Split-spectrum amplitude-decorrelation angiography with optical coherence tomography

Abstract

Amplitude decorrelation measurement is sensitive to transverse flow and immune to phase noise in comparison to Doppler and other phase-based approaches. However, the high axial resolution of OCT makes it very sensitive to the pulsatile bulk motion noise in the axial direction. To overcome this limitation, we developed split-spectrum amplitude-decorrelation angiography (SSADA) to improve the signal-to-noise ratio (SNR) of flow detection. The full OCT spectrum was split into several narrower bands. Inter-B-scan decorrelation was computed using the spectral bands separately and then averaged. The SSADA algorithm was tested on in vivo images of the human macula and optic nerve head. It significantly improved both SNR for flow detection and connectivity of microvascular network when compared to other amplitude-decorrelation algorithms.

1. Introduction

Optical coherence tomography (OCT) is an imaging modality for high-resolution, depth-resolved cross-sectional, and 3-dimensional (3D) imaging of biological tissue [1]. Among its many applications, ocular imaging in particular has found widespread clinical use. In the last decade, due to the development of light source and detection techniques, Fourier-domain OCT, including spectral (spectrometer-based) [2, 3] and swept-source OCT [4, 5], have demonstrated superior performance in terms of sensitivity and imaging speed over those of time-domain OCT systems [6–8]. The high-speed of Fourier-domain OCT has made it easier to image not only structure, but also blood flow. This functional extension was first demonstrated by Doppler OCT that images blood flow by evaluating phase differences between adjacent A-line scans [9–11]. Although Doppler OCT is able to image and measure blood flow in larger blood vessels [10, 11], it has difficulty distinguishing the slow flow in small blood vessels from biological motion in extravascular tissue [12, 13]. In the imaging of retinal blood vessels, Doppler OCT faces the additional constraint that most vessels are nearly perpendicular to the OCT beam, and therefore the detectability of the Doppler shift signal depends critically on the beam incident angle [14, 15]. Thus other techniques that do not depend on beam incidence angle are particularly attractive for retinal and choroidal angiography.

Several OCT-based techniques have been successfully developed to image microvascular networks in human eyes in vivo [16–25]. One example is optical microangiography (OMAG), which can resolve the fine vasculature in both retinal and choroid layers [18]. OMAG works by using a modified Hilbert transform to separate the scattering signals from static and moving scatters [26]. By applying the OMAG algorithm along the slow scanning axis, high sensitivity imaging of capillary flow can be achieved [27]. However, the high-sensitivity of OMAG requires precise removal of bulk-motion by resolving the Doppler phase shift [28]. Thus it is susceptible to artifacts from system or biological phase instability. Other related methods such as phase variance [23] and Doppler variance [24] have been developed to detect small phase variations from microvascular flow. These methods do not require non-perpendicular beam incidence and can detect both transverse and axial flow. They have also been successful in visualizing retinal and choroidal microvascular networks. However, these phase-based methods also require very precise removal of background Doppler phase shifts due to the axial movement of bulk tissue. Artifacts can also be introduced by phase noise in the OCT system and transverse tissue motion, and these also need to be removed.

To date, most of the aforementioned approaches have been based on spectral OCT, which provides high phase stability to evaluate phase shifts or differentiates the phase contrast resulting from blood flow. Compared with spectral OCT, swept-source OCT introduces another source of phase variation from the cycle-to-cycle tuning and timing variabilities [29]. This makes phase-based angiography noisier. To use phase-based angiography methods on swept-source OCT, more complex approaches to reduce system phase noise are required [29, 30]. On the other hand, swept-source OCT offers several advantages over spectral OCT, such as longer imaging range, less depth-dependent signal roll-off, and less motion-induced signal loss due to fringe washout [31]. Thus an angiography algorithm that does not depend on phase stability may be the best choice to fully exploit the advantages of swept-source OCT.

In this context, amplitude-based OCT signal analysis may be advantageous for ophthalmic microvascular imaging. A technique termed “speckle variance” using swept-source OCT [32, 33] has demonstrated a significant improvement in capillary detection in tumors by calculation of the variance of the OCT signal intensity. A key advantage of the speckle variance method is that it does not suffer from phase noise artifacts and does not require complex phase correction methods. Correlation mapping is another amplitude-based algorithm that has also recently demonstrated swept-source OCT mapping of animal cerebral and human cutaneous microcirculation in vivo [34, 35]. These amplitude-based angiography algorithms are well suited to swept-source OCT and offer valuable alternatives to the phase-based methods.

The purpose of this paper is to present an improved amplitude-based OCT angiography algorithm. The algorithm is called “split-spectrum amplitude-decorrelation angiography” (SSADA). Splitting the spectrum reduces the predominant bulk-motion noise in the axial dimension where OCT resolution is higher than that in the transverse dimension. This noise reduction is achieved without significant sacrifice in the flow signal, which in the ocular fundus is predominantly in the transverse rather than axial dimension. Thus the SSADA algorithm is particularly optimal for imaging of retinal and choroidal flow. This paper describes the algorithm and its initial results in live human retinal, choroidal, and optic nerve head (ONH) imaging.

2. System setup

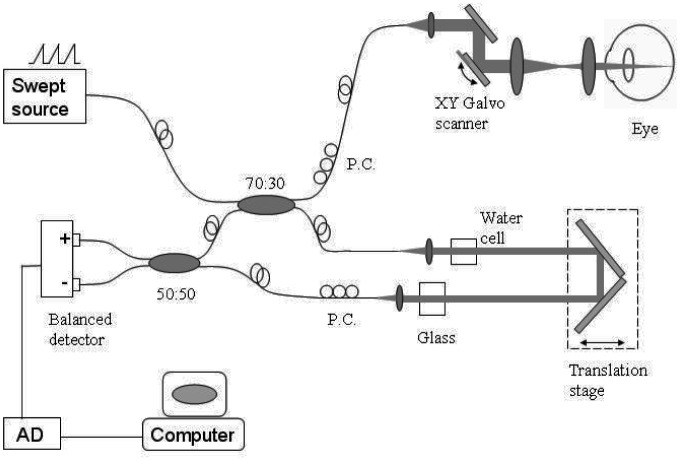
A recently described [31] high-speed swept-source OCT system (Fig. 1 ) was used to demonstrate SSADA imaging of microcirculation in the human ocular fundus. The system used a commercially available short cavity laser at 1050 nm (Axsun Technologies, Inc, Billerica, MA, USA) with a 100-nm tuning range. The tuning cycle of the laser has a repetition rate of 100 kHz and a duty cycle of 50%. The OCT system has a measured axial resolution of 5.3 µm (full-width-half-maximum amplitude profile) and imaging range of 2.9 mm in tissue. One portion (70%) of the light proceeds to the sample arm (the patient interface), and the other portion (30%) to the reference arm. In the sample arm, the average output power of the laser is 1.9 mW, consistent with safe ocular exposure limits set by the American National Standards Institute (ANSI). In the sample arm, the light was coupled to a retinal scanner that consisted of a collimating lens, a XY galvanometer scanner, an objective lens, and an ocular lens. A focused spot diameter of 18 µm (full-width-half-maximum amplitude profile) was calculated on the retinal plane based on an eye model [36]. In the reference arm, dispersion in the ocular media and sample-arm optics was compensated by using a water cell and glass block. The light returning from the reference and sample arms interfered at a 50/50 coupler and was detected by a balanced receiver (Thorlabs, Inc, Newton, NJ, USA). The interference fringes were recorded by a high speed digitizer (Innovative Integration, Inc.) at 400 MHz with 14-bit resolution. This analog-digital signal acquisition was driven by the optical clock output of the Axsun laser. The system sensitivity measured with a mirror and neutral density filter was 95 dB, and the sensitivity roll-off was 4.2 dB/mm.

Fig. 1.

Schematic of the swept-source OCT system used to collect the 3D image cube for split-spectrum amplitude-decorrelation angiography in a live human fundus. PC = polarization controller. AD = analog-digital conversion.

For the following study, the swept-source OCT system was operated at 100-kHz axial scan repetition rate. In the fast transverse scan (X) direction, the B-scan consisted of 200 A-scans over 3 mm. In the slow transverse scan (Y) direction, there were 200 discrete sampling planes over 3 mm. Eight consecutive B-scans were acquired at each Y position. This is referred to as the “M-B-scan mode” because it enables detection of motion between consecutive B-scans at the same position. Thus, it took 3.2 sec to obtain a 3D volumetric data cube comprised of 1600 B-scans and 32,0000 A-scans.

Normal human subjects were imaged to demonstrate SSADA imaging, which is approved by Institutional Review Board (IRB). The subject’s head was stabilized by chin and forehead rests. A flashing internal fixation target was projected by an attenuated pico projector using digital light processing (DLP) technology (Texas Instruments, Dallas, TX, USA). The imaging area on the fundus was visualized by the operator using real-time en face view of a 3 mm × 3 mm OCT preview scan.

3. Theoretical analysis

Speckle decorrelation has long been used in ultrasound imaging [37, 38] and in laser speckle technique [39] to detect optical scattering from moving particles such as red blood cells. This phenomenon is also clearly exhibited by the real-time OCT reflectance images. The scattering pattern of blood flow varies rapidly over time. This is caused by the fact that the flow stream drives randomly distributed blood cells through the imaging volume (voxel), resulting in decorrelation of the received backscattered signals that are a function of scatterer displacement over time. The contrast between the decorrelation of blood flow and static tissue may be used to extract flow signals for angiography.

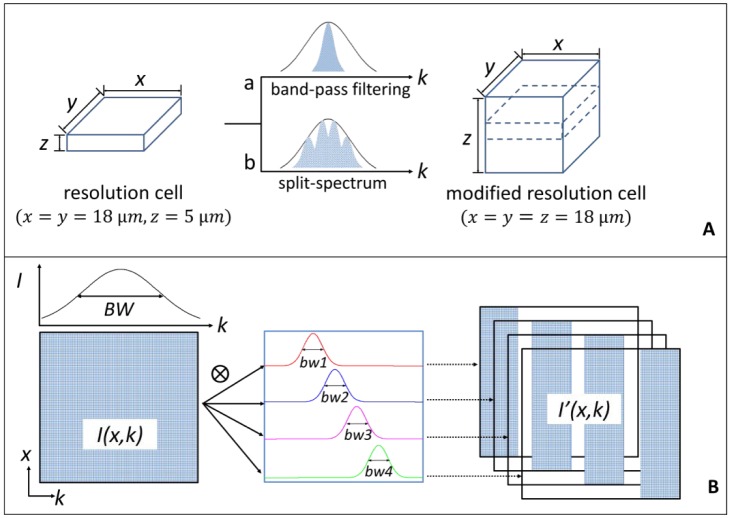
Each pixel in a B-scan OCT image is formed from backscattered signals of a 3D volume in space, referred to as a resolution cell (Fig. 2(A) ). The statistical changes in the envelope intensity are related to the motion of scatterers through the OCT resolution cell. For a typical swept-source OCT setup, the axial (Z direction) resolution, determined by the source central wavelength and its spectral bandwidth, is much higher than the lateral resolution determined by the laser beam profile in both X and Y directions. For example, in the current OCT system, using the full-width-half-maximum (FWHM) amplitude profile definition, the axial resolution (~5 µm) is four times higher than the lateral resolution (~18 µm) if both are defined as full-width-half-maximum amplitude profiles (Fig. 2(A)). This anisotropic resolution cell, with higher axial than transverse resolution, will result in higher decorrelation sensitivity for axial motion [40]. In the fundus, ocular pulsation related to heart beat, driven by the retrobulbar orbital tissue, mainly occurs along the axial direction. The anisotropic resolution cell of retinal OCT imaging is very sensitive to this axial motion noise [40]. On the other hand, retinal and choroidal blood flow vectors are primarily transverse to the OCT beam, along the wider (less sensitive) dimensions of the OCT resolution cell. Therefore, to improve the signal-to-noise ratio (SNR) of flow detection, it is desirable to lower the axial resolution and dampen the axial decorrelation sensitivity. This reduces the axial motion noise without sacrificing the transverse flow signal.

Fig. 2.

Diagrams of the modification of the OCT imaging resolution cell and the split-spectrum method used for this purpose. (A) The resolution cell in the current configuration can be modified into a new resolution cell by using band-pass filtering and split-spectrum methods. (B) Steps showing how the original 2D spectral interferogram I(x, k) was split into four new spectra I’(x, k) with smaller k bandwidth. “BW” and “bw” indicate the bandwidth of full-spectrum and Gaussian filters, respectively. The regions with non-zero values in the data block are indicated by the blue pattern.

One straightforward way to achieve this resolution modification is band-pass filtering of the spectral interferogram (method “a” shown in Fig. 2(A)). Unfortunately, this also sacrifices most of the speckle information in the spectral interferogram and decreases the flow signal. Thus this is not an effective way to increase the SNR of flow (decorrelation) detection. A better way to decrease axial resolution without losing any speckle information is to split the spectrum into different frequency bands (method “b” shown in Fig. 2(A)) and calculate decorrelation in each band separately. The decorrelation (flow) images from the multiple spectral bands can then be averaged together to make full use of the speckle information in the entire OCT spectrum. The details of the split-spectrum procedure (Fig. 2(B)) are explained below.

3.1 Split spectrum

The spectral interference signal recorded by a high speed digitizer in swept-source OCT, after subtracting background and autocorrelation terms, can be simply given by

$$I\left(x,k\right)={\displaystyle {\int }_{-\infty }^{\infty }R(k)A(x,k, z)cos(2kz)dz}$$ (1)

Where x is the transverse position of focus beam spot on the sample along the fast scan axis,k is the wavenumber, I(x, k) is the light intensity, R(k) is the amplitude of light reflected from the reference arm, A(x, k, z) is the amplitude of the light backscattered from the sample, and z is the optical delay mismatch between the sample reflections and the reference reflection in the free space equivalent. The Gaussian shape above the 2D interferogram I(x, k) was used to express the received interferometric fringe at one position (Fig. 2(B)). In our method, we first defined the bandwidth of this full-spectrum fringe, and then created a filter bank to divide this full-spectrum fringe into different bands. The specifications of this filter bank depend on some factors, including 1) filter type, 2) bandwidth of each filter, 3) overlap between different bands, and 4) number of bands. In this study, a Gaussian filter was introduced whose function was defined by

$$G(n)=\exp [-\frac{{(n-m)}^2}{2{\sigma }^2}]$$ (2)

where n is the spectral element number that varies from 1 to 1400 and is linearly mapped to wavenumber k [31]. The range of sampled k was 10000 to 9091 cm⁻¹, corresponding to a wavelength range of 1000 to1100 nm [31]. The bandwidth “BW” of the full spectrum is 69 nm, which provides a FWHM axial spatial resolution of 5.3 µm. m is the position of the spectral peak. In this study, the peaks of the spectral Gaussian filters were placed at 9784, 9625, 9466, and 9307 cm⁻¹. And σ² is the variance of the Gaussian filter in terms of the number of spectral elements. The FWHM amplitude bandwidth “bw” of the bandpass filters in Fig. 2(B) is equal to $\text{2}\sqrt{2\ln 2}\sigma$, covering 378 spectral elements, corresponding to a wavelength range of 27nm or a wavenumber range of 245 cm⁻¹. The 4 bandpass filters overlap so that none of the frequency components of the original signal were lost in the processing. The signals from each individual frequency band were then passed into conventional Fourier-domain OCT algorithms. That means the OCT signals could be directly calculated from the decomposed interferograms I′(x, k) by applying Fourier transform upon wavenumber . The computed OCT signal is a complex function, $\tilde{I}\left(x,z\right)$,which can be written as,

$$\tilde{I}\left(x,z\right)=FFT\left\{I\text{'}\left(x,k\right)\right\}=A\left(x,z\right)\exp [i\phi (x,z)]$$ (3)

where $\phi (x,z)$is the phase of the analytic signal $\tilde{I}\left(x,z\right)$. Note that only the amplitudes of the OCT signals, A(x, z), are used for the following decorrelation algorithm.

3.2 Decorrelation

3.2.1 Full-spectrum decorrelation

As mentioned above, the decorrelation calculation is achieved purely through processing the amplitude signal and does not require phase information. To evaluate the flow signals coming from the scattering tissue, the average decorrelation image $\overline{D}\left(x,z\right)$at each position was obtained by averaging N-1 decorrelation image frames computed from N reflectance amplitude images frames from M-B mode scanning. Each decorrelation frame was computed from 2 adjacent amplitude frames: $A_n\left(x,z\right)$and $A_{n+1}\left(x,z\right)$. Using the full spectrum, it is given by

$$\overline{D}\left(x,z\right)=1-\frac{1}{N-1}{\displaystyle \sum }_{n=1}^{N-1}\frac{A_n\left(x,z\right)A_{n+1}\left(x,z\right)}{[\frac{1}{2}{A}_n{\left(x,z\right)}^2+\frac{1}{2}{A}_{n+1}{\left(x,z\right)}^2]}\left(N=8\right)$$ (4)

where x and z are lateral and depth indices of the B-scan images and n denotes the B-scan slice index. In this equation, the decorrelation signal-to-noise ratio acquired from full spectrum can only be increased by increasing the number N of B-scans taken at the same position. However, more scans require more imaging time which may not be practical.

3.2.2 Decorrelation with pixel-averaging

To suppress the spurious noise and discontinuities in the vasculature, P by Q window moving average can be implemented over the X-Z 2D map. To fairly compare this pixel averaging method with the following split-spectrum method in the result section, we created a 1 by 4 window, which means we only applied pixel-averaging along the Z direction, the same direction we used for splitting the spectrum. The average decorrelation image $\overline{D}\left(x,z\right)$ can be expressed by

$$\begin{array}{l}\overline{ D}\left(x,z\right)=1-\frac{1}{N-1}\frac{1}{PQ}{\displaystyle \sum }_{n=1}^{N-1}{\displaystyle \sum }_{p=1}^P{\displaystyle \sum }_{q=1}^Q\frac{ A_n\left(x+p,z+q\right)A_{n+1}\left(x+p,z+q\right)}{[\frac{1}{2}{A}_n{\left(x+p,z+q\right)}^2+\frac{1}{2}{A}_{n+1}{\left(x+p,z+q\right)}^2]}\\ \left(P=1,Q=4,N=8\right)\end{array}$$ (5)

where P and Q are the averaging window widths in the X and Z directions, respectively [35].

3.2.3 Split-spectrum decorrelation

After splitting the spectrum by applying M (M = 4 in our current implementation) equally spaced bandpass filters, we obtain M individual decorrelation images between each pair of B-scans, which can be averaged to increase decorrelation SNR along both the lateral (X) and axial (Z) directions. So, in the SSADA technique, the decorrelation image $\overline{D}\left(x,z\right)$can be described by

$$\overline{D}\left(x,z\right)=1-\frac{1}{N-1} \frac{1}{M}{\displaystyle \sum }_{n=1}^{N-1}{\displaystyle \sum }_{m=1}^M\frac{ A_n\left(x,z\right)A_{n+1}\left(x,z\right)}{[\frac{1}{2}{A}_n{\left(x,z\right)}^2+\frac{1}{2}{A}_{n+1}{\left(x,z\right)}^2]}(M=4,N=8)$$ (6)

where M is the number of split-spectrums. By increasing the number M (up to a point), the decorrelation signal-to-noise ratio can be improved without increasing the scan acquisition time.

Whichever above method is used, the resulting average decorrelation image frame $\overline{D}\left(x,z\right)$ should be a value between zero and one, indicating weak and strong decorrelation, respectively.

4. Methods of noise reduction and image presentation

Decorrelation of OCT signal amplitude between B-scans taken at the same nominal position could be caused by several sources: (1) flow (2) bulk tissue motion or scanner position error (3) background noise. The following steps are taken to suppress decorrelation due to bulk motion and background noise. This helps accentuate true flow in the images and improves the signal-to-noise ratio for flow detection.

4.1 Removal of high decorrelation generated by background noise

Background noise is random and therefore has high decorrelation between B-scan frames. Noise predominates in pixels with low OCT signal amplitude and therefore flow cannot be assessed in these pixels with any accuracy. We assign zero decorrelation values to pixels in the average decorrelation frame where the respective pixels in the average amplitude frame has subthreshold amplitude value. The threshold was set to 2 standard deviations above the mean background value measured when the sample beam was blocked. The subthreshold pixels are also excluded from the histogram analysis in section 4.2.

4.2 Elimination of decorrelation frames corrupted by rapid eye movement

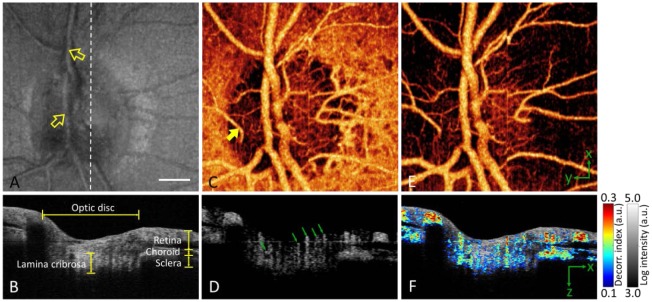
Saccadic and micro-saccadic eye movements [41] are rapid and cause a high degree of decorrelation between B-scans (Fig. 3 ). Such movements can be seen in a set of 7 decorrelation images of the region around the ONH, computed from eight OCT B-scans at the same Y location (Fig. 3(A)). Each decorrelation image frame was calculated from a pair of adjacent B-scan amplitude frames. In 6 of the 7 decorrelation frames, flow pixels could be distinguished from non-flow pixels by their higher decorrelation values. But in frame D4, both flow and non-flow pixels had high decorrelation values due to rapid eye movement. The high bulk motion in frame D4 was detected by the high median decorrelation value in pixel histogram analysis (Fig. 3(B)). The histogram analysis was performed within a high reflectivity band starting at the retinal inner limiting membrane and spanning 30 pixels below (between two red lines in Fig. 3(A)). By comparing the median decorrelation value to a preset threshold, we determined that frame D4 was a statistical outlier (Fig. 3(B)) and should be eliminated. After eliminating frame D4 (Fig. 3(C)), the remaining individual frames were averaged to obtain the final average decorrelation flow image (Fig. 3(D)). The corrected average decorrelation image (Fig. 3(D)) had higher contrast between vessels and static tissue than the uncorrected averaged decorrelation image (Fig. 3(E)).

Fig. 3.

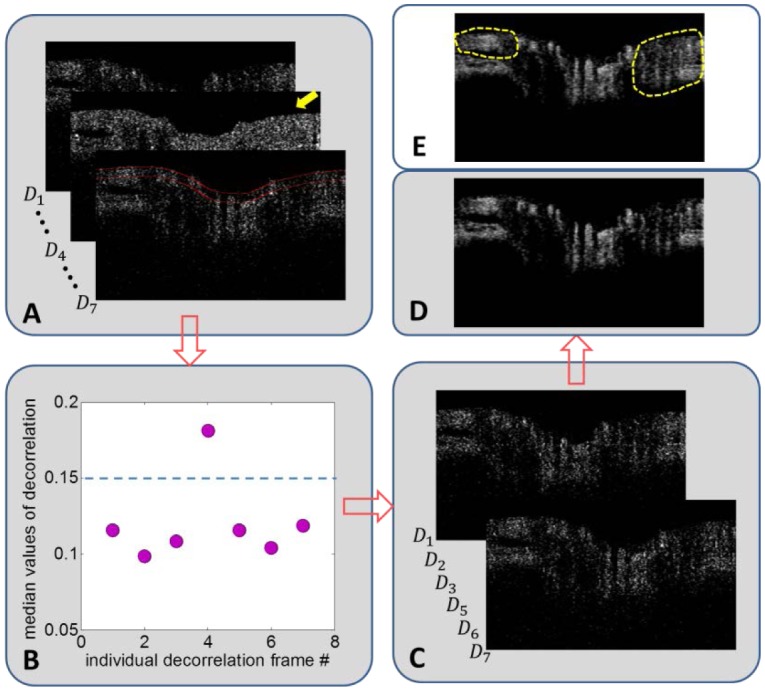
Flow chart showing the steps for removing a decorrelation frame with high bulk motion, using an OCT section across the optic nerve head as an example. (A) A series of 7 decorrelation frames (Dn) at one Y position. To avoid clutter, only frames D1, D4, and D7 are shown. Frame D4 (yellow arrow) showed high decorrelation in both flow (vessel) and non-flow (bulk) tissue, possibly due to saccadic eye movement. To detect bulk motion, the median decorrelation value in the first 30 pixels of the inner retina and disc (between two red lines) was determined. (B) Plot of median values from the 7 frames showed frame D4 as an outlier. The threshold (dotted blue line) was set at 0.15, two standard deviations above the mean median decorrelation value. (C) After removing frame D4, the remaining six decorrelation images were averaged. (D) The cleaned decorrelation image showed high contrast between flow pixels (bright areas in retinal vessels and choroid) and non-flow dark regions. (E) If frame D4 were not removed, the uncleaned decorrelation image showed less contrast between flow and non-flow pixels, which was evident by the lack of completely dark space between retinal vessels in the peripapillary areas (circled by dotted yellow lines).

4.3 Segmentation and maximum decorrelation projection of retinal and choroidal vasculatures

The 3D SSADA data set comprises a stack of 200 corrected average decorrelation cross-sectional images, along with the associated average reflectance images, that together spans 3 mm in the slow transverse scan (Y) direction. The 3D data is separated into retinal and choroidal regions with the dividing boundary set at the retina pigment epithelium (RPE). The depth (Z position) of the highly reflective RPE was identified through the analysis of the reflectance and reflectance gradient profiles in depth [18]. The region above the RPE is the retinal layer and the region below is the choroidal layer. The en face X-Y projection angiograms were produced by selecting the maximum decorrelation value along the axial (Z) direction in each layer. In ONH scans, the RPE depth just outside the disc boundary was used to set an interpolated RPE plane inside the disc.

5. In vivo testing of SSADA algorithm

To demonstrate the performance of the SSADA algorithm, macular and ONH imaging were performed on three normal volunteers using the swept-source OCT system described in Section 2. In this demonstration, the system captured 200 A-scans to cover ~3 mm for each B-scan. For 3D data acquisition, the entire scan volume was evenly divided into 200 steps, with eight repeated B-scans in each step. In doing so, it required 3.2 seconds to complete one 3D volumetric scan. Under this scanning protocol, the SSADA algorithm was applied to the repeated frame sequences at each step. Finally, the 200 calculated B-scan SSADA frames were combined to form 3D blood perfusion images of posterior part of the human eye.

5.1 Optic nerve head angiography

From one 3D volumetric data set, both reflectance intensity images and decorrelation (angiography) images were obtained. For the ONH scan, the en face maximum projection of reflectance intensity showed the major retinal blood vessels and the second order branches, but finer branches and the microcirculation of the retina, choroid, and optic disc were not visible (Fig. 4(A) ). In the vertical cross-sectional intensity image, the connective tissue struts (bright) and pores (dark) of the lamina cribosa could be visualized deep within the optic disc (Fig. 4(B)). Around the disc, the retina, choroid, and sclera can be delineated.

Fig. 4.

In vivo 3D volumetric [3.0 (x) × 3.0 (y) × 2.9 (z) mm] OCT of the optic nerve head in the right eye of a myopic individual. White bar, 500 µm. The images in the bottom panels have been cropped from 2.9 mm to 1.5 mm axially. (A) En face maximum reflectance intensity projection showed branches of the central retinal artery and vein (yellow arrows point to superior branches). (B) OCT cross-section at the plane marked by white dashed line in (A). (C) En face maximum decorrelation projection angiogram computed with the SSADA algorithm. It showed many orders of branching from the central retinal artery and vein, a dense capillary network in the disc, a cilioretinal artery (yellow arrow), and a near continuous sheet of choroidal vessels around the disc. (D) Decorrelation cross-section (same plane as B) showed blood flow in disc vessels (green arrows), peripapillary retinal vessels, and choroid. (E) En face maximum decorrelation projection angiogram after removing the choroid (pixels below the retinal pigment epithelium). (F) Fly-through movie ( Media 1 ^{(39.8MB, AVI)} ), in which flow (color scale representing decorrelation) was merged with structure (gray scale representing reflectance intensity), showed how the disc, retina, and choroid are perfused in a 3D volumetric fashion. A fixed pattern artifact originated from the swept laser source and resulted in a horizontal lines across the image [31].

The ONH angiogram obtained by the SSADA algorithm showed both many orders of vascular branching as well as the microcirculatory network. The en face maximum decorrelation projection angiogram (Fig. 4(C)) showed the major retinal branch vessels as well as many fine branches that could not be visualized well on the en face intensity image. It is of interest to point out that the angiogram also showed a cilioretinal artery that emerged at the nasal disc margin. This artery is not part of the central retinal circulation but arises from the posterior ciliary artery and can be recognized by its fish-hook shape just inside the disc margin [42]. The vertical SSADA cross-section (Fig. 4(D)) showed blood vessels in the disc that form columns from the surface to a depth of ~1.0 mm. It is unclear if this represents deep penetrating vessels or if this is a decorrelation projection artifact. Projection artifact refers to the fact that light reflected from deeper static structures may show decorrelation due to passing through a more superficial blood vessel. This type of artifact is evident where the peripapillary retinal vessels seem thicker than they should be (Fig. 4(D, F)). Due to this artifact, these vessels extended down the full depth of the nerve fiber layer (NFL), and the decorrelation signal appeared in the subjacent pigment epithelium (RPE), which should be avascular.

To separately view the retinal vessels and superficial disc vessels, we removed pixels below the level of the peripapillary RPE. The resulting en face angiogram (Fig. 4(E)) showed that the superficial vascular network that nourishes the disc ends at the disc boundary. By comparison, the choroidal circulation formed an almost continuous sheet of blood flow under the retina (Fig. 4(C)). The en face images (Fig. 4(A, C, E)) show RPE atrophy in a temporal crescent just outside the disc margin. Inside the crescent there was also a small region of choriocapillaris atrophy (Fig. 4(C)). Overlaying the cross-sectional gray scale reflectance intensity image with the color scale flow (decorrelation) image showed that the major retinal branches vessels were at the level of the peripapillary NFL (Fig. 4(F)). It also showed the blood flow within the full thickness of the choroid. The combined image also showed that the deeper disc circulation resides primarily in the pores of the lamina cribosa and not in the connective tissue struts. To our knowledge, it is the first time that the disc microcirculation has been visualized noninvasively in such a comprehensive manner.

5.2 Macular angiography

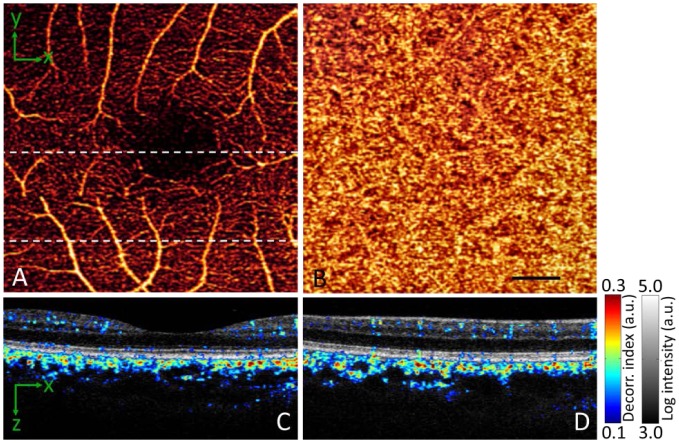
The macular region of the fundus is responsible for central vision. Capillary dropout in the macular region due to diabetic retinopathy is a major cause of vision loss [43]. Focal loss of the choriocapillary is a likely causative factor in the pathogenesis of both dry and wet age-related macular degeneration [44], the leading cause of blindness in industrialized nations [45]. Thus macular angiography is important. The SSADA algorithm was used to demonstrate macular angiography of both the retinal and choroidal circulations in a normal eye (Fig. 5 ). The vascular pattern and capillary networks visualized by SSADA were similar to those previously reported using phase-based OCT angiography techniques [27, 46]. The flow pixels formed a continuous microcirculatory network in the retina. There was an absence of vascular network in the foveal avascular zone (Fig. 5(A)) of approximately 600µm diameter, in agreement with known anatomy [47, 48]. There were some disconnected apparent flow pixels within the foveal avascular zone (Fig. 5(A)) due to noise. Inspection of Fig. 5(C) shows these false flow pixels to be decorrelation noise in the high reflectance layers of the RPE and photoreceptors. The choriocapillaris layer forms a confluent overlapping plexus [49], so it is to be expected that the projection image of the choroid circulation shows confluent flow (Fig. 5(B)).

Fig. 5.

In vivo 3D volumetric [3.0 (x) × 3.0 (y) × 2.9 (z) mm] OCT of the macula processed with the SSADA algorithm. The images in the bottom panels have been cropped from 2.9 mm to 1.5 mm axially. (A) En face maximum decorrelation projection angiogram of the retinal circulation. (B) En face maximum decorrelation projection angiogram of the choroidal circulation. Black bar, 500 µm. (C) Horizontal OCT cross section through the foveal center (upper dashed line in A) with merged flow (decorrelation represented in color scale) and structure (reflectance intensity represented in gray scale) information. (D) Merged horizontal cross section of the inferior macula (lower dashed line in A).

The cross sections (Fig. 5(C, D)) showed retinal vessels from the NFL to the outer plexiform layer, in agreement with known anatomy [50]. The flow in the inner choroid had higher velocity as based on decorrelation seen in the color scale. The volume was also greater than the retinal circulation (Fig. 5(C, D)), again consistent with known physiology that the choroidal circulation has much higher flow than the retinal circulation [49]. There were signal voids in the outer choroid which may be due to fringe washout from high flow velocity and the shadowing effect of overlying tissue. The cross sections (Fig. 5(C, D)) also showed a few spots of decorrelation in the RPE layer. These must be artifacts because the RPE is known to be avascular. As mentioned in the last section, this is likely due to the projection of decorrelation of flow in a proximal layer (i.e., inner retinal layers) onto distal layers with a strong reflected signal (i.e., RPE). There was also a tendency for vessels to form vertical arrays in the inner retina, which may in some instances be due to the projection artifact as well.

6. Comparison between three amplitude-decorrelation angiography algorithms: full-spectrum, pixel-averaging, and split-spectrum

6.1 Comparison on visualization

The differences between full-spectrum, pixel-averaging, and split-spectrum algorithms for decorrelation-based angiography can be appreciated by visual inspection of the images (Fig. 6 ). To obtain the angiograms, we followed the algorithm described by Eqs. (4)-(6), respectively. For fair comparison, the identical motion error reduction, noise threshold, and en face projection methods were used.

Fig. 6.

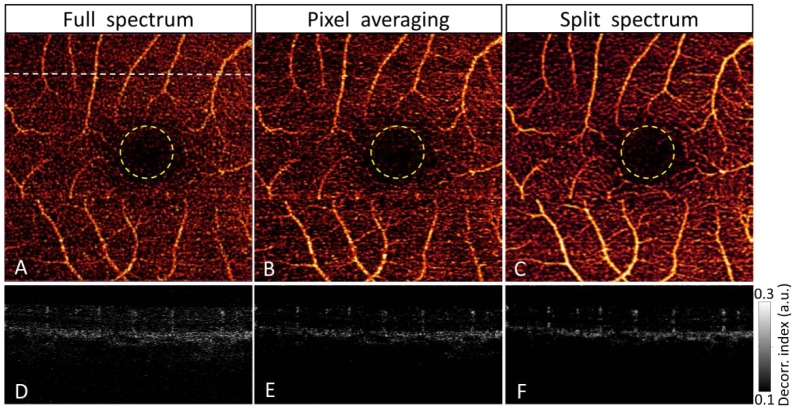
Comparison of amplitude-decorrelation angiography using three different algorithms: full-spectrum (A, D), pixel-averaging (B. E) and split-spectrum (C, F). The macula was scanned in a 3x3 mm area. En face maximum decorrelation projections of retinal layers (A-C) showed the macular vascular network around the central foveal avascular zone (yellow circles) of 600-µm diameter. The cross-sectional angiograms (D-F) scanned across a horizontal line in the superior perifoveal region (upper dashed line of A). White bar, 500 µm.

En face angiograms of the macular retinal circulation (Fig. 6(A-C)) showed that while all three algorithms could provide good visualization of major macular vessels, the capillary network looked the cleanest and most continuous with the split-spectrum algorithm. The pixel-averaging algorithm was second best, while the full-spectrum method showed significantly more disconnected flow pixels that were likely to be noise. The noise can be most easily appreciated in the foveal avascular zone (inside the yellow circles), which should not have any retinal vessels, including capillaries. In the split-spectrum angiogram, there was a near continuous visualization of the capillary network just outside the avascular zone, while this loop appeared broken up using the other two algorithms. The cross-sectional angiogram (Fig. 6(D-F)) showed that the split-spectrum algorithm provided the cleanest contrast between distinct retinal vessels and dark background. Again, the pixel-averaging method was second best, and the full-spectrum method showed visible snow-like background noise.

6.2 Comparison of connectivity and signal-to-noise ratio

To obtain quantitative figures of merit to compare the three decorrelation-based angiography algorithms, we made use of two pieces of anatomic knowledge. One is that the retinal vessels form a continuous network, and the other is that there are no retinal vessels within the foveal avascular zone.

To assess vessel connectivity, we converted projection images obtained by three different methods (Fig. 6(A-C)) to binary images (1st column of Fig. 7 ) based on a fixed threshold. Then a skeletonizing morphological operation [51] was applied to obtain a vascular network made of 1-pixel wide lines and dots (2nd column of Fig. 7). Next the unconnected flow pixels were separated from the connected flow skeleton (3rd column of Fig. 7). The vascular connectivity was defined as the ratio of the number of connected flow pixels to the total number of flow pixels on the skeleton map. Connectivity was analyzed on the OCT macular angiograms of six eyes of the three participants (Table 1 ). A comparison of the three algorithms based on paired t-tests showed that the split-spectrum algorithm had significantly better connectivity relative to the pixel-averaging (p = 0.037) and full-spectrum algorithms (p = 0.014). The split-spectrum algorithm reduced the number of unconnected flow pixels (18%) by more than a factor of 2 when compared with the full-spectrum algorithm (39%).

Fig. 7.

(A) Full-spectrum, (B) pixel-averaging, and (C) split-spectrum amplitude decorrelation angiography algorithms were applied to map the retinal circulation in a normal macula. The en face maximum projection decorrelation images (Fig. 6(A-C)) were binarized (Column 1), skeletonized (Column 2), and then filtered to remove unconnected flow pixels (Column 3). The ratio of the number connected flow pixels to the total number of flow pixels on the skeleton map is the vascular connectivity. The algorithms were also compared in terms of the decorrelation signal-to-noise ratio, where the noise region was inside the foveal avascular zone (Column 4 yellow circles), and the signal region was the parafoveal annulus (Column 4 between two red circles). R1 = 0.3 mm, R2 = 0.65 mm, and R3 = 1 mm.

Table 1. Vascular Connectivity and Signal-to-Noise Ratio of Three Angiography Algorithms.

Amplitude decorrelation	Connectivity (mean ± sd)	Improvement of connectivity	DSNR (mean ± sd)	Improvement of DSNR
full-spectrum	0.61 ± 0.08	N/A	3.30 ± 0.81	N/A
pixel-averaging	0.70 ± 0.06	14.8%	4.57 ± 1.08	38.5%
split-spectrum	0.82 ± 0.07	34.4%	6.78 ± 0.82	105%

DSNR = dcorrelation signal-to-noise ratio. Statistical analysis is based on 6 eyes of 3 normal human subjects.

To compute a SNR for the decorrelation signal, we needed to define relevant signal and noise regions. For the macula, fortuitously, the central foveal avascular zone (FAZ) is devoid of blood vessels, including capillaries [47, 48]. The parafoveal capillary network nourishes the fovea and the loss of these capillaries in diabetic retinopathy is an important mechanism in the loss of vision [43]. Thus the ratio of decorrelation value in the parafoveal region relative to the FAZ is a clean and clinically relevant way to compute SNR. The radius of the FAZ is approximately 0.3 mm [47, 48]. Therefore we chose the noise region as the central FAZ with a radius of 0.3 mm (yellow circles on the last column of Fig. 7), and we chose the signal region as the annular parafoveal region between 0.65 and 1.00 mm radii (between two red circles in column 4 of Fig. 7). Then we defined the decorrelation signal-to-noise ratio DSNR using the following formula,

$$DSNR=\frac{{\overline{D}}_{Parafovea}-{\overline{D}}_{FAZ}}{\sqrt{{\sigma }_{FAZ}^2}}$$ (7)

where ${\overline{D}}_{Parafovea}$and ${\overline{D}}_{FAZ}$are the average decorrelation values within the parafoveal annulus and FAZ, respectively; and ${\sigma }_{FAZ}^2$is the variance of decorrelation values within the FAZ. These computations were performed over the en face maximum projection images.

The DSNR was analyzed on the OCT macular angiograms performed on six eyes of the three participants (Table 1). The paired t-test showed that the DSNR of the split-spectrum algorithm was significantly higher than the pixel-averaging algorithm (p = 0.034) and the full-spectrum algorithm (p = 0.012). The split-spectrum algorithm improved the DSNR by more than a factor of 2 compared to the full-spectrum algorithm.

7. Discussion

Using the new SSADA algorithm, we have demonstrated the visualization of both larger blood vessels and the capillary network in the retinal and choroidal circulations. This visualization can also been achieved using Doppler [9–11] and other phase-based flow detection techniques [20, 23, 24, 27, 46]. The SSADA technique has several potential advantages over phase-based techniques. Insensitivity to phase noise is one advantage. Another potential advantage of SSADA is the possibility of quantifying microvascular flow. Because the effective resolution cell in SSADA is isotropic (having the same size in X, Y, and Z dimensions, Fig. 2(A)), it is equally sensitive to transverse (X, Y) and axial (Z) flow. This contrasts with all phase-based techniques, which are intrinsically more sensitive to flow in the axial direction over which Doppler shift occurs. Thus in SSADA result, the decorrelation value is a function of the flow velocity regardless of direction. The faster blood particles move across the laser beam, the higher the decorrelation index of the received signals within a velocity range set by the scan parameters. In theory the saturation velocity should be approximately the size of the resolution cell (0.018 mm) divided by the interframe time delay (0.002 sec), or 9 mm/sec. The minimum detectable flow velocity is determined by the decorrelation noise floor, which is based on the decorrelation distribution statistics of the non-flow tissue voxels. In this study, the projection view of SSADA showed the vascular pattern within the macular capillary zone (parafoveal region). This suggests that SSADA is able to detect retinal capillary flow, which is within the range of 0.5-2 mm/sec [52, 53]. For a more precise determination of the minimum detectable flow velocity we will require the calibration of velocity to decorrelation values using in vitro flow phantom experiments.

One limitation of SSADA technique is the projection of flow from proximal (shallower) layers to distal (deeper) layers. It was apparent from our results that flow in the major peripapillary retinal arteries and veins (Fig. 4) and larger macular vessels in the inner retina (Fig. 5) projects onto the highly reflective RPE, which should not contain any blood vessels. There were also probable projection of flow from the more superficial inner retinal layers (i.e. nerve fiber layer and ganglion cell layer) to the deeper inner retinal layers (i.e. inner and outer plexiform layers). This does not affect the accuracy of en face projection of the retinal circulation, but it could affect the accuracy of cross-sectional angiograms and en face projection of the choroidal circulation. One possible solution is to raise the threshold decorrelation value for flow identification in deeper voxels if a more superficial voxel has a suprathreshold decorrelation value; however, this will inevitably introduce a potential shadow artifact in place of a flow projection artifact. Thus the SSADA images of deeper vessels should be interpreted with this artifact in mind.

Another limitation of the SSADA technique is that it is still subject to noise from bulk tissue motion. In this paper, we made no attempt to compensate for X-Z motion between consecutive B-scan frames by the use of frame-shift registration. This registration could potentially reduce the effect of bulk motion in the X-Z dimensions (though not in the Y direction) and improve the accuracy of flow detection. It is also apparent from the en face angiograms that there are saccadic motion artifacts in the 3D data set. This could potentially be reduced by the use of 3D registration algorithms [54]. These potential improvements will be the subject of future investigations.

8. Summary

We have presented a novel optical angiography technique based on the decorrelation of OCT signal amplitude due to flow. By splitting the full OCT spectral interferograms into several spectral (wavenumber) bands, the OCT resolution cell in each band is made isotropic and less susceptible to axial motion noise. Recombining the decorrelation images from the spectral bands yields angiograms that use the full information in the entire OCT spectral range. The isotropic resolution cell of the SSADA algorithm could also theoretically be used to quantify flow with equal sensitivity to axial and transverse flow.

We tested SSADA in the imaging of retinal and choroidal circular in the macular and ONH regions of healthy human subjects. The resulting angiograms demonstrated improved SNR of flow detection and high connectivity in the peri- and parafoveal retinal microcirculatory networks. Non-invasive angiography of these ocular circulatory beds may be useful in the diagnosis and management of important blinding diseases such as glaucoma, diabetic retinopathy, and age-related macular degeneration. This algorithm may also be useful outside the eye, for example in the investigation of cerebral circulation and tumor angiogenesis.