The Effect of Variation in the Effective Population Size on the Rate of Adaptive Molecular Evolution in Eukaryotes

Abstract

The role of adaptation is a fundamental question in molecular evolution. Theory predicts that species with large effective population sizes should undergo a higher rate of adaptive evolution than species with low effective population sizes if adaptation is limited by the supply of mutations. Previous analyses have appeared to support this conjecture because estimates of the proportion of nonsynonymous substitutions fixed by adaptive evolution, α, tend to be higher in species with large N_e. However, α is a function of both the number of advantageous and effectively neutral substitutions, either of which might depend on N_e. Here, we investigate the relationship between N_e and ω_a, the rate of adaptive evolution relative to the rate of neutral evolution, using nucleotide polymorphism and divergence data from 13 independent pairs of eukaryotic species. We find a highly significant positive correlation between ω_a and N_e. We also find some evidence that the rate of adaptive evolution varies between groups of organisms for a given N_e. The correlation between ω_a and N_e does not appear to be an artifact of demographic change or selection on synonymous codon use. Our results suggest that adaptation is to some extent limited by the supply of mutations and that at least some adaptation depends on newly occurring mutations rather than on standing genetic variation. Finally, we show that the proportion of nearly neutral nonadaptive substitutions declines with increasing N_e. The low rate of adaptive evolution and the high proportion of effectively neutral substitution in species with small N_e are expected to combine to make it difficult to detect adaptive molecular evolution in species with small N_e.

Introduction

Population genetic theory predicts that the effective population size (N_e) of a species should be a major determinant of the rate of adaptive evolution if adaptive evolution is limited by the supply of new mutations. There are two reasons for this. First, the rate of adaptive evolution is expected to be proportional to N_es if $N_{\text{e}}s\gg 1$, where s is the strength of selection. This is because the fixation probability of a new advantageous mutation is proportional to N_es/N, where N is the census population size, if $N_{\text{e}}s\gg 1$ and s is small (Kimura 1983), and the rate at which new advantageous mutations occur is Nu; hence, the rate of adaptive evolution is expected to be proportional to Nu × N_es/N = uN_es. Second, in large populations, a higher proportion of mutations are expected to be effectively selected because a higher proportion are expected to have $N_{\text{e}}s\gg 1$. Previous analyses have suggested that the proportion of adaptive substitutions (α) is correlated to the effective population size because there is evidence of widespread adaptive amino acid substitutions in species such as Drosophila, house mice, bacteria, and some plant species with large N_e (Bustamante et al. 2002; Smith and Eyre-Walker 2002; Sawyer et al. 2003; Bierne and Eyre-Walker 2004; Charlesworth and Eyre-Walker 2006; Haddrill et al. 2010; Ingvarsson 2010; Slotte et al. 2010; Strasburg et al. 2011), whereas there is little evidence in hominids and other plant species that appear to have small N_e (Chimpanzee Sequencing and Analysis Consortium 2005; Zhang and Li 2005; Boyko et al. 2008; Eyre-Walker and Keightley 2009; Gossmann et al. 2010). There are, however, some exceptions. Maize, for example, has a relatively large effective population size, approaching that of wild house mice, but shows little evidence of adaptive protein evolution (Gossmann et al. 2010), and the yeast Saccharomyces paradoxus, which presumably has a very large N_e, also shows little evidence of adaptive protein evolution (Liti et al. 2009). Furthermore, Drosophila simulans does not appear to have undergone more adaptive evolution than D. melanogaster, even though it is thought to have a larger N_e (Andolfatto et al. 2011).

However, the correlation between α and N_e might be misleading because α depends on the rate of effectively neutral and advantageous substitution, variation in either of which could be caused by N_e (Gossmann et al. 2010), that is, α = D_adaptive/(D_adaptive + D_nonadaptive) where D_adaptive and D_nonadaptive are the rates of adaptive and nonadaptive substitutions, respectively. There is evidence that the proportion of effectively neutral mutations is negatively correlated to N_e across many species (Popadin et al. 2007; Piganeau and Eyre-Walker 2009), so a positive correlation between α and N_e might be entirely explained by variation in the number of effectively neutral substitutions. As a consequence, it has been suggested that ω_a, the rate of adaptive substitution relative to the rate of neutral evolution is a more appropriate measure of adaptive evolution for the purpose of comparison between genomic regions or species (Gossmann et al. 2010, see also Bierne and Eyre-Walker 2004; Obbard et al. 2009), that is, ω_a = D_adaptive/D_neutral where D_neutral is the substitution rate at sites that evolve neutrally. Contrary to expectation, Gossmann et al. (2010) failed to find any evidence of a correlation between ω_a and N_e in plants; but many of the plant species they considered appeared to have low N_e, and there may have been insufficient information from species with larger N_e to reveal a significant positive correlation. In contrast, Strasburg et al. (2011) have recently reported a significant positive correlation between ω_a and N_e within sunflowers, including some species that have very large N_e. There are two interpretations of a positive correlation between ω_a and N_e in sunflowers. First, the correlation could be due to a higher rate of adaptive substitution, or second, it could be due to an artifact of population size change (Strasburg et al. 2011). It has long been known that approaches to estimate adaptive evolution by methods related to the MK test are sensitive to changes in N_e, if there are slightly deleterious mutations (McDonald and Kreitman 1991; Eyre-Walker 2002; Eyre-Walker and Keightley 2009). For example, if the population has recently expanded, then ω_a and α will tend to be overestimated because slightly deleterious mutations, which would have become fixed in the past when the population size was small, no longer segregate as polymorphisms. This bias might be a particular problem in the sunflower data set because each species was contrasted against a common outgroup species, so that each comparison shared much of its divergence with all other comparisons. Therefore, any differences in N_e between the species must have occurred since they split and may have caused a genuine or an artifactual increase in ω_a. It is difficult to differentiate between these effects.

In contrast to the pattern in sunflowers, Jensen and Bachtrog (2011) recently estimated the rate adaptive evolution in D. pseudoobscura and D. miranda; they estimated that the two species probably had similar ancestral population sizes but that D. miranda had gone through a recent severe bottleneck. Despite this, the estimate of α along the two lineages was quite similar.

It is also evident that estimates of α or ω_a and N_e are not independent because N_e is usually estimated from the neutral diversity, which is also used to estimate α or ω_a. Sampling variation will therefore tend to induce a positive correlation between estimates of adaptive evolution and effective population size. This can be dealt with by randomly splitting the neutral sites into two halves, one of which is used to estimate N_e and the other to estimate the rate of adaptive evolution (Piganeau and Eyre-Walker 2009; Stoletzki and Eyre-Walker 2011). This correction is accurate whether or not the sites are linked (Piganeau and Eyre-Walker 2009).

Materials and Methods

Preparation of Data

Polymorphism data were retrieved from GenBank http://www.ncbi.nlm.nih.gov/Genbank or in case of Arabidopsis thaliana downloaded from http://walnut.usc.edu/2010. A summary of the analyzed data sets is shown in table 1. Phylogenetic trees for the plant and Drosophila species used in our analysis are given in supplementary figures S1 and S2 (Supplementary Material online), respectively (Drosophila 12 Genomes Consortium et al. 2007; Tang et al. 2008; Stevens 2010). Sequences were aligned using ClustalW using default parameter values (Thompson et al. 1994). Coding regions were assigned using protein-coding genomic data coordinates or, if given, derived from the information in the GenBank input files. An outgroup was assigned using the best Blast (Altschul et al. 1990) hit against the outgroup genome or, if included, taken from the GenBank Popset database (http://www.ncbi.nlm.nih.gov/popset). For all analyses, synonymous sites served as the neutral standard. Because some loci had been sampled in more individuals than others and other loci had missing data, we obtained the site frequency spectra (SFS) for each number of chromosomes for each species (e.g., we obtained the SFS for those sites with 4, 5, . . . etc. chromosomes separately). As a consequence, there was usually more than one SFS and its associated divergence data for each species. The estimation of the distribution of fitness effects (DFE), and ω_a was done jointly using all available SFS and divergence data for a given species. Summary statistics, such as π, were calculated as weighted averages. The numbers of synonymous and nonsynonymous sites and substitutions were computed using the F3×4 model implemented in PAML (Yang 1997) in which codon frequencies are estimated from the nucleotide frequencies at the three codon positions.

Table 1.

Summary of Data Sets Used for the Analyses

Species	Outgroup	Loci	Data Set
Drosophila melanogaster	Drosophila simulans	373	Shapiro et al. (2007)
Drosophila miranda	Drosophila affinis	76	Haddrill et al. (2010)
Drosophila pseudoobscura	Drosophila persimilis	72	Haddrill et al. (2010)
Homo sapiens	Macaca mulatta	445	EGP/PGAa
Mus musculus castaneus	Rattus norvegicus	77	Halligan et al. (2010)
Arabidopsis thaliana	Arabidopsis lyrata	932	Nordborg et al. (2005)
Capsella grandiflora	Neslia paniculata	251	Slotte et al. (2010)
Helianthus annuus	Lactuca sativa	34	Strasburg et al. (2011)
Populus tremula	Populus trichocarpa	77	Ingvarsson (2008)
Oryza rufipogon	Oryza spp.	106	Caicedo et al. (2007)
Schiedea globosa	Schiedea adamantis	23	Gossmann et al. (2010)
Zea mays	Sorghum bicolor	437	Wright et al. (2005)
Saccharomyces paradoxus	Saccharomyces cerevisiae	98	Tsai et al. (2008)

^aEGP: http://egp.gs.washington.edu and PGA: http://pga.gs.washington.edu, August 2010.

It is important in this type of analysis to count the numbers of synonymous and nonsynonymous sites correctly and consistently across the divergence and polymorphism data. It is appropriate to use a “mutational opportunity” definition of a site (Bierne and Eyre-Walker 2003) since we are interested in the relative numbers of mutations that can potentially occur at synonymous and nonsynonymous sites. PAML provides estimates of the proportion of sites that are nonsynonymous (and hence also synonymous) from the divergence data, and these were used to calculate the number of nonsynonymous and synonymous sites for the polymorphism data.

Estimation of N_e and ω_a

We assumed that synonymous sites were neutral, except when we estimated the strength of selection on synonymous mutations (see below). We estimated N_e from the level of nucleotide diversity, π, at synonymous sites and estimates of the rate of nucleotide mutation per generation, μ, from the literature, since

(1)

We estimated the mutation rate per generation in Populus tremula in the following manner. Tuskan et al. (2006) note that sequence divergence in putatively neutral sequences is approximately six times slower in P. tremula than in A. thaliana and that the average generation time for P. tremula is ≈15 years. We therefore estimated the mutation rate per generation in P. tremula by multiplying the mutation rate estimated in A. thaliana from mutation accumulation lines by 15/6 = 1.75 × 10⁻⁸.

The DFE and ω_a, the rate of adaptive substitutions relative to the rate of synonymous substitutions (Gossmann et al. 2010), were estimated using a modified version of the method of Eyre-Walker and Keightley (2009). First, the DFE and demographic parameters of the population are simultaneously estimated from the SFS of nonsynonymous and synonymous sites using the method of Keightley and Eyre-Walker (2007). The DFE is then used to estimate the average fixation probability of mutations $\stackrel{-}{f_{\text{n}}}$ at nonsynonymous sites relative to that at neutral sites:

(2)

where S = 4N_es, s is the strength of selection, M(S) is the distribution of S as inferred by the method of Keightley and Eyre-Walker (2007) and

(3)

is the fixation probability of a new mutation relative to the fixation probability of a neutral mutation (Kimura 1983). The rate of adaptive nonsynonymous substitution relative to the rate of synonymous substitution, ω_a, can then be estimated as

(4)

where d_n and d_s are the rates of nonsynonymous and synonymous substitution, respectively. The method of Eyre-Walker and Keightley (2009) does not take into account the fact that some substitutions between species are polymorphisms. This was taken into account in the following manner (Keightley and Eyre-Walker 2012). The Keightley and Eyre-Walker (2007) method estimates the DFE and demographic parameters by generating vectors representing the allele frequency distributions for synonymous and nonsynonymous sites by a transition matrix approach and using these to calculate the likelihood of the observed SFS. Let the density of mutations at i of 2N copies be v_n(i) and v_s(i) for nonsynonymous and synonymous sites, respectively, and let us assume that we have sampled a single sequence from each species to estimate the divergence. The contribution of polymorphisms to apparent divergence is therefore

(5)

for nonsynonymous sites, with an analogous expression for synonymous sites. The factor of two appears because polymorphism in both lineages contributes to apparent divergence, and we assume that the diversity is the same in the two lineages. We can now estimated ω_a taking into account the contribution of polymorphism to divergence as

(6)

We also estimated ω_a using a model in which there was negative selection upon synonymous mutations. We assume that all synonymous mutations are subject to the same strength of selection. Unfortunately, it is not possible to simultaneously estimate the demographic parameters and the strength of selection on synonymous mutations unless one includes information about which codons are preferred by selection (Zeng and Charlesworth 2009), and this is not known for most of the species in our analysis. We therefore infer the strength of selection at synonymous sites from the SFS using the transition matrix approach described in Keightley and Eyre-Walker (2007) assuming a constant population size. The strength of selection at synonymous sites allows us to calculate the probability of fixation of synonymous mutations f_s and obtain a corrected estimate of ω_a as

(7)

It is also necessary to adjust our estimate of N_e to take into account the action of natural selection at synonymous sites. This was performed in one of two ways, depending upon whether our estimate of the mutation rate was a direct estimate from a pedigree or mutation accumulation experiment, as in the Drosophila species, Arabidopsis, Capsella, Populus, and Saccharomyces, or indirectly from phylogenetic analysis, as in Mus, Helianthus, Oryza, Schieda, and Zea. Kimura (1969) showed that the nucleotide diversity at a site subject to recurrent mutation and semidominant selection, of strength s (positive s for advantageous mutations), relative to that at a neutral site is

(8)

For those species in which the mutation rate had been estimated directly, we corrected the estimate of N_e obtained from equation (1), by dividing it by H(S), where S is the strength of selection acting at synonymous sites; for those species in which the mutation rate came from a phylogenetic analysis, we corrected for selection at synonymous sites by multiplying the estimates by Q(S)/H(S). Synonymous codon bias was measured using the effective number of codons (ENC; Wright 1990) and ENC taking into account base composition bias (ENC′; Novembre 2002). To investigate whether the proportion of effectively neutral nonsynonymous mutations was correlated to N_e, we calculated a variant on the ψ statistic suggested by Piganeau and Eyre-Walker (2009):

(9)

where P_n and P_s are the numbers of nonsynonymous and synonymous polymorphisms, and L_n and L_s are the numbers of nonsynonymous and synonymous sites. ψ is expected to be less biased than P_n/P_s.

Creation of Independent Data Sets

Estimates of ω_a and N_e are not independent because they both depend on neutral diversity, so sampling error will tend to induce a positive correlation between N_e and ω_a. We avoided this problem by splitting the synonymous site data into two independent sets (which is similar to splitting the data set into odd and even codons as in Smith and Eyre-Walker 2002; Piganeau and Eyre-Walker 2009; Stoletzki and Eyre-Walker 2011) by generating a random multivariate hypergeometric variable as follows:

(10)

(11)

where L_s is the number of sites and P a vector consisting of the number of nonmutated sites and the site frequency spectrum so that ∑P = L_s. We use P_s1 and P_s2 to compute two corresponding independent variables N_e1 and ω_a2. Note that N_e2 and ω_a1 could be obtained in a similar manner, however, results were qualitatively comparable and we therefore only show results for N_e1 versus ω_a2. The same strategy was used to investigate the relationship between ψ and N_e.

Results

To investigate the correlation between the rate of adaptive evolution and N_e, we compiled data from 13 phylogenetically independent pairs of species (table 1; supplementary figures S1 and S2, Supplementary Material online). We measured the rate of adaptive evolution using the statistic ω_a, which is the rate of adaptive substitution at nonsynonymous sites relative to the rate of synonymous substitution, using a method that takes into account the contribution of slightly deleterious mutations to polymorphism and divergence (Eyre-Walker and Keightley 2009; Keightley and Eyre-Walker 2012). We estimated N_e by dividing the synonymous site nucleotide diversity by an estimate of the mutation rate per generation, taken from the literature. We also divided the synonymous sites into two groups when estimating ω_a and N_e in order to ensure that the estimates were statistically independent. Estimates of ω_a and N_e are given in table 2.

Table 2.

Summary of the Nucleotide Diversity for Silent Sites π, Mutation Rate per Generation μ from the Literature, Estimates of Effective Population Sizes N_e, ω_a, ENC, and ENC′ for the 13 Analyzed Species

								Selection on Silent Sites
Species	π	μ × 109	Ne	ωa	N2/N1	ENC	ENC′	4Nes	Nea	ωaa
Drosophila melanogaster	0.019	5.8 [1]	822,351	0.03	2.31	53.56	54.42	−0.0002	822,379	0.04
Drosophila miranda	0.008	5.8 [1]	334,502	−0.00	4.95	43.27	49.27	−0.0002	334,513	0.01
Drosophila pseudoobscura	0.019	5.8 [1]	798,607	0.27	4.5	43.28	48.62	−0.0008	798,714	−0.06
Homo sapiens	0.001	11 [2]	20,974	−0.04	4.09	53.39	54.61	−1.2118	26,127	0.02
Mus musculus castaneus	0.008	3.4 [3]	573,567	0.18	2.79	52.95	54.51	−0.4946	483,026	0.31
Arabidopsis thaliana	0.007	7 [4]	266,769	−0.04	4.95	54.98	56.46	−0.0016	266,840	0.03
Capsella grandiflora	0.018	7 [4]	641,262	0.06	2.8	55.08	56.11	−0.0186	643,257	0.04
Helianthus annuus	0.024	10 [5]	593,436	0.11	4.5	57.23	58.92	−0.2328	548,293	0.14
Populus tremula	0.011	17.4 [4,6]	156,368	0.06	1.5	55.98	57.43	−0.0002	156,373	0.08
Oryza rufipogon	0.005	10 [7]	131,083	−0.07	10	59.10	58.83	−3.4624	28,643	0.06
Schiedea globosa	0.013	95 [8,9]	34,075	−0.12	4.5	56.58	57.62	−0.001	34,054	−0.14
Zea mays	0.019	10 [7]	464,010	−0.00	3.07	59.05	59.01	−2.4864	168,117	0.03
Saccharomyces paradoxus	0.002	0.2 [10]	256,2065	−0.02	4.5	53.31	56.85	−0.0002	256,2150	−0.06

Note.—ω_a was estimated under a simple demographic model assuming a step change of N_e (k = N₂/N₁), where the ratio of N₂/N₁ > 1 and <1 indicates recent population size expansion and contraction, respectively. Estimates of the strength of selection on synonymous sites 4N_es and corresponding corrected estimates of N_e and ω_a. The strength of selection s on synonymous mutations was estimated assuming a constant population size. Literature sources for mutation rates: [1] Haag-Liautard et al. (2007); [2] Roach et al. (2010); [3] Keightley and Eyre-Walker (2000); [4] Ossowski et al. (2010); [5] Strasburg and Rieseberg (2008); [6] Tuskan et al. (2006); [7] Swigonová et al. (2004); [8] Filatov and Burke (2004); [9] Wallace et al. (2009); [10] Fay and Benavides (2005).

^aCorrected for the effect of selection on synonymous sites.

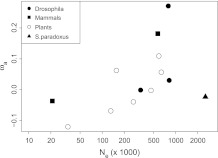
There is a nonsignificant positive correlation between ω_a and N_e for the individual data points (Pearson's correlation r = 0.16, P = 0.61; fig. 1). However, there is also a positive correlation between the two variables for all groups for which we have two or more data points (Plants: r = 0.74, P = 0.056; Drosophilidae: r = 0.55, P = 0.63; Mammals: r = 1.00, P not given because there are just two data points), suggesting that differences between taxonomic groups may obscure a significant correlation within the groups. To investigate this further, we performed an analysis of covariance (ANCOVA), grouping organisms as mammals, plants, Drosophila, and fungi. In ANCOVA, a set of parallel lines are fitted to the data, one for each group. This enables a test of whether the common slope of these lines is significantly different from zero, and one can also investigate whether the groups differ in the dependent variable for a given value of the independent variable by testing whether the lines have different intercepts. Using ANCOVA, we find that ω_a and N_e are significantly positively correlated (P = 0.017). Furthermore, there is significant variation between the intercepts (P = 0.044). There is also a positive correlation between ω_a and log(N_e) (P = 0.018), although the difference between intercepts is no longer significant (P = 0.12). The results therefore suggest that ω_a and N_e are positively correlated and that the level of adaptive evolution may vary between groups for a given N_e.

FIG. 1.—

The rates of adaptive evolution (ω_a) versus the effective population size (N_e) for 13 species grouped into four phylogenetic sets. Details concerning the analyzed species can be found in table 1.

The correlation between ω_a and N_e might be genuine, but it might also have arisen as an artifact, generated by changes in population size. For example, if species with large current N_e tend to have undergone population expansion and/or species with small N_e population size contraction, then a positive correlation between ω_a and N_e would be induced because population size expansion leads to an overestimate of ω_a and contraction to an underestimate if there are slightly deleterious mutations (Eyre-Walker 2002). We investigated whether changes in population size explain the correlation between ω_a and N_e by taking advantage of the fact that the method we used to estimate ω_a simultaneously fits a demographic model to the data. In this model, the population experiences a k-fold change in population size t generations in the past. The results of our analysis suggest that the correlation between the estimates of N_e and log(k) are weak and nonsignificant (Pearson: r = −0.41, P = 0.15; ANCOVA: slope P = 0.61) or between log(N_e) and log(k) (Pearson r = −0.15, P = 0.61; ANCOVA: slope P = 0.93); thus, there is no evidence that species with large current N_e have undergone recent expansion and/or that species with small current N_e have undergone recent contraction. We also find little evidence that ω_a is correlated to log(k) (Pearson: r = 0.17, P = 0.57; ANCOVA: P = 0.97), implying that the correlation between ω_a and N_e is not an artifact of changes in population size. It should be noted, however, that this test is not definitive because MK-based approaches are sensitive to differences in the N_e experienced by the polymorphism and the divergence data (McDonald and Kreitman 1991; Eyre-Walker 2002; Eyre-Walker and Keightley 2009). For example, a species might have experienced an expansion that predates the origin of the polymorphism data but is nevertheless recent in comparison with the overall divergence between the species being considered. In this case, there would be no evidence of expansion in the polymorphism data, but N_e for the polymorphism data would be greater than the average N_e during the divergence of the species. This would artifactually increase the estimate of ω_a.

A second explanation for the correlation between ω_a and N_e could be selection at synonymous sites. If the effectiveness of selection on synonymous sites increases with N_e, then this predicts a decrease in the level of synonymous divergence relative to polymorphism, leading to overestimation of adaptive nonsynonymous evolution. Although we might expect the effectiveness of selection on synonymous sites to increase with N_e, the evidence is mixed. Selection appears to be more effective on synonymous codon bias in Drosophila simulans than D. melanogaster (Akashi 1996; McVean and Vieira 2001), and N_e is thought to be larger in the former species (Aquadro et al. 1988; Akashi 1996). However, in mammals, selection appears to be more effective on synonymous sites in hominids than rodents (Eory et al. 2010), yet N_e is substantially larger in wild mice than hominids (Eyre-Walker 2002; Halligan et al. 2010). Furthermore, selection on synonymous codon use appears to have little effect on estimates of α in D. pseudoobscura, D. miranda, and D. affinis (Haddrill et al. 2010).

To investigate whether the correlation between ω_a and N_e might be due to selection on synonymous sites, we performed two analyses. First, we investigated whether ω_a and our estimate of N_e were correlated to codon usage bias, as measured by the ENC and ENC taking into account base composition (ENC′). ω_a is negatively correlated to ENC and ENC′, as expected if selection on synonymous codon use was causing an artifactual increase in ω_a, but in neither case was the correlation significant (ENC vs. ω_a: r = −0.481, P = 0.096; ANCOVA slope: P = 0.40; ENC′ vs. ω_a: r = −0.495, P = 0.085; ANCOVA slope: P = 0.430). Furthermore, the correlation between N_e or log(N_e) and ENC or ENC′ are nonsignificant (ENC vs. N_e: r = −0.15, P = 0.61; ANCOVA slope: P = 0.61; ENC′ vs. N_e: r = −0.04, P = 0.89; ANCOVA slope: P = 0.66; ENC vs. log(N_e): r = −0.23, P = 0.44; ANCOVA slope: P = 0.87; ENC′ vs. log(N_e): r = −0.15, P = 0.61; ANCOVA slope: P = 0.86). Hence, there is little evidence that the correlation between ω_a and N_e is a consequence codon usage bias.

In the second analysis, we estimated ω_a while simultaneously estimating the strength of negative selection on synonymous sites. We also corrected our estimate of the effective population size for the effect of selection on synonymous sites. Estimates of N_e, ω_a and the strength of selection on synonymous mutations are given in table 2. The results of this analysis show some evidence of selection on synonymous sites in four species: Oryza rufipogon, Zea mays, human, and mouse. There is independent evidence of selection in Homo sapiens (Iida and Akashi 2000; Hellmann et al. 2003; Chamary et al. 2006; Keightley et al. 2011) and mouse (Chamary and Hurst 2004; Gaffney and Keightley 2005; Keightley et al. 2011) but also in P. tremula (Ingvarsson 2010), D. melanogaster (Zeng and Charlesworth 2009), D. pseudoobscura (Akashi and Schaeffer 1997; Haddrill et al. 2011), and D. miranda (Bartolomé et al. 2005; Haddrill et al. 2011) for which we do not find evidence of selection at synonymous sites. The failure to detect selection on synonymous sites may be due to the strength of the selection being weak, and furthermore, we have assumed a model with constant population size. This was necessary because it is not possible to simultaneously fit a model that allows demographic change and selection on synonymous codon use in the absence of detailed information about codon preferences (Zeng and Charlesworth 2010). Correcting for selection on synonymous sites, we find that the correlation between ω_a and N_e is positive but not significant, whereas the correlation between ω_a and log(N_e) is positive and significant with ANCOVA (slope P = 0.028, intercept P = 0.032). Although not conclusive, these results suggest that the correlation between ω_a and N_e is not due to selection on synonymous codon use.

A third possible explanation for the correlation between ω_a and N_e is biased gene conversion (BGC). Like selection upon synonymous codon use, BGC can elevate the ratio of polymorphism to divergence relative to neutral expectations. However, it is less clear that this will affect synonymous sites preferentially.

We might expect that just as the number of adaptive substitutions increases with N_e, the number of effectively neutral substitutions will decline. We estimated the number of effectively neutral substitutions as ${\text{ω}}_{\text{na}}=\text{ω}-{\text{ω}}_{\text{a}}$, and found that ${\text{ω}}_{\stackrel{-}{\text{a}}}$ is significantly negatively correlated to N_e (r = −0.24, P = 0.43; ANCOVA slope P = 0.05; intercept P = 0.04) and log(N_e) (r = −0.53, P = 0.06; ANCOVA slope P = 0.14; intercept P = 0.23). The slopes of the regression lines, from the ANCOVA, between ${\text{ω}}_{\text{na}}$ and N_e are similar in magnitude to those between ω_a and N_e (−2.4 × 10⁻⁸ vs. 2.5 × 10⁻⁸). We also investigated whether aspects of the DFE of deleterious mutations, as estimated from the polymorphism data, are correlated to N_e. We find a significant negative correlation between ψ and N_e with ANCOVA controlling for the nonindependence between these variables (Pearson r = −0.24, P = 0.42; ANCOVA slope P = 0.014; intercepts P = 0.006) and between ψ and log(N_e) with Pearson (Pearson r = −0.64, P = 0.018; ANCOVA slope P = 0.016; intercepts P = 0.041), but correlations between the shape parameter of the DFE and the mean value of N_es and N_e are nonsignificant. The lack of a significant correlation between mean N_es and N_e could be a consequence of the low precision of estimates mean N_es (Keightley and Eyre-Walker 2007).

Discussion

We have presented evidence that the rate of adaptive protein evolution is positively correlated to N_e. We have shown that it is unlikely that this is due to recent demographic changes or selection on synonymous sites. Such a result is not unexpected. If the rate of adaptive evolution is limited by the supply of new mutations, then species with larger N_e are expected to undergo more adaptive evolution than species with small N_e because a greater number of advantageous mutations appear in the population and a higher proportion of these mutations are effectively selected.

The positive correlation between ω_a and N_e is consistent with a model in which the rate of adaptive evolution is limited by the supply of new mutations. The correlation seems less consistent with a model in which adaptation comes from standing genetic variation (Pritchard et al. 2010; Pritchard and Rienzo 2010) for two reasons. First, although the level of advantageous, neutral, and slightly deleterious genetic variation is expected to be correlated to N_e, this correlation appears to be weak; levels of diversity, at least in mammalian mitochondrial DNA (mtDNA), are poorly correlated to effective population size (Piganeau and Eyre-Walker 2009). This is probably due to a negative correlation between the rate of mutation per generation and the effective population size (Lynch 2007; Piganeau and Eyre-Walker 2009). Second, the level of diversity of strongly deleterious mutations is expected to be either independent of the effective population size or negatively correlated to it, since species with long generation times, and small effective population size, appear to have higher rates of mutation per generation (Keightley and Eyre-Walker 2000; Piganeau and Eyre-Walker 2009).

We have shown that species with large N_e undergo more adaptive substitutions than species with small N_e. However, this does not necessarily mean that these species adapt faster, though this is likely. This is because the total rate of adaptive evolution is a product of the number of adaptive substitutions and the effects of those substitutions. It is possible that species with large N_e undergo more adaptive substitutions but that these are smaller in magnitude. We have also not considered adaptive evolution outside of protein-coding genes.

The positive correlation between the rate of adaptive evolution and N_e implies that detecting the signature of adaptive evolution using MK approaches is likely to be difficult in species with small N_e because they are expected to have undergone low levels of adaptive evolution. Furthermore, they are likely to have a higher proportion of effectively neutral mutations, which tends to obscure the signature of adaptive evolution. For example, assume that we have two species with the same number of synonymous polymorphisms (20) and substitutions (100) in a sample of genes. Assume that the two species have undergone the same number of adaptive nonsynonymous substitutions (15) but that species A has experienced no neutral mutations, whereas species B has undergone as many effectively neutral nonsynonymous mutations as synonymous mutations. Under the assumption that adaptive mutations contribute little to polymorphism the MK tables for the two species would be as given in table 3. It is evident that adaptive evolution would be detected in species A using a standard MK test (i.e., a χ² test of independence), but not in species B, because although both species have undergone the same amount of adaptive evolution, this is obscured by the large number of effectively neutral substitutions in species B. The fact that large numbers of effectively neutral substitutions obscure the signature of adaptive evolution means that it will be more difficult to detect adaptive evolution in poorly conserved regions of the genome, such as regulatory sequences.

Table 3.

Power to Detect Adaptive Changes in Species with Different Effective Population Sizes

	Nonsynonymous Sites
	Adaptive	Effectively Neutral	Synonymous Sites	α (%)	ωa (%)	MK Test P Value
Species A (large Ne)
Polymorphisms	n.a.	0	20
Substitutions	15	0	100
				100	15	0.024
Species B (low Ne)
Polymorphisms	n.a.	20	20
Substitutions	15	100	100
				13	15	0.685

Note.—Comparison between two hypothetical species (A and B) that have the same number of adaptive changes but different effective population sizes illustrated by a difference in the number of effectively neutral nonsynonymous sites. n.a., not applicable.

We have found some evidence that the rate of adaptive evolution varies between groups of organisms for a given N_e. In particular, it is striking that the fungus S. paradoxus has the largest N_e among the species we have considered, but shows no evidence of adaptive evolution. If we remove S. paradoxus from the ANCOVA, we find no evidence that the rate of adaptive evolution differs between groups (ANCOVA intercepts P = 0.47), although ω_a is correlated to N_e (ANCOVA slope P = 0.017). It is possible that S. paradoxus has a low rate of adaptive evolution, despite its large N_e, because it is largely asexual (Tsai et al. 2008). Consistent with this, we note that there is a negative correlation between d_n/d_s and some measure of effective population in a number of nonrecombining genetic systems. In mammalian mtDNA, d_n/d_s is correlated to body size (Popadin et al. 2007), which is believed to be correlated to N_e, and in both mammals and birds, the largely nonrecombining Y and W chromosomes, which are believed to have lower N_e than the autosomes, have higher d_n/d_s values (Wyckoff et al. 2002; Berlin and Ellegren 2006). In contrast, we find no evidence of a significant correlation between d_n/d_s and N_e in our analysis (r = −0.37, P = 0.21; ANCOVA slope P = 0.34). This might be due to our small sample size, but it also may reflect a difference between recombining and nonrecombining loci. In our analysis, we find that the rate of adaptive substitution increases with N_e at a similar rate to the rate at which the effectively neutral substitutions decreases; this leaves the d_n/d_s uncorrelated to N_e. It might be that rates of adaptive evolution are lower in nonrecombining systems, and hence, the decline in the number of effectively neutral substitutions dominates the relationship between d_n/d_s and N_e, and species such as S. paradoxus undergo little adaptive evolution.

Supplementary Material

Supplementary figures S1 and S2 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).