An integrated in vitro and in situ study of kinetics of myosin II from frog skeletal muscle

Abstract

A new efficient protocol for extraction and conservation of myosin II from frog skeletal muscle made it possible to preserve the myosin functionality for a week and apply single molecule techniques to the molecular motor that has been best characterized for its mechanical, structural and energetic parameters in situ. With the in vitro motility assay, we estimated the sliding velocity of actin on frog myosin II (V_F) and its modulation by pH, myosin density, temperature (range 4–30°C) and substrate concentration. V_F was 8.88 ± 0.26 μm s⁻¹ at 30.6°C and decreased to 1.60 ± 0.09 μm s⁻¹ at 4.5°C. The in vitro mechanical and kinetic parameters were integrated with the in situ parameters of frog muscle myosin working in arrays in each half-sarcomere. By comparing V_F with the shortening velocities determined in intact frog muscle fibres under different loads and their dependence on temperature, we found that V_F is 40–50% less than the fibre unloaded shortening velocity (V₀) at the same temperature and we determined the load that explains the reduced value of V_F. With this integrated approach we could define fundamental kinetic steps of the acto-myosin ATPase cycle in situ and their relation with mechanical steps. In particular we found that at 5°C the rate of ADP release calculated using the step size estimated from in situ experiments accounts for the rate of detachment of motors during steady shortening under low loads.

Key points

• Force and shortening in muscle are due to the ATP-powered motor protein myosin II, polymerized in two bipolar arrays of motors that pull the two overlapping actin filaments toward the centre of the sarcomere.

• The parameters of the myosin motor in situ have been best characterized for the skeletal muscle of the frog, from which single intact cells can be isolated allowing fast sarcomere level mechanics to be applied.

• Up to now no reliable methods have been developed for the study of frog myosin with single molecule techniques.

• In this work a new protocol for extraction and conservation of frog muscle myosin allows us to estimate the sliding velocity of actin on myosin (V_F) and its modulation by pH, myosin density, temperature and substrate concentration.

• By integrating in vitro and in situ parameters of frog muscle myosin we can relate kinetic and mechanical steps of the acto-myosin ATPase.

Introduction

The motor protein myosin II produces force and shortening in muscle during cyclical ATP-driven interactions of its globular portion (the myosin head) with the actin filament. In each sarcomere, the structural unit of striated muscle, myosin II molecules polymerize in two bipolar arrays of motors that, following actin attachment, undergo a conformational change (the working stroke, d) that pulls the actin filament, originating from the Z line at the sarcomere extremity, toward the centre of the sarcomere. The array arrangement gives myosin II motors the property of generating steady force and shortening by the combination of single motor properties and cooperative mechanisms that still have to be clarified.

The ATPase activity of myosin II has been characterized by biochemical studies in solution (Lymn & Taylor, 1971): the energy liberation by the acto-myosin complex is mainly associated with release of the ATP hydrolysis products, phosphate and ADP. In the absence of ATP, a biochemical condition that in cells occurs only after death and is responsible for muscle rigor, all the nucleotide-free myosin motors are strongly bound to actin. Mechanics and energetics of the motor proteins of muscle can be described only in situ, where the contractile proteins act in the preserved filament lattice. As the load is reduced below the isometric force (T₀), the muscle shortens at a speed that is higher at lower load (Hill hyperbolic force–velocity relation; Hill, 1938), while the rate of acto-myosin interaction increases (Huxley, 1957), as shown by the increase in both the rate of energy liberation (Fenn, 1924) and the ATPase rate (Kushmerick & Davies, 1969). The motor function in situ can be studied with the best temporal and spatial resolution by applying sarcomere level mechanical methods to single fibres isolated from frog muscle (Huxley & Simmons, 1971; Piazzesi et al. 2002a,b, 2007). This approach enables estimating the stiffness of the myosin motor and the load dependence of the size and rate of the myosin working stroke, but does not allow the control of the biochemical milieu and relating the mechanical steps to the chemical transitions of the myosin–actin ATPase cycle. The coupling between mechanical and chemical steps can be investigated in situ in demembranated fibres from frog and mammalian muscle (see Goldman, 1987, and references therein), which, however, less consistently provide physiological responses at the sarcomere level, due to the loss of sarcomeric order in subsequent activations. In addition fibre mechanics implies the action of a large population of myosin motors and thus produces ambiguous interpretations of the function at the single molecule level.

The development of the in vitro motility assay (IVMA) (Sheetz & Spudich, 1983; Yanagida et al. 1984; Kron & Spudich, 1986; Ishijima et al. 1991; Finer et al. 1995) constituted a fundamental advance for the study of chemomechanical properties of the motor proteins. In fact, even if in IVMA the native three-dimensional arrangement of the myofilaments is lost, the mechanical output can be related to the kinetics of the single myosin–actin interaction under controlled biochemical conditions. A fundamental parameter in the coupling between mechanical and biochemical properties of the motor mechanism is the maximum shortening velocity or the velocity of sliding between the actin and myosin filaments under zero load (V₀). In terms of A. F. Huxley's (1957) mechanical–kinetic model, V₀ depends on the rate of motor detachment at the end of the working stroke. In addition V₀ from different muscle types is related to the rate at which the myosin extracted from the same muscles hydrolyses ATP in solution (k_cat) (Barany, 1967); both V₀ and the ATPase rate decrease by two orders of magnitude going from fast skeletal muscle to smooth muscle.

V₀ in muscle should be approximated in vitro by the velocity at which actin filaments move over a surface coated with myosin motors (V_F), as in IVMA the load exerted by the actin filament on the myosin motors is negligible (Howard, 2001). Actually, substantial differences are found comparing V_F and V₀ reported in the literature and their dependence on pH, temperature and ionic strength. In general V_F was found 2–8 times lower than V₀ (Homsher et al. 1992; Thedinga et al. 1999; Pellegrino et al. 2003), the difference being accounted for by the random orientation of myosin heads in the IVMA only for a minor contribution (Ishijima et al. 1996; Scholz & Brenner, 2003). All the IVMA measurements so far have been done with myosin extracted from mammalian muscle and V₀ used for the comparison has been determined in skinned fibres from the same muscle.

Skinned fibre preparations present a series of drawbacks (such as the loss of sarcomeric order induced by the diffusion limited Ca²⁺ activation and the large compliance of the end attachments to transducer levers) that limit the possibility to refer their responses to sarcomere mechanics. These drawbacks, together with the loss of soluble proteins and other native solutes, may account for the difference between skinned fibre and intact fibre mechanics. For instance, with reduction of ionic strength, V₀ in intact fibres increases (Edman & Hwang, 1977), while in skinned fibres it either does not change (Julian & Moss, 1981) or reduces (Thames et al. 1974). The skinned fibres swell as a consequence of membrane permeabilization, so that the distance between filaments increases. However, as demonstrated in intact frog fibres, changes in the interfilamentary distance per se should not affect either V₀ (Edman & Hwang, 1977) or the stiffness of the myosin motor (Piazzesi et al. 1994). On the contrary, reducing the lattice dimension of the skinned fibre back to the original value with the osmotic agent dextran increases the motor stiffness, revealing that in skinned fibres this parameter becomes sensitive to lattice dimension (Linari et al. 2007).

It is clear from the above considerations that the differences between the myosin motor parameters collected with in vitro mechanics and with fibre mechanics cannot find reliable explanations if both approaches have methodological limits. So far only intact fibre mechanics from frog skeletal muscle can provide a standard reference value for mechanical, kinetic and energetic parameters of the myosin motor. This is a compelling reason for the application of in vitro studies to the contractile proteins from frog skeletal muscle. Up to now a serious impediment for these studies has been caused by problems encountered in preserving the enzymatic activity of frog myosin during and after the purification process (Ferenczi et al. 1978; Pliszka et al. 1978; Focant & Huriaux, 1980). Inactivation was likely to have been favoured by dissolving purified myosins in high ionic strength solution, since these molecules in situ exist only in a polymerized form. Indeed, myosin enzymatic activity lost during the extraction could be recovered by dialysing the proteins against low salt solution (Ferenczi & Homsher, 1982).

Here we establish efficient protocols for purification and conservation of frog muscle myosin with stable IVMA functionality for more than 1 week. In this way we can determine the best (standard) conditions for V_F in terms of ionic strength and pH and define the dependence of V_F on temperature and [ATP]. By integrating in vitro data with the relevant data from in situ mechanics, such as the velocity of shortening and its dependence on the load and temperature, we can estimate the load on the myosin motors under the standard IVMA conditions and thus the step size of the unitary actin–myosin interaction and the kinetic correspondence between ADP release and detachment of the myosin motor from actin.

Methods

Ethical approval of the procedures for the specimen preparation

The skeletal muscle of Rana esculenta was used for both the preparation of myosin II and the dissection of single intact fibres. Frogs were kept in a humid environment at 4–6°C for no longer than 2 months. The animals were killed by decapitation followed by destruction of the spinal cord in agreement with the official regulation of the European Union (Directive 86/609/EEC) and with Schedule 1 of the UK Animals (Scientific Procedures) Act 1986. For in vitro experiments frog myosin II was extracted from muscles of thigh and legs, because these muscles contain mainly fast twitch fibres and are the source of a well established set of mechanical and energetic data on frog skeletal muscle. A single frog provided about 3–4 g of muscle tissue from hindlimb musculature. For in situ experiments single intact fibres were dissected from the lateral head of the tibialis anterior muscle. Actin for in vitro experiments was prepared from leg muscles of adult male New Zealand White rabbit (3–5 kg). Rabbits were killed in accordance with the official regulations of the institutions mentioned above.

In vitro experiments

Preparation of myosin

All steps were carried out on ice, maintaining the temperature at 4°C. Muscles were dissected in the presence of an incubation solution with composition: KP_i (KH₂PO₄ and K₂HPO₄) 170 mm, EGTA 5 mm, Na₂ATP 2.5 mm, MgCl₂ 5 mm, imidazole 10 mm, pH 7. This solution is similar to the physiological relaxing solution used for skinned fibres of the frog (Ferenczi et al. 1984). EGTA was added to prevent uncontrolled activation initiated by calcium release on rupture of the sarcoplasmic reticulum membrane. This procedure reduces the level of actin contamination in the final preparation below a measurable level (Fig. 1, see also Supplemental Material). Muscle pieces were finely minced with a scalpel and homogenized in the extraction solution (KCl 300 mm, KP_i 150 mm, DTT 10 mm, Na₂ATP 2.5 mm, MgCl₂ 5 mm, Na₄P₂O₇ 10 mm, EDTA-free antiprotease cocktail (1 tablet per 50 ml, Roche Complete®), pH 6.6) and then incubated for 15 min with constant stirring on ice. The mixture was centrifuged at 10,000 g for 10 min and the supernatant containing myosin was collected. The extraction solution is similar to that used for myosin extraction from mammalian muscle, except for the addition of Na₄P₂O₇ and the antiprotease cocktail to prevent proteolytic degradation (see Supplemental Material). Magnesium pyrophosphate (MgPP_i, 2 mm), which has a protective effect in reducing frog myosin inactivation (Kakol, 1971; Pliszka et al. 1978), was added to all solutions after extracting the myosin molecules from the lattice arrangement.

Figure 1. Polyacrylamide-gel electrophoresis (15% w/v) of frog myosin in the presence of sodium dodecyl sulphate (0.1%).

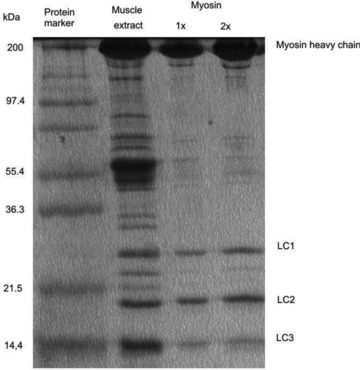
Lane 1: protein marker. Lane 2: proteins extracted from frog muscle. Lanes 3 and 4: final myosin preparation, with 1× and 2× concentration loadings. Myosin heavy chain: 200 kDa; myosin light chains: 25, 20 and 16.5 kDa.

For myosin purification we adopted the method of polymerization–depolymerization established for mammalian skeletal myosin (Margossian & Lowey, 1982). To polymerize myosin the high ionic strength of the supernatant was reduced by adding 15 × vol. of myosin precipitating solution (MES 5 mm, MgCl₂ 0.1 mm, DTT 1 mm, pH 5.8). Even after lowering the ionic strength of the extraction solution by 15 times, the rate of filament formation was minimum due to the inhibitory effect of pyrophosphate on filament formation (Davis, 1988). However, lowering pH from 6.4 to 6.1 increased the rate of filament formation (Ferenczi et al. 1978). The pH of the solution was therefore adjusted to 6.1–6.2 using acetic acid and the myosin was incubated in this solution to polymerize on ice for 30 min. Myosin filaments were collected by centrifugation at 10,000 g for 30 min. The myosin pellet was then dissolved with a depolymerizing solution (KCl 600 mm, MOPS 20 mm, MgCl₂ 5 mm, MgPP_i 2 mm, β-mercaptoethanol (βME) 1% at pH 7.1). The myosin was then dialysed overnight in a cold room against a solution with composition KCl 100 mm, Tris/HCl 20 mm, MgCl₂ 1 mm, Na₄P₂O₇ 2 mm, βME 1% at pH 7.1 to polymerize again. One cycle of polymerization–depolymerization–polymerization was adequate to extract frog myosin with a satisfactory level of purity. Repeating more polymerization–depolymerization cycles resulted in degradation of the quality of the preparation, in terms of fraction of myosin molecules active in the IVMA.

Myosin filaments formed overnight were mixed with glycerol 50% v/v and stored at −20°C. The degree of purification of the protein was checked by 15% SDS-polyacrylamide gel electrophoresis (Fig. 1). Protein concentrations were determined using the Bradford assay (Bradford, 1976). The molecular weight of frog myosin is taken as 480 kDa for further calculations.

The final preparation (Fig. 1, lanes 3 and 4) showed a strong staining heavy chain and three light chains with mobility corresponding to molecular masses of 25, 20 and 16.5 kDa. Following the extraction protocol, the yield was about 1% of the initial wet mass, that is about 30 mg of myosin from each extraction.

Preservation and evaluation of frog myosin function

Frog myosin deteriorates much more quickly than mammalian myosin and polymerization of the molecule into thick filaments after the extraction was dramatically effective in preserving the quality of frog myosin. For the optimization of our method the quality of the myosin was tested with IVMA at any stage of the myosin preparation. IVMA with freshly extracted frog myosin (15 min incubation with the extraction solution) showed a substantial number of actin filaments breaking and remaining stuck and this number progressively increased with time. Following overnight myosin re-polymerization in the presence of MgPP_i, most of the filaments showed smooth sliding and only a few filaments had a stop and go motion. Sliding could be seen for more than 30 min for most of the filaments. To explain the different quality of motility tests done on freshly extracted myosin and on overnight re-polymerized myosin, we cannot exclude the presence, in the freshly extracted myosin, of some denaturated myosin that was excluded in the IVMA tests done following the subsequent steps of overnight polymerization and centrifugation.

Storage of myosin in polymerized form at −20°C with glycerol 50% v/v was not enough to preserve the activity for a long time, as the quality of IVMA decreased within a couple of days. Polymerization of myosin molecules with bound MgPP_i into thick filaments represented the best storage conditions: this myosin, stored at −20°C with 50% glycerol, could be used for up to 1 week in IVMA experiments with preservation of the ability to move actin filaments at the same V_F (Fig. S5). MgPP_i and glycerol were removed from the myosin buffer and myosin was depolymerized just before the use. For this, 100 μl of polymerized myosin stored at −20°C was added to 400 μl of the base solution (imidazole 25 mm, KCl 25 mm, MgCl₂ 4 mm, EGTA 1 mm, pH 7.0) and centrifuged at 10,000 g in a Beckman desktop centrifuge at 4°C for 6 min. The myosin pellet was dissolved in a high salt solution (KCl 600 mm, Mops 20 mm, MgCl₂ 5 mm, DTT 10 mm, pH 7.0) with appropriate volume to get the final desired concentration of monomeric myosin in IVMA.

Figure 5. Effect of temperature on filament sliding velocity (V).

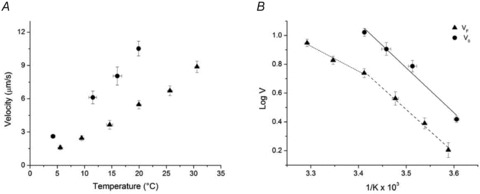
A, dependence on temperature of V_F (filled triangles, mean and SD) and of unloaded shortening velocity V₀ in fibres (filled circles, calculated as reported in the text from 11 fibres grouped in classes of temperature (°C) 2.5–5.5, 10–13, 15–18, 19–22). B, Arrhenius plot of data in A. The continuous line is the linear regression to V₀ data; the dashed line is the linear regression to V_F data for temperatures ≤ 20°C (1/K≥ 3.4 × 10⁻³); the dotted line is the linear regression to V_F data for temperatures ≥ 20°C (1/K≤ 3.4 × 10⁻³).

Preparation of actin filaments labelled with rhodamine-phalloidin

G-actin was prepared from rabbit leg muscles according to the method of Pardee & Spudich (1982). G-actin, frozen with liquid N₂, was stored at −80°C and used for up to one year. G-actin was polymerized into F-actin by adding Hepes 20 mm, KCl 10 mm, MgCl₂ 2 mm, ATP 100 μm, βME 0.01%. F-actin was fluorescently labelled according to the method of Kron et al. (1991), by incubating it overnight at 4°C, with excess of phalloidin-tetramethyl rhodamine isothiocyanate (TRITC: actin molar ratio 5:1). Labelled F-actin was stored at 4°C in aliquots covered with aluminium foil to avoid exposure to light and used for up to 1 week.

Preparation of the flow cell

Preliminary assays with frog myosin demonstrated that, even with a maximally coated myosin surface and at an ionic strength ≤60 mm, the actin filaments failed to show continuous sliding and diffused away. Such behaviour has been observed in mammalian myosin at higher ionic strength (Homsher et al. 1992). It is likely that frog myosin has lower affinity for actin than mammalian myosin. We could prevent actin filaments from diffusing away by enhancing the solution viscosity with the addition of methylcellulose 0.5% w/v to the flow cell (Uyeda et al. 1990).

The flow cell was prepared based on Spudich and collaborators’ method (Kron & Spudich, 1986), except for the coverslide coating used for myosin immobilization. In fact, using only a layer of nitrocellulose, the myosin molecules lost the ability to move the actin filaments, likely to be as a consequence of denaturation of the proteins. Instead, as previously found for myosin from insect flight muscle (Swank et al. 2001), myosin molecules maintained their motor function when spread over a layer of nitrocellulose covered with BSA. Nitrocellulose 0.1% dissolved in pentylacetate was smeared on the coverslide and allowed to dry. The treated coverslide was mounted over the microscope slide with double sticky tapes as spacers, to delimitate a chamber. Keeping the coverslide on ice, the following solutions were perfused in the flow cell by adding them from one side with a pipette while sucking by capillary action from the other side with filter paper: (1) BSA 1 mg ml⁻¹ dissolved in the base solution (imidazole 25 mm, KCl 25 mm, MgCl₂ 4 mm, EGTA 1 mm, pH 7.0) for 3 min; (2) myosin 0.5 mg ml⁻¹ for 5 min for experiments with saturating myosin surface density; for experiments with varying myosin surface density the perfusion time was kept constant at 1 min and myosin solution concentration was varied; (3) base solution with BSA 1 mg ml⁻¹ to wash away unbound myosin; (4) TRITC labelled F-actin (5 nm) for 1 min; (5) base solution with BSA 1 mg ml⁻¹ to wash away unbound F-actin, (6) the final reaction mix with desired pH, ionic strength, temperature and [MgATP] (see Table S1), also containing methylcellulose 0.5%, the anti-photobleaching agents catalase, glucose oxidase, glucose and DTT. Then the flow cell was sealed with silicone grease and mounted on the apparatus for data acquisition.

Table 1.

Activation energy determined in the temperature range 5–20°C for V at different loads, V₀ and V_F

	20 kPa	40 kPa	60 kPa	V0	VF
Ea (kJ mol−1)	60.77 ± 2.93	64.61 ± 3.17	68.06 ± 3.71	59.66 ± 6.12	57.27 ± 3.00

Solutions

The composition of the solution for the IVMA in control conditions was: saturating MgATP (>1.5 mm), free Mg²⁺ 1 mm, imidazole 25 mm, KCl 35.4 mm, MgCl₂ 3.1 mm, EGTA 1 mm, ionic strength 60 mm, pH 7.5 at room temperature (∼23°C). The ionic strength 60 mm was selected following an optimization process that discarded both a lower ionic strength, because it did not allow the KCl to be adjusted to keep the ionic strength constant when the [ATP] was raised, and a higher ionic strength, because in this case methylcellulose 0.5% did not prevent actin filaments from diffusing away. On the other hand 60 mm is the lower limit of the range where V_F of fast mammalian myosin is maximum (Homsher et al. 1992). For experiments in which pH or temperature or MgATP were changed, the final desired values of free [Mg²⁺] and [Na₂ATP] were obtained using a custom program similar to those already described (Brandt et al. 1972; Goldman et al. 1984). In the case of low ATP concentration (≤0.5 mm), an ATP regeneration system was also added (creatine phosphate 10 mm, creatine phosphokinase 1 mg ml⁻¹). Compositions of the base solutions for the various experimental conditions are shown in detail in Supplemental Material (Table S1). The pH of the solution was adjusted at the final temperature. Methylcellulose was prepared at 1.2 % in water and dialysed overnight to ensure the complete solubility.

Temperature control

The temperature of the IVMA flow cell was continuously monitored with a negative temperature coefficient (NTC) thermistor glued to the aluminium plate carrying the flow cell. The thermistor provided the feedback signal for a temperature control circuit, the output of which fed two thermoelectric modules (Melcor, CP 1.4-17-10L) stuck to the bottom of the aluminium plate carrying the flow cell. The sink for the hot surface of the two thermoelectric modules was made of an aluminium chamber with cold water circulation. The temperature inside the flow cell, tested with a miniaturized unsheathed type K thermocouple (diameter 25 μm, Omega Engineering, Manchester, UK) differed from that of the aluminium plate by less than ±0.5°C in the whole range of temperatures used.

Fluorescence imaging and data acquisition

The apparatus for recording fluorescent actin filaments was based on a custom-made inverted optical microscope that allows high mechanical stability and simultaneous use of optical tweezers and high-sensitivity wide-field fluorescence microscopy (Capitanio et al. 2005, 2007). Illumination for fluorescence microscopy was supplied by a frequency-doubled Nd:YAG laser (coherent, Verdi V-10, 532 nm wavelength) through a polarization-maintaining optical fibre. In all the experiments the polarization of the light after the fibre was circularized by a λ/4 wave-plate to maximize the excitation of all the chromophores regardless of their orientation in the sample plane. The laser power at the sample level was a few milliwatts, to obtain an optimal compromise between a high fluorescence signal and low photobleaching rate. The fluorescence signal collection was maximized by using a large NA objective (Nikon PlanApo water immersion 1.2 NA), a high efficiency EMCCD camera (Electron Multiplied CCD, photometrics cascade II) and efficient filters and dichroic mirrors with transmission spectra optimized for TRITC. The EMCCD camera was provided with a 512 × 512 pixel CCD sensor. The magnification of the fluorescence image was ∼200×, corresponding to ∼82 nm per pixel. Movies acquired with 50 ms, 200 ms and 500 ms exposure time were recorded for various time lengths and stored in the computer for further analysis.

Data analysis

Actin filament tracking was accomplished by analysing sequences of images with a custom built program in LabVIEW, as detailed in Supplemental Material. Filament velocity was determined from the change in the position of the centroid of the actin filament under inspection between two successive images.

Smooth continuous movement of actin filaments should correspond to the in situ movement due to the array of myosin motors in the half-sarcomere of a muscle fibre. Thus only in the case of smooth continuous movement should the sliding velocity (V_F) be comparable to fibre unloaded shortening velocity (V₀). The criteria used to select the filaments, the source of errors that limit the estimate of V_F and the optimization of the measurements are detailed in the Supplemental Material.

Statistical analysis of V_F

The mean sliding velocity and its standard deviation were obtained by fitting the velocity distribution with a Gaussian function (eqn (S2) in Supplemental Material; see also Fig. S2). In a preliminary phase two velocity distributions were evaluated for a given slide. The first comprised frame-to-frame velocities collected from all the actin filaments analysed in the slide. The second comprised the mean filament velocities. The details of the two procedures and the comparison of the results are reported in the Supplemental Material. V_F values obtained with the two procedures were equal within the experimental error. The second method has been adopted for the analysis shown here because it allows the discrimination of the weight of individual filaments to the generation of V_F and relating V_F of the individual filament to some other parameter of the filament, such as the filament length.

Fibre experiments

Single fibres (4–6 mm long, ∼2.15 μm sarcomere length) were dissected from the lateral head of the tibialis anterior muscle of Rana esculenta and horizontally mounted in a thermoregulated trough between the lever arms of a capacitance gauge force transducer (resonant frequency 35–50 kHz; Huxley & Lombardi, 1980) and a loudspeaker motor servo-system (Lombardi & Piazzesi, 1990). The physiological solution bathing the fibre (mm: NaCl 115, KCl 2.5, CaCl₂ 1.8, phosphate buffer 3, at pH 7.1) was set at the desired temperature by means of a servo-controlled thermoelectric module. Trains of stimuli of alternate polarity to elicit fused tetani were delivered by means of platinum plate electrodes 4 mm apart. A striation follower (Huxley et al. 1981) was used to record the changes in length of a population of sarcomeres in a 1–2 mm fibre segment. Details about preparation of fibres and on the apparatus have been already described (Lombardi & Piazzesi, 1990; Piazzesi et al. 1992). The force–velocity (T–V) relation was determined by imposing, on the isometric tetanus, constant velocity shortenings of 40–50 nm per half-sarcomere, at different temperatures ranging from 2.5 to 22°C.

T–V points were fitted with the hyperbolic Hill equation 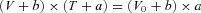, where a and b are constants related to the curvature of the relation and V₀ is the intercept of the relation on the velocity axis representing the unloaded shortening velocity.

A multifunction I/O board (PCI-6110E, National Instruments) and a program written with LabVIEW (National Instruments) were used for signal recording. Data have been collected from a total of 11 fibres.

Results

V_F in control conditions

The set of parameters chosen for defining the sliding velocity of actin over frog skeletal myosin in the ‘control’ condition were: saturating density of myosin on the surface (0.5 mg ml⁻¹ of myosin concentration in the solution and 5 min perfusion), ionic strength 60 mm, room temperature (∼24°C), pH 7.5, [Mg²⁺] 1 mm and [MgATP] >1.5 mm (saturating condition).

Under these conditions we found that F-actin filaments slide over frog myosin molecules at a velocity V_F = 5.28 ± 0.09 μm s⁻¹ (mean and SEM from a total of 388 filaments selected from 14 slides from 3 myosin extractions). As shown in Fig. 2, the statistical mean agrees with that provided by the Gaussian fit of the distribution of the number of filaments versus V_F. V_F determined for frog myosin is almost twice the value for the fast isoform from rabbit skeletal myosin under similar conditions (V_F = 2.58 ± 0.03 μm s⁻¹ at ionic strength 56 mm, 25°C, pH 7.2, MgATP 2 mm; Pellegrino et al. 2003), consistent with the different shortening velocity of the muscles of the two species at the same temperature.

Figure 2. Histogram of observed sliding velocities (V_F, μm s⁻¹) of actin over myosin molecules from frog skeletal muscle under control conditions.

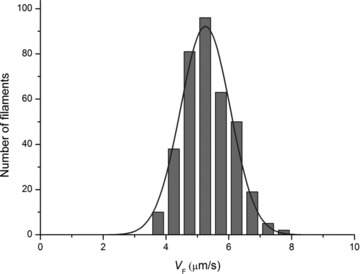
V_F was grouped in classes of 0.5 μm s⁻¹. The continuous line is the least-square fit, using the Gaussian equation (eqn (S2) in Supplemental Material), of the number of the observations (n) as a function of V_F. Estimated Gaussian parameters are: mean 5.25 μm s⁻¹ and σ 0.79 μm s⁻¹. Statistical mean ± SD is 5.28 ± 0.35 μm s⁻¹.

Effects of the myosin concentration

We determined if and how the myosin concentration affects the value of V_F in the range 0.1–0.9 mg ml⁻¹ (perfusion time 1 min). As shown in Fig. 3A, in the whole range of myosin concentrations used, V_F remained almost constant (average value 5.07 ± 0.20 μm s⁻¹, 7 slides). With the threshold conditions selected according to the criteria described in Supplemental material, no sliding was observed below the myosin concentration of 0.14 mg ml⁻¹.

Figure 3. Effect of the concentration of myosin on V_F and on the length of the actin filaments moving in the IVMA.

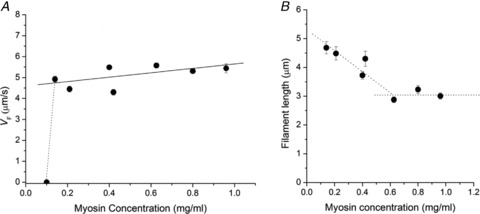
A, relation between the sliding velocity and the myosin concentration. All the data points (mean ± SEM from at least 20 filaments) belong to the same preparation. Continuous line is the linear fit to data, slope 1.05 ± 0.20 μm s⁻¹ ml mg⁻¹. B, relation between the length of moving actin filaments and the myosin concentration. Data points (mean ± SEM) are from the same slides as in A. The dotted lines are drawn to facilitate the visualization of the corner at 0.6 mg ml⁻¹. The average filament length for the three points above the myosin concentration 0.6 mg ml⁻¹ is 3.04 ± 0.18 μm.

Under control conditions the length of the actin filament did not influence per se the sliding velocity (see Fig. S6 in Supplemental Material). However, as shown in Fig. 3B, when the concentration of myosin in the incubation solution was reduced below a critical level (0.6 mg ml⁻¹), the length of the filaments selected for V_F measurements started to be correlated to the myosin concentration, increasing in proportion to the reduction of concentration. This suggests that there is a threshold of myosin density below which the average length of the actin filament has to increase to keep the number of myosin molecules adequate for continuous sliding.

Figure 6. Dependence of V_F on MgATP concentration at two temperatures.

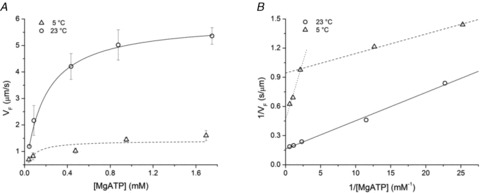
A, relation of V_Fversus[MgATP] at 23°C (circles) and at 5°C (triangles). Each data point (mean ± SD) is from at least 3 slides. The lines are data fits with the Michaelis–Menten equation (eqn (2)): the best fit parameters are at 23°C (continuous line): V_max = 5.92 ± 0.08 μm s⁻¹ and K_m = 0.174 ± 0.004 mm; at 5°C (dashed line) the values are: V_max = 1.41 ± 0.14 μm s⁻¹ and K_m = 0.051 ± 0.029 mm. B, plots of the reciprocal of V_Fversus the reciprocal of [MgATP]. Symbols as in A. The Michaelis–Menten parameters estimated from the linear fit (eqn (3)) are shown in the following table. For the relation at 5°C separate fits are done for [MgATP] < 0.4 mm (dashed line) and for [MgATP] > 0.4 mm (dotted line).

Effect of pH

To test the effect of pH on V_F, the pH of the solution was changed in the physiological range (6.5–7.5). As shown in Fig. 4, V_F does not change when reducing pH from 7.5 to 6.8 and then reduces at lower pH, falling to zero at pH 6.5. At this pH, within a few minutes after the addition of ATP to the bathing solution, filaments broke into pieces and stopped moving. This is similar to the effect of reduction of pH reported for rabbit myosin (Homsher et al. 1992).

Figure 4. Effect of pH on sliding velocity.

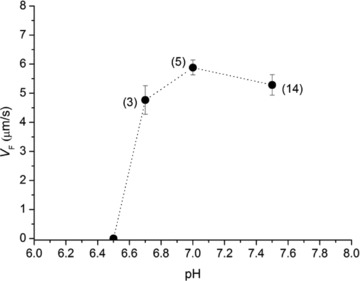
In brackets the number of slides contributing to the data points (mean and SD) are indicated.

Effect of temperature

The dependence of V_F on temperature was determined under otherwise control conditions in the range of temperatures between 5 and 30°C. As shown in Fig. 5A, in the whole range of temperatures used, V_F (triangles) increases with the increase in temperature from 1.60 ± 0.09 μm s⁻¹ at 5.5 ± 0.2°C (5 slides) to 8.88 ± 0.26 μm s⁻¹ at 30.6 ± 0.1°C (4 slides).

Note that filament sliding at 5°C was not observed in previous IVMA with mammalian skeletal myosin, very likely for an intrinsic temperature related difference in the two myosin motors: the working temperature (body temperature, 37°C) of mammalian myosin is ∼15°C higher than room temperature, while the muscle of a heterotherm, like the frog, works at temperatures that range from room temperature to a temperature as low as 5°C.

To better define the temperature dependence of V_F, the triangles of Fig. 5A were used to build the relation represented by triangles in Fig. 5B, where log V_F is plotted versus 1/K (the reciprocal of absolute temperature) according to the Arrhenius equation:

(1)

where E_a is the activation energy, R is the gas constant (8.314 J mol⁻¹ K⁻¹), and E_a/(2.303 ×R) and log(k) are the slope of the relation and the ordinate intercept, respectively. As previously found for mammalian myosin (Homsher et al. 2003; Rossi et al. 2005) the slope of the relation, and thus E_a, reduces at higher temperature.

Assuming that the corner between different slopes is at ∼20°C (1/K∼3.4 × 10⁻³), E_a is 33.30 ± 4.49 kJ mol⁻¹ in the range 20–30°C (dotted line) and 57.27 ± 3.00 kJ mol⁻¹ in the range 5–20°C (dashed line).

These values of activation energy are smaller than those reported previously for IVMA (70–120 kJ mol⁻¹, (Homsher et al. 1992; Grove et al. 2005; Rossi et al. 2005)). However E_a in the range 5–20°C is similar to E_a determined in situ in intact frog muscle fibres in the same range of temperatures (59.66 ± 6.12 kJ mol⁻¹, circles and continuous line in Fig. 5B (see also Cecchi et al. 1978)).

Effect of [MgATP]

The dependence of V_F on substrate concentration has been determined in the range of [MgATP] from 0.05 to ∼1.80 mm at both the control temperature (23°C, Fig. 6, circles) and 5°C (Fig. 6, triangles), that is the temperature at which in vitro data can be integrated with in situ data from fibre mechanics. As shown in Fig. 6A, V_F increases with [MgATP], following a saturation curve described by the Michaelis–Menten equation:

(2)

where V_max is V_F at saturating concentration of the substrate and K_m is the affinity constant for MgATP.

Since for [MgATP] < 100 μm the sliding velocity decreased at subsequent times during the measurement on the same slide, due to the progressive reduction of [MgATP], the ATP regenerating system, creatine phosphate (CrP) and creatine phosphokinase (CPK), was added to the solutions to prevent this.

It can be seen that at the lower temperature the data are not satisfactorily fitted by the Michaelis–Menten equation (the error of K_m is quite large). The reason of the deviation from a simple Michaelis–Menten relation at low temperature becomes explicit in Fig. 6B, where the reciprocal of V_F is plotted versus the reciprocal of [MgATP], according to the Lineweaver–Burk equation:

(3)

Temperature (°C)	[MgATP] (mM)	Vmax (μm s−1)	Km (mM)
5	<0.4	1.059 ± 0.022	0.021 ± 0.002
	>0.4	2.150 ± 0.194	0.515 ± 0.107
23		6.154 ± 0.530	0.179 ± 0.022

Under this form the Michaelis–Menten relation becomes linear with a slope K_m/V_max, an ordinate intercept 1/V_max and an abscissa intercept −1/K_m. It is evident that at 5°C (triangles) the slope of the relation is larger (and the ordinate intercept smaller) for [MgATP] > 0.4 mm, so that V_max becomes larger than the value estimated for values of [MgATP] < 0.4 mm (see the table in the legend of Fig. 6). Moreover K_m for [MgATP] > 0.4 mm is one order of magnitude larger than that for [MgATP] < 0.4 mm. This phenomenon is not present at higher temperature (circles and continuous line in Fig. 6) and has been already described for the myosin of the fast muscle of chicken in IVMA experiments at 25°C (Baker et al. 2002) (a temperature ∼15°C lower than the physiological temperature for that animal and thus comparable to the low temperature of IVMA experiment on frog myosin). In chicken myosin the [MgATP] for the shift between the two kinetics is smaller (∼0.1 mm). The phenomenon has not been seen in IVMA of other muscle myosins (either skeletal or smooth) and non-muscle myosins at different temperatures (Kron & Spudich, 1986; Harada et al. 1987; Warshaw et al. 1990; Homsher et al. 1992; Canepari et al. 1999). There is yet not a simple explanation for the presence of two regimes in the V_F-[ATP] relation (Baker et al. 2002), even if it can be hypothesized that there is a threshold [MgATP], below which the presence of the actomyosin rigor cross-bridges constitutes a substantial load that depresses V_F. Above that [MgATP], detachment would occur mostly from an actomyosin–ADP state with a strain sensitive kinetics (Nyitrai & Geeves, 2004) that prevents the generation of a V_F depressing load.

Unloaded shortening velocity in fibres

The dependence on temperature (range 2.5–22°C) of the unloaded shortening velocity (V₀) in single fibres from the frog tibialis anterior muscle is shown by circles in Fig. 5. V₀ was measured by the intercept of the force–velocity relation on the velocity axis (see Methods). V₀ rises with temperature from 2.62 ± 0.13 μm s⁻¹ at 4.2 ± 0.4°C (mean ± SEM from 8 fibres) to 10.52 ± 0.68 μm s⁻¹ at 19.9 ± 0.3°C (4 fibres). With respect to the relation between V_F and temperature in the same range of temperatures (4–20°C), the V₀–temperature relation is shifted up and has a larger slope, so that the ratio V₀/V_F goes from ∼1.6 at 4–5°C to ∼1.9 at 20°C. This is not in agreement with previous work on mammalian myosin showing that the difference between V_F in IVMA and V₀ in skinned fibres decreases with the increase in temperature (Homsher et al. 1992; Thedinga et al. 1999). The discrepancy may be related to the increase, in skinned fibres, of sarcomere inhomogeneity with temperature which generates an internal load and reduces V₀.

Comparison between V_F and isotonic shortening velocity at different loads

To investigate the reasons for the difference between V_F and V₀ and the limits of the comparison between in vitro and in situ measurements, we looked for an estimate of the extent of load able to justify the difference. For this we used the relation between the shortening velocity (V) and the force (T) determined in single fibres at different temperatures. Figure 7A shows the data and the procedure used to determine the temperature dependence of any given T–V point. Data are from a fibre where the T–V relation was determined at three different temperatures (7, 14.5 and 21°C). The force in the isometric contraction (T₀) was 195 kPa (7°C), 233 kPa (14.5°C) and 241 kPa (21°C). The continuous lines are the fit to data points at the three temperatures according to Hill's (1938) hyperbolic equation (see Methods):

Figure 7. Dependence of the force–velocity relation on temperature.

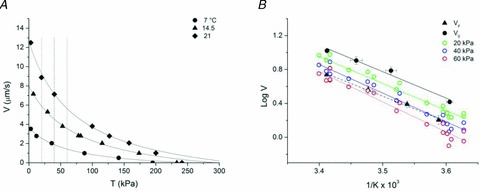
A, force–velocity (T–V) relation for a single muscle fibre at three different temperatures: circles, 7°C; triangles, 14.5°C; squares, 21°C. Data from a fibre with CSA 7600 μm², sarcomere length 2.11 μm. Continuous lines are Hill hyperbolic fits to data. Vertical dotted lines are drawn to intersect velocity points at constant load at the three temperatures. B, Arrhenius plots of V_F (triangles and dashed line from Fig. 5B), V₀ (black circles and continuous line from Fig. 5B) and V for loads of 20 kPa (green circles), 40 kPa (blue circles) and 60 kPa (red circles) estimated as shown in A in a total of 11 fibres. Coloured lines are the linear regressions to data points with corresponding colours.

(4)

The ordinate intercepts of the curves give the estimates of V₀ at the three temperatures. The vertical dashed lines are drawn to intersect velocity points (V) for the three different temperatures at any given constant load (20, 40 and 60 kPa).

In Fig. 7B the Arrhenius plots of V points determined in this way for loads of 20 kPa (green circles), 40 kPa (blue circles) and 60 kPa (red circles) are shown together with V₀ (black circles) and V_F (black triangles) from Fig. 5.

The Arrhenius plots are progressively shifted downward with the increase in load, but their slope is similar. Consequently the activation energy E_a, ∼60 kJ mol⁻¹ (Table 1), is similar and corresponds to E_a estimated for both V₀ and V_F in the same range of temperatures. Moreover the V relation that better superimposes to the V_F relation is that for 40 kPa, suggesting an estimate of the load exerted on the myosin motors in our IVMA measurements. The value of 40 kPa is ∼25% of the isometric force at 4–5°C and represents a progressively smaller fraction of the fibre isometric capability at higher temperature, because T₀ increases with temperature (Piazzesi et al. 2003; Decostre et al. 2005). Thus the same absolute load (40 kPa) represents a smaller fractional load in IVMA at higher temperature. However the difference between V_F and V₀ increases with increase in temperature (Fig. 5A). This result is a consequence of the larger effect of the increase in temperature on V₀ than on T₀ (Fig. 7A): the difference between V₀ and V at a load of 40 kPa (corresponding to V_F in IVMA) increases with the increase in temperature.

The finding that the reduction of V_F with respect to V₀ can be explained by a load that remains constant independent of temperature supports the hypothesis that this load is due to aspecific electrostatic interactions between the actin filament and the surface components.

Discussion

In this work we provide for the first time a protocol for studying the function of myosin II from frog skeletal muscle as a single molecule. This methodological achievement made it possible to accurately measure the sliding velocity of actin on frog muscle myosin and characterize its modulation by temperature and substrate concentration. The in vitro parameters can be integrated with the in situ mechanical and kinetic parameters of frog muscle myosin working in arrays in the muscle sarcomere. The following discussion concerns: (i) the comparison of the sliding velocity of the actin filament on a bed of frog myosins (V_F) with the unloaded shortening velocity determined in fibres (V₀) and its dependence on temperature and the identification of the mechanical conditions of correspondence between in vitro and in situ measurements; and (ii) the possibility to define, by making use of the integrated approach, fundamental kinetic steps of the acto-myosin ATPase cycle in situ and their relation with mechanical steps. In particular we can relate the rate of ADP release with the rate of detachment of myosin from actin.

Comparison between V_F and V₀

In the IVMA the sliding of the actin filament occurs in a regime where inertial effects are negligible and Brownian motion is dominant. There is negligible viscous drag on the filaments as they are propelled by myosin along their axis. Thus the velocity of the forward motion of the actin filament is set by the detachment rate of the myosin motor once it has completed the working stroke. Consequently the in vitro sliding velocity V_F should correspond to the in situ velocity of unloaded shortening V₀. Actually, as shown in Fig. 5, in the whole range of temperatures studied, V_F is smaller than V₀ by a factor that increases with temperature and becomes ∼2 at 20°C.

The finding that also in frog myosin, as in mammalian myosin, V_F is smaller than V₀ indicates the presence of systematic factors that reduce the sliding velocity in vitro. The effect may be explained considering that myosins are randomly oriented on the surface of the IVMA and those not properly oriented may interact with actin and generate a load. In favour of this interpretation, it has been found that, on a reconstituted thick filament of mammalian myosin, actin slides toward the centre of the filament 3–5 times faster than away from the centre (Scholz & Brenner, 2003). However the velocity of sliding with correct polarity remains smaller than V₀ reported by the same authors (Thedinga et al. 1999). Moreover, other works show the absence of a clear difference in V_F between myosin heads that are properly oriented in a track and myosin heads randomly oriented, suggesting that myosin heads attached to the surface can swivel to recover the correct direction of the stroke with respect to the actin orientation (Uyeda et al. 1990; Yamada & Takahashi, 1992; Yamada & Wakabayashi, 1993; Scholz & Brenner, 2003).

A factor that is likely to cause a reduction in V_F with respect to V₀ is the presence of a drag generated by some dead (rigor-like) myosin heads and/or by the ionic strength. The inhibitory effect on V_F of addition of a drag has been directly demonstrated by introducing in the IVMA slower myosin isoforms or non-cycling myosins (Warshaw et al. 1990; Cuda et al. 1997). Lowering the ionic strength below 80–100 mm is reported to reduce V_F, probably because it increases the aspecific interactions of the actin filament with any components of the surface like myosin tails or nitrocellulose (Homsher et al. 1992; Thedinga et al. 1999; Guo & Guilford, 2004; Grove et al. 2005). On the other hand, in our protocol the ionic strength could not be increased above 60 mm, because at higher (more physiological) ionic strengths even the addition of 0.5% methylcellulose did not prevent actin filament from flying away from the surface.

Another factor that could contribute to reduce V_F in our IVMA was the absence of the regulatory protein complex troponin–tropomyosin in the actin filament. In this respect it must be noted that V_F of the myosin proteolytic fraction HMM (heavy mero-myosin) has been found to be significantly larger when the actin filament contains the regulatory proteins, but only at temperatures higher than 12°C (Homsher et al. 2003). To give a quantitative estimate of the drag that can account for the difference between V_F and V₀ and for the limits of the comparison between in vitro and in situ measurements, we developed a comparative analysis of Arrhenius plots for V_F, V₀ and V during isotonic shortening at different loads (Fig. 7). The comparison suggests that V_F is reduced for the presence of a load on the actin, likely to be provided by aspecific electrostatic interactions of the actin with the surface components. This load corresponds to 25% of the isometric force developed by a fibre at low temperature (4–5°C). At this temperature the isometric force developed by a single frog myosin motor is ∼5 pN (Decostre et al. 2005; Piazzesi et al. 2007), and thus the average load imposed on each myosin on the surface of the IVMA by the aspecific interactions of the actin filament is ∼1 pN. The number of interactions and thus the load should increase with the length of the actin filament and this appears contradictory with the finding that in control conditions (saturating concentrations of myosin) V_F does not depend on the actin filament length (see SM). The contradiction however is solved considering that also the number of myosin motors interacting with the actin increases with the filament length, counteracting the increase in load and leaving the observed sliding velocity independent of the filament length.

Estimate of the kinetic parameters of the actin–myosin interaction

In a single actin–myosin interaction, the relation between the mechanically relevant step (the working stroke d) and biochemical steps can be represented as in Fig. 8: the time taken by a myosin motor to complete the ATPase cycle, τ_c ( = 1/k_cat), is much longer than the time, τ_on, during which the motor remains attached to actin and undergoes the working stroke.

Figure 8. Time course of a single interaction between the myosin motor and the actin, showing the length step d and the underlying biochemical transitions.

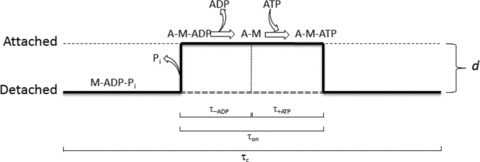
During the ATPase cycle time (τ_c), the motor may be detached (or weakly attached, M-ADP-P_i state) or attached (A-M states). The duration of the attachment (τ_on) is divided in the time for the ADP release (τ_-ADP) and the time for the ATP binding and actin dissociation (τ_+ATP) (modified from Tyska & Warshaw (2002)).

The transition leading to the strongly bound force generating state of the motor is linked to the release of P_i and the motor detachment from actin is linked to the binding of a new ATP. Thus, under the conditions that [P_i] and [ADP] are practically zero (∼physiological conditions), τ_on kinetically depends on two steps, the release of ADP, with a time constant τ_-ADP, and binding of ATP, with a time constant τ_+ATP: τ_on = τ_-ADP+τ_+ATP. In terms of rate constants the equation becomes:

(5)

where k_-ADP is the rate constant for the dissociation of ADP and k_+ATP is the second order rate constant for the binding of ATP. Thus the rate of ATP binding depends also on the ATP concentration. At saturating [ATP] the second term of the sum in eqn (5) becomes negligible compared to the first term. Consequently the detachment rate k_off, the reciprocal of τ_on, attains its maximum value, determined by the rate of ADP release. k_-ADP is strain dependent (Nyitrai & Geeves, 2004) and is maximum under unloaded conditions, that is when actin–myosin interactions occur in solution or in IVMA. Under these conditions and at saturating [ATP], τ_on ( = 1/k_-ADP) is minimum. The sliding velocity V depends on the rate of dissociation of myosin from actin at the end of the stroke d according to the equation:

(6)

where k_off ( = 1/τ_on) is the rate constant of dissociation determined by the slower of the two processes of ADP release and ATP binding.

From eqn (6) it follows that, knowing d, it would be possible to calculate k_off from mechanical measurements of V in vitro (that is from V_F). d is not known in IVMA experiments, but, for frog myosin, has been recently determined in single fibre experiments (Piazzesi et al. 2007). In that work it was demonstrated, with fibre mechanics and X-ray diffraction, that d of frog muscle myosin at 4°C changes in the range 5–11 nm depending on the load and shortening velocity: as shown in Figs 4C and 5B of Piazzesi et al. (2007), d is 5–6 nm at high load (velocity up to 1000 nm s⁻¹) and attains ∼10 nm only during the near zero load (velocity as high as 10,000 nm s⁻¹) experienced by the myosin motor following a large stepwise reduction in force or length. With a load on the fibre of 0.25T₀ (corresponding to a shortening velocity V∼1500 nm s⁻¹), that is comparable to the load on myosin motors during V_F measurements in our IVMA, d is ∼7 nm. We can use this estimate of d to calculate τ_on (eqn (6)), and thus the rate constant for detachment k_off, from our measurements of V_F.

Equation (3), reporting the dependence of V_F on [ATP] (Fig. 6B), can be rewritten multiplying both terms by d. Considering that τ_on = d/V_F and that, at saturating [ATP] and with [ADP]∼0, τ_on = d/V_max = 1/k_-ADP, we obtain an expression for the reciprocal of the rate constant of detachment of myosin from actin:

(7)

Since, with [ADP]∼0, 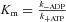(Palmiter et al. 1999):

(8)

that corresponds to eqn (5).

With d set to 7 nm, the V_F data of Fig. 6B, limited to those at low temperature and in the kinetic regime far from rigor conditions ([MgATP] > 0.4 mm), were used to plot τ_onversus 1/[MgATP] in Fig. 9. The slope of the relation estimates the reciprocal of the second order rate constant of ATP binding (k_+ATP) and is calculated multiplying by d the slope of the dotted line in Fig. 6B: 1.68 ± 0.21 × 10⁻⁶ s m; the ordinate intercept estimates the reciprocal of the detachment rate constant at saturating [ATP], that is the reciprocal of the rate constant of ADP release (k_-ADP), and is calculated multiplying by d the ordinate intercept of the dotted line in Fig. 6B: 3.26 ± 0.29 ms. Thus, from this analysis, during shortening against a low load (∼0.25T₀) k_+ATP is 0.60 ± 0.07 × 10⁻⁶ s m and k_-ADP is 307 ± 27 s⁻¹. These estimates of the two kinetic parameters are quite similar to those reported in the literature for skeletal muscle myosin of other species in both skinned fibre and IVMA experiments (Dantzig et al. 1991; Homsher et al. 1992; Baker et al. 2002), confirming the validity of the assumption made by taking the value of d from fibre experiments.

Figure 9. Plot of d/V_F (τ_on) versus the reciprocal of [MgATP] in the range of [MgATP] > 0.4 mm.

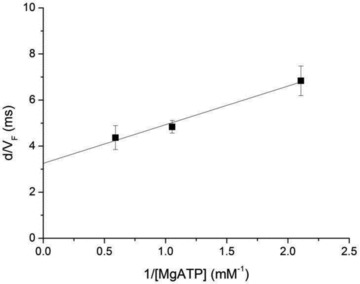
Data from triangles in Fig. 6B. The line is drawn according to the parameters from the fit in Fig. 6B multiplied by d (see text).

In turn the analysis provides a clue for estimating how strictly in situ at physiological [MgATP] the rate constant of detachment from actin of a motor depends on the rate of ADP release. In frog fibres at 4°C the rate constant of detachment at low load, calculated from the ratio between the velocity of shortening and the size of the working stroke, is ∼250 s⁻¹ (see Fig. 4C and D and Fig. 5B and C in Piazzesi et al. (2007)), which is largely accounted for by the k_-ADP calculated from the relation in Fig. 9 (300 s⁻¹).

Glossary

Abbreviations

d

working stroke of the myosin motor

E_a

energy of activation

HMM

heavy mero-myosin

IVMA

in vitro motility assay

k_cat

rate constant of ATP hydrolysis

k_off

rate constant of myosin motor detachment

k_-ADP

rate constant of ADP release

k_+ATP

second order rate constant of ATP binding

K_m

apparent binding constant for [MgATP]

T

force during isotonic shortening at velocity V in fibres

T₀

steady force exerted by fibres during the isometric contraction

τ_c

time of the ATPase cycle

τ_on

time the myosin motor remains strongly attached to actin during an ATPase cycle

τ_-ADP

time constant for release of ADP

τ_+ATP

time constant for binding of ATP

V

isotonic shortening velocity in fibres

V₀

unloaded shortening velocity in fibres

V_F

velocity of actin filament sliding in the IVMA

V_max

velocity of sliding at saturating [MgATP]

Author contributions

The experiments were performed at the European Laboratory of Non-Linear Spectroscopy, LENS, Firenze, Italy (in vitro experiments) and at the Laboratory of Physiology, Department of Evolutionary Biology, University of Florence, Italy (fibre experiments). The following authors participated in performing the experiments, data collection and drafting the article: R.E., M.C., L.M., F.P., V.L. and G.P. The following authors contributed to the conception and design of the experiments, analysis and interpretation of data, drafting the article or revising it critically for important intellectual content: R.E., M.C., V.L. and G.P. All authors approved the final version of the manuscript.

Author's present address

R. Elangovan: Indian Institute of Technology, Delhi, India.