Accurate extension of multiple sequence alignments using a phylogeny-aware graph algorithm

Abstract

Motivation: Accurate alignment of large numbers of sequences is demanding and the computational burden is further increased by downstream analyses depending on these alignments. With the abundance of sequence data, an integrative approach of adding new sequences to existing alignments without their full re-computation and maintaining the relative matching of existing sequences is an attractive option. Another current challenge is the extension of reference alignments with fragmented sequences, as those coming from next-generation metagenomics, that contain relatively little information. Widely used methods for alignment extension are based on profile representation of reference sequences. These do not incorporate and use phylogenetic information and are affected by the composition of the reference alignment and the phylogenetic positions of query sequences.

Results: We have developed a method for phylogeny-aware alignment of partial-order sequence graphs and apply it here to the extension of alignments with new data. Our new method, called PAGAN, infers ancestral sequences for the reference alignment and adds new sequences in their phylogenetic context, either to predefined positions or by finding the best placement for sequences of unknown origin. Unlike profile-based alternatives, PAGAN considers the phylogenetic relatedness of the sequences and is not affected by inclusion of more diverged sequences in the reference set. Our analyses show that PAGAN outperforms alternative methods for alignment extension and provides superior accuracy for both DNA and protein data, the improvement being especially large for fragmented sequences. Moreover, PAGAN-generated alignments of noisy next-generation sequencing (NGS) sequences are accurate enough for the use of RNA-seq data in evolutionary analyses.

Availability: PAGAN is written in C++, licensed under the GPL and its source code is available at http://code.google.com/p/pagan-msa.

Contact: ari.loytynoja@helsinki.fi

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Sequence alignment has numerous applications but its role is especially central in evolutionary analyses of molecular sequences. These inferences are based on the identities and differences detected between homologous characters and errors in these homology statements, that is errors in the alignment of the sequences, are likely to lead to errors in any downstream analyses. The generation of high-quality alignments can be computationally laborious and the solutions often require manual assessment or editing. When such alignments need to be extended, e.g. after new sequences become available, it may be preferable to keep the relative alignment of existing sequences intact and have the new sequences aligned to this reference alignment. Such addition of sequences should take into account the evolutionary relationships of all the sequences and be performed in the correct phylogenetic context.

Alignment extension has interesting applications in the analyses of next-generation sequencing (NGS) data. Fast profile-based methods have been used for the alignment of metagenomic sequence reads of unknown origin against a set of reference sequences in phylogenetic placement studies (Matsen et al., 2010; Stark et al., 2010). These do not use all information available in the data, however, and flatten the reference alignment into a consensus profile that only models conserved regions shared by most sequences. On the other hand, existing read placement methods based on phylogeny-aware alignment (Berger et al., 2011) handle the query sequences separately and delete sites inferred as insertions, limiting their use to phylogenetic placement only. Accurate alignment of complete NGS reads is of interest e.g. in analyses of RNA-seq data that come nearly exclusively from the gene regions of the genomes. With appropriate handling of short and noisy reads, RNA-seq data allow for inexpensive large-scale comparative studies of protein-coding genes, such as inferences of selection (Yang et al., 2000), and extend the use of NGS methods to evolutionary analyses of non-model organisms (e.g. http://www.onekp.com).

Popular progressive alignment programs (e.g. Katoh et al., 2002; Larkin et al., 2007) indirectly exploit the connection between alignment and phylogeny (Sankoff, 1975) as they divide the computationally intractable multiple alignment problem into many pairwise tasks. Yet, they ignore the phylogeny during the remainder of the alignment process and produce alignments whose gap patterns are not evolutionarily meaningful (Löytynoja and Goldman, 2008). We showed earlier that phylogenetic information can be used to distinguish insertions from deletions and these two very different mutation events can then be treated correctly in the progressive alignment (Löytynoja and Goldman, 2005). The phylogeny-aware algorithm based on these ideas and implemented in the program PRANK performs very well in evolutionary alignment comparisons (Dessimoz and Gil, 2010; Fletcher and Yang, 2010; Jordan and Goldman, 2012; Markova-Raina and Petrov, 2011).

Here, we outline a new general-purpose method for phylogeny-aware alignment of sequence graphs and apply it to phylogenetic extension of existing alignments. Our method, called PAGAN, is based on the same principle as PRANK and uses evolutionary information to distinguish insertions from deletions. In contrast to the greedy insertion-calling of the original approach, sequence graphs provide a flexible framework to model the phylogenetic evidence from related sequences and allow building a robust progressive aligner that tolerates errors in the guide phylogeny. The idea of using graphs to represent a sequence alignment is old (Kruskal and Sankoff, 1983) and has been revisited regularly (Hein, 1989; Lee et al., 2002; Paten et al., 2008). Our approach has similarities to earlier methods for global alignment of multiple sequences, especially the tree alignment method (Hein, 1989) and the sequence representation with partial-order graphs (Lee et al., 2002), but differs from these in its emphasis on phylogenetic calling of insertion and deletion events.

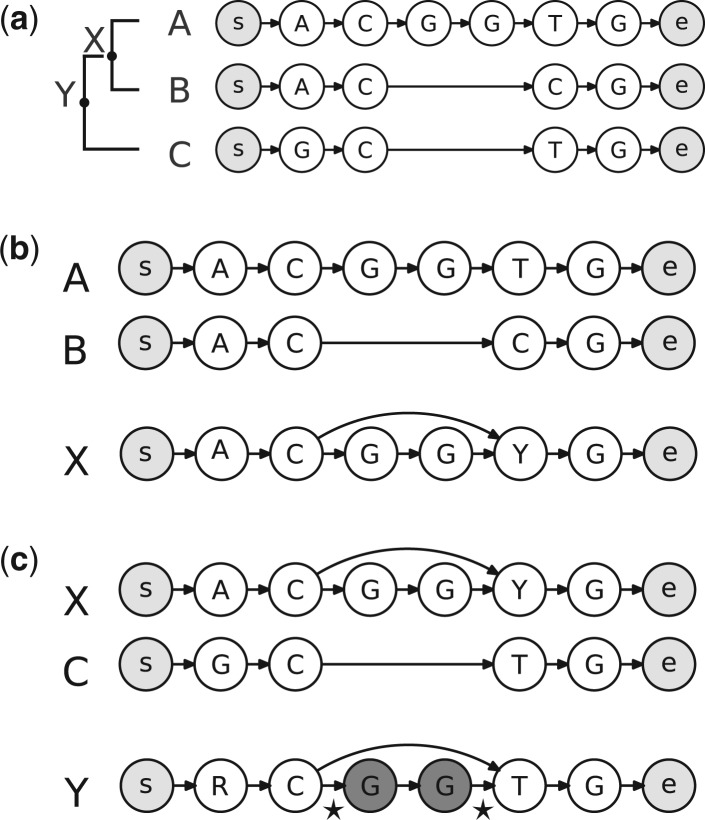
The key advantage of our graph representation of sequences is the ability to describe uncertainty regarding the presence of characters at certain sequence positions. This is beneficial during the progressive alignment of sequences (Fig. 1) but it can also be used to represent uncertainties in unaligned sequences or in the inferred ancestral sequences. As our approach considers all sequences as graphs that can be aligned against each other, it is easily extended to the placement of new sequences into existing reference alignments. Unlike most existing methods based on consensus sequence profiles, our approach correctly considers the phylogenetic context as it aligns new sequences against inferred ancestors. Moreover, it can add multiple related sequences to specific positions in the tree and thus correctly accounts for their relatedness and shared insertion and deletion events (Fig. 2).

Fig. 1.

(a) A progressive alignment of three sequence graphs consists of two pairwise alignments. (b) The first alignment creates graph X to represent the inferred ancestor of A and B. In X, the character state of vertex 5 is Y, representing both pyrimidines, and has two incoming edges, from vertices 2 and 4, to indicate that the presence of vertices 3 and 4 is uncertain. (c) The optimal alignment path for graphs X and C jumps from vertex 2 in graph X to vertex 5 using the direct connecting edge; the edges flanking the skipped-over fragment are recorded as unused (asterisks)

Fig. 2.

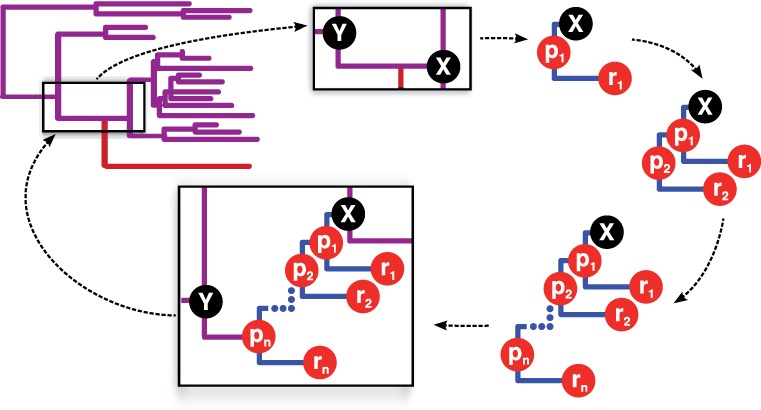
PAGAN can add multiple new sequences, assumed to come from the species shown in red, to the same target node in a progressive manner. It reconstructs sequence graphs to represent the ancestral nodes and aligns the new sequences against the ancestor of their sister clade, indicated by X. Each alignment of a sequence, r_n, creates a new parent node, p_n, against which the next sequence is aligned. After finishing the alignment, the sub-tree with the new sequences is inserted back to the tree structure

We tested PAGAN in the extension of real reference alignments with new protein and DNA sequences and found that it can successfully handle data of great variety in length and evolutionary divergence as well as different sizes of reference alignments. The accuracy of alignment cannot be tested with real data so we simulated datasets representing gene families of closely related paralogues. We used PAGAN to extend both protein and DNA reference alignments with new data and compared its performance with that of alternative extension approaches. To test larger problems, we used PAGAN and the best alternative method, hmmalign (Eddy, 2011), for a re-analysis of metagenomic data of Mirarab et al. (2012) consisting of reference alignments of 500 sequences and addition of 5000 sequence fragments. Finally, we quantified the effects of different factors on alignment accuracy and compared PAGAN and hmmalign under a simplified set-up that allowed changing the different parameters independently. Our results show that PAGAN produces exceptionally accurate alignments and its phylogenetic approach can efficiently use the evolutionary information available while remaining unimpaired by more distantly related sequences in the reference alignment.

2 METHODS

In the following sections we first describe the main concepts of our new method for phylogenetic alignment and placement of sequences using partial-order graphs. We then outline how we apply this method, called PAGAN, in the extension of DNA and protein alignments with new sequences and compare its performance with existing methods. Finally, we dissect in more detail the impact of the reference alignment and the query sequence on the performance of the best performing methods.

2.1 Phylogeny-aware graph alignment algorithm

The conversion of a regular sequence to a graph is trivial (Supplementary Fig. S1a) and two such graphs could be aligned with a standard dynamic-programming algorithm. Partial-order graphs can represent more than a sequence of characters, however, and allow modelling of e.g. evolutionary units of multiple characters, non-linear dependencies among the characters and uncertainties in the input data (Supplementary Figs S1 and S2).

The representation of sequences with graphs is especially attractive in progressive alignment that attempts to backtrack the tree-like hierarchical structure of relatedness among a set of sequences (Löytynoja and Goldman, 2009). Each alignment clusters two sister nodes, representing either single sequences or previous alignments, and defines a new node to represent this pairwise solution. The challenge of progressive alignment is that insertions cannot be distinguished from deletions at the time of aligning a pair of sequences but failing to account for their different properties is likely to cause alignment error (Löytynoja and Goldman, 2008).

A graph can describe this uncertainty regarding the type of mutation event with edges that connect vertices, representing characters in a sequence, to multiple preceding vertices; each edge is a hypothesis of the true structure of the ancestral sequence (Fig. 1 and Supplementary Fig. S3). Our new method, PAGAN, follows the ideas we implemented earlier in program PRANK (Löytynoja and Goldman, 2005) and uses phylogenetic information to distinguish insertions from deletions. However, instead of calling insertions based on one outgroup alignment only, PAGAN assigns weights to the graph edges—either skipping a deletion or connecting an insertion to the rest of the graph—and adjusts them according to the evolutionary evidence.

The algorithm for the alignment of two graphs and reconstruction of a new graph to represent this alignment is given in the Supplementary Material. The algorithm differs from the standard algorithm (Gotoh, 1982) in two aspects: it incorporates edge weights into the alignment cost; and, in the dynamic-programming computation, it chooses a move to the current state (match or two types of gaps) not only from the possible preceding states but also from all preceding cells connected to the current cell by incoming edges. The scoring function of PAGAN follows that of PRANK. Assuming that chr(x_i) gives the character associated to a vertex i of graph x, the score for matching characters at vertices x_i and y_j is:

(1)

where q(a) is the frequency of a, q_z=(q(chr(x_i))+q(chr(y_j)))/2, and P(a, b; t) is the substitution probability between characters a and b given the evolutionary distance t and the substitution model. A notable difference to the standard score is the additional term q_z , discussed in more detail in the Supplementary Material. As a further simplification, PAGAN uses weighted parsimony reconstruction of ancestral characters states and, for greater speed, the number of alternative character states for amino acid and codon data is limited to two (see Supplementary Material).

PAGAN can reconstruct ancestral sequences for an existing alignment and then extend that by aligning new sequences against the extant or inferred ancestral sequences. The reconstruction of ancestral sequence graphs for a reference alignment is not different from the de novo alignment except that the alignment solution is read from the input data. The addition of new sequences should be performed in their correct phylogenetic context: while PAGAN allows the user to define or constrain the possible phylogenetic positions for sequences coming from a known origin, it can also search for the optimal placement for unknown data. During the extension, PAGAN takes the target nodes, represented by sequence graphs, out of the tree structure and aligns the sequences assigned to each target using a progressive algorithm (Fig. 2). With data from mixed sources, the sequences for each target node can be aligned in a ranked order; on the other hand, the graph representation of reconstructed sequences tolerates inconsistencies between subsequent alignments and the algorithm can resolve conflicting gap patterns among a set of diverged sequences. Once finished, the extended sub-tree is put back to the alignment tree structure, the reference alignment is adjusted for insertions in the new sequences, and the process moves to the next node.

In this article, we focus on the extension of existing alignments with new sequences and phylogenetic placement of sequences. We test two approaches to decide the location for the new sequences, either ‘guided’ or ‘free’. The guided approach assumes that the approximate phylogenetic position of the query sequences is known and only the correct paralogue, if multiple exist, has to be resolved. The free approach is unsupervised and, in this study, is based on the use of an external local aligner to find the target node. The additional features implemented in PAGAN are explained in detail in the Supplementary Material.

2.2 Comparison of methods for alignment extension

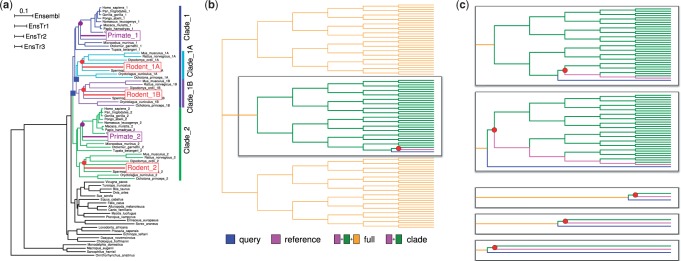
The test data for alignment extension were simulated using phylogenetic trees based on the Ensembl/UCSC tree (http://tinyurl.com/ensembltree; Fig. 3a). Three simulation trees representing different levels of evolutionary divergence, called EnsTr1, EnsTr2 and EnsTr3, were created by multiplying the branch lengths by 1.5, 2.0 and 2.5. The alignment simulator INDELible (Fletcher and Yang, 2009) was used to generate codon sequences (see Supplementary Material for details) and the resulting data were analyzed both as DNA and protein. For EnsTr1, EnsTr2 and EnsTr3, respectively, the alignments were in average 1489, 1800 and 2151 codons long; the base/amino acid identity between human and Primate was 89–90, 86–87 and 84–85 and between mouse and Rodent it was 80, 75–76 and 70–73%.

Fig. 3.

(a) The phylogeny used for the first analysis is based on the Ensembl mammalian tree but includes two additional species, Primate and Rodent shown in magenta and red, and has undergone two duplication events (blue squares). The target nodes provided for the PAGAN guided alignment are shown with dots of matching colour. (b) The first tree topology for the second analysis has ‘large’ ingroup and ‘close’ QS. (c) The ingroup of two other topologies have ‘large’ ingroup but ‘intermediate’ and ‘distant’ QSs (top). Three additional sets of reference alignments with ‘small’ ingroup are created by reducing the central sub-tree to two sequences (bottom). Full reference alignments are used with PAGAN; hmmalign analyses are performed with full sets of sequences (‘full’: 96 or 66 sequences) or just the central subgroup (‘clade’: 32 or 2 sequences). The target node for PAGAN is indicated with a red dot

The sequences for the hypothetical target species, Primate and Rodent, were removed from the simulated alignments and the rest of the aligned sequences were used as the reference alignment (RA). Of the sequences for the target species, 50 fragments of the given length were sampled from each and considered as the set of query sequences (QSs) to be aligned to the RA. We used fragment lengths of 30, 60 and 120 bases/amino acids as well as the original full-length sequences. To understand the impact of fragmented information and sequencing error on the alignment accuracy, we introduced NGS-like noise in the DNA fragment data (Massingham and Goldman, 2012). Two of the methods need a reference tree (RT) for the alignment extension: for those we used the true simulation tree and a tree inferred with RAxML (Stamatakis, 2006) using Ornithorhynchus anatinus (platypus) as the outgroup; the results were indistinguishable and the ones with the estimated tree are shown. The details of the methods and options used for the alignment are found in the Supplementary Material.

The accuracy of the resulting extended alignment was measured as the proportion of true homologies recovered between the QS and the closest human/mouse reference sequence. False homologies were not penalized and correctness of insertions inferred were not measured. The reported values are the mean accuracies over the 5000 aligned fragments (lengths 30, 60 and 120; 100 replicates, 50 fragments per sequence) or over the 100 full-length sequences for each target species paralogue.

2.3 Extension of large alignments

We downloaded the simulated test data of Mirarab et al. (2012) and analyzed the first ten replicates of the three different evolutionary scenarios. We used true simulated reference alignments and reference trees with RAxML-estimated branch lengths. We extended these alignments with the 5000 query sequences using PAGAN's experimental heuristics to quickly assign the queries to target nodes. These heuristics perform Exonerate local alignments (Slater and Birney, 2005) between the 5000 query sequences and 999 target sequences, the latter including extant sequences from the reference alignment and PAGAN-inferred ancestral sequences. The queries were assigned to their best-scoring target nodes and those not producing significant hits were discarded. We also aligned the same datasets with hmmalign from the HMMER package (Eddy, 2011): for that, the model was based on the full reference alignment and default options were used. More details can be found in the Supplementary Material.

The accuracy of the resulting extended alignment was measured as above except that each QS was compared with the closest reference sequence.

2.4 Impact of reference alignment

The impact of the RA composition on the accuracy of alignment extension was tested using the two best-performing methods from the first set of tests (see Section 3), PAGAN and hmmalign. The data were simulated using ultrametric trees that differed in the following parameters: (i) position of the QS; (ii) size of the ingroup; (iii) evolutionary divergence; and (iv) (for hmmalign) size of the outgroup. The simulation trees consisted of three 32-sequence sub-trees with one additional query sequence placed at different positions within the central subgroup (Fig. 3b and c). We call these basic topologies ‘close’, ‘intermediate’ and ‘distant’ and their ingroup (the central subgroup most closely related to the query) ‘large’. To study the effect of reduced phylogenetic information in the RA, further datasets were created with the ingroup cut down to two maximally divergent sequences. These three topologies are subsets of the full topologies but have ‘small’ ingroups. As the profile hidden Markov models (HMMs) of HMMER are affected by more distantly related reference sequences, we created six further sets of RA by keeping only the ingroup (either 2 or 32) sequences. In distinction to the ‘full’ sets, these sets are called ‘clade’. To mimic analyses of RNA-seq data, we again simulated protein-coding data and added NGS-like noise in the QS.

The simulation was repeated for tree depths of 0.30, 0.45 or 0.60 substitutions/codon with 50 replicates for each combination of tree topology and branch length. The average length of trees estimated from the full 96-sequence RA were (all lengths as substitutions/nucleotide site) 3.14, 4.70 and 6.25 for the three levels of evolutionary divergence and those of their leaf branches were 0.016, 0.025 and 0.033, respectively. The length of the branch leading to the query was (for ‘close’, ‘intermediate’ and ‘distant’) 0.020, 0.053 and 0.085 for the tree depth of 0.30; 0.029, 0.077 and 0.127 for the tree depth of 0.45; and 0.036, 0.102 and 0.167 for the tree depth of 0.60.

To mimic common practice used in metagenomic studies, the short-read simulator simNGS (Massingham and Goldman, 2012) was used to create NGS data with target fragment length of 181 bases (fragments under 130 bases excluded), 5× coverage and 125-base pair-end reads. This gave 74–76 reads for each RA with realistic noise in base call accuracy. To assess the effect of alignment error in the RA, the sequences were re-aligned with PAGAN and MAFFT (Katoh et al., 2002). The details of the data simulation and alignment are given in the Supplementary Material.

3 RESULTS

3.1 Phylogeny-aware graph alignment algorithm

PAGAN is capable of inferring de novo multiple alignments of DNA, protein and codon sequences when a guide tree is provided and, in the future, is meant to replace our earlier method PRANK. In this study, we focus on a novel feature of the method and a task that has no satisfactory existing solution, the extension of multiple alignments with new data in a phylogeny-aware manner.

We tested our new method in the extension of EnsemblCompara GeneTrees alignments with new sequences, focusing on plausible use cases such as update of an alignment repository after inclusion of new species (Supplementary Fig. S4) and analysis of RNA-seq data from a non-model organism (Supplementary Figs S5 and S6). The resulting alignments and the assembled sequence contigs are highly similar to the original ones but, as the original data may also contain errors, the analyses do not allow assessment of the true accuracy of the method. To further understand and illustrate the performance of the method we tested it with simulated data.

3.2 Comparison of methods for alignment extension

We compared methods for alignment extension using simulated data representing a mammalian gene family (Fig. 3a). The codon data, analyzed both as DNA and protein, were simulated under purifying selection [model M0 with ω=0.15 (Yang et al., 2000)] and many substitutions were synonymous on the protein level: despite the three-times greater number of sites for DNA, the sequence identity of DNA and protein sequences were similar, 84–90% between human and Primate and 70–80% between mouse and Rodent over the three levels of evolutionary divergence. Each reference alignment (RA), consisting of 67 sequences, was extended with 250 fragments of 30, 60 or 120 bases/amino acids (50 fragments per query sequence) or with five full-length sequences, and the accuracy of homology inference was measured.

We tested five alignment methods for both data types and two additional methods that only support DNA or protein data. The methods tested for both were PAGAN/guided, PAGAN/free (v.0.33), hmmalign (from the HMMER package, v.3.0; Eddy, 2011), MAFFT (v.6.860b; Katoh et al., 2002) and ClustalW (v.2.1; Larkin et al., 2007); for DNA we also used PaPaRa (RAxML v.7.2.6; Berger and Stamatakis, 2011) and for protein ClustalO (v.1.0.3; Sievers et al., 2011). All methods were provided with the true simulated RA and the QSs while PAGAN/free and PaPaRa were additionally given an inferred and PAGAN/guided the true RT. For PAGAN/guided, the species of origin (but not the correct paralogous copy) for the QSs were provided, giving two or three target nodes for the query sequences (Fig. 3a).

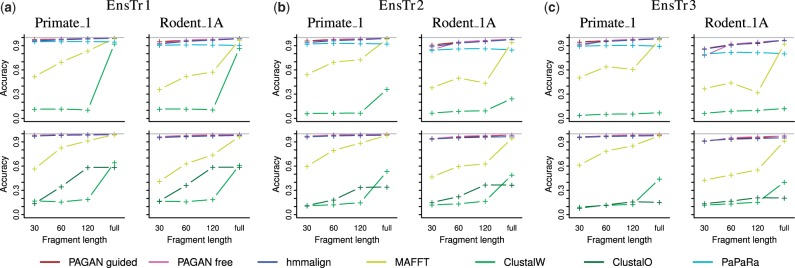
PAGAN and hmmalign were consistently the two most accurate methods for the extension of alignments with new DNA and protein sequences (Fig. 4). The two modes of running PAGAN, the ‘guided’ approach with pre-defined locations to place the sequences and the ‘free’ approach using heuristic local alignment to find the best location, had slightly different performance on different datasets. PAGAN/guided did better on the alignment of very short fragments that contain little information to infer their correct placement. Despite the prior information, also the guided approach was affected by multiple target nodes and a proportion of shorter sequences were misplaced (Supplementary Fig. S7).

Fig. 4.

The accuracy of alignment of DNA (top row) and protein (bottom row) QSs against the corresponding reference alignment using different alignment methods. The x-axis indicates the length of the fragments aligned and the sub-panels show two of the five query species analyzed. Columns (a)–(c) correspond to trees with branch lengths multiplied by 1.5, 2.0 and 2.5, respectively. The accuracy is measured as the correctness of the site-wise homology inference with respect to the closest human/mouse reference sequence

PAGAN/free slightly outperformed the guided approach in the alignment of longer fragments (Supplementary Fig. S8) and it did this despite a high fraction of the new sequences being placed to incorrect nodes (Supplementary Fig. S7). An explanation of this considers the long branches around the query sequence in our simulation tree: it is often advantageous to use outgroup information to resolve the mutation events that have taken place in the descendants of the true target node and place the sequence at a deeper location. On the other hand, the placement algorithm visits the tip nodes first and, if no mutations have occurred in the descendants, the greedy approach places the sequences to nodes visited earlier: up to 7% of short fragments from Primate_1 are placed at the node visited very first (Supplementary Fig. S7).

The performance of other methods shows that classical global alignment methods, MAFFT, ClustalW and ClustalO, struggle in the alignment of short sequence fragments (Fig. 4). MAFFT performed relatively well with full length sequences whereas the accuracy of two Clustal variants was unacceptably low. In contrast to these, hmmalign aligned short fragments nearly as well as full length sequences and was consistently one of the best performing methods. Hmmalign's excellent results should be taken with a grain of salt, however, as our accuracy score is based on sites shared by the query and reference only. By ignoring sites inserted since the species split, this score is overly lenient with profile-based methods that leave many insertions unaligned.

The performance of PaPaRa, based on a variant of phylogeny-aware algorithm, was good in the alignment of closely related DNA sequences but as it does not produce real multiple alignments—it deletes sites in the query sequences that are inferred as insertions—the method is only meaningful for its original task, phylogenetic placement of sequences. On the other hand, results for PaPaRa are based on reconstructed full-length query sequences (see the Supplementary Material for details) and in phylogenetic placement analyses its error may be smaller than reported.

We repeated the PAGAN and hmmalign analyses of DNA fragment data after adding NGS-like errors. The added noise had only a small negative impact on their accuracy (Supplementary Fig. S9).

The run times and peak memory usage of different methods were compared on a workstation with 2.40 GHz Intel Xeon CPUs. Two of the methods, MAFFT and hmmalign, are exceptionally fast and perform an alignment in seconds (Table 1). In contrast, PAGAN/free and PaPaRa needed 3.3 and 4.7 min for the most time-consuming alignment. These are the first versions of each software, however: the authors of PaPaRa have reported forthcoming speed-ups for their method and we are also working to accelerate ours. Of the methods tested, ClustalO is the most memory hungry but even that can easily be used on a standard personal computer. The memory usage of PAGAN is dominated by the dynamic programming matrix and, due to a more complex data structure needed for the graph representation, the requirements are, for example, somewhat higher than that of MAFFT with a comparable alignment strategy.

Table 1.

Execution time and peak memory usage for the extension of EnsTr2 reference alignment with 250 sequence fragments

Method		DNA fragments		Protein fragments
		60 nt	120 nt	60 aa	120 aa
Time (s)	MAFFT	1.9	1.0	0.4	0.3
	hmmalign	2.2	4.4	1.9	4.6
	ClustalO	–	–	16.5	26.3
	ClustalW	75.8	143	27.0	48.7
	PAGAN/guided	73.6	137	26.2	46.0
	PAGAN/free	186	200	47.2	57.9
	PaPaRa	144	284	–	–
Memory (Mb)	MAFFT	103	103	103	103
	hmmalign	198	198	198	198
	ClustalO	–	–	569	518
	ClustalW	31	31	16	16
	PAGAN/guided	298	334	133	155
	PAGAN/free	356	413	153	175
		(+104 for placement)		(+104 for placement)
	PaPaRa	84	85	–	–

nt, nucleotide; aa, amino acids.

3.3 Extension of large alignments

Our graph alignment algorithm is not yet well-optimized for speed and the first version of PAGAN is mainly targeted at small and medium-sized alignment tasks. An obvious application for the method is in metagenomic studies, however, so we performed a preliminary analysis to see how the method scales to larger tasks.

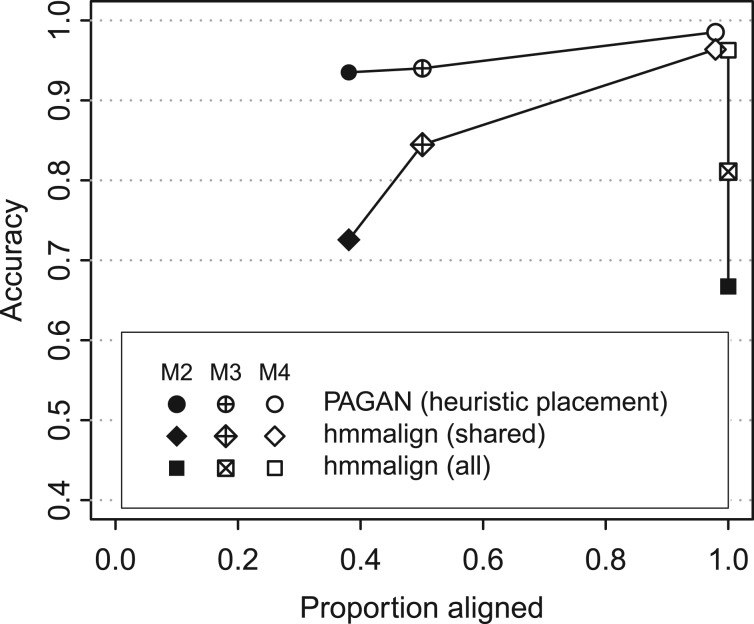
We analyzed the simulated test data of Mirarab et al. (2012) that consist of 500 reference sequences related by a phylogeny and 5000 query sequence fragments, a mixture of short and long ones, from related species. The alignment of 5000 query sequences to 999 possible target nodes (extant plus inferred ancestral sequences) with the graph alignment algorithm is too slow and we used an experimental acceleration for the placement step. These heuristics worked well for the easy case [M4 dataset from Mirarab et al. (2012)] and PAGAN aligned 97.9% of query sequences with an accuracy of 98.5 (Fig. 5). In the alignment of moderate (M3) and hard (M2) problems, the heuristics were less successful: the accuracy was high, 94.0 and 93.5%, respectively, but only 50 and 38% of query sequences were actually included in the resulting alignments.

Fig. 5.

The accuracy of PAGAN and hmmalign in the extension of reference alignments of 500 DNA sequences with 5000 query fragments. For the easy set (M4 dataset from Mirarab et al., 2012; open symbols), both methods align >96 sites correctly; for the moderate (M3; crossed) and hard (M2; solid) sets, the accuracy of PAGAN is high (circles) but the fast heuristics fails to place half of the queries. Hmmalign aligns all the queries but its accuracy for M2 and M3 is low (squares). For the fragments aligned by both methods, the alignments by hmmalign are less accurate (diamonds)

The method of Mirarab et al. (2012) divides the alignment extension problem into smaller sub-problems and performs alignments within each subgroup using hmmalign. That does not produce full multiple alignments of all sequences and the results cannot be meaningfully compared with those produced with PAGAN. We therefore used hmmalign only and aligned the query fragments to a model constructed from the full reference alignment. Hmmalign does not discard any query sequences but for the more challenging datasets, the alignments it produces were clearly less accurate. Importantly, the lower accuracy of hmmalign compared with PAGAN is not only explained by the latter discarding the difficult queries: also for the subset of sequences aligned by both methods the alignments from hmmalign were less accurate (Fig. 5).

Hmmalign is fast and, on our test system, it builds a model for a M4 dataset and aligns the queries to that in 12.5 s with the peak memory usage of 84 Mb. PAGAN reconstructs graphs for all internal and extant nodes (totalling 10 999 for a full alignment) and needs 627 s and 2070 Mb for the analysis of the same data.

3.4 Impact of reference alignment

As shown by the previous analysis, PAGAN has the potential to scale up to large alignment extension tasks while its approach for modelling of insertions/deletions and uncertainty is especially well-suited for analyses of short and noisy NGS data. Hmmalign has been used for the extension of reference alignments with new sequences in metagenomic analyses (Matsen et al., 2010; Stark et al., 2010) and recently Mirarab et al. (2012) developed an approach that applies hmmalign on subsets of the reference alignment. The latter mainly focused on computation time, however, and did not systematically study the strategies for choosing the optimal RA for alignment extension analyses, nor its effect on homology inference.

To understand the factors affecting alignment extension with phylogenetic and profile-based methods, we tested PAGAN and hmmalign with idealized data mimicking an RNA-seq study (see Section 2 Fig. 3b, c). Our set-up lets us assess the effects of (i) phylogenetic position of the query species; (ii) the number of closely related reference species; (iii) the evolutionary divergence of the reference; and (iv) the inclusion of more-distantly related reference species. To assess the impact of sequence divergence on the ancestor reconstruction, we constrained the placement of the QS with the guide phylogeny. Incorrect topologies, or correct topologies but with incorrect root position, could cause alignment/placement errors. A full investigation of this, beyond typical use cases with known reference trees or inferred trees as studied here, is beyond the scope of this article but will be considered in future work.

Although the magnitude of difference and the relative performance of alternative approaches varies, the phylogenetic approach of PAGAN with full data (ingroup ‘large’) consistently produces the most accurate alignments (Table 2). With ‘close’ sets, the removal of sequences does not affect PAGAN's reconstruction of the target ancestor and its performance on full and reduced RA (ingroup ‘large’ versus ‘small’) is nearly identical. When the query sequence branches out deeper in the tree (‘intermediate’ and ‘distant’), PAGAN shows the benefit from the phylogenetic information provided by denser sequence sampling: the alignments on the full RA are more accurate than those on the reduced ones, the difference growing with the increasing evolutionary divergence.

Table 2.

The accuracy of extending reference alignments with new sequences

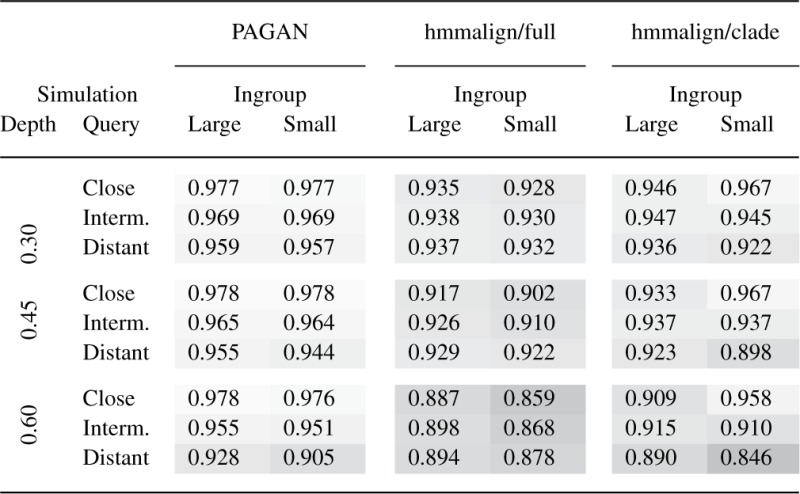Similarly, it is understandable that hmmalign's best performance is in the alignment of reads from a closely related query sequence against a profile based only on the two sequences from the sister sub-tree (‘clade’, ‘small’); the information from more distant subgroups only brings noise and the noise-to-signal ratio is at its worst when the central subgroup is represented by two sequences only (‘full’, ‘small’). The position of the query sequence is crucial, however, and the approach giving the best result for the closely related query sequence gives clearly the least correct alignments when the query sequence is deep and has a long history of its own. Although the profiles built from the full RA (‘full’, ‘large’) give marginally better results in the alignment of the most difficult cases (Table 2, bottom row), the inclusion of large numbers of sequences in the profile is generally not the best policy. Crucially, this conflicts with the requirements of real-life studies such as phylogenetic placement where the RA should be maximally representative.

As expected, decreasing similarity between the query and the RA makes the alignment more difficult (Table 2, depths 0.45 and 0.60). Although both methods lose accuracy, PAGAN is more consistent in its performance and the improvement over hmmalign grows with evolutionary divergence. As a demonstration of its efficient use of phylogenetic information, the relative improvement of PAGAN with the full RA over any other approach is greatest on the analyses of most diverged datasets (Table 2, bottom row). The correct use of phylogenetic information is important for real-life analyses: de novo alignment of distantly related sequences is error-prone and good aligners produce much better reference alignments if long evolutionary branches are cut shorter by additional sequences.

To understand the effects of alignment error on the different approaches, we re-aligned the reference sequences using MAFFT and PAGAN. The relative performance of the methods does not change with noisier RA (Supplementary Table S1). With PAGAN, the extension of densely sampled alignments (ingroup ‘large’) is more accurate than that of sparsely sampled ones (ingroup ‘small’), the effect further growing with the evolutionary divergence of the QS and the reference sequences. The results for hmmalign using the different sized re-aligned RA mirror those from the true simulated RA. Regardless of the placement method used, the RAs generated with PAGAN give a better starting point for the alignment of NGS reads than those generated with MAFFT.

4 DISCUSSION

We have generalized the concepts of our phylogeny-aware alignment algorithm and developed a method for phylogenetic alignment of partial-order sequence graphs. In this article, we focus on one specific application for the new method that has no satisfactory previous solution, the phylogeny-aware extension of existing alignments with new data.

Re-computation of alignments for largely the same sets of sequences is wasteful and may occasionally introduce errors that require manual verification and corrections. Extension of existing alignments with new sequences avoids these problems and guarantees that the relative alignment of reference sequences is not changed. The new sequences should also be accurately aligned, however, and we strongly believe that this is best achieved by aligning them in their phylogenetic context, against the targets resembling them most. This is true for all sequences but its importance is even more pronounced in the alignment of short sequence fragments containing little information.

We performed comprehensive simulation studies to compare the performance of our new method, PAGAN, to that of alternative methods for alignment extension and to test how the different approaches utilize the information available in related sequences. We focused on the accuracy of inferred evolutionary homology with the aim of using the resulting alignments for evolutionary studies. Our analyses show that PAGAN's phylogenetic approach clearly outperforms most alternative methods, the improvement being especially striking in the alignment of short sequence fragments. We were impressed by the good performance of hmmalign but also noticed that its performance is highly dependent on the reference alignment used for the construction of the profile HMM.

With a carefully chosen reference alignment, hmmalign's accuracy was in some cases comparable to that of PAGAN. In real-life analyses, one cannot typically maximize both the sensitivity of the profile HMM and the breath of sequences included, and the widely used practice of including all the diversity available heavily penalizes hmmalign's performance. In contrast, PAGAN is a truly phylogenetic method and, while it efficiently uses the information from closely related sequences, it is not affected by the inclusion of more distantly related ones in the reference set.

We tested PAGAN in the extension of large alignments and found the initial results very promising. We believe that improvements in the assignment of queries to target nodes and speed-ups in the algorithm will make PAGAN also a competitive method for large-scale metagenomic analyses. Unlike alternative methods for the task, PAGAN aligns also insertion sites and includes full-length sequences in the resulting multiple alignment. The latter may not be crucial in phylogenetic placement of query fragments relative to the reference sequences but it will provide additional information to resolve the relations between the newly added sequences and will allow connecting related fragments to longer contigs.

Alignment extension and phylogenetic placement has interesting applications in the analyses of increasingly abundant sequencing data produced by NGS technologies and we have implemented extensive support for such data. Falling costs per base will allow the sequencing of full genomes for many new non-model species and transcriptomes for even more species. We believe that there remains a need for comparative methods like ours, e.g. in the integration of transcriptome datasets into large reference alignments of closely related species, including the precise differentiation of close paralogues. We also envision extending our approach to the alignment of graphs produced by the de novo assemblers and using phylogenetic information to disambiguate these graphs into the correct separate sequences.

In addition to their alignment, we want to emphasize the advantages of graphs in the representation of the input sequence data. Graphs have direct applications in the modelling of NGS data from specific sequencing platforms but they can also be used to represent other features, such as repeat structures, that affect sequences' evolution and thus have an impact on their alignment. The evolutionary process varies across sequence sites and many features related to this may one day be inferred by sophisticated alignment methods from the input sequences along with their alignment. It seems easier, however, to start with separate tools for the annotation of sequences, such as detection of low-complexity repeat sequences, and pass this information to a generic alignment method. We believe that partial-order graphs are ideal for carrying that information.