OnlineCall: fast online parameter estimation and base calling for illumina's next-generation sequencing

Abstract

Motivation: Next-generation DNA sequencing platforms are becoming increasingly cost-effective and capable of providing enormous number of reads in a relatively short time. However, their accuracy and read lengths are still lagging behind those of conventional Sanger sequencing method. Performance of next-generation sequencing platforms is fundamentally limited by various imperfections in the sequencing-by-synthesis and signal acquisition processes. This drives the search for accurate, scalable and computationally tractable base calling algorithms capable of accounting for such imperfections.

Results: Relying on a statistical model of the sequencing-by-synthesis process and signal acquisition procedure, we develop a computationally efficient base calling method for Illumina's sequencing technology (specifically, Genome Analyzer II platform). Parameters of the model are estimated via a fast unsupervised online learning scheme, which uses the generalized expectation–maximization algorithm and requires only 3 s of running time per tile (on an Intel i7 machine @3.07GHz, single core)—a three orders of magnitude speed-up over existing parametric model-based methods. To minimize the latency between the end of the sequencing run and the generation of the base calling reports, we develop a fast online scalable decoding algorithm, which requires only 9 s/tile and achieves significantly lower error rates than the Illumina's base calling software. Moreover, it is demonstrated that the proposed online parameter estimation scheme efficiently computes tile-dependent parameters, which can thereafter be provided to the base calling algorithm, resulting in significant improvements over previously developed base calling methods for the considered platform in terms of performance, time/complexity and latency.

Availability: A C code implementation of our algorithm can be downloaded from http://www.cerc.utexas.edu/OnlineCall/

Contact: hvikalo@ece.utexas.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Recent development of next-generation sequencing platforms has enabled cost-effective whole-genome sequencing and resequencing, reinvigorated transcriptomics, and has provided an essential tool for research in functional and comparative genomics, epigenetics and metagenomics (Mardis, 2008). However, before the promised benefits of widespread applications of DNA sequencing come to fruition, sequencing technology requires further improvements. Although next-generation sequencing systems are cost-effective and capable of providing very high number of reads in a relatively short time, their accuracy and read lengths are still lagging behind those of conventional Sanger sequencing method. In this article, we focus on Illumina's sequencing platform (Bentley et al., 2008) and, relying on a mathematical model of sequencing-by-synthesis, propose a fast online algorithm for unsupervised learning of the parameters of the model and a computationally efficient technique for sequential base calling. The model captures the different sources of uncertainty in the sequencing process and signal acquisition procedure. Illumina's current base calling software, Bustard, is very fast but its performance leaves a lot of room for improvement. Consequently, several novel base calling methods for Illumina's sequencing platform have been proposed in recent years (Lederberger and Dessimoz, 2011). Elrich et al. (2008) developed an approach referred to as Alta-cyclic which relies on a supervised training stage (using a rich DNA library with a known reference genome on a control lane) to find parameters of a model, and uses support vector machines for optimal basecalling. Rougemont et al. (2008) proposed model-based clustering and information theoretic ideas for basecalling. The developed method, referred to as Rolexa, uses a Gaussian mixture model for classification, and uses filters which cut off bases/reads with quality scores that are below a certain threshold. Kircher et al. (2009) proposed Ibis which uses a machine learning scheme similar to Alta-cyclic, and relies on base-specific parameters and multiclass support vector machines with polynomial kernels for acceleration of the algorithm. Recently, Kao et al. (2009) proposed a Bayesian inference method for base calling. In particular, this approach relies on a batch expectation–maximization algorithm to infer parameters of a detailed mathematical model of sequencing-by-synthesis on Illumina's platform, and applies the Markov Chain Monte Carlo technique to perform base calling. The approach, named BayesCall, was shown to significantly improve base calling error rates over state-of-the-art techniques. However, the approach turned out to be computationally demanding and therefore infeasible for basecalling millions of reads obtained from Illumina's sequencing platforms. The follow-up article by the same authors presents naiveBayesCall (Kao and Song, 2010), a simplified heuristic, which runs significantly faster than BayesCall at the cost of small-to-moderate deterioration of the error rate performance.

The basecalling method we propose, OnlineCall, relies on a mathematical model that is a simplified version of the model used by BayesCall and naiveBayesCall. Parameters of the proposed model can be inferred in a computationally efficient manner. As a result, the parameter estimation step of OnlineCall is more than 3500 times faster than the parameter estimation step of BayesCall and naiveBayesCall. Moreover, the adopted efficient estimation procedure allows us to treat parameters in the model as tile-dependent, and makes tile-by-tile inference of parameters computationally affordable. The base calling step of OnlineCall is orders of magnitude faster compared to some other publicly available schemes (50 times faster than naiveBayesCall and approximately 750 times faster than Bayescall). Both parameter estimation and basecalling steps are implemented as online (as opposed to batch) algorithms. Performance of the proposed techniques is tested on a full lane of DNA sequencing reads of bacteriophage phiX 174 acquired by Illumina's Genome Analyzer II. It is demonstrated on this data that allowing tile-dependent model parameters translates to improved error rates as compared to other practically feasible basecalling methods—a significant improvement over Bustard and a moderate improvement over naiveBayesCall.

2 METHOD

2.1 Mathematical model

The mathematical model described in this subsection is based on presentation in (Kao et al., 2009).

Phasing, pre-phasing and the generated signal: in the Illumina's reversible terminator chemistry, dNTPs with removable protecting group are added in each test cycle. Ideally, only the first unpaired base of each template should bind with the dNTP that is its Watson–Crick complement. However, incorporation of dNTPs into complementary strands is not perfect and phasing and pre-phasing occur. The former refers to the event where no base is incorporated while the latter denotes the event where the complementary strand is extended by more than one base. Phasing and pre-phasing are significant sources of erroneous basecalls, especially towards the ends of the reads as the phasing and pre-phasing effects accumulate.

We adopt the representation of a template sequence of length L by a 4×L matrix S, where the ith column of S, S_i, has a single non-zero entry which is equal to 1 and which indicates the type of the base in the ith position of the template sequence. We use the convention where the first component of S_i corresponds to A, the second to C, the third to G and the fourth to T. Phasing and pre-phasing are treated probabilistically, and described as Bernoulli random variables. Let p_ph denote the probability that no base is incorporated into a complementary strand (i.e. the probability of phasing), and let p_pr denote the probability of incorporating more than one base (i.e. the probability of pre-phasing). For computational tractability, it is assumed that at most two bases can be incorporated in a single test cycle. Define an (L+1)×(L+1) transition matrix P with entries P_i,j (0<i,j<L) given by

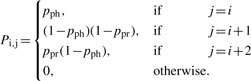The signal generated over N cycles of the synthesis process affected by phasing and pre-phasing can be expressed as Z=SE^T, where E=(E_i,j) is an N×L matrix with entries E_i,j=[Pⁱ]_0,j, the probability that a template terminates in state j after i cycles. We denote the ith column of the 4×N matrix Z by Z_i.

Cross-talk: during the data acquisition step, the clusters are exposed to lasers with two different emission wavelengths. The excited fluorescent labels attached to incorporated nucleotides emit light, and the image containing information about the type of each incorporated nucleotide is acquired and processed. However, the emission spectra of the fluorescent labels overlap, resulting in significant cross-talk. The cross-talk is quantified by a 4×4 matrix K having off-diagonal elements which are reflective of the level of the emission spectrum overlap between signals generated in the same cycle.

Signal decay/droop: signal decay observed in sequencing-by-synthesis platforms is not necessarily smooth, that is, it may exhibit variations that are conveniently represented as being probabilistic. In particular, the decay can be modeled by a cycle-dependent scalar parameter λ_i which evolves over time according to

(1)

where d denotes a droop factor presumed to be common to all cycles and reads, σ is the standard deviation of a scalar Gaussian random variable and ∣ denotes conditioning. Consequently, the signal generated in the ith cycle is given by X_i=λ_i(SE^T)_i.

Signal leakage: acquired raw data shows considerable evidence of signal leakage from one cycle into the next. Let Y_i denote the four-dimensional vector comprising signal intensities acquired in each of the four channels during the ith test cycle. Collect the vectors Y₁, Y₂,…, Y_N into a 4×N matrix Y, where N denotes the number of cycles. It is assumed that the signal leakage from cycle i−1 to cycle i is a constant fraction α, 0<α<1, of the signal acquired in cycle i−1, Y_i−1.

Noise: measurement uncertainties are assumed to primarily originate from fluctuations in K and are modeled by multiplicative noise of the form ∑_s=1^s=4X_i(s)ν_s, where ν_s are 4×1 zero mean independent identically distributed Gaussian random vectors each having covariance Σ. Thus, the covariance Σ_i in the ith cycle is

Full model: the full model which incorporates all of the listed effects is of the form

(2)

Time-dependent windowing: bayesCall (Kao et al., 2009) relies on time-dependent parameters to significantly improve the performance of basecalling. To this end, cycles are separated into ‘windows’, the length of which W is sufficiently small to capture local variations in parameters. Therefore, the set of parameters associated with the ith window, 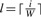, is in general different from those associated with other windows.

2.2 Revised model

Analysis of experimental data reveals that the coefficient of variation (ratio of the standard deviation to the mean) of λ_i in equation (1) is small, typically below 0.1 for cycles i≥20, and below 0.06 in the latter cycles which are more prone to erroneous basecalls than the early ones. Therefore, approximating decay by its mean may provide sufficient information about this phenomenon to a basecalling scheme. Nevertheless, to remain capable of capturing small variations in λ_i, we allow the droop factor to vary from one cycle to another and model the decay as 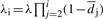, where λ denotes the transduction coefficient which maps synthesis events to the generated signal intensity and 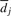denote cycle-dependent droop factors.

On another note, the intricate way in which p_ph and p_pr affect generated signal is a major reason for needing a computationally intensive parameter estimation step. Note that the signal generated in the ith cycle X_i can be expressed as

where 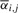and 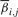are evaluated from p_ph, p_pr and 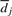, and where we assume that no more than L cycles leading and L cycles following the ith one affects the signal generated in the ith cycle. Assuming that the values of p_ph, p_pr and 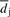do not vary much from the (i−L)^th to the (i+L)th cycle, we approximate X_i by

The above expression describes dependence (induced by phasing effects) of the signal generated in the ith cycle on signals generated in cycles preceding and following the ith one. If there were no measurement noise, the same relation would hold for Y_i, Y_i−j and Y_i+j – pre-multiplication of both sides of (2.2) with the cross-talk matrix K would result in Y_i being approximately equal to

However, measurements are perturbed by noise and hence we use the above expression to approximate the mean value of Y_i, while the associated uncertainty is modeled by a Gaussian noise of appropriate variance (as discussed in section 2.1). Therefore, the overall model is given by

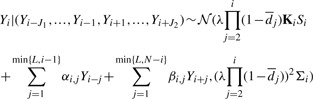(3)

where J₁=min{i−1,L}, J₂=min{L,N−i}, i=1,….N. Note that within a given window l, all parameter values are constant, for example for W=6 and l=1, K₁=K₂…=K₆. Similar expressions hold for the other parameters.

To summarize, we introduce the following modifications of the model equation (2):

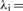
1. Expression for the signal decay (1) is replaced by the relation 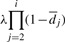and

2. Effects of phasing and prephasing are modeled implicitly by adding a fraction α_i,j and β_i,j of the jth lagging and leading cycle signals to the ith cycle signal. It is assumed that no more than L such leading and lagging bases contribute to the signal.

Note that the form of cross-talk and noise remain unchanged. It will be clarified in later sections why this revised model offers computational advantages over the original one.

2.3 Final model

Fitting the data to the model reveals that only the base immediately following or preceding the tested base makes a significant contribution to the signal generated by the test. This observation is consistent with the results reported in Elrich et al. (2008); Kao et al. (2009); Kircher et al. (2009). Therefore, we set L=1 and retain only α_i,1 and β_i,1 in our model. Then, the final model is of the form

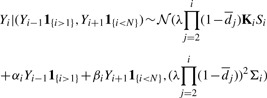(4)

where 1 is an indicator function equal to 1 if the tested condition is true and 0 otherwise, α_i,1 and β_i,1 are renamed as α_i and β_i and i=1,…,N. Note that we may, in principle, use L>1. The additional computational costs incurred by doing so are relatively small. There is, however, a price to be paid in terms of latency, that is, in the number of cycles that must pass before parameter estimation/basecalling can start.

2.4 Unsupervised online parameter estimation

An unsupervised learning scheme allows for a more economical use of resources and is, therefore, preferred over a supervised scheme. The latter suffers from the disadvantage that it requires training data, for example, in the form of known sequences analyzed in a dedicated control lane. Our unsupervised learning scheme has an additional, potentially major advantage of relying on an online, as opposed to a batch, algorithm. The online algorithm starts parameter estimation after only a few cycles of the sequencing run; hence, the latency between the start of the sequencing run and the completion of basecalling may be significantly reduced. In each cycle of a sequencing run, images of all lanes are acquired. Our online learning scheme, in combination with an adequately fast image processing algorithm capable of providing raw data in a timely manner, can perform calling of bases only a few cycles after their incorporation.

Scheme for the online parameter estimation: to facilitate unsupervised estimation of the parameters in equation (4), we rely on an online EM algorithm (Mclachlan and Krishnan, 1997) and use a training set of R=250 reads randomly selected across a tile. The EM algorithm iteratively solves the following optimization problem

(5)

where the scalar coefficient λ and the template sequence matrix S are latent variables, α, β, K, Σ and 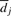(henceforth collectively referred to as Θ) are the parameters to be optimized over, and 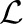denotes the log-likelihood function. The expectation is taken over the latent variables given the current estimate of Θ (i.e. given Θ_n−1).

As previously stated, we divide the sequencing run into windows and estimate parameters sequentially (i.e. window-by-window). Parameters for the lth window are initialized using the values of the parameters estimated in the (l−1)st window. To prevent over-fitting, optimization equation (5) is performed over two windows, l and l+1 and the resulting Θ is used as the set of parameters for window l. We empirically found that the choice of the window length W = 6 leads to a very good performance in terms of basecalling error rates, while requiring practically feasible CPU run times.

Following model equation (4), for the lth window, we need to maximize expectation of the log-likelihood function

(6)

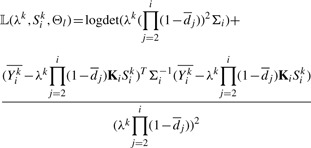(7)

where 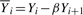for i=1, 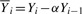for i=N and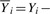 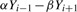for i>1, i<N. The superscript k is an index of a read in the training set and ranges from 1 to R.

E-step for the first window: given the initial parameter estimates, the E-step entails finding the expectation of the log-likelihood function in equation (6) over continuous and discrete variables λ and S. Closed form expressions are not available, while the numerical Monte-Carlo methods are computationally very intensive. As an alternative, we use the following method. In the first window, we call S using Bustard's approach since, in general, it performs well in the first few cycles. As a result, the E-step can be reduced to find the expectation of the log-likelihood function over the continuous-valued variable λ^k for k=1, 2,…,R. For this, we use an importance sampling scheme.

Finding 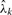: using the parameters Θ and S, for each read k we can find 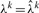by maximizing the log-likelihood function equation (7). The part of the objective function in equation (7) which is dependent on λ^k is given by

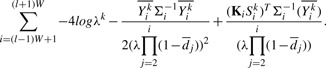(8)

Differentiating with respect to λ^k, we arrive at the following expression,

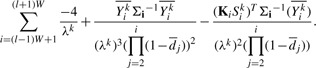(9)

Setting this to 0, we get an equation quadratic in λ_k. Since λ^k > 0, the unique solution 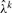is obtained by solving equation (9). The fact that the maximum of the log-likelihood function over λ^k can easily be found is used in various parts of the remaining sections.

Importance Sampler: to evaluate the log-likelihood function equation (7), we use an importance sampling scheme. It is empirically observed that the distribution of λ^k has a relatively small coefficient of variation, that is, its distribution is heavily concentrated around 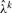. We found that a normal distribution with mean 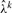and standard deviation 0.1 has a heavier tail than the empirical distribution of λ^k. We use the aforementioned normal distribution as a proposal density, sampling points from it and calculating their weights. In particular, N_IS=500 samples are generated from the proposal density . Following equation (7), our log-likelihood function is computed numerically according to

(10)

where λ_j^k is the generated samples and w_j,k denote their corresponding normalized weights.

M-step for first window: the objective function in equation (7) is not convex over the parameter vector Θ. However, the function is separately differentiable and convex over each of the parameters in Θ. To maximize it, we use a cyclic co-ordinate descent scheme which rotates among the components of Θ. Such a method is guaranteed to converge to a local minimum as long as there is a unique minimum over each of the coordinates. Differentiating equation (10) with respect to each of the variables, we find that this condition is indeed satisfied. We omit further details of this step for the sake of brevity of the presentation.

Stopping criteria: when the ratio of the change in the value of the objective function to the value of the objective function in a previous iteration is less than ϵ=0.003, the co-ordinate descent is terminated. A similar stopping criterion is used for the EM algorithm as well.

A brief comment on the convergence of the EM algorithm for parameter estimation in the first window is in place. It can be observed that the empirical log-likelihood may fluctuate (especially, when the algorithm is nearing termination), and hence the convergence of this stochastic EM is not monotonic. However, it can be shown that for such a stochastic EM algorithm, convergence is guaranteed provided N_IS is increased with every EM step (Celeux and Diebolt, 1992). In particular, increasing N_IS ensures that the difference between empirical expectation and true expectation of the log-likelihood function remains small. In our implementation, N_IS is increased by 30% in every iteration.

E-step for subsequent windows: the simple parameter estimation scheme which we use in the first time window performs well primarily because phasing effects are tolerable in the early cycles of the synthesis process. As the cycle number grows, cumulative effects of phasing, signal decay and measurement noise cause deterioration of performance and demand a more sophisticated parameter estimation and basecalling procedure. Since the simple basecalling procedure used to call bases in the first window is no longer adequate, we must resort to numerical evaluation of the expected value of the log-likelihood function in equation (6). However, this is computationally demanding because the expectation is over both the continuous variable λ^k and the discrete variables S_i^k. To make the inference practically feasible, we approximate expression equation (6) by fixing the value of the parameter λ^k to the value 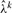obtained by the EM algorithm in the previous time window. Consequently, expectation of the log-likelihood function is evaluated over the discrete variables S_i^k only, and hence we replace equation (6) by

(11)

The probabilities ℙ(S_i,A^k|Y),ℙ(S_i,C^k|Y), ℙ(S_i,G^k|Y) and ℙ(S_i,T^k|Y) can be obtained from equation (4).

M-step for subsequent windows: the M-step for subsequent windows is very similar to the M-step for the first window, with the only difference stemming from the fact that the particle weights are now the probabilities of each symbol. The remaining steps are exactly the same as those described earlier. Note that because the E-step is evaluated in a closed form equation (11), the EM algorithm converges monotonically.

Updating 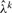: after each step of the EM algorithm used for estimating parameters in a given window, MAP calls for S_i^k are made. The calls and the most recent parameters are then used to update 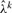by solving equation (9). The updated value of 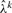is then used by the EM algorithm in the next window.

2.5 Base calling

Base calling requires solving the following maximization problem

for each read. On the basis of equation (4), this is equivalent to maximizing the log-likelihood function

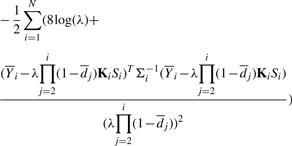(12)

Base calling follows in the lines of parameter estimation. Initialization is done by assuming that the bases in the first two windows can be called correctly using the simple scheme used by Bustard. Given S_i for the first two windows, the initial 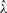is found by solving quadratic equation (9). For the next window, each of the four possibilities for S_i are tested to obtain the corresponding log-likelihoods. The choice of S_i that leads to the maximum value of the log-likelihood function is declared as the call. The associated likelihood is declared as the quality score for the call. Once all bases in a window have been called, 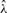is updated by solving equation (9) anew. Such updates allow for both local and global variations in λ to be accounted for, and ensure that noisy cycle intensities do not have a prolonged effect on future calls. The described basecalling procedure is repeated until all the bases in all the windows are called.

2.6 Quality scores

Although error rates provide a ground for benchmarking the performance of various base calling algorithms, quality scores enable assessment of the confidence of a base calling procedure. To assess the ‘goodness’ of quality scores (and thus measure the performance of an algorithm), we consider their discrimination ability (Ewing and Green, 1998; Smith et al., 2008). The discrimination ability for a given error rate is obtained by sorting all bases according to their quality scores in descending order and finding the number of bases called before the error rate exceeds the predefined threshold. In our base calling scheme, the quality scores assigned is the likelihood for the called base obtained from equation (12).

3 RESULTS

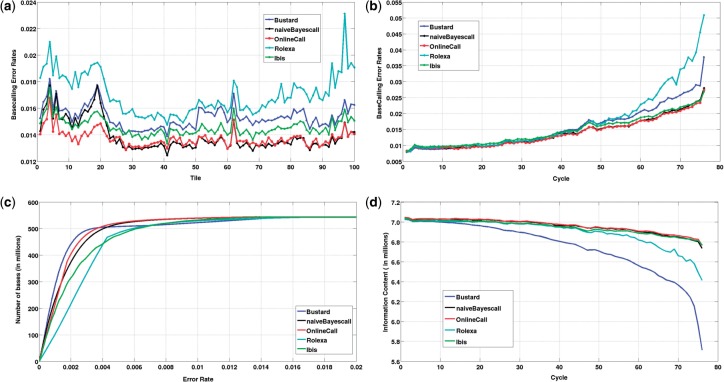
The Illumina flowcell has 8 lanes, each lane having 100 tiles. Performance of OnlineCall is verified on a full lane data obtained by sequencing phiX174(EMBL/NCBI accession number J02482) bacteriophage using Illumina's Genome Analyzer II, generating reads of length 76. After basecalling the lane by Bustard, naiveBayesCall, Rolexa, Ibis and OnlineCall, the calls were mapped onto the known reference sequence comprising 5386 bases. The optimal alignment which relies on computing the Hamming distance is found ( the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different). Any read that maps with <30% of erroneously called bases is retained while reads having more erroneously called bases are removed to ensure that there is no ambiguity in the alignment. This results in approximately 7.15 million reads and 544 million bases which are used to compare the performance of the considered basecalling schemes. Average error rates over the lane comprising 100 tiles are compared in Table 1.

Table 1.

A comparison of error rates, information content and running times (per lane) for different base callers (note that Bustard's running time is underestimated since it does not account for the parameter estimation step)

Decoding strategy	Error rate	IC(in mil)	Running times (min)
Rolexa	0.0171	514.3	720
Bustard	0.0154	512.7	40
Ibis	0.0147	526.9	480
NaiveBayescall	0.0139	528.9	1500
OnlineCall	0.0137	529.3	30

Figure 1a compares the per-tile error rates of five basecalling schemes: Bustard, naiveBayesCall, Rolexa, Ibis and OnlineCall. For the first 22 tiles, OnlineCall's tile-dependent parameter estimation strategy enables significant reduction of error rates as compared to other schemes. For the remaining tiles, performance of OnlineCall is very close to that of naiveBayesCall. Figure 1b shows the dependence of basecalling error rates on cycle number. OnlineCall and naiveBayesCall have similar performance, and are increasingly better than Bustard for cycles beyond the 30th one. Figure 1c is a plot of the discrimination ability of the five basecalling schemes. Up to an error rate 0.0038, Bustard's quality scores are the best, after which OnlineCall has the most reliable quality scores.

Fig. 1.

Comparison of the five basecalling strategies under different performance metrics.

4 DISCUSSION

4.1 Implementation and running times

We implemented our codes on an Intel i7 machine @3.07GHz using only a single core. With our codes written in C, it takes ∼20 s to read in an intensity file, perform the parameter estimation step on 250 reads, call bases for the whole tile and write it in fastq format. Processing an entire lane requires about 30 min. naiveBayesCall, on the other hand, takes 19 h just for a single parameter estimation step where as its basecalling step takes 6 h. Thus, our implementation is 50 times faster than naiveBayesCall. Note that the run times of naiveBayesCall are reported for an implementation on a processor with eight cores; we expect that a parallel implementation of our algorithm would reduce the total running time by roughly eight times. In addition, if the acquired images could be processed in real-time, our proposed scheme, being sequential in nature, would be able to almost instantaneously provide very high-quality base calls to the end user. A comparison of the running times ( for processing an entire lane) between our OnlineCall and the other basecallers is shown in Table 1.

4.2 Information content of base calling

A major drawback of the discrimination ability metric is the fact that it does not take into account absolute values of quality scores—any scaling of the quality scores leads to the same value of discrimination ability. Moreover, it is not clear how to use this measure to compare different base callers which may be calling different numbers of reads/bases. For a fair comparison between different base calling strategies, we suggest a new metric referred to as the information content of a tile/lane, defined as

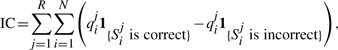where q_i^j is the quality score associated with the ith call of the jth read, S_i^j is the corresponding call, N is the number of cycles and R is the number of reads in the tile/lane. A justification for such a metric is the following: For a correct call, it is desirable that the quality score to be as large as possible, and hence we reward the correct call by the amount of its quality score. On the other hand, calling a base incorrectly is penalized with its corresponding quality score. (Not calling a base is not penalized.) Since base callers are invariably followed by downstream applications like de novo assemblers, which can exploit redundancy in reads to correct errors, the base callers purpose should be to provide as much reliable information as possible to the subsequent stages. Rejecting somewhat subpar reads will undoubtedly improve error rates, but will also feed those downstream applications with less information and therefore in the overall scheme of things, may lead to poor performance in the particular applications.

Table 1 shows the information content measure of performance of the different schemes applied to base calling a lane comprising 100 tiles. We see that OnlineCall and naiveBayesCall have comparable performance with ∼3.25% more information being extracted compared to Bustard. Figure 1d plots the information content as a function of cycle number. These figures imply that Bustard aggressively makes low quality score calls in later cycles, somewhat compensating (from the information content point of view) for the poorer error rates it achieves. The information content metric may reflect performance better than quality scores and error rates, especially in a situation where different base calling strategies result in different number of calls.

4.3 Impact of improved base calling on DeNovo assembly

We investigated the impact of improved base calling on de novo assembly. For this study, we relied on VELVET (Zerbino and Birney, 2008), version 1.2.03. A tile was randomly chosen from the whole lane and reads at coverage of 5X, 10X, 15X and 20X were randomly selected for the assembly. A k-mer size of 31 was used for the analysis. The experiment was repeated 100 times and average values for the maximum contig length and N50 are reported in Table 2.

Table 2.

Results of de novo assembly using different base calling strategies

Coverage	Bustard		NaivebayesCall		OnlineCall
	Max	N50	Max	N50	Max	N50
5X	635	276	580	268	613	285
10X	1502	985	1644	1061	1656	1096
15X	2936	2500	3513	3241	3524	3328
20X	3821	3677	4178	4097	4496	4429

N50 is a statistic commonly used to measure the goodness of an assembler. For this, all contigs are sorted in descending order according to their lengths, the minimum set of contigs whose lengths total 50% of the total length of all contigs is determined, and N50 is declared as the length of the shortest contig in this set. As can be seen, OnlineCall and naiveBayesCall outperform Bustard on all the different metrics at all coverages except for the 5X coverage maximum contig length. Moreover, OnlineCall performs better than naiveBayesCall. This clearly demonstrates the superiority of our algorithm compared to the competing schemes.

CONCLUSION

In this article, we proposed a novel model and developed a fast online parameter estimation and base calling scheme for Illumina's next-generation sequencers. The error rates and discrimination ability of the proposed method are better than those of the existing competing schemes. At the same time, the proposed method is three orders of magnitude faster than some of the recently proposed competing schemes, and is practically feasible. We demonstrated positive impact of the developed method on downstream applications (in particular, extended lengths of the contigs in sequence assembly). Improved base calling will enable performance advancements of genome and transcriptome assembly as well as genotype/SNP calling. As a part of our future work, we will investigate the impact of read-by-read parameter estimation and base calling on the overall platform performance. Studies of intertile and intratile parameter variations presented in the current article are a useful starting point. We also intend to investigate the information content metric in more details and explore fundamental relationships between quality scores, error rates and read/base rejection.