Identifying differentially expressed transcripts from RNA-seq data with biological variation

Abstract

Motivation: High-throughput sequencing enables expression analysis at the level of individual transcripts. The analysis of transcriptome expression levels and differential expression (DE) estimation requires a probabilistic approach to properly account for ambiguity caused by shared exons and finite read sampling as well as the intrinsic biological variance of transcript expression.

Results: We present Bayesian inference of transcripts from sequencing data (BitSeq), a Bayesian approach for estimation of transcript expression level from RNA-seq experiments. Inferred relative expression is represented by Markov chain Monte Carlo samples from the posterior probability distribution of a generative model of the read data. We propose a novel method for DE analysis across replicates which propagates uncertainty from the sample-level model while modelling biological variance using an expression-level-dependent prior. We demonstrate the advantages of our method using simulated data as well as an RNA-seq dataset with technical and biological replication for both studied conditions.

Availability: The implementation of the transcriptome expression estimation and differential expression analysis, BitSeq, has been written in C++ and Python. The software is available online from http://code.google.com/p/bitseq/, version 0.4 was used for generating results presented in this article.

Contact: glaus@cs.man.ac.uk, antti.honkela@hiit.fi or m.rattray@sheffield.ac.uk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

High-throughput sequencing is an effective approach for transcriptome analysis. This methodology, also called RNA-seq, has been used to analyze unknown transcript sequences, estimate gene expression levels and study single nucleotide polymorphisms (Wang et al., 2009). As shown by other researchers (Mortazavi et al., 2008), RNA-seq provides many advantages over microarray technology, although effective analysis of RNA-seq data remains a challenge.

A fundamental task in the analysis of RNA-seq data is the identification of a set of differentially expressed genes or transcripts. Results from a differential expression (DE) analysis of individual transcripts are essential in a diverse range of problems such as identifying differences between tissues (Mortazavi et al., 2008), understanding developmental changes (Graveley et al., 2011) and microRNA target prediction (Xu et al., 2010). To perform an effective DE analysis, it is important to obtain accurate estimates of expression for each sample, but it is equally important to properly account for all sources of variation, technical and biological, to avoid spurious DE calls (Robinson and Smyth, 2007; Anders and Huber, 2010; Oshlack et al., 2010). In this contribution, we address both of these problems by developing integrated probabilistic models of the read generation process and the biological replication process in an RNA-seq experiment.

During the RNA-seq experimental procedure, a studied specimen of transcriptome is synthesized into cDNA, amplified, fragmented and then sequenced by a high-throughput sequencing device. This process results in a dataset consisting of up to hundreds of millions of short sequences, or reads, encoding observed nucleotide sequences. The length of the reads depends on the sequencing platform and currently typically ranges from 25 to 300 basepairs. Reads have to be either assembled into transcript sequences or aligned to a reference genome by an aligning tool, to determine the sequence they originate from.

With proper sample preparation, the number of reads aligning to a certain gene is approximately proportional to the abundance of fragments of transcripts for that gene within the sample (Mortazavi et al., 2008) allowing researchers to study gene expression (Cloonan et al., 2008; Marioni et al., 2008). However, during the process of transcription, most eukaryotic genes can be spliced into different transcripts which share parts of their sequence. As it is the transcripts of genes that are being sequenced during RNA-seq, it is possible to distinguish between individual transcripts of a gene. Several methods have been proposed to estimate transcript expression levels (Katz et al., 2010; Li et al., 2010; Nicolae et al., 2010; Turro et al., 2011). Furthermore, (Wang et al., 2010) showed that estimating gene expression as a sum of transcript expression levels yields more precise results than inferring the gene expression by summing reads over all exons.

As the transcript of origin is uncertain for reads aligning to shared subsequence, estimation of transcript expression levels has to be completed in a probabilistic manner. Initial studies of transcript expression used the expectation–maximization (EM) approach (Li et al., 2010; Nicolae et al., 2010). This is a maximum-likelihood procedure which only provides a point estimate of transcript abundance and does not measure the uncertainty in these estimates. To overcome this limitation, Katz et al. (2010) used a Bayesian approach to capture the posterior distribution of the transcript expression levels using a Markov chain Monte Carlo (MCMC) algorithm. Turro et al. (2011) have also proposed MCMC estimation for a model of read counts over regions that can correspond to exons or other suitable subparts of transcripts.

In this contribution, we present BitSeq (Bayesian inference of transcripts from sequencing data), a new method for inferring transcript expression and analyzing expression changes between conditions. We use a probabilistic model of the read generation process similar to the model of Li et al. (2010) and we develop an MCMC algorithm for Bayesian inference over the model. Katz et al. (2010) developed an MCMC algorithm for a similar generative model, but our model differs from theirs because we allow for multialigned reads mapping to different genes. Furthermore, we infer the overall relative expression of transcripts across the transcriptome whereas Katz et al. (2010) focus on relative expression of transcripts from the same gene. We have implemented MCMC using a collapsed Gibbs sampler to sample from the posterior distribution of model parameters.

In many gene expression studies, expression levels are used to select genes with differences in expression in two conditions, a process referred to as a DE analysis. We propose a novel method for DE analysis that includes a model of biological variance while also allowing for the technical uncertainty of transcript expression which is represented by samples from the posterior probability distribution obtained from the probabilistic model of read generation. By retaining the full posterior distribution, rather than a point estimate summary, we can propagate uncertainty from the initial read summarization stage of analysis into the DE analysis. Similar strategies have been shown to be effective in the DE analysis of microarray data (Liu et al., 2006; Rattray et al., 2006) but given the inherent uncertainty of reads mapping to multiple transcripts, we expect the approach to bring even more advantages for transcript-level DE analyses. Furthermore, this method accounts for decreased technical reproducibility of RNA-seq for low-expressed transcripts recently reported by Łabaj et al. (2011) and can decrease the number of transcripts falsely identified as differentially expressed.

2 METHODS

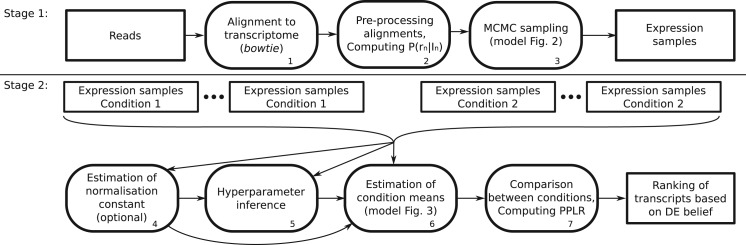
The BitSeq analysis pipeline consists of two main stages: transcript expression estimation and DE assessment (Fig. 1). For the transcript expression estimation, the input data are single-end or paired-end reads from a single sequencing run. The method produces samples from the inferred probability distribution over transcripts' expression levels. This distribution can be summarized by the sample mean in the case that only expression level estimates are required.

Fig. 1.

Diagram showing the BitSeq analysis pipeline divided into two separate stages. In Stage 1, transcript expression levels are estimated using reads from individual sequencing experiments. In Step 1, reads are aligned to the transcriptome. In Step 2, the probability of a read originating from a given transcript P(r_n|I_n) is computed for each alignment based on Equation (1). These probabilities are used in Step 3 of the analysis, MCMC sampling from the posterior distribution in Equation (3). In Stage 2 of the analysis, the posterior distributions of transcript expression levels from multiple conditions and replicates are used to infer the probability that transcripts are differentially expressed. In Step 4, a suitable normalization for each experiment is estimated. The normalized expression samples are further used to infer expression-dependent variance hyperparameters in Step 5. Using these results, replicates are summarized by estimating the percondition mean expression for each transcript, Equation (4), in Step 6. Finally, in Step 7, samples representing the distribution of within-condition expression are used to estimate the probability of positive log ratio (PPLR) between conditions, which is used to rank transcripts based on DE belief

The DE analysis uses posterior samples of expression levels from two or more conditions and all available replicates. The conditions are summarized by inferring the posterior distribution of condition mean expression. Samples from the posterior distributions are compared with score the transcripts based on the belief in change of expression level between conditions.

2.1 Stage 1: transcript expression estimation

The initial interest when dealing with RNA-seq data is estimation of expression levels within a sample. In this work, we focus on the transcript expression levels, mainly represented by θ=(θ₁,…, θ_M), the relative abundance of transcripts' fragments within the studied sample, where M is the total number of transcripts. This can be further transformed into relative expression of transcripts θ_m^(*)=θ_m/(l_m(∑_i=1^M θ_i/l_i)), where l_m is the length of the m-th transcript. Alternatively, expression can be represented by reads per kilobase per million mapped reads, RPKM_m=θ_m×10⁹/l_m, introduced by Mortazavi et al. (2008).

We use a generative model of the data, depicted in Figure 2, which models the RNA-seq data as independent observations of individual reads r_n∈R={r₁,…, r_N}, depending on the relative abundance of transcripts' fragments θ and a noise parameter θ^act. The parameter θ^act determines the number of reads regarded as noise and enables the model to account for unmapped reads as well as for low-quality reads within a sample.

Fig. 2.

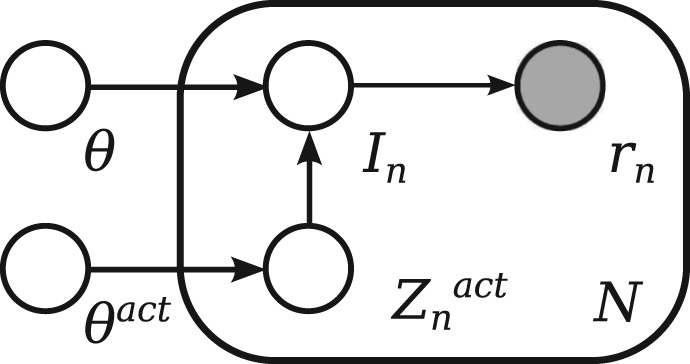
Graphical representation of the RNA-seq data probabilistic model. We can consider the observation of reads R=(r₁,…, r_N) as N conditionally independent events, with each observation of a read r_n depending on the transcript (or isoform) it originated from I_n. The probability of sequencing a given transcript I_n depends on the relative expression of fragments θ and the noise indicator Z_n^act. The noise indicator variable Z_n^act depends on noise parameter θ^act and indicates that the transcript being sequenced is regarded as noise, which enables observation of low-quality and unmappable reads

Based on the parameter θ^act, indicator variable Z_n^act∼Bern(θ^act) determines whether read r_n is considered as noise or a valid sequence. For a valid sequence, the process of sequencing is being modelled. Under the assumption of reads being uniformly sequenced from the molecule fragments, each read is assigned to a transcript of origin by the indicator variable I_n, which is given by categorical distribution I_n∼Cat(θ).

For a transcript m, we can express the probability of an observed alignment as the probability of choosing a specific position p and sequencing a sequence of given length with all its mismatches, P(r_n|I_n=m)=P(p|m)P(r_n|seq_mp). For paired-end reads, we compute the joint probability of the alignment of a whole pair, in which case, we also have to consider fragment length distribution P(l),

(1)

Details of alignment probability computation including optional position and sequence-specific bias correction methods are presented in Supplementary Material. For every aligned read, we also calculate the probability that the read is from neither of the aligned transcripts but is regarded as sequencing error or noise P(r_n|noise). This value is calculated by taking the probability of the least probable valid alignment corrupted with two extra base mismatches.

The joint probability distribution of the model can now be written as

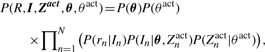(2)

where we use weak conjugate Dirichlet and Beta prior distributions for θ and θ^act, respectively. The posterior distribution of the model's parameters given the data R can be simplified by integrating over all possible values of Z^act:

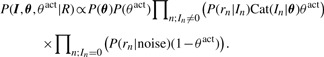(3)

According to the model, any read can be a result of sequencing either strand of an arbitrary transcript at a random position. However, the probability of a read originating from a location where it does not align is negligible. Thus, the term P(r_n|I_n)Cat(I_n|θ)θ^act has to be evaluated only for transcripts and positions to which the read does align. To accomplish this, we first align the reads to the transcript sequences using the Bowtie alignment tool (Langmead et al., 2009), preserving possible multiple alignments to different transcripts. We then precompute P(r_n|I_n) only for the valid alignments. (See Steps 1 and 2 in Fig. 1.)

The closed form of the posterior distribution is not analytically tractable and an approximation has to be used. We can analytically marginalize θ and apply a collapsed Gibbs sampler to produce samples from the posterior probability distribution over I_n (Geman and Geman, 1993; Griffiths and Steyvers, 2004). These are used to compute a posterior for θ, which is the main variable of interest. Full update equations for the sampler are given in Supplementary Material.

In the MCMC approach, multiple chains are sampled at the same time and convergence is monitored using the 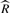statistic (Gelman et al., 2003). The 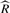statistic is an estimate of a possible scale reduction of the marginal posterior variance and provides a measure of usefulness of producing more samples. We use the marginal posterior variance estimate and between chain variance to calculate the effective number of samples for each transcript as described by Gelman et al. (2003), to determine the number of iterations needed for convergence.

Posterior samples of θ provide an assessment of the abundance of individual transcripts. As well as providing an accurate point estimate of the expression levels through the mean of the posterior, the probability distribution provides a measure of confidence for the results, which can be used in further analyses.

2.2 Stage 2: combining data from multiple replicates and estimating DE

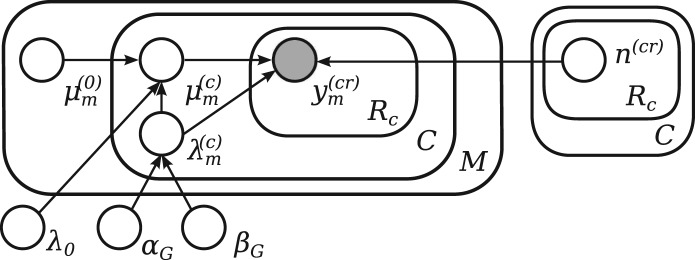
To identify transcripts that are truly differentially expressed, it is necessary to account for biological variation by using replication for each experimental condition. Our method summarizes these replicates by estimating the biological variance and inferring percondition Mean expression levels for each transcript. During the DE analysis, we consider the logarithm of transcript expression levels y_m=logθ_m. The model for data originating from multiple replicates is illustrated in Figure 3. We use a hierarchical log-normal model of within-condition expression. The prior over the biological variance is dependent on the mean expression level across conditions and the prior parameters (hyper-parameters) are learned from all of the data by fitting a nonparametric regression model. We fit a model for each gene using the expression estimates from Stage 1.

Fig. 3.

Graphical model of the biological variance in transcript expression experiment. For replicate r, condition c and transcript m, the observed log-expression level y_m^(cr) is normally distributed around the normalized condition mean expression μ_m^(c)+n^(cr) with biological variance 1/λ_m^(c). The condition mean expression μ_m^(c) for each condition is normally distributed with overall mean expression μ_m⁽⁰⁾ and scaled variance 1/(λ^(c)_mλ₀). The inverse variance, or precision λ^(c)_m, for a given transcript m follows a Gamma distribution with expression-dependent hyperparameters α_G, β_G, which are constant for a group of transcripts G with similar expression

A novel aspect of our Stage 2 approach is that we fit models to posterior samples obtained from the MCMC simulation from Stage 1, which can be considered ‘pseudo-data’ representing expression corrupted by technical noise. A pseudo-data vector is constructed using a single MCMC sample for each replicate across all conditions. The posterior distribution over per-condition means is inferred for each pseudo-data vector using the model in Figure 3 (described below). We then use Bayesian model averaging to combine the evidence from each pseudo-data vector and determine the probability of DE. This approach allows us to account for the intrinsic technical variance in the data; it is also computationally tractable because the model for a single pseudo-data vector is conjugate and therefore inference can be performed exactly. This effectively regularizes our variance estimate in the case that the number of replicates is low. As shown in Section 3.5, this provides improved control of error rates for weakly expressed transcripts where the technical variance is large.

For a condition c, we assume R_c replicate datasets. The log expression from replicate r, y_m^(cr) is assumed to be distributed according to a normal distribution with condition mean expression μ_m^(c), normalized by replication-specific constant n^(cr), and precision λ_m^(c), y_m^(cr)∼Norm(μ_m^(c)+n^(cr), 1/λ_m^(c)). As our parameters represent the relative expression levels in the sample, BitSeq implicitly incorporates normalization by the total number of reads or the RPKM measure, as Was done when generating the results in this publication. Further more, normalization can be implemented using the normalization constant n^(cr), which is constant for all transcripts of a given replicate and can be estimated prior to probabilistic modelling using, for example, a quantile-based method (Robinson and Oshlack, 2010) or any other suitable technique.

The condition mean expression is normally distributed μ_m^(c) ∼ Norm (μ_m⁽⁰⁾, 1/(λ_m^(c)λ₀)) with mean μ_m⁽⁰⁾, which is empirically calculated from multiple samples and scaled precision λ_m^(c)λ₀. The prior distribution over pertranscript, condition-specific precision λ_m^(c) is a Gamma distribution with hyperparameters α_G, β_G, which are fixed for a group of transcripts with similar expression level, G.

The hyperparameters α_G, β_G determine the distribution over pertranscript precision parameter λ_m which varies with the expression level of a transcript (see Supplementary Figure 3). For this reason, we inferred these hyperparameters from the dataset for various levels of expression, prior to the estimation of precision λ_m and mean expression μ_m. We used the same model as Figure 3 applied jointly to multiple transcripts with similar empirical mean expression levels μ_m⁽⁰⁾. We set a uniform prior for the hyperparameters, marginalized out condition means and precision, and used an MCMC algorithm to sample α_G, β_G. The samples of α_G, β_G were smoothed by Lowess regression (Cleveland, 1981) against empirical mean expression to produce a single pair of hyperparameters for each group of transcripts with similar expression level.

This model is conjugate and thus leads to a closed-form posterior distribution. This allows us to directly sample λ_m and μ_m given each pseudo-data vector y_m constructed from the Stage 1 MCMC samples:

(4)

Samples of μ_m^(c₁) and μ_m^(c₂) are used to compute the probability of expression level of transcript m in condition c₁ being greater than the expression level in condition c₂. This is done by counting the fraction of samples in which the mean expression from the first condition is greater, that is P(μ_m^(c₁)>μ_m^(c₂)|R)=1/N∑_n=1^N δ(μ_m,n^(c₁)>μ_m,n^(c₂)) which we refer to as the PPLR. Here, n=1… N represents one sample from the above posterior distribution for each of N independent pseudo-data vectors. Subsequently, ordering transcripts based on PPLR produces a ranking of most probable upregulated and downregulated transcripts. This kind of one-sided Bayesian test has previously been used for the analysis of microarray data (Liu et al., 2006).

3 RESULTS AND DISCUSSION

3.1 Datasets

We performed experiments evaluating both gene expression estimation accuracy as well as DE analysis precision. For the evaluation of bias correction effects as well as comparison with other methods (Table 1), we used paired-end RNA-seq data from the microarray quality control (MAQC) project (Shi et al., 2006) (Short Read Archive accession number SRA012427), because it contains 907 transcripts which were also analyzed by TaqMan qRT-PCR, out of which 893 matched our reference annotation. The results from qRT-PCR probes are generally regarded as ground truth expression estimates for comparison of RNA-seq analysis methods (Roberts et al., 2011). We used RefSeq refGene transcriptome annotation, assembly NCBI36/hg18 to keep results consistent with qRT-PCR data as well as previously published comparisons by Roberts et al. (2011).

Table 1.

Comparison of expression estimation accuracy against TaqMan qRT-PCR data

Read model	BitSeq	Cuff. 0.9.3	RSEM	MMSEQ
Uniform	0.7677	0.7503	0.7632	0.7614
Non-uniform	0.8011	0.8056	0.7633	0.7990a

The table shows the effect of non-uniform read distribution models using correlation coefficient R² of average expression from three technical replicates with the 893 matching transcripts analysed by qRT-PCR, highest correlation is highlighted in bold. The sequencing data (SRA012427) are part of the MAQC project and was originally published by Shi et al. (2006).

^aWe were not able to use the default bias correction provided by MMSEQ (Turro et al., 2011) due to an error in an external R package mseq used for the bias correction. Instead, we provided the MMSEQ package with effective lengths computed by BitSeq bias correction algorithm to produce results for this comparison.

The second dataset used in our evaluation was originally published by Xu et al. (2010) in a study focused on identification of microRNA targets and provides technical as well as biological replicates for both studied conditions. We use this data to illustrate the importance of biological replicates for DE analysis (Fig. 5; Supplementary Fig. 3 for biological variance) and the advantages of using a Bayesian approach for both expression inference and DE analysis (Fig. 4).

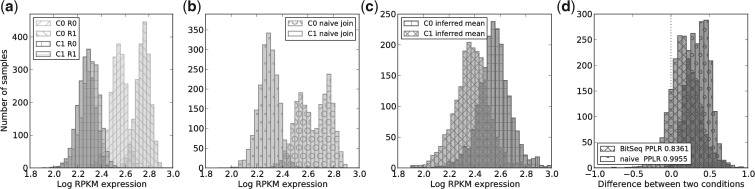
Fig. 5.

Comparison of BitSeq to naive approach for combining replicates within a condition for transcript uc001avk.2 of the Xu et al. dataset. (a) Initial posterior distributions of transcript expression levels for two conditions (labelled C0, C1), with two biological replicates each (labelled R0, R1). (b) Mean expression level for each condition using the naive approach for combining replicates. The posterior distributions from replicates are joined into one dataset for each condition. (c) Inferred posterior distribution of mean expression level for each condition using the probabilistic model in Figure 3. (d) Distribution of differences between conditions from both approaches show that the naive approach leads to overconfident conclusion

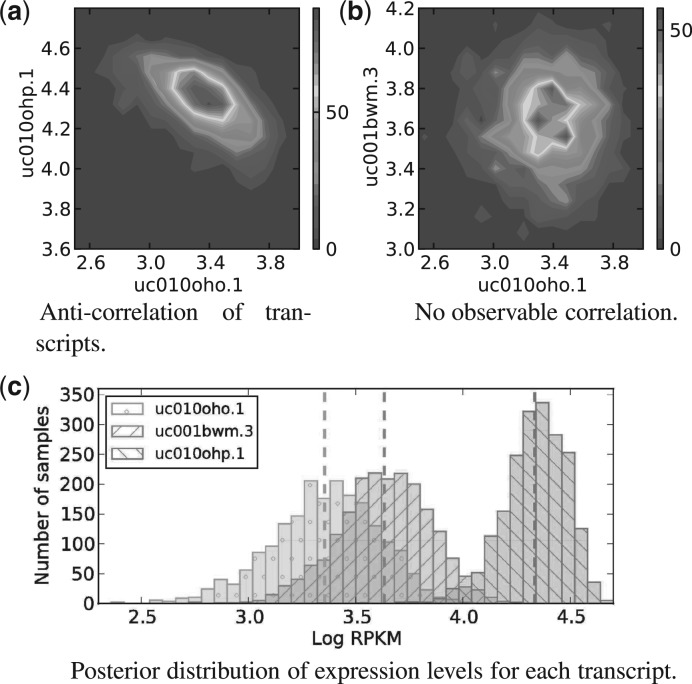
Fig. 4.

In plots (a) and (b), we show the posterior transcript expression density for pairs of transcripts from the same gene. This is a density map constructed using the MCMC expression samples for these three transcripts. In (c), we show the marginal posterior distribution of expression levels of the same transcripts as illustrated by histograms of MCMC samples. The sequencing data are from miRNA-155 study published by Xu et al. (2010)

For the purpose of evaluating and comparing BitSeq to existing DE analysis methods, we created artificial RNA-seq datasets with known expression levels and differentially expressed transcripts. We selected all transcripts of chromosome 1 from human genome assembly NCBI37/hg19 and simulated two biological replicates for each of the two conditions. We initially sample the expression for all replicates using the same mean relative expression and variation between replicates as were observed in the Xu et al. data estimates. Afterwards, we randomly choose one-third of the transcripts and shift one of the conditions up or down by a known fold change. Given the adjusted expression levels, we generated 300 k single-end reads uniformly distributed along the transcripts. The reads were reported in Fastq format with Phred scores randomly generated according to empirical distribution learned from the SRA012427 dataset. With the error probability given by a Phred score, we generated base mismatches along the reads.

3.2 Expression-level inference

Figure 4 demonstrates the ambiguity that may be present in the process of expression estimation. In Figure 4a and 4b, we show the density of samples from the posterior distribution of expression levels for two pairs of transcripts. The expression levels of transcripts uc010oho.1 and uc010ohp.1 (Fig. 4a) are negatively correlated. On the other hand, transcripts uc010oho.1 and uc001bwm.3 exhibit no visible correlation (Fig. 4b) in their expression-level estimates. Even though this kind of correlation does not have to imply biological significance, it does point to technical difficulties in the estimation process. These transcripts share a significant amount of sequence and the consequent read mapping ambiguity leads to greater uncertainty in expression estimates (see Supplementary Fig. 1d for transcript profile). Bayesian inference can be used to assess the uncertainty due to such confounding factors, unlike the maximum-likelihood point estimates provided by an EM algorithm. The marginal posterior probability of transcript expression for each transcript is shown in Figure 4c. In our analysis pipeline, the marginal posterior distributions are propagated into the DE estimation stage, thus the uncertainty from expression estimation is taken into account when assessing whether there is strong evidence that transcripts are differentially expressed.

3.3 Expression estimation accuracy and read distribution bias correction

Initially, it was assumed that high-throughput sequencing produces reads uniformly distributed along transcripts. However, more recent studies show biases in the read distribution depending on the position and surrounding sequence (Dohm et al., 2008; Roberts et al., 2011; Wu et al., 2011). Our generative model for transcript expression inference (Fig. 2) includes a model of the underlying read distribution which is included in the P(r_n|I_n=m) term that is calculated as a preprocessing step. The current BitSeq implementation contains the option of using a uniform read density model or using the model proposed by Roberts et al. (2011) which can account for positional and sequence bias. The effect of correcting for read distribution was analyzed using the SRA012427 dataset and results are presented in Table 1. We also compare BitSeq with three other transcript expression estimation methods: Cufflinks v0.9.3 (Roberts et al., 2011), MMSEQ v0.9.18 (Turro et al., 2011) and RSEM v1.1.14 (Li and Dewey, 2011).

The dataset contains three technical replicates. These were analyzed separately and the resulting estimates for each method were averaged together. Subsequently, we calculated the squared Pearson correlation coefficient (R²) of the average expression estimate and the results of qRT-PCR analysis. All four methods used with the default uniform read distribution model provide similar level of accuracy with BitSeq performing slightly better than the other three methods.

Both BitSeq and Cufflinks use the same method for read distribution bias correction and provide improvement over the uniform model similar to improvements previously reported by Roberts et al. (2011). We used version 0.9.3 of Cufflinks (as used by Roberts et al.) since we found that the most recent stable version of Cufflinks (version 1.3.0) leads to much worse performance for both uniform and bias-corrected models (see Supplementary results Section 2.2). The RSEM package uses its own method for bias correction based on the relative position of fragments, which in this case did not improve the expression estimation accuracy for the selected transcripts.

In the case of BitSeq, the major improvement of accuracy originates from using the effective length normalization. To compare the results with qRT-PCR, the relative expression of fragments θ has to be converted into either relative expression of transcripts (θ^*) or RPKM units. Using the bias-corrected effective length for this conversion leads to the higher correlation with qRT-PCR (Supplementary Table 1). This means that using an expression measure adjusted by the effective length, such as RPKM, is more suitable than normalized read counts for DE analysis.

We also evaluated the accuracy of the four methods using three different expression measures on simulated data. First, we compared with transcripts' RPKM as an absolute expression measure. Second, we used relative within-gene expression in which transcript expression is the relative proportion within transcripts of the same gene. Finally, we used gene expression RPKM, the sum of transcript expression levels for each gene. The results are presented in Table 2. MMSEQ provides the best absolute expression accuracy with BitSeq and RSEM showing almost equally good results. For the relative within-gene expression levels, BitSeq is more accurate than the other methods. In spite of providing slightly better results in absolute measure, RSEM and MMSEQ show worse correlation in the relative within-gene measure as they tend to assign zero expression to some transcripts within one gene. This is most likely due to the use of maximum- likelihood parameter estimates as the starting point for the Gibbs sampling algorithm.

Table 2.

The R² correlation coefficient of estimated expression levels and ground truth

Expression	Cutoff	BitSeq	Cuff. 0.9.3	RSEM	MMSEQ
Transcript	1	0.994	0.764	0.995	0.997
Relative	10	0.945	0.724	0.876	0.886
Relative	100	0.963	0.773	0.946	0.948
Gene	1	0.994	0.823	0.996	0.998

Three different expression measures were used: absolute transcript expression, relative within-gene transcript expression and gene expression. Comparison includes sites with at least 1 read per transcript for transcript expression, either 10 or 100 reads pre gene for within-gene transcript expression and at least 1 read per gene for gene expression. The highest correlation is in bold.

For more details and results comparing the transcript expression estimation accuracy, please refer to Supplementary Material Section 2.3.

3.4 DE analysis

We use the Xu et al. dataset to demonstrate the DE analysis process of BitSeq. This dataset contains technical and biological replication for both studied conditions. We observed significant difference between biological and technical variance of expression estimates (Supplementary Fig. 3). Furthermore, the prominence of biological variance increases with transcript expression level. We illustrate how BitSeq handles biological replicates to account for this variance in Figure 5, by showing the modelling process for one example transcript given only two biological replicates for each of two conditions.

Figure 5a shows histograms of expression-level samples produced in the first stage of our pipeline. BitSeq probabilistically infers condition mean expression levels using all replicates. For comparison, we used a naive way of combining two replicates by combining the posterior distributions of expression into a single distribution. The resulting posterior distributions for both approaches are depicted in Figures 5b and 5c.

The probability of DE for each transcript is assessed by computing the difference in posterior expression distributions of the two conditions. Resulting distributions of differences for both approaches are portrayed in Figure 5d with obvious difference in the level of confidence. The naive approach reports high confidence of upregulation in the second condition, with the PPLR being 0.995. When biological variance is being considered by inferring the condition mean expression, the significance of DE is decreased to PPLR 0.836.

3.5 Assessing DE performance with simulated data

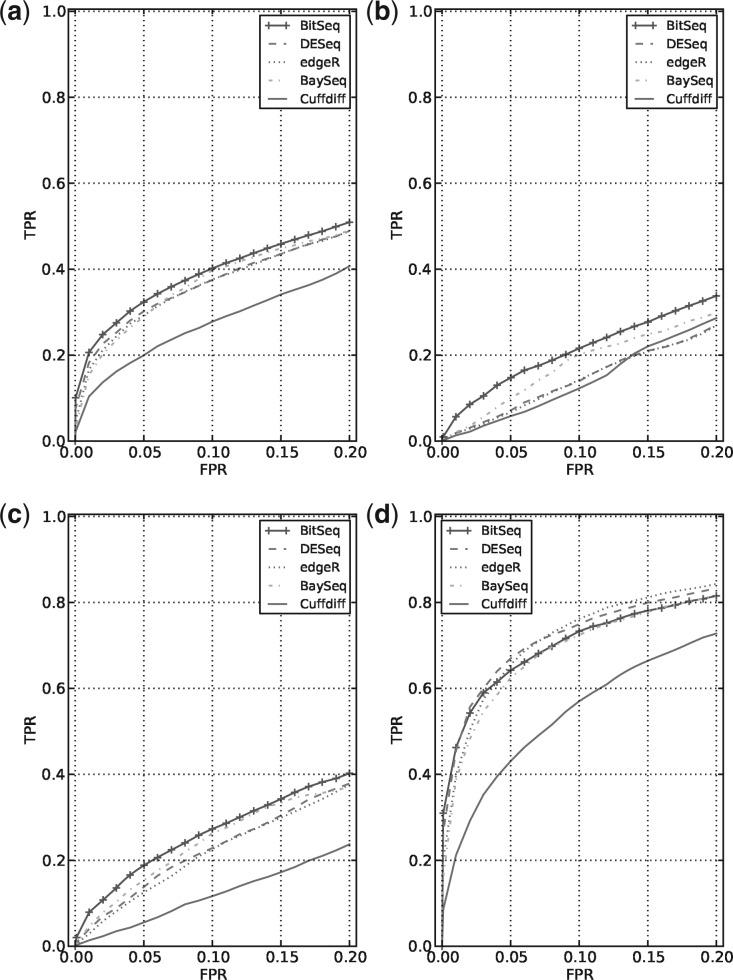
Using artificially simulated data with a predefined set of differentially expressed transcripts, we evaluated our approach and compared it with four other methods commonly used for DE analysis. DESeq v1.6.1 (Anders and Huber, 2010), edgeR v2.4.3 (Robinson et al., 2010) and baySeq v1.8.1 (Hardcastle and Kelly, 2010) were designed to operate on the gene level and Cuffdiff v1.3.0 (Trapnell et al., 2010) on the transcript level. Despite not being designed for this purpose, we consider the first three in this comparison as the use case is very similar and there are no other well-known alternatives besides Cuffdiff that would use replicates for transcript level DE analysis. All other methods beside Cuffdiff use BitSeq, Stage 1 transcript expression estimates converted to counts. Details regarding use of these methods are provided in the Supplementary material, Section 2.5. Figure 6 shows the overall results as well as split into three parts based on the expression of the transcripts. The receiver-operating characterization curves were generated by averaging over five runs with different transcripts being differentially expressed and the figures are focused on the most significant DE calls with false-positive rate below 0.2.

Fig. 6.

ROC evaluation of transcript level DE analysis using artificial dataset, comparing BitSeq with alternative approaches. DESeq, edgeR and baySeq use transcript expression estimates from BitSeq Stage 1 converted to counts. The curves are averaged over five runs with different set of transcripts being differentially expressed by fold change uniformly distributed in the interval (1.5,3.5). We discarded transcripts without any reads initially generated as these provide no signal. Panel (a) shows global average behaviour whereas in (b), (c) and (d) transcripts were divided into three equally sized groups based on the mean generative read count: [1,3), [3,19) and [19, ∞), respectively

Overall (Figure 6a), BitSeq is the most accurate method, followed first by baySeq, then edgeR and DESeq with Cuffdiff further behind. This trend is especially clear for lower expression levels (Fig. 6b and 6c). The overall performance here is fairly low because of high level of biological variance. For highest expressed transcripts (Fig. 6d), DESeq and edgeR show slightly higher true positive rate than BitSeq and baySeq, especially at larger false- positive rates. Furthermore details and more results from the DE analysis comparison can be found in Supplementary material Section 2.5.

3.6 Scalability and performance

As BitSeq models individual read assignments, the running time complexity of the first stage of BitSeq increases with the number of aligned reads. Preprocessing the alignments and sampling a constant number of samples scales linearly with the number of reads. However, with more reads, the data become more complex and the Gibbs sampling algorithm needs more iterations to capture the whole posterior distribution.

In Table 3, we present the running time for Stage 1, using simulated data generated from the UCSC NCBI37/hg19 knownGene reference. We ran the preprocessing of the reads with a uniform read distribution model on a single CPU and sampling with four parallel chains on four Intel Xeon 3.47 GHz CPUs. We set the sampler to run until it generates 1000 effective samples for at least 95% of transcripts. At the end, almost all transcripts converged according to the 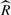statistic. The number of iterations necessary to produce the desired amount of effective samples seems to increase logarithmically with the number of reads.

Table 3.

Scalability and run-time complexity of BitSeq on different-sized datasets using simulated data with 9.9 up to 158.5 million paired-end reads

Read pairs (M)	4.9	9.1	19.8	39.6	79.2
Alignments (M)	16	32	64	129	258
Preprocessing (m)	8	15	29	57	115
1000 samples (m)	7	14	32	56	71
Total time (h)	0:55	2:18	5:42	16:23	33:19
Convergence it.	5269	6900	8920	11970	15979

The table shows wall clock running times to preprocess the aligned reads, generate 1000 samples and full time for the sampling algorithm on four CPUs. The last row contains the estimated number of iterations needed to reach convergence for at least 95% of transcripts.

Running time of the DE analysis in Stage 2 does only depend on the number of reference transcripts, replicates and samples generated in Stage 1 for the analysis. Producing the result presented in Section 3.4 took 97 min on the Intel Xeon 3.47 GHz CPU.

4 CONCLUSION

We have presented methods for transcript expression level analysis and DE analysis that aim to model the uncertainty present in RNA-seq datasets. We used a Bayesian approach to provide a probabilistic model of transcriptome sequencing and to sample from the posterior distribution of the transcript expression levels. The model incorporates read and alignment quality, adjusts for non-uniform read distributions and accounts for an experiment-specific fragment length distribution in case of paired-end reads. The accuracy of inferred expression is comparable and in some cases, outperforms other competing methods. However, the major benefit of using BitSeq for transcript expression inference is the availability of the full posterior distribution which is useful for further analysis.

The inferred distributions of transcript expression levels can be further analyzed by the second stage of BitSeq for DE analysis. Given biological replicates, BitSeq accounts for both intrinsic technical noise and biological variation to compute the posterior distribution of expression differences between conditions. It produces more reliable estimates of expression levels within each condition and associates these expression levels with a degree of credibility, thus providing fewer false DE calls. We want to highlight that to make accurate DE assessment, experimental designs must include biological replication and BitSeq is a method capable of combining information from biological replicates when comparing multiple conditions using RNA-Seq data.

In our current work, we aim to reduce the computational complexity of BitSeq by replacing MCMC with a faster deterministic approximate inference algorithm and we are generalizing the model to include more complex experimental designs in the DE analysis stage.

Funding: European ERASysBio+ initiative project SYNERGY by the Biotechnology and Biological Sciences Research Council [BB/I004769/2 to M.R.] and Academy of Finland [135311 to A.H.]; Academy of Finland [121179 to A.H.]; and IST Programme of the European Community, under the PASCAL2 Network of Excellence [IST-2007-216886]. This publication only reflects the authors' views.

Conflict of Interest: none declared.