Abstract
The flow of information within a cell is governed by a series of protein-protein interactions that can be described as a reaction network. Mathematical models of biochemical reaction networks can be constructed by repetitively applying specific rules that define how reactants interact and what new species are formed upon reaction. To aid in understanding the underlying biochemistry, timescale analysis is one method developed to prune the size of the reaction network. In this work, we extend the methods associated with timescale analysis to reaction rules instead of the species contained within the network. To illustrate this approach, we applied timescale analysis to a simple receptor-ligand binding model and a rule-based model of Interleukin-12 (IL-12) signaling in näive CD4+ T cells. The IL-12 signaling pathway includes multiple protein-protein interactions that collectively transmit information; however, the level of mechanistic detail sufficient to capture the observed dynamics has not been justified based upon the available data. The analysis correctly predicted that reactions associated with JAK2 and TYK2 binding to their corresponding receptor exist at a pseudo-equilibrium. In contrast, reactions associated with ligand binding and receptor turnover regulate cellular response to IL-12. An empirical Bayesian approach was used to estimate the uncertainty in the timescales. This approach complements existing rank- and flux-based methods that can be used to interrogate complex reaction networks. Ultimately, timescale analysis of rule-based models is a computational tool that can be used to reveal the biochemical steps that regulate signaling dynamics.
Keywords: Bayesian statistics, JAK-STAT signaling, model-based inference, cellular signal transduction
Introduction
Cellular response to extracellular stimuli is governed by biochemical reactions that allow the transfer of information from the cell membrane to the nucleus and back.1 This flow of information within cells can be described in terms of reaction networks. Reaction networks are constructed from a collection of nodes and edges. The nodes correspond to the specific reacting species that are thought to participate in the flow of information. The edges connect two or more nodes and correspond to the velocity of information flow due to the interaction between the corresponding nodes. These reaction networks can be depicted qualitatively as, for example, signaling cartoons (e.g., a KEGG canonical pathway) or depicted quantitatively in the form of a mathematical model. Mathematical models extend our reasoning abilities by predicting the consequence of assumptions that may not be interpreted or understood through human intuition alone.2
To create a mathematical model, one must first specify the causal relationships among the interacting proteins involved in a reaction network (i.e., the network topology). The topology of the network can be assembled from two perspectives: a node versus an edge perspective. Historically, the topology of a reaction network has been assembled from a node perspective. A priori knowledge of the key proteins involved in the signaling pathway of interest (i.e., the nodes) provide the framework for the network. The nodes are connected via a judicious use of simplifying assumptions (e.g.,3-5). These manually assembled networks have provided insight into many signaling pathways.6 However, the implicit assumptions required for manual assembly of reaction networks impose bias and limit wider application.7 More recently, reaction networks have been generated with the assistance of software that repetitively applies reaction rules that encode the distinct molecular transformations associated with information flow (i.e., a network edge) to an initial set of nodes and their progeny. Examples of applications include reaction networks that contain hydrocarbons,8-11 immobilized binding sites,12 metabolites,13,14 and multi-state proteins.15-21 Using reaction rules to construct a reaction network is considered an edge perspective.
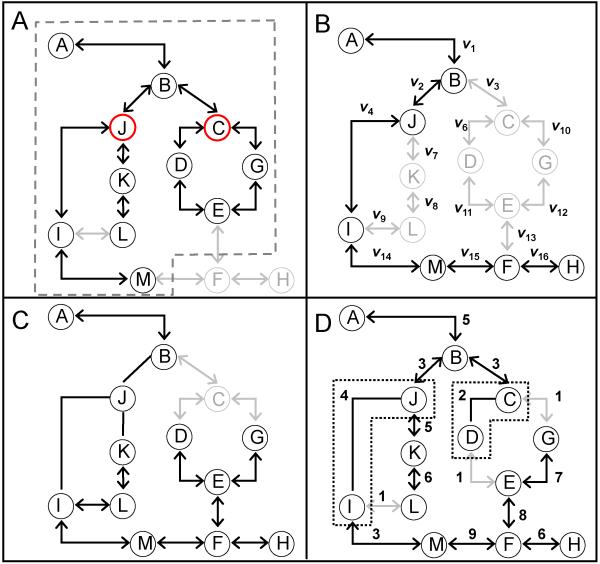
Application of the rules to reacting species can create reaction networks that exhibit combinatorial complexity,22 leading to a combinatorial explosion in the number of unique species represented in the model.19 However, computational tools have been developed to prune the reaction network based upon specific criteria and to facilitate intuitive interpretation of model behavior.11,23-28 In Figure 1, four different schemes for pruning rule-based models are illustrated using a generalized reaction network. The simplest scheme is a rank-based criterion, depicted in Figure 1A (e.g.,11,29). Repetitive application of the set of reaction rules to species generates a progressively larger set of species upon each application of the rule set. Species are assigned a rank based upon number of iterations required to generate a particular species. A rank-based criterion limits the reaction network to include only those species with a rank below a defined cut-off. One of the advantages of this approach is that knowledge of the rate parameters is not required to prune the reaction network. More generally, this implies that a rank-based criterion can be used for both qualitative reaction networks - such as Bayesian networks, Boolean networks and Petri-Nets (e.g.,30-32) - and quantitative reaction networks. For the remainder of this study, we will focus on quantitative models of reaction networks that are designed to make explicit predictions in species state space as a function of time.
Figure 1. Comparison of model analysis schemes for rule-based models.
A generalized reaction network is used to depict four different schemes for interrogating rule-based models: (A) a rank-based criteria (e.g.,11,29), (B) a rate-based criteria (e.g.,25), (C) timescale analysis of species (e.g.,35,36), and (D) timescale analysis of reaction rules (this work). In panel A, the dashed box indicates a reaction network of rank 2 generated using species J and C as starting reactants. Species and the corresponding reactions that are included in a rank 2 reaction network are shown in black. Neglected species and reactions are shown in gray. In panel B, reactions are included in the overall reaction network, as indicated by the black lines between the species, if the molecular flux, as indicated by vi, is above a threshold value. Panel C depicts the results of a time scale analysis of species where species J is determined to correspond to a fast kinetic manifold and be at pseudo-equilibrium. The relationships between species J and other interacting species can be represented as an algebraic relationship. In addition, species C corresponds to a stationary manifold and can be removed from the network. In Panel D, edges are annotated with a number that corresponds to reaction rule used to generate the edge. In this example, reaction rules 2 and 4 correspond to a fast kinetic manifold, as shown by undirected edges, and reaction rule 1 corresponds to the stationary manifold. As the protein-protein interactions between species J and I and species C and D are fast, the corresponding species are represented as multi-protein complexes (dotted boxes).
The other three network reduction schemes illustrated in Figure 1B - 1D require knowledge of the rate parameters. A rate-based criterion, as depicted in Figure 1B, includes edges (i.e., reactions) in an emerging network if the molecular velocity down the potential edge, as indicated by vi, is above a threshold value (e.g.,25). A similar idea has been proposed in the form of a kinetic Monte Carlo method for rule-based modeling (see additional comment in Supplemental File 1, Section 1).33 In this method, applying a rule during a time step depends on a probabilistic sample of the set of all rules that are weighted by molecular velocity of the associated reactions. The remaining two schemes shown in Figure 1 are related to timescale analysis.
Events associated with the transfer of cell signaling information exhibit a broad range of timescales.34 A classical approach for simplifying reaction networks that are described in dynamic terms is based upon timescale analysis.35,36 A timescale analysis aids in simplifying the response of a system by parsing system components and their corresponding dynamics into different kinetic manifolds (e.g.,37). The evolution in the system is constrained by the slow variables (i.e., the observable kinetic manifold) while the variables that correspond to the fast kinetic manifold exist at a pseudo-equilibrium. Moreover, variables that exhibit timescales significantly longer than the observable timescale can be considered stationary (i.e., a stationary manifold). This timescale separation phenomenon has been termed the slaving principle.38 From these differences in timescales, we can infer that the important species that regulate the system dynamics correspond to the slow kinetic manifold. Species that correspond to a stationary manifold do not need to be represented explicitly as their contributions can be lumped into appropriate rate parameters. Reacting species that correspond to a fast kinetic manifold can be described using static (e.g., algebraic) instead of dynamic (e.g., ordinary differential equations) relationships. The results of a classical timescale analysis of species is depicted in Figure 1C, where species J is determined to correspond to a fast kinetic manifold and be at pseudo-equilibrium. The relationship between species J and other interacting species can be represented as an algebraic relationship, which is shown as an undirected edge. In addition, species C corresponds to a stationary manifold and can be removed from the network. Timescale analysis is a classical technique used to identify key enzymes that control flux within39 and quantify hierarchical relationships among elements of a complex metabolic network.40 Prior implementation of timescale analysis has focused on identifying timescales associated with nodes.
The objective of this study is to describe how timescale analysis can be used to identify timescales associated with reaction rules (i.e., an edge perspective). This edge perspective in pruning reaction networks is depicted in Figure 1D, where the edges are annotated with numbers that indicate the specific reaction rules used to generate the edge. In this generalized example, reaction rules 2 and 4 correspond to a fast kinetic manifold, as shown by undirected edges, and reaction rule 1 corresponds to a stationary or slow kinetic manifold. In the following sections, we will review classical timescale analysis applied to reacting species and, by analogy, illustrate how timescale analysis can be applied to reaction rules. Finally, we will apply this timescale analysis approach to two examples: a simple receptor-ligand binding model and a mathematical model of Interleukin-12 signaling in näive CD4+ T cells.41
Methods
Mathematical modeling
Two mathematical models are used to illustrate the timescale analysis described in the following section. The first example is a simple rule-based model that describes ligand-induced receptor activation (see Figure 2A). The detailed equations and parameters for this simple model are described in Supplemental File 1: Tables S1-S4. Model equations and elements of the Jacobian were encoded in MatLab V7.11, and the MatLab code used to perform these calculations are provided as Supplemental File 3: MatLab Files. In the second example, a series of reaction rules, depicted in Figure 3A, were used to develop a mathematical model that describes the early signaling events following stimulation of IL-12R and represents the regulatory aspects of the IL-12 pathway. The details of the mathematical model and the calibration data is described previously.41 Briefly, a collection of 28 molecular species and the corresponding rate laws associated with each reaction rule were compiled into coupled system of ordinary differential equations that describes the evolution of the system with time (i.e., the Full IL-12 Model). The kinetic parameters for each reaction were assigned based upon the association of a particular reaction with a reaction rule, based upon the assumption that kinetic parameters are determined based upon local protein motif-motif interactions.42 A priori nonidentifiable parameters were assigned values based upon estimates reported in the literature. The remaining parameters were calibrated to experimental measurements of IL-12Rβ2 expression, the activity of STAT4 (i.e., phosphorylated STAT4), the dynamics of IL-12 binding to the IL-12 receptor, and activity of STAT4 normalized to IL-12Rβ2 expression as a function of time, as previously reported.41 The model equations were encoded and evaluated in MatLab V7.0 (The MathWorks, Natick, MA). Summed squared error between experimental and simulated measurements was used to determine goodness-of-fit. An empirical Bayesian approach, as described previously,41 was used to estimate the uncertainty associated with the parameter values given the available data.44 Using the posterior distributions in parameter values, timescales for each reaction rule were estimated using singular value decomposition of the derivative of the sum of the rate laws for a particular reaction rule with respect to species concentrations (i.e., the reaction rule Jacobian - ), as described in the following section. Posterior distributions in the timescales were estimated from 10,000 parameter sets obtained from the converged segments of 3 independent Markov chains, as reported previously.41 Posterior distributions were obtained by kernel density estimation in R using the collection of timescales calculated for each parameter set. The Full IL-12 Model was simplified based upon the timescale analysis (i.e., the Simplified IL-12 Model). The collection of molecular species, rate laws, and governing ordinary differential equations included in the Simplified IL-12 Model are described in Supplemental File 1: Tables S5-S7. An empirical Bayesian approach was used to quantify the uncertainty in the Simplified IL-12 Model parameters given the available information, as similarly described previously.41 The trace of the Simplified IL-12 model parameters, Gelman-Rubin convergence plot, posterior distribution in the model prediction for each chain, and posterior distribution in the model parameters are shown in Supplemental File 1: Figures S3-S6. The Maximum Expectation values for the parameters of the Simplified IL-12 Model are described in Supplemental File 1: Table S8.
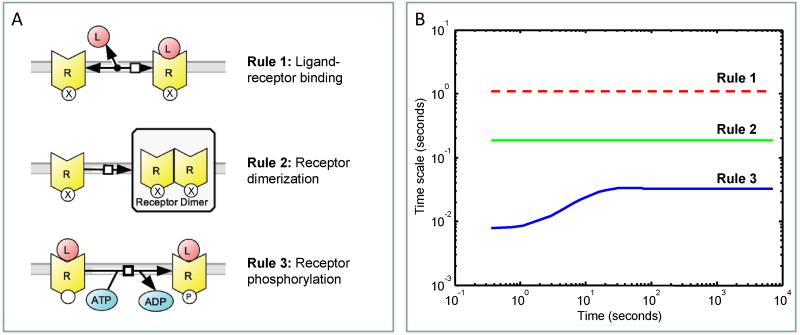
Figure 2. Simple rule-based model of ligand-induced receptor activation.
(A) Schematic of the rule-based model of ligand-induced receptor activation, inspired by insulin receptor signaling. The model represents insulin (ligand, L) binding to its receptor (R) and includes three reaction classes: Rule 1, insulin-receptor binding; Rule 2, receptor dimerization; and Rule 3, ligand-induced receptor phosphorylation. (B) Temporal profiles for the time scales associated with the three reaction classes: Rule 1 - red dotted, Rule 2 - green, and Rule 3 - blue.
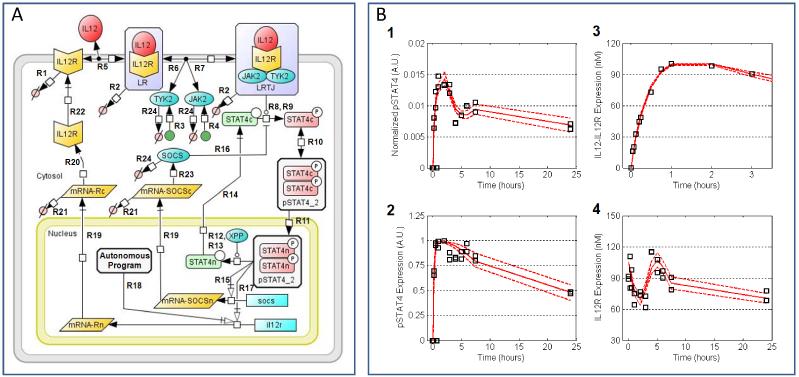
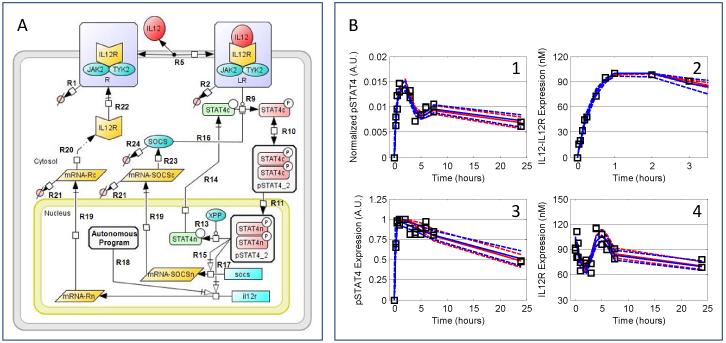
Figure 3. A rule-based model for early signaling events associated with IL-12 signaling reproduces the early dynamics for activation of the STAT4.
(Panel A) Schematic of the full IL-12 signaling model described previously.41 The model represents IL-12R synthesis and degradation; IL-12 binding to IL-12R; STAT4 dimerization and phosphorylation; JAK2 and TYK2 association with the receptor; activation of the signaling pathways associated with the interaction between STAT4 and the bound receptor complex (LRTJ); dimerization and localization of phosphorylated STAT4; deactivation following the dephosphorylation by STAT4 protein phosphatase; positive feedback regulation of STAT4 activity through IL-12R transcription; and negative feedback regulation of STAT4 activity by SOCS and protein phosphatase. Labels that annotate the arrows in the diagram correspond to the reaction rules shown in Table 1. (Panel B) Posterior distribution in the simulated results compared against the experimental observations (squares) used to calibrate the mathematical model. The most likely predictions are represented by the solid lines. The dashed lines enclose the 95% confidence intervals. (subpanel 1) Phosphorylated STAT4 normalized to the level of IL-12Rβ2 expression on a cellular basis. (subpanel 2) Phosphorylated form of STAT4 reported as a percentage of the maximum STAT4 activity. (subpanel 3) IL-12 bound to IL-12R (data from43). (subpanel 4) Total IL-12Rβ2 expression.
Results and Discussion
The difference between a node versus an edge perspective is a subtle but important distinction. To clarify this distinction, we will first establish the terminology and notation by explaining classical timescale analysis. In the subsequent section, we will describe how the analysis is modified to identify timescales associated with subgroups of edges generated by distinct reaction rules.
Classical timescale analysis
The evolution in time for a collection of n reacting species, , can be described by a non-linear function of the reacting species and rate parameters, :
| (1) |
For small increments in time, a first-order Taylor series can be used to approximate the non-linear rate function, , as a linear function:
| (2) |
where is the Jacobian of the rate function with respect to species concentrations and evaluated at the time origin of the Taylor expansion. By neglecting higher order terms, the rate of change for a perturbation in species concentrations,
| (3) |
can be integrated to provide a linear estimate of concentrations at a future time point:
| (4) |
One commonly used decomposition of into a Jordan’s normal form is an eigenspace decomposition such that
| (5) |
where Σ is a diagonal matrix of the eigenvalues, λi’s, and contains the right eigenvectors as column vectors. Using an eigenspace representation, the propagation in time of small changes in species concentrations is expressed as:
| (6) |
Geometrically, Equation 6 can be interpreted as follows:
| (7) |
Evolution in time in eigenspace is along a series of orthogonal directions whose distance, for a given time interval, is characterized by the eigenvalues. The inverse of the real part of the eigenvalue corresponds to a characteristic timescale:
| (8) |
The timescales are then distributed among the species based upon weighting coefficients contained within the rows of . The weighting coefficients are related to the fraction of the total evolution in species space that is represented by a particular timescale. For instance, a value of 0.975 for element V3,4 of means that 95% (100 × 0.9752) of change in species 3 is described by timescale 4.
This connection between timescales and changes in species concentrations (i.e., the reactive flux) has been used as a basis for simplifying reaction networks. Changes in the concentration of species that exhibit fast timescales can be considered at pseudo-equilibrium and can be represented as algebraic equations. In other words, the reactions that contribute to the reactive flux of a species are non-zero. After an initial transient period, the reactions that increase a species concentration (i.e., net producers) are identically balanced by reactions that decrease a species concentration (i.e., net consumers). This balance in reactive fates of the species is considered as a pseudo-equilibrium state. When the reactive flux of a species is at a pseudo-equilibrium, the dynamic relationship is converted into an algebraic constraint that eliminates some of the associated kinetic parameters. Alternatively, the reaction rates can be approximately zero. If the net producers and net consumers are balanced and both close to zero, then the reactive flux of the corresponding species is zero and exhibits a slow timescale (i.e., it is stationary). Species with slow timescale can be integrated into other parameters instead of being represented explicitly. This is a form of kinetic lumping. The reactive flux of the remaining species are non-zero during the time frame of interest. These species exhibit intermediate timescales and involve interactions between species that control the overall dynamics of the observed system response. As the connection between timescales and temporal changes in species space are used as a basis for simplifying reaction networks, we propose a similar connection between timescales and changes in reaction rule space as a basis for applying the slaving principle to reaction rules.
Timescale analysis of rule-based reaction networks
As an alternative to lumping all of the kinetic relationships for a given species into a single rate function (), the change in concentrations of reacting species can be described in terms of a series of competing reaction pathways. These reaction pathways may be comprised of elementary steps or non-elementary steps that define distinct molecular transformations (i.e., reaction rules). The rate of reaction i within a reaction pathway is described by a rate law, Li, that is expressed typically as a product of the reactant concentrations, Cj, and a proportionality constant, ki, that defines the frequency of a molecular reaction. This is in the form of mass action kinetics, although more empirical relationships may be also specified as a rate law. Collectively, the flow of molecules with the reaction network corresponds to a reaction rate vector:
| (9) |
where m is the number of unique reaction rate laws. The consumption or production of a species within a reaction is represented by the stoichiometric coefficients, where Sij is the stoichiometric coefficient for species i in rate law j. The rate of change in species concentrations can then be expressed as:
| (10) |
where is the overall stoichiometric matrix. The stoichiometric matrix also describes the topology of the reaction network, expressed in the form of a sparse directed graph. Nodes of the graph represent the species while edges of the graph represent directional relationships between the species. The magnitude of the molecular flow within an edge is quantified by the rate law. Geometrically, represents a transformation of m-dimensional reaction rate law space onto n-dimensional species space.
Given the unique association of a rate law with a particular reaction rule, we propose a linear transformation of the rate law space of dimension m onto the nRS-dimensional reaction rule space, :
| (11) |
where is an invertible nRS × m transformation matrix. Combining equations, the rate of change in species concentrations is a function of the reaction rules:
| (12) |
where is a linear transform that maps a dynamic trajectory in reaction rule space onto species concentration space. Similarly, the change in species space in response to a perturbation is expressed as:
| (13) |
where . If and are regular matrices then is a square matrix of the same rank as . By analogy with classical time scale analysis,
| (14) |
which implies that exhibits the same characteristic timescales as by the fact that is a dimensionally conserved linear transformation matrix. The linear transform of the temporal expansion in eigenspace onto reaction rule space, , corresponds to:
| (15) |
This linear transform also allows one to associate a timescale with a reaction rule instead of species.
As assumed in the previous derivation, the simplest implementation of the concept of reaction “rules” would be to create a unique rule for each rate law that describes the net rate of change in a given species (i.e., a rate function ). This implies that the dimension of the reaction rule space, nRS, would be equal to the dimension of the reaction rate law space (i.e., nRS = m). However, is typically not invertible as there is a contraction of rate law space onto the reaction rule space. While different species may participate in each specific rate law, the kinetics of a set of rate laws may be similarly governed by local energetics, such as the strength of motif-motif interactions, and entropic considerations.45 These thermodynamic considerations suggest that different rate laws may be grouped together into reaction rules, whereby the reaction rules represent these local atomistic events. This approach helps reduce the total number of unknown rate parameters as the number of unknown parameters is proportional to the number of reaction rules rather than the number of rate laws. This grouping of reaction rate law into reaction rule classes means that nRS is typically less than m. Correspondingly, is not square. However, can be decomposed using singular value decomposition,
| (16) |
to identify the singular values, , associated with the reaction rule space. The columns of form a set of orthonormal basis vectors for , called the left singular vectors that are equivalent to eigenvectors of . The inverse of the real part of the singular values can be interpreted as characteristic timescales:
| (17) |
The timescales are then assigned to the different reaction rules based upon weighting coefficients contained within the rows of . Similar to the classical timescale analysis, the weighting coefficients are related to the fraction of the total evolution in reaction rule space that is represented by a particular timescale. This spatial contraction of rate law space onto reaction rule space also breaks the ability to apply the characteristic timescales of reaction rules to predict dynamic evolution in species space, as suggested by Equation 15. The spatial contraction violates this equality as it is impossible to perform an operation in a lower dimensional space (i.e., rule space) and uniquely redistribute the result into a higher dimensional space (i.e., species space). However to provide useful results, it is not necessary for the timescales determined from singular value decomposition to be retranslated back into species concentration space but to distribute the timescales among the reaction rules. Reaction rules that exhibit fast timescales can be considered at pseudo-equilibrium and can be represented as algebraic equations. Reaction rules that exhibit exceedingly slow timescales can be considered stationary and do not need to be represented explicitly. Reaction rules that exhibit intermediate timescales involve interactions between species that control the overall dynamics of the observed system response. This is illustrated by the following examples.
Applying timescale analysis to rule-based reaction networks
A simple example: Ligand-induced receptor activation
To illustrate how timescale analysis can be applied to rule-based models, the approach, described in the previous paragraphs, was applied to a simple rule-based model of ligand-induced receptor activation, inspired by insulin binding and activation of the insulin receptor.46,47 The model includes three reaction rules: ligand binding to the receptor, receptor dimerization, and autophosphorylation of the ligand-bound receptor (see Figure 2A). The insulin receptor, R has three reaction motifs. The first motif consists of a ligand binding site that can be occupied, state ‘L’, or unoccupied, state ’0’. The second reaction motif represents a ligand-induced post-translational modification site that can be phosphorylated, state ’P’, or remain in a native, unphosphorylated state ’0’. The final reaction motif enables the receptor to form dimers. Given the four possible receptor monomer configurations, recombination of the different receptor monomer states gives rise to a total of ten dimer states. A total of 25 rate laws were derived from the three reaction rate laws. The species, rate laws, and initial conditions are given in Supplemental File 1: Tables S1-S4.
For the simple rule-based model described above, three reaction rules (nRS = 3) are used to generate 17 unique species (n = 17) and 25 rate laws (m = 25). The Jacobian, (i.e., ) is therefore a 3 × 17 matrix, where Kij is the derivative of rate law i with respect to the concentration of species j, and can be evaluated at a particular time point. The singular values of the Jacobian were calculated at each time point, and the inverse of the real parts of the singular values of the Jacobian of the reactions associated with each reaction rule were used to estimate the timescale of reaction rule i (i.e., τi) as a function of time. The timescales associated with the model of insulin-receptor binding during the course of the model simulation are shown in Figure 2B, with ligand-receptor binding being the slowest and receptor phosphorylation being the fastest.
STAT4 activation by Interleukin-12
Besides the simple rule-based model described in the previous section, we also applied timescale analysis to a rule-based model of the Interleukin-12 (IL-12) signaling pathway.41 The IL-12 signaling network is a member of the Janus kinase (JAK) and signal transducer and activator of transcription (STAT) family of signaling pathways. Signal transduction originates with the IL-12 receptor, a member of the type 1 cytokine receptor family and comprised of two subunits: IL-12Rβ1 and IL-12Rβ2. These receptor subunits lack intrinsic enzymatic activity and require association with specific Janus kinases, JAK2 and TYK2, to transmit cellular signals. Binding of a natural ligand to an IL-12 receptor precipitates a series of biochemical events: the receptor changes conformation, the tyrosine residues on the receptor become phosphorylated by receptor-associated Janus kinases, signaling proteins associate with the activated receptor (e.g., STAT4), and the signaling proteins in turn become phosphorylated. In the IL-12 signaling network, phosphorylated STAT4 translocates to the nucleus to promote the transcription of various response genes. A subset of these signaling pathways that lead to different cellular behaviors is depicted in Figure 3. These signaling proteins contain multiple functional protein motifs such as modification sites (tyrosine residues), protein interaction domains (e.g., SH2 domains on STAT4), and enzymatic sites.42 These transformations can be depicted as a series of reaction rate laws, as enumerated in Supplemental file 1: Table S6, that can be grouped into reaction rules, shown in Table 1. These reaction rules were used to generate a reaction network for the signaling events associated with IL-12 signaling. We assumed a priori that reactions associated with ATP exchange and changes in protein conformation are associated with the fast kinetic manifold and were not explicitly represented. The resulting reaction network was encoded into a series of ordinary differential equations, as described previously.41 The mathematical model was calibrated to dynamic measurements of components of the IL-12 signaling pathway obtained using primary näive CD62L+ CD4+ T cells, as shown in Figure 3B.
Table 1. Reaction Rules.
List of reaction rules used to describe early signaling events following IL-12 stimulation of CD4+ T cells.
| Reaction rule |
Description | Timescale (seconds) |
|---|---|---|
| R1 | Degradation of inactive receptor | 8.51 × 103 |
| R2 | Degradation of active (ligand-bound) receptor | 4.46 × 103 |
| R3 | Basal synthesis of TYK2 | 1.58 × 1015 |
| R4 | Basal synthesis of JAK2 | 1.00 × 1016 |
| R5 | Ligand binding to receptor | 1.29 × 103 |
| R6 | TYK2 binding to receptor | 3.55 × 10−4+ |
| R7 | JAK2 binding to receptor | 8.37 × 10−4+ |
| R8 | Inactive STAT4c binding to activated receptor complex | 3.10 × 10−3+ |
| R9 | Phosphorylation of STAT4c by the activated receptor complex | 2.06 × 100+ |
| R10 | Dimerization of phosphorylated STAT4 | 6.00 × 102+ |
| R11 | Export of STAT4 from cytosol to nucleus | 2.00 × 102 |
| R12 | Protein phosphatase binding to active STAT4 in nucleus | 1.30 × 10−3+ |
| R13 | Dephosphorylation of STAT4n by protein phosphatase | 2.39 × 102+ |
| R14 | Export of inactive STAT4 from nucleus to cytosol | 2.00 × 101 |
| R15 | Transcription of SOCS mRNA by active STAT4 | 3.16 × 105+ |
| R16 | SOCS binding to activated receptor complex | 7.24 × 102 |
| R17 | Transcription of IL-12R mRNA by active STAT4 | 1.00 × 1021 |
| R18 | Autonomous program for basal synthesis of IL-12R mRNA | 8.91 × 10−2 |
| R19 | Export of mRNA from nucleus to ribosomes in cytosol | 3.55 × 103 |
| R20 | Synthesis of IL-12R from mRNA | 3.16 × 1019 |
| R21 | Degradation of mRNA in the cytosol | 1.26 × 103 |
| R22 | Transport of intracellular IL-12R to cell membrane | 2.57 × 103 |
| R23 | Synthesis of SOCS from mRNA | 4.07 × 103 |
| R24 | Protein degradation | 6.46 × 103 |
timescale changes as a function of time (see Figure 5). Average value is reported.
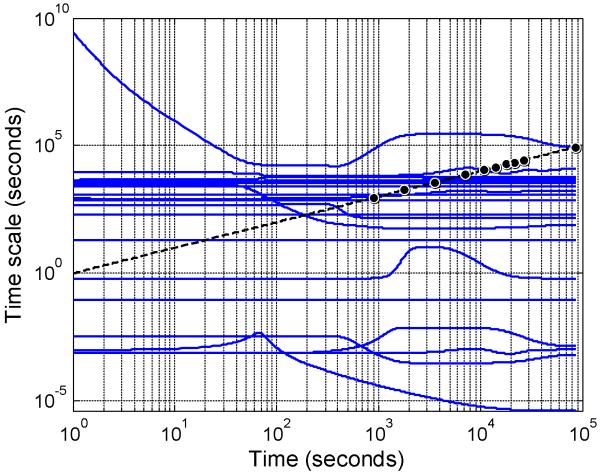
This mathematical model predicts the change in concentration of 28 species (i.e., n = 28) using 48 rate laws (i.e., m = 48). These rate laws were derived from 24 reaction rules (i.e., nRS = 24). Using the dynamic trajectories in species space, the Jacobian of the reaction rules with respect to species (i.e., ) were calculated at a series of time points and used to estimate the timescale of reaction rule i (i.e., τi) as a function of time. A representative , evaluated at 30 minutes, and the corresponding timescales are shown in Supplemental File 2. Collectively, the timescales associated with the simulation of IL-12 signaling in CD4+ T cells are shown in Figure 4. As highlighted by the circles shown along the dotted line in Figure 4, the time points associated with experimental observations bracket the range of timescales that can be observed during a given experiment. Generally, there are three groups of timescales that can be identified: (1) “fast” kinetic events, (2) “observable” kinetic events, and (3) “exceedingly slow” or stationary kinetic events. In this experiment, reactions associated with rules that exhibit timescales greater than 1 × 105 seconds are considered exceedingly slow or stationary. Reaction rules that exhibit timescales less than 1 × 103 seconds are considered fast and may exist at pseudo-equilibrium during the experiment. Reaction rules that exhibit timescales between 1 × 103 and 1 × 105 seconds are considered observable. Observing the system at longer time points (e.g., 24, 48, and 72 hours) would increase the range of observable timescales. However, these longer times points may also increase the influence of extrinsic factors (e.g., consumption of metabolites or growth factors in the cell culture media) on the observed system response and render the model unable to capture these additional influences.
Figure 4. Temporal profiles of timescales associated with singular value decomposition of the Jacobian of the set of reaction rules, .
The dotted line is a diagonal line where the biological timescale (y-axis) equals the experimental time (x-axis). The experimental time points are indicated along the dotted line by the circles. Timescales for reaction rules that are below 103 or are above 105 seconds are not practically identifiable, given the experimental design. Time scales associated with the 21 largest singular values are shown (solid blue lines). Three additional singular values were determined and correspond to timescales greater than 1.0 × 1010 seconds (data not shown).
Using the weighting coefficients contained within , we identified timescales associated with each reaction rule, as shown in Table 1. Many of the reaction rules exhibited constant timescales during the simulation period, as highlighted by the horizontal lines in Figure 4. A subset of the reaction rules exhibited dynamically changing timescales due to underlying changes in protein expression, as highlighted in Figure 5. It is possible for reactions associated with specific reaction rules to move between the timescale categories, and this might occur, for example, in response to the change in either protein expression or activation state. One example was Reaction Rule 10, dimerization of pSTAT4, that switched from an observable timescale (τ10 = 3.2 × 103 seconds) to a faster time scale (τ10 = 1.0 × 102 seconds) around 102 seconds. This occurred at approximately the same time as STAT4 was becoming phosphorylated in response to IL-12 stimulation (see Figure 3B). The faster timescale associated with pSTAT4 dimerization is consistent with a diffusion-limited on-rate.48 However, the fast timescale may also suggest that STAT4 may exist as pre-formed dimers prior to receptor-induced phosphorylation, as experimentally observed by Ota et al.49
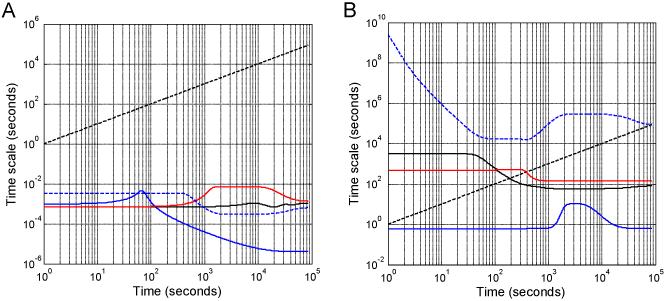
Figure 5. The reaction rules are shown with timescales that dynamically change.
In panel A, temporal profiles are shown for timescales associated with reaction rules: TYK2 binding to receptor (R6 - blue solid line), JAK2 binding to receptor (R7 - black solid line), inactive STAT4c binding to activated receptor complex (R8 - red solid line), and protein phosphatase binding to active STAT4 in nucleus (R12 - blue dashed line). In panel B, the timescales for phosphorylation of STAT4c by the activated receptor complex (R9 - blue solid line), dimerization of phosphorylated STAT4 (R10 - black solid line), dephosphorylation of STAT4n by protein phosphatase (R13 - red solid line), and transcription of SOCS mRNA by active STAT4 (R15 - blue dashed line) are also shown as a function of time. The dotted line is a diagonal line where the biological timescale (y-axis) equals the experimental time (x-axis).
The reaction rules can be associated with different kinetic manifolds based upon their associated timescales. The reaction rules identified as kinetically important with respect to the observed biological response are of particular interest if one wishes to modify the dynamics of cellular response. For example, binding of IL-12 to its receptor was found to have a timescale similar to the observed biological response - approximately 20 minutes. IL-12 binding to the receptor was slightly faster than the dynamics of receptor turnover (e.g., IL-12R transport and IL-12R degradation). Although we did not include trafficking of the bound receptor to internal endosomal compartments, the timescales identified by this analysis are consistent with nanoscale transport, which occurs on the order of minutes.50,51 In addition, timescale analysis suggests that binding of TYK2 and JAK2 with IL-12R was at pseudo-equilibrium and that these Janus kinases have already formed a complex with the receptor before the system sees IL-12. This is consistent with the experimental results from Zou et al. who reported that TYK2 and JAK2 are pre-associated with IL-12R via cytoplasmic regions of the receptor.52 In contrast to TYK2 and JAK2 binding, the basal synthesis of JAK2 and TYK2 exhibited slow timescales. This was expected as the reaction rules for JAK2 and TYK2 were specified as constitutive rate laws, whose derivative with respect to concentration is zero. The difference in timescales between pSTAT4-induced and autonomous program-regulated transcription of mRNA for the IL-12 receptor is consistent with the reaction flux reported by Finley et al.41 In particular, the mathematical model predicted that IL-12 receptor expression is regulated via a dynamic, autonomous program that was independent of STAT4 activation. In summary, this analysis suggests that the reaction rules associated with JAK2 and TYK2 association with IL-12R do not need to be explicitly represented. Instead, the receptor can be represented as a multi-protein complex that includes IL-12R and the associated Janus kinases. Moreover, the rapid dimerization of pSTAT4 suggests that STAT4 does not need to be represented separately as a monomer and homodimer but can be represented as a single entity with two activation states.
As the timescale estimates for the reactions associated with each reaction rule should be thought of as probabilistic distributions rather than single point estimates,53 we used an empirical Bayesian approach to estimate the uncertainty in the timescale estimates.44 Specifically, we used samples drawn from the converged segment of three Markov chains, reported previously,41 that describe the posterior distribution in the model parameters, given the available data. The distributions in timescales for a subset of the reaction rules are shown in Figure 6, with the remaining reaction rules shown in Supplemental File 1: Figure S1. The distribution in timescales for the reaction rules that are associated with the different kinetic manifolds are consistent with the slaving principle,38 which is analogous to the concept of a rate-limiting step. The slaving principle suggests that the dynamic evolution in the system is constrained by the observable variables (i.e., the slow kinetic manifold). In contrast, the fast variables, which exist at a pseudo-equilibrium, and the stationary variables have minimal impact on system response. This implies that the timescales associated with the fast and stationary kinetic manifolds exhibit one-sided distributions, as shown in Figure 6. The timescales associated with a variable contained within the fast kinetic manifold may be decreased below a threshold value with minimal impact on the dynamic response of the system. Above the threshold value, the dynamics of the corresponding variables impinge upon the observational kinetic manifold altering the dynamic response of the system and ability of the model to capture the experimental trends. In contrast, the timescales of reaction rules that correspond to the observable kinetic manifold exhibit posterior distributions that are bounded. As these distributions in timescales are empirical Bayesian estimates, the variance in the distributions can be interpreted as how well does the given data inform or constrain the estimated timescales. The reaction rules that correspond to receptor turnover (i.e., R1 and R2) are highly informed by the available data and exhibit low variance (i.e., we are highly confident in the estimated values). In contrast, the reaction rules associated with JAK2 and TYK2 binding to the receptor (i.e., R6 and R7) are not well constrained by the data. We are only confident that the timescales for these two reaction rules are less than 1 second.
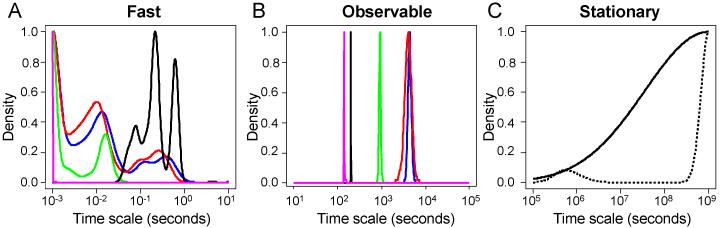
Figure 6. The posterior distribution in timescales associated with a subset of reaction rules.
The posterior distribution in timescales for reactions associated with reaction rules that associate with the fast (panel A), observable (panel B), and stationary (panel C) kinetic manifolds. In panel A, the fast kinetic manifold includes phosphatase binding to pSTAT4 in nucleus (R12 - purple), pSTAT4 dimerization (R10 - black), STAT4 phosphorylation (R9 - green), JAK2 binding to receptor (R7 - red), and TYK2 binding to receptor (R6 - blue). In panel B, the observable kinetic manifold includes pSTAT4 dimer deactivation (R13 - purple), nuclear import of pSTAT4 (R11 - black), IL-12 binding to receptor (R5 - green), degradation of activated IL-12R (R2 - red), and degradation of unactivated IL-12R (R1 - blue). In panel C, the stationary kinetic manifold includes pSTAT4-induced IL12R mRNA transcription (R17 - black dotted) and JAK2 and TYK2 synthesis (R3/R4 - black).
Using this timescale information, we created a simplified model of the IL-12 signaling network where reactions associated with rules that exhibited fast timescales were eliminated in favor of pseudo-equilibrium relationships, as similarly described for competitive binding of ligands to a receptor.54 Specifically, pseudo-equilibrium relationships were developed for STAT4 and SOCS interacting with the activated IL-12 receptor complex (i.e., Reaction rules 8 and 16, respectively) and for nuclear protein phosphatase (XPP) interacting with activated STAT4 (i.e., reaction rule 12). In addition, the interaction of the Janus kinases, JAK2 and TYK2, with the IL-12 receptor were assumed to be a pre-formed complex instead of dynamically assembling upon ligand binding (i.e., reaction rules 6 and 7). As summarized in Figure 7A, the IL12R species in the simplified model represents a multi-protein complex comprised of IL12Rβ1, IL12Rβ2, Tyk2, and Jak2. The resulting reaction network was reduced from 28 species to 15 species. The time required to evaluate the likelihood function in the empirical Bayesian algorithm was reduced from 1.705 to 0.451 seconds, which reduced the time needed to calculate an AMCMC chain containing 500,000 steps from 10 to 2.5 days. The posterior distributions in the model predictions (see Figure 7B) and model parameters were similar between the Full and Simplified models (i.e., compare Figure 5 in41 to Supplemental File 1: Figure S5).
Figure 7. Timescale analysis was used to create a simplified rule-based model for early signaling events associated with IL-12 signaling.
(Panel A) Schematic of the Simplified IL-12 signaling model based upon the timescale analysis of the full model. The major modifications include: representing the IL-12 receptor as a multi-protein complex comprised of IL-12Rβ1, IL-12Rβ2, JAK2, and TYK2; representing STAT4 and SOCS interacting with the IL-12 receptor as a competitive pseudo-equilibrium process; and representing nuclear STAT4 interacting with protein phosphatase (XPP) as a pseudo-equilibrium process. Labels that annotate the arrows in the diagram correspond to the reaction rules shown in Table 1. (Panel B) The experimental observations (squares41,43) are compared against the posterior distribution in the simulated results for the simplified model (blue lines) and for the full model (red lines). The most likely predictions are represented by the solid lines. The dashed lines enclose the 95% confidence intervals. (subpanel 1) Phosphorylated STAT4 normalized to the level of IL-12Rβ2 expression on a cellular basis. (subpanel 2) IL-12 bound to IL-12R. (subpanel 3) Phosphorylated form of STAT4 reported as a percentage of the maximum STAT4 activity. (subpanel 4) Total IL-12Rβ2 expression.
Concluding thoughts
While the use of rule-based methods to model biochemical reaction networks is an area of contemporary interest (e.g.,20), it is analogous to using reaction rules to model conventional complex chemical systems, like organic chemistry.21 In the analysis of these conventional chemical systems, there is a rich history in applying rule-based methods (see55,56 for pertinent reviews). Common attributes include the use of computer algorithms to encode species and developing reaction networks that account for combinatorial complexity. One of the major differences is in our prior knowledge of the relevant thermodynamics and kinetics for the system of interest. In conventional chemical systems with relatively small molecules, computational quantum chemistry methods and kinetic correlations have been useful for constraining the reaction energetics and corresponding kinetic parameters. Kinetic correlations, such as the Evans-Polanyi linear free energy relationships, provide a first-order adjustment to the rate constants assigned to a particular reaction using a reactivity index, such as the change in Gibbs free energy upon reaction. In contrast to conventional chemical systems, the computational burden associated with modeling large biological molecules coupled with observing distributions in conformational states experimentally present significant technological challenges in biochemical systems. However, recent developments on both the computational (e.g.,57) and experimental sides (e.g.,58) provide encouraging signs. As a bridge between prior knowledge and the desire to better understand a new system, empirical Bayesian methods, as used here, provide a mechanism to establish a level of confidence in the kinetic parameters that can be obtained from the specific data at hand, given prior knowledge of relevant proteins and their interactions (i.e., reaction thermodynamics, kinetics, and rules).
In summary, timescale analysis is one approach typically used to identify important aspects that regulate system behavior.59 Classical timescale analysis focuses on identifying the timescales associated with net changes in the concentrations of reacting species - i.e., the nodes in reaction networks. In this work, we have refined the theory associated with timescale analysis to enable identifying timescales associated with similar patterns or rules in which reacting species interact or are transformed - i.e., subsets of similar edges in reaction networks. This shift from a focus on nodes to edges is a subtle but important distinction, especially considering the iterative nature of model-based inference. In the context of rule-based models, classical timescale analysis is an ad hoc approach applied to an existing reaction network and is used to identify nodes that can be removed from the network. This approach may be more difficult to implement in an iterative model-based inference setting, as one needs to be able to generate the reaction network before the network can be simplified. By identifying the timescales associated with particular rules, new rules can be created that reflect this timescale information and can be used as prior information in the subsequent iteration of model-based inference. The IL-12 signaling example illustrates this step, whereby rules associated with STAT4 binding with protein phosphatase and TYK2/JAK2 association with the IL-12 receptor were revised to reflect the existence of pre-formed multi-protein complexes. By limiting network generation to a smaller subset of rules, the computational efficiency of model-based inference was improved by limiting the size of the overall reaction network. From the biological perspective, complexes comprised of multiple proteins - i.e., macromolecular machines - regulate most cellular processes. One of the current challenges in systems biology is trying to understand the cellular context in which multi-protein complexes are formed. The IL-12 signaling example also illustrates how timescale analysis of reaction rules can be used to identify proteins that exist as pre-formed multi-protein complexes and that are dynamically regulated. Ultimately, this approach complements existing rank- and flux-based methods that can be used to interrogate complex reaction networks, as summarized in Figure 1. Collectively, these analysis methods provide a suite of computational tools that can be used to reveal additional insight into how the underlying biochemistry within a cell regulates cellular behavior.
Supplementary Material
Supplemental File 1 - Simple Rule-based Model Example and Simplified IL-12 Model definition
The supplemental PDF file provides additional information regarding: 1) Comment on kinetic Monte Carlo methods for generating reaction networks; 2) a simple example of calculating the timescales of reaction rules; 3) the posterior distribution in the timescales associated with a subset of reaction rules, not shown in Figure 6; 4) the specification of the mathematical model for the Simplified IL-12 signaling network; and 5) the empirical Bayesian results for obtaining the posterior distribution in Simplified IL-12 model predictions.
Supplemental File 2 - Timescale values at 30 minutes
The supplemental Excel file contains two worksheets that provide additional information regarding: 1) values for the weighting coefficient of a given timescale (column) onto a reaction rule (row) evaluated at 30 minutes; and 2) values for the singular values, , and timescales, τi, at 30 minutes.
Supplemental File 3 - MatLab code for Ligand-induced receptor activation example
The supplemental zipped MatLab file contains the MatLab scripts that encode and execute the timescale analysis of the simple ligand-induced receptor activation example.
Acknowledgments
The authors thank Adam M. Halász and Miles S. Okino for their constructive comments and Brandon Dolly for assistance in analyzing the data. This work was supported by grants from the National Science Foundation (NSF) CAREER 1053490, the National Cancer Institute (NCI) R15CA123123, and the National Institute of Allergy and Infectious Disease (NIAID) R56AI076221. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NSF, the NCI, the NIAID, or the National Institutes of Health.
Literature Cited
- [1].Asthagiri AR, Lauffenburger DA. Bioengineering Models of Cell Signaling. Ann Rev Biomed Eng. 2000;2:31–53. doi: 10.1146/annurev.bioeng.2.1.31. [DOI] [PubMed] [Google Scholar]
- [2].Yaffe MB. Signaling Networks and Mathematics. Sci Signal. 2008;1:eg7. doi: 10.1126/scisignal.143eg7. [DOI] [PubMed] [Google Scholar]
- [3].Kholodenko BN, Demin OV, Moehren G, Hoek JB. Quantification of short term signaling by the epidermal growth factor receptor. J Biol Chem. 1999;274:30169–30181. doi: 10.1074/jbc.274.42.30169. [DOI] [PubMed] [Google Scholar]
- [4].Schoeberl B, Eichler-Jonsson C, Giles ED, Muller G. Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors. Nat Biotechnol. 2002;20:370–376. doi: 10.1038/nbt0402-370. [DOI] [PubMed] [Google Scholar]
- [5].Birtwistle MR, Hatakeyama M, Yumoto N, Ogunnaike BA, Hoek JB, Kholodenko BN. Ligand-dependent responses of the ErbB signaling network: experimental ad modeling analyses. Mol Syst Biol. 2007;3:1–16. doi: 10.1038/msb4100188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Bhalla US. Models of cell signaling pathways. Curr Opin Genet Dev. 2004;14:375–381. doi: 10.1016/j.gde.2004.05.002. [DOI] [PubMed] [Google Scholar]
- [7].Forsythe RG, Mavrovouniotis ML. Model Reduction in the Computational Modeling of Reaction Systems. J Chem Inf Comput Sci. 1997;37:258–264. doi: 10.1021/ci950184e. [DOI] [PubMed] [Google Scholar]
- [8].Broadbelt LJ, Stark SM, Klein MT. Computer generated pyrolysis modeling: On-the-fly generation of species, reactions, and rates. Ind & Eng Chem Res. 1994;33:790–799. [Google Scholar]
- [9].Broadbelt LJ, Stark SM, Klein MT. Termination of computer-generated reaction mechanisms: species rank-based convergence criterion. Ind & Eng Chem Res. 1995;34:2566–2573. [Google Scholar]
- [10].Broadbelt LJ, Stark SM, Klein MT. Computer generated reaction modelling: decomposition and encoding algorithms for determining species uniqueness. Comput & Chem Eng. 1996;20:113–129. [Google Scholar]
- [11].Klinke DJ, Broadbelt LJ. Mechanism Reduction during Computer Generation of Compact Reaction Models. AIChE J. 1997;43:1828–1837. [Google Scholar]
- [12].Klinke DJ, Broadbelt LJ. Construction of a Mechanistic Model of Fischer-Tropsch Synthesis on Ni(111) and Co(0001) Surfaces. Chem Eng Sci. 1999;54:3379–3389. [Google Scholar]
- [13].Hatzimanikatis V, Li C, Ionita JA, Henry CS, Jankowski MD, Broadbelt LJ. Exploring the diversity of complex metabolic networks. Bioinformatics. 2005;21:1603–1609. doi: 10.1093/bioinformatics/bti213. [DOI] [PubMed] [Google Scholar]
- [14].Finley SD, Broadbelt LJ, Hatzimanikatis V. Computational Framework for Predictive Biodegradation. Biotechnol Bioeng. 2009;104:1086–1097. doi: 10.1002/bit.22489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Blinov ML, Faeder JR, Goldstein B, Hlavacek WS. BioNetGen: software for rule-based modeling of signal transduction based on the interactions of molecular domains. Bioinform. 2004;20:3289–3291. doi: 10.1093/bioinformatics/bth378. [DOI] [PubMed] [Google Scholar]
- [16].Fages F, Soliman S, Chabrier-Rivier N. Modelling and querying interaction networks in the biochemical abstract machine BIOCHAM. J Biol Phys Chem. 2004;4:64–73. [Google Scholar]
- [17].Lok L, Brent R. Automatic generation of cellular reaction networks with Moleculizer 1.0. Nat Biotechnol. 2005;23:131–136. doi: 10.1038/nbt1054. [DOI] [PubMed] [Google Scholar]
- [18].Meier-Schellersheim M, Xu X, Angermann B, Kunkel EJ, Jin T, Germain RN. Key role of local regulation in chemosensing revealed by a new molecular interaction-based modeling method. PLoS Comput Biol. 2006;2:e82. doi: 10.1371/journal.pcbi.0020082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Blinov ML, Faeder JR, Goldstein B, Hlavacek WS. A Network Model of Early Events in Epidermal Growth Factor Receptor Signaling That Accounts for Combinatorial Complexity. Biosystems. 2006;83:136–151. doi: 10.1016/j.biosystems.2005.06.014. [DOI] [PubMed] [Google Scholar]
- [20].Faeder JR, Blinov ML, Hlavacek WS. Rule-Based Modeling of Biochemical Systems With BioNetGen. Methods Mol Biol. 2009;500:113–167. doi: 10.1007/978-1-59745-525-1_5. [DOI] [PubMed] [Google Scholar]
- [21].Feret J, Danos V, Krivine J, Harmer R, Fontana W. Internal coarse-graining of molecular systems. Proc Natl Acad Sci USA. 2009;106:6453–6458. doi: 10.1073/pnas.0809908106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Hlavacek WS, Faeder JR, Blinov ML, Perelson AS, Goldstein B. The Complexity of Complexes in Signal Transduction. Biotechnol Bioeng. 2003;84:783–794. doi: 10.1002/bit.10842. [DOI] [PubMed] [Google Scholar]
- [23].Neurock M, Libanati C, Nigam A, Klein MT. Monte-Carlo Simulation of Complex-Reaction Systems - Molecular-Structure and Reactivity in Modeling Heavy Oils. Chem Eng Sci. 1990;45:2083–2088. [Google Scholar]
- [24].Libanati C, Broadbelt L, Lamarca C, Klein MT, Andrews SM, Cotter RJ. Mechanistic Modeling Of Polymer Pyrolysis Using Monte-Carlo Methods. Mol Simulation. 1993;11:187–204. [Google Scholar]
- [25].Susnow RG, Dean AM, Green WH, Broadbelt LJ. Rate-Based Construction of Kinetic Models for Complex Systems. J Phys Chem A. 1997;101:3731–3740. [Google Scholar]
- [26].Borisov NM, Chistopolsky AS, Faeder JR, Kholodenko BN. Domain-oriented reduction of rule-based network models. IET Syst Biol. 2008;2:342–351. doi: 10.1049/iet-syb:20070081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Conzelmann H, Saez-Rodriguez J, Sauter T, Kholodenko B, Gilles E. A domain-oriented approach to the reduction of combinatorial complexity in signal transduction networks. BMC Bioinformatics. 2006;7:34. doi: 10.1186/1471-2105-7-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Koschorreck M, Conzelmann H, Ebert S, Ederer M, Gilles ED. Reduced modeling of signal transduction - a modular approach. BMC Bioinformatics. 2007;8:336. doi: 10.1186/1471-2105-8-336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Klinke DJ. Signal Transduction Networks in Cancer: Quantitative Parameters Influence Network Topology. Cancer Res. 2010;70:1773–1782. doi: 10.1158/0008-5472.CAN-09-3234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Sachs K, Perez O, Peer D, Lauffenburger DA, Nolan GP. Causal protein-signaling networks derived from multiparameter single-cell data. Science. 2005;308:523–529. doi: 10.1126/science.1105809. [DOI] [PubMed] [Google Scholar]
- [31].Schaub MA, Henzinger TA, Fisher J. Qualitative networks: a symbolic approach to analyze biological signaling networks. BMC Syst Biol. 2007;1:4. doi: 10.1186/1752-0509-1-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Ruths D, Muller M, Tseng JT, Nakhleh L, Ram PT. The signaling petri net-based simulator: a non-parametric strategy for characterizing the dynamics of cell-specific signaling networks. PLoS Comput Biol. 2008;4:e1000005. doi: 10.1371/journal.pcbi.1000005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Yang J, Monine MI, Faeder JR, Hlavacek WS. Kinetic Monte Carlo Method for Rule-Based Modeling of Biochemical Networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2008;78:031910. doi: 10.1103/PhysRevE.78.031910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Papin JA, Hunter T, Palsson BO, Subramaniam S. Reconstruction of Cellular Signalling Networks and Analysis of Their Properties. Nat Rev Mol Cell Biol. 2005;6:99–111. doi: 10.1038/nrm1570. [DOI] [PubMed] [Google Scholar]
- [35].Maas U, Pope SB. Simplifying Chemical-Kinetics - Intrinsic Low-Dimensional Manifolds in Composition Space. Combust Flame. 1992;88:239–264. [Google Scholar]
- [36].Lam SH, Goussis DA. The CSP Method for Simplifying Kinetics. Int J Chem Kinet. 1994;26:461–486. [Google Scholar]
- [37].Okino MS, Mavrovouniotis ML. Simplification of chemical reaction systems by time-scale analysis. Chem Eng Commun. 1999;176:115–131. [Google Scholar]
- [38].Haken H. Synergetics Introduction and Advanced Topics. Springer-Verlag; New York, NY: 2004. [Google Scholar]
- [39].Delgado J, Liao JC. Control of Metabolic Pathways by Time-Scale Separation. Biosystems. 1995;36:55–70. doi: 10.1016/0303-2647(95)01528-s. [DOI] [PubMed] [Google Scholar]
- [40].Jamshidi N, Palsson BO. Top-Down Analysis of Temporal Hierarchy in Biochemical Reaction Networks. PLoS Comput Biol. 2008;4:e1000177. doi: 10.1371/journal.pcbi.1000177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Finley SD, Gupta D, Cheng N, Klinke DJ. Inferring Relevant Control Mechanisms for Interleukin-12 Signaling within Naive CD4+ T cells. Immunol Cell Biol. 2011;89:100–110. doi: 10.1038/icb.2010.69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Pawson T, Nash P. Assembly of cell regulatory systems through protein interaction domains. Science. 2003;300:445–452. doi: 10.1126/science.1083653. [DOI] [PubMed] [Google Scholar]
- [43].Chizzonite R, Truitt T, Desai BB, Nunes P, Podlaski FJ, Stern AS, Gately MK. IL-12 receptor I. Characterization of the receptor on phytohemagglutinin-activated human lymphoblasts. J Immunol. 1992;148:3117–3124. [PubMed] [Google Scholar]
- [44].Klinke DJ. An empirical Bayesian approach for model-based inference of cellular signaling networks. BMC Bioinform. 2009;10:371. doi: 10.1186/1471-2105-10-371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Moore JW, Pearson RG. Kinetics and Mechanisms. A Study of Homogeneous Chemical Reactions. Third edn John Wiley & Sons; New York: 1981. [Google Scholar]
- [46].Wanant D, Quon MJ. Insulin receptor binding kinetics: modeling and simulation studies. J Theor Biol. 2002;205:355–364. doi: 10.1006/jtbi.2000.2069. [DOI] [PubMed] [Google Scholar]
- [47].Sedaghat AR, Sherman A, Quon MJ. A mathematical model of metabolic insulin signaling pathways. A J Physiol Endocrinol Metab. 2002;283:E1084–E1101. doi: 10.1152/ajpendo.00571.2001. [DOI] [PubMed] [Google Scholar]
- [48].Moran U, Phillips R, Milo R. SnapShot: key numbers in biology. Cell. 2010;141:1262, e1. doi: 10.1016/j.cell.2010.06.019. [DOI] [PubMed] [Google Scholar]
- [49].Ota N, Brett TJ, Murphy TL, Fremont DH, Murphy KM. N-Domain-Dependent Nonphosphorylated STAT4 Dimers Required for Cytokine-Driven Activation. Nat Immunol. 2004;5:208–215. doi: 10.1038/ni1032. [DOI] [PubMed] [Google Scholar]
- [50].Lauffenburger DA, Linderman JJ. Receptors: Models for binding, trafficking and signaling. Oxford University Press; New York: 1993. [Google Scholar]
- [51].Linderman JJ, Lauffenburger DA. Analysis of intracellular receptor/ligand sorting. Biophys J. 1986;50:295–305. doi: 10.1016/S0006-3495(86)83463-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Zou J, Presky DH, Wu CY, Gubler U. Differential associations between the cytoplasmic regions of the Interleukin-12 receptor subunits beta1 and beta2 and JAK kinases. J Biol Chem. 1997;272:6073–6077. doi: 10.1074/jbc.272.9.6073. [DOI] [PubMed] [Google Scholar]
- [53].Chen WW, Niepel M, Sorger PK. Classic and contemporary approaches to modeling biochemical reactions. Genes Dev. 2010;24:1861–1875. doi: 10.1101/gad.1945410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Klinke DJ. The ratio of p40 monomer to dimer is an important determinant of IL-12 bioactivity. J Theor Biol. 2006;240:323–335. doi: 10.1016/j.jtbi.2005.09.022. [DOI] [PubMed] [Google Scholar]
- [55].Broadbelt LJ, Pfaendtner J. Lexicography of kinetic modeling of complex reaction networks. AIChE J. 2005;51:2112–2121. [Google Scholar]
- [56].Green WH. Predictive kinetics: A new approach for the 21st century. Adv Chem Eng. 2007;32:1–50. [Google Scholar]
- [57].Schlick T, Collepardo-Guevara R, Halvorsen LA, Jung S, Xiao X. Biomolecular modeling and simulation: a field coming of age. Q Rev Biophys. 2011;44:191–228. doi: 10.1017/S0033583510000284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Bai F, Branch RW, Nicolau DV, Pilizota T, Steel BC, Maini PK, Berry RM. Conformational spread as a mechanism for cooperativity in the bacterial flagellar switch. Science. 2010;327:685–689. doi: 10.1126/science.1182105. [DOI] [PubMed] [Google Scholar]
- [59].Klinke DJ. A Multiscale Systems Perspective on Cancer, Immunotherapy, and Interleukin-12. Mol Cancer. 2010;9:242. doi: 10.1186/1476-4598-9-242. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental File 1 - Simple Rule-based Model Example and Simplified IL-12 Model definition
The supplemental PDF file provides additional information regarding: 1) Comment on kinetic Monte Carlo methods for generating reaction networks; 2) a simple example of calculating the timescales of reaction rules; 3) the posterior distribution in the timescales associated with a subset of reaction rules, not shown in Figure 6; 4) the specification of the mathematical model for the Simplified IL-12 signaling network; and 5) the empirical Bayesian results for obtaining the posterior distribution in Simplified IL-12 model predictions.
Supplemental File 2 - Timescale values at 30 minutes
The supplemental Excel file contains two worksheets that provide additional information regarding: 1) values for the weighting coefficient of a given timescale (column) onto a reaction rule (row) evaluated at 30 minutes; and 2) values for the singular values, , and timescales, τi, at 30 minutes.
Supplemental File 3 - MatLab code for Ligand-induced receptor activation example
The supplemental zipped MatLab file contains the MatLab scripts that encode and execute the timescale analysis of the simple ligand-induced receptor activation example.