Rapid acquisition but slow extinction of an attentional bias in space

Abstract

Substantial research has focused on the allocation of spatial attention based on goals or perceptual salience. In everyday life, however, people also direct attention using their previous experience. Here we investigate the pace at which people incidentally learn to prioritize specific locations. Participants searched for a T among Ls in a visual search task. Unbeknownst to them, the target was more often located in one region of the screen than in other regions. An attentional bias toward the rich region developed over dozens of trials. However, the bias did not rapidly readjust to new contexts. It persisted for at least a week and for hundreds of trials after the target’s position became evenly distributed. The persistence of the bias did not reflect a long window over which visual statistics were calculated. Long-term persistence differentiates incidentally learned attentional biases from the more flexible goal-driven attention.

Introduction

Humans live in a complex visual environment. At any moment, the amount of visual input exceeds what one can perceive and respond to. Adaptive functioning depends on our ability to prioritize a subset of visual input. Previous research has emphasized the significance of two sources of attention: an observer’s goal and perceptually salient stimuli. In everyday life, spatial attention is also frequently driven by one’s previous experience, often in an implicit manner (Chun & Jiang, 1998; Reber, 1993). Here we ask: How quickly can people incidentally learn to prioritize important locations from experience, and how quickly does the learned bias adjust after training has discontinued?

Our research focuses on the adaptability of experience-driven attention, particularly how incidentally learned attention generalizes to new contexts. Unlike goal-driven attention, experience-driven attention requires neither the intention to learn nor the intention to use past experience to bias spatial attention. Goal-driven attention is flexible and can be adjusted on a trial-by-trial basis. For example, endogenous cuing often relies on a spatial cue, such as a centrally presented arrow, that informs people where to attend next (Posner, 1980). The cue changes from trial to trial, yet within about 300 ms of seeing the cue, people can effectively attend to the cued location (Müller & Rabbitt, 1989). Rapid readjustment is also demonstrated when the cue informs people what to attend to, as opposed to where (Vickery, King, & Jiang, 2005; Woodman & Arita, 2011).

Similarly, bottom-up (or stimulus-driven) attention produces relatively short-lived effects. In studies on the phenomenon of “priming of pop-out”, participants search for an odd colored target such as a red diamond presented among green diamonds. The specific feature of the target on trial N, such as its color (red) and location (upper left), influences search speed on subsequent trials. Response time (RT) is faster if the target on trial N has the same color or location as the target on trial N-1 (Maljkovic & Nakayama, 1994, 1996). However, the facilitation is transient. It becomes undetectable when there are more than 8 intervening trials between the repetitions (Maljkovic & Nakayama, 1994, 1996).

These studies suggest that spatial attention can be quickly adjusted based on endogenous cues or the recent history of target features. Does a similar level of adaptability apply to incidentally learned attentional biases? Some evidence suggests that it does. Statistical learning of visual displays occurs rapidly. Within several repetitions, people can incidentally learn that certain shapes often co-occur or that there is a consistent association between a target’s location and its spatial context (Chun & Jiang, 1998; Fiser & Aslin, 2001; Turk-Brown, Jùnge, & Scholl, 2005). One way to characterize this type of visual statistical learning is that it reflects environmental regularities. As a result, attentional biases that reflect environmental regularities may be expected to rapidly emerge and flexibly adjust to new environmental contexts. However, the pace at which attentional biases are incidentally learned, and their adaptability to new contexts have not been directly investigated.

In addition to examining the adaptability of experience-driven attention to environmental changes, the present study addresses an unresolved debate about the relative importance of transient priming and long-term learning in location probability learning. In location probability learning the spatial distribution of a target in a search task is uneven: targets are more likely to appear in some locations (rich) than in others (sparse). Several studies have shown that participants locate a target more quickly when it appears in a rich location than in a sparse location (Geng & Behrmann, 2002, 2005; Logan, 1998; Miller, 1988; Shaw & Shaw, 1977; Umemoto, Scolari, Vogel, & Awh, 2010; Walthew & Gilchrist, 2006). Two factors could contribute to this advantage (Walthew & Gilchrist, 2006). One is transient priming, or better search when the target’s location on trial N matches the target’s location on trial N-1. Because location repetitions are more likely to occur in the rich locations than in the sparse locations, transient priming contributes to the RT advantage in the rich locations. Second is visual statistical learning. Visual statistical learning is the incidental learning of the target’s spatial distribution, or where the target is most likely to appear. Learning can be used to bias spatial attention toward the rich locations. Both transient priming and visual statistical learning could influence performance when the target is unevenly distributed.

Although other attempts to disentangle the effects of transient priming and visual statistical learning have been made, these studies have reached conflicting conclusions. In one study, Geng and Behrmann (2005) measured transient priming from the most recent trial or two-trials back. They found that location repetition significantly facilitated visual search RT. However, the facilitation was greater in the rich locations than in the sparse locations. The interaction between transient priming and the probability manipulation suggested to Geng and Behrmann (2005) that probability learning influenced search. The inference about learning is indirect, however, leaving open the possibility that probability learning is a relatively minor component. Indeed, a different conclusion was reached in a subsequent study. Walthew and Gilchrist (2006) presented items in 8 locations, 4 on one side and 4 on the other. The target appeared on the rich side 80% of the time. In one condition, the target’s location was unconstrained and could repeat from one trial to the next. Visual search, as measured by the accuracy of the first saccade toward the target, was superior when the target fell on the rich side of the screen rather than the sparse side. However, when the target’s location was constrained such that it did not repeat for four consecutive trials, the advantage in the rich side was eliminated. In other words, the removal of immediate repetition that produced transient priming also eliminated an advantage in locating the target on the rich side. Walthew and Gilchrist (2006) concluded that the target’s uneven distribution produced transient priming, but not long-term statistical learning.

Walthew and Gilchrist (2006)’s study is important in highlighting the significance of transient priming when learning a target’s likely location. At the same time, however, it may have gone too far in rejecting probability learning as an important source of spatial attention. To remove repetitions across four consecutive trials it was necessary to constrain the target’s location. This constraint may have introduced non-random visual statistics that could have interfered with probability learning.

An alternative approach to isolating the impact of probability cuing is to evaluate learning in a transfer (or testing) phase where transient priming is dissociated from probability cuing. The training phase involves an uneven distribution of the target’s location. During this phase transient priming and probability cuing are confounded – they both contribute to an advantage in the rich locations. The testing phase involves an even distribution of the target’s location. Because the target is evenly distributed, transient priming is equally likely to occur in any location. In addition, because transient priming is short-lived, soon (e.g., 8 trials) after the testing phase has started, the difference between the previously rich and sparse locations should disappear. On the other hand, probability cuing depends on the accumulation of visual statistics across multiple trials. Even if the learned attentional bias can be flexibly adjusted, the readjustment will likely take longer than just a few trials.

The present experiments therefore used a testing phase. The testing phase allowed us to 1) examine the persistence of experience-driven attentional biases in the face of changes in target distribution, and 2) to dissociate these effects from those of transient priming. In these experiments, we asked participants to search for a T among several Ls. Unbeknownst to them, the T appeared in one visual quadrant more often than in any of the other quadrants. After several hundred trials, training ended, and the spatial distribution of the target was modified. In Experiments 1, 2, and 4, the target was equally likely to appear in any quadrant during testing. In Experiment 3, the previously rich quadrant became sparse whereas a previously sparse quadrant became rich.

We expect that RT will be faster when the target appears in the rich rather than in the sparse quadrants during training. Of interest is whether or for how long the advantage remains after the spatial statistics have changed. The pace of extinction may differentiate experience-driven attention from the more flexible goal-driven attention. It will also bear on whether the advantage for targets that appear in rich locations reflects visual statistical learning rather than transient priming alone.

Experiment 1. Uneven, then even

In Experiment 1 participants searched for a T among 11 Ls. Unlike previous studies that have used a small number of item locations, the items could appear in any of 100 locations. This design reduced the likelihood that the target would repeat its location on consecutive trials. In the first half of the experiment the T appeared in one quadrant on 50% of the trials, three times more often than in any of the remaining three quadrants. For the second half of the experiment the T appeared in each of the four quadrants on 25% of the trials.

The main purpose of this experiment is to characterize i) the pace at which an advantage in the rich quadrant emerges during training, and ii) the pace at which this advantage disappears during testing.

Method

Participants

Participants in all experiments were students from the University of Minnesota. They were naïve to the purpose of the study. They all had normal or corrected-to-normal visual acuity. We obtained informed consent prior to the experiment. Participants were compensated $10/hour or extra course credits for their time.

There were 8 participants, 4 females and 4 males, in Experiment 1. Their mean age was 21 years old.

Materials and equipment

Participants completed the experiment individually in a room with normal interior lighting. Viewing distance was approximately 57cm but was unconstrained. Stimuli were presented on a 19” CRT monitor controlled by Psychtoolbox (Brainard, 1997; Pelli, 1997) implemented in MATLAB (http://www.mathworks.com).

Participants searched for a 90° rotated T among 0°, 90°, 180°, or 270° rotated Ls. Each item subtended 1.25°×1.25° and was positioned at randomly selected locations from an invisible 10×10 matrix (20°×20°). Items were white presented against a black background.

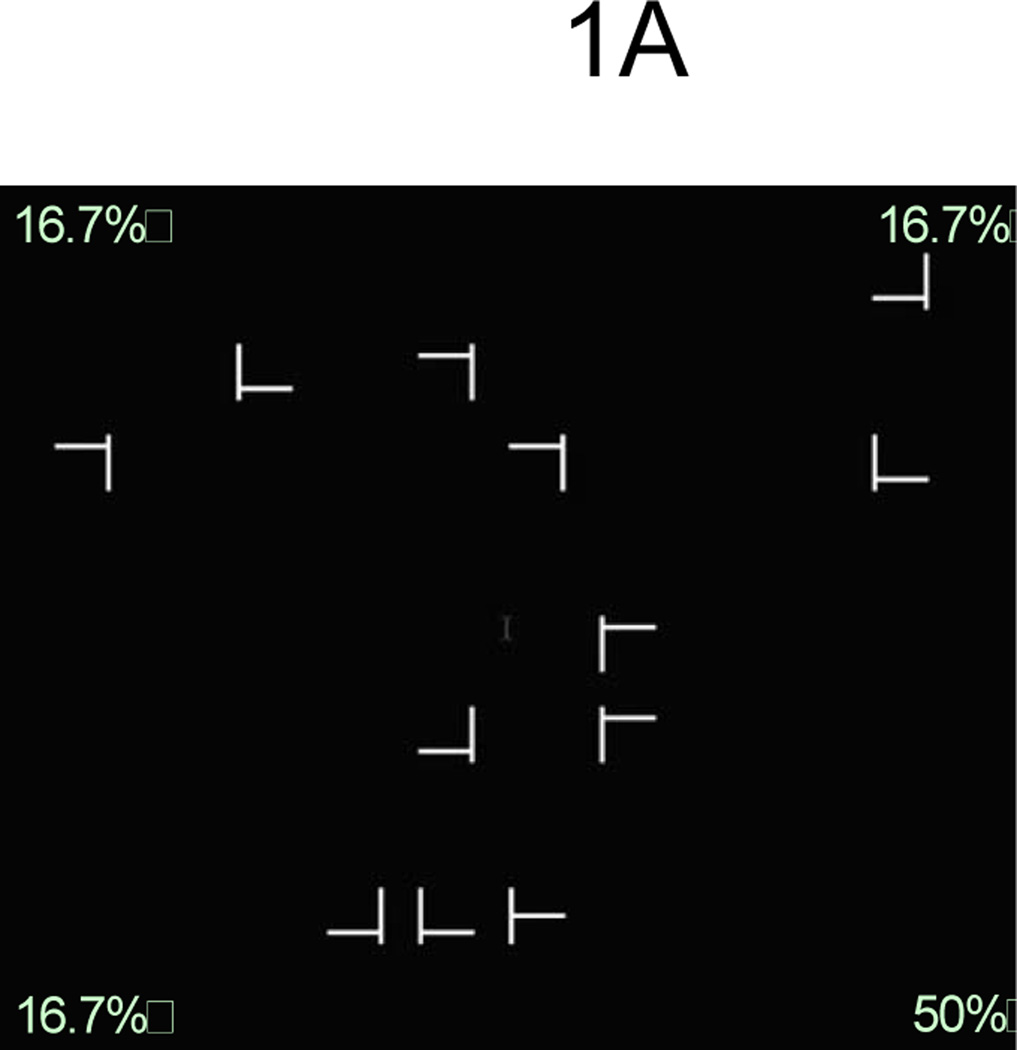
On each trial, participants viewed a display of 12 items: 1 T and 11 Ls. There were always 3 items in each quadrant (Figure 1A). The task was to find the T as quickly and as accurately as possible, and press either the left or right arrow to report the orientation of the T (left or right, equally often). The search display was presented until a response was made. A correct response was followed by three pleasant rising tones (for a total of 300 ms). An incorrect response was followed by a buzz (for 200 ms) and a blank timeout period of 2000 ms. The next trial commenced after a 500 ms blank interval. Participants were given a chance to take a break every 96 trials.

Figure 1.

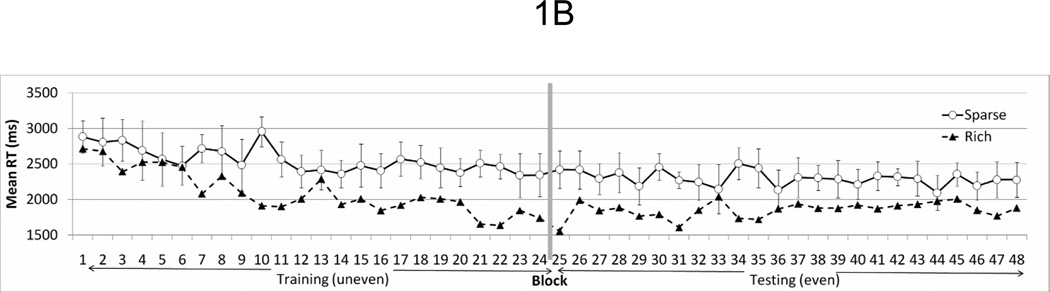
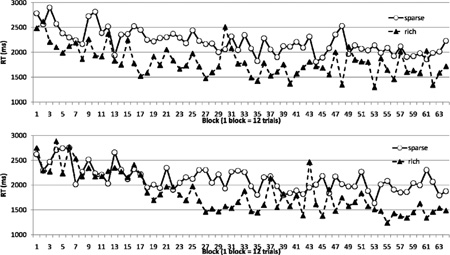
A. A sample visual search display. Participants searched for a T among Ls and reported the direction of the T. There were 3 items per quadrant. During training the target was located in a specific quadrant on 50% of trials (illustrated as the lower right quadrant on this figure), and in each of the other three quadrants on 16.7% of trials. The rich quadrant was counterbalanced across participants. The numbers illustrating target probability are shown here for illustrative purposes only. B. Results from Experiment 1. The target’s location was uneven in Blocks 1–24 and was even in Blocks 25–48. Error bars showed ±1 S.E. of the RT difference between rich and sparse conditions.

Procedure and Design

Participants completed 60 trials of practice, 576 trials of training, and 576 trials of testing. Training and testing were carried out continuously without further instructions or interruptions. At the end of the experiment, participants answered a question that assessed their awareness of the experimental manipulation.

Practice

The 60 trials of practice were used to tailor the difficulty of visual search to individual participants. During practice the target was equally probable in all quadrants. Search was conducted among displays with varying degrees of target-distractor similarity. The offset at the intersection of the two segments of L changed from 2 to 7 pixels. To increase the likelihood that learning would be observed, initial search RT was titrated to 3000 ms to allow plenty of room for improvement. The type of L that produced an RT of about 3000 ms for each individual was used in the main experiment.

Training

The first 576 trials involved an uneven spatial distribution of the target. The target appeared in a randomly selected rich quadrant on 50% of the trials. On the remaining trials it was randomly presented in one of the other three quadrants (each quadrant contained the target on 16.7% of the trials). Which quadrant was rich was maintained throughout training and was counterbalanced across participants. Participants were not told that the target’s distribution would be uneven, neither were they informed of the transition between training and testing.

Testing

For the next 576 trials the spatial distribution of the target was even, with the target appearing in each quadrant on 25% of the trials.

Final question

At the end of the experiment, participants were given a 5-alternative-forced-choice question. They were asked whether they thought that the target was equally probable across all quadrants, or whether it more often appeared in the upper left, upper right, lower left, or lower right quadrants.

Results

In all experiments reported here, overall accuracy was high (over 98%) and was unaffected by any experimental manipulations, all p-values > .05. Accuracy data are listed in the Appendix. Our analyses focus on RT. Trials that took longer than 10 seconds to complete were considered outliers and removed (less than 0.3% of the data were removed). Mean RT for correct trials was calculated for each participant.

We binned 24 trials into a “block”. Figure 1B plots data from Experiment 1.

Training

An ANOVA on block (1–24) and target quadrant (rich vs. sparse) indicated that search RT was faster as training progressed, leading to a significant main effect of block, F(23, 161) = 4.21, p < .001. In addition, search RT was faster when the target appeared in the rich quadrant than in the sparse quadrants, F(1, 7) = 6.42, p < .039. The interaction between the two factors was marginally significant, F(23, 161) = 1.44, p = .10. The lack of an interaction may be attributed to the early onset and subsequent maintenance of a quadrant effect. Binning the 24 training blocks into 4 epochs (1 epoch = 6 blocks), we observed a significant interaction between epoch and target quadrant, F(3, 24) = 5.58, p < .006. Response times in the sparse and rich conditions were initially indistinguishable in epoch 1 (p > .40), but diverged subsequently (e.g., p < .03 in epoch 2).

Testing

If the search advantage in the rich quadrant was driven primarily by transient priming, then it should rapidly disappear in the testing phase when the target was evenly distributed. This was not the case. Search RT continued to be faster in the previously rich quadrant than the previously sparse quadrants throughout the testing phase. An ANOVA on block (25–48) and target quadrant (previously rich or previously sparse) revealed a significant main effect of target quadrant, F(1, 7) = 12.59, p < .009, but no main effect of block or interaction between target quadrant and block, Fs < 1. The RT difference between rich and sparse quadrants did decline from 553 ms in the first testing epoch to 346 ms in the last testing epoch. A trend analysis on the RT difference across blocks revealed a significant linear trend, F(1, 7) = 5.95, p < .045.

Training vs. testing

To directly compare the magnitude of probability cuing between the training and testing phases, we conducted an ANOVA using phase (training vs. testing), target quadrant (rich or sparse), and block within phase as factors. This analysis showed no interaction between target quadrant and phase, and no interaction between target quadrant, phase, and block, Fs < 1. Thus, probability cuing did not significantly decrease in the testing phase compared with the training phase.

Transient priming

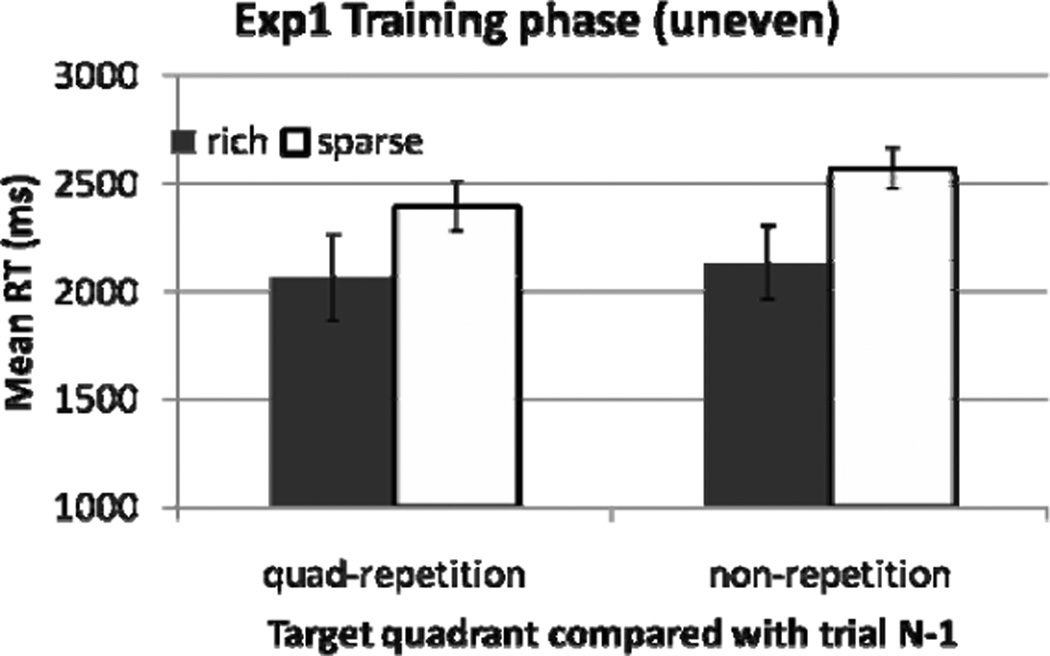
In the training phase, transient priming (due to spatial proximity) and target’s location probability were confounded. Did transient priming contribute to the effect of unevenly distributed targets in the training phase? To answer this question, we separated trials based on whether the target was in the rich or sparse quadrant, and whether the target was in the same quadrant as the target in the preceding trial. This analysis allowed us to examine effects of spatial proximity (defined by quadrant repetition on consecutive trials), as well as probability cuing (defined by whether the target on the current trial was in a rich or sparse quadrant). Figure 2 shows mean RT in the four conditions for the training (uneven) phase of the experiment.

Figure 2.

Experiment 1’s search RT as a function of whether the target’s quadrant was rich or sparse, and whether the current trial’s target was in the same quadrant as the preceding trial’s target. Error bars showed ±1 S.E. of the mean.

This analysis confirmed that quadrant repetition improved search RT, F(1, 7) = 4.32, p < .08 in the training phase. Importantly, the effect of probability cuing (rich vs. sparse quadrants) was significant even on trials without an immediate quadrant repetition. RT was faster in the rich quadrant than the sparse quadrant on non-repetition trials (p < .04). The interaction between quadrant repetition and probability cuing was not significant (p > .19). Thus, although spatial proximity for targets on consecutive trials sped up RT, probability cuing did not depend on the proximity of target locations on consecutive trials.

Recognition

The final recognition question served as a crude measure of participant’s explicit insight into the experimental manipulations. Seven of the 8 participants reported that the target was evenly distributed. The remaining participant correctly identified the rich quadrant. Removing this participant’s data did not change the overall pattern of results.

Discussion

Experiment 1 showed that the uneven spatial distribution of a search target across trials led to faster RT in the rich locations than the sparse locations. This advantage was observed relatively early (after about 100 trials). It was maintained for more than 500 trials after the target’s distribution became even [footnote¹]. The very long persistence of a search advantage in the rich quadrant argues against transient priming as the sole mechanism underlying the search advantage. This is because during testing the target was no more likely to repeat its location in the previously rich quadrant than in the previously sparse quadrants. Instead, the data convincingly demonstrated that visual statistical learning occurred and influenced search. In addition, the learned attentional bias did not rapidly readjust to changes in the underlying visual statistics.

Unlike previous studies that were concerned only with the difference in performance in rich and sparse regions (e.g., Geng & Behrmann, 2005; Walthew & Gilchrist, 2006), this study was specifically designed to address the development of attentional biases over time (Figure 1B). This study revealed that about 100 trials were sufficient for the initial learning. Although the pace of acquisition was faster than the pace of extinction, learning was not instantaneous. In addition, in the training phase the difference between the rich and sparse locations increased over time. These results provided additional support for the presence of probability learning. If transient priming had been the sole source of the RT advantage, then it should have occurred sooner and should not have grown over time. Moreover, the RT advantage should have been weaker when the target appeared in a different quadrant than on the previous trial. These data do not contest the claim that transient priming contributes to search RT (Geng & Behrmann, 2005; Walthew & Gilchrist, 2006). However, they also make it clear that probability cuing is a major and powerful component of the search advantages afforded by location probability learning.

Probability cuing occurred in this study even though participants were not informed of the manipulation or told to use this information. In addition, most participants reported that the target was evenly distributed. Although participants’ verbal reports may have been different if we had probed explicit awareness immediately after training, the final verbal report did not reflect participants’ behavior even at the end of testing. Explicit knowledge is unlikely a necessary component of probability cuing.

Experiment 2. Primacy effects and long sampling window

The next three experiments were designed to provide deeper insight into the persistence of an incidentally learned attentional bias. In Experiment 2 we tested the possibility that the persistence of the attentional bias reflects two effects: a long sampling window and a primacy effect.

In order to learn where a target is likely to appear, information about the target’s location must be aggregated over some number of trials (τ). One possibility is that the number of trials over which statistical information is sampled exceeds the length of the testing session in Experiment 1. To produce a bias towards the previously rich quadrant, at the end of testing the sampling window would need to contain trials from the training phase in which the target was unevenly distributed. Therefore, τ would need to be longer than the 576 trials in the testing phase. It follows from this account that if an even phase precedes an uneven phase, the initial even phase should weaken or slow subsequent learning in an uneven phase.

A second explanation for the persistence of the learned attentional bias is the concept of primacy. One’s early experience with an environment may have a disproportionately large influence on learning (Jùnge, Scholl, & Chun, 2007). For example, in their study on contextual cuing Jùnge et al. (2007) asked participants to search for a target on displays that occasionally repeated. Under standard conditions, search is faster on repeated than on unrepeated displays (Chun & Jiang, 1998). However, when 144 trials of unrepeated displays were completed before the displays started repeating, contextual cuing was not observed (Jùnge et al., 2007). Jùnge et al. (2007) proposed that learning was blocked by the initial experience with unrepeated displays. By the same logic, the presence of a learning signal in Experiment 1 early on may have blocked the adjustment to new statistics during testing.

To assess the whether either a primacy effect or a long sampling window can account for the persistence of probability cuing in Experiment 1, we conducted an experiment on two groups of participants. The experiment was divided into four epochs of 192 trials each. In some epochs the target was equally probable in all quadrants (even epochs). In other epochs the target’s location was biased toward a specific quadrant (uneven epochs). The two groups of participants were tested using different epoch orders. The order of the four epochs was “even, uneven, even, uneven” for the even-first group, and “uneven, even, uneven, even” for the uneven-first group. In Experiment 2 we tested a relatively broad definition of primacy: any statistical information present at the beginning of a task has a disproportionately large influence on learning and behavior than later statistical information. Specifically, we asked whether, like contextual cuing (Jùnge et al., 2007), initial exposure to a task that lacks statistical structure impairs learning once a new structure is introduced. If so, then participants in the even-first group should show less learning than those in the uneven-first group. Similarly, if probability cuing reflects statistics sampled in the preceding τ trials and τ is greater than 576, then even epochs should weaken probability cuing in subsequent uneven epochs.

Method

Participants

There were 16 participants in Experiment 2. Eight were tested in the even-first group (7 females and 1 male, mean 24 years old) and eight others were tested in the uneven-first group (5 females and 3 males, mean age 23 years old).

Procedure

The procedure was identical to Experiment 1, save for one important change. On each trial a fixation square (0.5°×0.5°) was presented in a random location within 3° of the center of the screen. Participants were required to click on the square to start each trial. Because participants had to look at the square to click it, this procedure ensured that they fixated near the center of the screen before the onset of the search display. The fixation task slowed down the pace of the experiment, so the total number of trials was reduced.

After the mouse click, the fixation square disappeared, and 500 ms later the search display was presented until participants pressed a key to report the T’s orientation. In this experiment we minimized practice to 10 trials (the target was randomly distributed). The offset between the two segments of the Ls was 5 pixels for all participants.

Design

Participants completed 768 self-initiated visual search trials, binned into 4 epochs of 192 trials each. In the even epochs, the target appeared in each of the four quadrants on 25% of the trials. In the uneven epochs, the target appeared in a randomly selected quadrant on 50% of the trials and in each of the other quadrants on 16.7% of the trials. Which quadrant was rich was counterbalanced across participants, but it was held constant throughout the experiment for a given participant. The order of the four epochs was “even, uneven, even, uneven” for participants in the even-first group. The order was “uneven, even, uneven, even” for those in the uneven-first group. Participants were not informed about the target’s spatial distribution or the transition from one epoch to the next.

At the end of the experiment, participants answered a 5-alternative-forced-choice question (same as Experiment 1) to provide a crude measure of explicit awareness.

Results

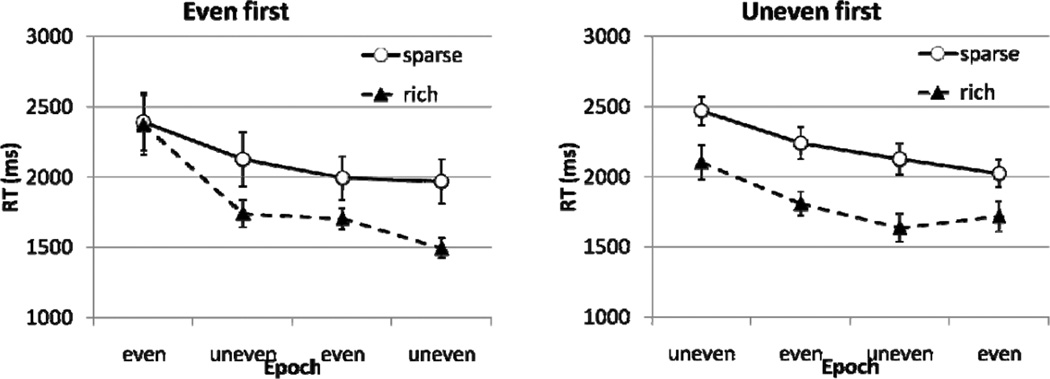
Figure 3 plots mean RT for the four different experimental epochs, separately for the even-first and uneven-first groups.

Figure 3.

Results from Experiment 2. Visual search RT in two groups of participants tested in different epoch order. Error bars showed ±1 S.E. of the mean for each condition.

If probability cuing is subject to a primacy effect, then the visual statistics of the first epoch should disproportionately influence the overall pattern of learning. People tested in the even-first group should show a weaker attentional bias than people in the uneven-first group. This was not supported by our data. Averaged across the two uneven epochs for each group, the RT difference between the rich and sparse quadrants was 431 ms for people tested in the even-first group, which was not any less than the 429 ms difference shown in people tested in the uneven-first group, F < 1.

The concept of a long sampling window does not specifically emphasize the beginning of training. However, it predicts that probability cuing in an uneven epoch should be weakened if this epoch was preceded by an even epoch, as long as the length of these epochs is shorter than the statistical sampling window. Based on Experiment 1, this window should be at least 576 trials long, long enough to encompass two 192 trial epochs of Experiment 2. To test whether performance in the uneven epoch is influenced by a preceding even epoch, we contrasted performance in the two groups for the first uneven epoch. For people tested in the uneven-first group, the only available history of visual statistics was an uneven distribution. In contrast, for people tested in the even-first group, the first uneven epoch was preceded by an even epoch. If the relevant statistics encompassed both epochs, then probability cuing in the first uneven epoch should be weakened. However, our data were inconsistent with this prediction. The RT advantage in the first uneven epoch for people tested in the even-first group was 385 ms, which was not any less than the 369 ms effect for people tested in the uneven-first group, F < 1 for the main effect of group. A finer-grained analysis that divided each epoch into 16 blocks (of 12 trials each) yielded similar results (Appendix Figure 1).

Appendix Figure 1.

Results from Experiment 2, finely divided into 64 blocks of 12 trials. Note: We performed an ANOVA for the first uneven epoch of each group (blocks 1–16 in the uneven-first group and blocks 17–32 in the even-first group). This analysis showed no interaction between group and target quadrant, F < 1, and no interaction between group, target quadrant, and block, F<1.

Although having searched for targets with an even distribution did not weaken probability cuing in the uneven epochs, biases acquired during the uneven epochs persisted into subsequent even epochs. In the uneven-first group, the subsequent even epochs showed faster RT in the previously rich quadrant than in the previously sparse quadrants (ps < .03). Similarly, in the even-first group, once an attentional bias had developed (the first uneven epoch), the subsequent even epoch showed a residual bias toward the previously rich quadrant (p < .09; 7 of the 8 participants were faster in the previously rich quadrant).

In the forced-choice question, 13 of the 16 participants reported that the target was evenly distributed. The remaining 3 correctly identified the rich quadrant. While these data do not rule out explicit awareness as a contributing factor to probability cuing, they do suggest that explicit learning is not a major component.

Discussion

Data from Experiment 2 supported neither the broad definition of primacy effect nor the concept of a long statistical sampling window. Probability cuing was equivalent during the uneven epochs regardless of whether people started out with an even or uneven epoch. Unlike Jùnge et al. (2007)’s contextual cuing study, the visual statistics that occurred in the beginning of the experiment did not disproportionately influence probability cuing. The primacy effect, broadly defined, was not supported in location probability learning. In addition, learning an uneven target distribution was not weakened by a preceding epoch of evenly distributed targets. A long sampling window also failed to account for our data.

Both a primacy effect, broadly defined, and the long sampling window failed to explain the persistence of an incidentally learned attentional bias. The failure arises because neither account distinguishes between how a spatial bias is acquired and how it is extinguished. The primacy effect only distinguishes the beginning and the end of training. It does not assign different weights to the extraction of a bias and the removal of that bias. A long sampling window only considers the length of averaging. It does not differentiate between different types of statistical information when the averaging is performed. The failure of these two accounts suggests that the acquisition of an attentional bias differs from the unlearning of that bias. We will return to this point in the General Discussion.

Experiment 3. Uneven-1, Uneven-2, Even

The persistence of an incidentally learned attentional bias distinguishes experience-driven attention from goal-driven attention. Endogenous cuing can be adjusted on a trial-by-trial basis (Müller & Rabbitt, 1989; Posner, 1980; Vickery et al., 2005; Woodman & Arita, 2011). In addition, cue validity is a defining feature of endogenous cuing. Endogenous cuing is only effective when the cue is predictive. In contrast, the first two experiments strongly suggest that experience-driven attention is insensitive to changes in cue validity. However, the change in probability cue validity may have been too subtle to encourage the abandonment of the cue when prioritizing search. Although the likelihood that a target was in the previously rich quadrant was lower in the even than uneven epochs, it was just as likely to be in the previously rich as in the previously sparse quadrants. Thus, there was little cost associated with continuing to search the previously rich quadrant first.

Experiment 3 provides a stronger test of whether experience-driven attention adjusts to changes in cue validity. In this experiment the validity of the cue is changed from one uneven distribution to another uneven distribution. After the first training epoch, a new quadrant becomes rich and all the other quadrants become sparse. After training, the learned attentional bias not only ceases to be valid (as in Experiments 1 and 2), it also competes with a new, valid attentional bias. Does a learned attentional bias persist even if it interferes with performance?

Experiment 3 also presents another opportunity to evaluate whether information learned at the beginning of a task more strongly influences performance than information acquired later in the task. The broad definition of primacy we introduced in Experiment 2 stated that any statistical information experienced early would have a disproportionately large impact on later learning and performance. This definition was not supported by Experiment 2’s data. However, it is possible that the primacy effect in location probability cuing may depend upon learning an uneven target distribution rather than on any exposure to the task. If so, then acquiring an attentional bias early in the experiment could reduce learning of a new bias later on.

Method

Participants

Twelve college students, 7 females and 5 males, completed Experiment 3. Their mean age was 23 years.

Procedure and Design

The procedure was similar to that used in Experiment 2. Each participant completed 576 trials divided into 3 epochs (of 192 trials each). The epochs were uneven-1, uneven-2, and even. One quadrant (“rich-first”) was randomly selected to be the rich quadrant during the first epoch. It contained the target on 50% of the trials whereas each of the other quadrants contained the target on 16.7% of the trials. In the second epoch, the rich quadrant changed to one of the other three quadrants. This new rich quadrant (“rich-second”) contained the target on 50% of the trials in the second epoch, whereas the rich-first quadrant and each of the other quadrants contained the target on 16.7% of the trials. Finally, in the third epoch, all quadrants were equally likely to contain the target.

In this design, we examined data in three types of quadrants: rich-first, rich-second, and always-sparse. The assignment of quadrants to each type was fully counterbalanced across participants. Participants were not informed of the statistical distribution.

All other aspects of the experiment were the same as in Experiment 2.

Results

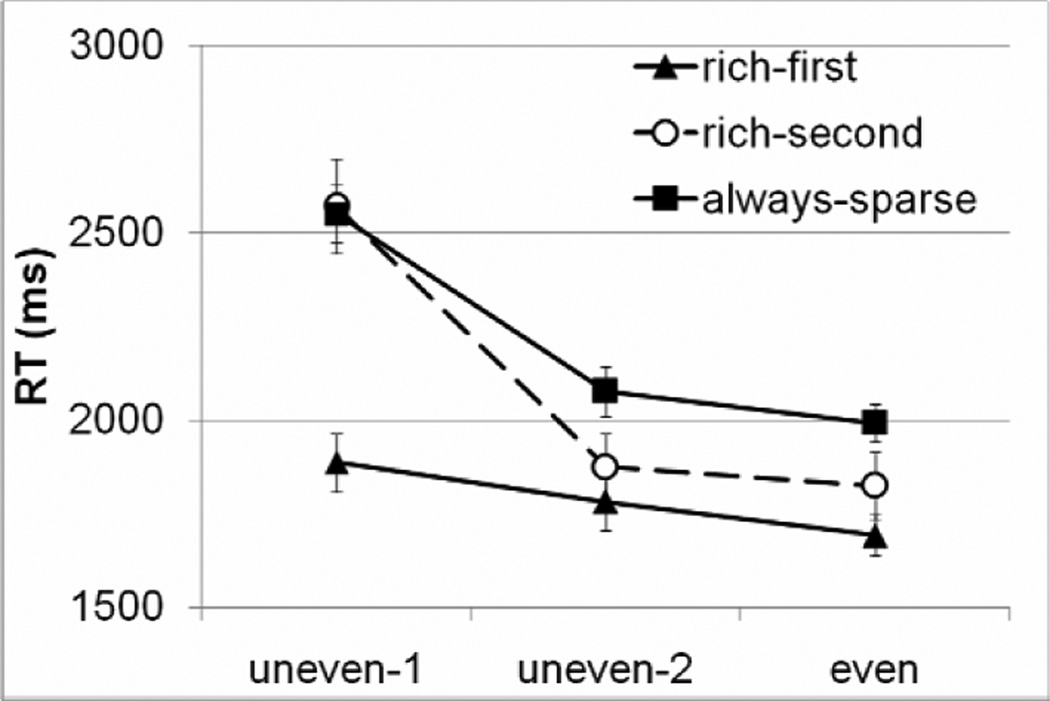
Figure 4 plots mean RT for the three types of quadrants across the three experimental epochs. In epoch 1, the target was more likely to appear in the rich-first quadrant. RT was faster when the target fell in the rich-first quadrant rather than in the other quadrants, F(2, 22) = 22.71, p < .001.

Figure 4.

Results from Experiment 3. Error bars showed ±1 S.E. of the mean for each condition.

In epoch 2, the target was more likely to appear in the rich-second quadrant. The change in visual statistics invalidated the attentional bias toward the rich-first quadrant. Nonetheless, participants retained that bias. RT was significantly faster in the rich-first quadrant than the always-sparse quadrants, t(11) = 2.56, p < .027, and was numerically but not statistically faster than in the rich-second quadrant, t(11) = 0.84, p > .30. Learning of an uneven target distribution in epoch 1 interfered with the acquisition of a new bias toward the currently valid quadrant. RT in the rich-second quadrant was not significantly faster than that in the always-sparse quadrants, t(11) = 1.75, p = .10.

Finally, in epoch 3 the target became evenly distributed across quadrants. A clear persistence of the previously learned bias was observed. RT was significantly faster when the target fell in the rich-first quadrant than in the always-sparse quadrants, t(11) = 3.77, p < .003, and was numerically but not statistically faster when the target fell in the rich-second quadrant than in the always-sparse quadrants, t(11) = 1.54, p = .15.

Of the 12 participants, 7 reported that the target was evenly distributed. Among the five participants who thought the distribution was uneven, only 2 identified a quadrant that was either the rich-first or rich-second quadrant. Similar to the other experiments, evidence for explicit awareness was weak.

Discussion

This experiment examined whether an incidentally learned attentional bias would persist when it became counter-productive. Our data showed that it did. For example, after an initial training epoch where the target was more often located in the upper left quadrant, an attentional bias toward that quadrant persisted even when the target was now more often located in the lower right quadrant. In addition, the outdated attentional bias interfered with the acquisition of a new spatial bias. These findings suggest that the persistence of an incidentally learned attentional bias is a robust phenomenon. It is observed even when the outdated spatial bias is maladaptive. The lack of rapid readjustment differentiates incidentally learned attention from goal-driven attention.

Experiment 3 also suggests that the acquisition of an attentional bias in space is influenced by prior experience. In particular, after a spatial bias has developed, it interferes with the development of a second bias. These data are consistent with a modified definition of primacy, where the first learned bias persists and slows down the acquisition of a second bias (Gebhart, Aslin, & Newport, 2009). Experiment 3 can be contrasted with Experiment 2’s data, where an initial block with an even spatial distribution did not interfere with learning in a subsequent uneven epoch. How can we reconcile the presence of a primacy effect in Experiment 3, but a lack of a primacy effect in Experiment 2? We suggest that the nature of prior experience – exposure to an even or uneven distribution – affects the likelihood that subsequent learning will be affected. Primacy effects were observed when the initial experience involved a spatial bias (Experiment 3), but not observed when the initial experience did not involve a spatial bias (Experiment 2). We will return to this point in the general discussion.

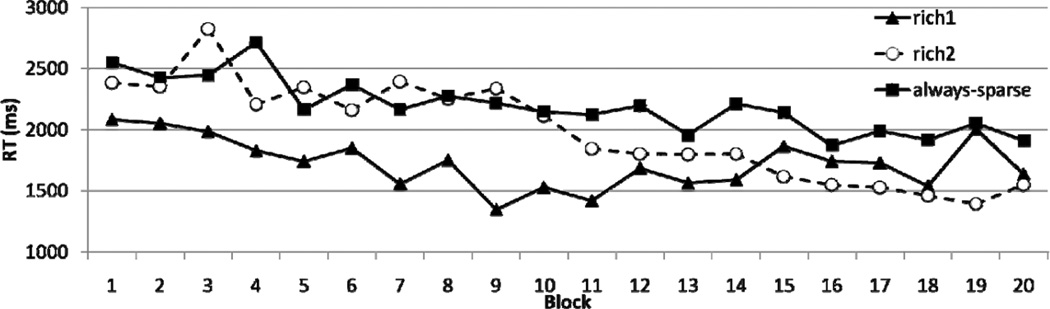
Although the outdated attentional bias appears to be stronger than the new attentional bias in Experiment 3, it is likely that with additional training the new attentional bias will strengthen. To examine this possibility, we tested 8 new participants (6 females and 2 males, mean age 21 years) in an experiment with 720 trials. We describe the experiment here briefly because the procedure was similar to that of Experiment 3. The target was unevenly distributed throughout the experiment, but the rich quadrant differed for the first and second halves of the experiment. Because training of the new attentional bias was relatively long, we were able to observe a gradual crossover in search RT in the rich-first and rich-second quadrants. Figure 5 shows data from this experiment, divided into 20 blocks of 36 trials each.

Figure 5.

Data from the follow-up experiment for Experiment 3. Each block has 36 trials.

For the first half of the uneven-2 epoch (blocks 11–15), search RT was significantly faster in the rich-first quadrant compared with the rich-second (p < .05) or the always-sparse (p < .001) quadrants. However, as training progressed, the attentional bias toward the new rich quadrant became stronger. For the second half of the uneven-2 epoch (blocks 16–20), the order of search RT was rich-second, rich-first, and always-sparse. During this time search RT was significantly slower in the always-sparse quadrants compared with the rich-first (p < .01) or rich-second (p < .01) quadrants, which did not differ significantly (p > .25). These data replicated the persistence of an outdated attentional bias in the face of a new attentional bias. In addition, they suggest that there is readjustment of spatial attention based on incidental learning, although the readjustment takes a long time. Primacy effects may slow the learning of new visual statistics in this task, but they do not eliminate it.

Experiment 4. One week delay

In Experiment 4 we examined the possibility that the learned attentional bias could survive several days of interruption. A one-week interval separated the initial training phase from a subsequent testing phase. The target’s spatial distribution was uneven in the training phase and even in the testing phase.

Several factors may lead to the elimination of a persistent attentional bias from training to testing. First, memory for the learned information may decay over one week. Second, new visual experience with one’s daily environment may interfere with the learned spatial bias. Third, the delay marks the transition between the two phases. The spatial bias acquired initially may reset after the transition. If persistence still remains under these conditions, it would strengthen the idea that persistence is a major characteristic of experience-driven attention.

Method

Participants

Eight college students, 5 females and 3 males, completed Experiment 4. Their mean age was 22 years. Participants were scheduled to complete the two sessions one-week apart. However, 3 participants rescheduled. The average delay between the two sessions was 7.8 days (range 7–10 days).

Procedure and Design

Participants completed 384 trials of training and 384 trials of testing. During training the target appeared in one quadrant on 50% of the trials and in each of the other quadrants on 16.7% of the trials. The quadrant that was rich was counterbalanced across participants. During testing the target was equally probable in all quadrants. Participants completed 10 trials of practice before training.

At the completion of the testing session, participants were queried about their explicit awareness. The recognition procedure was modified from the 5-choice question (as in Experiments 1–3) to a sequence of two questions. First, participants were asked whether they thought the target was evenly distributed or not. After their response, they were told that the target was not evenly distributed and were asked to select the quadrant that was rich.

Results and Discussion

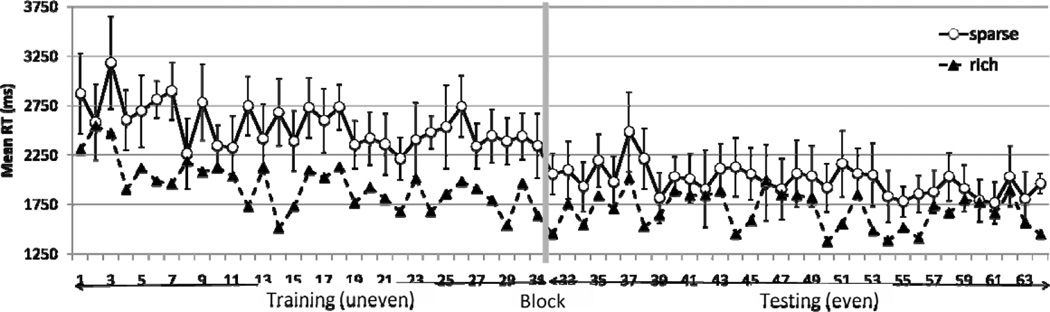
Mean RT is plotted in Figure 6.

Figure 6.

Results from Experiment 4. The training (Blocks 1–32) and testing (Blocks 33–64) phases were separated by at least a week. Error bars showed ±1 S.E. of the RT difference between rich and sparse conditions.

Training

Search was faster when the target fell in the rich quadrant than the sparse quadrants, F(1, 7) = 20.35, p < .001. In addition, RT decreased as the experiment progressed, F(31, 217) = 2.08, p < .001 for the main effect of block. The interaction between the two factors was not significant, F < 1. Similar to Experiment 1, the advantage occurred early (it reached significance in Block 6, p < .03) and was sustained for most of the training phase.

Testing

The learned bias survived the week-long delay. In the testing phase, participants continued to be faster when the target appeared in the previously rich quadrant, F(1, 7) = 11.21, p < .012. This advantage was observed even though the target was evenly distributed during testing. RT did not significantly improve during the testing phase, F < 1 for the main effect of block, and there was no interaction between target quadrant and block, F < 1.

Aggregated across all blocks, the RT advantage in the rich quadrant was 596ms during training, which was statistically comparable to that shown in Experiment 1’s training phase, F < 1. After a week-long delay and after the uneven statistics were removed, the RT advantage in the previously rich quadrant declined to 304ms. This was significantly less than the effect during the training phase (interaction between phase and target quadrant was significant, F(1, 7) = 30.44, p < .001). However, it was comparable to the size of the effect in at the end of Experiment 1 (346ms in the last testing epoch; the interaction between experiment and target quadrant was not significant, F < 1).

When asked the recognition question, 3 of the 8 participants reported that the target’s distribution was uneven. One of these participants correctly reported the rich quadrant in the forced-choice question. Of the 5 who reported that the target was evenly distributed, 3 participants correctly identified the rich quadrant. Overall more participants (4) identified the rich quadrant than would be expected by chance (2). Unlike contextual cuing (Chun & Jiang, 2003), there was greater evidence that explicit awareness occurred in target location probability learning. Location probability learning may be more comparable to unsupervised statistical learning, such as the learning of shape associations (Fiser & Aslin, 2001; Turk-Browne et al., 2005). In those studies, learning was incidental, but participants rated the learned information as more familiar than unlearned information.

What enables the learned bias to persist even after a one-week delay? Without additional experiments, we do not know whether the learned spatial bias is widespread (e.g., it affects participants’ daily activities), context-specific (it only shows up in the laboratory), or task-specific (it only shows up when participants engage in the same T/L search task). Based on unpublished preliminary data, we speculate that the learned bias is task-specific, such that when the same task is introduced again, it will be influenced by the spatial bias learned previously. Additional studies are needed to examine the conditions in which a learned spatial bias does or does not persist.

General Discussion

Visuospatial attention is an important mechanism for selection. Previous research has shown that spatial attention may be driven by an observer’s goal or by salient stimuli (Desimone & Duncan, 1995; Wolfe, 1994). Here we focused on a third source of spatial attention: one’s previous experience. Using target location probability learning, we demonstrated that people prioritize locations that were more likely to contain the target in their previous experience. This prioritization occurs in an incidental manner. The main finding from this study is that although an attentional bias to a region of space can be acquired rapidly, once acquired, it persists for a surprisingly long time. The stubborn persistence of this learned attentional bias, even in situations where they could impair performance, differentiates experience-driven attention from goal-driven attention.

In a previous study, Walthew and Gilchrist (2006) demonstrated that transient priming could underlie the search advantages that are observed when targets are unevenly distributed in space. In particular, when the target’s location is constrained such that it does not repeat across consecutive trials, then visual search (as indicated by the first saccade) is equivalent for rich and sparse locations (Walthew & Gilchrist, 2006). The data from the present study, however, suggest that location probability learning does influence search. Whereas Walthew and Gilchrist focused on the learning process, our study focused on how the learned bias is used after training has discontinued. Across four different experiments we showed that a learned attentional bias is used for hundreds of trials after training has terminated and the targets were evenly distributed. Because we did not manipulate location repetition during training, our study does not rule out the possibility that transient priming is an important component of location probability learning (Walthew & Gilchrist, 2006). What is clear though, is that probability cuing facilitates performance even when the target’s location changes across trials (Experiment 1; Geng & Behrmann, 2005), and when repetitions are equally likely to occur in the rich and sparse quadrants (Experiments 1–4).

The slow extinction of a learned bias cannot be simply accounted for by a long sampling window of prior experience. Consider people who were tested in 192 trials of an even distribution, and then 192 trials of an uneven distribution (Experiment 2). If a long sampling window of prior statistics always highly influenced subsequent behavior, then the initial exposure to 192 trials of an even distribution should have delayed the acquisition of an attentional bias subsequently. This was not the case.

Our study demonstrates a large discrepancy between the number of trials needed to establish a spatial bias and the number of trials needed to extinguish that bias. This observation raises doubts about the degree to which visual statistical learning is a mechanism for extracting statistical information in the visual environment. Had behavior been driven purely by statistical information, it should have faithfully reflected the current visual statistics, allowing for a lag in acquiring the new information. When the target is unevenly distributed one’s attentional prioritization should reflect this; when the target is evenly distributed one’s attention should be unbiased. An information-sampling view of visual attention and learning cannot adequately account for the persistence of experience-driven attention.

Rather these data suggest that not all visual statistics are created equal. The presence of statistical regularities is relatively easy to acquire, but the absence of statistical regularities does not easily extinguish a learned bias or interfere with learning a new one. In other words, there is an asymmetry in visual statistical learning. Visual statistical learning likely occurs as a means of extracting regularities from an inherently complex and chaotic environment. Information that helps simplify the environment and guide behavior is likely prioritized, resulting in the relatively rapid acquisition of an attentional bias that reflects these regularities. Learning could be supported by the reinforcement of behaviors and stimuli that are associated with detecting a target. In contrast, when regularities are removed from the environment, adaptation to the change requires finding chaos. However, accumulating statistics about chaos is likely less useful than extracting regularities. Adapting to chaos does not easily translate into a clear course of action. Adaptation to change may require finding another source of structure (see for example, the gradual acquisition of a new bias in Experiment 3). In the absence of another source of structure, it may be difficult to abandon a learned bias. Indeed, every re-appearance of a target in the previously rich location may reinforce the attentional bias. The visual system may therefore have evolved to extract regularities from the environment, but not necessarily to seek evidence that these regularities are no longer present. We suggest that both the rapid acquisition and slow extinction of a learned attentional bias may reflect a bias towards detecting the presence of regularities rather than their absence.

This proposal does not imply that the visual system lacks the means to correct an outdated bias. The extent to which previous experience biases attention may be sensitive to a change in the task (e.g., from visual search to a working memory task), a change in the environment (e.g., from the computer monitor to the outside world), and the presence of a goaldriven cue (e.g., an arrow that tells people where to attend to). We are currently exploring whether these factors modulate or eliminate the persistence of experience-driven attention.

To what degree can the learned spatial bias be attributed to a change in covert attention, as opposed to learning where to move one’s eyes? Although eye movements and covert attention are often directed to the same location (Kowler, 2011), it is possible to attend to one place while looking at another. The current set of experiments cannot tease apart oculomotor learning from a change in covert attention. However, preliminary data from our lab suggest that probability cuing influences covert attention. Specifically, probability cuing was observed in an experiment where the display was presented for only 200ms, which was too brief to induce a saccadic eye movement to the target (see also Geng & Behrmann, 2005, where items were shown for 150ms). Future eye-tracking studies are needed to further elucidate the role of eye movements in probability cuing.

Traditional models of attention emphasize the importance of an observer’s goal and stimulus saliency in driving attention (Desimone & Duncan, 1995; Wolfe, 1994). Increasing evidence suggests that the dichotomous view is inadequate in accounting for factors that modulate attention. In addition to incidental learning, a recent study has uncovered “value-driven” attention (Anderson, Laurent, & Yantis, 2011). Stimuli that were previously associated with monetary reward captured attention in visual search, even though these stimuli were not perceptually salient. Value-driven attentional capture shows long-term persistence - it was observed after a delay of several days between the training with monetary reward and subsequent testing. However, important differences exist between value-driven attentional capture and location probability learning. First, value-driven attentional capture is about what item should be attended, whereas location probability learning is about the location to which one should attend. Second, value-driven attentional capture depended on trial-by-trial monetary reward, whereas location probability learning was acquired in the absence of any monetary reward. Third, value-driven attentional capture is a relatively small effect, slowing down RT by about 3%. Location probability learning, on the other hand, speeds up RT by 10–25%. Despite clear differences, value-driven attention and incidentally learned attention both suggest that there are additional sources of attention to an observer’s goal and salient stimuli.

In summary, we have shown that people are highly sensitive to the uneven spatial distribution of targets in a visual search task. Learning occurs rapidly and largely incidentally. Once acquired, however, the learned attentional bias persists for several hundred trials after training has discontinued and after several days of delay. The stubborn persistence of a learned attentional bias, even in situations where the bias is no longer valid, differentiates experience-driven attention from goal-driven attention. It raises doubts about the degree to which visual statistical learning can be conceptualized as a way of acquiring the true visual statistics in the environment. Future studies should examine ways in which a learned attentional bias can be rapidly eliminated or reset.

Appendix

Table 1.

Percent correct in Experiment 1 during the training and testing phases. Standard error of the mean is in parenthesis.

	Training		Testing
	sparse	rich	sparse	Rich
Mean	98.7 (0.3)	98.5 (0.5)	98.4 (0.6)	98.7 (0.6)

Table 2.

Percent correct in Experiment 2. Standard error of the mean is in parenthesis.

	Uneven-first
	Epoch1 (uneven)	Epoch2 (even)	Epoch3 (uneven)	Epoch4 (even)
Sparse	97.0 (2.0)	97.9 (0.6)	97.4 (0.9)	98.2 (0.8)
Rich	97.3 (1.4)	97.9 (1.0)	98.6 (0.7)	96.2 (1.6)
	Even-first
	Epoch1 (even)	Epoch2 (uneven)	Epoch3 (even)	Epoch4 (uneven)
Sparse	98.4 (0.5)	98.6 (0.5)	98.9 (0.5)	98.0 (0.5)
Rich	99.0 (0.6)	97.9 (1.0)	97.9 (0.8)	98.4 (0.6)

Table 3.

Percent correct in Experiment 3. Standard error of the mean is in parenthesis.

	Epoch1 (uneven-1)	Epoch2 (uneven-2)	Epoch3 (even)
Rich-first	98.3 (0.3)	98.5 (0.5)	98.1 (0.7)
Rich-second	97.1 (0.7)	98.6 (0.5)	99.3 (0.3)
Always-sparse	98.3 (0.6)	97.9 (0.6)	98.5 (0.3)

Table 4.

Percent correct in Experiment 4 during the training and testing phases. Standard error of the mean is in parenthesis.

	Training		Testing
	sparse	rich	sparse	Rich
Mean	98.8 (0.2)	98.7 (0.4)	98.8 (0.3)	99.2 (0.3)