Low Cost, High Performance GPU Computing Solution for Atomic Resolution CryoEM Single-Particle Reconstruction

Abstract

Recent advancements in cryo-electron microscopy (cryoEM) have made it technically possible to determine the three-dimensional (3D) structures of macromolecular complexes at atomic resolution. However, processing the large amount of data needed for atomic resolution reconstructions requires either accessing to very expensive computer clusters or waiting for weeks of continuous computation in a personal computer (PC). In this paper, we present a practical computational solution to this 3D reconstruction problem through the optimal utilization of the processing capabilities of both commodity graphics hardware [i.e., general purpose graphics processing unit (GPGPU)]. Our solution, which is implemented in a new program, called eLite3D, has a number of advanced features of general interests. We construct interleaved schemes to prevent the data race condition intrinsic in merging of 2D data into a 3D volume. The speedup of eLite3D is up to 100 times over other commonly used 3D reconstruction programs with the same accuracy, thus allowing completion of atomic resolution 3D reconstructions of large complexes in a PC in 1–2 hours other than days or weeks. Our result provides a practical solution to atomic resolution cryoEM (asymmetric or symmetric) reconstruction and offers useful guidelines for developing GPGPU applications in general.

1. Introduction

Cryo-electron microscopy (cryoEM) is a fast emerging tool in structural biology for three-dimensional (3D) structure determination of macromolecular complexes. Several recent hardware improvements in cryoEM instrumentation together have made it possible to obtain cryoEM images containing atomic resolution information. From such images, it is possible to determine 3D structures at near atomic resolution (~4Å) (Jiang et al. 2008; Ludtke et al. 2008; Yu et al. 2008a; Zhang et al. 2008a; Cong et al. 2010; Zhang et al. 2010a), and more recently at atomic resolution (Zhang et al. 2010a; Zhang et al. 2010b).

However, due to the intrinsic poor signal/noise ratio in cryoEM images, the number of images required for high-resolution studies increases exponentially as the targeted resolution improves; hence the computation time for 3D reconstruction also increases exponentially, creating a bottleneck for routine applications of cryoEM. Computer-controlled cryoEM instrument and automation in data collection have enabled the acquisition of this large number of particle images in a few days (Stagg et al. 2006). However, processing this huge amount of image data, especially reconstructing a large size density map from the particle images, takes a long period of time (from days, weeks or even months, depending on the targeted resolution and particle sizes) and has become the de facto time-limiting step in high-resolution cryoEM reconstruction. In addition, the clock speed of computer processors has remained roughly unchanged for the past several years and may remain so for the near future due to an upper limit of transistor switching time. Taken together, there is an urgent need for high performance computation solution of the 3D reconstruction problem.

The process of obtaining a 3D structure from 2D cryoEM images consists of two main tasks: orientation determination/refinement and 3D reconstruction (DeRosier and Klug 1968; Crowther et al. 1970c; Crowther 1971b). The orientation determination/refinement task can be accomplished on individual particle images thus is embarrassingly parallel in nature. Various applications and software kits have been developed to handle this task efficiently through distributed computing (e.g., Smith et al. 1991; Johnson et al. 1994; Martino et al. 1994; Baker and Cheng 1996; Crowther et al. 1996; Frank et al. 1996a; van Heel et al. 1996; Zhou et al. 1998; Ludtke et al. 1999a; Liang et al. 2002; Sorzano et al. 2004; Grigorieff 2007; Heymann and Belnap 2007; Tang et al. 2007; Yan et al. 2007; Yang et al. 2007). The latter task, 3D reconstruction, requires combining many particle images to form a single 3D volume. This task, however, has data dependency (see below) and has not been optimized for multi-core and many-core computing. In fact, it has become the computational bottleneck of cryoEM data processing in atomic resolution structure determination of large complexes. For example, a single iteration of 3D reconstruction of a middle size virus particle (~700Å in diameter) to 3–4Å resolution takes 1–2 weeks of computation to complete. Because several iterations are required for each structure, such approach quickly becomes unrealistic when pushing the reconstruction resolution further to the 2–3Å range.

Addition of advanced capabilities, such as random memory access and in-order execution, to commodity graphics processing unit (GPU) has led to the development of general purpose GPU (GPGPU) in recent years. This development makes it possible to use stream-processing on non-graphical data, thus providing a very cost-effective solution to computation-intensive problems. Inherited from the superior characteristics of GPU, GPGPU offers high floating point calculation power by devoting more transistors to data processing. Moreover, the dedicated memory of GPGPU alleviates the limitation due to the so called von Neumann bottleneck (i.e., competition for memory access by processing units sharing the same system bus) (Backus 1978). These characteristics make GPGPU an attractive choice for large-scale, data-parallel processing tasks with high arithmetic intensity and high spatial locality. However, GPGPU has a limited cache and only implements simple flow control (NVIDIA 2009b), in contrast to CPU, which has a large cache and implements sophisticate flow control in order to minimize latency for arbitrary system memory (sMEM) access for serial process. In addition, severe race conditions (Netzer and Miller 1992) exist in the operation of 3D Fourier interpolation in the data merging step. Other important factors, such as thread mapping, graphics memory (gMEM) management and coalescing access etc., should also be carefully considered to fully exploit the massive computation power of GPGPU.

In this paper, we present a practical solution to the 3D reconstruction problem using GPGPU and its implementation as an integrated program, eLite3D. This solution drastically reduces the computation time needed to compute an atomic resolution reconstruction of large complexes to only a small fraction (1% – 5%) of that needed by other commonly used reconstruction programs, permitting completion of weeklong reconstruction tasks within 1–2 hours in a personal computer (PC). Our solution represents a practical and cost effective approach to atomic resolution cryoEM reconstruction and offers general guidelines for GPGPU implementation of other computation and data intensive problems.

2. Single Particle 3D Reconstruction

Fourier space reconstruction method (Crowther et al. 1970a; Crowther et al. 1970b; Crowther 1971a) is currently the standard algorithm for single particle 3D reconstruction. The most notable advantage of this method is speed at the algorithmic level comparing to other methods, such as the weighted back-projection method (Radermacher 1988) and its variants. When merging 2D Fourier transforms of images in 3D Fourier space, it is necessary to properly interpolate and weigh the 2D Fourier data to fill the 3D Fourier space at regular grid points. For interpolation, we choose the nearest-neighbor interpolation method (1x1x1 voxel interpolation) with proper weighting based on their amplitude of contrast transfer function, which has been demonstrated to be adequate for high-resolution reconstructions (Liang et al. 2002; Grigorieff 2007; Liu et al. 2008; Yu et al. 2008b; Zhang et al. 2008b; Zhang et al. 2010b).

In order to develop a most computationally efficient and GPGPU- friendly 3D reconstruction method, we decided to start writing a completely new program, eLite3D. This process also provided us the opportunity to integrate many desirable features commonly recognized in the 3D reconstruction modules of the following software packages, including IMIRS (Liang et al. 2002), EMAN (Ludtke et al. 1999b), Spider (Frank et al. 1996b), Frealign (Grigorieff 2007), and AUTO3DEM (Yan et al. 2007) et al.. Our new program eLite3D embodies a light style and supports asymmetric (C1) and symmetric (C2-C9; D2-D9; tetrahedral, octahedral and icosahedral symmetries) reconstructions. eLite3D consists of two subprograms, C3D and G3D, specifically optimized for performances in personal computers equipped with low-end graphics cards (i.e., multi-cores/CPUs-based) and high-end graphics cards (i.e., GPU-based), respectively. These subprograms can be launched either automatically based on available gMEM size or manually by specifying a command-line option. eLit3D runs on both Unix-like (e.g. Linux) environments and Microsoft Windows platforms.

3. Data dependency and solutions

One property of the Fourier transform data used in 3D reconstruction is that they have data dependency. Data dependency is a situation in which a program statement (instruction) refers to the data of a preceding statement. For every grid point in the 3D Fourier space, we sum many Fourier data points from 2D Fourier transforms of particle images (see above). A simple sequential summation of these data points will lead to a data dependency situation – a latter summation operation depends on the result of the immediate proceeding summation operation. Data dependency often results in race condition in parallel processing. Race condition occurs when separate processors (or computation threads) access shared data simultaneously, thus potentially resulting in collisions and loss of data (Netzer and Miller 1992).

One straight-forward approach to avoid data dependency is to keep several identical 3D Fourier volumes in sMEM and process them separately, as employed by EMAN and other packages (Ludtke et al. 1999b; Yan et al. 2007; Yang et al. 2007). However, this approach requires storing a 3D Fourier volume and its 3D weighting matrix in the sMEM of each CPU or core (e.g., >6 GB for reconstruction of 1024 image dimension; i.e., >48 GB for eight processors in each node for full speed execution) and is not economical for multi-core/CPU parallel processing for large reconstructions at high resolution.

A careful analysis of data dependency existed in data merging step of 3D reconstruction allows us to design a solution to deal with this condition. Consider 2D sample point P located in the Cartesian coordinate (x, y) and its neighborhood Q located at (x+a, y+b) (here a and b can be any integer numbers). Suppose O is the corresponding 3D grid point of P. Then, the relationship between P s 2D coordinate (x, y) and 3D coordinate (X, Y, Z) is related by the following transformation:

$$\left|\begin{array}{c}\text{X}\\ \text{Y}\\ \text{Z}\end{array}\right|=\text{R}·\left|\begin{array}{c}\text{x}\\ \text{y}\\ \text{0}\end{array}\right|$$ (1)

Where R is the rotation matrix and has the form of $\left[\begin{array}{lll}{\text{a}}_{00}\hfill & {\text{a}}_{01}\hfill & {\text{a}}_{02}\hfill \\ {\text{a}}_{10}\hfill & {\text{a}}_{11}\hfill & {\text{a}}_{12}\hfill \\ {\text{a}}_{20}\hfill & {\text{a}}_{21}\hfill & {\text{a}}_{22}\hfill \end{array}\right]$. Since we only use the rotation operation here, the distance between P and Q remains the same when transforming the coordinate to 3D from 2D and this means that we can compute the 3D distance between P and Q from their 2D coordinates. From this distance, we can determine whether the two data points will collide with the same voxel point in 3D by judging from their 2D relationship, as illustrated below. Thus, data dependency can be judged from their distance in 2D plane.

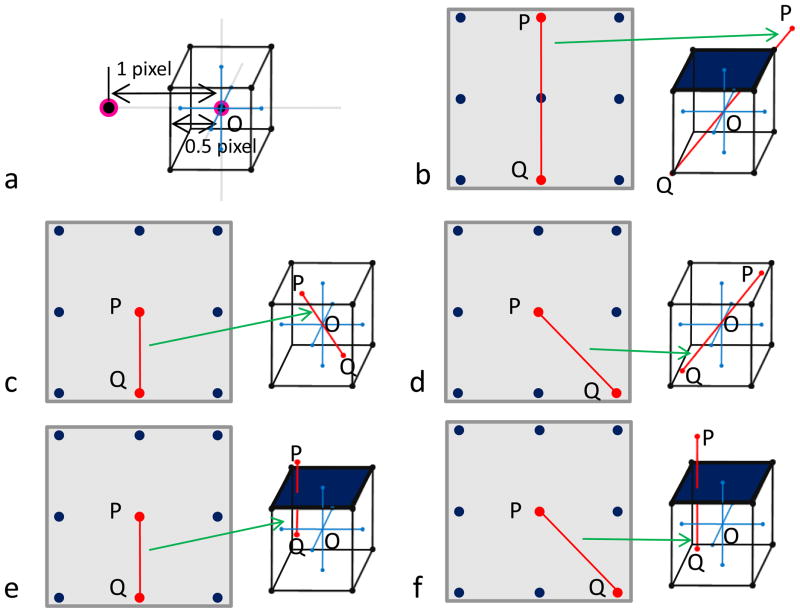
For simplicity, let us place grid point O at the origin (Figure 1a), and draw lines of 0.5 pixel length on both positive and negative directions along X, Y, Z axes (grey lines in the center of Figure 1a). Based on the interpolation plan discussed in problem description section, all possible contributing data points should be located within a 1x1x1 voxel cube (Figure 1a), then the longest distance of any two points contributing to the same 3D voxel is the length of the diagonal line of the cube, i.e., $\sqrt{1^2+1^2+1^2}=\sqrt{3}$. In other words, any two points with a distance larger than $\sqrt{3}$ will surely not coincide with the same grid point (Figure 1b), since the 3D line between them cannot fully fit within a single cube around the grid point.

Figure 1. Illustration of data dependency during merging of Fourier data in 3D reconstruction.

(a) Illustration of a voxel centered at a grid point in 3D Fourier space.

(b – f) The grey square at the left side of each panel represents the 2D Fourier plane, in which each point is a discrete data point. The cube at the right side of each panel represents a possible space which contains all points that may contribute to the central 3D voxel during interpolation. Here, several cases of 2D sample point combination and their possible 3D placements are illustrated. In each, two points of interest are highlighted in red are connected by a red line. In (b), we illustrate that any two points with a distance of 2 pixels (e.g., P and Q) can’t be placed within a single voxel, thus will not coincide with the same central 3D grid point (O). We also illustrate that, in some circumstances (c, d), a data point (P in each panel) and one of its eight neighboring points (e.g., Q in each panel) within one pixel distance may be merged into the same central 3D grid point (O in each panel). But in other circumstances (e, f), one point (P in each panel) and one of its eight neighboring points (e.g., Q in each panel) within one pixel distance won’t be merged into the same central 3D grid point (O in each panel).

In 2D Fourier plane, the lines joining a point (e.g., point P in Figure 1b) and one of its eight neighboring points can be classified into either axial or diagonal. The red lines in the 2D Fourier plans in Figure 1c and Figure 1e are axial and those in Figure 1d and Figure 1f are diagonal. The distances between the two points with an axial relationship and those with a diagonal relationship are 1 and $\sqrt{2}$, respectively. Because these distances are not greater than $\sqrt{3}$, when placed in the 3D Fourier space, the two points joined by the red lines may (Figure 1c, d) or may not (Figure 1d, f) be merged into the same voxel. Thus, data on these points may have data dependency and parallel operations on them may cause race condition.

For those data points that are not neighboring to one another in 2D Fourier plane, the distance between them are ≥ 2, i.e. greater than $\sqrt{3}$ (Figure 1f). There is no data dependency among them and they can be updated simultaneously without causing race condition. Hence, a pixel distance of 2 is the dividing criterion which differentiates data dependency existing in 3D reconstruction.

Based on this dividing criterion, we can group 2D Fourier data points into different categories and within each category, there is no data dependency. Below, we describe our implementations based on this idea in both multi-cores/CPUs and GPU platforms.

3.1 1D interleaved scheme for multi-core platform

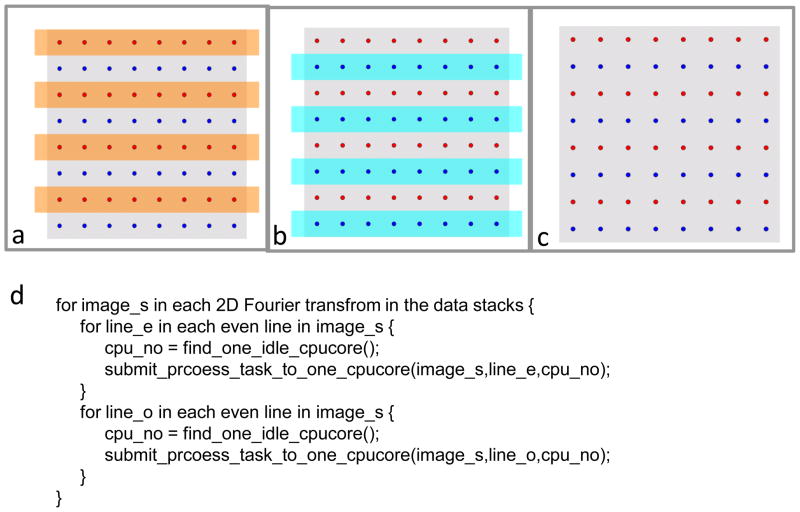
For multi-core platform, we use an interleaved striping scheme to group data points and then eliminate data dependency. As illustrated in Figure 2c, we split all source data points on the 2D plane into two groups, either odd or even, and color them in red or blue. Points on the same row form a stripe. According to what we have discussed before, data dependency of data points come from any two of the stripes which have the same parity can be updated simultaneously because the nearest distance between any two points on them are 2 (thus > $\sqrt{3}$, see the section on Race condition and solution) pixels and exceeds the diagonal length of a single 3D grid voxel. Therefore, we can safely and simultaneously update the odd group stripes (Figure 2a) first and then the even group stripes (Figure 2b) without causing an update race condition.

Figure 2. 1D interleaving scheme to overcome race condition.

The grey square (c) represents a 2D Fourier transform, containing data points that can be grouped into either odd stripes (red) (a) or even stripes (blue) (b). Data points in the same color group do not contribute to the same 3D voxel point during merging. (d) Pseudo-code showing the implementation of our 1D interleaving scheme.

This scheme is implemented in a sub-program, C3D. In this sub-program, a full 3D Fourier volume and its weighting matrix are stored in the sMEM, only a series of interpolated planes are stored in the gMEM.

3.2 2D interleaved scheme for GPGPU platform

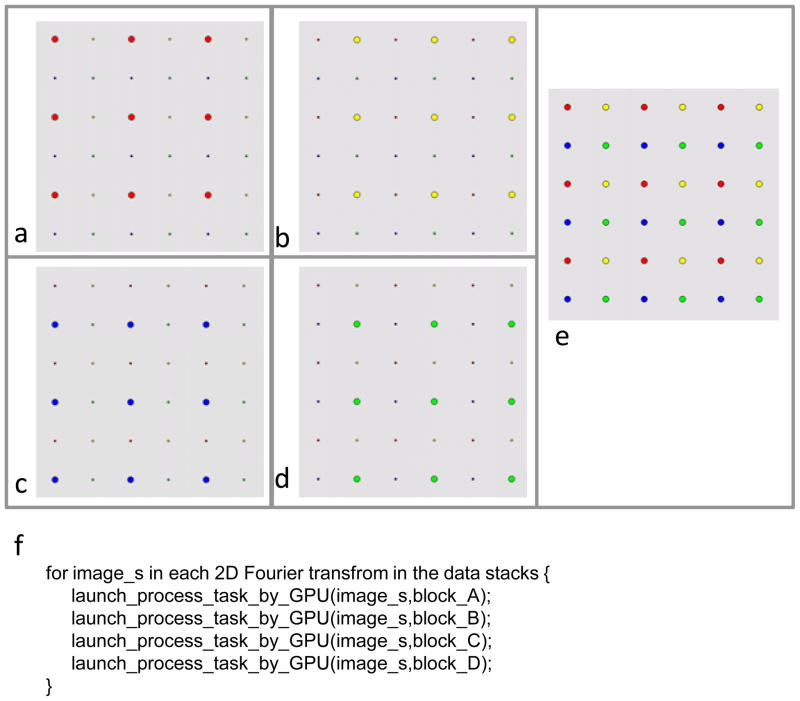
For GPGPU, simply reusing the above described 1D interleaved strategy would not fully utilize the vast GPGPU computing power due to the “Multiple Instruction Multiple Data (MIMD)” architecture of GPGPU. Here we introduce a 2D interleaved, or “abcd blocks” update scheme (Figure 3) to gain further performance enhancement. In this scheme, we group the sample points from 2D Fourier transforms not only horizontally but also vertically, thus turning them into four blocks. Like the nature of 1D interleaved scheme we described above, any two points of the same block can be updated simultaneously because the nearest distance between them are 2 pixels (thus > $\sqrt{3}$, see the section on Data dependency and solution), which exceeds the maximum allowed length (i.e., $\sqrt{3}$) in the same 3D grid point. Therefore, we can safely update the points in a block simultaneously and then b block, c block, d block (Figure 3a–d).

Figure 3. 2D interleaving scheme to overcome race condition.

The grey square (e) represents a 2D Fourier transform, containing data points grouped into red (a), yellow (b), blue (c) or green (d) blocks. Data points of the same color do not contribute to the same 3D voxel point during merging. (f) Pseudo-code showing the implementation of our 2D interleaving scheme.

The 2D interleaved scheme enables us to map elements of large dataset to many more parallel processing threads on GPGPU than the 1D interleaved scheme. Having many more working threads can effectively hide gMEM accessing latency (~400 to 600 clock cycles) (NVIDIA 2009b; a). Of equal importance is to keep the gMEM access to follow a pattern that ensures continuous address access to gain the best bandwidth performance to gMEM.

This scheme is implemented in a sub-program, G3D. In this sub-program, only a portion of 3D Fourier volume and its weighting matrix are stored in the gMEM. At the final stages, this portion will be merged into a full 3D Fourier volume and its weighting matrix stored in the sMEM.

4. Accuracy and performance evaluations of eLite3D

For execution of the GPU-based programs, a desktop and a workstation as listed in Table 1 are assembled. Here we used the desktop to represent a low-end computer and the workstation to represent a high-end computer.

Table 1.

Test System Configuration

	CPU	System Memory	Graphics Card(s)
System A (Desktop)	Intel® Core™2 Q6600	8GB DDR2 SDRAM	nVidia® GeForce™ GTX 295
System B (Workstation)	Intel® XEON™ E5504 *2	48GB DDR3 SDRAM	nVidia® GeForce™ GTX 285 *2

We first test our program using projection images computed from known atomic structures and then evaluate the performance of our programs by applying it to process two sets of experimental data. The first evaluation uses a middle size data set with an image size of 880x880 pixels, containing 44,250 Bordetella bacteriophage particle images. The second evaluation is based on a large dataset with an image size of 1024x1024 pixels, containing 18,425 of the grass carp reovirus (GCRV) particle images.

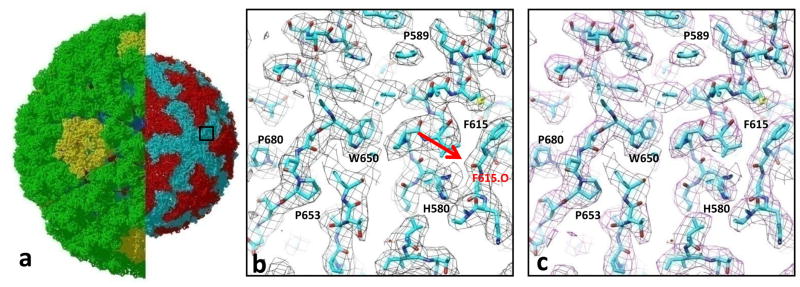
In this evaluation of the GCRV data, we compare the mass densities of the 3D maps reconstructed to the same resolution (3.3Å), by eLite3D and by the serial reconstruction program of Frealign. GCRV is a dsRNA virus and a member of the aquareovirus genus of Reoviridae family (Cheng et al. 2010). GCRV virion consists of three protein layers (~850Å diameter), and during infection, the outermost layer must be removed to generate an ~800Å diameter infectious subvirion particle (ISVP), which penetrates cell membrane to releases the virus core into host cytoplasm during infection. Here we show a side-by-side comparison between the 3.3Å resolution 3D maps of GCRV ISVP reconstructed by eLite3D and serial program Frealign. In these two maps, side chain densities are clearly resolved, and densities of some carboxyl oxygen atoms can also be observed. These high-resolution features are identical in both maps (Figure 4). The results demonstrate that the GPGPU reconstruction by eLite3D has essentially the same accuracy as that of the serial reconstruction program.

Figure 4. Accuracy of the cryoEM density map computed by eLite3D.

(a) Atomic model of the GCRV ISVP derived from a 3.3Å 3D reconstruction. The left half shows both its coat and core. In the right half, the coat shell is removed to reveal the core. The box demarcates the region displayed in (b) and (c). (b) and (c) Close-up views of the boxed area in (a), showing cryoEM densities (mess) calculated using the eLite3D GPGPU software (b) and serial CPU software(Frealign) (c). The atomic models are shown using sticks with numbers indicating amino-acid residues. Sidechain densities of the core protein are clearly resolved in both maps, and some of the carboxyl oxygen atoms are also resolved [e.g., the carboxyl oxygen of F615, arrow in (b)].

In order to demonstrate the practical effectiveness of our solution, we will only consider the overall performance of our program and take the runtime ratio between our GPGPU solution and leading software packages running on CPU-only environments. We note that many previous GPGPUs programs measure only the relative speedup of individual computation tasks to CPUs, not counting factors such as I/O operations that seriously affect the overall performance.

For the middle size reconstruction (image size: 880x880 pixel), 3D reconstruction by Frealign in a desktop PC (Table 1, system A) took ~90 hours. Running C3D of eLite3D on both low-end and high-end computer systems (Table 1, system A and B) reduces the runtime to 4.8% (4.3 Hrs) or 4.6% (4.1 Hrs) (Figure 5a). Better yet, due to GPGPU s own dedicated bus and multi-GPGPU support, G3D of eLite3D can further reduce the runtime to only 2% (1.8 Hrs) when using a desktop computer (Table 1, system A), and to an impressive 0.8% (0.71 Hrs) on a workstation computer (Table 1, system B) (Figure 5a).

Figure 5. Speedup benchmarks of eLite3D.

The runtimes of eLite3D are plotted in percentiles as compared to the runtimes of serial program Frealign (100%) for 3D reconstructions of either middle (880x880x880) dimension size data (dimension of 880) (a) or large (1024x1024x1024) dimension size data (b). Here, abbreviations: sA, system A (Intel® Core™2 Q6600 + 8GB DDR2 SDRAM + nVidia® GeForce™ GTX 295); sB, system B (Intel® XEON™ E5504 *2 + 48GB DDR3 SDRAM + nVidia® GeForce™ GTX 285 *2).

Calculating a large size reconstruction (e.g., image size: 1024x1024 pixel) using G3D requires larger gMEM. Therefore, if gMEM is limited (e.g., system A of Table 1), we can use C3D subprogram. The performance of our program is still significantly better than serial programs even for such configuration. For example, reconstruction of a large size map of GCRV with Frealign took nearly 5 days (Table 1, system B), while it took 3.2 hours (2.7%) using the C3D on system A (Table 1), and to 2 hrs (1.7%) on system B (Figure 5b). The results also demonstrate that a larger sMEM bandwidth will greatly enhance performance of C3D (system B has a relatively larger sMEM bandwidth than that of the system A). These results demonstrate that C3D is a robust solution for large size reconstructions when high-end graphical card is not available.

Conclusion

We have solved the major time-limiting computational problem in atomic resolution cryoEM reconstruction by developing eLite3D. Our solution makes PCs equipped with GPGPU as competitive as expensive computer clusters for high-resolution 3D reconstructions of large complexes. Our interleaved schemes for eliminating data dependency described in this study are generally applicable to developing high-performance GPGPU solutions for other computation-intensive, data-rich problems.