Variance analysis of x-ray CT sinograms in the presence of electronic noise background

Abstract

Purpose: Low-dose x-ray computed tomography (CT) is clinically desired. Accurate noise modeling is a fundamental issue for low-dose CT image reconstruction via statistics-based sinogram restoration or statistical iterative image reconstruction. In this paper, the authors analyzed the statistical moments of low-dose CT data in the presence of electronic noise background.

Methods: The authors first studied the statistical moment properties of detected signals in CT transmission domain, where the noise of detected signals is considered as quanta fluctuation upon electronic noise background. Then the authors derived, via the Taylor expansion, a new formula for the mean–variance relationship of the detected signals in CT sinogram domain, wherein the image formation becomes a linear operation between the sinogram data and the unknown image, rather than a nonlinear operation in the CT transmission domain. To get insight into the derived new formula by experiments, an anthropomorphic torso phantom was scanned repeatedly by a commercial CT scanner at five different mAs levels from 100 down to 17.

Results: The results demonstrated that the electronic noise background is significant when low-mAs (or low-dose) scan is performed.

Conclusions: The influence of the electronic noise background should be considered in low-dose CT imaging.

INTRODUCTION

Low-dose x-ray computed tomography (CT) is clinically desired. It can be achieved by delivering less x-ray energy to the patient via lowering the x-ray tube mAs or kVp values in data acquisition.^{1, 2} However, the quality of low-dose CT images would be severely degraded due to excessive x-ray quanta fluctuation and system inherent electronic noise background in the acquired data,^{3, 4} if there is no adequate noise treatment in processing the data for image reconstruction. Accurate statistical modeling of the data is a fundamental issue for low-dose CT imaging via either statistics-based sinogram restoration^{2, 5, 6, 7} or statistical iterative image reconstruction.^{8, 9, 10} For a clinical x-ray CT detection system, the quanta noise is introduced as x-ray flux being generated from the x-ray source and propagates along as the x-ray flux traversing the patient, while the electronic noise is intrinsic to the detection system.^{11, 12}

The two principal sources of causing the CT data noise, i.e., the photon counting statistics and the electronic noise background, have been investigated individually.^{4, 11, 12} For polychromatic x-ray generation, the signal statistics follows the compound Poisson distribution.¹³ While the mathematical formula of the compound Poisson distribution has been explicitly derived,¹³ its manipulation seems numerically intractable¹⁴ and encounters more severe challenges if the electronic noise background is included. To consider the electronic noise background, the x-ray source is usually assumed approximately as monochromatic and the signal statistics is then described by the Poisson distribution.^{5, 6, 9} For a clinical x-ray CT detection system, the electronic noise background follows a normal distribution,^{4, 6, 12} where the mean and variance reflect the dark current and readout noise of electronics, respectively. For low-dose CT imaging, the electronic noise background has been conjectured as an important factor affecting the image quality.^{4, 15} This work extends the previous study¹⁶ to consider explicitly the electronic noise background. Because the variance of data measurements is an important factor and determines the relative weight for each measurement in either statistics-based sinogram restoration or statistical iterative image reconstruction,^{5, 6, 7, 8, 9, 10} this work focuses on the variance analysis, where a mean–variance relationship with inclusion of the electronic noise background is derived and validated and the contribution of the electronic noise to the data variance is measured.

The remaining sections of this paper are organized as follows. In Sec. 2, we first briefly describe the previously gained knowledge on the noise properties of low-dose CT measurements and then present a statistical moment analysis on the measurements in CT transmission domain. Based on the analysis, we develop a new noise model to reflect the relationship between the mean and variance of the measurements in CT sinogram domain. Finally, to validate the presented noise model and get insight into the associated parameters, experimental design for data acquisition is outlined. In Sec. 3, experimental results are reported, followed by discussion and conclusion in Sec. 4.

METHOD

Statistical model of CT transmission data

Previous investigations have revealed the two principal sources from which the CT transmission data noise arises, i.e., x-ray quanta noise and system electronic noise. The quanta noise is due to the limited number of x-ray photons collected by the detector and the electronic noise is the result from electronic fluctuation in the detector photodiode and other electronic components.^{4, 12} For polychromatic x-ray generation and ignoring the beam hardening effect, the acquired CT transmission data by energy integrating detection can be described by a statistically independent compound Poisson distribution plus a statistically independent Gaussian or normal distribution. By the mathematical notations in Refs. ^{5, 6, 7}, the transmission data can be expressed as

$$I=\mathrm{compound}\mathrm{Poisson}(\lambda ,\Theta )+\mathrm{Normal}\left(m_e,{\sigma }_e^2\right),$$ (1)

where the functional form of compound Poisson (λ, Θ) is given in Ref. 13, notation Θ represents the x-ray energy spectrum, and parameter λ is the average number of x-ray photons having traversed the patient, i.e., the expectation value of the number of photons, and is a measure of the radiation intensity collected by the detector. Given the mAs and kVp setting and body size, λ reflects the radiation dosage level. $\mathrm{Normal}(m_e,{\sigma }_e^2)$ denotes the normal distribution of the electronic noise with mean m_e and variance ${\sigma }_e^2$. In modern CT systems, the mean m_e of the electronic noise, arising from the detector dark current, can be determined immediately before each scan by sampling the signals in unexposed detectors over some time interval.^{7, 12} The variance ${\sigma }_e^2$ of the electronic noise can be estimated from the sample variance of a series of dark current measurements. If a detector element is indexed by i, then all the three parameters, (λ, m_e, ${\sigma }_e^2$) in Eq. 1 shall have a subscription of i, i.e., ( λ_i, m_{e, i}, ${\sigma }_{e,i}^2$). With the assumption of monochromatic x-ray generation, Eq. 1 reduces to

$$I=\mathrm{Poisson}\left(\lambda \right)+\mathrm{Normal}\left(m_e,{\sigma }_e^2\right).$$ (2)

Equation 2 represents a noise model of the CT transmission data, ignoring the polychromatic nature of x-ray generation and other measurement errors. An analysis on the statistical moment properties of this noise model is given in Sec. 2B.

Statistical moment analysis of CT transmission data

In statistics, given a random variable X, the moment generating function is defined as ϕ_X(t) = E[e^tX], where E[^.] indicates the expectation operation.¹⁷ It is well-known that the moment generating function for the sum of independent random variables is just the product of the individual moment generating functions.¹⁷ Thus, for the CT measurement model of Eq. 2, let I = X + Y, where the random variables X and Y are independent from each other and follow the Poisson and Gaussian distributions, respectively, we have the following moment generating functions:

1. For the Poisson statistics, Poisson(λ), with parameter λ > 0, the moment generating function of X is

   $${\varphi }_X\left(t\right)=\exp \left\{\lambda (e^t-1)\right\}.$$ (3)
2. For the Gaussian statistics, $\mathrm{Normal}(m_e,{\sigma }_e^2)$, with parameters $(m_e,{\sigma }_e^2)$, the moment generating function of Y is

   $${\varphi }_Y\left(t\right)=\exp \left\{m_{e}t+\frac{{\sigma }_e^2{t}^2}{2}\right\}.$$ (4)
3. For the mixture distribution, $\mathrm{Poisson}\left(\lambda \right)+\mathrm{Normal}(m_e,{\sigma }_e^2)$, the moment generating function of I = X + Y can be calculated by

   $$\begin{array}{ccc}\hfill {\varphi }_I\left(t\right)& =& {\varphi }_{X+Y}\left(t\right)=E\left[e^{t(X+Y)}\right]={\varphi }_X\left(t\right){\varphi }_Y\left(t\right)\hfill \\ \hfill & =& \exp \left\{\lambda (e^t-1)+m_{e}t+\frac{{\sigma }_e^2{t}^2}{2}\right\}.\hfill \end{array}$$ (5)

According to the properties of the generating function, we have the following results:

$$E\left[I\right]={\varphi }_I^{\prime }\left(0\right)=\lambda +m_e,$$ (6)

$$E\left[I^2\right]={\varphi }_I^{\prime \prime }\left(0\right)={(\lambda +m_e)}^2+\left(\lambda +{\sigma }_e^2\right),$$ (7)

$$\begin{array}{c}\hfill E\left[I^3\right]={\varphi }_I^{\prime \prime \prime }\left(0\right)={(\lambda +m_e)}^3+3(\lambda +m_e)\left(\lambda +{\sigma }_e^2\right)+\lambda ,\end{array}$$ (8)

where the superscript notation " ′ " reflects the derivative operator. Furthermore, the second and third center moments of I can be calculated as

$$E\left[{(I-EI)}^2\right]=E\left[I^2\right]-{\left(E\left[I\right]\right)}^2=\lambda +{\sigma }_e^2,$$ (9)

$$\begin{array}{c}\hfill E\left[{(I-EI)}^3\right]=E\left[I^3\right]-3\left(E\left[I^2\right]\right)\left(E\left[I\right]\right)+2{\left(E\left[I\right]\right)}^3=\lambda .\end{array}$$ (10)

Equations 6, 9 indicate the mean and variance of the measurement I, respectively. Equations 6, 7, 8, 9, 10 will be used in Sec. 2C. For simplicity purpose, the expectation operation E[^.] will be replaced by E hereafter.

Variance analysis of the transmission data in CT sinogram domain

According to the results of the above statistical moment analysis, the mean and variance of I in Eq. 2 can be written as follows:

$$EI=\lambda +m_e\mathrm{and}\mathrm{Var}\left(I\right)=\lambda +{\sigma }_e^2.$$ (11)

Based on the Lambert–Beer’ law, the measurement p of the line integral along an attenuation path can be approximately calculated by

$$p=\ln \frac{I_0}{I}=\ln \left(I_0\right)-\ln \left(I\right),$$ (12)

where I₀ represents the radiation intensity prior to arrival at the body and can be measured by system calibration, e.g., by air scans. Therefore, I₀ is usually treated as a nonrandom factor. According to the Appendix at the end of this paper, by the use of the relationship of Eq. 12 and the three-order Taylor expansion about the functions ln (x) and ln ²(x) at the expectation point of EI, the variance of measurement p can be expressed as follows:

$$\begin{array}{ccc}& & \mathrm{Var}\left(p\right)=\mathrm{Var}\left(\ln \left(I\right)\right)\approx {\left({\ln }^{\prime }\left(EI\right)\right)}^2\mathrm{Var}\left(I\right)\hfill \\ & & -\frac{{\left({\ln }^{\prime \prime }\left(EI\right)\right)}^2{\mathrm{Var}}^2\left(I\right)}{4}+T=\frac{\mathrm{Var}\left(I\right)}{{\left(EI\right)}^2}-\frac{{\mathrm{Var}}^2\left(I\right)}{4{\left(EI\right)}^4}+T,\hfill \end{array}$$ (13)

where

$$\begin{array}{ccc}& & T=\left(\frac{{\left({\ln }^2\left(EI\right)\right)}^{\prime \prime \prime }}{3!}-2\left(\ln \left(EI\right)+\frac{{\ln }^{\prime \prime }\left(EI\right)}{2!}\mathrm{Var}\left(I\right)\right)\frac{{\ln }^{\prime \prime \prime }\left(EI\right)}{3!}\right.\hfill \\ & & \left.-{\left(\frac{{\ln }^{\prime \prime \prime }\left(EI\right)}{3!}\right)}^{2}E{(I-EI)}^3\right)E{(I-EI)}^3.\hfill \end{array}$$ (14)

According to Eq. 11, Var(p) in Eqs.13, 14 can be expressed as

$$\begin{array}{ccc}& & \mathrm{Var}\left(p\right)=\frac{\lambda +{\sigma }_e^2}{{(\lambda +m_e)}^2}+\frac{-{\left(\lambda +{\sigma }_e^2\right)}^2}{4{(\lambda +m_e)}^4}\hfill \\ & & +\left(\frac{-\lambda }{{(\lambda +m_e)}^3}+\frac{\lambda \left(\lambda +{\sigma }_e^2\right)}{3{(\lambda +m_e)}^5}-\frac{{\lambda }^2}{9{(\lambda +m_e)}^6}\right).\hfill \end{array}$$ (15)

In reality, in order to reduce the effect of detector dark current, the mean m_e of the electronic noise is often calibrated to be zero.^{7, 12} Thus, the variance of the line-integral measurement in Eq. 15 with m_e = 0 can be written as

$$\begin{array}{ccc}\hfill \mathrm{Var}\left(p\right)& =& \underset{T_1}{\underbrace{\frac{\lambda +{\sigma }_e^2}{{\lambda }^2}}}+\underset{T_2}{\underbrace{\frac{-{\left(\lambda +{\sigma }_e^2\right)}^2}{4{\lambda }^4}}}\hfill \\ & & +\underset{T_3}{\underbrace{\left(-\frac{1}{{\lambda }^2}+\frac{\left(\lambda +{\sigma }_e^2\right)}{3{\lambda }^4}-\frac{1}{9{\lambda }^4}\right)}}.\hfill \end{array}$$ (16)

Based on the rational function expansion,¹⁸ Var(p) in the three-order Taylor expansion 16 can be further expressed as

$$\begin{array}{ccc}\hfill \mathrm{Var}\left(p\right)& =& \underset{{\tilde{T}}_1}{\underbrace{\frac{1}{\lambda }}}+\underset{{\tilde{T}}_2}{\underbrace{\frac{{\sigma }_e^2-\frac{5}{4}}{{\lambda }^2}}}+\underset{{\tilde{T}}_3}{\underbrace{\frac{-\frac{1}{2}{\sigma }_e^2+\frac{1}{3}}{{\lambda }^3}}}\hfill \\ & & +\underset{{\tilde{T}}_4}{\underbrace{\frac{-\frac{1}{4}{\left({\sigma }_e^2\right)}^2+\frac{1}{3}{\sigma }_e^2-\frac{1}{9}}{{\lambda }^4}}}.\hfill \end{array}$$ (17)

The difference between the rational function expansion 17 and the original Taylor expansion 16 is the ordering along the parameter λ. Since λ reflects the mean radiation intensity of detected x-ray photons, Eq. 17 might be more meaningful than Eq. 16 in analyzing the relative importance of those different terms ${\tilde{T}}_i$ (or mean radiation intensity) for low-dose CT imaging. The first term in Eq. 17 reflects the variance which is mainly due to the quanta noise or Poisson statistics. The electronic noise affects the second and higher terms in the total variance of Eq. 17. Therefore, the significance of the electronic noise can be measured with respect to λ. From previous reports,^{9, 10, 19, 20} λ is in the range of tens for ultra low-dose scans¹⁰ up to thousands for normal-dose scans.^{9, 19, 20} In this study, the minimum order of λ was assumed at O(10¹), i.e., an extremely low count imaging. Using the first term ${\tilde{T}}_1=1/\lambda$ of Eq. 17 as a reference, we performed an order analysis on the other terms in Eq. 17 under the conditions of different ratios $\lambda /{\sigma }_e^2$. The results are shown in Table 1.

Table 1.

Order analysis of different terms in Eq. 17 under conditions of different ratios $\lambda /{\sigma }_e^2$.

	$\lambda /{\sigma }_e^2=O\left({10}^0\right)$	$\lambda /{\sigma }_e^2=O\left({10}^1\right)$	$\lambda /{\sigma }_e^2=O\left({10}^2\right)$	$\lambda /{\sigma }_e^2=O\left({10}^3\right)$	$\lambda /{\sigma }_e^2=O\left({10}^4\right)$	$\lambda /{\sigma }_e^2=O\left({10}^5\right)$
${\tilde{T}}_2/{\tilde{T}}_1$	O(100)	O(10−1)	O(10−2)	O(10−3)	O(10−4)	O(10−5)
${\tilde{T}}_3/{\tilde{T}}_1$	O(10−2)	O(10−2)	O(10−3)	O(10−4)	O(10−5)	O(10−6)
${\tilde{T}}_4/{\tilde{T}}_1$	O(10−3)	O(10−3)	O(10−5)	O(10−7)	O(10−11)	O(10−13)

In the extremely low-dose CT imaging situation, the order of $\lambda /{\sigma }_e^2$ may approach to O(10⁰), see the second column of Table 1, i.e., the x-ray signal is at the same magnitude as the electronic noise background. In this case, the second term is at a similar order as the first term and so it must be considered. The third and higher terms are at a level more than two orders lower than the first term and so they may be ignored. At the low-dose scanning level with $\lambda /{\sigma }_e^2$ at the order O(10¹), see the third column of Table 1, the second term is only an order lower than the first term and so it shall be considered. The other terms may be ignored. In other cases from relatively low-dose to normal-dose imaging, i.e., the order of $\lambda /{\sigma }_e^2$ is higher than O(10¹), (see the fourth and higher columns in Table 1), the second and higher terms (i.e., the electronic noise background) may be ignored.

Assuming that the ratio T_i/T₁ (i = 2, 3, 4 ) is less than the order of O(10⁻²) for low-dose CT imaging, we obtain a new approximation of Var( p) in Eq. 17 with consideration of the electronic noise background as follows:

$$\mathrm{Var}\left(p\right)=\frac{1}{\lambda }+\frac{{\sigma }_e^2-1.25}{{\lambda }^2}.$$ (18)

where the constant term “−1.25” may vary slightly when different order Taylor expansion is used.

For comparison purposes, we performed a similar ordering analysis using the original Taylor expansion form of Eq. 16. Since λ indicates the mean radiation intensity, then ${\tilde{T}}_1=1/\lambda$ was used as the reference (i.e., the case of ignoring the electronic noise background). The results are shown in Table 2. It can be observed that both the second and third terms in Eq. 16 may have noticeable contributions to the total variance if assuming that the ratio $T_i/{\tilde{T}}_1$ (i = 1, 2, 3 ) would be less than the order of O(10⁻²) in low-dose CT imaging. In other words, if Eq. 16 is used for CT image reconstruction, the second and third terms in Eq. 16 shall be included for all dose level imaging. The inclusion of these two terms can introduce significant computing complexity for the image reconstruction task.

Table 2.

Order analysis of different terms in Eq. 16 under conditions of different ratios $\lambda /{\sigma }_e^2$.

	$\lambda /{\sigma }_e^2=O\left({10}^0\right)$	$\lambda /{\sigma }_e^2=O\left({10}^1\right)$	$\lambda /{\sigma }_e^2=O\left({10}^2\right)$	$\lambda /{\sigma }_e^2=O\left({10}^3\right)$	$\lambda /{\sigma }_e^2=O\left({10}^4\right)$	$\lambda /{\sigma }_e^2=O\left({10}^5\right)$
$T_1/{\tilde{T}}_1$	O(100)	O(100)	O(100)	O(100)	O(100)	O(100)
$T_2/{\tilde{T}}_1$	O(10−1)	O(10−1)	O(10−1)	O(10−1)	O(10−1)	O(10−1)
$T_3/{\tilde{T}}_1$	O(10−1)	O(10−1)	O(10−1)	O(10−1)	O(10−1)	O(10−1)

Considering the different expansion properties in Eqs. 16, 17, we selected the rational function expansion of Eq. 17 for the following studies. For the low-dose CT image reconstruction in the ratio range T_i/T₁ (i = 2, 3, 4 ) of less than the order of O(10⁻²), we conjecture that the variance of Eq. 18 shall be considered.

By the Lambert–Beer’ law, the mean λ of the transmission datum and the mean $\overline{p}$ of the line-integral measurement p can be approximately expressed as¹¹

$$\lambda =I_0\exp (-\overline{p}).$$ (19)

Considering the use of Bowtie attenuating filtration on the x-ray flux and system calibration operations among all detector elements or bins,¹² the incident radiation intensity I₀ will no longer remain constant for all detector bins. For a detector bin i, Eq. 19 then becomes

$${\lambda }_i=I_0^i\exp (-{\overline{p}}_i).$$ (20)

Thus, Var( p_i) of Eq. 18 for each detector bin i can be expressed as

$$\begin{array}{ccc}& & {\sigma }_{p_i}^2=\mathrm{Var}\left(p_i\right)=\frac{1}{{\lambda }_i}+\frac{{\sigma }_{e,i}^2-1.25}{{\lambda }_i^2}=\frac{1}{{\lambda }_i}\left(1+\frac{{\sigma }_{e,i}^2-1.25}{{\lambda }_i}\right)\hfill \\ & & ={\Gamma }_i\exp \left({\overline{p}}_i\right)\left(1+{\Gamma }_i\exp \left({\overline{p}}_i\right)\left({\sigma }_{e,i}^2-1.25\right)\right),\hfill \end{array}$$ (21)

where ${\Gamma }_i=1/I_0^i$. Considering the polychromatic nature of x-ray generation and system calibration, Γ_i may no longer be exactly equal to $1/I_0^i$, but can be measured by repeated scans. Obviously, if ignoring the electronic noise background in Eq. 2, the variance estimation by Eq. 21 would reduce to a similar one as that in Ref. 2. Validation of the new mean–variance relationship 21 with inclusion of the electronic noise background at different mAs levels and study of its associated parameters (Γ_i, ${\sigma }_{e,i}^2$) are performed by the following experimental design. The main goal in the experimental studies is to estimate the parameters {Γ_i, ${\sigma }_{e,i}^2$} and analyze their roles in the data variance ${\sigma }_{p_i}^2$.

Data acquisition

Experimental phantom data were acquired using a clinical CT scanner (Siemens SOMATOM Sensation 16 CT scanner). An anthropomorphic torso phantom (Radiology Support Devices, Inc., Long Beach, CA) was used as shown in Fig. 1. The phantom was scanned repeatedly 150 times by a cine mode at a fixed bed position, i.e., each time the scanner rotated 360º or a full circle around the phantom while the bed position remains the same. Each of the repeated scanning of 150 times was set at a specific mAs level. A total of five different mAs values were used from 100 down to 17, i.e., 100, 80, 60, 40, and 17 mAs. By each mAs value, the tube voltage was set as the same as 120 kVp. In other words, the phantom was scanned at five different mAs levels; and at each mAs level, the scanner rotated around the phantom 150 times. The parameters of scanning geometry were as follows: (1) Each rotation included 1160 projection views evenly spaced on a circular orbit. (2) Each view contained 672 data elements each from one of the 672 detector bins. (3) The distance from the detector arrays to the x-ray source was 1040 mm. (4) The distance from the rotation center to the x-ray source was 570 mm. (5) The space of each detector bin was 1.407 mm.

Figure 1.

Illustration of an anthropomorphic torso phantom (a), an acquired dataset in sinogram format from one slice of the 16 detector rows (b), and a CT image reconstructed by a filtered back-projection (FBP) method from the sinogram dataset (b).

In modern CT systems, the CT transmission measurements are usually calibrated and outputted as scaled line-integral measurements or sinograms, {${\widehat{p}}_i$}. In order to match the physics meaning of the line integrals {p_i} in the sinogram domain [i.e., the Lambert–Beer’ law of Eq. 19] and also to give a reasonable estimation about the parameter λ_i in Eq. 20, according to the calibrated output of sinograms as described in Ref. 16, the outputted sinograms in this study were scaled by a scaling factor 2294.5, which relates to the number of bits stored in the computer. In other words, the stored digital number and the physical line integral are related by ${\widehat{p}}_i=2294.5p_i$. In Sec. 3, we will focus on the experimental studies of the relationship between the mean and variance of Eq. 21.

RESULTS

To estimate the two parameters (Γ_i, ${\sigma }_{e,i}^2$) in Eq. 21, we first calculated the sample mean ${\overline{p}}_i$ and variance ${\sigma }_{p_i}^2$ using the 150 samples of the scaled outputted sinograms or the physical line-integral measurements {p_i} from each channel i in one of the 16 detector rows at each mAs value. Since each rotation contained 1160 projection views, there were a total of 1160 calculated pairs (${\overline{p}}_i$,${\sigma }_{p_i}^2$) for each channel i for each mAs level. A set {${\overline{p}}_i$}, i = 1, 2, 3, …, 672, makes up a projection view for a detector band. All the 1160 projections on this detector band around the phantom make up a sinogram. Figure 1b shows an example of such a sinogram. A presentation in sinogram format of the variance images {${\sigma }_{p_i}^2$} is shown in Fig. 2 for different mAs levels.

Figure 2.

The sinogram presentation of variance images calculated from the 150 repeated samples of the scaled outputted sinogram for each channel i in one of the 16 detector rows at each mAs value. From (a) to (e), the corresponding mAs value is 17, 40, 60, 80, and 100, respectively.

Comparing the variance image at 100 mAs level with that at 17 mAs level, the effect of the electronic noise background is noticeable by the following observations. Since the electronic noise is relatively uniform across all detector bins, the data variance image shall be less uniform at 100 mAs level than that at 17 mAs level. This is observed in the figure. At 100 mAs level, the variance shall be smaller at less attenuated areas and remains nearly the same at heavily attenuated areas where the electronic noise dominates. This is also observed in the figure. One of the heavily attenuated areas in the sinogram representation is at the bins from 200 to 500 and views from 200 to 400 and another area is at the bins from 200 to 500 and views from 750 to 950.

In the previous study,¹⁶ the mean–variance relationship involves one parameter for each detector bin i, i.e., Γ_i, and so this parameter at each bin i was first calculated from the corresponding pair (${\overline{p}}_i$, ${\sigma }_{p_i}^2$) and then averaged over the 1160 views. In this work, there are two parameters {Γ_i, ${\sigma }_{e,i}^2$} in the variance estimation model 21, and the previous method is no longer applicable. Therefore, we took an alternative approach of estimating the parameters Γ_i and ${\sigma }_{e,i}^2$ by fitting the 1160 paired data for each bin i. Each set {Γ_i} or {${\sigma }_{e,i}^2$} can be plotted as a curve along the bin index, i = 1, 2, 3,…, 672, i.e., across the field-of-view (FOV). In the parameters fitting experiments, the MATLAB function “lsqcurvefit” was used together with the “trust-region-reflective method.” To ensure computing accuracy, the associated optimization settings were as follows: (1) the termination tolerance on the function value was 1 × 10⁻⁶; (2) the termination tolerance on the variable was 1 × 10⁻⁶; and (3) the maximum iteration is 400. To perform the goodness-of-fit for evaluating the presented model 21, we used the sum of squares due to error (SSE), the coefficient of determination (or R-square), and the root mean squared error (RMSE).

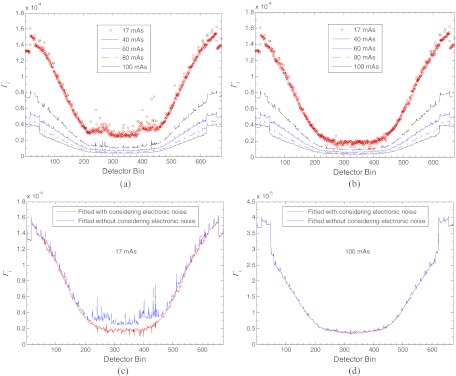
Figure 3 shows the fitted parameter factors {Γ_i} in Eq. 21 from the 150 repeatedly measured samples at the five different mAs levels. The curves in Fig. 3a were fitted from the variance estimation model 21 without considering the electronic noise background (i.e., set ${\sigma }_{e,i}^2=0$). These curves are similar, as expected, to those in Ref. 16. Some variations from those curves in Ref. 16 can be seen because of the use of different mean–variance relationship formulae and different implementations of the calculation procedure. The similarity at higher mAs levels (⩾40) indicates the domination of the Poisson statistics of the quanta noise where including or ignoring the electronic noise does not make a noticeable difference. The noticeable difference at the low mAs level, e.g., 17 mAs indicates the influence of the electronic noise (i.e., the difference occurs because of the electronic noise presented in the acquired data, but was ignored in the calculation procedure). The above observations from Fig. 3a with comparison to the results in Ref. 16 can also be seen with comparison to Fig. 3b. The curves in Fig. 3b were fitted from the variance model 21 with consideration of the electronic noise. Those curves at higher mAs levels (⩾40 ) are similar in shape to that in Fig. 3a, indicating the domination of the Poisson statistics at relatively higher dose imaging cases. The curve at 17 mAs level is noticeably different from that in Fig. 3a, indicating the influence of the electronic noise.

Figure 3.

An illustration of the fitted factor {Γ_i} in model (21) from 150 repeated measurements at the five different mAs levels: (a) the fitted results from the variance estimation model 21 without considering the electronic noise (i.e., set ${\sigma }_{e,i}^2=0$); (b) the fitted results from the variance estimation model 21 with consideration of the electronic noise; (c) a comparison of the fitted {Γ_i} with/without consideration of the electronic noise in model 21 at 17 mAs level; and (d) a comparison of the fitted {Γ_i} with/without consideration of the electronic noise in model 21 at 100 mAs level.

To more clearly see the difference between Figs. 3a, 3b, we plotted the curves by continuous lines in Figs. 3c, 3d. These continuous lines compare the fitted {Γ_i} with/without considerations of the electronic noise in model 21 at 17 mAs and 100 mAs, respectively. The most different line segment ranges from bin 200 to bin 500, concurring with the heavily attenuated area in Fig. 2. In summary, it is observed that the shapes of {Γ_i} curves from the variance model 21 are similar at all the mAs levels in the presence of electronic noise, see Fig. 3b. This is expected, because of ${\Gamma }_i\approx 1/I_0^i$, that (1) each curve shall be symmetric from left to right to reflect the symmetrical effect of the Bowtie filtration and (2) the amplitude of each curve shall increase from center toward both sides to reflect the inverse proportional relationship between Γ_i and $I_0^i$ (or the Poisson characteristics). It is further observed that the difference of the fitted {Γ_i} with/without consideration of the electronic noise in model 21 is noticeable in the low-dose imaging case of 17 mAs level, see Fig. 3c. This difference demonstrates that in low-dose CT imaging, the electronic noise can have a noticeable influence for ideal singoram estimation and image reconstruction. At the normal-dose level with mAs value of 100, the similarity in Fig. 3d demonstrates that the electronic noise background can be ignored. This experimental observation concurs with the current practice in x-ray CT applications at the normal-dose level. By comparing Fig. 3a with Fig. 3b for this phantom/body size, the electronic noise may be ignored at a mAs level greater than 40.

The above graphical observations from Fig. 3 can be documented by quantitative validation measures. For example, Table 3 shows the corresponding coefficients of determination with 95% confidence bounds and the goodness-of-fit for fitting model 21 at the detector bin 300 and bin 450. It can be seen that in all the cases, the goodness-of-fit measures with consideration of the electronic noise are better than those without considering the electronic noise in model 21. Another example is the consistency measure between the fitted parameters {Γ_i} with and without considering the electronic noise in model 21 at different mAs levels. This measure is usually given by the Lin's concordance correlation coefficients.²¹ Table 4 shows the results of this measure. It can be seen that the Lin's concordance coefficients increase as the mAs level increases from 17 to 100, and all the lower bounds of the 95% confidence interval of the correlations are larger than 0.9, except in the case of 17 mAs. This consistency measure indicates that the difference is significant at 17 mAs level with and without considering the electronic noise in model 21, and suggests that the influence of electronic noise at lower mAs level must be considered.

Table 3.

The coefficients of determination with 95% confidence bounds and the goodness-of-fit for fitting model 21 at the detector bin 300 and bin 450 using the 150 repeated measurements at the five different mAs levels.

			Coefficients of determination
			(with 95% confidence bounds)		Goodness-of-fit
mAs level	Detector bin	Consideringelectronic noise	Γi	${\sigma }_{e,i}^2$	SSE	R-square	RMSE
17	300	Yes	(1.999, 2.121) × 10−5	(6.162, 8.202)	1.006×10−2	0.9718	2.947 × 10−3
		No	(2.686, 2.747) × 10−5	–	1.476 × 10−2	0.9587	3.568 × 10−3
	450	Yes	(2.778, 2.938) × 10−5	(12.40, 17.24)	1.906 × 10−3	0.9686	1.283 × 10−3
		No	(3.511, 3.577) × 10−5	–	2.439 × 10−3	0.9598	1.451 × 10−3
40	300	Yes	(8.342, 8.839) × 10−6	(14.07, 19.06)	1.604 × 10−3	0.9734	1.177 × 10−3
		No	(1.091, 1.113) × 10−5	–	2.192 × 10−3	0.9636	1.375 × 10−3
	450	Yes	(1.379, 1.446) × 10−5	(11.01, 18.06)	3.303 × 10−4	0.9714	5.341 × 10−4
		No	(1.559, 1.584) × 10−5	–	3.586 × 10−4	0.9689	5.562 × 10−4
60	300	Yes	(6.188, 6.471) × 10−6	(6.668, 10.78)	5.036 × 10−4	0.9791	6.594 × 10−4
		No	(6.958, 7.065) × 10−6	–	5.485 × 10−4	0.9773	6.879 × 10−4
	450	Yes	(9.193, 9.615) × 10−6	(8.13, 17.43)	1.307 × 10−4	0.9718	3.359 × 10−4
		No	(9.950, 10.10) × 10−6	–	1.356 × 10−4	0.9708	3.421 × 10−4
80	300	Yes	(4.334, 4.583) × 10−6	(10.54, 18.14)	3.869 × 10−4	0.9688	5.780 × 10−4
		No	(4.961, 5.054) × 10−6	–	4.161 × 10−4	0.9664	5.992 × 10−4
	450	Yes	(6.884, 7.218) × 10−6	(5.008, 17.65)	8.110 × 10−5	0.9674	2.646 × 10−4
		No	(7.298, 7.416) × 10−6	–	8.253 × 10−5	0.9668	2.669 × 10−4
100	300	Yes	(3.536, 3.703) × 10−6	(10.61, 18.09)	1.732 × 10−5	0.9777	3.867 × 10−4
		No	(3.944, 4.008) × 10−6	–	1.956 × 10−5	0.9748	4.108 × 10−4
	450	Yes	(5.490, 5.736) × 10−6	(1.991, 16.21)	4.403 × 10−5	0.9711	1.950 × 10−4
		No	(5.726, 5.812) × 10−6	–	4.427 × 10−5	0.9710	1.954 × 10−4

Table 4.

Lin's concordance coefficient between the fitted parameters Γ_i at the detector bins from 200 to 500 with and without considering the electronic noise in model 21 at different mAs levels.

			95% confidence interval of
mAs level	Sample size N	Lin's concordance coefficient	concordance coefficient
17	301	0.6340	(0.5611, 0.6970)
40	301	0.9504	(0.9382, 0.9603)
60	301	0.9836	(0.9795, 0.9869)
80	301	0.9901	(0.9875, 0.9921)
100	301	0.9912	(0.9890, 0.9930)

Figure 4 shows the fitted parameter factor {${\sigma }_{e,i}^2$} in model 21 at five different mAs levels, where the median value of each fitted {${\sigma }_{e,i}^2$} is shown by the horizontal lines. To get insight into these fitted results about {${\sigma }_{e,i}^2$}, we look back to Figs. 23.

Figure 4.

An illustration of the fitted factor {${\sigma }_{e,i}^2$} in model 21 from 150 repeated measurements at the five different mAs levels and the median value of the fitted {${\sigma }_{e,i}^2$} (a)–(e); and the fitted curve with an exponential functional from the calculated five median values (f).

At the 17 mAs level, we have observed from Figs. 2a, 2e that the electronic noise plays a significant role in the data (or total) noise. Thus, we expect that at the 17 mAs level, the system calibration on the detected signals for the outputted sinograms would not alter too much the electronic noise variance. In other words, the fitted {${\sigma }_{e,i}^2$} at low mAs level would reflect more closely to the actual variance of the electronic noise than that at high mAs level. Therefore, the fitted {${\sigma }_{e,i}^2$} are relative-uniformly distributed among all detector bins, see Fig. 4a, concurring with the expectation, and the median value is around 10, agreeing with the previously reported values.^{4, 7, 11, 12}

At 40 and higher mAs levels, the electronic noise plays less and less role in the total data noise, and the nonstationary nature of Poisson noise becomes noticeable. In these cases, the second term $({\sigma }_{e,i}^2-1.25)$ in Eq. 21 approaches to negligible, as compared to the first term. Therefore, the fitted {${\sigma }_{e,i}^2$} would be affected more and more by the contribution of the first term (i.e., the Poisson noise). In other words, the fitted {${\sigma }_{e,i}^2$} would be less uniformly distributed as the mAs value increases. The nonuniform distribution shall happen in the range from bin 200 to bin 500, concurring with the heavy attenuation area in Fig. 2. Considering that median value can rule out the interference of the extreme values, Fig. 4f shows the tendency of the median values of electronic noise at all channels about five mAs levels. It can be seen that median value decreases as the mAs value increases. To be seen below, the amplitude of the median value variation is small as compared to the first term in Eq. 21.

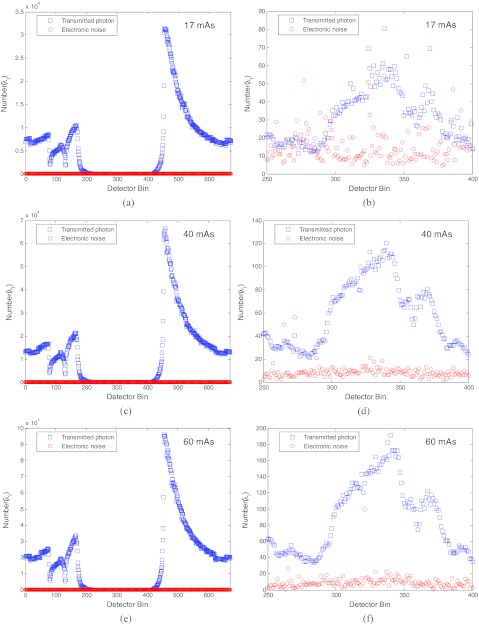
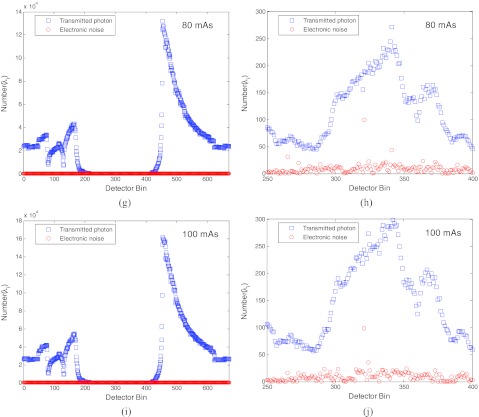
To get more insight into the results about the electronic noise in the total data noise in Fig. 4, we performed another analysis. The results are shown in Fig. 5. The top row shows the mean number of the transmitted photons (i.e., ${\lambda }_i=I_0^i\exp (-{\overline{p}}_i)$) and the variance of the electronic noise (i.e., ${\sigma }_{e,i}^2$) along one projection view at 17 mAs level. The bottom row shows the results at 100 mAs level. The other rows show the results at other mAs levels. The left column shows the results across all the detector bins. The right column shows the zoomed-up image of the left column for those bins from 250 to 400 where heavy attenuation occurs, referring to Fig. 2.

Figure 5a.

Number of transmitted photons and electronic noise along one projection view at different mAs levels of (a) −17, (c) −40, (e) −60, (g) −80, and (i) −100. Pictures (b), (d), (f), (h), and (j) show the details for those detector bins between 250 and 400 at the different mAs levels, respectively.

Figure 5b.

Figure 5c.

Figure 5d.

Figure 5e.

Figure 5f.

Figure 5g.

Figure 5h.

Figure 5i.

Figure 5j.

It is clearly seen that at the 17 mAs level, the mean number of the transmitted photons (which is equal to the variance of the transmitted data of Poisson statistics) and the variance of the electronic noise are at the same order in the heavily attenuated area between bin 250 and bin 400. However, at the 100 mAs level, the domination of the Poisson noise is clearly seen, while the electronic noise remains at the same order as that at 17 mAs level.

Putting Figs. 45 together, the left column of Fig. 5 shows the global picture of both variances of the Poisson noise and the electronic noise, while Fig. 4 and the right column of Fig. 5 show the zoomed or local picture of the Poisson and electronic noises. From the global picture, it is clear that at the heavily attenuated areas, the data quality is severely affected at all mAs levels from 17 up to 100. From the local picture, the different roles of the Poisson noise and the electronic noise in the total data noise are seen. At higher mAs levels (⩾60 ), the electronic noise background can be distinguished from the x-ray photon counts and, therefore, it may be corrected by subtraction or simply be ignored. At lower mAs levels, the electronic noise contaminates the photon counts. In such cases, it shall be considered via modeling of the data statistics.

In addition to the observations in the global and local pictures, we also noted from Fig. 4f the decreasing of the median value of the electronic noise as the mAs level increases. While the decreasing of the median value as the mAs level increases is observable, the change is so small as compared to the changing of the Poisson noise variance as mAs level increases. If this changing of the overall variance level of the electronic noise is not ignorable, it can be incorporated via Eq. 21 into a statistical image reconstruction.

So far, we have presented a global picture of Fig. 2 to show the effect of the electronic noise background in the sinograms, showed the effect of the Bowtie filtration on the variance of the sinogram data in Fig. 3, and revealed the relative influence of the electronic noise at five different mAs levels by Figs. 45. In the following, we report the experimental studies on the effect of the electronic noise {${\sigma }_{e,i}^2$} on the linearity of the {Γ_i} and on the variance estimation of Eq. 21.

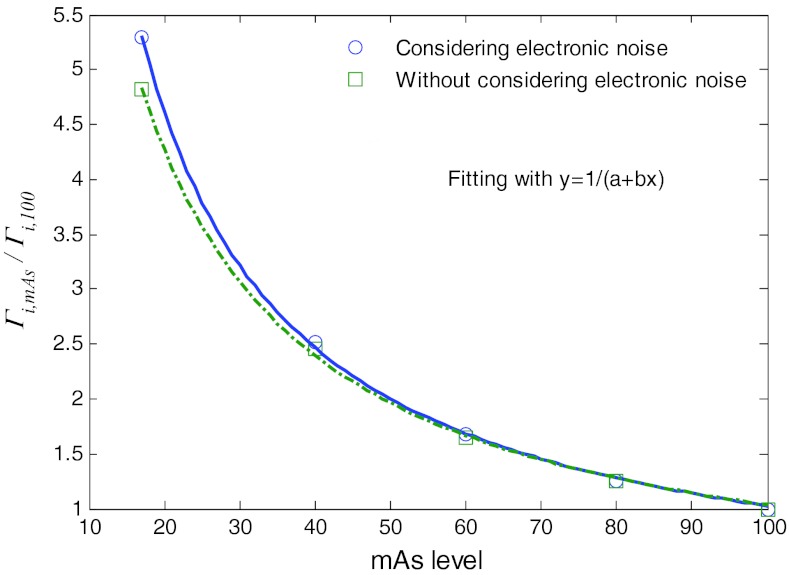
The similarity of {Γ_i} curves for different mAs levels can be further seen by plotting the paired points {Γ_{i, 100}, Γ_{i, mAs}}, where {Γ_{i, 100}} are the {Γ_i} values at the 100 mAs level while {Γ_{i, mAs}} are the values at a lower mAs level. Figure 6 shows the plots of the paired points at the five different mAs levels with/without consideration of the electronic noise background. A linear relationship can be observed for each of the four (17, 40, 60, and 80) mAs levels, similar to the results in Ref. 16. The slope of the four lines in each of the two cases (i.e., with and without consideration of the electronic noise) was determined by linear fitting and the results are shown by the four points at 17, 40, 60, and 80 mAs in Fig. 7.

Figure 6.

Illustration of a linear relationship between factors {Γ_i} at 100 mAs level and at other lower mAs levels from the variance estimation model 21. (a) is from model 21 without considering the electronic noise (i.e., set ${\sigma }_{e,i}^2=0$) and (b) is from model 21 with consideration of the electronic noise.

Figure 7.

Factors {Γ_{i, mAs}/Γ_{i, 100}} at five different mAs levels with/without considering electronic noise and their fitted curves with a reciprocal functional.

Essentially, all the four slope values are closely represented by the corresponding ratios of {Γ_{i, mAs}/Γ_{i, 100}}, see Fig. 6. A noticeable difference between Fig. 6a (without considering the electronic noise) and Fig. 6b (with consideration of the electronic noise) can be seen at the lower left corners of the figures for low mAs levels of 17 and 40. This observation further indicates that the electronic noise shall be considered at the low mAs levels for low-dose CT imaging. The relationship between the ratio of {Γ_{i, mAs}/Γ_{i, 100}} and the mAs values can be described by a reciprocal function as shown in Fig. 7. It illustrates that when the mAs level is not greater than 40, the difference between the two cases, i.e., considering electronic noise and without consideration of the electronic noise, becomes noticeable. In other words, when the mAs level is less than a threshold, the influence of the electronic noise should be considered in such a low-dose CT imaging.

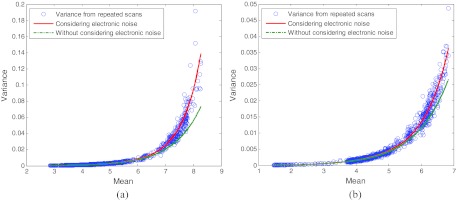
To further show the difference between the two cases with/without consideration of the electronic noise, we first directly calculated the variance of the acquired sinogram data from the repeated scans at 17 mAs level. The plots of the mean–variance of the line-integral measurements at two different bins are shown by the circles in Fig. 8 as an example. We then calculated the mean–variance curves based on the variance model 21 with consideration (the solid lines) and without consideration (the dotted lines) of the electronic noise. From this figure, it can be observed that the results from both the repeated scans and the theoretical model 21 with consideration of the electronic noise agree with each other better than the results without considering the electronic noise. To quantitatively measure the consistency between the variances of the line-integral measurements from the repeated scans and the predicted variances from the theoretical model 21 at two different detector bins with and without considering the electronic noise, we calculated the associated SSE, R-square, and RMSE as shown in Table 5. Both the graphical observation and the quantitative consistency measure further indicate the importance of considering the electronic noise background for low-dose CT imaging.

Figure 8.

Plots of the mean–variance of the line-integral measurements at two different detector bins from the repeated scans and from the analytical formulas 21 with and without considering the electronic noise. (a) is the result at bin 300 and (b) is the result at bin 450.

Table 5.

Quantitative evaluation of the consistency between the variances of the line-integral measurements from the repeated scans and the predicted variances from the theoretical model 21 at two different detector bins with and without considering the electronic noise.

Detector	Considering
bin	electronic noise	SSE	R-square	RMSE
300	Yes	1.393×10−2	0.9662	3.464 × 10−3
	No	4.336×10−2	0.7612	6.114 × 10−3
450	Yes	2.176×10−3	0.9583	1.370 × 10−3
	No	6.004×10−3	0.8296	2.275 × 10−3

CONCLUSION AND DISCUSSION

In our previous work,^{1, 2, 10, 16} a nonlinear relationship between the mean and variance of the measurements in the singoram domain was presented without consideration of the electronic noise background. In this experimental study, we extended our previous mean–variance model in the sinogram domain to include the electronic noise background for low-dose CT imaging.

Based on the presented statistical moment analysis of the measurements in the transmission domain via the Taylor expansion approximation of a continuous function, the variance of the sinogram data at a specific detector bin can be determined by four physical quantities, as shown in formula 15: (i) the line integral (i.e., ${\overline{p}}_i$) of the attenuation coefficients along the x-ray path i; (ii) the incident photon number (i.e., 1/Γ_i); (iii) the mean (i.e., m_e) of the electronic noise; and (iv) the variance (i.e., ${\sigma }_e^2$) of the electronic noise. In modern CT systems, some parameters in the mean–variance model 15 can be measured as part of the standard routine calibration operation. For example, from our systematic studies using the repeated measurements in Ref. 16 and above, it can be observed that parameter Γ_i primarily depends on both the incident photon number (or the mAs level) and the shape of the Bowtie attenuating filter across the FOV, as shown in Fig. 3, and therefore can be estimated from measurements of air scans. Another parameter in the mean–variance model 15, i.e., the mean m_e of the electronic noise, arising from the detector dark current, can be determined immediately before each scan by sampling the signals in those unexposed detectors over some time interval.^{6, 7, 12} From Figs. 45, it can be observed that another parameter, i.e., the variance ${\sigma }_e^2$ of the electronic noise, reduces slightly as the mAs value increases, and can be determined by the exponential relationship of Fig. 5f. In practice, the variance ${\sigma }_e^2$ of the electronic noise may be estimated from the sample variance of a series of dark current measurements.^{6, 7} Given the above four physical quantities, Eq. 15 provides a theoretical means to estimate the variance, which reflects the relative importance of each measurement for various data processing tasks, for example, a statistical image reconstruction task in the sinogram domain.¹⁰

In the special case where the mean of the electronic noise is calibrated to zero, we obtained the mean–variance model 21, which reflects the ground-truth for an accurate statistical modeling of the low-dose CT data in the sinogram domain. Based on Eq. 21, the sinogram variances can be predicted accurately from the corresponding transmission data acquired at a specific mAs level. Figures 345 illustrate that, because the mean and variance relationship of Eq. 21 includes explicitly the electronic noise background, the difference between the two cases with and without considering the electronic noise at a mAs level, e.g., lower than 60 mAs for the phantom body, is visually noticeable. This observation on the difference between the two cases indicates that inclusion of the electronic noise is needed for low-dose CT imaging.

The observation that the variance ${\sigma }_e^2$ of the electronic noise reduced slightly as the mAs value increased seems contradictory to our intuition that the variance should be independent from the mAs level. This intuition is based on the assumption that the detection system is perfectly linear in the concerned energy and count rate ranges. In general, the detection system is made by the manufacturer to do so. If the assumption does not hold, then the dependence would be reflected by the small variation of Fig. 4f. If the assumption holds, then the dependence may be due to several factors in the data calibration. For example, both I_i and $I_0^i$ in their relationship of $I_i=I_0^i\exp (-p_i)$ of Eq. 12 contain the electronic noise. If the scanner calibration uses a different way to handle the electronic noise in I_i than that in $I_0^i$, the outcome may affect the intuition. By common perception, $I_0^i$ is treated as a parameter (nonstatistical). Therefore, the outcome may affect the intuition. Another factor which may affect the intuition is the calibration or correction for the beam hardening. Since the energy spectrum of $I_0^i$ is altered by the body attenuation, the energy spectrum of I_i becomes unknown. Using the energy spectrum of $I_0^i$ to correct for the beam hardening on I_i may affect the intuition. Another factor may be the calibration for m_i = 0. It is very interesting to see that by fixing the electronic noise variance at the level found at 17 mAs [i.e., Fig. 4a], the fitting on the Gamma parameter {Γ_i} remained almost the same (no noticeable difference) as that in Fig. 3. The same outcome was also observed when fitting the Gamma parameter {Γ_i} by using the mean–variance level from the five mAs levels. Based on these fitting experiments, we would conjecture that the fitting on {${\sigma }_e^2$} is relatively sensitive to the error in the measured data. This may be another factor affecting the intuition. Despite these influencing factors, the slight decrease of variance ${\sigma }_e^2$ as mAs level increases is so small as compared to the amplitude of the signals at those mAs levels. So the small change will not affect the conclusion of this experimental work.

It is expected that the gained knowledge on the noise properties of the low-mAs sinogram data in this experimental work would assist the development of a statistical image reconstruction algorithm in currently available CT scanners to achieve low-dose CT clinical applications, such as that in Ref. 15. In the reconstruction algorithm development, since the relationship between the mean and variance is no longer linear, a Poisson model for the sinogram data is no longer valid. Other statistical models are needed. Without an explicit expression to describe the sinogram data statistics, the penalized weighted least squares approach¹⁰ can be a choice with accuracy up to the second order statistical moment. Searching for an adequate expression to describe the sinogram statistics remains a research topic, and our recent exploratory study indicates that the information divergence theory can be a potential choice to describe the sinogram statistics.²²

APPENDIX: VARIANCE ANALYSIS OF A FUNCTION OF ONE RANDOM VARIABLE

Suppose x ∈ X is a random variable and f(·) is a smooth function, ∀ɛ > 0 and ∃c > 0, applying three-order Taylor expansion at point EX, we can have

$$\begin{array}{ccc}& & f\left(x\right)=f\left(EX\right)+f^{\prime }\left(EX\right)(x-EX)+\frac{f^{\prime \prime }\left(EX\right)}{2!}{(x-EX)}^2\hfill \\ & & +\frac{f^{\prime \prime \prime }\left(EX\right)}{3!}{(x-EX)}^3+\frac{f^{\prime \prime \prime }\left(\xi \right)}{4!}{(x-EX)}^4,\hfill \end{array}$$ (A1)

where ξ ∈ [EX − c, EX + c] and c is a constant. Equation A1 holds for all x ∈ [EX − c, EX + c] because the Taylor expansion works for a function in a bounded closed interval. In our case, only the first four terms were considered in the Taylor expansion because these four terms are sufficient for data analysis. Including more terms can be conducted straightforwardly if needed. The expectation of f(x) for the first four terms can be expressed as

$$\begin{array}{ccc}\hfill Ef\left(X\right)& \approx & f\left(EX\right)+\frac{f^{\prime \prime }\left(EX\right)}{2!}\mathrm{Var}\left(X\right)\hfill \\ & & +\frac{f^{\prime \prime \prime }\left(EX\right)}{3!}E{(X-EX)}^3.\hfill \end{array}$$ (A2)

Similar to the Taylor expansion of function f(x), the expansion of f ²(x) can be written as

$$\begin{array}{ccc}\hfill f^2\left(x\right)& \approx & f^2\left(EX\right)+2f\left(EX\right)f^{\prime }\left(EX\right)(x-EX)\hfill \\ & & +\frac{2({\left(f^{\prime }\left(EX\right)\right)}^2+f\left(EX\right)f^{\prime \prime }\left(EX\right))}{2!}{(x-EX)}^2\hfill \\ & & +\frac{{\left(f^2\left(EX\right)\right)}^{\prime \prime \prime }}{3!}{(x-EX)}^3.\hfill \end{array}$$ (A3)

The expectation of f²(x) for the first four terms can be expressed as

$$\begin{array}{ccc}& & E{f}^2\left(X\right)\approx f^2\left(EX\right)+[{\left(f^{\prime }\left(EX\right)\right)}^2+f\left(EX\right)f^{\prime \prime }\left(EX\right)]\mathrm{Var}\left(X\right)\hfill \\ & & +\frac{{\left(f^2\left(EX\right)\right)}^{\prime \prime \prime }}{3!}E{(X-EX)}^3.\hfill \end{array}$$ (A4)

The formula for the variance of f(X) then can be expressed as

$$\begin{array}{c}\hfill \begin{array}{c}\mathrm{Var}\left(f\left(X\right)\right)=E{(f\left(X\right)-Ef\left(X\right))}^2=E\left(f^2\left(X\right)\right)-{\left(E\left(f\left(X\right)\right)\right)}^2\hfill \\ \approx \left\{\begin{array}{c}{\displaystyle f^2\left(EX\right)+[{\left(f^{\prime }\left(EX\right)\right)}^2+f\left(EX\right)f^{\prime \prime }\left(EX\right)]\mathrm{Var}\left(X\right)+\frac{{\left(f^2\left(EX\right)\right)}^{\prime \prime \prime }}{3!}E{(X-EX)}^3}\hfill \\ -{\left({\displaystyle f\left(EX\right)+\frac{f^{\prime \prime }\left(EX\right)}{2!}\mathrm{Var}\left(X\right)+\frac{f^{\prime \prime \prime }\left(EX\right)}{3!}E{(X-EX)}^3}\right)}^2\hfill \end{array}\right\}\hfill \\ =\left\{\begin{array}{c}{\displaystyle f^2\left(EX\right)+[{\left(f^{\prime }\left(EX\right)\right)}^2+f\left(EX\right)f^{\prime \prime }\left(EX\right)]\mathrm{Var}\left(X\right)+\frac{{\left(f^2\left(EX\right)\right)}^{\prime \prime \prime }}{3!}E{(X-EX)}^3}\hfill \\ -{\left({\displaystyle f\left(EX\right)+\frac{f^{\prime \prime }\left(EX\right)}{2!}\mathrm{Var}\left(X\right)}\right)}^2\hfill \\ -\left({\displaystyle 2\left({\displaystyle f\left(EX\right)+\frac{f^{\prime \prime }\left(EX\right)}{2!}\mathrm{Var}\left(X\right)}\right)\frac{f^{\prime \prime \prime }\left(EX\right)}{3!}E{(X-EX)}^3+{\left({\displaystyle \frac{f^{\prime \prime \prime }\left(EX\right)}{3!}E{(X-EX)}^3}\right)}^2}\right)\hfill \end{array}\right\}\hfill \\ =\left\{\begin{array}{c}{\displaystyle f^2\left(EX\right)+{\left(f^{\prime }\left(EX\right)\right)}^2\mathrm{Var}\left(X\right)+f\left(EX\right)f^{\prime \prime }\left(EX\right)\mathrm{Var}\left(X\right)+\frac{{\left(f^2\left(EX\right)\right)}^{\prime \prime \prime }}{3!}E{(X-EX)}^3}\hfill \\ -\left({\displaystyle f^2\left(EX\right)+f\left(EX\right)f^{\prime \prime }\left(EX\right)\mathrm{Var}\left(X\right)+\frac{{\left(f^{\prime \prime }\left(EX\right)\right)}^2{\mathrm{Var}}^2\left(X\right)}{4}}\right)\hfill \\ -\left({\displaystyle 2\left({\displaystyle f\left(EX\right)+\frac{f^{\prime \prime }\left(EX\right)}{2!}\mathrm{Var}\left(X\right)}\right)\frac{f^{\prime \prime \prime }\left(EX\right)}{3!}E{(X-EX)}^3+{\left({\displaystyle \frac{f^{\prime \prime \prime }\left(EX\right)}{3!}E{(X-EX)}^3}\right)}^2}\right)\hfill \end{array}\right\}\hfill \\ {\displaystyle ={\left(f^{\prime }\left(EX\right)\right)}^2\mathrm{Var}\left(X\right)-\frac{{\left(f^{\prime \prime }\left(EX\right)\right)}^2{\mathrm{Var}}^2\left(X\right)}{4}+T.}\hfill \end{array},\end{array}$$ (A5)

where

$$\begin{array}{c}\hfill \begin{array}{c}T=\left\{\begin{array}{c}{\displaystyle \frac{{\left(f^2\left(EX\right)\right)}^{\prime \prime \prime }}{3!}E{(X-EX)}^3-}\hfill \\ {\displaystyle 2\left({\displaystyle f\left(EX\right)+\frac{f^{\prime \prime }\left(EX\right)}{2!}\mathrm{Var}\left(X\right)}\right)\frac{f^{\prime \prime \prime }\left(EX\right)}{3!}E{(X-EX)}^3-{\left({\displaystyle \frac{f^{\prime \prime \prime }\left(EX\right)}{3!}E{(X-EX)}^3}\right)}^2}\hfill \end{array}\right\}\hfill \\ \\ =\left({\displaystyle \frac{{\left(f^2\left(EX\right)\right)}^{\prime \prime \prime }}{3!}-2\left({\displaystyle f\left(EX\right)+\frac{f^{\prime \prime }\left(EX\right)}{2!}\mathrm{Var}\left(X\right)}\right)\frac{f^{\prime \prime \prime }\left(EX\right)}{3!}-{\left({\displaystyle \frac{f^{\prime \prime \prime }\left(EX\right)}{3!}}\right)}^{2}E{(X-EX)}^3}\right)E{(X-EX)}^3.\hfill \end{array}\end{array}$$ (A6)