Mosquitoes survive raindrop collisions by virtue of their low mass

Abstract

In the study of insect flight, adaptations to complex flight conditions such as wind and rain are poorly understood. Mosquitoes thrive in areas of high humidity and rainfall, in which raindrops can weigh more than 50 times a mosquito. In this combined experimental and theoretical study, we here show that free-flying mosquitoes can survive the high-speed impact of falling raindrops. High-speed videography of those impacts reveals a mechanism for survival: A mosquito’s strong exoskeleton and low mass renders it impervious to falling drops. The mosquito’s low mass causes raindrops to lose little momentum upon impact and so impart correspondingly low forces to the mosquitoes. Our findings demonstrate that small fliers are robust to in-flight perturbations.

One of the technological feats of the 21st century is the construction of insect-sized flying robots, micro-airborne vehicles (MAVs), made possible by rapidly shrinking manufacturing and elecronics (1–7). These robots have numerous applications such as deployment in swarms for surveillance and search-and-rescue operations. In parallel with the engineering of MAVs, vigorous efforts continue to be made into understanding flight in the natural world, such as by birds and insects (8–11). Much progress has been made in understanding straight-path flight in unidirectional flow. However, much remains to be understood about the abilities of birds and insects to fly through complex conditions such as wind and rain. Such knowledge clearly has implications for ecology in terms of understanding the evolution of animals in rain forests and near waterfalls. The adaptations of these animals may also serve engineering via biological inspiration for the design of robust MAVs.

Previous studies on bats have shown that rain doubles their energetic cost of flight (12). The remainder of our knowledge of the effect of precipitation is restricted to large aircraft, although they operate upon very different principles from flapping fliers. Field testing on the effects of heavy rain on aircraft (13) confirms that precipitation generally hinders locomotion. Aircraft experience greater drag (2–5%), reduced lift (7–29%), and a reduction in stall angle of 1–5°, as measured (14, 15) during a rainfall intensity of 100–1,000 mm/h. Aircraft can reduce these losses by using wing designs that can funnel rivulets and control their diameter. These design principles may explain some of the water-repellent features common in birds’ wings (16). However, they clearly do not apply for much smaller fliers such as insects which are closer in size to raindrops.

Flying insects likely perceive raindrop impacts as in-flight perturbations. There have been many studies of such perturbations, although none have considered the influence of a wetting fluid such as rain. For instance, bees exposed to turbulent air resist rolling instabilities by extending their legs to increase their moment of inertia (17). Following in-flight perturbation, fruit flies actively restabilize themselves by flapping (18, 19). Even symmetric wing beats of a rotating insect will dampen insect rotation (20). Many of these restabilizing maneuvers rely upon delaying stall and interacting with wakes created by flapping wings (21). They are thus sensitive to the wing’s ability to deform under flapping (22). All together, these studies indicate that flying insects are highly maneuverable and able to quickly correct many kinds of perturbations (roll, pitch, yaw). However, such abilities may be affected if the wing is wet or must flap through a field of drops. Thus, to truly gain insight on the ability to fly through rain, we turn to in-flight experiments with wetting drops of fluid.

Previous experiments on flying insects through fields of drops were conducted toward the development of insecticides. Such experiments show that many insects possess adaptations to contend with water, including a dense layer of wax-coated hairs that repel water. This layer causes flying insects to be considerably more water-repellent than both aquatic and terrestrial insects (16). For instance, water drops on mosquitoes have contact angles of approximately 180° on the thorax and 75–95° on the legs and wings (23). To cope with this high water-repellency, insecticides are composed of a fog of very small drops, of sizes 20 μm, which adhere to mosquitoes midflight. It remains unknown how a mosquito’s water repellency is beneficial during high-speed impacts of much larger drops such as rain.

To investigate how flapping flight is affected by rain, we care for and film mosquitoes Anopheles, a species that is found in moist climates and is likely to face rainy conditions regularly. These mosquitoes have a body length of 3 mm and a mass of m₂ = 2 mg. As shown in Fig. 1A, raindrops are of comparable size (24), with a radius R₁ = 0.1–0.4 cm. However, the raindrops are of much larger mass m₁ = 4–100 mg: The mass ratio of the raindrops to mosquitoes is m₁/m₂ = 2–50. Two objects with the same mass ratio are a person laying underneath the wheel of a bus, a scenario whose outcome suggests that mosquitoes should not survive raindrop collision.

Fig. 1.

(A) Impact of a 3-mm drop on a mosquito supported from below, meant to show the relative size of raindrop to a mosquito. (B) Schematic of our drop impact chamber. (C) Time sequence of a mosquito spun by a falling drop. Graph shows the time course of angular position of a mosquito where the pink shaded area denotes the duration of contact with the drop. (D) Time sequence of a mosquito pushed by a drop. Graph shows the time courses of vertical positions of the mosquito (black) and drop (blue). In both impacts (C and D), the mosquito easily recovers and continues flying.

To gain insight into the collision forces, we consider a simplified scenario. Consider raindrop impact force onto a mosquito resting on an unyielding surface such as a tree branch. The dynamics of drop impact onto unyielding surfaces (25) (e.g., of infinite mass) has been well studied. Upon striking such a surface, raindrops exhibit a spreading stage and a receding stage. Given the terminal velocity of rain, u₁ = 6–9 m/s (26), the duration of the spreading is an exceedingly short τ = R₁/u₁ ≈ 1 ms. Therefore, the impact force associated with the transfer of momentum on an unyielding surface is F ∼ m₁u₁/τ ≈ 5 × 10⁴ dyn, which is 10⁴ times the weight of a mosquito. This large force further suggests raindrop impacts should be deadly to mosquitoes.

The likelihood of a raindrop impact can be predicted by considering the mosquito as a target for a raindrop. A vertically falling raindrop encounters a plan view of the insect given by its wings, legs, and remainder of the insect’s body, whose total surface area A_m = 30–40 mm². During the heaviest rain (27) with drops of mass m₁ = 16 mg, falling with an intensity I ≈ 50 mm/h, a stationary mosquito will receive an impact on average every Δt = m₁/(IρA_m) = 25 s, where ρ is the density of water. Thus it is quite likely that a free-flying mosquito will be struck by a drop during a rainstorm.

The mosquito’s long legs and wings account for three-fourths of the potential impact area, with the body accounting for only one-fourth. If a drop falls with uniform probability on these surfaces, impacts on the wings and legs are three times more probable than on the body. We will test this prediction in our experiments.

Results

Jet Impacts Cause Mosquitoes to Tumble.

We constructed a flight arena composed of a small acrylic cage of width 5 cm, covered with a mesh top to both contain the mosquitoes but permit the entry of drops (Fig. 1B). To prevent the insects from landing on the walls, the cage was vibrated manually every few seconds. In this confined environment, we observed insects made no attempt to escape being struck by drops.

In our first series of experiments, we desired to strike a mosquito with a terminal-velocity raindrop; this requires releasing drops at a height of about 10 m, which was nearly impossible to aim into our flight arena. Instead, we employed a jet of water to simulate rainfall. We used a gear pump to shoot a 9 m/s jet of water point-blank into a container of flying mosquitoes (Fig. 2). Jet speed and mosquito position were confirmed using high-speed filming at 4,000 fps (see Experimental Methods). Due to fortuitous cavitation in the pump, the jet was pulsatile, a combination of drops and jetting streams.

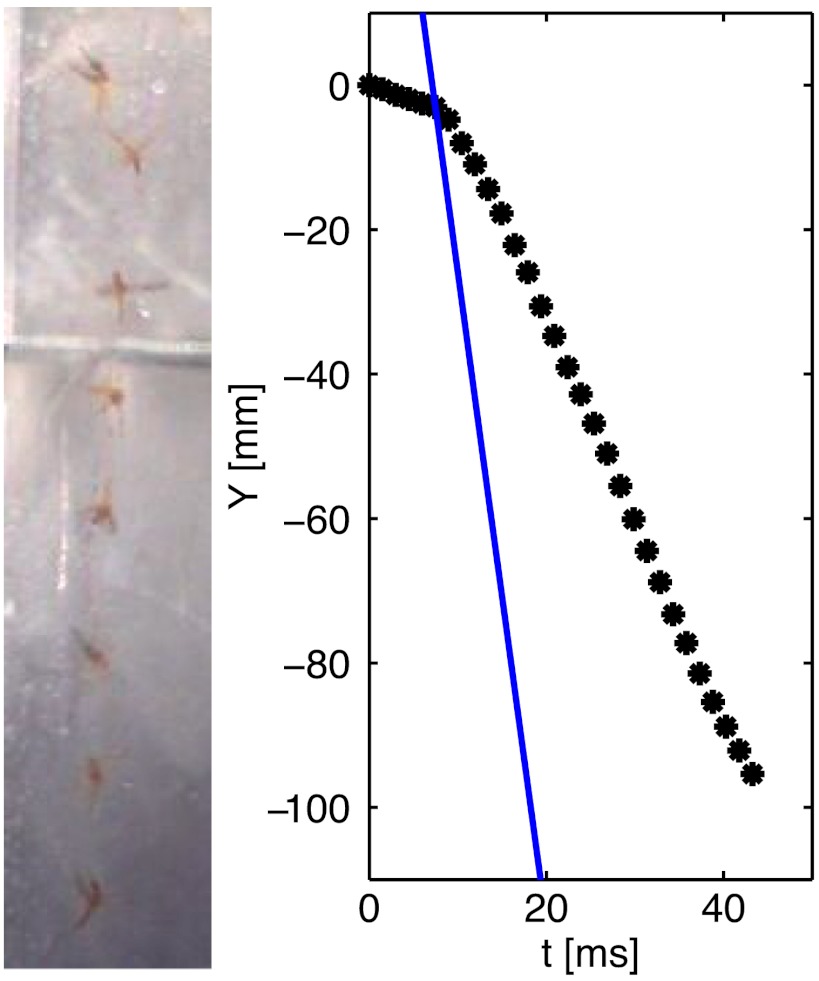
Fig. 2.

Mosquito being pushed and tumbled by a vertical jet traveling at 9 m/s. The graph indicates the time course of the vertical position of the jet and mosquito, shown in blue and black, respectively.

Using this setup, we observed six mosquitoes struck with high-speed jets. A mosquito is rapidly accelerated downward upon collision with the jet. Continued perturbations with the jet tumble the mosquito repeatedly. Fig. 2 shows one example: Impact by a 9 m/s jet accelerates the mosquito to a velocity of 2.1 m/s within a duration of 1.5 ms. After tumbling a distance of 39 mm, or 13 body lengths, the mosquito finally separates laterally from the jet and lands on the side of the container. The six mosquitoes tested each separated from the jet before striking the bottom of the 20-cm tall chamber. It was noteworthy that all the mosquitoes survived the collision, as shown by their flight after a brief resting period. These experiments confirm that mosquitoes can survive impact with terminal-velocity raindrops, which have even less momentum than the jets used.

Drop Impacts on Mosquitoes.

To obtain films at higher resolution as well as more accurate body tracking, we filmed free-flying mosquitoes subjected to drops falling at a lower speed than the jets. A small nozzle of variable height ejected individual drops of radius 0.15–0.25 cm at speeds of 10–260 cm/s (Fig. 1 C and D).

We observed impacts on the wings and legs are far more likely (N = 13) than on the body (N = 4), as predicted. These glancing blows cause a pitch, yaw, or roll rotation to the insect, depending on the point of impact. An impact on the wing is shown in Fig. 1C and the Movie S1. The mosquito rolls an amplitude of θ ≈ 50° ≈ 0.9 rad with a contact duration τ = 10^-2 s with the drop. The insect subsequently recovered its original position in 10^-2 s. We can estimate the forces involved using the geometry of the insect and neglecting aerodynamic losses in this short duration. The torque applied by the drop is r × F = Iα, where the mass moment of inertia of the insect , R_e is the effective radius of its mass, and the force is applied to the wing at a distance r ∼ 1 mm from the center of mass. Using the observed angular acceleration of α = θ/τ² ∼ 10⁴ rad/s², we find the impact force is F ≈ 3.5 dyn, or nearly two mosquito masses, and from which the mosquito easily recovered.

If the drop makes a direct hit with the insect’s center of mass, such as between the wings, a very different outcome from a glancing blow occurs. The insect is pushed downward a distance of several body lengths at the same speed of the drop. A direct impact is shown in Fig. 1D and Movie S1. Upon impact the drop remains intact and nearly at the same speed. These features suggest little force is imparted, in contrast to the splash observed due to impact upon an immobile surface. A mosquito is always able to laterally separate itself from the drop and recover its flight (N = 17). The mosquito’s falling distance while pinned by the drop varies from 5–20 body lengths. Thus it is imperative a mosquito does not fly too low during rain or it will suffer an secondary impact with the ground.

Drop Impacts on Mosquito Mimics.

Clearly, mosquitoes are able to survive impacts from both low- and high-speed drops. In the collision of two bodies, the outcome is known to be highly dependent on the masses involved (28). We thus hypothesize that mosquitoes survive drop impacts by virtue of their low mass: Specifically, the low mass of mosquitoes causes a falling drop to maintain most of its speed after impact and apply a correspondingly low impact force to the mosquitoes.

To test this hypothesis, we conducted tests with mimics of the same mass as mosquitoes. We constructed insect mimics using Styrofoam spheres of varying mass (0.4–1.8 mg) and radius (1.65–2.75 mm), as shown in Fig. 3A. Our use of mimics enabled us to investigate the dynamics of drop impact at drop speeds up to 2.60 m/s, which are closer to the terminal velocities of raindrops. The mimics were held in place using a solenoid that was rigged to drop instantaneously by the incoming drop, leaving the sphere momentarily suspended and poised for impact (Fig. 3C). We tracked the position of the drop and spheres, both before and immediately after impact (Fig. 3 D and E) to determine their change in velocity. Initial drop speeds highlighted in Fig. 3 D and E are 2.3 and 0.31 m/s, respectively. We generated drops with mass ratios of m₁/m₂ = 1–300 with respect to our mimics. We expect the behavior of the impact within the range m₁/m₂ = 1–50 to be dynamically similar to our mosquito experiments.

Fig. 3.

(A) Insect mimics composed of variably sized Styrofoam spheres. Both small and large size are shown with respect to a drop. (B) Schematic of inelastic impact between drop and insect. (C) Schematic of apparatus used to strike insect mimics with drops, where (A) nozzle, (B) infrared laser sensor, (C) controller, (D) power supply, (E) pull-type solenoid, (F) material holder. (D and E) Video sequences of drop impact onto small (D) and large (E) insect mimics with respect to the drop. Graphs indicate the time course of the vertical positions of the drops and mimics, shown in blue and black, respectively. Note, in both cases, the velocity of the drop is only slightly influenced.

Consider the collision of a drop of mass m₁ and speed u₁ with a stationary insect of mass m₂ hovering in midair. From our experiments of direct hits with mosquitoes, we observed the collision is inelastic, namely, that the insect and drop adhere immediately after impact into a combined lump of mass (m₁ + m₂) of speed u^′ (Fig. 3B). Conservation of linear momentum indicates the final velocity u^′ of the combined mass system is

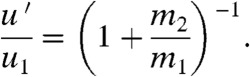[1]

Measurements of the dimensionless drop speed after impact u^′/u₁ are given in Fig. 4A for a range of dimensionless drop masses m₁/m₂. The drop is only slowed slightly (2–17%). Notice that direct impacts, which cause no rotation, follow the prediction in Eq. 1 well. Departure from the prediction occurs when a drop glances the mimic, rotates around it, and pulls it downward. More kinetic energy is lost in this rotation, as compared to the direct impacts.

Fig. 4.

Relations between dimensionless drop mass and (A) dimensionless final drop velocity, (B) dimensionless drop deformation ratio, and (C) object acceleration in gravities.

The blue X in Fig. 4A corresponds to a direct impact with a mosquito and fits the prediction, Eq. 1, well. Here, the final velocity u^′ = 0.9 u₁, indicating the drop’s speed decreases only 10%: The drop continues in its path unimpeded by the mosquito. It is noteworthy that this result is strongly dependent on the mosquito’s low mass. For instance, according to Eq. 1, a much heavier dragonfly with a mass of 1 g will cause the drop to decrease in speed by 91%, stopping the drop in its tracks.

From our tests with mosquito mimics, we observed raindrops do not splash upon mosquitoes, but simply deform. We rationalize this surprising result by comparing drop deformation χ in our experiments to the results observed by Clanet et al. (29). For water, Clanet et al. found a relation for the drop deformation, χ/R₁ ∼ We^1/4, when a drop impacts a solid surface, where 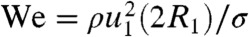. In particular, they saw a drop with R₁ = 1.65 mm impacting rigid plastic at u₁ = 0.81 m/s experienced a maximal deformation of χ/R₁ = 1.1 and did not splash. The highest χ/R₁ value we witnessed in our mosquito mimic experiments was a lower value of 0.77 (Fig. 4B) and so we conclude splashing on mosquitoes is not possible.

We can predict the deformation radius of drops at various impact speeds using methods inspired by those of Okumura et al. (30). Using a coordinate frame fixed on the drop, the relation between the change in speed of a drop u₁-u^′ and its internal pressure p is given by Euler’s equation, 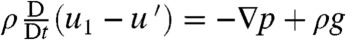. Assuming the drop’s radius undergoes a small deformation during impact, we may scale the duration of impact τ ∼ χ/(u₁-u^′) and the pressure gradient 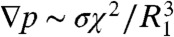, where σ is the surface tension of water. Euler’s equation at low Bond numbers (Bo = ρgl²/σ = 0.003–0.009 as found in our experiments), yields 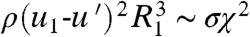. The dimensionless deformation may be written as

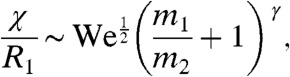[2]

where 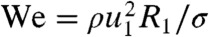and the predicted exponent γ from literature is -1. Our measurements of the dimensionless drop deformation χ/R₁ are shown in Fig. 4B. Our power-law fit for our drop deformations is excellent (with an R² value of 0.93), and moreover has an exponent of -0.85, very close to the prediction of -1. Thus we find drop deformation is inversely proportional to drop size: A small drop suffers a larger change in speed and larger deformation than a large drop, keeping all other conditions the same.

Impact Force by a Raindrop.

If drops do not splash on mosquitoes, we can easily estimate the force of direct impacts on the mosquito. During inelastic impact, a mosquito experiences a change in momentum m₂u^′ over an impact duration τ, yielding a impact force

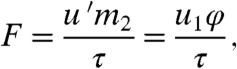[3]

where the reduced mass of the system is φ = m₁m₂/(m₁ + m₂) and the measured range of impact durations was τ ≈ 0.5-1.8 ms. In the limit of insects much lighter than drops, m₂ ≪ m₁, the force scales as m₂u₁/τ. This scaling indicates that the applied force decreases in proportion with insect size, consistent with our hypothesis.

Fig. 4C shows the associated number of gravities g, experimentally measured on our insect mimics. At first glance, it appears that this force is quite high, as shown by the range of accelerations of 100–300 g, equivalent to 50–150 mosquito weights. However, this range is two orders of magnitude less than impact on a unyielding surface (10,000 dyn); moreover, it amounts to very low absolute values that the insect can clearly survive. For example, a 2 dyn mosquito experiencing 300 g will feel a force of 600 dyn or 0.61 g force, the weight of a small feather. These estimates remain robust when we increase the speed of the drop to terminal raindrop speeds. The six mosquitoes struck by jets, as demonstrated in Fig. 2, experienced 80 ± 35 g, a fraction of the force due to a direct impact. Glancing blows, which cause tumbling, vastly reduce impact force.

Although the impact force of F ≈ 200–600 dynes is many times the insect’s body weight, it is easily survivable because the insect’s exoskeleton enables small insects to support large loads (31). To confirm survival in this range of forces, we performed compression tests using an analytical balance and a micromanipulator to determine mosquito’s threshold to force. When subjected to a sustained compressive force, a mosquito survived up to about 3,000–4,000 dyn (N = 3) and was still able to fly. When subjected to a larger force of 8,000–10,000 dyn, the mosquito did not survive. Because these values exceed by an order of magnitude the impact forces applied by raindrops, we conclude a flying mosquito cannot be killed by the impact of falling rain.

Discussion

We performed raindrop impact experiments on both mosquitoes and their mimics, finding that the momentum and force imparted to the insect is determined entirely by the insect’s mass relative to the drop. The mosquito is so lightweight that the resulting force imparted upon it is low, enabling a mosquito to survive flying in the rain. This result is in stark contrast to the resulting force on immobile surfaces for which splashing and large momentum transfers occur.

Although the raindrop force imparted to a mosquitoes is low, the mosquito’s low mass causes the concomitant acceleration to be quite high. Insects struck by rain may achieve the highest survivable accelerations (100–300 g) in the animal kingdom. In comparison, the current champions of generating acceleration are fleas, which experience 135 g when jumping (32). The similarity between these maximal accelerations may suggest a fundamental limit to survival among organisms.

Mosquitoes may experience life-threatening impacts if flying very low to the ground. Without sufficient distance to recover from impact, the insect could strike the ground with the speed of a falling drop or be immersed in pools of water from which it cannot escape. Such an effect was evidenced in our jet and drop chamber experiments. A mosquito which landed into a puddle ultimately perished, not from the impact of drops, but by drowning due to adhesion of its body with the water surface. Although the insect is covered in water-repellent hairs, these hairs do not seem to confer any advantage with respect to the force imparted. The hydrophobicity, however, may be advantageous in enabling the insect to separate from the drop as is necessary for recovery postimpact. The hairs may also be advantageous in surviving puddles.

It remains unknown whether flying insects can dodge raindrops, given their remarkable abilities to fly sideways and take off in reverse (11). Mosquitoes were unable to employ drop-avoidance maneuvers in our experiments. Their maximum flight speed (33) is about 1 m/s, which is far less than the average raindrop speed (26) 6–9 m/s. Suppose a mosquito were visually aware of incoming objects within a radius of 10 cm. Given the speed of raindrops, it would have 10 ms to move out of the path of an incoming drop. If the mosquito could achieve half of its maximum speed in avoidance, it would travel a distance of 0.5 cm in 10 ms, which is insufficient to avoid collision in most cases. However, it may make the difference between a direct and a glancing blow.

In this study, we only studied drop impacts from above. If rain falls vertically, the relatively slow flight-speed of mosquitoes will not appreciably increase the frequency of frontal impacts. Even so, it is advantageous for an insect to fly as quickly as possible when flying from one dry area to another through rain to decrease the total number of impacts from above (34).

Studies of aircraft (13–15) and flying animals (12) have shown rain acts to slow flight. In contrast, mosquitoes may be propelled forward by a glancing blow in their hind region. Such events could be a hazardous to the flier when flying close to other objects. Design parameters for MAVs may be adapted from the body plan of mosquitoes. For instance, hydrophobicity allows glancing drops to roll off the body quickly. Sprawled legs create an aerodynamic freeing torque that allows the mosquito to separate from the drop during direct impacts, minimizing the distance pushed upon impact.

Experimental Methods

Insect Care.

Non-blood-fed, 2–5 d old adult Anopheles mosquitoes were obtained from the Malaria Research and Reference Reagent Resource Center at the Center for Disease Control. They were housed with cotton balls of sugar water in our lab. Insects were filmed one at a time to avoid pseudoreplication.

Insect Mimic Experiments.

To capture the effects of drop impact on inanimate objects in flight, we collided them with drops freely and without support. The apparatus is shown in Fig. 1B. A syringe was used to generate a single drop from a nozzle suspended as high as 1.5 m above the subject. The falling drop passed through an infrared beam (modified photo gate) which triggered a high-speed pull-type solenoid leaving the object momentarily airborne and poised to be struck by a drop. Attached to the solenoid is a supporting arm composed of two thin wires, sufficiently stiff to support insect mimics, but thin enough not to drag the objects down its wake when retracted.

Rain Simulators.

For studying the behavior of living insects, we enclosed a group of insects in a closed acrylic container with length and width of size 5 cm and height of 20 cm for experiments where a high-speed jet was employed. A nozzle was positioned at the roof of the container and jet was produced by a Cole Parmer 75211-10 Gear Pump. The impacts were captured with a Phantom V210 high-speed camera at 4,000 fps.

For drop experiments, the container height was reduced to 10 cm to increase the probability of impact, as shown in Fig. 1C. Wet plastic mesh was placed at the top of the container, so that drops hitting the mesh released water collected upon it, allowing high-speed drops to enter the cage without letting mosquitoes escape. Impacts occurred opportunistically, and the recovery of the insects is captured with a Phantom Miro 4C high-speed camera at 6,400 fps.