Quantification of the relative roles of niche and neutral processes in structuring gastrointestinal microbiomes

Abstract

The theoretical description of the forces that shape ecological communities focuses around two classes of models. In niche theory, deterministic interactions between species, individuals, and the environment are considered the dominant factor, whereas in neutral theory, stochastic forces, such as demographic noise, speciation, and immigration, are dominant. Species abundance distributions predicted by the two classes of theory are difficult to distinguish empirically, making it problematic to deduce ecological dynamics from typical measures of diversity and community structure. Here, we show that the fusion of species abundance data with genome-derived measures of evolutionary distance can provide a clear indication of ecological dynamics, capable of quantifying the relative roles played by niche and neutral forces. We apply this technique to six gastrointestinal microbiomes drawn from three different domesticated vertebrates, using high-resolution surveys of microbial species abundance obtained from carefully curated deep 16S rRNA hypervariable tag sequencing data. Although the species abundance patterns are seemingly well fit by the neutral theory of metacommunity assembly, we show that this theory cannot account for the evolutionary patterns in the genomic data; moreover, our analyses strongly suggest that these microbiomes have, in fact, been assembled through processes that involve a significant nonneutral (niche) contribution. Our results demonstrate that high-resolution genomics can remove the ambiguities of process inference inherent in classic ecological measures and permits quantification of the forces shaping complex microbial communities.

Ecological species distributions are determined by the interplay between environmental factors and evolutionary processes. In classic ecological theory, niches characterized by nutrients and other environmental factors, for example, determine species abundance distributions and populations primarily through deterministic partitioning of resources among species (1). Species populations are limited by niche-carrying capacity rather than by interspecies competition, thus tending to promote coexistence (2). In niche theory, diversity is determined primarily by the number of available niches, raising the issue of how to account quantitatively for the apparent observed diversity (3–6) from well-documented instances of niche differences (7).

An alternative perspective is the class of neutral theories in which species are functionally equivalent and stochastic factors, such as immigration, birth/death processes, and speciation, are the primary drivers of ecological diversity and community structure (8–13). This class of models has been reported to be capable of accurate predictions for the species abundance distributions in riverine fish populations (14) or microbial populations (15), for example, in addition to the early successes in forest ecosystems, a planktonic copepod community, and a bat community on Barro Colorado Island (BCI) (10). However, the methodology used in such comparisons is contentious when examined carefully (16, 17), with sampling issues, parameter estimation, and model definition being some of the key factors that require careful attention. The assumptions of neutral theory, particularly functional equivalence, are not transparently biological (18); in addition, they have been criticized on a variety of empirical grounds (19, 20), including predictions for species lifetimes, speciation rates, and incidence of rare species (21). Other technical assumptions, for example, that the number of individuals competing for a resource is a constant (the “zero-sum” assumption), may be unrealistic but can be extended or relaxed (13, 22, 23). Perhaps a more useful insight into the applicability of neutral theory comes from considering the interplay between niche stabilization mechanisms and fitness (24). A recent study of a sagebrush steppe community, where strong niche stabilization mechanisms were identified even in the presence of apparently small fitness differences (25), underscores the fact that weak functional inequivalence need not necessarily mean that niche dynamics are negligible. On the other hand, a study that attempted to infer pairwise interaction strengths among the most abundant species at the BCI site found that interspecies interactions were much weaker than intraspecies ones, in apparent agreement with neutral assumptions (26).

Despite their fundamental differences, and the plethora of studies nominally supporting each side of the niche-neutral dichotomy, these theories predict species abundance distributions that are difficult to distinguish empirically (5, 27), with similar mathematical properties for asymptotically large diversity (28). The inverse problem of inferring ecological dynamics from measures of diversity does not appear to have a unique solution, either theoretically or empirically. Accordingly, a more nuanced perspective has arisen (2, 19, 29) in which elements of both types of theory may contribute to a proper description of the ecological dynamics, and a variety of mathematical frameworks for accomplishing this type of synthesis have recently appeared (26, 30–35). Nevertheless, it remains an open question as to how to characterize community dynamics properly and how to quantify the relative roles of niche and neutral processes usefully in the evolutionary dynamics of ecosystems.

These questions are of particular relevance to microbial communities, which play functionally important roles in ecosystems but are typically rich in diversity, suggesting the presence of subpopulations shaped primarily by stochastic forces. Such communities would not be expected to represent end members of the niche-neutral continuum, and quantification of their structuring process represents a complex problem that has recently attracted attention. Most studies find evidence for a mixture of neutral and niche processes in microbial community assembly (36–40). These seem to arise for different physical reasons. One indication is that the neutrally assembling taxa are generalist microbes that can exist in a wide variety of environments (38), whereas the niche portion of the microbiota is adapted to the media conditions (41). There are also indications that that microorganismal cooccurrence patterns are shaped by the same processes and interactions that shape macroorganismal cooccurrence patterns (42).

In this paper, we propose a methodology for addressing the problem of quantifying the relative role of niche and neutral processes in structuring microbial communities by fusing measures of abundance with phylogenetic information. The merging of classic ecological measures with phylogenetic analysis is growing in importance but is still in its infancy (43–47). The method presented here is particularly applicable to uncultured microbial communities that are characterized by a high level of diversity and are amenable to modern metagenomic tools, such as pyrosequencing.

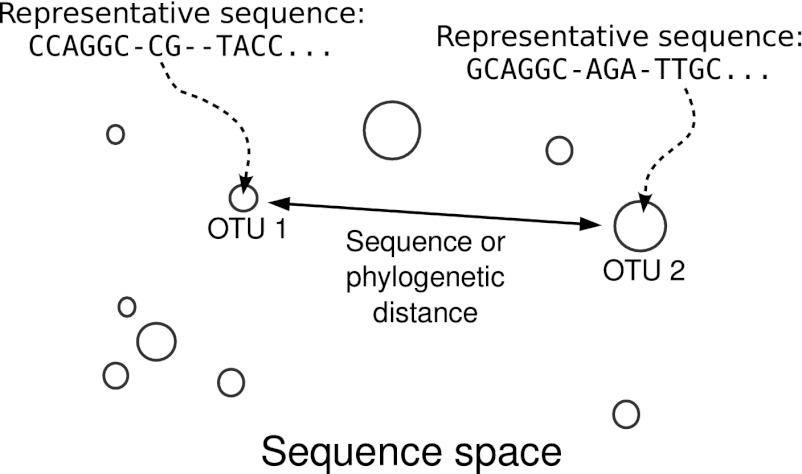
To explain the basic idea of how we quantify an ecosystem on the niche-neutral continuum, it is necessary to recall how microbiomes can be probed by genomic methods. The first step in an ecological study of a microbiome, following sequencing, cleanup, and alignment, is the assignment of sampled sequences into operational taxonomic units (OTUs) through a clustering process (48). The OTUs are then used as a proxy for estimating microbial species abundance (49). The OTU data are twofold. On the one hand, the OTUs have relative abundances that are estimations of the species’ abundances in the environment. On the other hand, the OTUs also have representative sequences associated with them. Typically, a representative sequence of an OTU is the most abundant of the identical clones within the OTU, and it is also more than 97% similar to every other sequence within that OTU. These genomic data associated with the representative sequence allow us to think of OTUs as points in a sequence space as illustrated in Fig. 1. We can think of distances between points in this space as corresponding to the phylogenetic or sequence distances between the sequences in these OTUs.

Fig. 1.

Sketch of the starting point for a metagenomic analysis of an environment. Circles indicate OTUs, and abundance (number of sequences within the OTU) is labeled by the size of the circle. A representative sequence is associated with each OTU. The OTUs are embedded in a sequence space, such that the distance between the circles in the sequence space corresponds to, for example, sequence or phylogenetic distance between the representatives.

This cloud of points in high-dimensional sequence space can also be labeled by OTU abundance. In our work, this is determined by sequence abundance (after every effort has been made to account for artifacts); however, in principle, OTU abundance labels could be obtained from any other source, such as quantitative PCR. In this space, we can categorize the OTUs into two sorts: the most abundant OTUs (which we term modal OTUs and define precisely below) and the other, less abundant, OTUs (which we term rare OTUs and define precisely below). The correlations between the modal and rare OTUs will depend on the evolutionary dynamics and, in fact, exhibit sharp mathematical differences that can be used to discriminate different putative dynamics. To see the essential idea, we will now explain how this would work in two caricatures of ecosystem dynamics: a simplified neutral model and a simplified niche model. A significantly more elaborate analysis is carried out below, in the main body of this paper, but the key concepts are captured by these simplified models.

First, suppose that the evolutionary dynamics are themselves neutral, such that the rare and modal OTUs are distributed at random in the high-dimensional sequence space. We are going to be interested in measuring the distances between sequences corresponding to different OTUs and comparing their similarity. Let us assume that the sequences being analyzed are all of the same length, containing 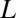nucleotide bases from the usual four-letter alphabet (ACGT); here, we are ignoring real-life complications, such as insertions, deletions, and gaps. We label the sequences by 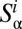, where 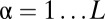labels the position along the sequence and 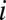labels the OTU; 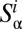can take the values 1, 2, 3, 4 corresponding to the alphabet of bases ACGT. We define the normalized Hamming distance, 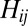, between two sequences 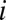and 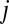as the fraction of bases in 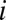that is different from the base in the corresponding position in :

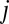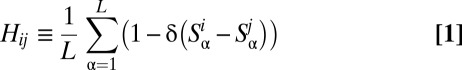where 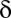denotes the Kronecker delta. The mean 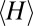of 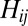averaged over a large sample of random sequences would be 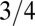, because there is a 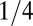chance that two bases at the same position are identical. Thus, the probability distribution of 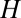would be expected to be a roughly bell-shaped curve, peaked around 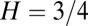, with a width dependent on the number of sequences. In practice, there are complications attributable to insertions, deletions, and gaps as well as to, most importantly, conserved positions. Bases that are highly conserved cannot be appropriately modeled as being chosen randomly from the alphabet. This can be taken into account by simply restricting the above analysis to bases that are strongly nonconserved: Let us call the number of highly conserved bases 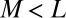, such that the expected value of 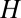will now be reduced by the fraction of conserved bases: 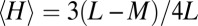. Thus, taking into account conservation, the bell-shaped curve will shift its peak to a smaller value of 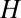. In the data presented below, we found that 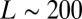and 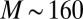, such that the distribution of should be peaked at about 0.15 in the case of a neutral system. Now consider a subset 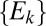of distances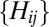. For each rare OTU 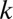, we rank all the distances between OTU 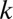and each modal OTU 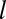. Then, we select the shortest such distance and label it 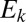. In this way, the set 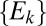is the set of distances of rare OTUs to their nearest niche neighbor. For the above case, where the evolutionary dynamics are neutral-like, the distribution of 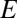is also a bell-shaped curve like the distribution of 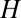. However, its mean is slightly shifted to the smaller values and its SD is smaller (because 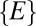is the subset of shortest distances from the set of 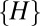). In other words, .

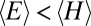Second, let us consider a caricature of a system that is dominated by niche dynamics. In the extreme (and unrealistic) case in which there is only one niche, occupied by one particular modal OTU, the probability distribution of 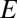will be a delta distribution peaked at 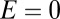. In a more realistic model, where there is a cloud of rare OTUs surrounding the modal OTU, having evolved from it by a few point mutations, one would expect the probability distribution of 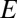to be peaked at 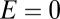and then to decrease monotonically for 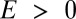. In the case of a system with several niches, the probability distribution for 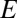will be somewhat more complicated, because one needs to calculate the normalized 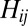from each rare OTU to the nearest modal OTU, and this requires making a Voronoi polyhedron construction in sequence space. 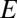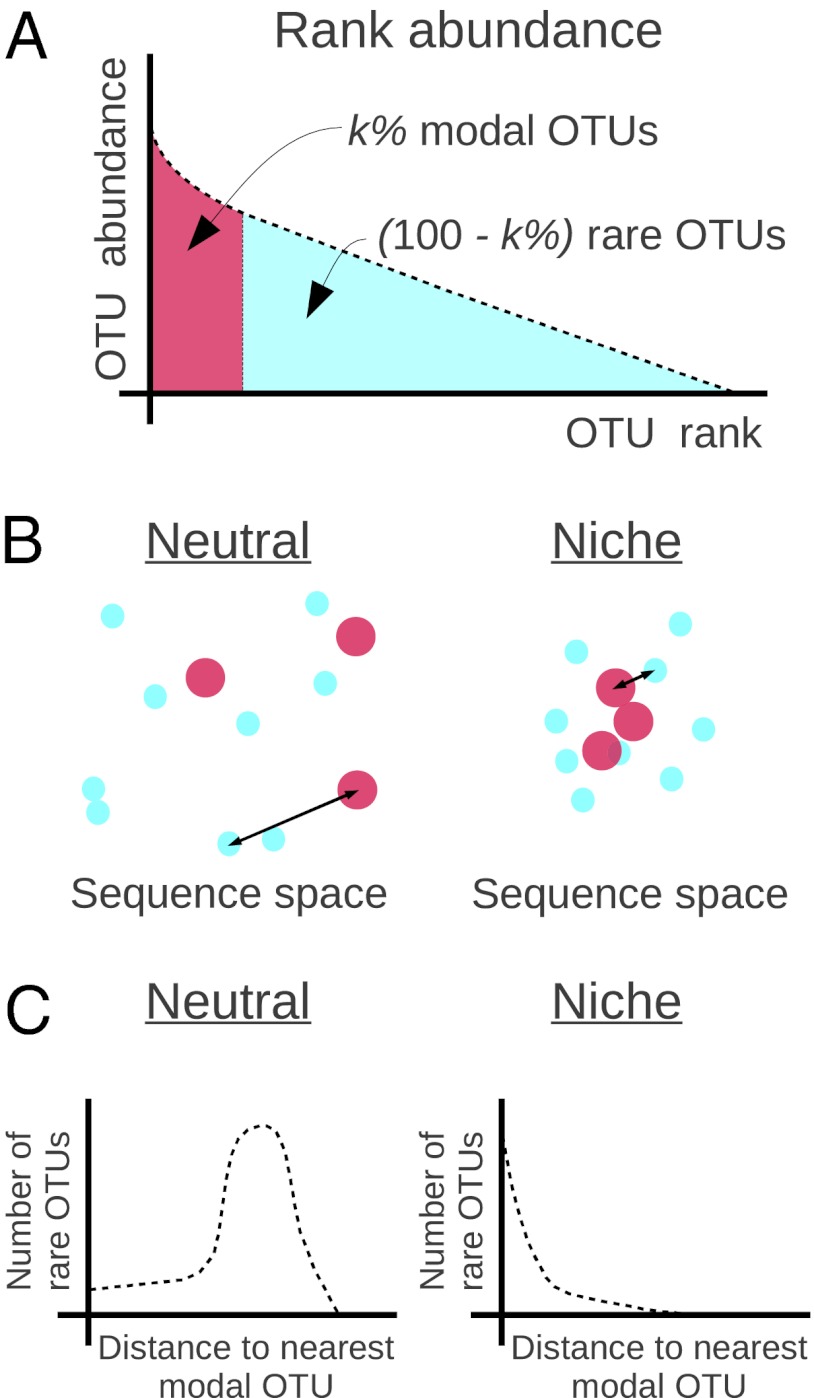Nevertheless, for small values of , the probability distribution will be dominated by the single niche argument given above and the functional form will be unchanged: peaked at the origin and monotonically decreasing for 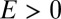. These two caricatures for simplified models of ecosystem structure are sketched in Fig. 2 and show that there are clear and distinct signatures arising from the nature of the processes that have structured the community.

Fig. 2.

(A) Classification of the OTUs into two groups based on the rank abundance. The top 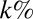of OTUs are labeled modal, whereas the remaining OTUs are labeled rare. (B) Sketch of the neutral and niche evolution processes in sequence space. Light blue OTUs are rare, whereas red OTUs are modal. For the neutral process, the average distance of a rare OTU to its closest modal OTU is large (indicated by the arrow). For the niche process, this distance is much smaller because rare OTUs cluster about the modal OTUs that define the niches. (C) Sketch of the expected distributions of distance to the closest modal OTU. For the neutral process, this distribution is peaked around some nonzero distance, which is close to the average distance between the OTUs in the dataset. In the niche process, the distribution monotonically decays with distance because the rare OTUs are attracted to the niches.

In the remainder of this paper, we numerically evaluate the metric for model systems to confirm quantitatively and concretely the above heuristic description. We then describe how we have implemented these ideas in a proof-of-principle study of vertebrate gastrointestinal (GI) microbiomes. These experimental systems were chosen not only because of the growing recognition of the importance of microbiomes as a determinant of host health (50) but because these are systems that have high diversity and are likely to be shaped by both stochastic and niche processes. Indeed, as we will see, they can be well described naively by neutral theory, although, in fact, niche processes play a fundamental role in structuring these communities.

Model Calculations

In this section, we evaluate our metric on model systems parametrized by a single parameter, 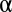, the proportion of the system undergoing a niche dynamic. We perform 5,000 Monte Carlo simulations of the following process. We simulate 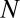OTUs (here, 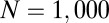), each with representative sequences of length 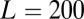. A subset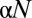 of the OTUs undergoes a niche dynamic in the following way. A single random OTU is chosen to be the center of the niche. The remaining 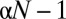OTUs (niche OTUs) are generated by performing random mutations of the genome of the OTU representing the niche center. The placement and number of the mutations were chosen randomly in the following way. Placements of mutations were sampled uniformly (without replacement) across the entire genome. The number of mutations for each of the niche OTUs was sampled from an exponential distribution, thereby modeling the evolution of OTUs under multiplicative fitness pressure (a larger number of mutations corresponds to smaller fitness, and hence to a smaller abundance of OTU). The remaining 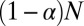OTUs (neutral OTUs) are randomly distributed throughout the sequence space, and they represent the sequences undergoing dynamics under no evolutionary pressure (neutral dynamics).

Each OTU in the model system is associated with an abundance. The abundances of neutral OTUs are randomly sampled from an exponential distribution. (In the Hubbell Neutral Model, the OTU rank abundances are exponentially distributed.) On the other hand, the abundance of niche OTUs exponentially scales with their closeness to the niche:

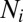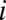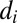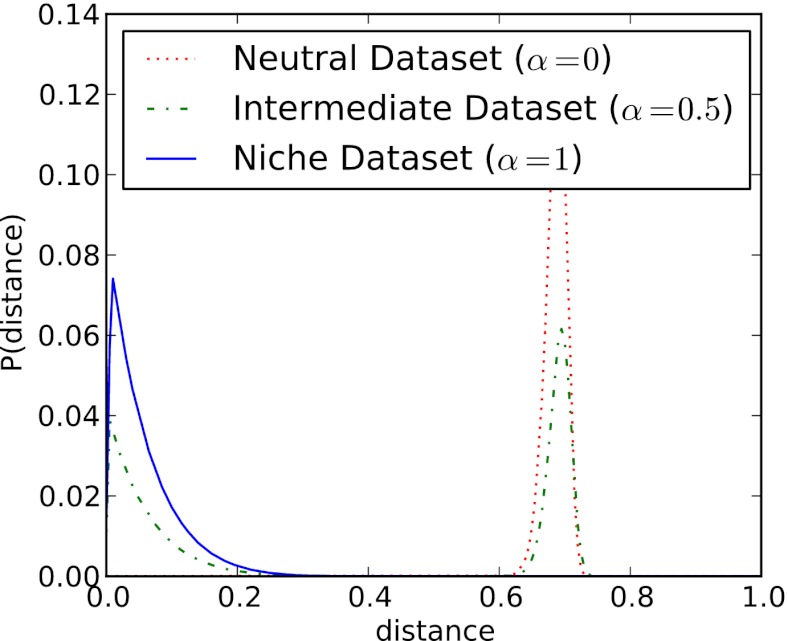
where is the abundance of OTU and is the distance from the OTU to the center of the niche (in sequence space). The results of our metric, the distributions of 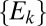, are shown in Fig. 3 for three model systems characterized by values of α = 0, 0.5, and 1. We see that the heuristic arguments we described in the previous section and sketched out in Fig. 1C are consistent with these model numerical calculations.

Fig. 3.

Results of our metric, the distributions of 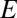shown for a fully niche-like model dataset 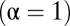, a fully neutral-like model dataset 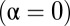, and an intermediate dataset 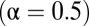. The results shown are the average of 5,000 Monte Carlo simulations for each dataset.

It is instructive to demonstrate the effects of two factors on our metric so as to highlight some of the mathematical considerations that went into the design of the metric, particularly our use of an extremal measure (the shortest distance aspect of our metric) and the influence of sampled abundance distributions. First, we demonstrate the role of extremality introduced by choosing the subset 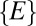. Instead, if we choose to plot the distribution of 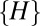, we obtain qualitatively the same results for neutral-like models (compare models 1 and 2 in Fig. S1). However, for niche-like models, the peak at zero moves to a nonzero peak that corresponds to the average size of the niche (compare models 5 and 6 in Fig. S1). Thus, the choice of an extremal measure is important in making sure that the end-member distributions (pure niche and pure neutral) are clearly distinct.

Second, we demonstrate what might appear at first to be a rather counterintuitive fact: The distribution of distances is only weakly dependent on the abundance distribution of the OTUs. If the abundance of an OTU 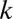is 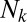, we could then imagine modifying our procedure by weighting the contribution of 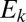in the distribution 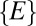by a factor of 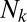. Such a weighting introduces no change whatsoever in the neutral dataset (compare models 2 and 4 in Fig. S1) and no qualitative change in the niche dataset (models 6 and 8 in Fig. S1). Finally, we can also weigh the distribution of 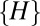in such a way that each distance 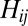between OTUs 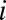and 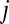gets weighted by a factor of 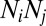. The results are exactly the same as with no weighing for the neutral dataset (compare models 1 and 3 in Fig. S1) and are qualitatively the same for the niche dataset (compare models 5 and 7 in Fig. S1).

Results

We performed a pyrosequencing study of the GI microbiomes of three pairs of domesticated vertebrates: two swine, two cattle, and two chickens. These pairs of organisms were chosen as pilots for probing specific microbiome issues of relevance to animal science. In particular, we attempted a comparative study looking at the effects of diet on identically cloned swine and the effects of a microbial challenge on two identically raised chickens. For the purposes of this paper, these comparisons and the outcomes of the experiments are not of interest: Full details of the comparisons and other studies will be published elsewhere. In this study, two genetically identical cloned swine were fed different diets and their fecal samples were then collected for sequencing. Cattle rumen 1 and cattle rumen 2 were rumen fistulae sampled at 0 and 8 h after feeding, respectively (51). Chicken cecum 94 was inoculated with Campylobacter jejuni 1 wk before cecal sampling. Chicken cecum 1 was kept under the same conditions but without oral gavage of C. jejuni (52). Details regarding the laboratory protocols are provided in Materials and Methods. The GI samples were subjected to deep hypervariable 16S rRNA tag sequencing using a 454 Life Sciences Genome Sequencer GS FLX (49). Table S1 shows the average read length and number of reads obtained for each sample.

Following their acquisition, we aligned the pyrosequenced reads using NAST (53) to the SILVA (54) database. We also aligned the reads using the front end of the Ribosomal Database Project (RDP) (55) to the Infernal (56) structural aligner. For each dataset, the NAST + SILVA and RDP + Infernal multiple alignments were merged and hand-curated using the methodology and tools described by Sipos et al. (48). Short reads and sequences with unknown nucleotides were removed. Spurious “tails” in the multiple alignment, sequences that extend beyond the region of 16S common to all the sequences in the dataset, were also removed. Distance matrices were generated from the multiple alignments and were then fed to a complete linkage clustering algorithm to generate the OTUs. The careful multiple alignment procedure led to a vast reduction in the number of resulting OTUs in the datasets, as previously reported by Sipos et al. (48). Multiple alignment, species diversity, and richness metrics for each of the six GI microbiome samples are provided in Table S1. Rarefaction curves show how the number of sampled OTUs varies as a function of the number of organisms sampled. Our rarefaction curves are shown in Fig. S2 for each of the six datasets.

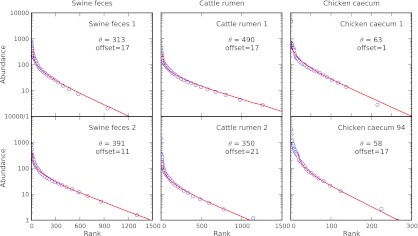
We plotted the abundances of the OTUs for each of the six datasets in our study, and we find very good agreement with the neutral model. These are displayed in rank-abundance form in Fig. 4 and in alternative forms in Figs. S3 and S4. The early ranks (high-abundance OTUs) show some systematic deviation from the abundances expected from neutral theory; however, at face value, these results are consistent with the majority portion (thousands) of the OTUs evolving in the absence of any apparent selection acting on the individual OTUs. Given all the factors that influence the GI microbiome (57–62) and the reproducible, and thereby seemingly host-selected, microbial abundances (63), it seems counterintuitive that there should be no apparent selection for the vast majority of OTUs in the exponential tail of the rank abundance. However, if we compare taxonomic assignments of microbes across each pair of animals in our study (Fig. S5), we find that there is a correlation between the relative abundances of taxa in members of each animal pair. Specifically, we observe that the most abundant taxonomic orders are the same for each animal pair (Clostridiales for swine and chickens and Pseudomonadales for cattle). This correlation also extends to other taxonomic orders. Hence, our dataset indicates that certain taxa are favored more than others within the GI tract of these six vertebrates.

Fig. 4.

Comparison of rank-abundance curves and neutral model fits for the six animal GI microbiomes. Lines indicate fits to Hubbell’s neutral metacommunity model. Parameter of the model is fit to correspond to the exponential tail in rank abundance. Offset represents the number of high-abundance OTUs that do not fit the neutral model.

We now attempt to resolve this apparent contradiction, namely, that the neutral theory fits the rank-abundance patterns well, with only two fitting parameters, even though the taxonomic data suggest niche selection. To do this, we must turn our attention to other information contained within the pyrosequenced reads. As shown in Fig. 1, the OTUs with their characteristic sequences and associated abundances form patterns within a high-dimensional space. Each read constitutes a point in this space, defined by its nucleotide sequence. One way in which we can attempt to comprehend the structure of this space is through dimensional reduction. We use principal component analysis (PCA) to place the OTUs into a 2D space spanned by the two principal components. We perform a weighted version of PCA (64), where we assign a weight to the OTUs proportional to their abundance. The resulting patterns in the space of two principal components are shown in Fig. S6. Each circle in the figure is an out, and the circles’ size and color indicate the logarithm of the OTU abundance.

As a control, we generate datasets of artificially generated sequences (hereafter referred to as neutral datasets). We generate a neutral dataset for each of the six experimental datasets to facilitate a one-to-one comparison. Each neutral dataset is constructed in such a way that it has the same number of OTUs and the same OTU abundance distribution as the associated experimental dataset. However, the representative sequence for each OTU is artificially generated and has a randomized sequence, with the constraint that it has the same sequence statistics as the original dataset (probability of observing a nucleotide at a position in the multiple alignment) and column conservation. This ensures that the sequences are randomly distributed along a realistic submanifold of sequence space (the subset of 16S sequences that are allowed by secondary structure). We then run the PCA on the neutral datasets (Fig. S7). Comparing Figs. S6 and S7, we notice the following pattern in the experimental GI data: the low-abundance OTUs cluster around the high-abundance OTUs in the dimensionally reduced space. In the neutral datasets, this is not observed; instead, the PCA distributes the OTUs approximately uniformly in the dimensionally reduced space.

We now formulate a heuristic to discriminate clearly between the randomly assembled model sequences and those assembled from a niche-driven process. On a rank-abundance curve, we label the k% of the most abundant OTUs as modal OTUs. We label the remaining OTUs as rare OTUs (Fig. 2A). Instead of using the whole-dataset rank-abundance curve, one can use per-order rank-abundance curves if additional resolution is necessary. Once modal and rare OTUs have been assigned, for each rare out, we compute the distance to the modal OTU that is closest to it. The motivation behind this heuristic is the following. The spread pattern of sequence abundances gives us an indication of whether organisms are evolving neutrally or toward defined niches. In long-time behavior, neutral evolution leads to the expectation that organisms have an equal chance of being anywhere in this space. Niche selection, however, suggests a very biased distribution of organisms. In particular, organisms would be densely clustered about the local optimum for each niche (Fig. 2B). These two scenarios lead to very different distributions of distance to nearest niche. If the OTUs are undergoing a niche-driven dynamic, the rare OTUs will tend to drop off exponentially in abundance around the modal OTUs. If, on the other hand, the OTUs have been sampled from a community shaped by neutral evolutionary dynamics, the rare OTUs’ distance to closest modal OTU will be peaked around some nonzero distance that is the average distance between any two OTUs in the dataset (Fig. 2C).

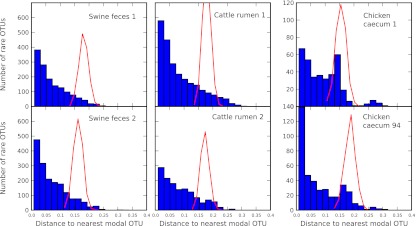
We apply the above analysis to the case of GI microbiome datasets of the six vertebrates. The results are summarized in Fig. 5. In this figure, the blue bars indicate the results of our metric applied to experimental data. The dashed red lines indicate the results of the metric applied to a dataset of sequences that were randomized in the way described above. The results indicate that the GI tracts of the six vertebrates largely undergo niche dynamics, with the possible exception of a subpopulation of the chicken GI tracts. The chicken datasets have a small nonzero peak corresponding to the average distance between sequences chosen at random. Our study indicates that the sequences within this peak may be undergoing neutral dynamics. The results that we obtain are robust in that they do not qualitatively depend on the choice of the cutoff 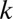. In Fig. S8, we show the metric for 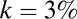and 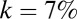. Similarly, the results of the metric on model systems are virtually unchanged when 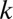is changed between 2% and 10% (Fig. S9), indicating robustness. Although our metric is robust in this way, the reader is reminded that phylogenetic resolution is nevertheless important: Some niches may appear as single OTUs at 97% sequence identity.

Fig. 5.

Histogram of distances of rare OTUs to the nearest modal OTU for each of the six GI microbiomes with the cutoff 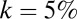(blue bars indicate experimental data). Red lines indicate the results of the metric applied to sequences that were randomized while preserving rank abundance and sequence statistics (main text). Cattle and swine datasets share the same y axis.

Discussion

In this work, we set out to construct genomic-based measures of ecosystem diversity and abundance that can provide evidence for process. We focused on understanding the processes that structure microbial communities because these play functionally important roles in many ecosystems yet are rich in diversity. Thus, such systems would, a priori, be expected to contain at least subpopulations shaped primarily by stochastic forces. The dual features of high diversity and foundational role in their host ecosystem suggest that microbial communities would not be simple to characterize as either niche or neutral. At the same time, theoretical arguments suggest that such high-diversity communities might appear, for fundamental statistical reasons, as neutral.

We succeeded in creating a quantitative metric that fuses abundance and genomic data to determine whether an ecological system is dominated by neutral evolution or by niche selection. The key concept was to explore the correlations and associated probability distributions between the most abundant members of the community and the long, low-abundance tail members. We showed that the signature of the probability distribution describing the distance in genomic sequence space from each rare OTU to the nearest modal OTU provided a signature of the strength of niche dynamics. We tested this construct on large datasets from six animal GI tract microbiomes, finding that the results are inconsistent with neutral assembly in all cases. We conclude that niche selection largely dominates within the GI microbiome, despite the fact that the rank-abundance patterns are apparently well-modeled by neutral theory.

Our results provide firm evidence from an empirical dataset that apparently neutral patterns of diversity and abundance can arise from niche-dominated dynamics, in agreement with earlier theoretical expectations (2, 5, 19, 27–29). Our results establish definitively that simple ecological measures need to be, and can be, augmented by genomic data to provide insight into the processes that structure communities.

Materials and Methods

Sample Preparation.

All procedures involving animals were approved by the Institutional Animal Care and Use Committee of the University of Illinois. For each animal, we used two different samples for our test that vary in some aspect, such as diet or sampling times. The Duroc sow (University of Illinois at Urbana–Champaign 2-14; T. J. Tabasco) was used as the genomic template for producing cloned animals using somatic cell nuclear transfer. T. J. Tabasco was used to produce the CHORI 242 BAC library, which was used to generate the full pig genome sequence (65). The clones were born by vaginal delivery and allowed to suckle. They were weaned at 4 wk of age and continuously housed together. They were not vaccinated or ever in contact with other pigs after weaning. Pigs were fed once daily in the morning and had free access to water. Fecal samples were collected on day 14 (the last day of that feed rotation) of each diet for a total of four samples for each animal. Samples were collected from the rectum into a sterile tube and frozen at −80 °C until time of analysis. Bovine rumen samples were collected as previously reported (51). Chicken caeca were collected as previously reported (52).

Sequencing.

Swine and cattle samples were sequenced using PCR product from PCR-specific primers flanking the V1–V3 region of bacterial 16S rDNA (66). The forward fusion primers for pyrosequencing included 454 Life Science’s A adapter and barcode A fused to the 5′ end of the V1 primer 27F. The V3 primer 341F was used in chickens. In all samples, the reverse fusion primer included 454 Life Science’s B adapter (lowercase) fused to 5′ end of V3 primer 534R. The fragments in the amplicon libraries were subjected to a single pyrosequence run from the V3 primer end using a 454 Life Science Genome Sequencer GS FLX (Roy J. Carver Biotechnology Center, University of Illinois). The sequence reads for chicken 1, cattle 1 and 2, and swine 1 and 2 have been deposited in the National Center for Biotechnology Information Sequence Reads Archive (accession no. SRA052136.3). Chicken 94 reads have been previously deposited as reported (48).

Rank Abundance, Species Abundance, Preston Plots, and Taxa Distributions.

The reads from cattle and swine microbiomes were cleaned up using the method recommended by Kunin et al. (67). For the chicken cecum microbiome, we removed all sequences shorter than 100 bp. The ends of all reads were trimmed so that the sequences start and end in the same place in the 16S rRNA consensus structure. All remaining sequences were then aligned using the method described by Sipos et al. (48). The OTUs were clustered using the complete linkage method of Schloss et al. (68) with a cutoff of 3% sequence identity with the denominator 4 from the method of May (69) (counting indels as differences). The OTU abundance data for rank abundance were then binned into a histogram using the method described by Adami and Chu (70). Species-abundance and Preston plots were generated according to the method of Gray et al. (71). Neutral model curves were generated using the algorithm for the sampling organisms from a neutral metacommunity (10). Hubbell’s parameter was fixed to match the exponentially decaying tail of the rank abundance. Offset was chosen by a least-squares method. Taxonomy assignments and comparison of libraries were made with the Library Compare tool (72) at the RDP (55).

PCA Ordination.

In Fig. S6, we show the results of PCA on our OTU data. In performing this calculation, each OTU was associated with a vector of real numbers of dimension 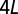, where 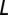is the length of the multiple alignment. The elements of the vectors were calculated in the following way. Each nucleotide within the multiple alignment is represented by a subvector of four numbers: A is 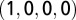, C is 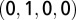, G is 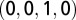, and T is , whereas the gap is represented as 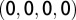. The vector associated with the OTU is then the arithmetic average of the vectors associated with each sequence within the OTU. We then perform the weighted PCA procedure (64), where we weigh each OTU by its abundance.

Closest-Distance Metric.

We used the percent sequence distance metric in Fig. 5. The randomized dataset (red line) was generated in the following way. Each OTU (with its associated abundance) was replaced by a representative randomized sequence. This sequence was generated by selecting each nucleotide from a distribution of probabilities generated from the sequence reads. In this way, the base pair distribution for each position in the multiple alignment of the model dataset is the same as that of the experimental dataset. Furthermore, because the abundances of OTUs are kept, the rank abundance of the model dataset is exactly the same as that of the experimental dataset.