Biomimetic emulsions reveal the effect of mechanical forces on cell–cell adhesion

Abstract

Cell–cell contacts in tissues are continuously subject to mechanical forces due to homeostatic pressure and active cytoskeleton dynamics. In the process of cellular adhesion, the molecular pathways are well characterized but the role of mechanics is less well understood. To isolate the role of pressure we present a dense packing of functionalized emulsion droplets in which surface interactions are tuned to mimic those of real cells. By visualizing the microstructure in 3D we find that a threshold compression force is necessary to overcome electrostatic repulsion and surface elasticity and establish protein-mediated adhesion. Varying the droplet interaction potential maps out a phase diagram for adhesion as a function of force and salt concentration. Remarkably, fitting the data with our theoretical model predicts binder concentrations in the adhesion areas that are similar to those found in real cells. Moreover, we quantify the dependence of the area of adhesion on the applied force and thus reveal adhesion strengthening with increasing external pressure even in the absence of active cellular processes. This biomimetic approach reveals a physical origin of pressure-sensitive adhesion and its strength across cell–cell junctions.

Cell–cell adhesion is important in biology because it underlies the structure of tissues and their dynamic reorganization during processes as important as morphogenesis (1, 2), cell locomotion (3, 4) and signaling (5, 6). In addition to the high level of complexity in the identified biochemical pathways, it has recently become clear that mechanical effects also play an important role. For example, pushing cells together or increasing their contractile forces by changing the substrate stiffness reinforces the strength of contacts (7–9). Furthermore, because homeostatic pressure arising from the balance of cell division and cell death is important in achieving the mechanical integrity of tissues (10) it should also affect cell–cell adhesion. Despite these important observations, the physical origin of force-sensitive adhesion remains an open question. In fact, theoretical models are derived from the behavior of simplified model membranes that lack mechanical resilience (11). Although these models successfully describe the kinetics and energetics of adhesion in the absence of rigidity (12, 13), they cannot address the effects of force. In an individual cell, the cytoskeleton scaffold coupled to the membrane gives rise to a cortical tension of ≈0.035 mN/m (14). Moreover, the interplay between cortical tension and adhesive interactions with surrounding neighbors gives rise to a different surface tension in cellular aggregates (15, 16) and measures ≈1–20 mN/m (17, 18).

To mimic the dense packing of cells in tissue with a homeostatic pressure of ≈10 kPa (19, 20), we use a 3D assembly of biomimetic emulsion droplets under an external compression. In the emulsion system the compression of individual droplets with an interfacial tension of ≈10 mN/m leads to pressures in a similar range to those found in tissues (21). In addition to mechanical similarities, the chemical composition of the emulsion system reproduces the attractive and repulsive interactions that govern adhesion between cells. By experimentally tuning the interaction potential and the elasticity of the emulsion we show the conditions under which a pushing force is necessary to create adhesion, which suggests a possible role for homeostatic pressure for tissue integrity. The dependence of this threshold force on the interparticle interaction is captured by a free energy model, which results in a phase diagram in agreement with our experiments.

Results and Discussion

Biomimetic Emulsions.

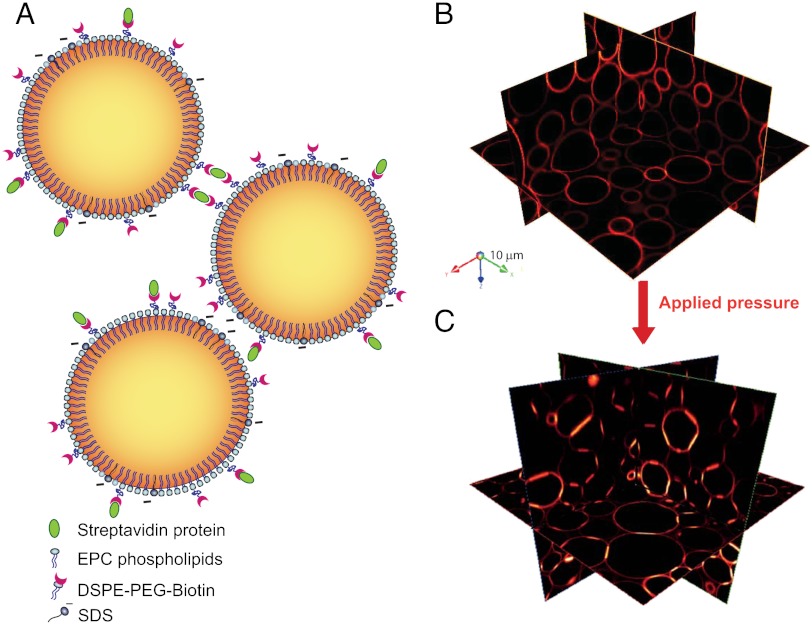
In the model system illustrated in Fig. 1A, adhesion mediated by homophilic cadherins in cells is replaced by a biotin–streptavidin–biotin complex bridging two droplet interfaces. A biotin–streptavidin complex on one droplet surface diffuses until it binds to another biotin on a neighboring surface through a second binding site, which is the molecular basis for adhesion in this model system (22, 23). While the presence of the intermediary streptavidin modifies the kinetics and statistics of bonds compared to homophilic interactions, the energy associated with forming such a ligand-receptor bond is on the same order as that of cellular adhesive junctions (24–26). The emulsion is stabilized by a mixture of surface active agents that serve different biomimetic purposes: EPC phospholipids are the major interfacial component that replace the outer leaflet of cell membranes; SDS ionic surfactant introduces electrostatic repulsion between the droplet surfaces (27), analogous to the charge repulsion between cell surface macromolecules; PEG-biotinylated lipids act as a polymer brush to induce steric repulsion (28) and also provide biotin ligands for the binding with streptavidin to mimic adhesion. In order to visualize the droplet assembly in 3D shown in Fig. 1B we match the refractive indices of the aqueous and oil phases and use fluorescent streptavidin to label the biotinylated lipids on the droplet surface. The homogeneous fluorescence of the lipids at the interface (29) provides a quantitative measure of the concentration of PEG-biotinylated lipids. In this case, the equilibrium separation between the droplet surfaces exceeds the distance over which the proteins can interact and the fluorescence remains homogeneous. We therefore compress the droplets by centrifugation at rates ranging from 1 to 1,000 times the acceleration due to gravity to deform them such that their surfaces are closer together. A given centrifugation rate gives rise to a broad distribution of deformation areas corresponding to a distribution of interdroplet forces within the 3D packing (30). To extend the force range even further and increase the statistical accuracy of our results we centrifuge each emulsion at different rates and pool together data from different 3D stacks. When the interdroplet force leads to a surface-to-surface distance that allows for protein interactions, we observe a redistribution of the proteins into adhesive patches that give rise to a much higher fluorescence intensity at the center of the droplet deformation sites shown in Fig. 1C.

Fig. 1.

(A) Schematic representation of functionalized emulsions. The oil–water interface is stabilized by a mixture of phospholipids and negatively charged SDS. Some of the lipids hold a PEG-biotin group that allows binding through biotin-streptavidin interactions, as shown on the upper droplets. (B) Three-dimensional representation of confocal images shows Texas red-streptavidin fluorescence on the surface of the droplets. Packing under gravity is not sufficient to create adhesion between the droplets (top image), whereas an applied pressure triggers the formation of adhesions between the droplets, shown as the areas of brighter fluorescence in the bottom image.

Model for Adhesion Between Droplets.

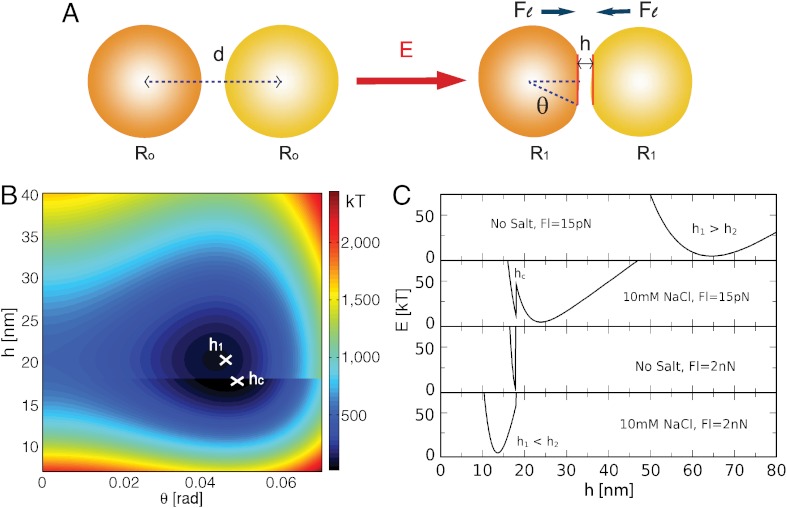
To quantitatively assess adhesion in the emulsion system, we develop a local model that takes into account the various energy terms that play a role in the interaction between two droplets in contact, as illustrated in the schematic in Fig. 2A. The binding energy E_b of the lock and key proteins and the work W_l done by the external pressure both favor adhesion. By contrast, the electrostatic repulsion E_e and the surface energy E_d oppose adhesive patch formation. Van der Waals interactions, which are negligible in cell–cell contacts, are ignored because the system is refractive index matched. For a given set of experimental conditions, the minimization of the total free energy E = E_d + E_e + E_b + W_l with respect to the distance h between the droplet surfaces and the deformation angle θ sets the equilibrium adhesion patch size, as shown in Fig. 2A.

Fig. 2.

(A) Idealized droplet deformation under a compressive force F_l. The total energy E depends on the interdistance h and the deformation angle θ. (B) A typical energy landscape as a function of the deformation parameters. Patch adhesion occurs when the global energy minimum is located at h ≤ hc. (C) The model predicts that two droplets adhere spontaneously either by the addition of salt or an applied force. The energy profiles correspond to the conditions of four points in the phase diagram presented in Fig. 5C.

For clarity, we describe a simplified model in the limit of small deformations that neglects emulsion polydispersity, which is relaxed in SI Text. The work done by the external pressure on the droplets is given by W_l = Fd, where F is the interdroplet force and 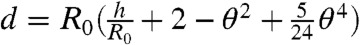is the distance between the droplet centers and R₀ is their undeformed radius. This compression of the droplets does work against the energy of deformation given by 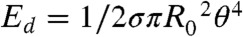, where σ is the surface tension. Our model system neglects the effects of variable interfacial tension that have been identified as important in adhesion in tissues (31, 32). Moreover, in our emulsion system all the energy is spent on deforming the surface of the oil droplets, whereas the cortical network in real cells would give rise to an additional bending energy. The work done in bringing the surfaces closer together also serves to overcome electrostatic repulsion, modeled as 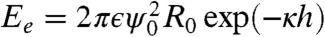(27) where ϵ is the dielectric constant, ψ₀ is the electrical potential at the droplet surface, and κ is the inverse of the Debye length. If the resulting interparticle distance h is smaller than a critical length h_c, the interaction of the surface proteins leads to an adhesive state with an additional binding energy term. The distance h_c of about 18 nm is set by the size of the biotinylated lipids and the streptavidin between them. The binding energy is given by 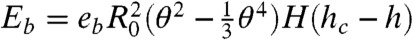, where e_b = c_bϵ_b is the binding energy per unit area, c_b is the binder concentration in the adhesion patch, ϵ_b is the binding energy of an individual binder (33), and H(t) is the Heaviside function that determines whether binding is allowed.

The resulting energy landscape reveals two local minima, E₁ = E(θ₁,h₁) and E₂ = E(θ₂,h₂), as shown in Fig. 2B, corresponding to the deformed yet nonadhesive and adhesive states of the contacting droplets. These energy states are separated by an energy barrier and a discontinuity at h = h_c that comes from the additional binding energy E_b for h < h_c. Adhesion can only occur if the global minimum is found at h < h_c or if the energy difference between the two minima is within thermal energy. The solutions of the model in different regimes give

• 

• 

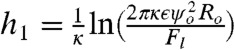
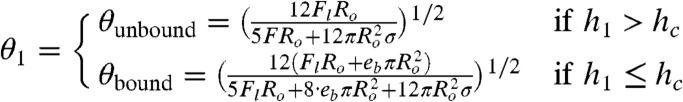
• θ₂ = θ_bound

Decreasing the Debye length or compressing the droplets with force F_l modifies the energy landscape in favor of the adhesive state, as shown in Fig. 2C. These parameters are varied in the experiment to probe the validity of the model.

Quantitative Analysis of Force-Dependent Adhesion.

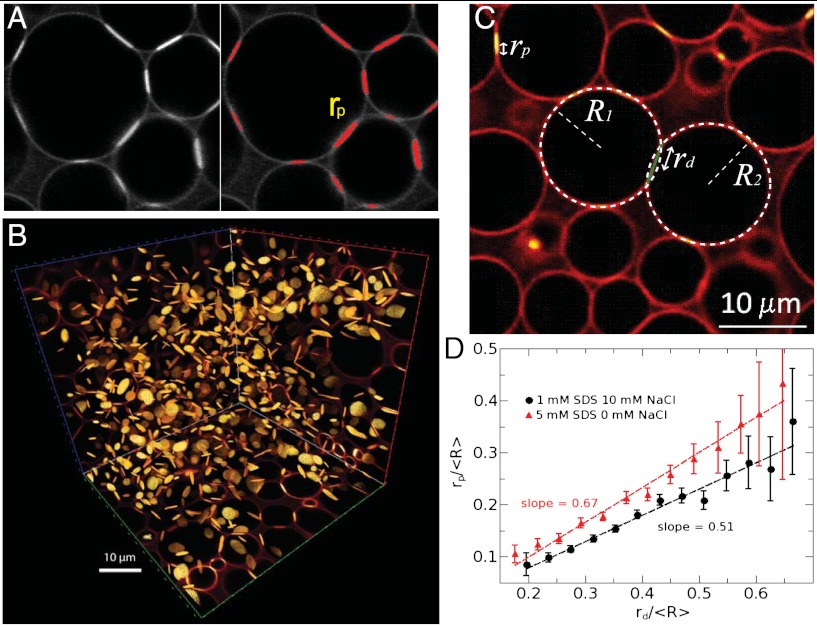
In order to compare the experimental findings with the model we first extract ≈1,000 adhesion patches from 3D reconstructions of confocal images. As shown in Fig. 3A, the adhesion patches are identified by a thresholding algorithm because they fluoresce brighter than the surface of the droplets or the aqueous background (see SI Text). The homogeneous spatial distribution of the adhesion discs within the volume of the packing is shown in Fig. 3B in a typical experiment. For every droplet pair in contact we therefore measure the adhesion patch radius r_p.

Fig. 3.

(A) The radii of fluorescent adhesive patches are determined by thresholding the intensity of the images. (B) All patches are thus identified in the 3D structure of the packing. (C) The radii of deformation between droplets are derived from the overlap between identified spheres of radii R1 and R2. (D) This analysis reveals the linear correlation between the adhesion and deformation radii of each contacting droplet pair in the packing.

Second, the images reveal the radius of deformation r_d between contacting droplets from the geometric overlap between the identified spheres of radius R shown in Fig. 3C (34). Whereas we assume that the adhesion patch spans the full area of deformation in the theoretical model, experimentally we observe r_p < r_d. We find that r_p = αr_d with the slope α giving the coverage of the adhesion (Fig. 3D). We use the measured r_p, r_d, R, and the model parameters introduced above (see SI Text for values) to obtain the electrostatic, adhesion and deformation forces (F_e, F_b, F_d) for each droplet contact in the pile. Assuming mechanical equilibrium, we thus deduce the interdroplet compression force as F_l = F_e + F_d - F_b.

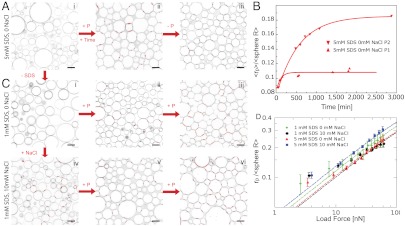
This analysis allows us to test how electrostatic repulsion, surface tension, and the screening of charges influence the force-dependent adhesion in terms of the time scale, size, and number density of the protein links. By varying the SDS concentration from 1 to 5 mM in the emulsions, we simultaneously increase the charge repulsion and decrease the surface tension of the droplets. In the 5 mM case, the charge repulsion prevents adhesion under gravity (Fig. 4Ai) and requires an applied pressure by centrifugation as well as a long waiting time before the patches form (Fig. 4A, ii). The fact that patches persist after relaxing the applied pressure to 0.2 kPa, corresponding to gravitational compression, confirms that they arise from protein links across contacting surfaces (Fig. 4A, iii). This irreversibility indicates a kinetic barrier to removing the adhesive patches. The mean patch radius grows toward steady state size to form adhesions on a characteristic time scale of hours, as shown in Fig. 4B, where the patch growth dynamics is displayed for two different global pressures. Interestingly, these time scales on the order of hours are slower than the second time scales measured in functionalized model membranes (35). However, the ≈30 minutes observed for individual cellular adhesions (9, 36) or the 90 min measured in centrifugation-based bulk adhesion assays (37) are similar to the ≈120 min measured under the low emulsion compression. Decreasing the electrostatic repulsion by lowering the SDS concentration to 1 mM or by screening charges with salt leads to patches growing on much faster time scales (below 20 min), independent of the centrifugation rate (Fig. 4 C, ii–vi).

Fig. 4.

Two-dimensional confocal slices are shown for different conditions. When the droplets are stabilized with 5 mM SDS, centrifugation and waiting time are necessary to observe the formation of adhesive patches, which are irreversible (A, i–iii). (B) The growth of the mean adhesive radius for the emulsion in A is shown for two different applied compressions corresponding to average forces of 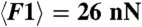and 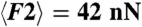and fit with exponentials (red lines). Lowering the SDS concentration to 1mM still requires compression to induce adhesion (C, i–iii). However, when salt is added to the solution (C, iv–vi) gravity alone triggers droplet adhesion and the patches formed under compression are more numerous (C, vi) than in the no salt cases (A, iii, and C, iii). (D) Normalized patch radius for all emulsion conditions grows as a function of the applied force, in good agreement with the model at high forces (dashed lines). Bars = 10 μm.

Image analysis of the local microstructure reveals the dependence of each patch size on the corresponding interdroplet force. To probe a wide range of forces we centrifuge each emulsion at different rates and image multiple stacks to collect a large statistical pool of data. We find that higher compression visibly increases the adhesion patch sizes under all conditions (Fig. 4C, iii and vi). To quantify this effect we bin the local interdroplet forces and plot the corresponding average patch size as a function of the average force for all conditions, as shown in Fig. 4D. In all cases, the increase of patch size with load force follows the model prediction of a square root law at high forces, but there is a pronounced deviation toward larger patches at low forces due to the onset of protein binding. The high force dependence makes sense because the energy of deformation dominates the total free energy and predicts that the force is proportional to the square of the deformation radius, consistent with the Princen model (38). While the force dependence is similar between the datasets, they differ in the prefactor. This prefactor corresponds to the adhesion coverage α of the area of deformation identified in Fig. 3D, which is larger for the 5 mM SDS emulsion with salt. A possible explanation is that a line tension develops as the protein complexes displace the other surface molecules and increase the local surface tension, similar to domain formation. The coverage efficiency then depends on the surface properties of the emulsion and the resulting line tension.

Although the increase of patch sizes with force follows the model prediction independent of the emulsion conditions, the number of droplet contacts that are covered with adhesion patches N_p divided by the total number of droplet contacts N_c reveals interesting distinctions, as shown in Fig. 5A. In the absence of screening by salt no patches are observed in the 1 mM and 5 mM SDS emulsion under gravitational compression with forces of F_g ≈ 15 pN (corresponding to deformations below the resolution limit of the microscope). On the other hand, applying the smallest measurable force of ≈2 nN leads to 20% and 35% of droplet contacts with adhesions, respectively. This result is consistent with the force tilting the energy landscape in the model to favor the adhesive minimum. However, the low probability of adhesion remains constant over the entire force range up to 50 nN, which indicates a kinetic barrier that is insensitive to force. Instead, this barrier can be overcome by screening the electrostatic repulsion with 10 mM salt, which allows some adhesions (5%) to form even under gravity. Upon compression of the screened emulsions the probability of adhesion reaches almost 1, also evidenced by the large number of patches seen in Fig. 4C, v and vi. The effects of these experimental scenarios on the model are shown in Fig. 2C for the 5 mM SDS emulsion. These results demonstrate that increasing external pressure is required to observe adhesion in the biomimetic system. Even though this observation suggests a possible role of homeostatic pressure in achieving the mechanical integrity in biological tissues (10), cells contain other active mechanisms, such as the remodeling of the cortical network due to signaling molecules or cytoskeletal forces, that are known to affect adhesion through active processes (39).

Fig. 5.

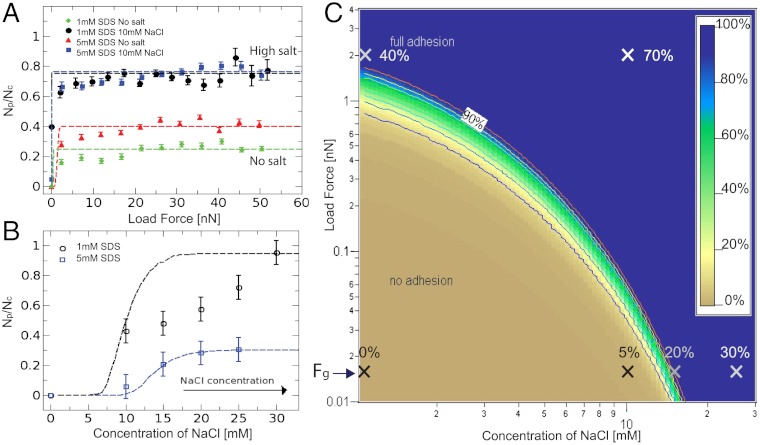
The probability of finding a patch increases as a function of the applied force in A or salt concentration in B, in agreement with the model (dashed lines). The observed trends are predicted by the model phase diagram of adhesion in C, in which the fitting parameters are consistent with the literature (see SI Text). Crosses are experimental data points with labels that denote the percentage of adhesive contacts (Np/Nc) for each experiment. The background color map denotes the same quantity in the model phase diagram.

An alternative to using force to populate droplet contacts with adhesions is to screen the charges by increasing the salt concentration, as shown in Fig. 5B and the image in Fig. 4C, iv. This trend is in agreement with the model, in which the corresponding decrease in the Debye length changes the energy landscape, favoring the adhesive state and decreasing the barrier to it. Because the model assumes a constant compression force of 15 pN between droplets, the transition appears sharper than in the emulsion where the patch fraction is derived from a distribution of forces in a given droplet packing under gravity. Under physiological conditions of 100 mM salt the model predicts the spontaneous nucleation of adhesions in both emulsions. Under gravity alone, the model predicts adhesions on the scale of 200 nm in radius from the estimated concentration of cadherins on the cell surface (16, 40). As shown above, nanonewton forces are necessary to grow adhesions that span the entire cell–cell interface.

Phase Diagram for Adhesion.

Finally, we construct phase diagrams for adhesion from the probabilities of forming a patch as a function of the applied force and the concentration of NaCl, as shown in Fig. 5C for the 5 mM SDS emulsion. The model prediction of the phase diagram, fixed by literature values for the surface tension of our emulsions, the binding energy per streptavidin–biotin bond, and the measured value for the electrical potential, yields a binder concentration of 47 molecules/μm² in the 5 mM SDS case and 60 molecules/μm² in the 1 mM SDS case to fit the phase boundaries identified by the data. Therefore, the fact that the theoretical model fits the data in both cases using only one fit parameter (i.e., the binder concentration) for the adhesion fraction as a function of two experimental variables gives strong validity to the model. However, the transition from nonadhesive to adhesive regimes is typically sharper in the model than the data. This may be due to the fact that the model considers only pairwise interactions, while the data is extracted from the statistical analysis of a 3D network of contacts where a distribution of forces and packing geometry also play a role.

Remarkably, the range of binder densities is similar to that of cadherins (80–800 molecules/μm²) on the cell surface. The fact that all the parameters that describe the biomimetic system are to within a factor of two in agreement with the values measured in cells under physiological conditions (see SI Text) lends strong support to this synthetic approach in biology. While it is known that the concentration of adhesive molecules on the cell surface tune the strength of adhesion, our model system shows how this concentration depends on the balance between factors such as the osmolyte concentration, membrane surface tension, and cytoskeletal pushing forces as well. More specifically, the phase diagram demonstrates that the global screening of charges facilitates the formation of adhesions and that external pressure contributes to the size increase of droplet contacts.

In real tissues, the strengthening of adhesive contacts on long time scales depends strongly on the interactions between cadherins and the active actin cytoskeleton. Nevertheless, our results suggest possible additional mechanisms in which cell–cell adhesions are strengthened by the regulation of the local electrostatic environment and cortical tension or the global regulation of the tissue homeostatic pressure and surface tension. Experiments should be performed to test these possibilities in biological tissues using the biomimetic phase diagram as a guide. Furthermore, the versatility of our simplified system will enable the quantitative study of specific constituents in the mechano-sensitive regulation of cellular adhesion.

Materials and Methods

The protocol for the emulsion preparation is inspired by experiments described in ref. 29. Here, the oil droplets contain egg L-α-phosphatidylcholine (EPC) lipids and the DSPE-PEG(2000) biotinylated lipids from Avanti Polar Lipids at a molar ratio of 92∶8, respectively, and a total mass of 19 mg. The solvent containing the lipids is evaporated under nitrogen before 10 mL of silicone oil is added to the dried lipids. This mixture is then sonicated during 30 min at room temperature and heated at 50 °C during 3 h. After cooling to room temperature the lipid containing oil (10 mL) is first coarsely emulsified in 22 mL of buffer (5 mM SDS, w_t = 18% dextran). This crude emulsion is then injected into a narrow gap couette mixer, with a gap size of 100 μm, and sheared at 22 rpm. The resulting emulsion is washed twice in an aqueous solution of 1 or 5 mM SDS before a last wash in the index matching buffer containing 50∶50 glycerol∶water. This emulsion is stable over several weeks at 4 °C. The emulsion is dyed on the surface with Texas Red conjugated streptavidin (Invitrogen), 500 μL of 1 or 5 mM SDS emulsion is mixed with 1 mg/mL streptavidin (25 uL) and 1.5 mL of buffers containing 2 mM Tris pH = 7, 1 or 5 mM SDS, 0 to 30 mM NaCl. This solution is incubated 1 h at room temperature to allow the streptavidin to bind to the biotinylated lipids on the droplets. The sample can be observed after creaming under gravity as shown in Fig. 1B or centrifuged a 20 °C at accelerations ranging from 50 to 1,400 g during 20 min. The top layer of the compressed emulsion is then transferred into another observation cell to isolate it from the continuous phase and therefore avoid relaxation. The sample is imaged using a fast scanning confocal microscope (Leica TCS SP5 II).