Reversible voltammograms and a Pourbaix diagram for a protein tyrosine radical

Abstract

Reversible voltammograms and a voltammetry half-wave potential versus solution pH diagram are described for a protein tyrosine radical. This work required a de novo designed tyrosine-radical protein displaying a unique combination of structural and electrochemical properties. The α₃Y protein is structurally stable across a broad pH range. The redox-active tyrosine Y32 resides in a desolvated and well-structured environment. Y32 gives rise to reversible square-wave and differential pulse voltammograms at alkaline pH. The formal potential of the Y32-O^•/Y32-OH redox couple is determined to 918 ± 2 mV versus the normal hydrogen electrode at pH 8.40 ± 0.01. The observation that Y32 gives rise to fully reversible voltammograms translates into an estimated lifetime of ≥30 ms for the Y32-O^• state. This illustrates the range of tyrosine-radical stabilization that a structured protein can offer. Y32 gives rise to quasireversible square-wave and differential pulse voltammograms at acidic pH. These voltammograms represent the Y32 species at the upper edge of the quasirevesible range. The square-wave net potential closely approximates the formal potential of the Y32-O^•/Y32-OH redox couple to 1,070 ± 1 mV versus the normal hydrogen electrode at pH 5.52 ± 0.01. The differential pulse voltammetry half-wave potential of the Y32-O^•/Y32-OH redox pair is measured between pH 4.7 and 9.0. These results are described and analyzed.

Proton-coupled electron transfer (PCET) represents a fundamental component of catalytic and long range radical-transfer processes involving tyrosine radicals (1–4). The thermodynamic and kinetic effects of coupled tyrosine oxidation/reduction and acid/base chemistry at the protein matrix are likely to play a key role in activating the aromatic residue for redox chemistry and for fine tuning its functional properties. This prediction is largely based on three sets of experimental observations that include the thermodynamic properties of aqueous tyrosine (5–7), the hydrogen-bonding properties of the kinetically well-characterized Y_Z and Y_D radicals in photosystem II (PSII) (7–10), and data derived from small-molecule model systems designed to delineate the PCET processes associated with tyrosine/phenol oxidation (4, 11–16). Tyrosine redox chemistry involves three redox couples and two pK_a values. The cation Y-OH^•+/Y-OH redox pair exists at pH below the pK_a of the oxidized state (pK_oY) whereas the tyrosinate Y-O^•/Y-O^- couple is observed at pH above the pK_a of the reduced state (pK_rY). The neutral tyrosine Y-O^•/Y-OH redox couple operates in the pK_oY < pH < pK_rY region. With pK_oY and pK_rY values of -2 and 10 for aqueous tyrosine, respectively (5), Y-O^•/Y-OH is predicted to be the dominant protein redox pair. Consequently, long-range electron transfer involving protein tyrosine residues is coupled to short-range proton motions between the radical species and the protein matrix. Indeed, studies on Y_Z and Y_D suggested early on that electron and proton transfers associated with tyrosine oxidation/reduction are strongly coupled events (7–9). Studies on solvated small-molecule tyrosine/phenol model systems have reinforced the key observation that local interactions critically determine the redox properties of tyrosine and the PCET mechanism by which the radical state is formed (for a recent review, see ref. 4).

The involvement of tyrosine radicals in biochemical processes has been known for decades. Yet, there is essentially a complete lack of thermodynamic data available for these redox species with published reduction potentials limited to two single-pH estimates (ref. 17 and references therein). This situation underlines the experimental challenges associated with probing the potentials of these highly oxidizing PCET molecules when they reside in a protein environment. Here we present a reduction potential vs. solution pH (Pourbaix) diagram (18) for a protein tyrosine radical. This was made possible by adopting a model protein approach guided by the following criteria. Obtaining a Pourbaix diagram for a protein tyrosine radical requires: (i) a protein system; i.e., a system that exhibits classic protein properties of cooperative structure and stability; (ii) that this protein contains a solvent-sequestered redox-active tyrosine whose potential can be measured by voltammetry across a broad pH range; (iii) that the protein voltammogram reflects a reversible electrode process from which formal tyrosine potentials can be derived. Here we report voltammetry studies of a de novo designed tyrosine radical model protein that fulfills these unique requirements.

Results and Discussion

α₃Y Is a Well-Structured Protein.

The synthetic α₃Y model protein used here is a member of a family of de novo designed radical proteins (2, 17, 19–21). This family is based on a 67-residue scaffold containing three interacting α-helices linked by two glycine loops (Fig. S1). The radical site (position 32) is located in the middle of the central helix and occupied by a tyrosine (to form the α₃Y protein), a tryptophan (α₃W), or a cysteine (α₃C). C32 in α₃C has been used as a chemical link for phenol ligation (22). α₃Y, α₃W, and α₃C exhibit main characteristics associated with well-folded native proteins. They form thermodynamically stable, highly helical structures across a broad pH range. Folding occurs in a reversible, cooperative manner and is driven by the hydrophobic effect. Their tertiary structures are well defined. Importantly, residue 32 resides in a desolvated and highly structured environment. This latter property uniquely separates α₃Y from all previously described tyrosine/phenol radical model systems in which the radical species typically resides in a highly solvated and dynamic environment (4, 23).

α₃Y Voltammetry Control Studies.

Cyclic voltammetry (CV) (24) data cannot be obtained for α₃Y due to the poor electrochemical response when using this relatively insensitive technique [see ref. 17 for a comparison in the CV response of a small-molecule tyrosine system and α₃Y]. Differential pulse voltammetry (DPV) (24, 25) has better sensitivity than CV and generates a well-defined Faradaic response from α₃Y at both acidic and alkaline conditions. Site-directed mutagenesis unambiguously assigned the observed current to Y32 and showed that the protein scaffold itself is redox inert to at least 1.3 V vs. NHE (17, 22). Examples of raw and background-corrected differential pulse voltammograms, details regarding data processing, and error analyses are provided in SI Text. To prove that α₃Y is an electrochemically reversible system we employ the similarly sensitivity technique square-wave voltammetry (SWV) (24, 26, 27). In SWV, the applied potential is stepped progressively in fixed increments, and at each increment, a forward (in this study, oxidative) potential pulse is applied followed by a reverse (reductive) pulse. This generates a forward (I_for), a reverse (I_rev), and a net (I_net = I_for - I_rev) voltammogram. The time between sampling I_for and I_rev is set by the pulse width (t_p), which is determined by the square-wave frequency (f = 1/2t_p). The forward and reverse square-wave voltammograms resemble a cyclic voltammogram and can be used to assess the reversibility of the electrode process (26, 27). For a reversible electrode process, the peak potential of the net current (E_net) equals the voltammetry half-wave potential (E_1/2). Typically, the half-wave potential closely approximates the formal potential (E⁰’). For a diffusion-controlled reversible redox system, E_1/2 equals E⁰’ when the ratio of the diffusion coefficients of the reduced and oxidized species equals unity (24).

DPV conducted with a glassy carbon (GC) working electrode generates α₃Y voltammograms with good signal-to-noise ratio (S/N) (17) (Fig. S2). In contrast, SWV in combination with a GC electrode generates α₃Y voltammograms with significant lower S/N and this approach was not perused beyond a preliminary assessment. A series of control measurements were conducted to refine a pyrolytic graphite “edge” (PGE) electrode system for a SWV analysis of the α₃Y electrode process. Fig. S3 summarizes experiments conducted to optimize sample conditions (Fig. S3 A and B) and to determine whether α₃Y gives rise to diffusion-controlled or surface-confined electrode kinetics (Fig. S3D). Fig. S4 displays typical raw and background-corrected α₃Y square-wave voltammograms collected at optimized sample conditions and provides details regarding data processing and analyses. Finally, Fig. S5 illustrates the reproducibility observed between data replicates and independent SWV measurements. The main conclusions from the data displayed in Figs. S2–S5 are summarized below and we refer to the SI Text for further details. (i) SWV samples were optimized at 20–100 μM α₃Y in 20 mM sodium acetate, 20 mM potassium phosphate, 20 mM sodium borate (APB buffer), and 80–140 mM KCl. The S/N of the α₃Y Faradaic current decreases above and below the 20–100 μM protein concentration range. The α₃Y peak potential is independent of the KCl concentration above 10 mM KCl at alkaline pH (pH 8.4) and above 60 mM KCl at acidic pH (pH 5.5). The S/N of the α₃Y voltammogram declines as the KCl concentration rises and accurate determination of peak amplitudes and potentials becomes increasingly difficult above 140 mM KCl. Based on these results, subsequent SWV studies were conducted at 80 μM α₃Y dissolved in a 20 mM APB, 80 mM KCl buffer. (ii) The SWV net potential (E_net) and the DPV half-wave potential (E_1/2) are displayed as a function of the α₃Y concentration in Fig. S3 B and C, respectively. The SWV and DPV measurements were conducted using a PGE and GC electrode, respectively, and the α₃Y concentration series was collected at both acidic and alkaline pH. A very weak to no correlation (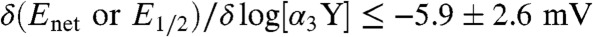 per decade) is observed for both electrode systems. We conclude that there are no distorting protein/working electrode surface interactions (such as self-inhibition, e.g., ref. 28) present at any conditions used in this report. (iii) Voltammograms were recorded at large SW pulse amplitudes to investigate the kinetic characteristics of α₃Y on the PGE electrode (27, 29) (Fig. S3D). The observed response is consistent with diffusion-controlled electrode kinetics at both acidic and alkaline pH. (iv) The reproducibility in E_1/2 obtained with the DPV/GC system is ± 3 mV for data replicates (Fig. S2 A and D–F) and ± 4 mV for independent measurements (Fig. S2I). The reproducibility in E_net observed for the SWV/PGE system is ± 3 mV for data replicates (Fig. S5 A–F) and ± 3 mV for independent measurements (Fig. S5 G–I). After correcting for small differences in pH, we find no significant difference (5 ± 5 mV) in the α₃Y DPV E_1/2 value obtained using a GC electrode (Figs. S2 and S3C) relative to a PGE electrode (Fig. S3A). This concludes the description of control experiments done in preparation for a SWV analysis of the α₃Y electrode process and obtaining a Pourbaix diagram for the tyrosine radical protein.

α₃Y Gives Rise to Reversible Voltammograms.

Voltammetry measurements on α₃Y are expected to follow an EC mechanism where “E” represents the electrode reactions (electron and proton transfers associated with the electrode-driven oxidation/reduction of Y32) and “C” represents coupled chemical reactions (i.e., side reactions of the formed Y32-O^• radical). The kinetic and thermodynamic properties of both the E and C processes will influence the observed voltammogram (26, 27, 30–32). In SWV the time between the oxidative and the reductive pulse is set by the SW frequency, which has a practical range of 8–2,000 Hz (t_p 62.5 ms–250 μs). This predicts that for an EC system with a very long-lived radical (i.e., t_1/2 on the tens of milliseconds time scale), the SW frequency can be set to outcompete the follow-up chemical reaction(s). This would generate voltammograms with properties that only reflect the E process. Remarkably, the protein environment stabilizes the Y32-O^• radical into the required time frame such that voltammograms representing a fully reversible electrode process could be obtained. This is shown below.

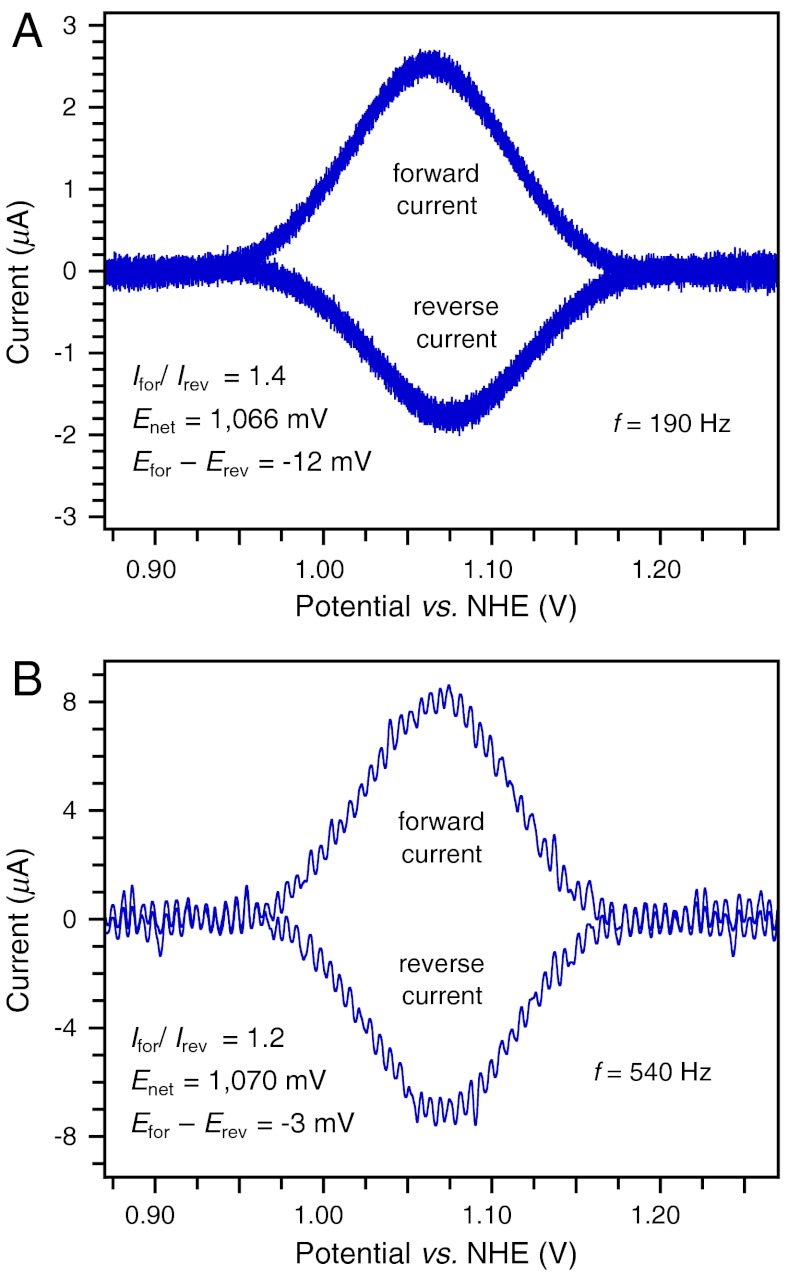
α₃Y square-wave voltammograms were recorded using a frequency ranging from 30 Hz (t_p 16.7 ms) to 960 Hz (t_p 521 μs). The three top boxes in Fig. 1 display voltammograms from this data series. Background-corrected forward and reverse square-wave voltammograms collected at 190 Hz (t_p 2.63 ms), 540 Hz (t_p 926 μs), and 750 Hz (t_p 667 μs) are shown in Fig. 1 A–C, respectively. Fig. S4 illustrates the quality of the raw voltammograms from this data series and describes methods used for background corrections and data analyses. The key results from the SW frequency series are summarized in Fig. 1 D and E. Fig. 1D shows the change in the peak potentials as a function of the SW frequency. Importantly, the net peak potential (E_net) and the peak potentials of the forward (E_for) and reverse (E_rev) currents become independent of the SW frequency at 750 Hz (Fig. 1D). This is a hallmark characteristic of a fully reversible electrode process (26, 27). We further observe that I_for/I_rev declines from 1.71 ± 0.14 at 30 Hz and reaches a limiting value of 1.01 ± 0.02 for the 750 - 960 Hz range (Fig. 1E). Whereas E_for - E_rev varies between -14 ± 1 and -8 ± 2 in the quasireversible range (30–540 Hz), the effects on E_net remain small with a change of 8 ± 2 mV between 30 and 120 Hz and only 4 ± 2 mV for the 120–960 Hz range (Fig. 1D). E_net equals 918 ± 2 mV vs. NHE for the 750–960 Hz range and represents the formal potential (E⁰’) of the Y32-O^•/Y32-OH redox couple at pH 8.40 ± 0.01. This statement assumes that the diffusion coefficient of α₃Y does not change as a function of the protein redox state. The diffusion coefficient of reduced α₃Y was determined to be 1.47 ± 0.01 × 10^-6 cm² s^-1 by pulsed field gradient NMR experiments (33) (Fig. S6). This value is typical for a small soluble protein and is not likely to change significantly as Y32 loses an electron and a proton.

Fig. 1.

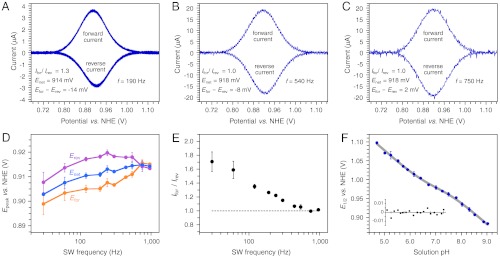
α₃Y forward (oxidation) and reverse (reduction) square-wave voltammograms obtained at pH 8.40 ± 0.01 and using a SW frequency of (A) 190 Hz (t_p 2.6 ms), (B) 540 Hz (t_p 926 μs), and (C) 750 Hz (t_p 667 μs). These voltammograms form part of a SW frequency series spanning from 30 Hz (t_p 16.7 ms) to 960 Hz (t_p 521 μs). (D) describes the change in the peak potential of the net (E_net), forward (E_for), and reverse (E_rev) currents as a function of the SW frequency. E plots the ratio of the peak currents of the forward (I_for) and reverse (I_rev) components as a function of the SW frequency. SWV settings: 80 μM α₃Y in 20 mM APB, 80 mM KCl, pH 8.40 ± 0.01; PGE working electrode, temperature 25 °C, step potential 0.15 mV, SW pulse amplitude 25 mV. (F) α₃Y differential pulse half-wave potential (E_1/2) of as a function of pH. The solid gray line represents a nonlinear regression curve fit to Eq. 1. The insert displays the corresponding fitting residuals. DPV settings: 200 μM α₃Y in 10 mM APB, 100 mM KCl, GC working electrode, temperature 23 °C, interval time 0.1 s, step potential 1.95 mV, scan rate 19.5 mV s^-1, modulation time 2 ms, modulation amplitude 25 mV.

The observation that Y32 gives rise to a fully reversible voltammogram means that the radical state is stable on the time scale of the electrochemical oxidation/reduction reactions. Theoretical treatments for EC systems where “E” represents a diffusion-controlled reversible electrode process and “C” is a coupled chemical reaction have been described for SWV (30, 31). They predict that the influence of the coupled chemical reaction on E_net approaches zero when log(2t_pk_EC) ≤ -1.5. This predicts that rate constants (k_EC) associated with Y32-O^• side reactions are ≤ 24 s^-1, which, in turn, translates into a radical lifetime of ≥30 ms. The well-structured protein environment of the Y32 site clearly suppresses radical side reactions with a remarkable efficiently. Possible side reactions include intermolecular radical-radical and radical-protein reactions as well as intramolecular radical-protein reactions. For example, for freely solvated tyrosine the oxidized species rapidly dimerizes (4–8 × 10⁸ M^-1 s^-1) to form C_ortho-C_ortho and C_ortho-O dityrosine as the major and minor products, respectively. Intermolecular radical reactions are not expected to occur for the Y32 system to any significant extent. The Y32 site is located inside the protein, and the global stability of α₃Y predicts that only 0.2% of the protein population is unfolded at any given time (17, 19). The absence of intermolecular side reactions is consistent with the insensitivity in the SWV E_net (190 Hz; Fig. S3B) and DPV E_1/2 (Fig. S3C) potentials to the protein concentration. As a comparison, aqueous N-acetyl-tyrosinamide (NAYA) displays a δE_1/2/δ log[NAYA] dependence of -30 ± 3 mV per decade (Fig. S3C) reflecting rapid intermolecular radical reactions. Intramolecular radical-protein reactions could occur in α₃Y. ¹H-¹H nuclear Overhauser effect spectroscopy (NOESY) spectra show that the Y32 site is comprised of numerous aliphatic C-H groups (17, 19). This suggests that hydrogen-atom abstraction from C-H bonds may represent the dominant route for chemical reduction of Y32-O^•. These reactions typically exhibit low rate constants (34). They are also predicted to be pH independent, which becomes important for the interpretation of the Pourbaix diagram derived for α₃Y (vide infra).

Collecting SW voltammograms in the pH 5.5 region was more challenging for two reasons. The Faradaic current decreases at lower pH (e.g., compare Fig. 1 A and B to Fig. 2 A and B) whereas the Y32 potential increases to above +1.0 V vs. NHE. This makes background currents (arising from the aqueous solvent and the electrode itself) more pronounced. Nonetheless, voltammograms of satisfactory S/N were collected at 190 and 540 Hz. Background-corrected forward and reverse voltammograms obtained at pH 5.52 ± 0.01 are shown in Fig. 2. Examples of raw data triplicates of the net, forward, and reverse components are shown in Fig. S5 D–F, respectively. The properties of the low-pH voltammograms exhibit the same overall frequency dependence as the high-pH data. I_for/I_rev drops from 1.44 ± 0.03 (190 Hz) to 1.15 ± 0.01 (540 Hz), E_for - E_rev decreases from -11 ± 1 mV (190 Hz) to -3 ± 1 mV (540 Hz), and a minor change from 1,066 ± 2 mV (190 Hz) to 1,070 ± 1 mV (540 Hz) is observed for E_net. These characteristics strongly suggest that the 540 Hz voltammogram represents the Y32 system at the upper edge of the quasireversible range and that E_net (pH 5.52; 540 Hz) deviates from E⁰’ (pH 5.52) by a few mV at most (27). We therefore conclude that 1,070 ± 1 mV vs. NHE closely approximates the formal potential of the Y32-O^•/Y32-OH redox couple at pH 5.52 ± 0.01.

Fig. 2.

α₃Y forward (oxidation) and reverse (reduction) square-wave voltammograms obtained at 5.52 ± 0.01 and using a SW frequency of (A) 190 Hz (t_p 2.6 ms) and (B) 540 Hz (t_p 926 μs). SWV settings: 80 μM α₃Y in 20 mM APB, 80 mM KCl, pH 5.52 ± 0.01; PGE working electrode, temperature 25 °C, step potential 0.15 mV, SW pulse amplitude 25 mV.

Pourbaix Diagram of α₃Y.

Fig. 1F shows the DPV E_1/2 potential of α₃Y as a function of the solution pH. The α₃Y potential displays a nonlinear relationship across the investigated 4.7–9.0 pH range. The SWV analysis described above provides an explanation to the observed pH dependence. The formal potential of the Y32-O^•/Y32-OH redox couple is 918 ± 2 mV at pH 8.40 ± 0.01. From the E_1/2 vs. pH plot in Fig. 1F we extract a potential of 916 ± 3 mV at pH 8.40. There is no significant difference between the formal potential of the Y32-O^•/Y32-OH redox couple as determined by SWV and the E_1/2 value derived by DPV. Consequently, the α₃Y SW voltammogram (pH 8.40; ≥750 Hz) and the DP voltammogram (pH 8.40) are both derived from a fully reversible electrode process.

The DPV E_1/2 (pH 5.52) value is 22 ± 3 mV lower relative to the 1,070 ± 1 mV (pH 5.52; 540 Hz) value determined by SWV. Tyrosine oxidation is a PCET event, that is, the kinetic and thermodynamic properties of the electron transfer depend on the position of one (or several protons) at any given time (35). It is well established that the hydrogen-bonding properties of the phenol OH group and the characteristics of the base accepting the phenolic proton upon oxidation strongly influence the oxidation mechanism and associated PCET rate constants. The small 22 mV shift in the DPV E_1/2 potential relative to the SWV E_net value is likely to arise from coupled protonic reactions lowering the Y32/electrode electron-transfer rate into the quasireversible regime for the DPV experiment. The alternative explanation is that k_EC increases as the pH decreases and makes the system quasireversible. We favor the former explanation because the effects of coupled protonic reaction are expected to be highly sensitive to the pH (e.g., by pH-induced changes in the hydrogen-bonding properties of Y32) whereas k_EC is not (vide supra).

Based on the discussion presented above, the α₃Y Pourbaix diagram is modeled by (36):

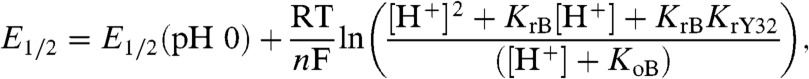[1]

where E_1/2(pH 0) is the half-wave potential at pH 0 (V); K_rY32 is the acid dissociation constant of Y32 in its reduced state (pK_app = 11.3, see ref. 17); K_rB and K_oB represent apparent acid dissociation constants (K_app) of a protein residue B when Y32 is in its reduced and oxidized state, respectively; n is the number of electron equivalents required to convert one mol of oxidant to one mol of reductant; T is the temperature (296 K); R is the gas constant (8.314 J mol^-1 K^-1); and F is the Faraday constant (96.485 kJ V^-1 mol^-1). Eq. 1 was fitted to the α₃Y Pourbaix diagram with the following results: E_1/2(pH 0) = 1.37 ± 0.02 V, ln(10)RT/nF = 59 ± 5 mV, pK_rB = 6.7 ± 0.2, and pK_oB = 7.4 ± 0.2. The fitted line is displayed in gray in Fig. 1F and the fitting residuals are shown in the Inset. In this model, Y32 is thermodynamically coupled to a residue B in the protein matrix. Residue B is protonated at low pH and unavailable to participate in the protonic reactions associated with the oxidation of Y32. As the pH increases and approaches the pK_rB range, residue B deprotonates and now becomes available to participate in the PCET reactions associated with Y32 oxidation. The redox-induced shift in the pK_a of residue B gives rise to the nonlinearity of the Pourbaix diagram describing the pH dependence of the Y32-O^•/Y32-OH redox couple.

Conclusions

This report describes three important experimental results. (i) Square-wave and differential pulse voltammograms representing a reversible electrode process have been obtained for a protein tyrosine radical. This represents a unique experimental demonstration of obtaining a formal potential for a protein Y-O^•/Y-OH redox pair. (ii) The observation of reversible voltammograms translates into an estimated lifetime for the tyrosine radical of ≥30 ms. This is a remarkably long lifetime for a phenol-based radical and illustrates that the protein environment can stabilize the Y32-O^• state by inhibiting deleterious radical side reactions. (iii) The first Pourbaix diagram for a protein tyrosine radical is described and analyzed. These results represent a significant advance that is long overdue considering that these important protein redox species were identified as early as 1977 (37). The historically prohibitive challenges associated with obtaining thermodynamic information for protein tyrosine radicals stem from the fact that electrochemical measurements must be performed at the very upper edge of the biological redox scale. Moreover, voltammetry on phenols typically follows an EC mechanism where the electrochemical reduction of the radical state is outcompeted by the coupled chemical reaction. This gives rise to irreversible voltammograms from which E_1/2 potentials cannot be derived without independent information on the rate of the chemical follow-up reaction. Finally, the voltammetry measurements must be conducted in a pH-stable protein background and be sensitive to interactions at the radical site to generate a meaningful Pourbaix diagram for this PCET cofactor. These experimental barriers have been successfully overcome by the α₃Y system.

The recently published high-resolution crystal structure of PSII provides a striking example as to why it is vital to understand the details associated with tyrosine-mediated PCET processes in nature. Seventeen years ago, Gerald T. Babcock and co-workers proposed a model for photosynthetic water oxidation in which PCET at the level of Y_Z provides the key mechanism by which protons formed during the water-splitting process are transported from the active site to the thylakoid lumen (38, 39). This hypothesis broke significantly with the contemporary metal-centered view of photosynthetic water oxidation as it proposed a mechanistically essential PCET function for the tyrosine rather than a traditional ET role in which Y_Z forms a simple link in an electron-transfer chain. The hypothesis of directional proton transfer driven by the Y_Z redox cycle gave rise to two core structural predictions: That Y_Z is in hydrogen-bonding contact with substrate molecules ligated to the metal cluster and that there is a proton exit channel from the tyrosine via its hydrogen-bonding partner D1-H190 to the thylakoid lumen. The recent 1.9 Å resolution crystal structure of PSII shows features remarkably consistent with these predictions (10). In light of the new PSII structure, a straightforward refinement of the 1995 hypothesis is to propose a “global” reprotonation of the Y_Z radical upon reduction with a proton from the extended hydrogen-bonding network connecting the metal/substrate/Y_Z molecules. This would allow directional PCET at the Y_Z site as originally proposed but remove the requirement of direct hydrogen-atom transfer from metal-ligated substrate to the Y_Z radical. Overall, the intriguing structural properties of the PSII active site will undoubtedly spark an even more intense interest in the amazing chemistry performed by protein tyrosine radicals.

Materials and Methods

Differential pulse and square-wave voltammetry measurements were performed using an Autolab PGSTAT12 potentiostat equipped with a three-electrode glass cell containing a GC or a PGE working electrode. The working electrode was carefully polished between each measurement. All samples were prepared using ultra-pure chemicals and the measurements made under an argon atmosphere. NMR spectra were collected using a 500 MHz Bruker Advance III spectrometer fitted with a cryo probe. Details regarding electrode preparations, voltammetry setup and measurements, data processing, and data analyses can be found in the SI Text.