An integrated catch-and-hold mechanism activates nicotinic acetylcholine receptors

Abstract

In neuromuscular acetylcholine (ACh) receptor channels (AChRs), agonist molecules bind with a low affinity (LA) to two sites that can switch to high affinity (HA) and increase the probability of channel opening. We measured (by using single-channel kinetic analysis) the rate and equilibrium constants for LA binding and channel gating for several different agonists of adult-type mouse AChRs. Almost all of the variation in the equilibrium constants for LA binding was from differences in the association rate constants. These were consistently below the limit set by diffusion and were substantially different even though the agonists had similar sizes and the same charge. This suggests that binding to resting receptors is not by diffusion alone and, hence, that each binding site can undergo two conformational changes (“catch” and “hold”) that connect three different structures (apo-, LA-bound, and HA-bound). Analyses of ACh-binding protein structures suggest that this binding site, too, may adopt three discrete structures having different degrees of loop C displacement (“capping”). For the agonists we tested, the logarithms of the equilibrium constants for LA binding and LA↔HA gating were correlated. Although agonist binding and channel gating have long been considered to be separate processes in the activation of ligand-gated ion channels, this correlation implies that the catch-and-hold conformational changes are energetically linked and together comprise an integrated process having a common structural basis. We propose that loop C capping mainly reflects agonist binding, with its two stages corresponding to the formation of the LA and HA complexes. The catch-and-hold reaction coordinate is discussed in terms of preopening states and thermodynamic cycles of activation.

INTRODUCTION

Nicotinic acetylcholine (ACh) receptor channels (AChRs) are pentameric ligand-gated ion channels (pLGICs) that mediate rapid signaling in the central and peripheral nervous systems. Resting AChRs cannot conduct ions, but active ones have an open channel that readily allows Na⁺ to pass across the cell membrane. Activating ligands (“agonists”) such as the neurotransmitter ACh increase the probability that the protein adopts the ion-conducting conformation and therefore initiate cell depolarization and signaling cascades.

Del Castillo and Katz (1957) proposed a simple reaction sequence for the activation of a neuromuscular AChR by an agonist:

(SCHEME 1)

A is the agonist, R is the protein in its resting (closed-channel) conformation, and R* is the protein in its active (open-channel) conformation. The two steps of this sequence are called “binding” and “gating.” We now know that there are two agonist-binding sites, so this scheme has been modified to include two sequential binding steps followed by a gating step.

Scheme 1 is useful for understanding pharmacological and cellular responses, but a cyclic model for allosteric conformational change provides a more complete basis for understanding the energetics of AChR activation (Karlin, 1967; Changeux et al., 1984; Auerbach, 2012) (Fig. 1 D). The stable R and R* structures each have a characteristic affinity for the agonist and can interconvert even when the binding sites are unoccupied by a ligand (Jackson, 1986; Purohit and Auerbach, 2009). In wild-type (wt) adult mouse neuromuscular AChRs, each binding site has an equilibrium dissociation constant for ACh that is ∼6,000 times lower in R* versus R, and it is this difference in agonist-binding energy that causes the gating equilibrium constant to increase substantially when the neurotransmitter ACh is bound at the transmitter-binding sites. From the logarithm of the equilibrium dissociation constant ratio, we estimate that each transmitter molecule provides approximately −5.1 kcal/mol to power the global gating isomerization (Jha and Auerbach, 2010; Jadey et al., 2011).

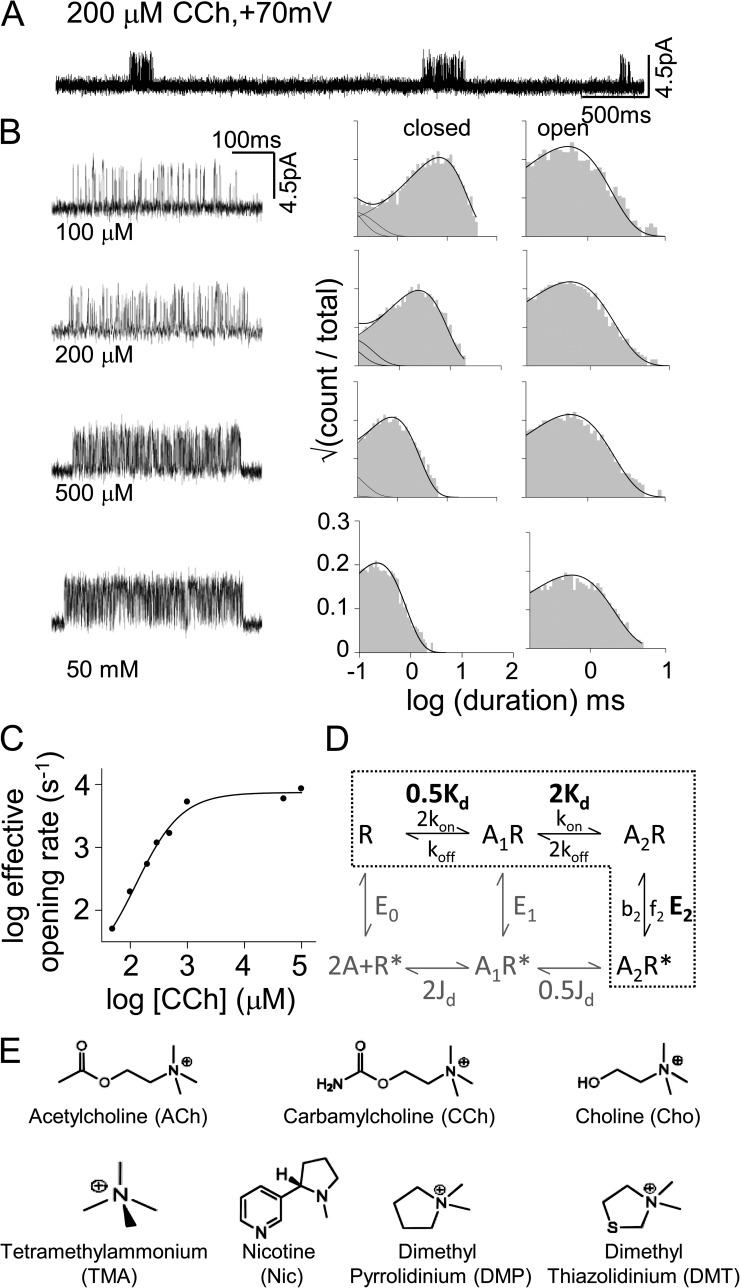
Figure 1.

Activation of AChRs by CCh. (A) Low resolution view of current clusters that reflect binding and gating activity of single AChRs (+70 mV; open is up). (B) Higher resolution view of clusters at different [CCh] and corresponding intra-cluster interval duration histograms. Solid lines are the global fit by boxed states in D. (C) With increasing [CCh], the effective opening rate reaches a plateau that is the diliganded opening rate constant. (D) Cyclic model for binding and gating. R, LA/closed-channel conformation; R*, HA/open-channel conformation; A, agonist; K_d, equilibrium dissociation constant of R; J_d, equilibrium dissociation constant of R*. E₀, E₁, and E₂ are gating equilibrium constants with zero, one, and two bound agonists. When the two binding sites are functionally equivalent, E₂/E₀ = (K_d/J_d)² and E₁/E₀ = E₂/E₁. The rate constants: k_on, LA association; k_off, LA dissociation; f₂, diliganded opening; b₂, diliganded closing. (E) Agonist structures.

Low affinity (LA) agonist binding determines the extent to which a ligand targets the resting receptor, and the switch of the binding site to its high affinity (HA) conformation is a trigger for the full channel-opening isomerization. Several experimental results have led to some assumptions regarding these early stages of receptor activation. First, the LA “on” association rate constant for ACh is ∼10⁸ M⁻¹s⁻¹, so it is often assumed that agonist binding is diffusion limited. Each of the binding pockets is comprised of several loop regions and in the ACh-binding protein (AChBP), a soluble homologue of the AChR extracellular domain; these show an inward displacement (“capping”) when agonists are present (Hansen et al., 2005; Rucktooa et al., 2009; Brams et al., 2011b). A second, common assumption is that loop C capping traps the agonist in the binding site and is the structural correlate of the LA↔HA conformational change of the binding site.

Some experimental results, however, are not consistent with these notions. The “on” rate constant for the partial agonist tetramethylammonium is <10⁷ M⁻¹s⁻¹, which suggests that the entry of this ligand into the resting binding site is not diffusion limited (Zhang et al., 1995). A similar conclusion was reached for agonists of GABA_A receptor channels (Jones et al., 2001). Second, in AChRs having the mutation αG153S (near the binding site), both the “on” and “off” rate constants are highly temperature dependent (Gupta and Auerbach, 2011). The high enthalpy of the LA-binding barrier (∼34 kcal/mol) is evidence that in this construct, this binding process is not by diffusion alone but requires a protein conformational change. Third, for a family of structurally related agonists there is a correlation between apparent affinities and efficacies in GABA_C receptors (Chang et al., 2000). This suggests that in this pLGIC, the processes that underlie LA binding and the LA↔HA conformational switch are not independent, as would be expected if agonist association was diffusion limited. Finally, the association rate constants for ACh are approximately the same for LA and HA binding (Grosman and Auerbach, 2001). This observation is not consistent with the idea that the capped position of the binding site increases affinity by creating a steric barrier with the bulk solution, because closing a lid will keep agonists in but will also keep them out.

To better clarify the nature of the early events in pLGIC activation, we have investigated agonist LA binding and gating rate and equilibrium constants in adult-type mouse AChRs. For a structurally related family of ligands, these constants suggest that LA binding is not by diffusion alone, and that there are protein conformational changes associated with both LA binding (“catch”) and the LA↔HA switch (“hold”). Further, for this agonist series affinity and efficacy are correlated, which indicates that these two conformational changes are not independent.

MATERIALS AND METHODS

Mutagenesis

The QuikChange Site-directed Mutagenesis kit (Agilent Technologies) was used to make mutant cDNAs of mouse AChR α, δ, and ε subunits, and their sequences were verified by dideoxy sequencing. Transient transfection of HEK 293 cells was performed using calcium phosphate precipitation. 3.5 µg of subunit cDNA was added in the ratio 2:1:1:1 (α/β/δ/ε) to each 35-mm culture dish of cells. Cells were incubated for ∼16 h at 37°C and were then washed with fresh media. Electrophysiological recordings (cell-attached patches) were performed ∼20 h after transfection.

Single-channel recording

Single-channel recordings were from cell-attached patches at 23°C. The bath solution contained (in mM): 142 KCl, 5.4 NaCl, 1.8 CaCl₂, 1.7 MgCl₂, and 1 HEPES, pH 7.4. The pipette solution contained the specified concentration of agonist dissolved in Dulbecco’s PBS (in mM): 137 NaCl, 0.9 CaCl₂, 0.5 MgCl₂, 1.5 KH₂PO₄, and 8.1 NaHPO₄, pH 7.4. The cell membrane potential (V_m) was held at +70 mV so the currents were in the outward direction. At this level of membrane depolarization, channel block by the agonist was minimal, and high concentrations of agonist could be used to fully saturate the transmitter-binding sites. The effects of depolarization on the gating constants were compensated for by adding the mutation εS450W (Jadey et al., 2011). The kinetic parameters correspond to wt AChRs at approximately −100 mV.

Single-channel currents were recorded using an Axopatch 200B (Axon Instruments), with analogue low-pass filtering at 20 kHz, and were digitized at a sampling frequency of 50 kHz (NIDAQ; National Instruments). QUB software was used to digitize and analyze the currents (http://www.qub.buffalo.edu). Intervals within clusters (selected by eye) were idealized into noise-free intervals using the segmental k-means algorithm (Qin, 2004). The interval durations were fitted by a C–O–C kinetic scheme by using a maximum interval likelihood algorithm (Qin et al., 1997) with an approximate missed-event correction (dead time = 50 µs). Subsections of these clusters were selected for further analysis by invoking a critical shut time (which varied with the agonist concentration) that removed intervals associated with desensitization.

Equilibrium and rate constant estimation

The equilibrium dissociation constant of the R conformation (K_d = k_off/k_on) and the diliganded gating equilibrium constant (E₂ = f₂/b₂) were estimated by fitting globally intra-cluster interval durations obtained at several different agonist concentrations (see below) by the scheme boxed in Fig. 1 D. k_on is the single-site LA agonist association rate constant, k_off is the single-site LA agonist dissociation rate constant, f₂ is the forward diliganded channel-opening rate constant, and b₂ is the backward diliganded channel-closing rate constant. In our preparation, the two binding sites are approximately equivalent with regard to both the LA and HA equilibrium dissociation constants for ACh and choline (Jha and Auerbach, 2010). The GlyB2 (αG153) mutants were activated by nicotine, and the TrpD (εW55) mutants were activated by ACh.

In all plots, each symbol is the average of two or more patches. The agonist structures are shown in Fig. 1 E. The rate constants and concentrations used for the K_d estimation are shown in Table 1. The equilibrium constants are shown in Table 2.

Table 1.

Activation rate and equilibrium constants for wt AChRs

Agonists	kon	koff	Kd	Concentrations
	mM−1s−1	s−1	M	mM
DMP	1,383	2,838	2.1 E-3	1, 2, 3
DMT	1,991	3,194	1.6 E-3	1, 2, 3
Nic	2,484	2,501	1 E-3	1, 2, 3
TMA	6,770	5,515	0.81 E-3	0.3, 0.5, 0.7
CCh	17,500	7,178	0.41 E-3	0.1, 0.2, 0.3, 0.5
ACh	106,108	17,614	0.16 E-3	0.03, 0.1, 0.3

Concentrations are those used for the estimation of K_d. In all cases, the SEM of the rate constants were <10% of the optimal values shown. k_on, k_off, agonist association and dissociation rate constants to resting receptors; K_d (=k_off/k_on), the LA agonist equilibrium dissociation constant to resting receptors; J_d, the HA agonist equilibrium dissociation constant to open-channel (R*) receptors.

Table 2.

Equilibrium constants for wt AChRs

Agonists	Kd	Jd	E2
	M	M
Choa	4.1 E-3	15.1 E-6	0.046
DMP	2.1 E-3	2.77 E-6	0.38
DMT	1.6 E-3	1.77 E-6	0.58
Nic	1 E-3	0.95 E-6	0.87
TMA	0.81 E-3	0.41 E-6	2.54
CCh	0.41 E-3	0.14 E-6	5.33
ACh	0.16 E-3	2.65 E-8	25.4

See Table 1. E₂, the diliganded gating equilibrium constant.

^aPurohit and Grosman, 2006.

The probability of being open within a cluster (P_o) was calculated as f₂/(f₂ + b₂). f₂ was the high concentration asymptote of the opening rate constant, and b₂ was the closing rate constant at a low agonist concentration where there was no channel block. These curves are equivalent to nonnormalized whole cell dose–response curves with rapid agonist application (without desensitization). The data were fitted by the Hill equation (Table 4).

Table 4.

Dose–response analysis

Agonists	Pomax	EC50	nH
		M
DMP	0.26	67.0 E-4	1.22
DMT	0.40	42.0 E-4	1.35
TMA	0.75	12.0 E-4	1.51
CCh	0.84	32.0 E-5	1.65
ACh	0.96	43.2 E-6	1.96

P_o^max, the maximal response to an agonist; EC₅₀, the concentration of agonist required to produce a half-maximal response; n^H, the Hill slope.

Chemicals

The agonists were purchased (Sigma-Aldrich), except for dimethyl pyrrolidinium tosylate (DMP) and dimethy thiazolidinium tosylate (DMT), which were synthesized as described elsewhere (Jadey et al., 2011).

Analysis of AChBP structures

19 Aplysia californica AChBP structures were analyzed using PyMOL (DeLano Scientific). The distance between residues C190 and (W147) TrpB (αC–αC) was measured using the distance measurement wizard. AChBPs in this analysis were (Protein Data Bank accession nos.): 2WN9, 2WNL, 2BYN (apo-), 2PGZ, 2W8F, 2W8G, 2XYT, 2WNJ, 2BYQ, 2BR7, 3C79, 2BYR, 2XYS, 3GUA, 3C84, 2WNC, 2XZ6, 2XZ5, and 2BYS. We excluded from the analysis AChBPs in which the αC–αC distance was greater than in the apo- structure.

The distances were segregated into clusters iteratively by using the k-means clustering algorithm (MacKay, 2003). The starting assignments were random. The goodness of fit index was the corrected Akaike information criterion (AICc) (Burnham and Anderson, 2002):

$$\text{AICc}=\text{n}\ast \text{ln (RSS}/\text{n})+\text{2k[2k(k}+\text{1})/(\text{n}-\text{k}-\text{1})],$$

where n is the number of distances measurements, k is the number of clusters, and RSS is the residual sum of squares. Software for this analysis (X-means web application) is available at http://www.qub.buffalo.edu.

Single-channel current simulations

Single-channel currents were simulated (by using QUB) at a sampling frequency of 100 GHz using the scheme shown in Fig. 5 A. The shut-interval duration histogram was computed directly from the simulated intervals (there was no idealization). The currents were then digitally filtered at 0.5 GHz and resampled by a factor of 100. These currents were idealized as with the experimental currents (described above); the 1-GHz shut-interval duration histogram pertains to this idealization. These currents were again filtered and resampled by a factor of 5 to generate currents at a 200-kHz sampling frequency. These currents were idealized, and the shut-interval duration histogram pertains to the idealization.

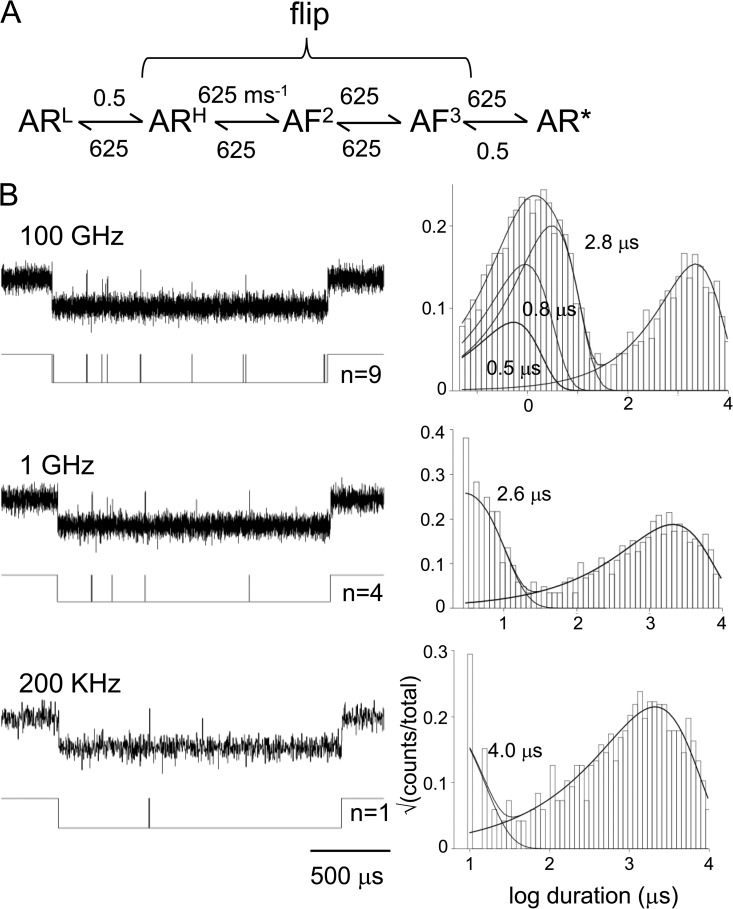
Figure 5.

The relationship between catch-and-hold and preopen states. (A) Scheme 4 was used to simulate single-channel currents. AR^H, AF², and AF³ each had a lifetime of 0.8 µs, and AR^L and AR* (the only open-channel state) had a lifetime of 2 ms. In this model, the forward hold conformational change (AR^L→AR^H) is the first step of a flip sojourn in the entire transition-state ensemble. (B; left) An example burst of openings shown at different sampling frequencies. The idealized current trace (determined after filtering to half of the sampling frequency) is shown below; n is the number of detected shut intervals in each burst. (Right) Shut-interval duration histograms from the idealization. At all sampling frequencies, a long-lived shut component is apparent that corresponds to sojourns in AR^L. The briefer components reflect sojourns in the aggregate [AR^H, AF², AF³] that merge into a single flip event with decreasing sampling rates. At 200 kHz, there is only a single ∼4-µs gap apparent.

RESULTS

An example analysis

Fig. 1 shows the action of the partial agonist carbamylcholine (CCh) on adult mouse neuromuscular AChRs having two wt transmitter-binding sites. Channel openings occurred in clusters that each represent binding and gating activity of a single AChR. The silent intervals between clusters reflect periods when all of the AChRs in the patch are in states associated with desensitization. The time required to bind CCh decreases with increasing agonist concentration, as do the intra-cluster shut-interval durations (Fig. 1 C). At very high concentrations this time is negligible, and the intervals within clusters reflect only the diliganded gating rate constants.

CCh also inhibits current flow by blocking the open pore. To reduce channel block, the membrane was depolarized so that current flowed in the outward direction. Depolarization also alters the gating rate constants, so we compensated for this effect by adding a background mutation (εS450W) that was far from both the binding sites and the pore and that had no effect on agonist binding. The mutation had equal but opposite effects on gating as did depolarization, so the binding and gating rate constants we measured pertain to AChRs at −100 mV (Jadey et al., 2011).

The diliganded gating rate and equilibrium constants were estimated by fitting a kinetic scheme to the open- and shut-interval durations within clusters (boxed in Fig. 1 D). The diliganded gating equilibrium constant for CCh was E₂^CCh ≈ 5.3, which was calculated from the high concentration asymptote of the opening/closing rate constant ratio (8,600/1,600 s⁻¹). The LA equilibrium dissociation constant for CCh (which is not voltage dependent) was estimated by fitting globally intra-cluster–interval durations from currents obtained at several lower [CCh] (Fig. 1 B and Table 1). The value was K_d^CCh ≈ 410 µM, which is the ratio of the single-site agonist dissociation/association rate constants (7,178 s⁻¹/17.4 µM⁻¹s⁻¹).

In the absence of an external energy source, the cyclic reaction scheme of Fig. 1 D requires that the products of the equilibrium constants for the clockwise and counterclockwise paths of the outer cycle are equal:

$${\text{E}}_{\text{2}}/{\text{E}}_0={(K_{\text{d}}/{\text{J}}_{\text{d}})}^{\text{2}}.$$ (1)

E₀ is the unliganded gating equilibrium constant, and J_d is the HA equilibrium dissociation constant. In adult mouse neuromuscular AChRs, E₀ ≈ 7 × 10⁻⁷ (Purohit and Auerbach, 2009; Jha and Auerbach, 2010), so from Eq. 1 and the above estimates of K_d^CCh and E₂^CCh, we calculate J_d^CCh ≈ 0.14 µM. The affinity of each binding site for CCh increases on average by 2,750-fold when the binding site undergoes the LA→HA switch in conformation. Or, each bound CCh molecule on average increases the gating equilibrium constant by −0.59 times the natural logarithm of this factor (−4.7 kcal/mol).

We used the above procedure to estimate binding and gating constants for the structurally related AChR agonists shown in Fig. 1 E (Tables 1 and 2).

LA binding involves a conformational change

Fig. 2 A (Table 1) shows the single-site LA association (k_on) and dissociation (k_off) rate constants (K_d = k_off/k_on) for wt AChRs. For all of the agonists, k_on was less than the diffusion limit, which for these small molecules (at 23°C) might be up to ∼10⁹ M⁻¹s⁻¹ in the absence of an electric field (Berg and von Hippel, 1985). That k_on for all agonists was slower than this limit is not surprising because orientation and desolvation processes can slow ligand association to protein-binding sites. What is notable is that k_on varied substantially among ligands that all have the same charge and were approximately the same size. For example, k_on^CCh is ∼6 times, k_on^TMA is ∼16 times, and k_on^DMP is ∼77 times smaller than k_on^ACh. We think it is improbable that the substantial differences in k_on among these structural-related ligands arise from differences in diffusion, orientation, or desolvation.

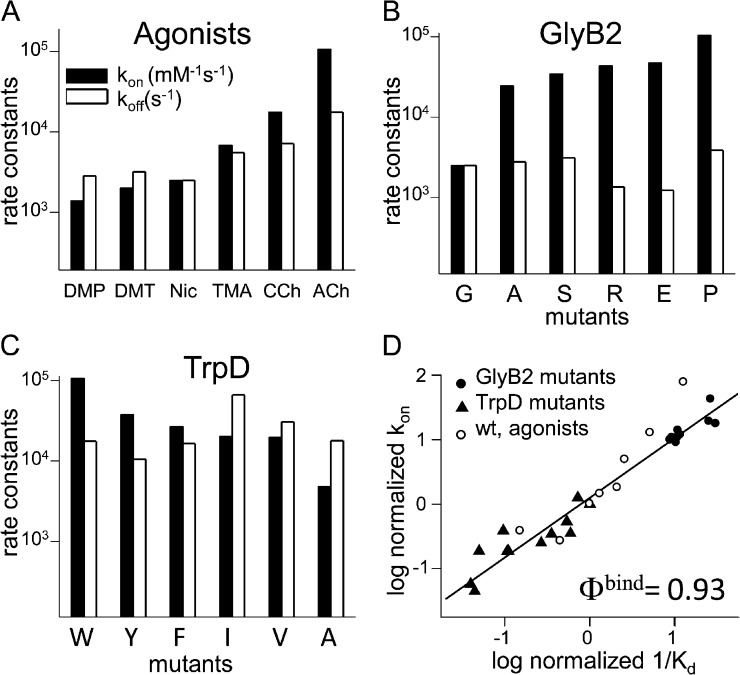
Figure 2.

Rate constants for binding to resting receptors. (A) LA association (k_on) and dissociation (k_off) rate constants for seven different agonists. k_on varies by ∼77-fold even though all agonists have approximately the same diffusion constant. (B) k_on and k_off for AChRs having a mutation of binding site residue GlyB2 (αG153) activated by nicotine (see Fig. 3). (C) k_on and k_off for AChRs having a mutation of binding site residue TrpD (εW55) activated by ACh (Bafna et al., 2009). (D) Rate–equilibrium plot for LA agonist binding. The slope, Φ^bind = 0.93 ± 0.04, indicates that at the binding TS, the agonist is boundlike in energy.

We made mutations to two AChR-binding site residues (see Fig. 3) and measured the ACh “on” and “off” rate constants. Fig. 2 (B and C) shows that all of the tested mutations of GlyB2 (αG153 in mouse AChRs) increased and all of TrpD (εW55) decreased k_on (Table 3) (Bafna et al., 2009). A mutation can induce large-scale changes in the size or charge of the binding pocket. However, the observed pattern is not consistent with an effect of the side-chain substitution on electrodiffusion of the agonist into the binding site. For example, at GlyB2 a large and positively charged Arg substitution caused a greater increase in k_on than Ala, and at TrpD a small Ala side-chain substitution caused a greater decrease in k_on than the larger Ile.

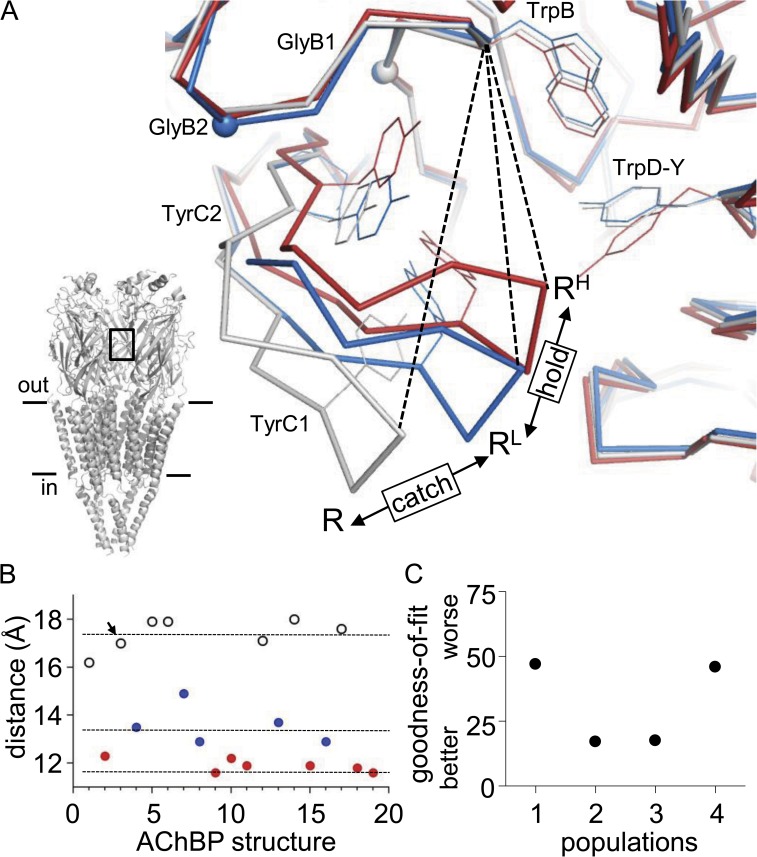
Figure 3.

Analysis of AChBP structures. Cluster analysis of the distances between the αC atoms of C190 (at the tip of loop C) and TrpB in Aplysia AChBPs. The distances were fitted by k clusters. (A) Example AChBP structures. Dashed line is the αC–αC distance. (Bottom) Putative relationship between structures and the catch-and-hold scheme for AChRs. (Inset) Unliganded Torpedo AChR (Protein Data Bank accession no. 2bg9; Unwin, 2005); a transmitter-binding site region is boxed. (B) Scatter plot of the distances, with each structure assigned to one of three populations. The mean ± SD for each population was 17.4 ± 0.5 (white), 13.6 ± 0.7 (blue), and 11.9 ± 0.3 (red) Å. The ligands were (from left to right): 4OH-DMXBA, anabasine, apo- (arrow), cocaine, compound 31, compound 35, d-tubocurarine, DMXBA, epibatidine, HEPES, imidacloprid, methylcaconitine, strychnine, sulfate, thiacloprid, tropisetron, Y53C-MMTS-Apo, Y53C-MMTS-ACh, and lobeline (see Materials and methods for Protein Data Bank accession nos.). (C) Model selection (number of populations) using the AICc goodness-of-fit index. The distribution of distances was optimally described by two or three populations.

Table 3.

Activation rate and equilibrium constants for mutant AChRs

Mutant	k+	k−	Kd	Jd
	mM−1s−1	s−1	M	M
GlyB2a	2,484	2,501	1 E-3	0.95E-6
Aa	24,300	2,776	0.11 E-3	9.6 E-8
Sa	34,300	3,135	0.09 E-3	7.9 E-8
Ra	43,308	1,365	0.03 E-3	2.6 E-8
Ea	47,111	1,234	0.03 E-3	2.6 E-8
Pa	104,001	3,891	0.04 E-3	3.5 E-8
TrpDb	106,108	17,614	0.16 E-3	2.65E-8
Yb	37,357	10,460	0.28 E-3	4.65E-8
Fb	26,612	16,500	0.62 E-3	10.3 E-8
Ib	19,972	66,310	0.33 E-4	0.5 E-8
Vb	19,641	30,640	0.15 E-4	0.2 E-8
Ab	4,783	17,890	0.37 E-4	0.6 E-8

GlyB2 (αG153) mutants were activated by nicotine, and TrpD (εW55) mutants were activated by ACh.

^aUnpublished data.

^bBafna et al., 2009.

The results for both agonists and mutations with regard to LA binding are summarized as a rate–equilibrium plot in Fig. 2 D. This plot illustrates the extent to which a perturbation (mutation or agonist change) alters the “on” versus the “off” rate constant of the binding process. If the perturbations changed K_d only by altering the “on” rate constant, the slope of this plot will be 1. If they change K_d only by altering the “off” rate constant, the slope will be 0. The slope of the plot was 0.93, which indicates that both agonist and side-chain substitutions alter mainly the “on” rate constant. That is, for the agonists and mutations we examined, K_d is determined mainly by k_on. Diffusion-limited rate constants are insensitive to small changes in ligand structure.

From the slope of the rate–equilibrium relationship (Φ^bind) we infer the energetic character of the agonist (or side chain) at the transition state (TS) for LA binding on a scale from 1 to 0. A slope of 1 (only k_on changes) implies that the local structure at the TS for binding was like that of the fully bound state, and a slope of 0 (only k_off changes) implies that this structure was like that of the apo- state (Fersht et al., 1987; Zhou et al., 2005). The result that Φ^bind is ∼0.93 for both agonists and mutations indicates that these perturbations are mostly “boundlike” in energy at the TS for LA binding. Energy and structure are related, so a boundlike energy implies a boundlike structure, and, hence, that there is contact between the agonist and protein at this TS. The high Φ^bind value is evidence that there is a chemical barrier to LA association.

Collectively, the results suggest that targeting of resting AChRs by agonists is an active process that involves, in addition to diffusion, a structural rearrangement of the protein. Temperature studies of LA binding to mutant AChRs provide strong support for this hypothesis (Gupta and Auerbach, 2011). We call the LA conformational change catch and the LA↔HA conformational change hold.

Structural correlates of catch and hold

The ligand-binding sites of AChRs and AChBPs share a common architecture. We attempted to associate the three AChR-binding site conformations inferred from kinetic analyses with structures of Aplysia AChBPs having various ligands at the binding site. The question we asked is, do these structures separate into distinct populations that might correspond to the apo-, LA, and HA conformations of the AChR?

The metric we used to classify AChBP structures was the distance between the αC atoms of (AChBP numbering) cysteine 190 (the tip of loop C) and Trp147 (TrpB, the middle of loop B) (Fig. 3 A) (Brams et al., 2011b). We measured this distance in 19 different Aplysia AChBPs and fitted the values by using a cluster analysis algorithm. Fig. 3 B shows a scatter plot of the distances, and Fig. 3 C shows the goodness of fit as a function of the number of clusters. The distribution of distances was equivalently described by two or three populations. The color code associates each AChBP structure with one of three populations. Most of the AChBPs belonged to the long- or short-distance groups. Five structures were in the intermediate population. The results were the same when the metric was the distance between the αC atoms of TrpB and Y188 (TyrC1) or S189.

The ligands of the long-distance group were apo- (Hansen et al., 2005), Y53C-apo, sulfate, compound 31, compound 35 (Ulens et al., 2009), methylcaconitine (Hansen et al., 2005), and 4-OH-DMXBA. None of these are AChR agonists. Those in the short-distance group were epibatidine, imidacloprid, thiacloprid (Talley et al., 2008), anabasine (Hibbs et al., 2009), Y53C-ACh (Brams et al., 2011a), lobeline (Hansen et al., 2005), and HEPES (Celie et al., 2005). Most, but not all, of these are agonists. In the intermediate-distance group were cocaine, d-tubocurarine, strychnine (Brams et al., 2011b), tropisetron, and DMXBA (Hibbs et al., 2009), which are either antagonists or partial agonists.

Although these results are not conclusive, these assignments are generally consistent with the possibility that in AChBP, loop C can adopt a metastable intermediate conformation that we provisionally associate with the LA-bound conformation of AChRs. We speculate that the three different AChBP conformations correspond to the apo-, LA, and HA states of the AChR and, hence, that capping is in part a structural correlate of both the LA catch and LA↔HA hold conformational changes. If so, the experimental equilibrium dissociation constants for AChBP would be an average arising from binding to multiple structures that are in rapid equilibrium.

LA binding and the LA↔HA switch share a common mechanism

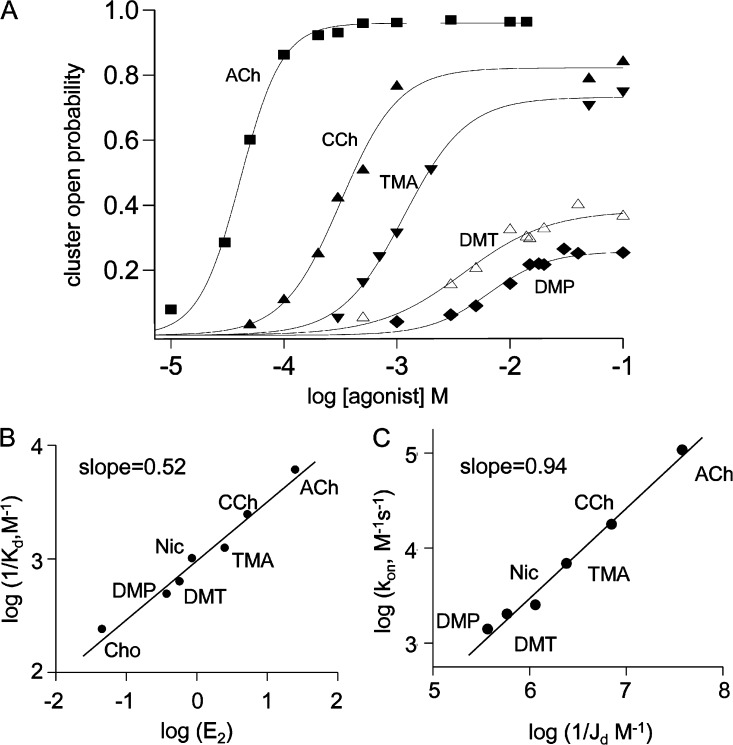
Dose–response curves for several agonists are shown in Fig. 4 A (Table 4). There was an inverse correlation between the maximal response to the agonist (maximum cluster open probability [P_o^max]) and the concentration of agonist required to produce a half-maximal response (EC₅₀). This correlation will not apply in general to all AChR agonists. There are antagonists (weak partial agonists) that have a HA for resting AChRs but a low efficacy, for instance, curare (Trautmann, 1982). However, for the structurally related ligands we examined, the correlation between affinity and efficacy was clear.

Figure 4.

Affinity–efficacy correlation for agonists. (A) The probability of being open within a cluster (P_o) versus agonist concentration. Agonists with higher maximum P_o values have lower EC₅₀ values (Table 4). Agonist structures are shown in Fig. 1 E. (B) Logarithmic plot of 1/K_d (resting affinity) versus E₂ (efficacy). Agonists that open the channel more effectively (have higher E₂ values) also bind to resting AChRs with higher affinity (higher 1/K_d values). Slope = 0.52 ± 0.03, intercept = −3.02 ± 0.03. (C) On a log–log scale, the LA association rate constant (k_on) is closely correlated with the equilibrium constant for HA binding (1/J_d).

Fig. 4 B illustrates this correlation in terms of the binding and gating equilibrium constants that determine the dose–response relationship. A log–log plot of 1/K_d versus E₂ (the diliganded gating equilibrium constant) shows that agonists that bind to resting receptors with a higher affinity (have a higher 1/K_d) also have a higher efficacy (have a higher E₂) (Table 2). For the agonists we examined, the correlation between the logarithms of 1/K_d and E₂ was linear with a slope of 0.52. That is, for these agonists, 1/K_d was approximately proportional to √E₂.

A correlation between binding and gating is not predicted by a view that posits these two processes are completely independent. The logarithm of an equilibrium constant is proportional to the free energy difference between the end states. The linear correlation between log 1/K_d and log E₂ for different agonists indicates that the free energy change of the LA catch conformational change is correlated with that of LA↔HA hold. Energy and structure are related, so this correlation in free energy also indicates that the structural rearrangements that occur in these two processes are related. The correlation would not be expected if LA binding and the LA↔HA switch in conformation arise from independent structural events, for instance, diffusion and capping. Rather, the close correlation between affinity and efficacy implies that binding and the affinity change are two stages of a single integrated process.

Preopen states

The above results suggest the following model of the primary events at each binding site in the presence of agonists:

(SCHEME 2)

The first step (“docking”) is the diffusion of the agonist between the bulk solution and the binding site. A–R is an encounter complex, where the agonist molecule has arrived at a binding site that still has its apo- shape, but the LA complex has not formed. The second step is the LA catch conformational change. R^L represents a binding site that has undergone this rearrangement, and AR^L is the LA complex. 1/K_d is the product of the first two equilibrium constants in Scheme 2, and k_on and k_off are the mean first-passage rates between the A and AR^L states. AR^H is a binding site that has undergone the LA→HA hold conformational change.

We can extend this model into a more complete one for the full gating isomerization of the pentamer. The AChR allosteric transition involves the asynchronous movements of many residues and passage through short-lived intermediate conformations that exist, briefly, between the stable end states R and R*, both with and without agonist at the binding site. An ∼5-µs gap in open intervals of AChR single-channel currents has been interpreted to reflect sojourns in a single such intermediate (Lape et al., 2008). With the incorporation of this intermediate (F, here for “flip”), the model for just the gating step (the second step of Scheme 1) is:

(SCHEME 3)

The LA↔HA affinity conformational change of the binding site occurs in the first step, and the closed↔open conductance change of the pore occurs in the second. Thus, the F state has a HA for agonists and a closed pore, as does AR^H in Scheme 2.

Before the detection of flip, intermediate states in AChR gating were revealed by using Φ-value analysis (Grosman et al., 2000). These experiments suggest that there are (at least) three brief states interposed between AR^L and AR* (Auerbach, 2010; Cadugan and Auerbach, 2010). These, again denoted as F (this time for “Φ”), can be incorporated into a model of the gating isomerization:

(SCHEME 4)

This scheme was proposed (Auerbach, 2005) and discussed (Auerbach, 2010) previously. The first transition is the LA↔HA conformational change. In AR^H (which could also be called AF¹), the agonist is bound with HA and the channel is nonconducting. The pore does not become conducting until the final step of the sequence, so all of the intermediate gating states (within the brackets) are HA and nonconducting, like the AF state of Scheme 3. The experimental forward (backward) channel opening (closing) gating rate constants reflect the mean first-passage rates across the entire state sequence (Fig. 4), and the gating equilibrium constant is the ratio of these aggregate values.

Fig. 5 shows how flip and the states inferred from Φ-value analysis may be related. If the three intermediate states of Scheme 4 each had a lifetime of 0.8 µs, in high resolution patch-clamp recordings they would only appear as a single brief gap with a lifetime of ∼4 µs. We hypothesize that the directly detected flip event reflects the mean first passage across a transition-state ensemble comprised of several brief intermediate states and thus incorporates the hold conformational change.

Schemes 2 and 4 can be combined into a general binding–gating activation sequence for AChRs:

(SCHEME 5)

Only AR* has an ion-conducting channel, and the bracketed states are all HA and nonconducting. The first step is docking, which is the diffusion of the agonist to the binding site, and all of the other steps require a conformational change somewhere in the protein.

Another model for AChR gating that incorporates preopening states and C-loop capping is called “priming” (Mukhtasimova et al., 2009). One motivation for the proposal of this mechanism was the complex interval duration distributions of unliganded gating activity, which show both brief and long open components (Jackson, 1986; Grosman and Auerbach, 2000; Purohit and Auerbach, 2009). The idea is that a capping movement of loop C at each binding site triggers a long-distance transfer of energy (priming) that increases the probability that the distant gate opens. In this model, brief unliganded openings reflect AChRs that are “singly primed” (only one C-loop capped), and the long unliganded openings reflect those that are “doubly primed” (both C-loops capped).

We, too, think that loop C capping is an early event in AChR activation. However, in our view, capping occurs in two stages that each involve interactions with the ligand. The first stage of capping is LA binding, and the second is the LA→HA transition. Evidence suggests that the brief population of unliganded openings, and the standard ones observed in the presence of agonists, reflects the same gating process (rather than singly vs. doubly primed) and can be linked in a thermodynamic cycle (Nayak et al., 2012). In the catch-and-hold model for gating (Scheme 4), there is no requirement for long-range energy transfer. Once loop C has fully capped and the HA conformation (AR^H) has been established, energy is transferred to the gate mainly by local interactions (Auerbach, 2010).

DISCUSSION

The results suggest that the first stages of AChR activation are dock, catch, and hold. This sequence is similar to that proposed for glutamate receptor channels (a tetrameric ligand-gated ion channel), where closure of lobes in the ligand-binding domain triggers the full gating isomerization (Armstrong et al., 1998; Jin et al., 2003). In this receptor, electrophysiological (Robert et al., 2005) and hydrogen–deuterium exchange experiments (Fenwick and Oswald, 2010) indicate that there is an intermediate conformation in the binding–gating process, which has been called a dock–isomerize–lock sequence of events, with only the dock processes being by diffusion. We observe a similar sequence in AChRs and further suggest that the two conformational changes share a common energetic basis.

If we use ∼10⁹ M⁻¹s⁻¹ as the upper limit for ACh diffusion, then k_on^ACh = 10⁸ M⁻¹s⁻¹ implies that each ACh molecule is released from the encounter complex back to the bulk solution up to ∼10 times before it is caught as a LA complex. Assuming that the docking rate constants are approximately the same for all agonists, the experimental k_on values are proportional to the rate constants of the forward catch conformational change. It is likely that different agonists promote (or select) the catch conformation to different extents.

Structural correlates of preopen states

The correlation between resting affinities and gating equilibrium constants indicates that for the agonists we examined, the catch-and-hold structural rearrangements were related energetically. We tentatively associate these energy changes with the structural differences apparent in AChBP structures and speculate that capping of the binding site occurs both in catch and in hold. The correlation between affinity and efficacy excludes the possibility that the HA form of the binding site is generated exclusively by structural elements that are completely independent of those that generate the LA complex.

Based on the putative R and R* structures of two prokaryote pLGICs (Hilf and Dutzler, 2008; Bocquet et al., 2009), we can associate provisionally the steps in Scheme 4 with specific structural changes in the AChR. Φ-value analysis of AChR gating (Auerbach, 2010) suggests that the first step in Scheme 4 (hold) reflects conformational changes of about a dozen residues in the vicinity of the binding sites, including in loops A, B, C, and D. Loop C capping is part of, but not all of, the AR^L↔AR^H conformational change. Away from the binding site there are also early energy changes in residues near the C terminus of the αM2 helix (the αM2 “cap”) (Bafna et al., 2008). It is not known whether or not these two widely separated regions change energy independently or if they are coupled. Regarding the remaining steps of Scheme 4, Φ values and pLGIC structures together suggest the following sequence of structural events in the AChR α subunit. AR^H↔AF² is an anticlockwise concerted twist of the extracellular domain β sandwich and a downward motion of loop 2. AF²↔AF³ is an upward movement of the M2–M3 linker and a radial tilting of the pore-lining M2 helix away from the channel axis that perturbs putative “gate” residues at 16–17′. AF³↔AR* may reflect the wetting of a hydrophobic section of the pore, between M2 residues 9′and 16′ (Jha et al., 2009). We think that the flip event represents the passage through all of these structural intermediates and not just loop C capping.

The energy correlation between catch and hold offers an explanation of how capping and the binding rate constants may be related. There is a strong correlation between an agonist’s LA “on” rate (k_on) and its HA equilibrium association constant (1/J_d) (Fig. 4 C). Agonists that promote (or select) catch effectively favor hold, which is an event that triggers the full gating isomerization. We speculate that without agonists wt AChRs open rarely because water supports a small equilibrium constant for catch, and therefore for hold and, hence, for channel opening.

The energy relationship between AR^L and AR^H suggests that the converse is also true: anything that promotes hold (for example, mutations) will also promote catch. Adopting the fully open AR* conformation favors hold, which in turn will favor the probability of catch. Rather than a simple lid closure, we hypothesize that agonists associate rapidly to fully open AChRs because having the hold conformational change in place increases the forward rate constant (and decreases the backward rate constant) of catch. This mechanism accounts for the observation that the ACh “on” rate constant increases when the hold position is adopted.

Thermodynamic cycle

Finally, the integrated catch-and-hold sequence can be incorporated into a standard thermodynamic cycle. The main assumption in this analysis is that the energetic consequences of the binding site perturbations have only local effects. That is, we interpret the observed changes in K_d (relative to a reference condition) for different side chains or ligands only to reflect changes in the catch equilibrium constant (A–R↔AR^L in Scheme 5) and not that for diffusion-limited “dock.” Similarly, we assume that the binding site perturbations only change the hold equilibrium constant (AR^L↔AR^H in Scheme 5) and none of the others contained within flip. With this assumption, we can relate the observed changes in K_d and E₂ caused by the binding site perturbations specifically to energy changes in the catch or hold processes.

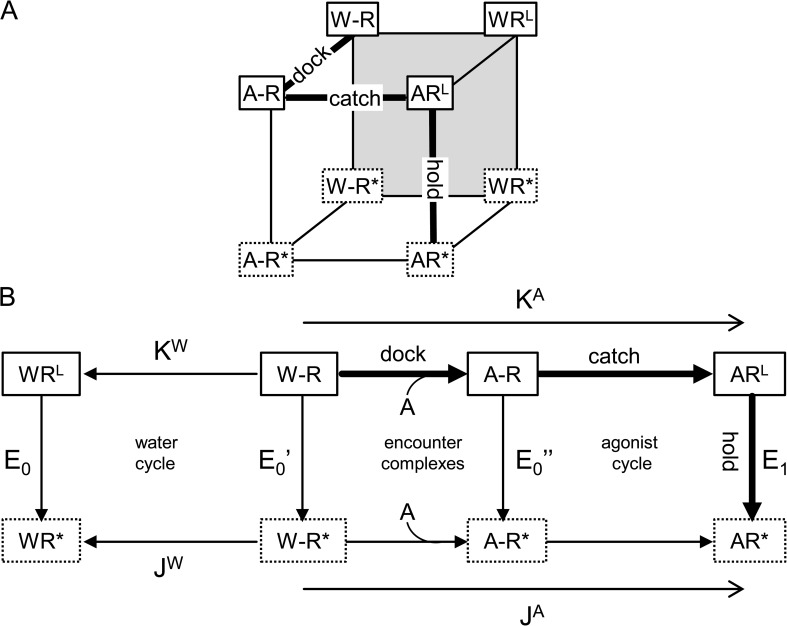
In Fig. 6 A, dock, catch, and hold events at the binding site are represented as dimensions of a cube. The front plane represents catch-and-hold activation by an agonist (Fig. 6 A, A), and the back plane is catch and hold in water only (W), where W–R is the resting apo- receptor that is equivalent to state R in the standard cycle for AChRs (Fig. 1 D). On the front plane, A–R is neither catch nor hold, AR^L is catch only, AR* is both catch and hold, and A–R* is a complex of unknown affinity that is hold only. The only state that is difficult to imagine is A–R*. We think this conformation is an AChR having all of the residues around the binding site (loops A, B, D, and elsewhere) in their “active” positions, but with loop C uncapped.

Figure 6.

Incorporating dock, catch, and hold into a thermodynamic cycle. (A) Each of the three processes is a dimension of the cube. Dock is by diffusion alone, and both catch and hold require a protein conformational change. The scheme pertains only to events related to agonist binding rather than the full gating isomerization; states boxed with dotted lines lead directly to open-channel R* states. Front plane, catch and hold with agonists; backplane (gray), catch and hold with water only; left plane, encounter complexes. W–R corresponds to R in the scheme shown in Fig. 1 D. Thick lines represent the main dock–catch–hold activation sequence. (B) If agonists (A) and water (W) exchange only at encounter complexes, the cycle is 2-D. K and J are the LA and HA equilibrium association constants (forward direction given by arrow). There are three kinds of unliganded openings: after catch (E₀) or with either water or agonist in the encounter complex (E₀′ and E₀″). From detailed balance, E₁/E₀ = λ^A/λ^W, where λ = K_d/J_d.

The cube can be reduced to a simpler 2-D cycle if we make the reasonable assumption that agonists exchange with water only at an encounter complex (Fig. 6 B). We can relate the states of the model for agonist binding to the constants derived from single-channel currents, with each of the vertical hold conformational changes associated with an experimental gating equilibrium constant. The equilibrium constants of the 2-D model are as follows (forward direction defined by the arrows). K is the equilibrium association constant when hold has not taken place. As discussed above, for agonists, K is the product of the docking and the catch equilibrium constant in the absence of hold. J is the equilibrium association constant after hold has taken place. The magnitude of J is also the product of docking and catch equilibrium constants, but in this case when the hold conformational change has occurred. The superscripts A and W refer to these constants in the presence of agonists and water. E₁ is the gating equilibrium constant with one agonist, after catch. The model predicts two open states for gating in water only, one after catch (E₀), and one pre-catch (E₀′). As discussed in the first paragraph of this section and in Scheme 4, we assume that the hold conformational change of the binding site is the first step of the channel-opening process. Open intervals arising from unliganded AChRs exhibit multiple open components (Jackson et al., 1990; Grosman and Auerbach, 2000), but it remains to be explored if these components do or do not correspond to those predicted by the scheme in Fig. 6 B.

Balancing the outer cycle, K^AE₁ = K^WE₀J^A/J^W or E₁/E₀ = (J^A/K^A)/(J^W/K^W). We define λ = J/K (=K_d/J_d), so E₁/E₀ = λ^agonists/λ^water. The energy supply for gating from an agonist is log(λ_A) − log(λ_w). For a series of agonists, the offset energy from water is a constant. Considering just the agonist cycle, λ^A = E₁/E₀″. Considering just the water cycle, λ^W = E₀/E₀′. Hence, λ^A/λ^W = (E₁/E₀)(E₀′/E₀″). From the balance of the outer cycle, we know that the second term of this equation must equal 1. Hence, we conclude that the equilibrium constant for the hold conformational change is the same regardless of whether water or an agonist occupies the encounter complex.

The integrated catch-and-hold mechanism is consistent with a standard thermodynamic cycle for activation. It will be interesting to learn the values of the correlation between affinity and efficacy for other agonists. Measurements of this correlation in AChRs with mutations of binding site amino acids may help unravel the events that constitute the critical initial stages of receptor activation.