Modulation of enrofloxacin binding in OmpF by Mg²⁺ as revealed by the analysis of fast flickering single-porin current

Abstract

One major determinant of the efficacy of antibiotics on Gram-negative bacteria is the passage through the outer membrane. During transport of the fluoroquinolone enrofloxacin through the trimeric outer membrane protein OmpF of Escherichia coli, the antibiotic interacts with two binding sites within the pore, thus partially blocking the ionic current. The modulation of one affinity site by Mg²⁺ reveals further details of binding sites and binding kinetics. At positive membrane potentials, the slow blocking events induced by enrofloxacin in Mg²⁺-free media are converted to flickery sojourns at the highest apparent current level (all three pores flickering). This indicates weaker binding in the presence of Mg²⁺. Analysis of the resulting amplitude histograms with β distributions revealed the rate constants of blocking (k_OB) and unblocking (k_BO) in the range of 1,000 to 120,000 s⁻¹. As expected for a bimolecular reaction, k_OB was proportional to blocker concentration and k_BO independent of it. k_OB was approximately three times lower for enrofloxacin coming from the cis side than from the trans side. The block was not complete, leading to a residual conductivity of the blocked state being ∼25% of that of the open state. Interpretation of the results has led to the following model: fast flickering as caused by interaction of Mg²⁺ and enrofloxacin is related to the binding site at the trans side, whereas the cis site mediates slow blocking events which are also found without Mg²⁺. The difference in the accessibility of the binding sites also explains the dependency of k_OB on the side of enrofloxacin addition and yields a means of determining the most plausible orientation of OmpF in the bilayer. The voltage dependence suggests that the dipole of the antibiotic has to be adequately oriented to facilitate binding.

INTRODUCTION

Antibiotics have to penetrate the outer membrane to enter Gram-negative bacteria. One possible pathway is the diffusion through the lipid phase (Ribeiro et al., 2011), especially for the hydrophobic first-generation quinolones (Delcour, 2009). However, the outer membrane also contains a plethora of channel-forming proteins called porins. Recent studies on multidrug resistance revealed modified porin patterns in the outer membrane. Resistant cells were found to reduce the number, to show mutated porins, or to express different porins (Pagès et al., 2008). These findings suggested that a reduced permeation through porins is one possible contribution to drug resistance and motivated studies on interactions between antibiotics and porins (James et al., 2009; Tran et al., 2010).

Here, the major outer membrane protein F (OmpF) isolated from Escherichia coli is in the focus (Nikaido, 2003) because it is suggested that newer, more hydrophilic quinolones like enrofloxacin use OmpF as an entrance to the cell interior (Delcour, 2009). OmpF forms a homotrimer, and each monomer forms a channel (pore) consisting of a 16-stranded antiparallel β-barrel (Cowan et al., 1992). At the periplasmic side, the β-strands are connected by short turns, and at the extracellular side they are connected by long loops. Loop 3 (L3) is folded back into the pore and constricts its size (Cowan et al., 1992). Molecules smaller than ∼600 D can pass the pore such as ions, carbohydrates, amino acids (Nikaido, 2003; Delcour, 2009), and small antibiotic molecules (Mortimer and Piddock, 1993).

Antibiotics interact with affinity sites in the pores of OmpF, thus transiently blocking the pathway and causing fluctuations of the measured ionic current. Molecular dynamic (MD) simulations (Mahendran et al., 2010a) have shown that each monomeric pore of OmpF has two binding sites for enrofloxacin called Mini Above at the external side of the constriction zone formed by L3 and Mini Below at the periplasmic side (see Fig. 5). Enrofloxacin is a fluoroquinolone and inhibits the activity of bacterial DNA gyrase (Lizondo et al., 1997). In the case of enrofloxacin (Mahendran et al., 2010a) or HPA3P, an analogue of the antimicrobial peptide HP(2–20) (Apetrei et al., 2010), the residence time at the OmpF binding site is in the millisecond range, leading to clear transitions between the current levels in the open and in the blocked state. In contrast, most other antibiotics bind very weakly to OmpF or OmpC. This leads to residence times in the range of 100 to 200 µs. In the case of weak binding, blocking by the antibiotic is indicated by short spikes, increased noise, or reduction of the apparent ionic current (Mahendran et al., 2010b). In that case, unphysiologically high concentrations of the antibiotics can be used to increase the number of transitions into the blocked state and thus to make them more obvious.

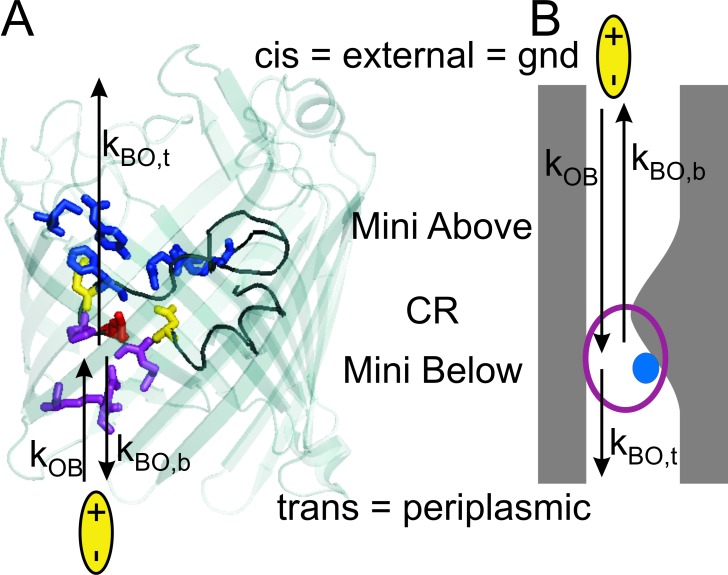
Figure 5.

Definition of the rate constants of blocking (k_OB) and unblocking (k_BO) under the assumption that the location of Mg²⁺ as found in crystal structure also applies to the electrophysiological studies here (Yamashita et al., 2008). The assignment periplasmic = trans results from the most plausible interpretation of the difference in accessibility described in Figs. 8 and 9 for the dominant F+ type insertion (flickering at positive potentials). (A) Crystal structure obtained by Yamashita et al. (2008). (PDB code 2ZFG, the water-coordinated Mg²⁺, and two detergent molecules have been removed for clarity.) Enrofloxacin (yellow bipolar ellipse) is given at the periplasmic side. Here, the issue of coloring the involved residues is showing the association of residues to the binding domains; thus, conventional coloring of amino acids has not been used. The binding domain of the (H₂O)₆-coordinated Mg²⁺ ion, including the residues D113, E117 (yellow), and L115 (red), is on the L3 loop (black) of the constriction zone CR. Residues on L3 are also involved in the periplasmic bindings site Mini Below for enrofloxacin (purple and red). The binding site Mini Above (blue) does not play a role in the fast blocking events investigated here. (B) For the definition of the rate constants that are involved when enrofloxacin is given at the external side, a cartoon is used. It highlights those features of the Ompf structure in A which are important for the understanding of the fast flickering events. The blue sphere presents (H₂O)₆-Mg²⁺, and the purple ring the binding site Mini Below.

Here, we demonstrate that the information about a fast blocking process can also be obtained at concentrations of the antibiotic below 1 mM if the noisy time series of the ionic current is analyzed by β distributions. We have investigated the fast-flickering binding of enrofloxacin to OmpF which occurs in the presence of Mg²⁺. Mg²⁺ itself has only a small influence on ionic current. In our experiments, addition of 5 mM MgCl₂ resulted in an increase of current of ∼10%, as expected from the increase in conductivity of the medium (unpublished data). The presence of Mg²⁺ has been selected for several reasons: first, the plasma concentration of Mg²⁺ in humans is 0.4 to 0.8 mM (Wang et al., 2002). The concentration here (5 mM) is higher than that in the plasma, but this concentration has been chosen to make the effects more obvious for a biophysical analysis. Second, in the presence of Mg²⁺, the crystal structure of OmpF shows an additional electron density arising from a (H₂O)₆-coordinated Mg²⁺ ion near D113, L115, and E117 in the L3 loop (Yamashita et al., 2008) which overlaps with the periplasmic binding domain Mini Below for enrofloxacin comprising M114, L115, and P116 on the L3 loop and Q262, R270 on the pore wall (Mahendran et al., 2010a). Mg²⁺ has been found nowhere else in the structure. If we assume that these findings of crystal structure analysis also apply to electrophysiological experiments, the presence of Mg²⁺ can help to discriminate between the periplasmic and the external binding site and reveal further details of the periplasmic site. Third, this region on L3 is of special interest as the removal of the negative charge by the point mutation D113N reduces the strong binding of enrofloxacin to OmpF, leading to shorter residence times in the range of 100 µs (Mahendran et al., 2010a). Fourth, the interpretation of the results can benefit from the knowledge of the crystal structure of OmpF obtained at 1.6-Å resolution (Yamashita et al., 2008). Together with the MD simulations of Mahendran et al. (2010a), this structure provides a molecular background for the interpretation of the electrophysiological results.

The experimental access for studying these binding phenomena is provided by the blocking-induced modulation of the ion current through the three pores of the trimeric porin. In contrast to the previously analyzed slow block in the absence of Mg²⁺ (Mahendran et al., 2010a), the flickery block in the presence of Mg²⁺ consists of blocking events shorter than the temporal resolution of the recording apparatus (5-kHz 4-pole Bessel filter). Thus, they cannot be observed as transitions between states of high and low conductivity in the time series of single-porin current but only as increased noise of the high-conductance state. The clue for the analysis of fast blocking processes is provided by this increase in open-pore noise and a reduction of the apparent open-pore current. The excess noise is evaluated by fitting the broadened and often non-Gaussian amplitude histograms by means of so-called β distributions (FitzHugh, 1983; Yellen, 1984; Sigworth, 1985; Heinemann and Sigworth, 1991; Weise and Gradmann, 2000; Schroeder and Hansen, 2006, 2009a,b; Abenavoli et al., 2009). In this analysis, the unavoidable low-pass filter of the recording set-up is not viewed as a nasty obstacle but as a part of the evaluation process as it converts short open times into current values (Hansen et al., 1997). The method yields the rate constants of the open-blocked transitions and the true single-pore current.

MATERIALS AND METHODS

OmpF was purified from E. coli by H. Weingart (Jacobs University, Bremen) with the final solution containing 1 mg/ml in 1% Octyl-(polydisperse)oligooxyethylene (Octyl-POE; Garavito and Rosenbusch, 1986). Enrofloxacin (Fluka Analytical) was dissolved in 100 mM KCl, 5 mM MgCl₂, and 5 mM HEPES, pH 7.0, to a concentration of 2 mM. This stock solution was added to the experimental buffer solution in appropriate amounts to create final concentrations of 0.1, 0.3, or 0.4 mM enrofloxacin.

The experimental set-up

The bilayer experiments were performed by the so-called solvent-free method (Montal and Mueller, 1972). In brief, two Teflon chambers were sealed together by silicone and separated by a 25-µm-thick Teflon foil (Goodfellow). The Teflon foil contained a 60–120-µm circular aperture and was pretreated with 1% hexadecane in hexane. After the hexane had evaporated, the chambers were filled with 2 ml buffer (100 mM KCl, 5 mM MgCl₂, 5 mM HEPES, pH 7). In this study, we used symmetric lipid membranes consisting of uncharged diphytanoylphosphatidylcholine (DPhPC; Avanti Polar Lipids, Inc.) as well as asymmetric membranes containing negatively charged lipopolysaccharides (LPSs) on the trans side, and on the cis side a mixture of phosphatidylethanolamine (PE) from E. coli, phosphatidylglycerol (PG) from E. coli, and cardiolipin (diphosphatidylglycerol, DPG), with the ratio PE/PG/DPG being 81:17:2. LPS was extracted from the E. coli strain WBB01 by the phenol/chloroform/petroleum ether method (Galanos et al., 1969), purified, and afterward lyophilized at the Research Center Borstel. The concentration of LPS dissolved in chloroform/methanol (9:1; Merck) was 2.5 mg/ml Lipids (Avanti Polar Lipids, Inc.) were dissolved in chloroform (2.5 mg/ml).

10 µl of the phospholipid solutions was added to the buffer surfaces on each side of the chamber. For asymmetric membranes, LPS was added only at the trans side. After the organic solvent had evaporated, the membrane could be formed by lowering and raising the buffer levels. For OmpF insertion, <1 µl of a stock solution of 1 mg/ml was diluted by a factor of at least 100,000. Starting with a minimum amount of 0.1 µl of the diluted solution, OmpF was always added on the cis (ground) side until the electrical activity of one porin could be observed. In the case of the asymmetric membranes, the cis (uncharged) side is the side from where OmpF also enters the bacterial membrane. We found that it did not insert from the LPS side. The time intervals between the additions were at least 3 min.

Single-trimeric porin currents were measured by an Axopatch 200B amplifier (Molecular Devices) connected to Ag/AgCl electrodes (World Precision Instruments). The electrode on the trans side was connected to the amplifier. The cis side was connected to ground. The signal was filtered by a 5-kHz four-pole low-pass Bessel filter and sampled at 50 kHz using a Digidata 1322A digitizer and pClamp 10.0 software (Molecular Devices). All measurements were performed at 37°C. During the experiments water evaporation was negligible as measured by conductance.

Determination of the noise

The knowledge of the rms of the baseline noise (σ) is crucial for the analysis. However, because of the extremely high open probability of OmpF, the baseline was never visible. Instead, the noise of the Gaussian distribution of time series measured at the same bilayer either at the same voltage without enrofloxacin or at negative potentials with enrofloxacin on the cis side was used. The absence of contributions from blocking-induced noise in these records was verified by the finding that all three observable levels, I₁, I₂, and I₃, could be fitted with Gaussian distributions of equal width (see Fig. 6 A). This baseline noise was σ = 2.1 pA ± 0.2 pA (n = 47) and was determined for each individual dataset.

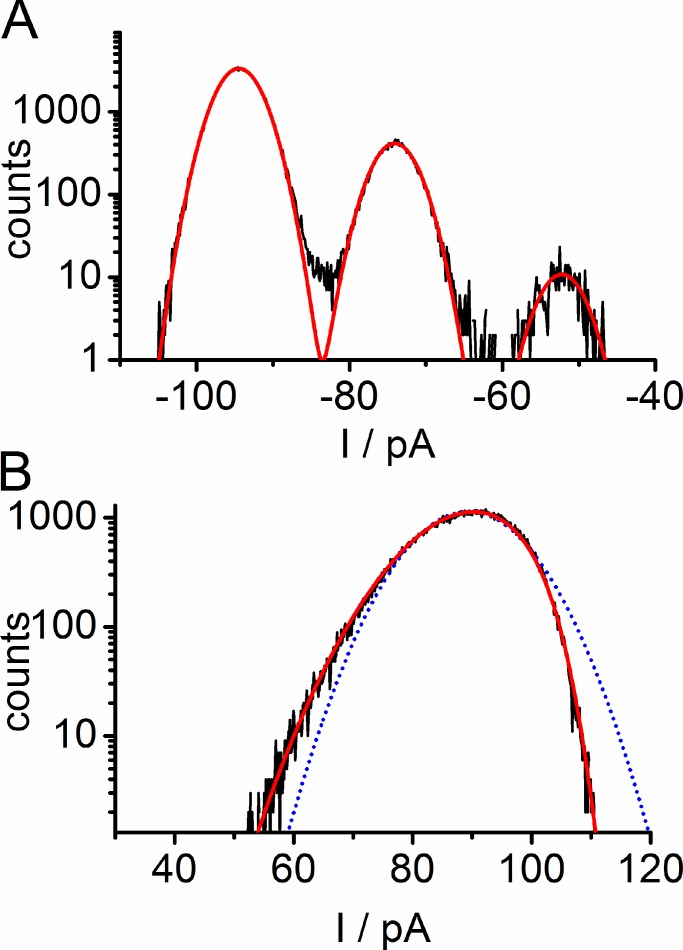
Figure 6.

Examples for fitting of amplitude histograms in the presence of 0.3 mM enrofloxacin on the cis side in an LPS membrane. Data are taken from Fig. 4 B. (A) Successful fitting of Gaussians (red) to an all-point amplitude histogram with slow blocking measured at −100 mV resulting in σ₀ = 2.6 pA and an estimated single-pore current I_app = 20.8 pA. (B) Failure of fitting an open-point histogram measured at +100 mV by a Gaussian distribution (blue dotted line). Successful fitting of the data with a β distribution (red solid line) resulting in I_true = 22.7 pA, I_B = 12 pA, k_OB = 20 700 s^-1, and k_BO = 67 000 s^-1 (Eq. 1, Figs. 1 C and 5).

Analysis: fitting amplitude histograms

When individual blocking or gating events can no longer be resolved in a time series, the amplitude histograms can be evaluated. They are fitted by means of β distributions as has been described in previous papers (Schroeder and Hansen, 2006, 2007, 2008, 2009a,b). The method applies when open-point histograms show broadening with respect to the baseline noise and/or are non-Gaussian (see Figs. 4, 6, and 7). Both phenomena indicate unresolved fast blocking or gating events. In brief, before starting the fit, the program KielPatch was used to extract the partial amplitude histogram of the largest open-level current (I₃) from time series of 4–60-s length (i.e., 200,000 to 3,000,000 sampling points). This so-called open-point histogram included fast flickering events and excluded the (rare) slow events (Schröder et al., 2004).

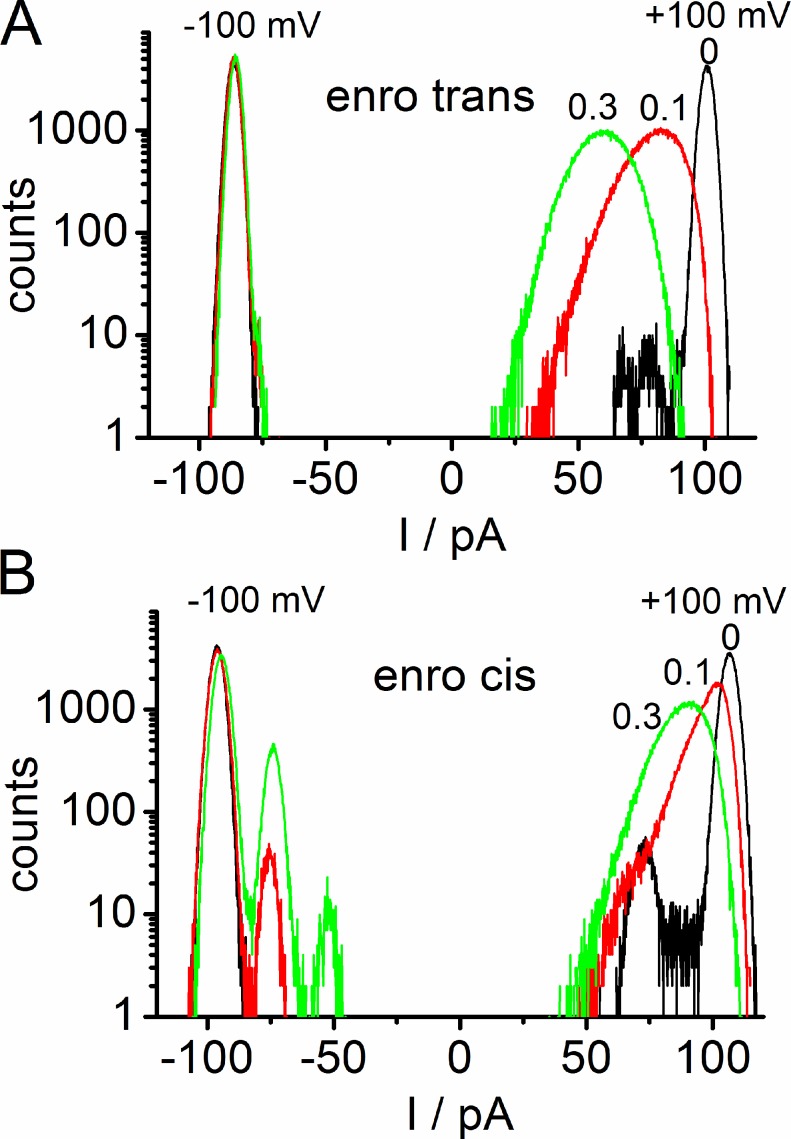
Figure 4.

Amplitude histograms from representative time series of OmpF in an asymmetrical LPS membrane similar to those in Fig. 2 with enrofloxacin given on the trans side (A) and the cis side (B) at −100 mV and +100 mV. Black lines are the controls with zero enrofloxacin, red with 0.1 mM enrofloxacin, and green with 0.3 mM enrofloxacin.

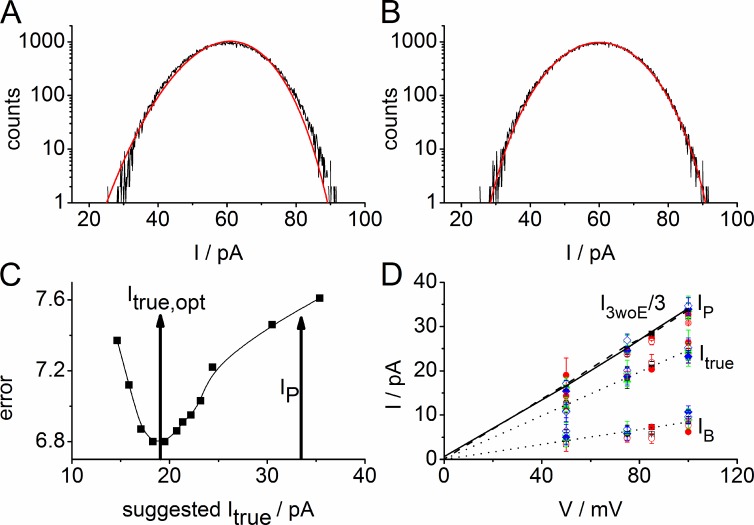
Figure 7.

Illustration of the determination of the amplitude of flickering single-pore current I_true (= the difference between the total current of state O (I_P) and of state B (I_B), I_true = I_P − I_B, see Fig. 1 C). (A and B) Effect of the choice of single-pore current, I_true, on the quality of the fit with β distributions. Open-point histogram of a time series recorded at +100 mV with 0.3 mM enrofloxacin on the trans side of an LPS membrane similar to that in Fig. 2 G. (A) Failure of the best fit with I_B = 0, I_true = 34.9 pA, equal to I_P = 1/3 of the total current obtained when all three pores are open in the absence of enrofloxacin (Fig. 2 E). (B) Successful fit of the same data with I_B = 8.3 pA, I_true = 22.8 pA, k_OB = 45,600 s⁻¹, and k_BO = 46,950 s⁻¹. (C) Dependence of the error sum on the value of the single-pore current I_true used in the fitting routine (for another example in LPS than in B). The optimum value obtained from the best fit is at I_true,opt = 19 pA, I_B = 8.4 pA. I_p = 33.5 pA marks the value obtained from records in the absence of enrofloxacin. Data from a single experiment at +100 mV with 0.3 mM enrofloxacin on the trans side. (D) IV curves of I_B and I_true obtained from β fits. The dotted lines present linear fits. The sum I_P = I_true + I_B should theoretically coincide with I_3woE/3 (Fig. 1 C) of the control measurements without enrofloxacin (I_3woE/3 in DPhPC: solid line; LPS: dotted line, obtained from averaging over data like those in Fig. 3). Assignment of the symbols: open for LPS membranes, closed for DPhPC membranes. Black squares: 0.1 mM enrofloxacin on the trans side; red circles: 0.3 mM trans; green triangles: 0.1 mM cis; blue diamonds: 0.3 cis. The same symbols are used for I_B, I_true, and the sum I_P. There is no significant influence of the concentration, side of addition, or membrane composition on I_B and I_true; all symbols overlap. Shown are two to five experiments per point with a total of 79 experiments. Error bars represent standard deviation.

For the analysis, a theoretical amplitude histogram had to be fitted to the measured amplitude histogram. The theoretical amplitude histogram was generated from a time series of flickering current by simulations on the basis of three identical copies of a two-state Markov model (see Eq. 1 and Fig. 1 C) and afterward convoluted with a Gaussian distribution representing baseline noise of adequate width (i.e., with the σ determined as described in the previous section). During the fit, the rate constants of the Markov model for the simulated time series were modified under the control of a simplex algorithm (Caceci and Cacheris, 1984) in the laboratory-made program bownhill, whereas the current levels (I_true and I_B, Fig. 1 C) were iteratively suggested in a dialog until a minimum error was found (see Fig. 7 C). Simulations had to be used for the generation of the theoretical histograms because there is no simple analytical approach for the calculation of β-distributions of higher order Bessel filters (Riessner, 1998). Shot noise resulting from the discrete nature of the electrical charge could be ignored (Schroeder and Hansen, 2009b). The programs KielPatch and bownhill are available at http://www.zbm.uni-kiel.de/aghansen/software.html.

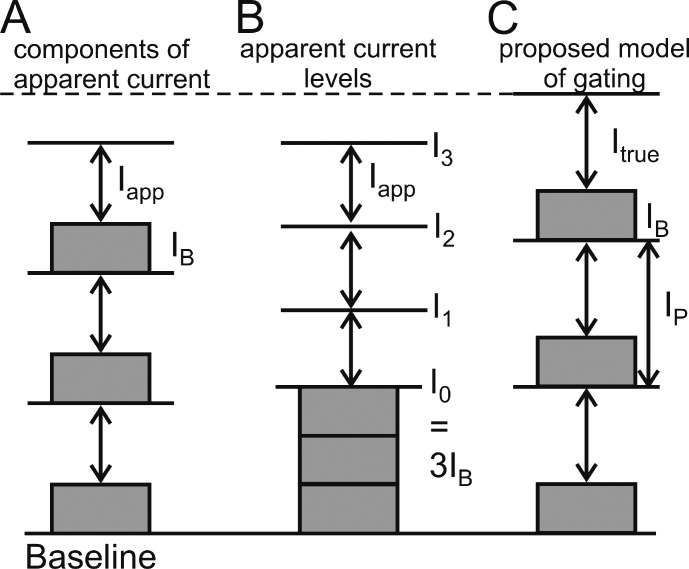
Figure 1.

Definitions of current components used in data analysis. (A) Contribution of the constant (I_B) and flickering components (I_app) of each pore to the measured single-porin current. (B) Illustration of the levels I₀ to I₃ observable in a measured time series. (C) Scenario used for fitting amplitude histograms. I_p is the sum of I_B and the true (reconstructed by fitting) single-pore current I_true.

Analysis: definition of currents

The study of transport of enrofloxacin here is more difficult than in the case of canonical ion transport. Because the primary transportee (the antibiotic) is zwitterionic under the conditions here (Lizondo et al., 1997), it does not contribute to electrical current. Instead, the measured current is carried by smaller ions, and transport of enrofloxacin has to be estimated from the modulation of this current as caused by the binding of enrofloxacin to the pore (Mahendran et al., 2010a). Here, we concentrate on the binding kinetics of enrofloxacin as obtained from the measured current and not on the net transport of the antibiotic.

Modeling the flickering currents in OmpF is also different from that of gating in ion channels (e.g., in the BK channel; Schroeder and Hansen, 2007, 2008) in two other aspects. First, as a result of the trimeric nature of OmpF, the theoretical curves are generated from a superposition of three identical models of fast flickering single-pore current. All models had the same rate constants and current levels (Fig. 1 C). Second, in each pore there is one state of high conductivity (O, open = unblocked) and one state of low conductivity (B, blocked), which turns out not to be zero in the analysis described in the Results section entitled Enrofloxacin blocks only 3/4 of the ionic current in the case of fast blocking. Thus, the canonical symbol C (closed) as used for modeling of ion channels is replaced by B (blocked). Because of this, single-pore current consists of two components: the constant current I_B of the blocked state and a flickering component I_app, (Fig. 1 A). In the measured time series, the constant components of the three pores cannot be distinguished. Thus, the lowest level observable in the presence of enrofloxacin is I₀ = 3 I_B (Fig. 1 B). In the flickering part of the porin current, a superposition of the three currents I_app can lead to four observable levels: I₀, I₁, I₂, and I₃, depending on the number of pores in the open state (Fig. 1 B). In the experiments here, the open probability is so high that mostly I₃ and rarely I₂ can be observed (Fig. 2). The flickering component is called I_app (apparent) because its original (true) value, I_true, is attenuated because the unavoidable low-pass filter of the set-up averages over the current values in the open and blocked state.

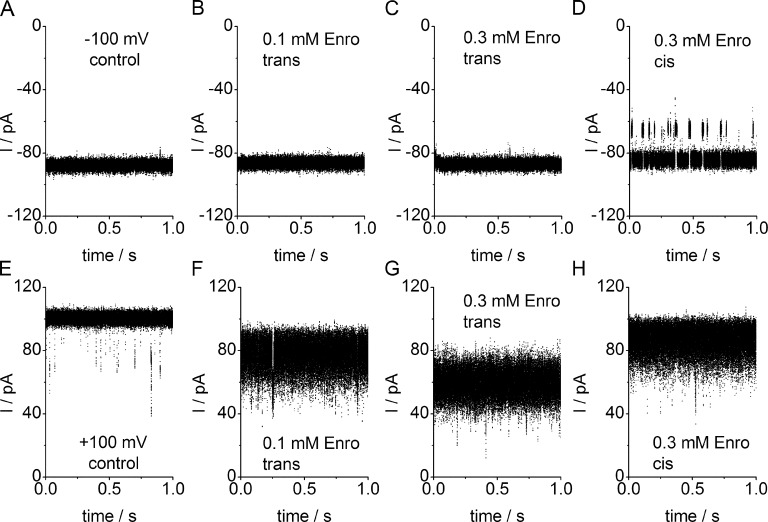
Figure 2.

Representative sections of current traces of a single OmpF porin recorded at −100 mV (A–D) and +100 mV (E–H) measured in an asymmetrical LPS membrane. Traces were obtained without antibiotic (A and E), with 0.1 mM (B and F) and 0.3 mM enrofloxacin (C and G) on the trans side and 0.3 mM enrofloxacin on the cis side (D and H). The level of full current (all three pores open) is not affected in the presence of enrofloxacin at negative potentials (B–D), regardless of whether it is applied at the trans (B and C) or cis (D) side. At +100 mV, enrofloxacin causes apparent current reduction and a strong increase in noise which is smaller when given at the cis side (H) than at the trans side (F and G). Enrofloxacin given at the cis side at −100 mV causes pronounced slow blocking events (D). All measurements of this and the following graphs were performed at 37°C.

The determination of I_app needs some comments. The amplitude histogram obtained from flickering time series (as in Fig. 2) normally is not Gaussian. Thus, the peak of the distribution is quite different from what the experimenter would intuitively consider the middle of the broad noisy current level. Furthermore, this value strongly depends on the low-pass filter of the set-up. I_app reaches an asymptotic constant value, when the filter frequency is low enough (Schroeder and Hansen, 2008). Thus, it is determined here from the peak of the nearly Gaussian distribution obtained after averaging >200 sampling points.

For the understanding of the biophysics of the process, the true flickering current I_true (Fig. 1 C) is relevant. I_true could be observed directly if the temporal resolution were high enough (for a proper definition of I_true see Hansen et al., 2003). Increasing temporal resolution has succeeded in the case of the Cs⁺ block in Chara (Draber and Hansen, 1994), but here flickering is too fast and has to be evaluated by means of β distributions.

RESULTS

Induction of fast blocking events (ion current flickering) in the single-porin current by enrofloxacin in the presence of Mg²⁺

Fig. 2 shows time series of single-porin ion current measured in an LPS membrane at −100 mV and +100 mV with no antibiotic or with enrofloxacin given at the trans or cis side, respectively. At negative membrane potentials, enrofloxacin has no measurable effect on the current level and on the open-pore noise (Fig. 2, B–D). Slow blocking events at negative voltages occur only when enrofloxacin is given at the cis side (Fig. 2 D). The slow block corresponds to the behavior in the absence of Mg²⁺ and has been analyzed previously (Mahendran et al., 2010a). Thus, it is not investigated here in more detail.

The remarkable effect occurs at positive membrane potentials, i.e., the induction of excess open-pore noise in the presence of enrofloxacin. This coincides with a reduction of the apparent open-pore current amplitude (Fig. 2, F–H as compared with E). The effect is strongest when enrofloxacin is given on the trans side (Fig. 2, F and G). When enrofloxacin is given on the cis side the current reduction is less pronounced (Fig. 2 H). As shown in more detail in Fig. 8 (A and C) and Table 1, the effect of 0.3 mM cis (Fig. 3 H) is similar to that of 0.1 mM trans (Fig. 2 F).

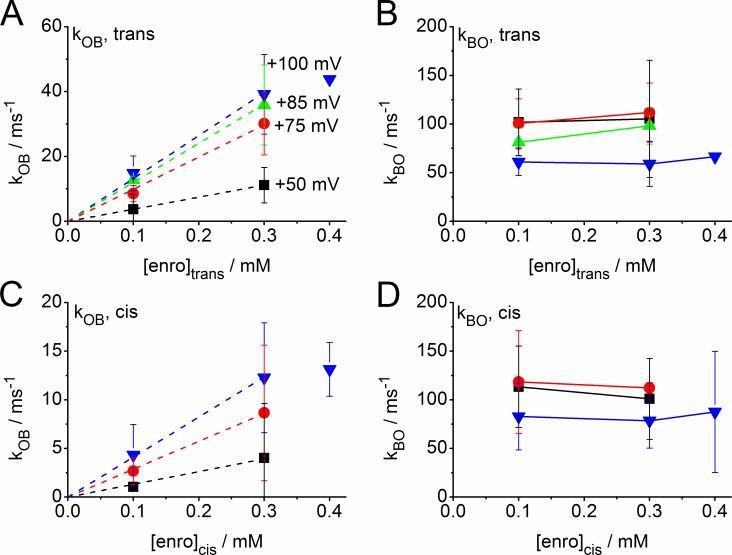
Figure 8.

Dependence of the rate constants (Eq. 1) of fast blocking on the concentration of enrofloxacin given at the trans side (A and B) or cis side (C and D). k_OB (A and C) is the rate constant of blocking (binding of antibiotic) and k_BO (B and D) of unblocking (dissociation of the antibiotic from the protein). Black squares: +50 mV; red circles: +75 mV; green upright triangles: +85 mV; blue inverted triangles: +100 mV. Dashed lines in A and C are linear fits through the origin. For the sake of clarity, the datasets from LPS and DPhPC membranes were pooled, and the symbols show mean and standard error. A separate presentation for both membrane types is given in Fig. 9 and Table 1, where the number of experiments is also given.

Table 1.

 Normalized rates (r_OB = k_OB/enrofloxacin concentration) for various transmembrane voltages

Enrofloxacin concentration/bilayer type	rOB 1/(mM × ms) at +100 mV	rOB 1/(mM × ms) at +75 mV	rOB 1/(mM × ms) at +50 mV
0.1 mM trans DPhPC	164 ± 82 (3)	78 ± 16 (2)	38 ± 24 (3)
0.3 mM trans DPhPC	119 ± 45 (2)	88 ± 29 (2)	37 ± 30 (2)
0.1 mM trans LPS	150 ± 33 (4)	99 ± 35 (2)	43 ± 5 (2)
0.3 mM trans LPS	147 ± 43 (3)	121 ± 34 (2)	46 ± 4 (2)
mean trans	148 ± 48 (12)	96 ± 28 (8)	41 ± 17 (9)
0.1 mM cis DPhPC	32 ± 9 (4)	22 ± 9 (2)	11 ± 4 (4)
0.3 mM cis DPhPC	35 ± 19 (5)	33 ± 30 (3)	13 ± 12 (2)
0.1 mM cis LPS	48 ± 16 (5)	37 ± 16 (2)	10 ± 4 (4)
0.3 mM cis LPS	54 ± 16 (5)	38 ± 17 (2)	11 ± 4 (4)
mean cis	46 ± 25 (19)	32 ± 19 (9)	11 ± 5 (14)

The same data is shown as in Fig. 8 (A and C). In parentheses: number of experiments.

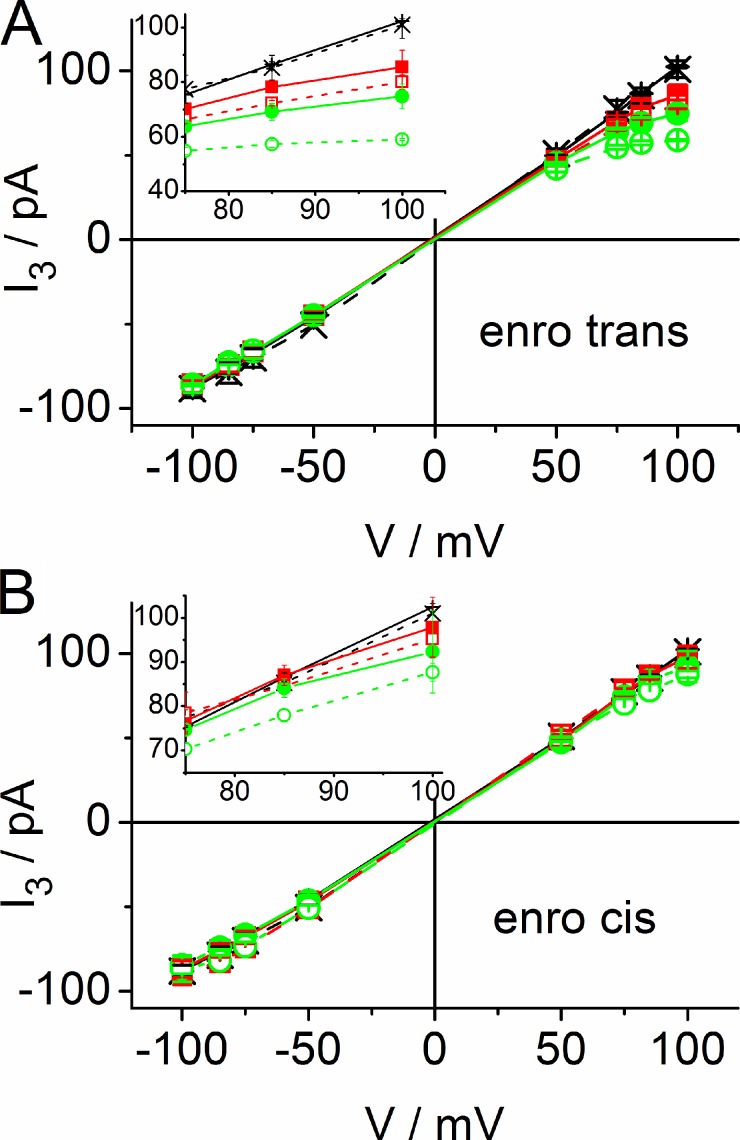
Figure 3.

IV curves of apparent single-OmpF current I₃ (sum of the three monomer currents) in the absence of the antibiotic (black crosses) and with enrofloxacin given at the trans side (A) and the cis side (B) at 0.1 mM (red squares) and 0.3 mM (green circles). LPS: open symbols and dashed lines; DPhPC: filled symbols and solid lines. The insets provide an enlarged presentation of the range where the IV curves differ. Data points are shown as mean and standard error, n = 2–9 per symbol, with a total of 199 current traces.

The scenario (type F+ = flickering at positive membrane potentials) shown in Fig. 2 was found in 10 out of 11 OmpFs inserted in LPS membranes and in 6 out of 9 OmpFs inserted in DPhPC membranes. The other type (F− = flickering at negative potentials) showed the same behavior as the F+ type when membrane potential was inverted and cis and trans were exchanged. From this finding, we concluded that OmpF can insert in different orientations into the membrane but that the F+ type is preferred, especially in asymmetric LPS membranes. We exploited this asymmetric occurrence of flickering (and a concomitant slight asymmetry in the IV curves without enrofloxacin, see means obtained from Fig. 3) to ensure that all channels investigated here have a single (F+ type) orientation.

In Fig. 3, the IV curves of the F+ type are shown for the apparent current I_app in LPS and DPhPC membranes with I_app being determined as described in Materials and methods. As a result of the high open probability of OmpF, they present the current at level 3 (I₃, all three pores open). There is no difference in the conductivity of the two different membrane types in the absence of enrofloxacin. The IV curves in the absence of the antibiotic are almost linear (black symbols in Fig. 3) with the current at −100 mV being ∼15% smaller (I₃ = −88.0 ± 3.4 pA, n = 3 experiments in DPhPC, and −88.2 ± 5.4 pA, n = 8 in LPS) than compared with that at +100 mV (I₃ = 102.4 ± 0.8 pA, n = 3 in DPhPC, and 101.5 ± 5.0 pA, n = 8 in LPS). This results in a first estimate of apparent single-pore currents (I₃/3 = 1/3 single-porin current) of −29.4 pA and 34 pA for −100 mV and +100 mV, respectively. However, these values have to be further analyzed in terms of the definitions given in Fig. 1. The interpolated values between −50 mV and +50 mV have been verified by voltage ramp protocols (unpublished data).

In the presence of enrofloxacin, the IV curves of the F+ type become sublinear at positive potentials according to the decrease in current as found in Fig. 2 (F–H). The effect is more pronounced when enrofloxacin is given at the trans side (Fig. 3 A) as compared with the cis side (Fig. 3 B). Furthermore, the effect is slightly stronger in LPS membranes (dashed lines with open symbols) than in DPhPC membranes (solid lines with filled symbols). Even though this difference is hardly greater than the error bars, it gets further support from the kinetic analysis described in the Results section entitled The rate constants of the enrofloxacin-induced fast blocking events. At −100 mV, the current I₃ in Fig. 3 is not significantly influenced by the presence of enrofloxacin or by the type of membrane (without: −88.0/−88.2 pA in DPhPC/LPS (n = 3/8), 0.3 mM trans: −86.2 ± 4.5 pA (n = 2) in DPhPC, −85.9 ± 0.8 pA (n = 3) in LPS, 0.3 mM cis: −87.0 ± 4.9 pA (n = 2) in DPhPC, and −86.6 ± 7.9 pA (n = 5) in LPS).

Amplitude histograms of the enrofloxacin-induced flickery block

As mentioned, flickering faster than the corner frequency of the recording set-up leads to averaging over open and blocked events decreasing the amplitude of the recorded signal. The resulting distortions of the open-point amplitude histogram (broadening and skewness) provide the key for revealing the original parameters of this fast process (Hansen et al., 1997; Schroeder and Hansen, 2006, 2009a). Thus, the analysis by means of β distributions starts from amplitude histograms like those in Fig. 4, which are created from time series of the F+ type shown in Fig. 2.

At negative potentials, enrofloxacin added at the trans side has no significant effect on the shape of the amplitude histogram (Fig. 4 A, left). Furthermore, the levels I₂ to I₀ are absent, corresponding to Fig. 2 (A–C). In contrast, enrofloxacin given at the cis side at negative potentials leads to the appearance of the conductance levels I₂ (2 pores open) and, very rarely, I₁ (1 pore open) in Fig. 4 B (left). The events related to evel I₁ in Fig. 4 B are not obvious in the trace of Fig. 2 D because their occurrence is <1% of that of I₃. Subtracting three times the difference I₃ − I₂ from I₃ (I₃ − 3 I_app in Fig. 1, A and B) leads to a mean value of I₀ = 20.6 ± 8.4 pA (n = 4) for 0.3 mM and 20.5 ± 0.7 pA (n = 3) for 0.1 mM enrofloxacin on the cis side. This nonzero value of I₀ (corresponding to 3 I_B in Fig. 1 B) indicates that the pores are not closed completely during enrofloxacin-induced blockage. However, the slow block as found at negative potentials (Fig. 2 D) has already been described by Mahendran et al. (2010a) and thus it is not discussed here in detail.

The interesting effects occur at positive potentials when fast flickering is induced. Corresponding to the noisy records and the apparent reduction of the current level (Fig. 2, F–H), the amplitude histograms in the presence of enrofloxacin become skewed and broadened (Fig. 4, A and B, right).

The kinetic model and the orientation of OmpF

As mentioned in Materials and methods, the theoretical amplitude histograms used for fitting have to be created from simulated time series on the basis of an adequate model. A two-state Markov model (Eq. 1) has been found to be sufficient to adequately fit the open-point histograms of I₃ (all three pores open):

$$B\underset{k_{OB}}{\overset{k_{BO}}{\rightleftharpoons }}O.$$ (1)

The definitions of the rate constants are illustrated in Fig. 5, A and B using two different representations of OmpF. For Fig. 5 A, the crystal structure of a single pore of the trimeric OmpF has been used (Yamashita et al., 2008), showing the two binding sites on either side of the constriction zone CR which is formed by the L3 loop (black; Mahendran et al., 2010a). Using PyMOL (DeLano Scientific, version v0.99), the β sheets of OmpF have been made transparent to open the view on the binding sites for (H₂O)₆-coordinated Mg²⁺ (yellow: D113, E117; red: L115; Yamashita et al., 2008) and for enrofloxacin at the periplasmic Mini Below (red: L115; purple: M114, P116 and Q262, R270) and at the external Mini Above (blue: Y32, M38, R82, F118, and R132). The residues D113 to F118 are located on L3.

In the binding domain Mini Above, the negative carboxylic end of enrofloxacin binds to R132 and R82. The antibiotic anchors in hydrophobic pockets at residues M38, F118 and the positive end is at Y32 (Fig. 4 in Mahendran et al., 2010a). In Mini Below, the negative carboxylic end forms hydrogen bonds with R270, Q262, and H-C bonds are formed with M114, P116, and L115 (Fig. 7 in Mahendran et al., 2010a). Important for the investigations here is the overlapping of the binding sites for (H₂O)₆–Mg²⁺ and those for enrofloxacin at Mini Below in the range of D113 to E117 on the L3 loop of the constriction zone. In Fig. 5 B, the structure of OmpF is given as a cartoon highlighting those parts of the OmpF structure, which are important for the discussion of the results reported below.

Fig. 5 A shows the rate constants of enrofloxacin binding to the periplasmic binding site for the case that enrofloxacin is added at the periplasmic side and Fig. 5 B for addition at the external side. The electrophysiological studies cannot distinguish between the off-rate constants k_BO,t, which leads to translocation (t) through the membrane, and k_BO,b, which brings enrofloxacin back (b) to the solution where it came from. Thus, the analysis in the next section only yields k_BO = k_OB,t + k_OB,b. An approach to calculate the fluxes from these rates constants has been suggested by Mahendran et al. (2010a).

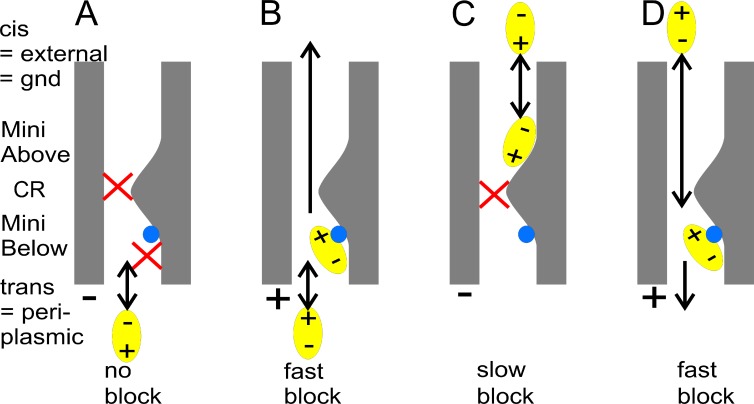
The orientation of OmpF in artificial bilayer membranes is still under discussion (for references, see the Discussion). Here, the suggestion that trans = periplasmic for the F+ type orientation as presented in Fig. 5 is based on the study of the accessibility of the binding sites. As considered in more detail in the Discussion, the validity of this assignment depends on whether the results from crystal structure analysis (Yamashita et al., 2008) and MD simulations (Mahendran et al., 2010a) also apply to the electrophysiological data here. However, keeping this caveat in mind we tentatively describe the results on the basis of the model in Fig. 5. For this model, we have to combine the following findings obtained for the dominant F+ type insertion: (1) Mg²⁺ interferes with Mini Below at the periplasmic side (Fig. 5 A; Yamashita et al., 2008); (2) flickering is related to the presence of Mg²⁺ (it is absent in experiments without Mg²⁺, Mahendran et al., 2010a); (3) flickering only occurs at positive membrane potentials (Fig. 2, F–H); (4) flickering is stronger when enrofloxacin is given at the trans side (compare Fig. 2, F and G vs. Fig. 3 H, and see evaluation of Fig. 8, A and C); and (5) in the presence of Mg²⁺, slow gating only occurs at negative potentials when enrofloxacin is given at the cis side.

Finding 3 yields a plausible suggestion for the orientation of OmpF when enrofloxacin is added on the cis side because orientation by positive potentials is required to pass the constriction zone from the external side (carboxyl group first, MD simulations of Mahendran et al., 2010a; see also Fig. 10 D). Item 4 leads to the conclusion that the lower binding rate of enrofloxacin from the cis side (details in Fig. 8, A and C) results from the necessity that enrofloxacin has to pass the constriction zone to reach Mini Below. Item 5 indicates that Mini Above can easily be reached from the cis side at negative potentials but not from the trans side, as it is hindered to pass the constriction as a result of the wrong orientation by the electric field. Collectively, these considerations lead to the assignments shown in Fig. 5 A, i.e., cis = external and trans = periplasmic in the experiments evaluated here. Nevertheless, the validity of this conclusion depends on the premise that the results of crystal structure analysis (Yamashita et al., 2008) also apply to the electrophysiological studies here. A more reliable approach based on the accessibility of blockers to adequately located mutations as used by Heginbotham et al. (1999) for KcsA in bilayers has not succeeded so far for OmpF because the porin lets agents up to 600 D pass the pore (Nikaido, 2003; Delcour, 2009).

Figure 10.

Schematic presentation of the effect of voltage (A and C: −; B and D: + at the trans side) and of the side of enrofloxacin addition (A and B: trans; C and D: cis) on the accessibility of the binding site Mini Below (purple in Fig. 5) for enrofloxacin. The blue sphere indicates the presence of (H₂O)₆-Mg²⁺. The cartoons are made for the dominant F+ type insertions (flickering at positive potentials) under the assumption that the location of Mg²⁺ found in crystal structure analysis (Yamashita et al., 2008) also applies to the electrophysiological studies used here.

Evaluation of fast gating by β distributions

In Fig. 6 A, it is shown that the amplitude histograms related to slow blocking (data from Fig. 4 B, −100 mV, 0.3 mM enrofloxacin at the cis side) can very well be fitted by Gaussian distributions of equal width (this is used for the determination of baseline noise σ), whereas such a fit is not possible at positive potentials in the presence of enrofloxacin (Fig. 6 B, blue dotted curve). However, a fit by a β distribution based on three identical two-state models (Fig. 1 C and Eq. 1) is successful (Fig. 6 B, red solid curve). For all cases, the two-state model of Eq. 1 has been found to be sufficient because analysis with a higher number of states (Schroeder and Hansen, 2009a) has not improved the quality of the fit.

Enrofloxacin blocks only 3/4 of the ionic current in the case of fast blocking

Experiments with planar lipid bilayers suffer less from leakage currents as compared with giga seals of patch pipettes. Thus, the analysis of the data with enrofloxacin by means of the scenarios in Figs. 1 and 5 yields a surprising result: the simple approach with I_B = 0, i.e., that enrofloxacin blocks the ion flow completely, leads to a failure of the fitting routine (Fig. 7 A). Instead, it has consistently been found that good fits can be achieved only when the B-O model (Eq. 1) is forced to switch the conductivity of the pore between ∼25 and 100% of the full conductivity (Fig. 1 C; and Fig. 7, B and C). Thus, the current I_B of the blocked state is not zero. Consequently, four parameters have to be determined from the β fits: the rate constants k_BO and k_OB, the current of the blocked state (I_B), and the amplitude (I_true) of the flickering current in the presence of enrofloxacin.

The values of I_B and I_true are shown in Fig. 7 D. The individual data points present averages over measurements with enrofloxacin given at the cis and trans side at concentrations from 0.1 to 0.3 mM. The symbols for the individual conditions (type of membrane, side of application, concentration of enrofloxacin) can hardly be distinguished in the graph. This is just the message, namely, that I_B and I_true do not significantly depend on these conditions. Averaging over all conditions in Fig. 7 D by means of the fitted linear lines yields the following conductivities: g(I_B) = 84 ± 3 pS and g(I_true) = 246 ± 2 pS (error of the fit), which implies that I_B is 25 ± 7% of I_P = I_B + I_true, the full current (Fig. 1 C), with the error being the averaged relative rms over all conditions.

The reliability of the fits is indicated by the fact that the sum of I_B + I_true = I_P (obtained in the presence of enrofloxacin) perfectly matches the line given by the single-pore current as estimated from dividing level I_3woE in time series without enrofloxacin (woE) by 3. The ratio 3I_P/I_3woE is 1.00 ± 0.05 as obtained from all 91 records with enrofloxacin.

The rate constants of the enrofloxacin-induced fast blocking events

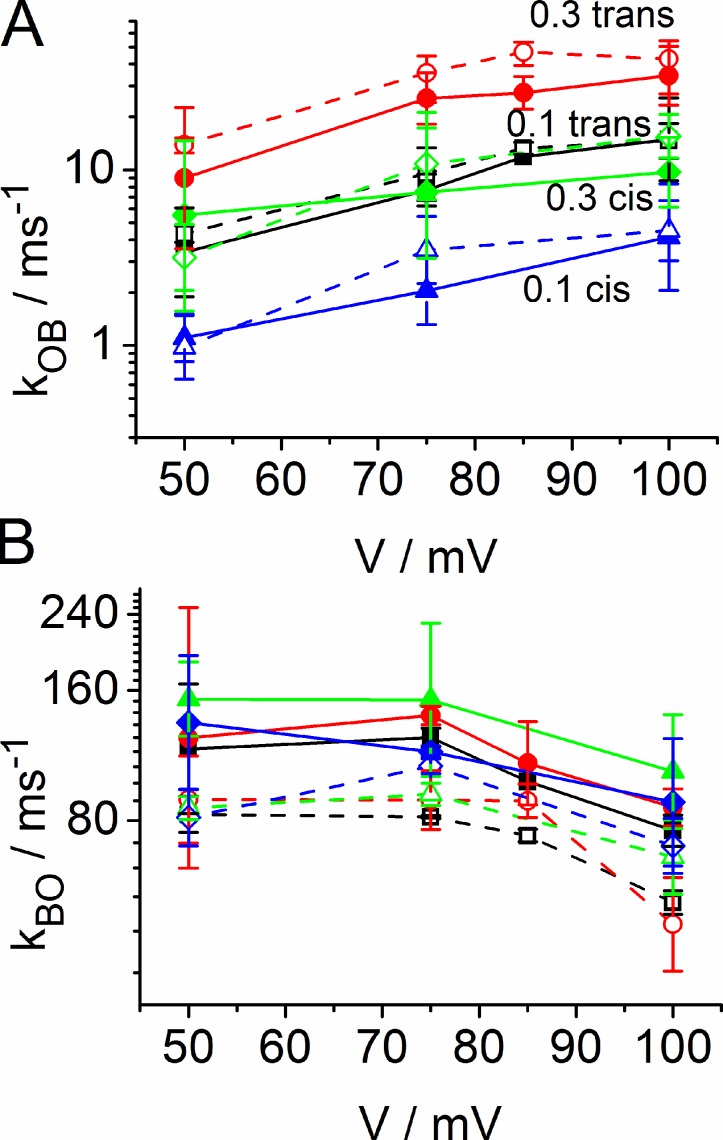
The analysis of the fast blocking events (Figs. 6 and 7) induced by enrofloxacin at positive membrane potentials by means of the simple B-O model of Eq. 1 leads to the rate constants of blocking, k_OB, and unblocking, k_BO (Fig. 5, A and B). For the sake of clarity, the rate constants from LPS and DPhPC membranes are pooled in Fig. 8. This is legitimate because of the small difference, which becomes obvious from the separate presentations in Table 1 and in Fig. 9.

Figure 9.

Voltage dependence of the rate constants of blocking (A, k_OB) and unblocking (B, k_BO) of the enrofloxacin-induced fast block (same set of experiments as in Fig. 8 and Table 1). Open symbols and dashed lines present data from LPS, and closed symbols and solid lines those from DPhPC. Red circles: 0.3 mM enrofloxacin trans; black squares: 0.1 mM trans; green diamonds: 0.3 mM cis; blue triangles: 0.1 mM cis. Symbols show mean and standard error, and the number of experiments is given in Table 1.

The rate constant of unblocking, k_BO, does not significantly depend on the concentration of enrofloxacin (Fig. 8, B and D) as expected for a dissociation of the antibiotic from the protein. The mean value obtained from averaging over all conditions is k_BO = 99,000 ± 38,000 s⁻¹.

The rate constant of blocking (i.e., binding), k_OB, increases with the concentration of enrofloxacin in the investigated range (Fig. 8, A and C). The concentration dependence of the effect on k_OB is similar when enrofloxacin is given on the cis or trans side. However, there is a remarkable difference: the curves in Fig. 8 C (cis) only coincide with the corresponding curves in Fig. 8 A (trans) when the rate constants, k_OB, are multiplied by a factor of 3.2. Thus, enrofloxacin given at the cis side is about threefold less effective than that given at the trans side.

Linearity up to 0.3 mM is indicated by the fact that the data can be fitted by a line through the origin. Furthermore, for all conditions the normalized rate k_OB,0.1mM/0.1 mM, is about equal to k_OB,0.3mM/0.3 mM, for all membrane potentials within the scatter (Table 1). This constant ratio (as well as the linear fit through zero by the dotted lines in Fig. 8) verifies a linear relationship between blocking rate constant k_OB and enrofloxacin concentration up to 0.3 mM. The ratios are not significantly different for LPS and DPhPC. It remains to be elucidated whether the single data point at 0.4 mM enrofloxacin in Fig. 8 indicates the beginning of saturation.

To provide more information for the discussion of the voltage dependencies of k_OB and k_BO, the same data in Fig. 8 is presented separately for LPS and DPhPC in Fig. 9. In the case of k_OB, there is a clear voltage dependence, but no significant difference between LPS and DPhPC.

In contrast to k_OB, the rate constant k_BO of unblocking seems to be quite independent of the enrofloxacin concentration and of the side of the application. There seems to be a slight dependence on membrane potential. Even though the scatter per data point is high, the parallel behavior of eight curves is convincing. Interestingly, the clouds of values obtained from LPS (dotted lines with open symbols in Fig. 9 B) and DPhPC (solid line in Fig. 9 B) are clearly separated. As a result of the parallel shift of the curves, the difference can be presented by a mean value for all concentrations and potentials: k_BO,DPhPC = 115,000 ± 42,000 (n = 55), k_BO,LPS = 76,000 ± 18,000 (n = 42).

DISCUSSION

The investigations here show that the analysis by β distributions has the power of resolving residence times of ∼10 µs (k_BO up to 120 ms⁻¹ in Figs. 8 and 9). This is a factor of 20 above the corner frequency of the experimental set-up and indicates that β distributions are an adequate means of resolving fast blocking events in porins. The necessity of such a gain in temporal resolution becomes obvious, for example, from the study of temperature dependence of ampicillin binding to OmpF (Mahendran et al., 2009). At higher temperatures, the rate constants could not directly be evaluated because of the limited temporal resolution of classical analytical approaches.

The temporal resolution of 10 µs can be further improved. In patch clamp experiments on BK channels, 0.1 µs could be reached by virtue of the lower noise of excised patches (Schroeder and Hansen, 2007, 2009a). With respect to noise, experiments in bilayers suffer from the wider membrane area and the resulting higher membrane capacitance. However, by virtue of the high single-pore current sometimes reaching 100 pA (Bredin et al., 2002), the temporal resolution may be even higher than that reached in BK channels when OmpF is expressed in cells, and patch clamping is used.

Nevertheless, the temporal resolution here is obviously sufficient for a complete evaluation of the kinetics of enrofloxacin binding in the presence of Mg²⁺ and leads to several findings which are listed.

(1) Polarity

Fig. 10 illustrates the dependency of the induction of slow and fast blocking events on the polarity of membrane potential and on the side of enrofloxacin addition. The finding that membrane potential has to be positive on the trans side to induce fast flickering and that negative potential does not induce a similar effect when enrofloxacin is given on the cis side is in contrast to the canonical blocking effects in ion channels like BK, where fast flickering is induced when the charged blocking ion (e.g., Tl⁺, Schroeder and Hansen, 2008; Cs⁺, Draber and Hansen, 1994) is pulled into the channel by the membrane potential. Our favorite hypothesis is based on the fact that enrofloxacin is zwitterionic under the experimental conditions used here (Lizondo et al., 1997). This suggests a need to orient the molecule before binding as illustrated in Fig. 10.

An alternative hypothesis may be based on the assumption that the positive membrane potential is required to induce an adequate conformational change of the protein for fast flickering binding. Voltage-induced conformational changes have been discussed by Nikaido (2003) starting from the observation that porins spontaneously close at high voltage, typically +100 mV or more (also shown in Fig. 2 E).

One suggestion is that transmembrane voltages make the channel narrower by bringing the cationic and anionic amino acid side chains closer to each other. However, the spontaneous closures still occur when the loop is fixed to the barrel wall by a disulfide bond (Phale et al., 1997; Bainbridge et al., 1998b). Alternatively, an atomic force microscopy study has shown that the application of voltage causes the movement of external loops, resulting in the closure of channel entrance (Müller and Engel, 1999). Nikaido (2003) also considers a third mechanism, which has been found in the α-toxin of Staphylococcus aureus, which is an empty 14-member β-barrel with no constrictions or infolding loops. It shows gating behavior in planar bilayers (Bainbridge et al., 1998a), presumably as a result of the fluctuation in the ionization of the charged groups either within or near the channel as also known from holes in a plastic film (polyethylene terephthalate, Korchev et al., 1997).

In the case of the experiments here, there are two indications that voltage-induced conformational changes may exist. First, the traces in Fig. 2 (A and E) and the black amplitude histograms in Fig. 4 B show that positive voltages lead to the appearance of a current level below I₂ in the absence of enrofloxacin, whereas negative voltages do not. These slow transitions occur with I_B = 0, indicating that a different mechanism is involved than that related to the blockage by enrofloxacin. (I_B = 0 becomes obvious in the location of the black peak in Fig. 4 B, but a detailed analysis will be given in a separate paper dealing with the slow transients). The second indication is related to item 2.

(2) Voltage dependence of k_BO

In Fig. 9 B, there is a slight voltage dependence of the rate constant of unblocking (k_BO). The effect is small, and nearly hidden by the scatter. However, the parallel behavior obtained under eight different conditions is intriguing. This may be a consequence of voltage-induced conformational changes mentioned in finding 1, especially as it occurs at potentials where the spontaneous slow transients have been observed. However, a major effect of surface charges can be excluded because the LPS and DPhPC curves are parallel in Fig. 9 B. Indications of a similar effect on k_off (corresponding to k_BO) have also been found for the dissociation of OmpF and an analogue of the HP(2–20) antimicrobial peptide (Apetrei et al., 2010). This effect may imply that the geometry of the pore is modified by the electric field (as discussed in finding 1). Alternatively, it may be assumed that the electric field exerts a force on the bound agent, especially as it cannot be excluded that the environment at the binding site may shift the distribution of zwitterionic and charged forms of enrofloxacin (Lizondo et al., 1997).

(3) Voltage dependence of k_OB

The rate constant of enrofloxacin binding strongly increases with positive voltage (Fig. 8, A and B). Here again, the putative mechanisms already mentioned in finding 1 can be involved. Nevertheless, our favorite hypothesis is that the main effect of voltage is mediated by the orientation of enrofloxacin. Then, this voltage dependence would reflect the mean number of adequately oriented approaches to the binding site. However, the voltage-induced effects on slow transients (Fig. 4, black curves) in the absence of enrofloxacin and on k_BO of fast flickering in Fig. 9 B may also indicate a direct effect of voltage on the conformation and dynamics of the protein, thus contributing to the strong voltage-dependence of k_OB in Fig. 9 A. A major role of surface charges (Green and Andersen, 1991) on the steepness of the voltage dependence can be excluded as there is no significant difference between negatively charged LPS and uncharged DPhPC membranes in Fig. 9 A.

One effect that also has to be considered is the putative inhomogeneity of the electric field in the pore, as caused by charged residues (Fig. 5 A). This makes the movement of dipoles sensitive to the field. Evaluating this kind of effect, however, is beyond the reach of this study.

Conclusion for findings 1–3

There is a great variety of possible mechanisms that may be involved in the voltage dependence of enrofloxacin-induced flickering, but there is no unequivocal preference for one of these mechanisms. Nevertheless, considering that a transmembrane field of course leads to an orientation of the zwitterionic antibiotic, and that MD simulations (Mahendran et al., 2010a) have shown that enrofloxacin has to be oriented to pass through the constriction zone, we favor the hypothesis that orientation by the positive potential is a salient factor to explain the scenarios in Fig. 10 (B and D).

(4) Concentration dependence

It is not surprising that k_OB increases linearly with the concentration of the antibiotic (Fig. 8, A and C; Table 1) because the included message is a priori expected, i.e., that the reaction between OmpF and the antibiotic is bimolecular. The same holds for the apparent independence of k_BO on concentration (Fig. 8, B and D).

(5) Incomplete block

An interesting finding is the incomplete occlusion of the pore by enrofloxacin as indicated by the remaining current I_B of the blocked state (Fig. 7). This is of special interest, as MD simulations suggested a space of ∼5 Ų accessible to ions at Mini Above and Mini Below when enrofloxacin was bound (Mahendran et al., 2010a).

(6) Effect of Mg²⁺

The charge reversion by Mg²⁺ in the region D113 to E117 on the L3 loop (Fig. 5 A) results in rate constants that are even faster than in the D113N mutant (Mahendran et al., 2010a). The weakening of binding in the presence of Mg²⁺ has also been found for the interaction of OmpF and an analogue of the HP(2–20) antimicrobial peptide (Apetrei et al., 2010). Furthermore, Yamashita et al. (2008) also found an interaction of Mg²⁺ and the unfolded N-terminal domain (T83) of the bacteriocin colicin E3, which is also translocated through OmpF. 1 M Mg²⁺ led to a complete suppression of colicin binding in OmpF crystals.

(7) Sidedness for slow and fast blocking effects

At negative membrane potentials (Fig. 10, A and C), enrofloxacin causes slow blocking when given at the cis side (Figs. 2 D and 10 C) but has no effect when given at the trans side (Fig. 2, B and C; and Fig. 10 A). This can be explained under the assumption that for OmpF in the F+ orientation the assignment periplasmic = trans holds (see discussion in the next section, Sidedness of k_OB). This sidedness in Fig. 2 indicates that enrofloxacin can reach the external binding site Mini Above (Fig. 5, A and B) from the cis side without having to pass the constriction zone (Fig. 10 C). According to the crystal structure analysis of Yamashita et al. (2008), there is no Mg²⁺ binding at Mini Above, and thus fast flickering should not be observed. In contrast, the orientation at negative potentials is not only inadequate for binding at the periplasmic site Mini Below but also for enrofloxacin passing the constriction zone to reach Mini Above when given at the trans side. In our experiments, passing the constriction zone is only possible when the positive voltage forces the correct orientation (Fig. 10 D).

In the case of scenario of Fig. 10 D, the question may arise why enrofloxacin from the cis side can pass the still existing high affinity binding site Mini Above on its way to Mini Below at the trans side of the constriction zone. There are two possible explanations: first, the binding rate constant k_OB,cis is by a factor of approximately three smaller than k_OB,trans. This may not only result from the necessity to pass through the constriction zone but also from the necessity to escape from being trapped by Mini Above. However, it is unlikely that this is valid in numerical terms. More likely is the second hypothesis; Fig. 2 D shows that slow gating only occurs at negative potentials and when enrofloxacin is given at the cis side. Thus, consistent with the MD simulations of Mahendran et al. (2010a) it may be concluded that enrofloxacin has to be oriented by a negative potential to bind to Mini Above. In that case, it would escape from trapping when oriented by a positive potential as in Fig. 10 D.

(8) Sidedness of k_OB

According to Figs. 8 and 9, the rate constants of binding, k_OB, are higher when enrofloxacin is given on the trans side (Fig. 10 B) than on the cis side (Fig. 10 D). This is consistent with the assumption that the trans side is the periplasmic side because the region D113 to E117 is located at the periplasmic side of the constriction zone (Fig. 5 A).

(9) Orientation

Fig. 5 A is drawn under the assumption that trans = periplasmic. This is plausible because of findings 7 and 8. The slight asymmetries in channel conductance (Fig. 3) and in the dependence of the kinetics on the side of enrofloxacin addition (Figs. 2, 4, 8, and 9) allow the distinction between two different modes of the orientation of the porin during reconstitution. As mentioned, 9 out of 11 OmpF had the dominant F+ configuration (flickering at positive membranes) in LPS membranes and 6 out of 9 in DPhPC membranes. The results of the kinetic evaluation of the dominant F+ type (findings 7 and 8) only correspond to those from MD simulations (Mahendran et al., 2010a) and crystal structure analysis (Yamashita et al., 2008) if the periplasmic side of the protein is assumed to be on the trans side of the membrane. In the native bacteria membrane, the orientation of OmpF has been determined (Hoenger et al., 1993). However, for reconstituted porins so far only weak hints are available. Inspection of accelerated MD modeling (Mahendran et al., 2010a) suggests that enrofloxacin can enter the porin from either side. Coming from the external side, it penetrates the constriction zone with the carboxylic (negative) end first. This corresponds to the situation in Fig. 10 D only when cis = external side. This is in contrast to the orientation in the bacterial membrane. However, a similar situation has been found for Maltoporin which is known to insert with the periplasmic side first in vitro. This is opposite to the situation in vivo, and the difference is supposed to originate from the involvement of chaperones in the bacteria (Danelon et al., 2003).

However, these conclusions about the orientations of OmpF are only valid if the exclusive location of Mg²⁺ at Mini Below (as determined by crystal structure analysis; Yamashita et al., 2008) also applies to the electrophysiological studies here. Thus, the orientation periplasmic = trans is very plausible but not proven. We have tried to introduce blocking sites by mutations that are only accessible from one side, similar to the approach of Heginbotham et al. (1999) for KcsA in bilayers. However, so far these experiments failed to give a definite answer. In OmpF, the situation is less favorable than in ion channels because of the wide diameter of the OmpF pore which allows putative blockers up to 600 D to pass the constriction zone (Nikaido, 2003; Delcour, 2009). This impedes the concept of accessibility. Nevertheless, this evaluation is at least a stimulus to verify the results from crystal structure analysis by mutational studies influencing Mg²⁺ binding.