Distinct subunit contributions to the activation of M-type potassium channels by PI(4,5)P₂

Abstract

Low-threshold voltage-gated M-type potassium channels (M channels) are tetraheteromers, commonly of two Kv7.2 and two Kv7.3 subunits. Though gated by voltage, the channels have an absolute requirement for binding of the membrane phospholipid phosphatidylinositol-4,5-bisphosphate (PI(4,5)P₂) to open. We have investigated the quantitative relation between the concentration of a water-soluble PI(4,5)P₂ analog, dioctanoyl-PI(4,5)P₂ (DiC₈-PI(4,5)P₂), and channel open probability (P_open) by fast application of increasing concentrations of DiC₈-PI(4,5)P₂ to the inside face of membrane patches excised from Chinese hamster ovary cells expressing M channels as heteromeric Kv7.2/7.3 subunits. The rationale for the experiments is that this will mimic the effect of changes in membrane PI(4,5)P₂ concentration. Single-channel conductances from channel current–voltage relations in cell-attached mode were 9.2 ± 0.1 pS with a 2.5-mM pipette [K⁺]. Plots of P_open against DiC₈-PI(4,5)P₂ concentration were best fitted using a two-component concentration–P_open relationship with high and low affinity, half-maximal effective concentration (EC₅₀) values of 1.3 ± 0.14 and 75.5 ± 2.5 µM, respectively, and Hill slopes of 1.4 ± 0.06. In contrast, homomeric channels from cells expressing only Kv7.2 or Kv7.3 constructs yielded single-component curves with EC₅₀ values of 76.2 ± 19.9 or 3.6 ± 1.0 µM, respectively. When wild-type (WT) Kv7.2 was coexpressed with a mutated Kv7.3 subunit with >100-fold reduced sensitivity to PI(4,5)P₂, the high-affinity component of the activation curve was lost. Fitting the data for WT and mutant channels to an activation mechanism with independent PI(4,5)P₂ binding to two Kv7.2 and two Kv7.3 subunits suggests that the two components of the M-channel activation curve correspond to the interaction of PI(4,5)P₂ with the Kv7.3 and Kv7.2 subunits, respectively, that channels can open when only the two Kv7.3 subunits have bound DiC₈-PI(4,5)P₂, and that maximum channel opening requires binding to all four subunits.

INTRODUCTION

M-type potassium channels are low-threshold, noninactivating voltage-gated potassium channels that regulate the excitability of many central and peripheral neurons (Brown and Adams, 1980; Brown and Passmore, 2009). They are composed of subunits of the Kv7 potassium channel family, principally, Kv7.2 and Kv7.3 arranged as a heterotetramer (Wang et al., 1998; Hadley et al., 2003). Though gated by membrane voltage, like several other ion channels (Hilgemann et al., 2001; Gamper and Shapiro, 2007; Suh and Hille, 2008; Logothetis et al., 2010), they require the presence of the membrane phospholipid phosphatidylinositol-4,5-bisphosphate (PI(4,5)P₂) to open (Suh and Hille, 2002; Zhang et al., 2003; Li et al., 2005). This is important physiologically because neurotransmitters such as acetylcholine can close the channels by stimulating the hydrolysis and depletion of membrane PI(4,5)P₂ through activating Gq-coupled receptors (Suh and Hille, 2002; Delmas and Brown, 2005; Winks et al., 2005; Hernandez et al., 2009). This causes postsynaptic depolarization and an enhanced neuronal excitability (Brown and Selyanko, 1985; Gahwiler and Brown, 1985; Jones, 1985).

Interestingly, when the two M-channel subunits Kv7.2 and Kv7.3 are expressed separately as homomeric channels, they show an approximately 100-fold difference in their sensitivities to PI(4,5)P₂, as measured by the concentration of the water-soluble analog dioctanoylphosphatidyl-4,5-bisphosphate (DiC₈-PI(4,5)P₂) required to open them (half-maximal effective concentration [EC₅₀] values of 205 and 2.6 µM for Kv7.2 and Kv7.3, respectively; Li et al., 2005). Channels generated by coexpressing the two subunits gave an intermediate EC₅₀ of 40 µM (Li et al., 2005).

To investigate the contributions of the individual subunits to the overall response of heteromeric M channels to PI(4,5)P₂, we have examined the sensitivity of heteromeric Kv7.2/7.3 channels to DiC₈-PI(4,5)P₂ in detail, using both coexpressed subunits and tandem Kv7.2-7.3 constructs (the latter to favor a fixed stoichiometry; Hadley et al., 2003). We have used an extended range of DiC₈-PI(4,5)P₂ concentrations to embrace the sensitivities of the individual subunits when expressed as homomeric channels. The results reveal distinctive components to the concentration dependence of the heteromeric channel activation that can be described by the interaction of DiC₈-PI(4,5)P₂ with the individual subunits.

MATERIALS AND METHODS

Cell culture

For most experiments on Kv7.2/7.3 channels, we used Chinese hamster ovary (CHO) cells stably cotransfected with cDNAs for the human Kv7.2 and Kv7.3 M-channel subunits (K2/3-CHO cells; Main et al., 2000). To ensure that the K2/3-CHO cell line generates tetraheteromeric M channels, we also performed experiments on CHO cells (stably expressing human muscarinic type 1 receptors [HM1-CHO]) that were transiently transfected with a concatenated Kv7.2-7.3 cDNA plasmid (Wickenden et al., 2000). These generate currents carried by a single species of channel with a unique sensitivity to tetraethylammonium appropriate to a 2×Kv7.2 + 2×Kv7.3 stoichiometry (Hadley et al., 2003). For some experiments, we used CHO cells transfected to express wild-type (WT) Kv7.2 subunits with mutated Kv7.3 subunits Kv7.3 [K425E/K432E/R434E] (provided by M.S. Shapiro, University of Texas Health Science Center, San Antonio, TX). When expressed to form homomeric channels, this mutant (abbreviated herein as Kv7.3(EEE)) is >100-fold less sensitive to PI(4,5)P₂ than the WT Kv7.3 channel (Hernandez et al., 2008). For studies of homomeric Kv7.2 and Kv7.3 channels, we also used the HM1-CHO cell line, which expresses the M1 muscarinic acetylcholine receptor (Mullaney et al., 1993) and which was then transiently transfected with Kv7.2 or Kv7.3 cDNA plasmids. For the latter, we used the A315T pore mutant (Kv7.3^T; provided by A. Villarroel, Campus Universidad el País Vasco, Leioa, Spain); this enhances Kv7.3 channel expression and P_open without affecting its sensitivity to PI(4,5)P₂ (Zaika et al., 2008; Gómez-Posada et al., 2010).

K2/3-CHO cells were incubated in MEM-α (Invitrogen) supplemented with 10% FCS, 1% l-glutamine, 1% penicillin/streptomycin, 0.2 mg/ml hygromycin, and 0.4 mg/ml neomycin (K2/3-CHO media). For HM1-CHO cells, we used HM1-CHO media, which was similar to K2/3-CHO media but did not contain hygromycin and neomycin. For transient transfections, HM1-CHO cells were incubated in Opti-MEM medium (Invitrogen) and cotransfected with the appropriate Kv7 DNA plasmid plus an enhanced green fluorescent protein cDNA plasmid using Lipofectamine 2000 reagent (following the manufacturer’s protocols). The media, Lipofectamine 2000, and all the supplements were purchased from Invitrogen. Both K2/3-CHO and HM1-CHO cell lines were maintained in a humidified incubator gassed with 5% CO₂/95% air. Cells were passaged every 2–3 d in a ratio of 1:10; Ca²⁺- and Mg²⁺-free phosphate-buffered Hanks’ balanced saline solution was used to detach the cells. This was subsequently followed by centrifugation at 800 g and resuspension in the aforementioned supplemented medium. For subsequent electrophysiological experimentation, K2/3-CHO and HM1-CHO cells were settled in specially designed silicon chambers (volume of ∼200 µl) within plastic Petri dishes and incubated for at least 24 h before being mounted on the stage of an inverted microscope equipped with phase-contrast optics and continuously superfused at ∼5 ml/min⁻¹.

Electrophysiological recordings

Single M-channel activity was recorded using patch electrodes in cell-attached and inside-out configuration at a controlled room temperature (22 ± 0.5°C). For current recording, we used an Axopatch 200A amplifier and Digidata 1440 A/D interface (Axon Instruments, Inc.) and pipette holder optimized for low-noise recordings (G23 Instruments). Membrane voltages were set in the range from −40 to 0 mV with 10-mV increments in cell-attached mode and at 0 mV in inside-out configuration. All recordings were filtered with an 8-pole Bessel filter (Harvard Apparatus) at 2 kHz and digitized at 5 kHz. The pipette resistance when filled with the intracellular solution was ∼5–10 MΩ. Data were analyzed using Clampfit 10.2 (Molecular Devices), Excel (2003; Microsoft Office), and Microcal Origin (6.0; OriginLab Corporation) software.

Bath and pipette solutions contained 144 mM NaCl, 2.5 mM KCl, 0.5 mM MgCl₂, 2 mM CaCl₂, 10 mMd-glucose, and 5 mM HEPES; pH was adjusted to 7.4 with Tris. Bath solutions for inside-out studies contained 165 mM KCl, 5 mM HEPES, and 10 mM EGTA; pH was adjusted at 7.2 by NaOH. 0.1 µM nonhydrolyzable ATPγS was constantly present in the bath solutions during inside-out studies to inhibit endogenous production of PI(4,5)P₂ by phosphatidylinositol kinases, which possibly remained associated with a patch after excision. DiC₈-PI(4,5)P₂ was applied to the isolated inside-out membrane patches in incremental concentrations from 0.1 to 300 µM using a fast piezoelectric-driven microperfusion system (delivery time of <1 s). All compounds for solutions and ATPγS were purchased from Sigma-Aldrich; DiC₈-PI(4,5)P₂ was purchased from Echelon Biosciences Inc.

Data analysis

Data were analyzed using Clampfit 10.2, WinEDR (Dempster, 2001), Excel (2003), and Microcal Origin (6.0) software. Single-channel current amplitudes were measured directly from each patch by fitting Gaussian functions to the all-point amplitude distribution. In patches containing multiple (two to six) channels, recordings made at low DiC₈-PI(4,5)P₂ concentrations where individual channel openings could be clearly observed were used to estimate channel amplitudes. Where patches contained multiple channels, the number of channels (N) in the patch was estimated by fitting the current variance (Var(I_m)) to mean current (I_m) relationship with the unit current (i_unit) constrained to the value estimated from the point amplitude distribution using the following parabolic function:

$$Var\left(I_m\right)={Var}_{background}+i_{unit}{I}_m-\frac{I_m^2}{N}\text{.}$$

Patch NP_open measurements were then corrected for the estimated number of channels in each patch to give channel P_open as a function of DiC₈-PI(4,5)P₂ concentration. Open probabilities were measured over the last 20 s of each DiC₈-PI(4,5)P₂ concentration application, when NP_open was stable (verified by stability plots constructed using NP_open measured in 0.5–2.0-s bins; see Fig. 5 D).

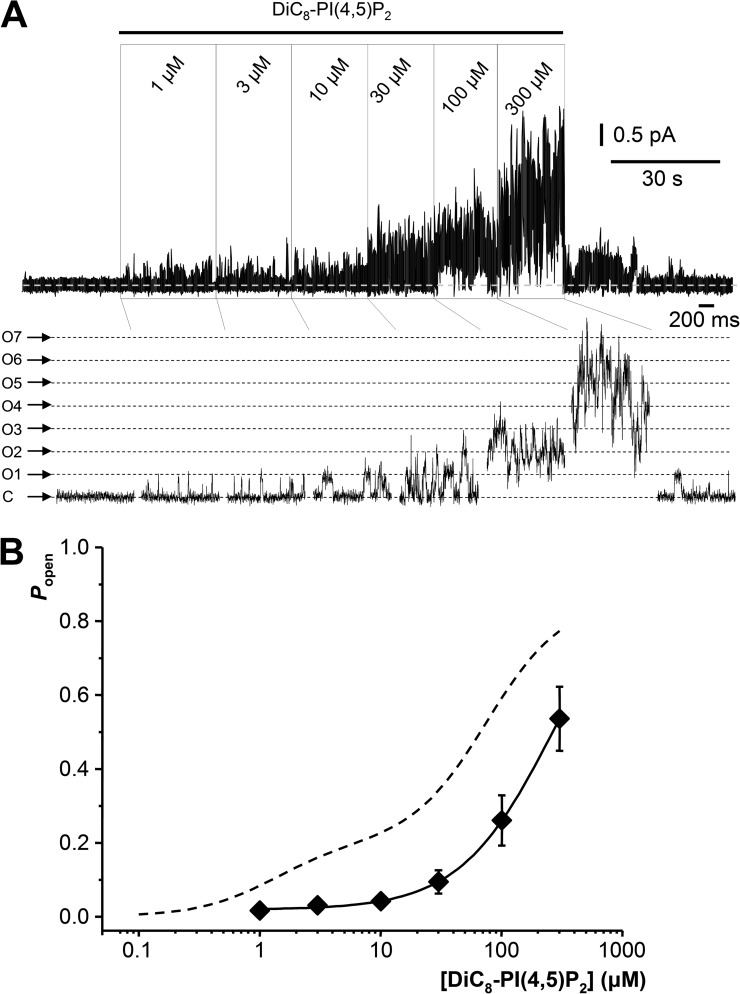
Figure 5.

Effects of reversed sequential and random applications of various concentrations of DiC₈-PI(4,5)P₂ on homomeric Kv7.3^T channels. (A) Multichannel recording in an excised inside-out membrane patch from an HM1-CHO cell transfected with Kv7.3^T cDNA. The patch contained up to 11 channels with current levels. 1, 10, and 100 µM DiC₈-PI(4,5)P₂ were applied sequentially in ascending order and then in reverse (descending) order. Holding potential is 0 mV. (B) Multichannel recording of Kv7.3^T channel activity induced by applications of different concentrations of DiC₈-PI(4,5)P₂ in random order. Holding potential is 0 mV. (C) Mean (±SEM) single-channel open probabilities (P_open), corrected for channel numbers, from five such patches exposed to the same sequences of DiC₈-PI(4,5)P₂ applications as in A. (D) Stability plot analysis (bin width of 2 s) of the response of a patch of membrane to a 60-s application of 100 µM DiC₈-PI(4,5)P₂.

DiC₈-PI(4,5)P₂ concentration values for half-activation (EC₅₀) were estimated by weighted least squares fitting of concentration-response data for P_open using Hill equations for single- and two-component curves, using

$$P_{open}=\frac{{Po}_{\left(Max\right)}}{1+{\left(\frac{E{C}_{50}}{\left[PIP\right]}\right)}^{nH}}\hspace{0.17em}\text{and}$$

$$P_{open}=\frac{{Po}_{\left(Max1\right)}}{1+{\left(\frac{E{C}_{50\left(1\right)}}{\left[PIP\right]}\right)}^{nH}}+\frac{{Po}_{\left(Max2\right)}}{1+{\left(\frac{E{C}_{50\left(2\right)}}{\left[PIP\right]}\right)}^{nH}},$$

where n_H represents the Hill coefficient and [PIP] represents DiC₈-PI(4,5)P₂ concentration. When fitting two-component curves, n_H was constrained to be the same for both components.

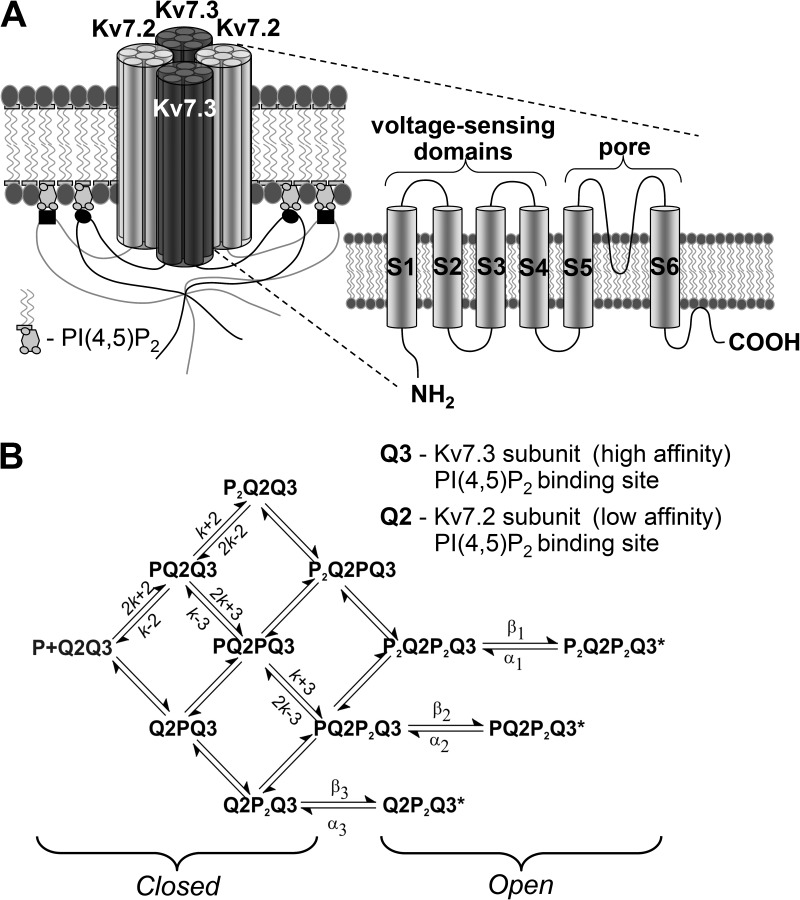
To gain insight into the subunit dependence of M-channel activation by PI(4,5)P₂, data were also fitted to an activation mechanism incorporating two pairs of independent high- and low-affinity PI(4,5)P₂ binding sites (see Fig. 6). Three open states were assumed to occur corresponding to opening when the two high-affinity binding sites are occupied, when two high-affinity sites and one low-affinity site are occupied, and when all four binding sites are occupied. Equilibrium occupancies of each state in the model were expressed according to the law of mass action, with the rates in each cycle in the mechanism constrained to conserve microscopic reversibility (Colquhoun, et al., 2004). Channel open probability was calculated as the sum of occupancies of the three open states (see Fig. 6 B) as a function of PI(4,5)P₂ concentration ([P]), the dissociation equilibrium constants for binding to the high-affinity (K₃) and low-affinity (K₂) sites, and the equilibrium constants for channel opening when only the two high-affinity sites are occupied (E₃), when two high-affinity sites and one low-affinity site are occupied (E₂), or when all four PI(4,5)P₂ binding sites are occupied (E₁), where E_i = β_i/α_i was defined as the ratio of channel opening (β) and closing rates (α). Thus,

$$\begin{array}{l}{P}_{Open}=\frac{1}{1+\frac{1}{E_1}\left\{\begin{array}{l}1+\frac{K_2^2{K}_3^2}{{\left[P\right]}^4}+\frac{2K_2^2{K}_3}{{\left[P\right]}^3}+\frac{2K_2{K}_3^2}{{\left[P\right]}^3}+\frac{K_2^2}{{\left[P\right]}^2}+\frac{4K_2{K}_3}{{\left[P\right]}^2}+\\ \frac{K_3^2}{{\left[P\right]}^2}+\frac{2K_2}{\left[P\right]}+\frac{2K_3}{\left[P\right]}+\frac{E_3{K}_2^2}{{\left[P\right]}^2}+\frac{2E_2{K}_2}{\left[P\right]}\end{array}\right\}}+\\ \frac{1}{1+\frac{1}{E_2}\left\{\begin{array}{l}1+\frac{K_2{K}_3^2}{2{\left[P\right]}^3}+\frac{K_2{K}_3}{{\left[P\right]}^2}+\frac{K_3^2}{{\left[P\right]}^2}+\frac{K_2}{2\left[P\right]}+\frac{2K_3}{\left[P\right]}+\frac{K_3^2}{2K_2\left[P\right]}+\\ \frac{K_3}{K_2}+\frac{\left[P\right]}{2K_2}+\frac{E_3{K}_2}{2\left[P\right]}+\frac{E_1\left[P\right]}{2K_2}\end{array}\right\}}+\\ \frac{1}{1+\frac{1}{E_3}\left\{\begin{array}{l}1+\frac{K_3^2}{{\left[P\right]}^2}+\frac{2K_3}{\left[P\right]}+\frac{2K_3^2}{K_2\left[P\right]}+\frac{4K_3}{K_2}+\frac{K_3^2}{K_2^2}+\frac{2\left[P\right]}{K_2}+\frac{2K_3}{K_2^2}+\\ \frac{{\left[P\right]}^2}{K_2^2}+\frac{2E_2\left[P\right]}{K_2}+\frac{E_1{\left[P\right]}^2}{K_2^2}\end{array}\right\}}.\end{array}$$

Figure 6.

Suggested model for M-type Kv7.2/7.3 channel activation by binding of PI(4,5)P₂ molecules. (A) Cartoon of an M-type potassium channel composed of two Kv7.2 and two Kv7.3 subunits arranged alternately around a central ion channel. Each subunit contains both voltage-sensing and pore-forming domains, as illustrated on the right, as well as a putative PI(4,5)P₂ binding region located within the C-terminal domain. (B) Model scheme of PI(4,5)P₂ binding and channel gating assuming that PI(4,5)P₂ binds independently to each subunit and that channels can gate to the open state (denoted by asterisks) when both Kv7.3 (Q3) subunits have bound PI(4,5)P₂ (Q2P₂Q3), when both Kv7.3 subunits and one Kv7.2 (Q2) subunit are occupied (PQ2P₂Q3), or when all four subunits are occupied (P2Q2P₂Q3). The equilibrium dissociation constants for PI(4,5)P₂ binding to Kv7.3 (K₃ = k₋₃/k₊₃) and Kv7.2 (K₂ = k₋₂/k₊₂) subunits and the equilibrium constants describing channel gating to each open state—E₁(β₁/α₁), E₂(β₂/α₂), and E₃(β₃/α₃)—are determined by their respective rate constants, as indicated.

Statistical comparisons were performed using one-way ANOVA, and the difference was considered as significant at the level of P < 0.05.

Online supplemental material

Fig. S1 shows development of a subunit-specific model to describe M-channel activation by PI(4,5)P₂. Fig. S2 shows an investigation of the contribution of changes in binding affinity and gating efficiency to the overall effect of the Kv7.3(EEE) mutation. Fig. S3 shows fidelity of channel subunit assembly. Table S1 shows model-fitted parameters. Table S2 shows parameter estimates from fitting Kv7.3(EEE) mutant channels to model 4 with efficacy or affinity constraints. Table S3 shows parameter estimates from fitting Kv7.3(EEE) mutant channels to a subunit dimer–dependent cooperativity model. Table S4 shows proportions of channel subtypes created with a random subunit assembly model and parameter estimates obtained by fitting the data with this model. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201210796/DC1.

RESULTS

Cell-attached recordings

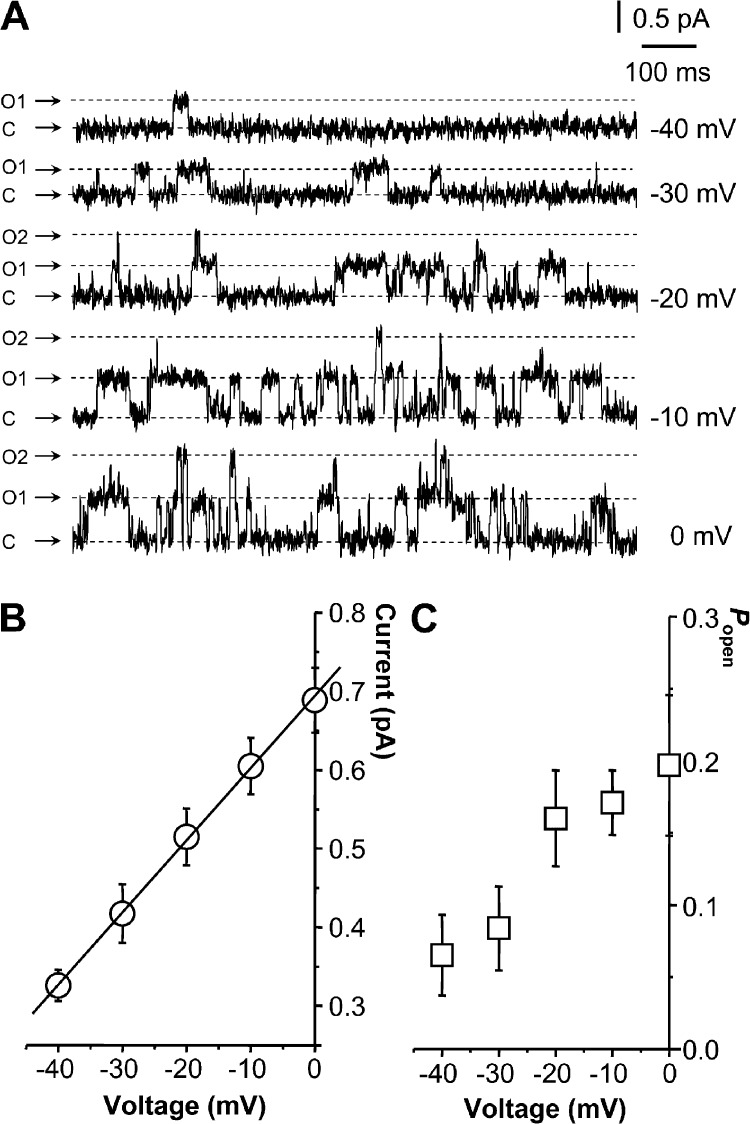
Single-channel activity recorded from K2/3-CHO cells showed a pronounced voltage sensitivity in both open probability (P_open) and single-channel current amplitude when the membrane potential was varied between −40 and 0 mV in 10-mV steps (patch potential of 20–60 mV and assumed resting potential of −60 mV; Fig. 1; Selyanko et al., 2001). Mean single-channel slope conductance (γ_slope) was 9.2 ± 0.1 pS (n = 6; Fig. 1 B). P_open at 0 mV was 0.2 ± 0.05 (Fig. 1 C). Values for both γ_slope and P_open at 0 mV accord with previous observations on these cells with on-cell patches (g_slope of 9.0 ± 0.3 pS and P_open of ∼0.27 in Selyanko et al. [2001] and P_open of 0.31 ± 0.4 in Li et al. [2005]).

Figure 1.

Single M-type Kv7.2/7.3 channel activity recorded in intact CHO cells with cell-attached patch electrodes. (A) Exemplar single-channel activity traces recorded in the voltage range from about −40 to 0 mV (patch electrode voltages of 20–60 mV) from a CHO cell stably expressing M-type Kv7.2/7.3 channels. C, closed channel; O1 and O2, open channel current levels for 1 and 2 channels. (B) Summary current voltage plot of single Kv7.2/7.3 channel currents. C, single-channel open probability (P_open) plotted against membrane voltage. (B and C) Points are means ± SEM from six patches.

Excised patches

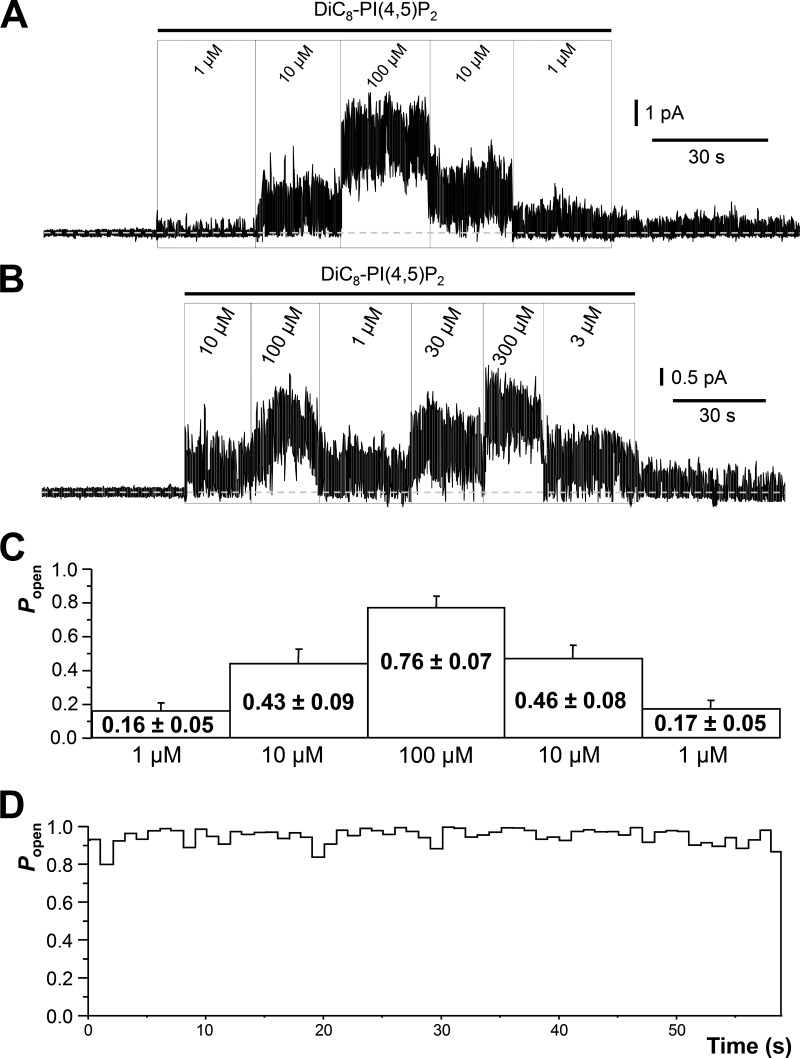
Patches active in cell-attached mode were excised to inside-out mode and voltage clamped at a pipette potential of 0 mV. After excision, the vast majority of patches showed no further activity. This was presumably because endogenous PI(4,5)P₂ was lost (Zhang et al., 2003; Li et al., 2005), and its synthesis by phosphatidylinositol kinases was impaired by lack of ATP and inclusion of ATPγS in the bath fluid. Very occasionally, some low-level residual activity persisted (e.g., Fig. 2 A [i]); this control P_open (0.0084 ± 0.0066; n = 31) was subtracted from that seen in DiC₈-PI(4,5)P₂ solution in quantifying responses to the latter.

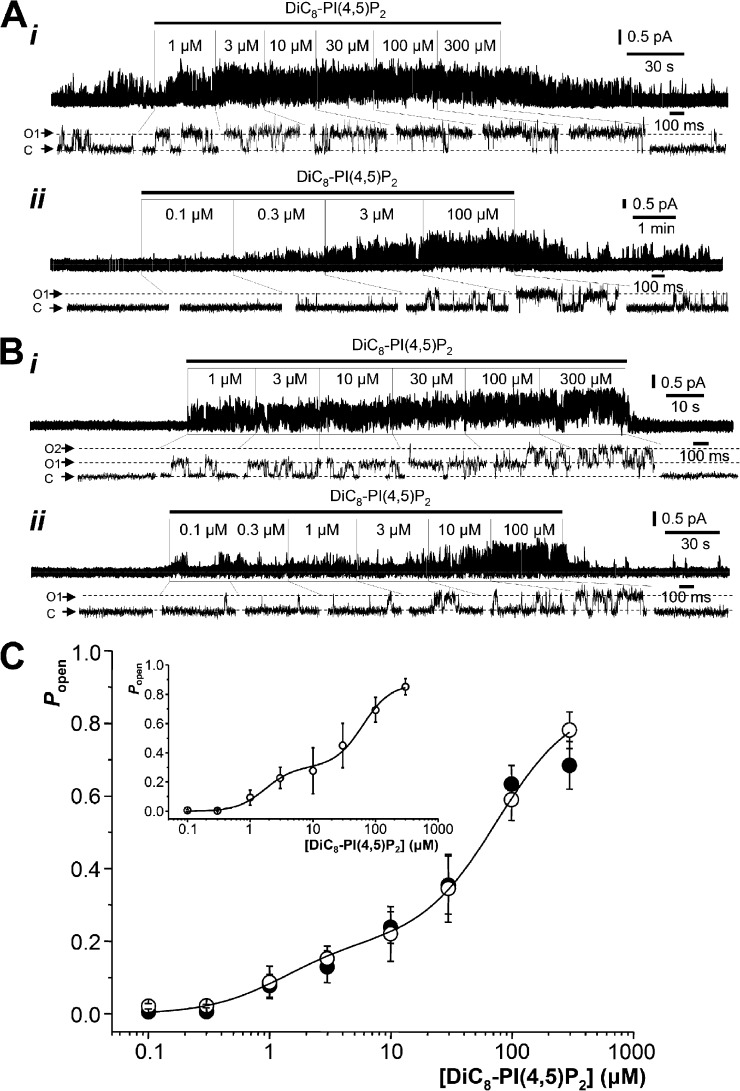
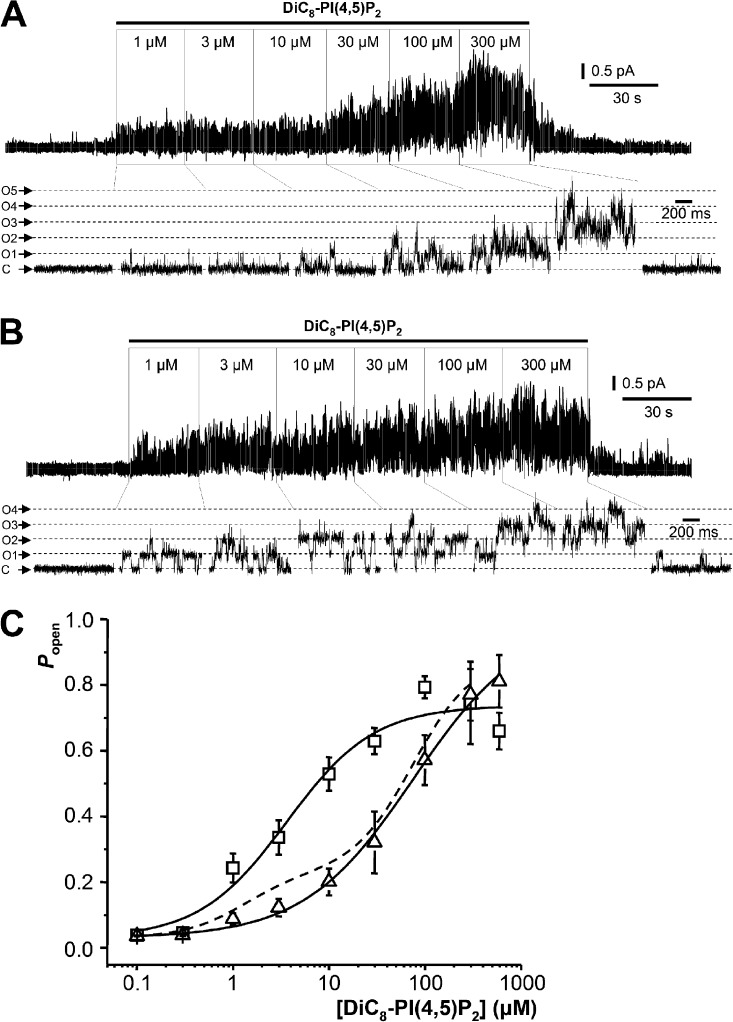
Figure 2.

Single M-type Kv7.2/7.3 channel activity in excised inside-out membrane patches activated by exogenous DiC₈-PI(4,5)P₂. (A) Examples of single-channel recordings showing effects of sequential increases of DiC₈-PI(4,5)P₂ concentrations applied to the inner leaflet of excised inside-out patches from K2/3-CHO cells stably expressing M-type Kv7.2/7.3 channels. Holding potential is 0 mV. C, closed channel current level; O, open channel current level. (B) As in A but with patches excised from HM1-CHO cells transiently transfected with a concatenated Kv7.2/7.3 channel cDNA. O1 and O2, open channel current levels for 1 and 2 channels. (C) Mean (±SEM) for P_open plotted against DiC₈-PI(4,5)P₂ concentration. Open circles represent K2/3-CHO cells stably transfected with coexpressed Kv7.2 and Kv7.3 channels. Filled circles represent HM1-CHO cells transiently transfected with a concatenated Kv7.2/7.3 cDNA. The solid line represents a least-squares fit of the open circle data to a two-component Hill equation (see Materials and methods) giving the parameter values indicated in the text. (inset) The mean (±SEM) channel P_open plotted against DiC₈-PI(4,5)P₂ concentration for patches where analysis indicated that only a single active channel was present (n = 5–14 patches at each concentration) is shown. The data were fitted with a two-component Hill equation with parameter values as given in the text.

Effects of DiC₈-PI(4,5)P₂ on Kv7.2/7.3 channel activity

Patches excised from stably cotransfected CHO cells (K2/3-CHOs) were exposed to incremental concentrations of DiC₈-PI(4,5)P₂ from 0.1 to 300 µM for 30 s to 2 min (Fig. 2, A and B). Patches with a single Kv7.2/7.3 channel showed a gradual augmentation in P_open with increasing DiC₈-PI(4,5)P₂ concentration (Fig. 2 A). In other patches, one or more superimposed channel openings appeared at the higher DiC₈-PI(4,5)P₂ concentrations (Fig. 2 B). The mean single-channel current amplitude at 0 mV was 0.532 pA (SD ± 0.073 pA; 95% confidence interval of 0.495–0.553 pA; n = 27). Amplitudes followed a normal distribution with distribution mean amplitude 0.531 ± SD of 0.080 pA.

Concentration-response curves for activation of Kv7.2/7.3 channels by DiC₈-PI(4,5)P₂ were constructed from recordings in both single- and pauci (one to six)-channel patches after correcting NP_o in the latter for the number of channels in the patch (Fig. 2 C; see Materials and methods). At each concentration tested, measurements were made from between 11 and 29 different patches. They were best fitted using a two-component Hill function, with EC₅₀(1) = 1.3 ± 0.14 µM and P_open(max1) = 0.2 ± 0.0073 (component 1) and EC₅₀(2) = 75.5 ± 2.5 µM and P_open(max2) = 0.6 ± 0.0012 (component 2) and with Hill coefficients (1.4 ± 0.06) constrained to be the same for the two components (open circles and interrupted line in Fig. 2 C). Fig. 2 C (inset) shows the concentration-response curve for patches where only a single channel was active (n = 1). At each concentration, measurements were made from between 5 and 14 different patches. The data were fitted using a two-component Hill function, with parameters of EC₅₀(1) = 1.5 ± 0.55 µM and P_open(max1) = 0.28 ± 0.045 and EC₅₀(2) = 61.1 ± 14.7 µM and P_open(max2) = 0.61 ± 0.0074 (component 2) and with Hill coefficients n_H = 1.6 ± 0.36.

We were concerned that the concentration-response curve might be affected by the presence of some homomeric Kv7.3 channels or heteromeric channels with different proportions of Kv7.3 and Kv7.2 subunits. To check this, we performed experiments using CHO cells transiently transfected with a single cDNA coding for concatenated Kv7.2 and Kv7.3 subunits (Hadley et al., 2003). These cells expressed channels with indistinguishable unitary current amplitude (0.519 ± SD of 0.053 pA; 95% confidence interval of 0.495–0.653; n = 21) from that in K2/3-CHO cells and yielded a very similar biphasic DiC₈-PI(4,5)P₂ concentration-response curve (n = 9–21; filled circles in Fig. 2 C).

Responses of homomeric Kv7.2 and Kv7.3 channels

The two-component concentration-response curves in Fig. 2 imply the presence of at least two distinguishable high- and low-affinity sites for PI(4,5)P₂ activation, differing by a factor of about 60 in their apparent affinities. The question then arises whether this relates to the differential sensitivities of the homomeric Kv7.2 and Kv7.3 subunits described by Li et al. (2005). In these latter experiments, activation curves for homomeric Kv7.3 and Kv7.2 channels were monotonic, with (respectively) EC₅₀ values of 2.6 and 215 µM and Hill slopes of 1.33 and 0.97. Accordingly, we investigated whether this held true in our test system or whether the DiC₈-PI(4,5)P₂ concentration-response curves for these homomers might themselves be biphasic. For this, we transiently expressed WT Kv7.2 or Kv7.3^T in CHO cells and recorded activation by DiC₈-PI(4,5)P₂ of single- and multichannel activity in excised membrane patches using the same protocols as used with the Kv7.2/7.3 heteromers. As shown in Fig. 3 and in agreement with Li et al. (2005), activation curves for the homomeric channels were well fitted with a single-component Hill equation, with EC₅₀ values and Hill coefficients (n_H) for Kv7.3^T of 3.6 ± 1.0 µM and 0.95 ± 0.2 (n = 7–15) and for Kv7.2 of 76.2 ± 19.9 µM and 0.76 ± 0.08 (n = 7–19), respectively. These EC₅₀ values are close to those for the two components of the activation curve for the heteromeric Kv7.2/7.3 channels.

Figure 3.

Effect of incremental DiC₈-PI(4,5)P₂ concentrations on homomeric Kv7.2 and Kv7.3 channel activity. (A and B) Examples of multichannel recordings in excised membrane patches from HM1-CHO cells transfected with cDNAs for Kv7.2 and Kv7.3^T cDNAs. C, closed state; O1–On, open-state current levels for 1 to n channels, as indicated. Holding potential is 0 mV. (C) Mean (±SEM) single-channel open probability corrected for the number of channels in each patch plotted against DiC₈-PI(4,5)P₂ concentrations. Triangles represent Kv7.2; squares represent Kv7.3^T. Curves show data fits to single-component Hill equations giving the parameters shown. The interrupted line shows the two-component fit from Fig. 2 obtained from K2/3-CHO cells stably expressing Kv7.2 + Kv7.3 subunits.

Coexpression of a mutated Kv7.3 subunit with WT Kv7.2

To further assess the influence of the different subunits in the response of heteromeric Kv7.2/7.3 channels to DiC₈-PI(4,5)P₂, we transiently coexpressed Kv7.3(EEE) with the WT Kv7.2 subunit. Kv7(EEE) channels are >100-fold less sensitive to DiC₈-PI(4,5)P₂ than WT channels when expressed as homomers (Hernandez et al., 2008), so they might be expected to modify the high-affinity component of the heteromeric Kv7.2/7.3 DiC₈-PI(4,5)P₂ concentration-response curve if this component reflects binding to Kv7.3. Single-channel current amplitudes following coexpression of Kv7.3(EEE) with Kv7.2 (0.52 ± 0.01 pA; n = 13 patches) were indistinguishable from those of coexpressed WT Kv7.3 with Kv7.2 (0.52 ± 0.01 pA; n = 27) but significantly different (P = 0.0017) from those of homomeric Kv7.3^T channels (0.45 ± 0.01 pA; n = 16), suggesting that the Kv7.3(EEE) subunit had indeed heteromerized with the WT Kv7.2 subunit. As shown in Fig. 4, the DiC₈-PI(4,5)P₂ concentration–P_open curve for the Kv7.3(EEE)/Kv7.2 heteromer was shifted to the right of that for the WT Kv7.3/7.2 heteromer and could now be fitted with a single-component equation, with EC₅₀ = 265.0 ± 74.0 µM (n_H = 1.1 ± 0.1). This might imply either that the two subunits now had broadly comparable sensitivities to PI(4,5)P₂ or (more probably perhaps, judging by the reduced Hill slope) that the curve remained fundamentally biphasic but with the Kv7.3(EEE) subunit now being the less sensitive of the two. If the latter, their practical discrimination was limited by the fact that the low sensitivity of the Kv7.3(EEE)/Kv7.2 channels precluded completion of the full concentration-response curve as a result of the high concentrations of DiC₈-PI(4,5)P₂ that would be required, and, so, the maximum P_open of the channel is undetermined here.

Figure 4.

Effect of incremental DiC₈-PI(4,5)P₂ concentrations on heteromeric Kv7.2/Kv7.3(EEE) channel activity. (A) Responses of a cluster of seven channels expressed from cotransfected Kv7.2 and Kv7.3(EEE) cDNAs to incremental concentrations of DiC₈-PI(4,5)P₂. C, closed state; O1–O7, open-state current levels for 1–7 channels, as indicated. Holding potential is 0 mV. (B) Mean (±SEM) single-channel open probability of 13 patches corrected for the number of channels in each patch plotted against DiC₈-PI(4,5)P₂ concentrations. The curve shows data fit to a single-component Hill equation (solid line). The interrupted line shows the two-component fit to data from coexpressed Kv7.2 + Kv7.3 subunits, illustrated in Fig. 2.

Stability analysis of the patch response to DiC₈-PI(4,5)P₂

The response of Kv7.2/7.3 channels to DiC₈-PI(4,5)P₂ would not be expected to desensitize, as native M channels display constant current for many minutes (or longer) at constant voltage and (presumably) constant PI(4,5)P₂ levels. However, our use of incremental concentrations might induce artifacts in the deduced concentration-response relations if (for example) the DiC₈-PI(4,5)P₂ gradually accumulated in the membrane. The Kv7.3^T channels provided a convenient tool to check this, as they responded well over a wide range of usable DiC₈-PI(4,5)P₂ concentrations. Accordingly, in a series of patches, we monitored their response to sequential incremental then decremental concentrations from 1 to 100 µM. As shown in Fig. 5 (A and C), there was no significant difference in the responses to the two sequences (i.e., no DiC₈-PI(4,5)P₂ concentration-dependent hysteresis), as might be expected if substantial membrane accumulation of DiC₈-PI(4,5)P₂ had occurred. This is supported by the effect of applying randomized concentrations of DiC₈-PI(4,5)P₂ (Fig. 5 B). For all recordings, the stability of the channel P_open was checked at each concentration of DiC₈-PI(4,5)P₂; an example stability plot is shown in Fig. 5 D for Kv7.2/Kv7.3 channels at 100 μM DiC₈-PI(4,5)P₂.

DISCUSSION

The principal new result of the present experiments is that by exploring the activation of expressed M-channel subunits (Kv7.2 + Kv7.3) over a wide range of concentrations of the PI(4,5)P₂ analog DiC₈-PI(4,5)P₂, we have revealed a complex PI(4,5)P₂ concentration dependence, resolvable into high- and low-affinity components (EC₅₀ values of ∼1.3 and ∼75 µM). Though superficially different from the monotonic response of coexpressed Kv7.2 and Kv7.3 subunits previously reported (Li et al., 2005), this biphasic activation curve became evident in the present studies only after extension of the DiC₈-PI(4,5)P₂ concentration range to lower concentrations and improved fast-flow DiC₈-PI(4,5)P₂ application, allowing multiple concentrations to be applied to a single patch.

Our data suggest that the biphasic concentration-response curve is not a result of the presence of separate homomeric Kv7.2 and Kv7.3 channels or of a mixed population of channels with varying posttranslational modification or subunit stoichiometries (Shapiro et al., 2000; Stewart et al., 2012) but (overwhelmingly, at least) to a single population of heteromeric Kv7.2/7.3 channels (also see Fig. S3). Our reasons for this assertion are as follows: (a) in previous experiments using this expression system (Hadley et al., 2003), currents generated by coexpressed Kv7.2 and Kv7.3 cDNAs were inhibited by TEA across its full concentration range according to a single binding site equation with unity Hill slopes (0.98 ± 0.02) and with no improvement in fit using two or more binding site equations (in contrast, the experiments of Shapiro et al. [2000] implying a much more random assembly yielded a Hill slope of 0.58); (b) in these same experiments, currents generated by the concatemeric Kv7.2/Kv7.3 dimer yielded the same monotonic TEA inhibition curves with the same unity Hill slope (0.97 ± 0.12) and EC₅₀ values indistinguishable from those obtained with the coexpressed channels (although McCormack et al. [1992] reported that tandem dimers of mutated Drosophila melanogaster Shaker subunits did not guarantee a fixed stoichiometry, as judged by voltage sensitivity; this has not been supported by others who deduced a fixed stoichiometry of concatenated TEA-sensitive and -insensitive Shaker subunits, including Kavanaugh et al. [1992] and Liman et al. [1992]); (c) channels formed from both coexpressed and concatenated Kv7.2 and Kv7.3 cDNAs gave the same constant unitary current (∼0.52 pA) with very low variance across the entire range of experiments and throughout the PIP₂ concentration range; this would not be expected if separate homomeric Kv7.2 and Kv7.3 channels were present, as these show different current amplitudes (Selyanko et al., 2001; Li et al., 2005); thus, in multichannel patches containing a mixed channel population, a higher proportion of openings from high-affinity Kv7.3 homomers with larger current amplitudes (Li et al., 2005) would be expected at low PIP₂ concentrations; and (d) although recent experiments using atomic force microscopy (Stewart et al., 2012) show that (unusually) Kv7.2 and Kv7.3 subunits can assemble in a random manner, these same experiments also indicated that the mature tetramer was predominantly composed of two molecules of each subunit when equal amounts of KCNQ2 and KCNQ3 cDNA were transfected, as in our experiments.

In contrast (and in agreement with Li et al. [2005]), homomeric Kv7.2 and Kv7.3 channels both showed an approximately monotonic DiC₈-PI(4,5)P₂ concentration dependence, with Kv7.3 channels being much the more sensitive. In our experiments, EC₅₀ values were 3.6 ± 1.0 µM for Kv7.3 (as the mutant Kv7.3^T) and 76 ± 19.9 µM for Kv7.2. Thus, an obvious explanation for the biphasic concentration dependence of the Kv7.2/7.3 heteromer might be that it results from the separable effects of DiC₈-PI(4,5)P₂ binding to the two subunits. This suggestion is reinforced by the fact that the original high-affinity component of the DiC₈-PI(4,5)P₂–Kv7.2/7.3 concentration-response curve was lost when the Kv7.3 subunit in the heteromer was replaced with the much less PI(4,5)P₂-sensitive Kv7(EEE) construct. Hence, we might envisage that, at low concentrations of DiC₈-PI(4,5)P₂, binding to the high-affinity Kv7.3 subunit induces partial channel opening to ∼25% of the maximum P_open at a given voltage (i.e., to P_open of ∼0.2 at 0 mV); then, with higher concentrations of the ligand, additional binding to the lower-affinity Kv7.2 subunits promotes full opening (to P_open of ∼0.8). As each component of the P_open–DiC₈-PI(4,5)P₂ concentration curve is well fitted with a Hill slope near 1.4, this would be consistent with the idea that both copies of each subunit have to bind DiC₈-PI(4,5)P₂ to efficiently trigger the channel opening conformational change and that maximum opening requires all four subunits to be ligand bound. This latter is also implicit in previous modeling of M-current responses to changes in membrane PI(4,5)P₂ (Hernandez et al., 2009).

Identifiable contributions of ligand binding to individual subunits to overall activity have been noted in some other ligand-gated multisubunit channels. Thus, Harpsøe et al. (2011) have recently described a biphasic ligand activation curve for (α4)₃(β2)₂ nicotinic acetylcholine receptor channels (very like the present data) that results from binding to distinct high- and low-affinity sites; and, individual subunit contributions to homomeric Kir potassium channel open probability as a result of PI(4,5)P₂ binding to each of the four subunits have previously been deduced from the use of mutant subunits (Jin et al., 2008). Contributions to channel gating by ligand binding to less than the maximal number of subunits, resulting in partial channel openings to subconductance levels, have also been shown for AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazolpropionate)-type homotetrameric glutamate receptors (Rosenmund et al., 1998) and heterotetrameric cyclic nucleotide–gated cation channels (Ruiz and Karpen, 1997). Interestingly, independent (noncooperative) subunit contributions to the voltage gating of homologous (but homomeric) Kv7.1 channels have also been postulated, again with each subunit movement proposed to result in distinct subconductance states (Osteen et al., 2010). In the present experiments (and those of Jin et al. [2008]), partial activation by incremental PI(4,5)P₂ binding to individual subunits was not manifest by increasing single-channel current amplitudes but instead by clearly defined increments in open probability at constant channel conductance. This has not been experimentally excluded for Kv7.1 gating (Osteen et al., 2010), so it might be a general feature of Kv7 channel gating.

Kinetic schemes

Interpretation of the two-component DiC₈-PI(4,5)P₂ concentration-response curve requires postulation of a suitable mechanism that may describe the data. Accordingly, we have attempted to draw up a minimal scheme that could explain the observed DiC₈-PI(4,5)P₂–P_open curves for activation of WT Kv7.2/7.3 and mutated Kv7.2/Kv7.3(EEE) channels in terms of the binding affinities for the individual subunits and the equilibrium constants for channel opening. For this, we have viewed the Kv7.2/7.3 channels as essentially a multisubunit ligand–gated channel, with PI(4,5)P₂ as the ligand, and so have used a similar approach to that previously used for analyzing the activation of other ligand-gated heterotetrameric channels such as the NMDA receptor channel (Nahum-Levy et al., 2002; Rycroft and Gibb, 2002; Erreger et al., 2005) and cyclic nucleotide–gated channels (Ruiz and Karpen, 1999). Voltage-gating steps have been ignored because all experiments were performed at a constant pipette voltage of 0 mV, and available evidence suggests that changes in PI(4,5)P₂, induced, for example, by muscarinic agonists or by overexpressing phosphatases or kinases, do not affect M-current voltage sensitivity but only the maximum current amplitude (e.g., Adams et al., 1982; Marrion, 1997; Suh et al., 2006; Hernandez et al., 2009). We were also guided by previous observations on M-channel open–shut time distributions indicating a minimum of two open states (Selyanko and Brown, 1999; Selyanko et al., 2001; Prole et al., 2003; Li et al., 2004). We have assumed ab initio independent PI(4,5)P₂ binding to the individual subunits, without cooperativity (possible cooperativity in subunit binding is considered further below and in Fig. S1). We have also assumed that channel opening might occur after at least two subunits bind PI(4,5)P₂ but that maximum open probability requires binding to all four subunits, as assumed in Hernandez et al. (2009). Although not excluding the possibility that binding to one subunit might induce some channel opening (as with PI(4,5)P₂-sensitive inward rectifier Kir channels; Jin et al., 2008), we start from the postulate that in a heteromeric channels, such monoliganded openings will be very rare and/or very brief (e.g., cyclic nucleotide–gated channels [Ruiz and Karpen, 1997], AMPA receptor glutamate channels [Rosenmund et al., 1998], NMDA receptor channels [Gibb and Colquhoun, 1992], and nicotinic acetylcholine receptor channels [Colquhoun and Sakmann, 1985]). It is worth noting that, in the Kir channels, binding to each subunit induces an additional open state (up to four), each with its own distribution of open times (Jin et al., 2008). In contrast, the reduction of PI(4,5)P₂ that is produced by stimulating muscarinic receptors (Delmas and Brown, 2005) did not change the number of open states but instead altered the proportions of the exponential components in the open time distribution (Selyanko and Brown, 1993). Finally, as the concatemeric channels formed from the KCNQ2/3 dimeric cDNA gave identical results to the coexpressed KCNQ2 and KCNQ3 cDNAs, we assume that the tetrameric channel is a dimer of dimers, like other Kv channels (Tu and Deutsch, 1999) and also like some other heterotetrameric ligand–gated channels (Traynelis et al., 2010). This seems equally likely for Kv7 channels, as Etxeberria et al. (2008) report that coexpressed KCNQ2 and KCNQ3 cDNAs form Kv7.2/7.3 dimers, and, in their recent experiments, Stewart et al. (2012) could only detect proteins of molecular volumes corresponding to dimers or tetramers, not trimers. In addition, Stewart et al. (2012) suggest that there was no constraint on subunit arrangement, i.e., that the subunits might be arranged 2-3-2-3 or 2-3-3-2 with equal likelihood. This contrasts with heteromeric NMDA receptors (Salussolia et al., 2011) and cyclic nucleotide–gated channels (He et al., 2000) in which the different subunits are arranged symmetrically. However, as PIP₂ probably binds to the individual K⁺ channel subunits, rather than at their interfaces (Hansen et al., 2011), we have assumed that the position of each subunit within the tetramer does not affect their affinities for PI(4,5)P₂. Hence, for simplicity in constructing operational models, we have used the symmetrical 2-3-2-3 arrangement for illustrative purposes (Fig. 6 A).

The scheme that provided the best combined fit to the activation curves for both the WT and Kv7.3-mutated Kv7.2/7.3 channels is illustrated in Fig. 6. Some alternative models tested are illustrated in Fig. S1.

To obtain a two-component DiC₈-PI(4,5)P₂ concentration-response curve, the model requires a minimum of two channel open states (in accordance with previous kinetic analyses of M-channel activity; see above), one open state occurring when the two high-affinity PI(4,5)P₂ binding sites are occupied, and one when all four sites are occupied (e.g., model 3 in Fig. S1). However, it is then logical to also allow channel opening when the two high-affinity sites and one of the two low-affinity sites are occupied, giving three open states in total (Fig. S1, model 4). In fitting the model to the data, the equilibrium constants for channel opening for partially (E₃ and E₂) and fully (E₁) liganded channels were free parameters along with the equilibrium constants for DiC₈-PI(4,5)P₂ binding, K₂ and K₃. To test the ability of this model to describe M-channel activation, the data for stably expressed WT Kv7.2/Kv7.3 channels and transiently transfected Kv7.2/Kv7.3 concatemer data (Fig. 2) were combined and fitted, and then, the data for the Kv7.2/Kv7.3(EEE) mutant from sequential (Fig. 4) and randomized DiC₈-PI(4,5)P₂ applications were combined and fitted with the Kv7.2 affinity constrained to be the same as for the WT channels (Fig. 7). The values of E₁, E₂, and E₃ were free parameters for each data set. Parameter values obtained from these fits are summarized in Table 1.

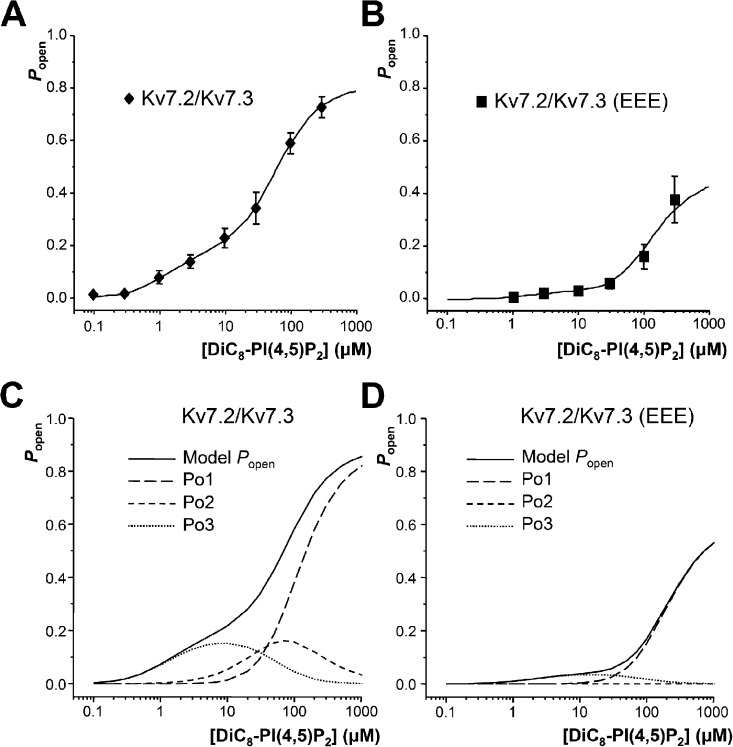
Figure 7.

Use of a subunit-specific model to predict the P_open of Kv7.2/7.3 channels. (A and B) Illustration of fitting of the model (solid lines), depicted in Fig. 6, to the steady-state open probability of Kv7.2/7.3 channels and Kv7.2/Kv7.3(EEE) mutant channels activated by DiC₈-PI(4,5)P₂. The fitted lines correspond to the parameter values given in Table 1 (data points show mean ± SEM; Kv7.2/Kv7.3, n = 20–49 patches; Kv7.2/Kv7.3(EEE), n = 8–13 patches). (C and D) Computed contribution of each of the open states (P_o1, P_o2, and P_o3) to the overall channel P_open. The model predicts that at low DiC₈-PI(4,5)P₂ concentrations, most channel openings result from binding of DiC₈-PI(4,5)P₂ to the Kv7.3 subunits, which peaks around 7 µM at 0.145 (dotted lines), whereas combined binding to both Kv7.3 and Kv7.2 subunits (dashed lines) underlies the steepening of the P_open curve and the high open probabilities observed at high DiC₈-PI(4,5)P₂ concentrations. In contrast, mutant Kv7.2/Kv7.3(EEE) channels are weakly activated by DiC₈-PI(4,5)P₂, with a maximum open probability for channels with both Kv7.3 binding sites occupied (P_o3) of 0.027 occurring at 10 µM DiC₈-PI(4,5)P₂.

Table 1.

Model parameters (±SD) derived from fitting the DiC₈-PI(4,5)P₂–P_open curve

	Kv7.2/Kv7.3	Kv7.2/Kv7.3(EEE)
K2 (µM)	96.0 ± 32	96 (fixed)
K3 (µM)	0.84 ± 0.29	0.94 ± 5.02
E1	4.42 ± 0.61	0.89 ± 0.43
E2	0.46 ± 0.39	0.00
E3	0.26 ± 0.07	0.04 ± 0.14
Po (max)	0.82	0.47

The steepness of the DiC₈-PI(4,5)P₂ concentration-response relationship (n_H > 1) is consistent with the idea that monoliganded channels do not open (or open with very low probability) and that with increasing number of occupied binding sites, the efficiency of channel gating increases, resulting in Hill coefficients >1 for the individual components fit to the P_open curve. This cooperativity in the DiC₈-PI(4,5)P₂ concentration-response relationship does not require any change in DiC₈-PI(4,5)P₂ binding affinity in response to DiC₈-PI(4,5)P₂ binding to other subunits.

We also considered the question of cooperativity of PI(4,5)P₂ binding affinity to the Kv7.2 and Kv7.3 subunits (Fig. S1, model 5). Here, the channel is considered as a dimer of dimers, each dimer composed of a Kv7.2/Kv7.3 pair. The possibility that a negative cooperativity in PI(4,5)P₂ binding within the dimer may contribute to the biphasic nature of the P_open curve was then investigated by fitting this model to the data. Although the results suggest that a modest cooperativity (a 1.4-fold decrease in affinity for the WT channel and fivefold for the Kv7.2/Kv7.3(EEE) mutant) improves the quality of the fit, allowing cooperativity in the binding also creates an extra functional state, and so, this model is less parsimonious than the other models tested. Hence, we retained the independent binding model 4 for our further analyses.

The results of fitting this model to the data illustrate that the two-component DiC₈-PI(4,5)P₂ concentration-response curve can be described by a mechanism in which the microscopic equilibrium binding constants are K₃ = 0.84 µM and K₂ = 96 µM. Both the half-maximum concentrations (EC₅₀ values) and maximum P_open values calculated for the data from heteromeric Kv7.2/Kv7.3 and homomeric Kv7.2 and Kv7.3 channels concur with previous observations (Li et al., 2005; Hernandez et al., 2009), confirming that under these experimental conditions, channel behavior is consistent.

The data obtained by expressing Kv7.2 with the Kv7.3(EEE) mutant strengthen the conclusion that M-channel opening begins when only the high-affinity subunits are bound to PI(4,5)P₂. Interpreting the effects of the triple EEE mutation of the Kv7.3 subunit using this model generates the surprising suggestion that, although moderate changes in affinity cannot be excluded from this analysis (the parameter SD for our estimate of K₃ indicates this parameter is relatively poorly defined), this mutation does not, per se, decrease the binding affinity of the channel (a low level of channel activity at 1, 3, and 10 µM was consistently observed for this mutant) but instead that the mutation results in a marked decrease in the ability of the channel to open when only the high-affinity subunits are occupied. The model also predicts some decrease in gating efficacy of the fully liganded channel (fourfold decreased E₁) for the mutant; this cannot be determined with precision because of the high concentrations of DiC₈-PI(4,5)P₂ that would be required to define accurately the maximum of the P_open curve for this mutant. In Fig. S2, this conclusion is further explored by fitting the Kv7.2/Kv7.3(EEE) data while constraining the channel-gating efficacy to that of the WT channels. The results show (Fig. S2, left) that the data can only be described by this model if these mutations also affect channel gating (Table S2). In contrast, constraining the value of K₃ to that predicted from the free energy calculations of Hernandez et al. (2009) can give a reasonably good description of the data (Fig. S2, middle), provided the channel-gating efficacy is also decreased.

The behavior of this model is further illustrated in Fig. 7 (C and D), in which the concentration dependence of the occupancy of the three open states (O1, O2, and O3) and the overall channel P_open are shown, calculated using the parameter values obtained from fitting WT heteromeric Kv7.2/Kv7.3 and from the fit to the heteromeric Kv7.2/Kv7.3(EEE) mutant channels. These emphasize the importance for this model of openings occurring when only the high-affinity Kv7.3 subunits have PI(4,5)P₂ bound, which are predicted to contribute almost all the open probability at low (<10 µM) DiC₈-PI(4,5)P₂ concentration, and how a large drop in overall PI(4,5)P₂ affinity shifts the equilibrium throughout the mechanism so that much higher concentrations of ligand are needed to achieve significant channel opening.

The fact that the effect of the Kv7.3 mutation appeared to result in a change in the equilibrium constants for channel opening rather than the binding constant K₃ seems counterintuitive, given that a plausible binding site in the C terminus of the Kv7 channel has been deduced from the changes in free energy of binding caused by the mutation (Hernandez et al., 2008). Notwithstanding, we verified that the shift of the DiC₈-PI(4,5)P₂–P_open curve could not be satisfactorily explained simply by altering K₃ without simultaneous and substantial changes in the opening and/or closing rates (Fig. S2). Inclusion of cooperativity between the PI(4,5)P₂ binding sites on the Kv7.2 and Kv7.3 subunits did not negate this conclusion, as the best fit still required a decrease in gating efficiency (Fig. S2, right). Recent structural work on PI(4,5)P₂-gated inward rectifier Kir2 channels (Hansen et al., 2011) suggests why this might be so: binding to PI(4,5)P₂ induces a large conformational change such that the cytoplasmic domain is drawn up to become attached to the transmembrane domain to allow the channel to open. One might then envisage that the weaker attachment of a channel containing the mutated subunit is manifest primarily as a less efficient gating. Comparable effects of binding-site mutations on the gating of other ligand-activated ion channels have been discussed extensively by Colquhoun (1998).

Physiological significance

The particular significance of the heteromeric nature of the Kv7.2/Kv7.3 channels is highlighted by comparison with the data from the homomeric channels. Whereas the low-affinity component of the heteromeric P_open curve is very similar to the homomeric Kv7.2 data, the high-affinity component tends to provide a region of M conductance on the P_open curve predicted to be relatively insensitive to small changes in PI(4,5)P₂ concentration.

This might be expected to counteract excessive increases in excitability resulting from strong activation of phospholipase C–coupled receptors. Thus, even though a muscarinic agonist can reduce membrane [PI(4,5)P₂] by ≥90% (Horowitz et al., 2005; Winks et al., 2005), it does not normally produce complete inhibition of the M current; the Kv7.2 subunits act as the primary sensors of changes in membrane PI(4,5)P₂, with the Kv7.3 subunits being, to an extent, constitutively active (Hernandez et al., 2009). On the other hand, the low-affinity component contributes a region of channel P_open that is more steeply sensitive to changes in PI(4,5)P₂ concentration than occurs with either Kv7.2 or Kv7.3 homomeric channels or would be expected in a cell simply expressing a mixture of channels like these.