Membrane Potential-Dependent Inhibition of the Na⁺,K⁺-ATPase by para-Nitrobenzyltriethylammonium Bromide

Abstract

Membrane potential (V_M)-dependent inhibitors of the Na⁺,K⁺-ATPase are a new class of compounds that may have inherent advantages over currently available drugs targeting this enzyme. However, two questions remain unanswered regarding these inhibitors: (1) what is the mechanism of V_M-dependent Na⁺,K⁺-ATPase inhibition, and (2) is their binding affinity high enough to consider them as possible lead compounds? To address these questions, we investigated how a recently synthesized V_M-dependent Na⁺,K⁺-ATPase inhibitor, para-nitrobenzyltriethylamine (pNBTEA), binds to the enzyme by measuring the extracellular pNBTEA concentration and V_M dependence of ouabain-sensitive transient charge movements in whole-cell patch-clamped rat cardiac ventricular myocytes. By analyzing the kinetics of charge movements and the steady-state distribution of charge, we show that the V_M-dependent properties of pNBTEA binding differ from those for extracellular Na⁺ and K⁺ binding, even though inhibitor binding is competitive with extracellular K⁺. The data were also fit to specific models for pNBTEA binding to show that pNBTEA binding is a rate-limiting V_M-dependent reaction that, in light of homology models for the Na⁺,K⁺-ATPase, we interpret as a transfer reaction of pNBTEA from a peripheral binding site in the enzyme to a site near the known K⁺ coordination sites buried within the transmembrane helices of the enzyme. These models also suggest that binding occurs with an apparent affinity of 7 μM. This apparent binding affinity suggests that high-affinity V_M-dependent Na⁺,K⁺-ATPase inhibitors should be feasible to design and test as specific enzyme inhibitors.

Introduction

Interest in small-molecule inhibitors of the P-type Na⁺,K⁺-ATPase has reemerged with the realization that pharmacological interventions targeting this enzyme might be relevant in a diverse array of disease processes. The Na⁺,K⁺-ATPase is well known for its critical role in developing and maintaining electrochemical gradients for Na⁺ and K⁺ across the plasma membrane (Glynn, 1985). In this role, the Na⁺,K⁺-ATPase controls contractility of cardiac muscle cells by regulating cell Ca²⁺ loading via the sarcolemmal Na⁺/Ca⁺ exchanger (Eisner et al., 1984). Manipulating the Na⁺ electrochemical gradient, and thereby cellular Ca²⁺, by Na⁺,K⁺-ATPase inhibition is believed to be the basis for the inotropic actions of the cardiac glycoside, digoxin (Akera and Brody, 1977), a classic pharmacological agent and, until recently, a first-line treatment for congestive heart failure (Gheorghiade et al., 2006). Mutations in the enzyme's α subunit have been linked to autosomal dominant forms of migraine (De Fusco et al., 2003) and Parkinson's disease (Blanco-Arias et al., 2009). A signaling function has also been postulated for the Na⁺,K⁺-ATPase via Src-dependent pathways (Haas et al., 2000; Tian et al., 2006). For example, the cardiac glycoside ouabain has been shown to regulate cell junctional contacts (Larre et al., 2010) and cell proliferation (Tian et al., 2009) at concentrations that have little or no significant effect on net ion transport. Such reports have generated interest in Na⁺,K⁺-ATPase inhibitors as potential chemotherapeutic agents (for review, see Newman et al., 2008) and suggest that the Na⁺,K⁺-ATPase might be an attractive drug target beyond its established roles in inotropic and antiarrhythmic therapeutics.

Cardiac glycosides are the most widely studied Na⁺,K⁺-ATPase inhibitors. Mutagenesis studies have identified amino acids in the enzyme's α subunit that are important for ouabain binding (for review, see Lingrel, 2010) and recent high-resolution structures of the Na⁺,K⁺-ATPase include bound ouabain (Ogawa et al., 2009; Yatime et al., 2011). Cardiac glycosides have been synthesized and tested in more than five decades of drug discovery efforts (Glynn, 1964; Güntert and Linde, 1981; Gobbini and Cerri, 2005). In addition, other high-affinity Na⁺,K⁺-ATPase inhibitors, such as cassaine (Tobin et al., 1975), have been reported and have served as the basis for recent efforts to synthesize novel enzyme inhibitors (Gobbini and Cerri, 2005). However, none of these inhibitors can distinguish between Na⁺,K⁺-ATPase located in different cellular or tissue compartments in which the enzyme resides. Selectivity in Na⁺,K⁺-ATPase inhibition, however, may provide advantages in treatment of congestive heart failure and is certainly relevant if Na⁺,K⁺-ATPase inhibitors are to be developed as chemotherapeutic agents. For this reason, the search for novel Na⁺,K⁺-ATPase inhibitors is a promising area of drug discovery.

In a previous study, we identified a compound, benzyltriethylamine (BTEA), that inhibits the Na⁺,K⁺-ATPase in a membrane-potential (V_M)-dependent fashion such that enzyme block is more pronounced at negative potentials (Peluffo et al., 2004). This compound seems to bind at a K⁺ coordination site within the enzyme although, unlike K⁺, it is neither occluded nor transported. What is intriguing about BTEA is that it is the first reported V_M-dependent blocker of the Na⁺,K⁺-ATPase, although several other V_M-dependent inhibitors have since been reported (Peluffo et al., 2009; Ratheal et al., 2010). These compounds offer the possibility of a class of Na⁺,K⁺-ATPase inhibitors that distinguish, to some degree, enzyme located in electrically polarized cells versus enzyme in cells with depolarized membrane potentials. As will be presented under Discussion, this property might be useful for the treatment of congestive heart failure. In addition, V_M-dependent Na⁺,K⁺-ATPase inhibitors might also be useful as chemotherapeutic agents.

BTEA is a low-affinity blocker, used in the millimolar concentration range (Forbush, 1988; Peluffo et al., 2004). For this reason, the para-nitro derivative of BTEA, pNBTEA, was synthesized and found to have similar V_M-dependent inhibitory effects on the Na⁺,K⁺-ATPase, but at a much lower concentration (Peluffo et al., 2009). These results were promising for development of similar compounds as high-affinity Na⁺,K⁺-ATPase inhibitors, but two important questions remained unanswered in previous work. First, although BTEA and pNBTEA seem to bind at a K⁺ site in the enzyme, their mechanism of V_M-dependent inhibition was not studied. Using pre–steady-state binding kinetics, we have compared different models for V_M-dependent binding in the present work to determine which best describes pNBTEA inhibition of the Na⁺,K⁺-ATPase. Second, we have not previously determined the apparent affinity for inhibition of the Na⁺,K⁺-ATPase by pNBTEA. Our analysis here shows it is a much more potent inhibitor than the parent BTEA. These results suggest that further development of V_M-dependent Na⁺,K⁺-ATPase inhibitors is warranted.

Materials and Methods

Whole-Cell Patch Clamp.

Ventricular myocytes were enzymatically isolated from rat hearts and voltage-clamped with patch electrodes (1.0–1.5 MΩ) as published previously (Ishizuka et al., 1996). Animals were treated according to the Guide for the Care and Use of Laboratory Animals (Institute of Laboratory Animal Resources, 1996) in a protocol approved by our institutional animal care and use committee. For measurements of transient charge movements, protocols were followed as outlined previously (Peluffo and Berlin, 1997; Peluffo et al., 2009). Experiments were performed at 18–20°C with Na⁺- and K⁺-free superfusion solutions containing 145 mM tetramethylammonium chloride, 2.3 mM MgCl₂, 0.2 mM CdCl₂, 5.5 mM dextrose, and 10 mM HEPES (pH 7.4 with Tris). The bromide salt of pNBTEA was added to this solution at the indicated concentrations. The patch electrode solution contained 130 mM K⁺, 20 mM tetraethyl ammonium chloride, 9.1 mM MgCl₂, 0.7 mM ATP-Mg²⁺ salt, 30 mM phosphate (H₂PO₄⁻ + HPO₄²⁻), 1 mM EGTA, 66 mM aspartic acid, and 10 mM HEPES, pH 7.3 (20°C). The magnesium phosphate concentration was calculated with MaxChelator to be 1.3 mM.

The experimental procedure to measure extracellular pNBTEA transient charge movements was to first superfuse a voltage-clamped myocyte with a pNBTEA-containing Na⁺- and K⁺-free solution and determine the current-voltage relationship between −160 and +100 mV two times, separated by 1 min. The myocyte was then perfused for 2 min with the same solution that also included 1 mM ouabain, and another current-voltage relationship was determined before switching back to the ouabain-free solution. Our previous experiments (Peluffo et al., 2009) have shown that 2 min of exposure to 1 mM ouabain is sufficient to completely block quaternary amine-dependent transient charge movements. Currents measured before and 2 min after addition of ouabain were then subtracted to yield ouabain-sensitive transient currents. These currents were integrated and divided by cell capacitance to yield a ouabain-sensitive charge (q; in units of femtocoulombs per picofarad). A more complete description of the experimental protocol is found in Peluffo et al. (2009).

Analysis, Curve-Fitting, and Model Selection.

Data are presented as means ± S.E.M. for the indicated number of replicates or cells. Cell capacitance was calculated as the integral of current elicited with 5-mV pulses. Indicated functions were fit to the data with a nonlinear least-squares algorithm available in commercial software (SigmaPlot, Systat Software Inc., San Jose, CA) using statistical weights proportional to (S.E.M.)⁻¹. Different binding models were evaluated by applying a second-order Akaike information criterion and Akaike weights (Yamaoka et al., 1978; Burnham and Anderson, 2002; González-Lebrero et al., 2002; Montes et al., 2004). The Akaike information criterion (AIC_c) with a limited data set was calculated for each model as

where L(θ|y) is the root mean square of the residuals between the data and fitted model function, n is the sample size, and K is the number of estimated parameters. To determine the weight of evidence that a particular model is actually the best model to describe the data, Akaike weights (w_i) were calculated as

where AIC_i is the AIC_c for the ith function out of the total number (N) of functions tested. The likelihood that the ith model is the best model for the data increases as w_i approaches a value of 1 (Burnham and Anderson, 2002). Experiments using 100 μM pNBTEA have been reported in Peluffo et al. (2009); however, analysis of the data set at all tested pNBTEA concentrations is presented here for the first time.

Reagents.

Reagents were from Sigma-Aldrich (St. Louis, MO) and were of analytical grade or higher. pNBTEA was synthesized as outlined previously (Peluffo et al., 2009).

Results

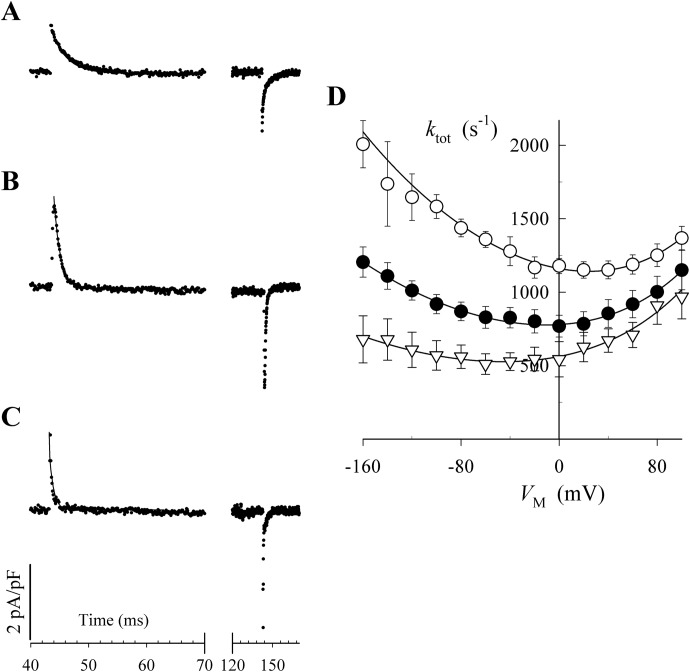
Peluffo et al. (2009) showed that BTEA competitively inhibits ⁸⁶Rb⁺ occlusion by the Na⁺,K⁺-ATPase. In the same study, pNBTEA was found to be a V_M-dependent inhibitor by examining the effects of 100 μM pNBTEA on steady-state Na⁺,K⁺-pump current and pNBTEA-dependent pre–steady-state transient charge movements at different membrane potentials. To gain greater insight into the mechanism of enzyme block by pNBTEA, we have also conducted measurements of transient charge movements with 33 and 300 μM concentrations of the quaternary amine added to the perfusion solution in patch-clamped rat ventricular myocytes (see Materials and Methods). Figure 1, A to C, shows representative 1 mM ouabain-sensitive difference currents recorded when the membrane potential was stepped from the holding potential, −40 mV, to 0 mV for 100 ms, before returning to the holding potential. Our previous work (Peluffo and Berlin, 1997; Peluffo et al., 2009) has shown that 1 mM ouabain is sufficient to completely block extracellular ion-dependent charge movements in rat ventricular myocytes. The ouabain sensitivity of these currents demonstrates that they arise from a V_M-dependent process in the Na⁺,K⁺-ATPase. In the absence of pNBTEA, ouabain-sensitive transient currents were not observed (Peluffo et al., 2009). Thus, these currents show that the inhibition of the Na⁺,K⁺-ATPase by the positively charged pNBTEA involves at least one V_M-dependent reaction.

Fig. 1.

Ouabain-sensitive pre–steady-state currents with various pNBTEA concentrations. Currents were recorded in response to a 100-ms depolarization to 0 mV in the presence and absence of 1 mM ouabain in superfusion solutions containing 33 μM (A), 100 μM (B), and 300 μM pNBTEA (C). Ouabain-sensitive difference currents are displayed without any capacitance correction or leak subtraction. The solid curve through the decaying phase shows the exponential function fit to the data. Note the change in the time scale. The rate of current decay (k_tot) is displayed as a function of V_M (D) for 33 μM (▿), 100 μM (●), and 300 μM pNBTEA (○). The solid curves were determined by fitting the entire data set to eq. 1. The calculated values of k_f⁰ and k_r⁰ were 58,600 ± 2000 s⁻¹ M⁻ⁿ and 282 ± 9 s⁻¹, respectively.

Ouabain-sensitive charge movements reflect a change of ion binding by the Na⁺,K⁺-ATPase in response to a change in V_M (Gadsby et al., 1993; Peluffo and Berlin, 1997). With transported cations (i.e., Na⁺ and K⁺), the kinetics of these charge movements are limited by subsequent electroneutral reactions involved in ion occlusion by the enzyme (Gadsby et al., 1993; Hilgemann, 1994; Wuddel and Apell, 1995). However, as we have previously shown, organic quaternary amine inhibitors of the Na⁺,K⁺-ATPase, such as pNBTEA, are not occluded (Peluffo et al., 2009). Therefore, the kinetics of pNBTEA-dependent transient charge movements are a direct measure of the rate of quaternary amine binding reactions.

As shown in Fig. 1, A to C, depolarization produced an outward current transient and hyperpolarization an inward current transient, consistent with the movement of a positive charge in the membrane electric field. An exponential function provided a good fit to the decaying portion of the current traces in Fig. 1, A to C, indicating a pseudo-first-order process. This fitting allowed us to derive a rate (k_tot) for the change in pNBTEA binding after a V_M jump. The rate of decay of the transient current increased at higher pNBTEA concentrations (Fig. 1D), as would be expected for a pseudo-first-order ligand binding reaction. Thus, the transient currents shown here result from the V_M-dependent binding of the quaternary amine as it inhibits the Na⁺,K⁺-ATPase.

The calculated k_tot is plotted as a function of V_M for all pNBTEA concentrations tested in Fig. 1D. This k_tot-V_M relationship has several interesting features. The relationship is U-shaped for all pNBTEA concentrations tested. This feature distinguishes quaternary amine binding kinetics from those for ions that are bound, occluded, and transported by the Na⁺,K⁺-ATPase (see Discussion). Of interest, the V_M at which k_tot was a minimum shifted to more positive V_M with increasing pNBTEA concentration, and the kinetics seemed to be more V_M-dependent at positive potentials. To describe the pNBTEA- and V_M-dependent properties of k_tot, the entire data set was fitted simultaneously with eq. 1, which is derived assuming that first-order kinetics of pNBTEA-dependent transient currents reflect a system in which Na⁺,K⁺-ATPase is amine-bound or free (i.e., a pseudo-two-state model),

where k_f⁰ and k_r⁰ are the forward and reverse rate constants for pNBTEA binding at 0 mV, [Q] is the extracellular pNBTEA concentration, n is the Hill coefficient for the reaction, λ_Q is the apparent charge moved in the V_M-dependent reaction, δ is a proportionality coefficient that distributes the effect of the electric field between the forward and backward reactions, and F, R, and T are the Faraday constant, the gas constant, and the absolute temperature, respectively. The calculated values for k_f⁰ and k_r⁰ are given in the legend to Fig. 1. This calculation showed that the apparent charge (λ_Q) equaled 0.41 ± 0.01, equivalent to a full charge dissipating 41% of the electric field during enzyme inhibition. This value was not significantly different from the 37% of the electric field dissipated by extracellular K⁺ during its activation of ion transport by the Na⁺,K⁺-ATPase (Peluffo and Berlin, 1997). This similarity along with the competitive nature of pNBTEA enzyme inhibition led us to conclude that these amines were binding at a K⁺ coordination site in the enzyme (Peluffo et al., 2009). The proportionality constant δ was 0.32 ± 0.01. This value reflects the steeper V_M dependence of k_tot at positive potentials and the shift in the V_M at which k_tot reaches a minimum with increased pNBTEA concentration (see eq. 1). The Hill coefficient was 0.52 ± 0.01, a value indicative of negative cooperativity in pNBTEA binding to the enzyme, which implies that more than one amine molecule binds to the enzyme.

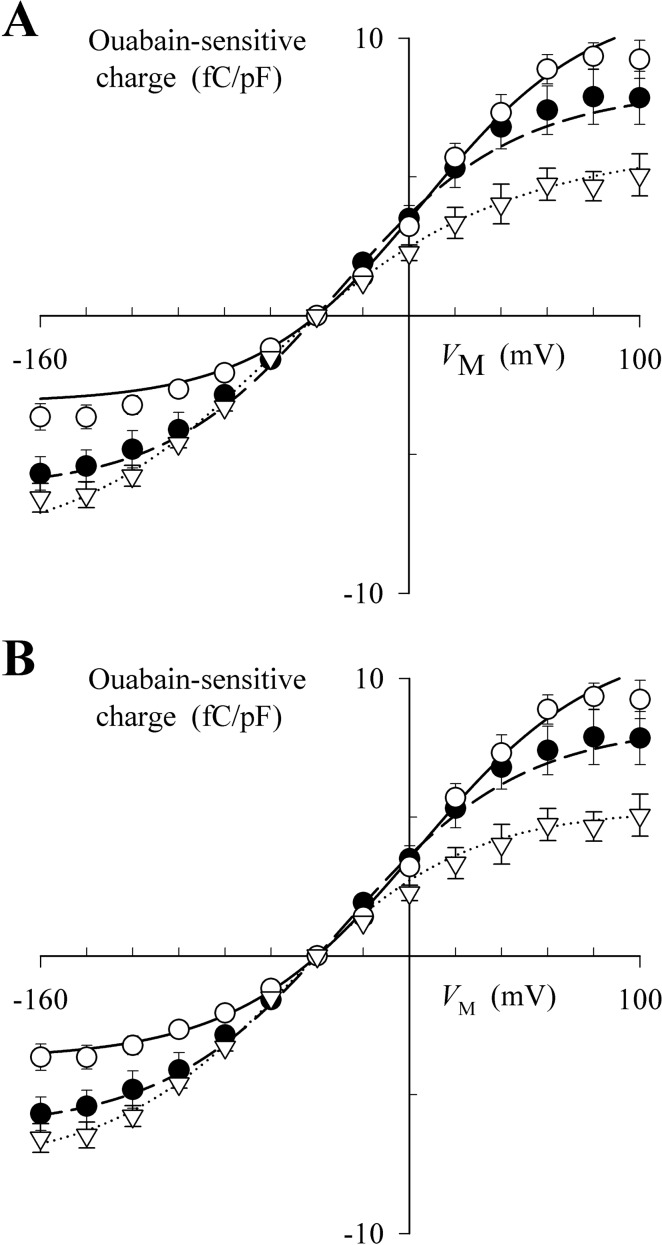
To further describe the V_M dependence of pNBTEA binding, charge (q) moved in response to step changes in V_M was calculated by integrating the area under ouabain-sensitive difference currents. The current integral at the beginning of the V_M step, q_ON, was the same as the current integral, q_OFF, measured after returning to the holding potential. Equality of q_ON and q_OFF is indicative of a reversible binding process for the quaternary amine (Peluffo and Berlin, 1997; Peluffo et al., 2009).

The values for q_ON were plotted against V_M, before (Fig. 2A) and after normalization to q_TOT, the total amount of charge moved (Fig. 2B). The data at each pNBTEA concentration were also fitted with a Boltzmann equation that describes the probability of the enzyme being in a pNBTEA-bound state as a function of V_M. Best-fit parameter values are shown in Table 1.

Fig. 2.

pNBTEA concentration and V_M dependence of charge movement. Charge (q) was calculated as the integral of the ouabain-sensitive difference current recorded in response to a step change in V_M (q_ON) divided by cell capacitance during superfusion with solutions containing 33 (▿), 100 (●), and 300 μM pNBTEA (○). A, charge. B, charge normalized to q_TOT calculated by fitting the data at each pNBTEA concentration with the following Boltzmann equation: q = q_min + q_TOT/(1 + exp[ − (V_M − V_q)/z_q]) Values for the best fit parameters are given in Table 1.

TABLE 1.

Pseudo-two-state Boltzmann function parameters for the V_M dependence of q

Parameter	[pNBTEA]
	33 μM	100 μM	300 μM
qTOT (fC/pF)	13.7 ± 0.6	14.9 ± 0.4	14.0 ± 0.5
qMIN (fC/pF)	−8.3 ± 0.5	−6.1 ± 0.2	−3.6 ± 0.2
Vq (mV)	−57.0 ± 3.4	−27.1 ± 1.8	0.5 ± 2.9
zq	0.56 ± 0.04	0.65 ± 0.03	0.72 ± 0.06

This analysis revealed V_M-dependent properties of pNBTEA binding reactions as well as limitations of the pseudo-two-state model analysis. q_TOT was unchanged with pNBTEA concentration, as if V_M could drive pNBTEA into or out of a fixed number of Na⁺,K⁺-ATPase binding sites over the range of concentrations tested; however, the quantity of charge moved by a large negative step in V_M (q_MIN) from the holding potential decreased as the pNBTEA concentration was increased. This shift in the V_M dependence of charge movement, shown more clearly in Fig. 2B, is consistent with increased amine binding at the holding potential as the pNBTEA concentration is increased (i.e., at a higher amine concentration, a smaller fraction of total Na⁺,K⁺-ATPase remains to be driven into the bound state at negative V_M). The magnitude of the shift in charge movement, 26 mV per e-fold change in pNBTEA concentration (Supplemental Fig. 1), would be consistent with one charge dissipating the equivalent of the entire electric field across the cell membrane during pNBTEA binding. Thus, V_M dependence of binding calculated in this manner seems to be much stronger than that determined by the value for λ_Q, the apparent charge calculated from the kinetics of transient current decay (Fig. 1).

Eyring rate theory suggests that the shift in charge movement depends on the effective charge of the V_M-dependent reaction and the molecularity of that reaction (Peluffo, 2004). Because the Hill coefficient for transient currents does not equal 1 (Fig. 1), the molecularity of the reaction is unknown, although clearly more than one pNBTEA molecule is involved in these reactions. Thus, there is no a priori expectation that V_M-dependent parameters derived from analyses of kinetics and quantity of charge movement will be consistent because the pseudo-two-state model used for analysis of data in Figs. 1 and 2 accommodates neither the molecularity nor the type of binding reaction.

To understand more about pNBTEA binding to the Na⁺,K⁺-ATPase, different ligand binding models were evaluated to determine which provides the best fit to the data. In evaluating potential binding models for pNBTEA, random schemes were excluded because Rb⁺ binding to the Na⁺,K⁺-ATPase is an ordered process (Forbush, 1987; González-Lebrero et al., 2002). Given that pNBTEA seems to bind at an extracellular K⁺ coordination site, the assumption of ordered binding is also likely to be valid. Furthermore, the effect of BTEA on Rb⁺ occlusion (Peluffo et al., 2009) is well described by postulating two amine binding sites in the enzyme. Although a greater number of sites cannot be excluded, there is no obvious rationale to include more. For this reason, only models with two pNBTEA binding sites were evaluated. The monoexponential decay of pNBTEA-activated transient charge movements also suggests that either 1) rate-limiting V_M-dependent reactions have similar kinetics or 2) multiple V_M-dependent reactions have very different kinetics. In both cases, these schemes simplify to an ordered reaction with a single V_M-dependent reaction.

In a broad sense, ordered reaction schemes fall into two categories shown as Schemes A and B. Scheme A is a classic sequential reaction mechanism for a two-site enzyme in which pNBTEA binding at site 1 and/or site 2 can be V_M-dependent. The rates of the binding reactions are described by pseudo-first-order forward (k_x) and reverse (k_−x) rate constants (where x = 1,2). Because the decay of pNBTEA-dependent transient currents is exponential, it can be assumed that for Scheme A either the sum of k₁ + k₋₁ is similar to the sum of k₂ + k₋₂ or these sums are very different. Scheme B is based on the work of Glynn et al. (1985), Forbush (1987), and González-Lebrero et al. (2002), whose analysis of Rb⁺ occlusion kinetics by the Na⁺,K⁺-ATPase suggested that Rb⁺ binding is in rapid equilibrium with the Na⁺,K⁺-ATPase but the sequential binding of each Rb⁺ is limited by the accessibility of the Rb⁺ binding sites, as if a gate with low open probability (“leaky gate”) limited access to the ion coordination sites. Because BTEA is not occluded (Peluffo et al., 2009), we have instead substituted a rate-limiting reaction of the pNBTEA-bound enzyme, illustrated in Scheme B as transfer of the bound amine between the first and second binding sites (see Discussion). Any or all of these reaction steps can be V_M-dependent.

Scheme A.

Scheme B.

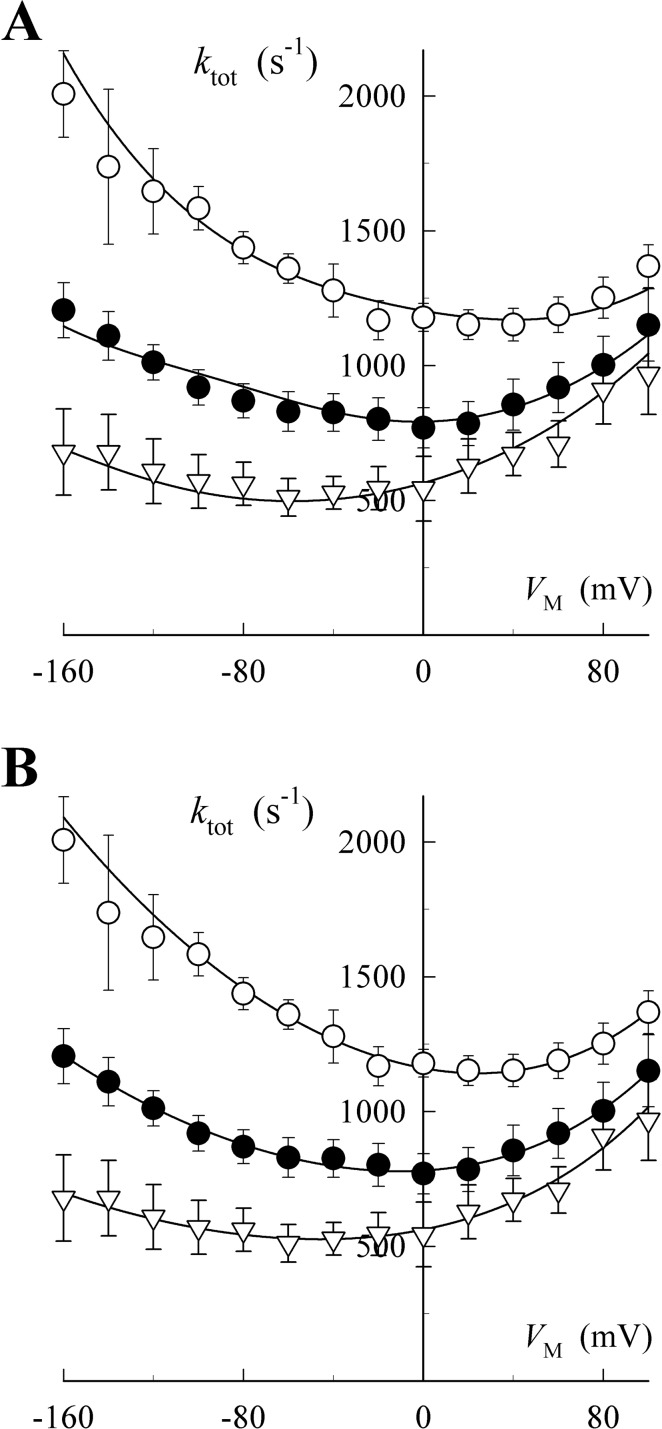
Given these two reaction schemes, there are a total of 10 possible model systems (3 for Scheme A and 7 for Scheme B) that derive from assigning V_M dependence to any one or combination of reaction steps. Some of these model systems are mathematically identical so that only eight model systems were fitted to the data for the k_tot-V_M relationship. Most models could not be fitted to the data without collapsing to a simpler system. Of the remaining models, the best-fitting models representative of Scheme A and Scheme B are presented in Fig. 3 for the k_tot-V_M relationship. Because these models have different numbers of free parameters, evaluations of goodness-of-fit were made using an Akaike information criterion (AIC_c).

Fig. 3.

Fitting charge movement kinetics with specific pNBTEA binding models. Data points are reproduced from Fig. 1D. Curves represent the functions solved for the best fit models based on Scheme A (A) and Scheme B (B) using eqs. A6 and B9, respectively. These equations and their best fit parameter values are listed in the supplemental data. Symbols are as indicated in Fig. 1D.

The best-fitting models for Schemes A and B both tracked the experimental data well (see supplemental data for the fitted functions and best-fit parameter values). However, it is clear that the Scheme B model provided the better fit. This graphical impression is substantiated by the AIC_c for Scheme A (AIC_c = 321.2) and for Scheme B (AIC_c = 226.8), which provide an Akaike weight (w_i) for Scheme A that approaches a value of 0, meaning that the model is highly unlikely, whereas the w_i for Scheme B approaches a value of 1, meaning that this model is quite likely to be the best one describing the V_M and pNBTEA concentration dependence of k_tot (see Materials and Methods). From this analysis, we conclude that the V_M-dependent step in pNBTEA inhibition of the Na⁺,K⁺-ATPase occurs as a rate-limiting reaction of the amine-bound enzyme. As presented under Discussion, we believe that this V_M-dependent step represents the transfer of bound pNBTEA from site 1 to site 2 within the enzyme.

Figure 4 shows the functions fitted to the q-V_M data for the same Scheme A and B models (see supplemental data). Again, both models seem to fit these steady-state data quite well; however, the model based on Scheme B seems to provide the better fit. In addition, both models show that the membrane electric field has a similar effect on the V_M dependence of charge kinetics and quantity. With Scheme A, binding of the first and second amine molecule is V_M-dependent, together dissipating between 80 and 100% of the electric field, for both charge kinetics (Fig. 3A) and quantity (Fig. 4A). Scheme B is also somewhat successful with the single V_M-dependent reaction predicted to dissipate between 41 and 64% of the membrane electric field (see supplemental data for values of λ_Q) for charge kinetics (Fig. 3B) and quantity (Fig. 4B). Thus, to a large degree, the apparent contradiction regarding the effectiveness of the membrane electric field on charge movement parameters derived from using a more generalized pseudo-two-state model is overcome by using a specific model that accounts for the molecularity of amine binding to the Na⁺,K⁺-ATPase.

Fig. 4.

Fitting the q-V_M relationship with specific pNBTEA binding models. Data points are reproduced from Fig. 2A. Curves show the functions solved for the best-fit models based on Scheme A (A) and Scheme B (B) using eqs. A9 and B11, respectively. These equations and their best fit parameter values are listed in the Supplemental Data. Symbols are as indicated in the legend to Fig. 2.

What is interesting about the best-fit functions for Scheme B is the prediction that the first pNBTEA binds to the Na⁺,K⁺-ATPase with high affinity. From the V_M dependence of steady-state charge distribution, the model calculates an apparent affinity of 7 μM (K_D1 = 1/K_a1 = 6.9 μM). Consistent with the negative cooperativity shown in Fig. 1, the second amine molecule binds with lower apparent affinity (e.g., K_D2 = 1/K_a2 = 65 μM from the V_M dependence of steady-state distribution of charge) (See supplemental data for parameter values when eq. B11 is solved.) Our previous experiments showed that binding of one molecule of pNBTEA inhibits the Na⁺,K⁺-ATPase (Peluffo et al., 2009). Thus, we conclude that the effect of negative V_M is to increase apparent affinity by driving the amine into the second binding site within the enzyme.

Discussion

In this report, pNBTEA reaction kinetics with the Na⁺,K⁺-ATPase were examined. We reported the first V_M-dependent Na⁺,K⁺-ATPase inhibitor, BTEA (Peluffo et al., 2004), and subsequently an initial characterization of its para-nitro derivative, pNBTEA (Peluffo et al., 2009). These compounds are competitive inhibitors of K⁺ activation of the Na⁺,K⁺-ATPase hydrolytic activity, extracellular K⁺ activation of steady-state ion transport, and ⁸⁶Rb⁺ occlusion. Their V_M dependence of inhibition, dissipating approximately 40% of the membrane electric field, is similar to that for extracellular K⁺ activation of the enzyme (Peluffo and Berlin, 1997), when analyzed using a pseudo-two-state model to describe binding. Our interpretation of these data is that these compounds bind at a K⁺ coordination site in the enzyme. In a recent study, guanidinium, acetamidinium, and formamidinium ions have also been reported to be V_M-dependent inhibitors of the Na⁺,K⁺-ATPase (Ratheal et al., 2010). With the discovery of these V_M-dependent inhibitors, we have begun to consider whether similar compounds can be developed into a useful class of Na⁺,K⁺-ATPase inhibitors. To explore this question, a more in-depth investigation of pNBTEA was undertaken to answer two questions relevant to its utility as a V_M-dependent enzyme inhibitor.

First, what is the mechanism of pNBTEA V_M-dependent Na⁺,K⁺-ATPase inhibition? BTEA and pNBTEA seem to bind at an extracellularly accessible K⁺ coordination site; however, they are neither occluded nor transported by the enzyme (Peluffo et al., 2004, 2009). pNBTEA binding also does not conform to the properties of ion binding in an ion well. V_M-dependent binding of Na⁺ and K⁺ in the Na⁺,K⁺-ATPase are diffusion-limited processes accompanied by slow conformational changes of the enzyme (Gadsby et al., 1993; Wuddel and Apell, 1995; Peluffo and Berlin, 1997) in which ion diffusion to its coordination site is V_M-dependent, whereas accompanying enzyme conformational changes seem to move little charge in the membrane electric field. For this reason, the proportionality coefficient “δ” in eq. 1 is approximately equal to 1 for K⁺, meaning k_tot is an asymptotic function of V_M (Peluffo and Berlin, 1997). In contrast, the properties of transient charge movements and our modeling calculations show that V_M-dependent pNBTEA binding must be much slower than would be expected for a diffusion-limited process. Kinetics of pNBTEA-dependent transient charge movements, measured as k_tot, have a U-shaped dependence on V_M that is reflected in the value of δ = 0.32, a value showing that the effect of the membrane electric field on forward and reverse binding reaction kinetics is experimentally measurable. This condition cannot occur when a V_M-dependent diffusion-limited process is kinetically limited by a slow electroneutral reaction (i.e., a conformational change). The fact that model Scheme B yields a far better fit to the data than Scheme A is also consistent with the V_M-dependent step being rate-limiting. Scheme B also stipulates that a rapid binding process occurs without movement of charge in the membrane electric field. This initial binding step is then followed by a slow charge moving reaction step. Thus, pNBTEA binding is clearly distinct from the mechanism involved in V_M-dependent extracellular K⁺ binding.

What is the V_M-dependent reaction that occurs during pNBTEA binding? Our present and previous data suggest a possible mechanism. Two general types of V_M-dependent reaction mechanisms are possible with a pNBTEA-bound enzyme. First, V_M dependence can arise from movement of intrinsic charges in the protein during a conformational change, and second, pNBTEA could move within the electric field even after binding. With Na⁺- and K⁺-dependent reactions, significant movement of intrinsic protein charges has not been observed during ion binding (Gadsby et al., 1993; Hilgemann, 1994; Wuddel and Apell, 1995; Peluffo and Berlin, 1997). There is no obvious reason to infer that such movements would become apparent after pNBTEA binding, so this first mechanism seems unlikely. As to the second possibility, simulations of BTEA binding to a homology model of the Na⁺,K⁺-ATPase α subunit [with sarco(endo)plasmic reticulum Ca²⁺-ATPase structure 3B9B as a template] suggest that there are two amine sites in the enzyme (Peluffo et al., 2009). One of those sites is located at the extracellular surface of the protein in a wide vestibule with an electronegative surface charge. The second site is located within the transmembrane domain between helices 4 and 6 at a K⁺ coordination site. We have postulated that the first site is outside the membrane electric field, whereas the second site is in the field such that extracellular K⁺ or BTEA binding dissipates approximately one-third of the total electric field. This postulate could explain why most quaternary amine blockers of the Na⁺,K⁺-ATPase are not V_M-dependent inhibitors (Peluffo et al., 2009); i.e., they would have low affinity for the second quaternary amine site located within the enzyme's transmembrane domain. Thus, data and modeling are consistent with the V_M-dependent reaction occurring when pNBTEA transfers from its initial binding site to the second site in the transmembrane domain. The reason this reaction would not be diffusion-limited is that the bulky p-nitrobenzyl moiety would have to be accommodated in the space between the transmembrane helices. The possibility that an enzyme conformational change could move bound pNBTEA in the electric field cannot be ruled out; however, that movement would have to dissipate the same fraction of the membrane electric field as extracellular K⁺ binding. This possibility also seems to be unlikely. Thus, a scenario to explain V_M-dependent inhibition by pNBTEA is that it moves to a K⁺ coordination site in the enzyme's transmembrane domain from its initial peripheral binding site. The effect of the membrane electric field is then to bias the binding site toward the transmembrane helices, deeper into a binding pocket in the enzyme.

The second question is whether pNBTEA inhibits the Na⁺,K⁺-ATPase with high enough affinity that these compounds warrant further investigation as possible enzyme blockers. Amine-containing compounds were first shown to inhibit the Na⁺,K⁺-ATPase in a manner that is competitive with extracellular K⁺ in the 1960s (Sachs and Conrad, 1968). In that article and subsequent reports (Kropp and Sachs, 1977; Forbush, 1988), amine concentrations were generally in the millimolar range, much too high to consider for pharmacological applications. Even BTEA, the first of the V_M-dependent inhibitors to be reported, inhibited Na⁺,K⁺-pump current (at 0 mV) by 50% at a concentration of 4 mM (Peluffo et al., 2004). Therefore, we synthesized pNBTEA to determine whether an amine-containing compound could inhibit the Na⁺,K⁺-ATPase at lower concentrations, and, in our initial report (Peluffo et al., 2009), its V_M-dependent inhibition was studied at a concentration of 100 μM. We did not, however, investigate the apparent binding affinity for pNBTEA. To determine that value, we have examined the concentration and voltage dependence of charge movements that, as shown previously (Peluffo et al., 2004, 2009), represent the binding steps for BTEA and pNBTEA. In our experiments, the Na⁺,K⁺-ATPase is trapped in phosphorylated E₂ states (Peluffo and Berlin, 1997). Therefore, charge movements represent net redistribution of enzyme conformations between two steady-state conditions and thereby provide an approximation of equilibrium pNBTEA binding. Thus, steady-state distribution of charge (q_ON) was used to estimate the apparent affinity of pNBTEA binding as 7 μM. In fact, even the Scheme A model, which fit the data with greater error, also predicted that binding occurred with similar affinity (8 μM). Thus, the prediction of high-affinity binding seems to be independent of the model used.

A final question is, could a V_M-dependent inhibitor of the Na⁺,K⁺-ATPase be a beneficial pharmacologic agent? To date, V_M-dependent Na⁺,K⁺-ATPase inhibitors contain ammonium moieties, as in pNBTEA, and thus all are likely to inhibit more strongly at negative membrane potentials. With these compounds, highly polarized tissues such as healthy cardiac ventricular muscle would be preferentially inhibited compared with more depolarized tissue, such as ischemic heart muscle whose membrane potential is reported to as much as 35 mV less negative than surrounding well perfused muscle (Wit and Janse, 1993). In fact, myocardial ischemia is a frequent complication in heart failure according to the Digitalis Investigation Group (1997), the largest clinical study of digoxin therapy for treatment of congestive heart failure, with 65% of patients having a history of myocardial infarction and 27% having on-going angina. This same study documented the finding that, given digoxin, patients with ischemic heart disease showed worse outcomes (higher rate of hospitalization and mortality) than patients with nonischemic heart failure. Likewise, digoxin was found to be an independent risk factor for excess mortality in patients surviving myocardial infarction (Leor et al., 1995). These clinical data suggest that myocardial ischemia increases the risk of digoxin-induced toxicity (i.e., arrhythmogenesis).

The reason for digoxin's excess morbidity and mortality with ischemic heart disease may well reflect the propensity for ischemic heart tissue to develop cardiac glycoside-induced arrhythmias compared with normal tissue (Lynch et al., 1986; Mazur and Anderson, 1998). Thus, one approach to minimizing arrhythmogenesis with ischemic tissue is to use a V_M-dependent Na⁺,K⁺-ATPase inhibitor that preferentially inhibits highly polarized (i.e., well perfused) heart muscle while being relatively less effective in depolarized, ischemic cardiac tissue. A V_M-dependent inhibitor with properties similar to those of pNBTEA will have such a preference to inhibit Na⁺,K⁺-ATPase in highly polarized cells.

Conceptually, it should also be possible to develop a Na⁺,K⁺-ATPase inhibitor that has the opposite V_M dependence, inhibiting depolarized tissues preferentially over highly polarized tissue. Such an inhibitor might be useful for a glycoside developed as a chemotherapeutic agent that would spare muscle and nerve tissue from unwanted drug actions. Whether clinically useful V_M-dependent Na⁺,K⁺-ATPase inhibitors can be developed remains to be determined; however, the present results suggest that the development of such agents should be feasible.

Authorship Contributions

Participated in research design: Berlin and Peluffo.

Conducted experiments: Berlin and Peluffo.

Contributed new reagents or analytic tools: Berlin.

Performed data analysis: Berlin and Peluffo.

Wrote or contributed to the writing of the manuscript: Berlin and Peluffo.