Folding Transition State and Denatured State Ensembles of FSD-1 from Folding and Unfolding Simulations

Abstract

Characterization of the folding transition state ensemble and the denatured state ensemble is an important step toward a full elucidation of protein folding mechanisms. We report an investigation of the free energy landscape of FSD-1 protein by a total of four sets of folding and unfolding molecular dynamics simulations with explicit solvent. The transition state ensemble was initially identified from unfolding simulations at 500 K and was verified by simulations at 300 K starting from the ensemble structures. The denatured state ensemble and the early stage folding have been studied by a combination of unfolding simulations at 500 K and folding simulations at 300K starting from the extended conformation. A common feature of the transition state ensemble was the substantial formation of the native secondary structures, including both α-helix and β-sheet, with partial exposure of the hydrophobic core in solvent. Both the native and non-native secondary structures were observed in the denatured state ensemble and early stage folding, consistent with the smooth experimental melting curve. Interestingly, the contact orders of the transition state ensemble structures were similar to that of the native structure and were notably lower than those of the compact structures found in early stage folding, implying significant roles that the chain and topology entropy may play in protein folding. Implications to FSD-1 folding mechanisms and the rate-limiting step are discussed. Analyses further revealed interesting non-native interactions in the denatured state ensemble and early stage folding and destabilization of these interactions could help to enhance the stability and folding rate of the protein.

Introduction

A detailed description of the transition state ensemble (TSE) is an important step toward full elucidation of the protein folding mechanisms. TSE is a set of non-native structures that collectively form the highest free energy barrier that a protein has to cross during its folding process. The functional significance of TSE lies in its strategic location on the free energy landscape of protein folding that crossing of TSE should lead to rapid process towards the native structure during folding reaction. It is generally recognized that TSE may contain those key tertiary and secondary contacts that are mostly responsible for both protein’s stability ^1,2 and its folding processes. Because of their key roles, attempts have been made both theoretically ^3–7 and experimentally ^8,9 to identify protein folding/unfolding TSE. Some of the examples include the seminal work of Fersht and co-workers who have characterized the TSE of several prototypical small proteins based on their Φ-value analyses ^10–14. In a recent collaboration, Fersht and Daggett and their co-workers¹⁵ combined the Φ-value analyses from experiments and unfolding simulations that helped them to elucidate the detailed information of the folding transition states. In this work, we extend the effort by combining folding and unfolding simulations to investigate three key areas on the free energy landscape.

Since TSE form the barrier of the free energy landscape and the associated structures are unstable and prone to go toward either side of the reaction coordinate, it is difficult to obtain high-resolution structures of the TSE from direct experimental measurements. The inherent heterogeneity of TSE implies that there may be wide variety of structures with common features. Therefore, experimental observations are averaged over the ensemble and the experimentally identified TS may represent the average features of the TSE. Nevertheless, the knowledge of the structural variation in TSE may help to understand the mechanism of narrowing the conformational space towards the native state. Due to the high spatial and temporal resolution, molecular dynamics (MD) simulation is advantageous to identify these transient structures.

One major problem in the computational studies of the protein folding process is the short timescale achievable from the simulations which limits the study to within several microseconds ¹⁶. Therefore, unfolding simulations have been performed to allow thorough sampling of the conformational space. An implicit assumption of this approach based on unfolding simulations is that folding and unfolding process follow the same or similar pathways in the reverse directions. However, because unfolding simulations are mostly carried out in high temperature conditions to allow fast unfolding be realized within the short simulation time, the free energy landscape may have been altered slightly¹⁷. Because of these potential complications, identification of TSE from unfolding simulations directly is not a straight-forward exercise. In this article we report our effort to combine both folding and unfolding simulations to identify the TSE of folding of a mini-protein FSD-1.

The denatured state ensembles of proteins were thought to be structureless random coils. However, NMR experiments¹⁸ indicated substantial residual structures in the denatured state. Since then, efforts have been made to characterize the denatured state residual structures by both experimental^19–22 and computational23 approaches. Unlike the native structure, the denatured ensembles are highly heterogeneous and are difficult to study experimentally. In this work, we combine both unfolding simulations at 500 K starting from the native structure and folding at 300K starting from the extended conformation to characterize the denatured structure ensemble and early stage folding. Analyses revealed detailed information on the interactions that were partially responsible to stabilize the non-native states. Further comparison between the structures of the denatured and the transition state ensembles allows proposal of a possible folding pathway.

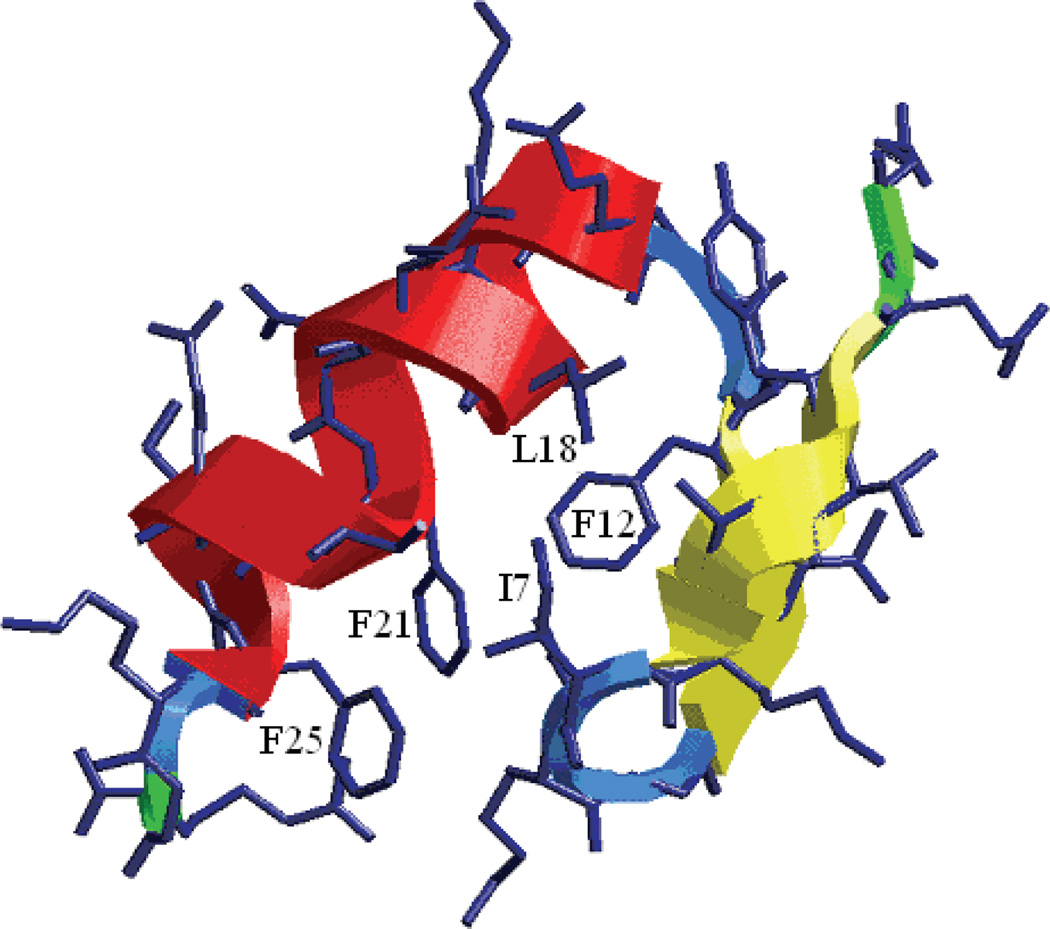
FSD-1 is a small α/β protein of 28 residues (QQYTAKIKGR₁₀TFRNEKELRD₂₀FIEKFKGR). It was designed based on the backbone structure of a zinc-finger protein domain using a fully-sequence-design protocol²⁴ by dead-end-elimination²⁵ with low sequence identity to the template. The NMR (Figure 1) structure of FSD-1 shows that residues 3–13 form a β–hairpin and residues 15–25 form a helix under its native condition. The α/β interface contained mostly hydrophobic residues including Ala₅, Ile₇, Phe₁₂, and Leu₁₈, Phe₂₁, Ile₂₂, Phe₂₅. The terminal residues were not well resolved in the NMR experiment.

Figure 1.

Native structure of FSD-1. The helix is in red and the β-hairpin is in yellow. The side chains at the helix/sheet interface have been labeled with single letter code and residue index.

Method

The initial structure for the unfolding simulations was taken from the NMR ensemble (PDB code 1FSD). The models 1–10 were chosen for the simulation. The initial structure was solvated using a truncated octahedron box of TIP3P model of water ²⁶ assuring that the edge of the solvent box was at least 9 Å away from the solute. This required a box of 50 Å side lengths and a total of ~11,000 atoms. The system was minimized and equilibrated via a constant pressure and temperature simulation. After the equilibration phase at each trajectory, constant volume and temperature simulations were performed and the coordinates were saved at every 20 ps. The MD simulations were conducted with AMBER simulation package²⁷ and the protein was represented using Duan et al force field (AMBER ff03)²⁸. Particle Mesh Ewald (PME) ²⁹ was applied to calculate long range electrostatic interaction; SHAKE ³⁰ was applied to freeze the vibration of the bonds connecting hydrogen atoms; a 2.0 fs time step was used.

The unfolding temperature was set to 500 K and 10 independent trajectories were run that each to 10.0 ns starting from the native structure. This set of trajectories is labeled as ‘UTRAJ’. For comparison, ten trajectories were run at 300 K for 10 ns each starting from the native state and this set has been marked as ‘NTRAJ’. Five independent simulations at 300.0 K were performed that each to 200.0 ns to investigate early folding process. In this set of simulations, the initial structure was the fully extended state. After initial collapsing process by a short simulation in Generalized-Born ^31,32 solvent model, the RMSD reached ~8Å. Five extended structures were selected from which the folding simulations continued using the same protocol and solvent models as those used in ‘UTRAJ’ and ‘NTRAJ’ sets. This trajectory set is labeled as ‘FTRAJ’.

Initial estimate of the TSE was obtained from the unfolding simulations at 500K by analyses of the free energy landscape which allowed identification of an area as defined by the RMSD = 4.0 +/− 0.2Å and radius of gyration of 9.1 +/− 0.2 Å. There are total of 42 snapshots in the defined area. Ten conformations were selected from this set of 42 structures for approximately 2 frames per each of the 5 trajectories that were structurally dissimilar from one another by visual inspection. Using these ten structures as the starting points, 10 different trajectories were run for 10.0 ns at 300K. This trajectory set is referred as ‘TSTRAJ’. A summary of the simulations is shown in Table I.

Table I.

summery of the simulations

Set	Starting point	Temperature	Length of each trajectory	Number of independent trajectory	description
UTRAJ	Native	500	10 ns	10	unfolding
NTRAJ	Native	300	10 ns	10	native
FTRAJ	Unfolded	300	200 ns	5	Early folding
TSTRAJ	Unfolding-TS	300	10 ns	10	Folding/unfolding

Results and Discussions

The native state ensemble

We first examined the stability of FSD-1 at room temperature. Consistent with our early observations ³³ and experimental findings ²⁴, FSD-1 was marginally stable at room temperature. The backbone root-mean-square-deviation (RMSD) from that of the native structure in the ten NTRAJ trajectories at 300K remained mostly within ~2.0Å, although it also reached ~3Å from time to time. In other trajectories, although the RMSD transiently reached ~5Å in some trajectories, it came back quickly to below 3Å. This level of RMSD is higher than the typical RMSD observed in simulations of other stable proteins. The radius of gyration (R_g), which measures the size and compactness of the protein, was relatively stable and fluctuated between 9Å–10.5Å, indicating that the protein remained roughly the similar size to that of the native structure.

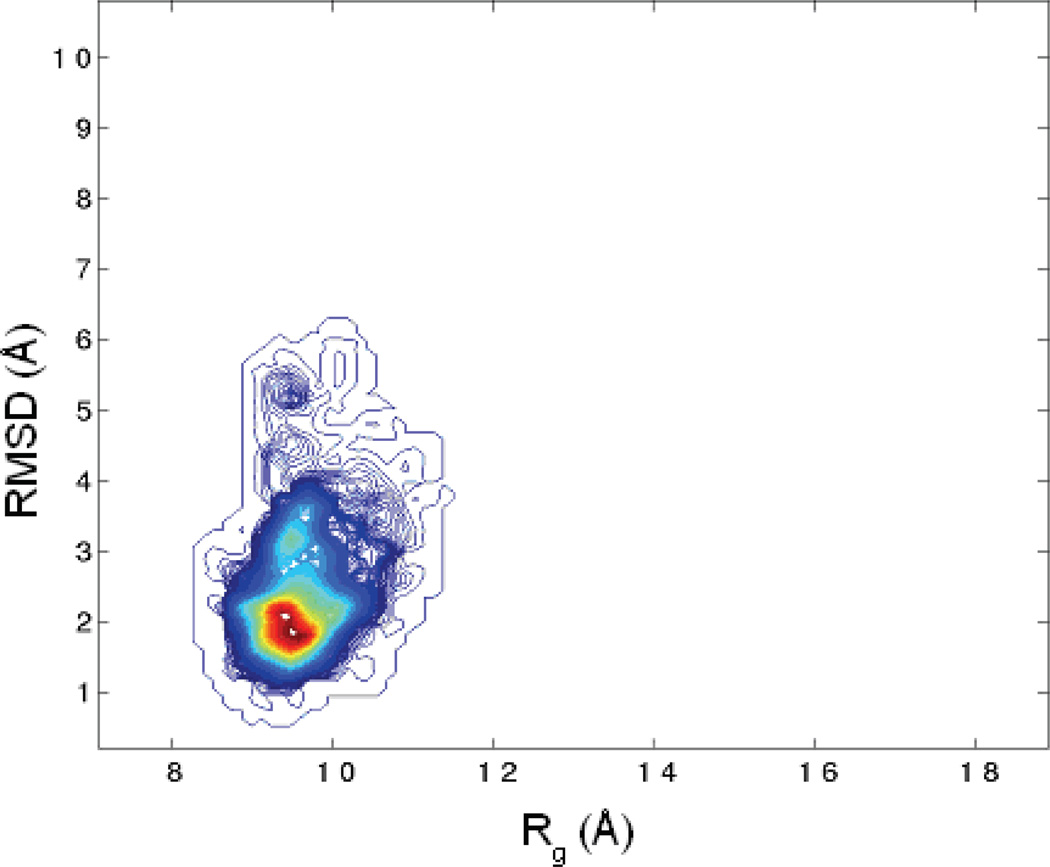
A two-dimensional contour map of the population density was generated from the data of ‘NTRAJ’ trajectories using WHAM ^34,35 (Figure 2) with RMSD (y-axis) and radius of gyration (R_g, x-axis) as the reaction coordinates. The figure shows that sampling in these 10 trajectories was mainly around the native state, consistent with our earlier observation. The most populated region was around RMSD ~1.5Å–2Å which is the native structure basin. Extension to the RMSD ~3.5Å region was also observed. The broad native basin enabled the protein to sample a wide range of conformational space. More importantly, it suggests that the folding transition state ensemble lies beyond 3.5Å RMSD. It is also found that the protein has a rather low tendency to cross a region of RMSD ~4Å, suggesting the presence of (free) energy barrier. Overall, these results are consistent with the observations that FSD-1 is a marginally protein^24,33 and its native basin appears to be relatively broad.

Figure 2.

The 2-dimensional population distribution around native state (NTRAJ) at 300K. The RMSD and R_g are the reaction coordinates. The population is represented by the color gradient where red is the most populated area.

General features of the unfolding trajectories

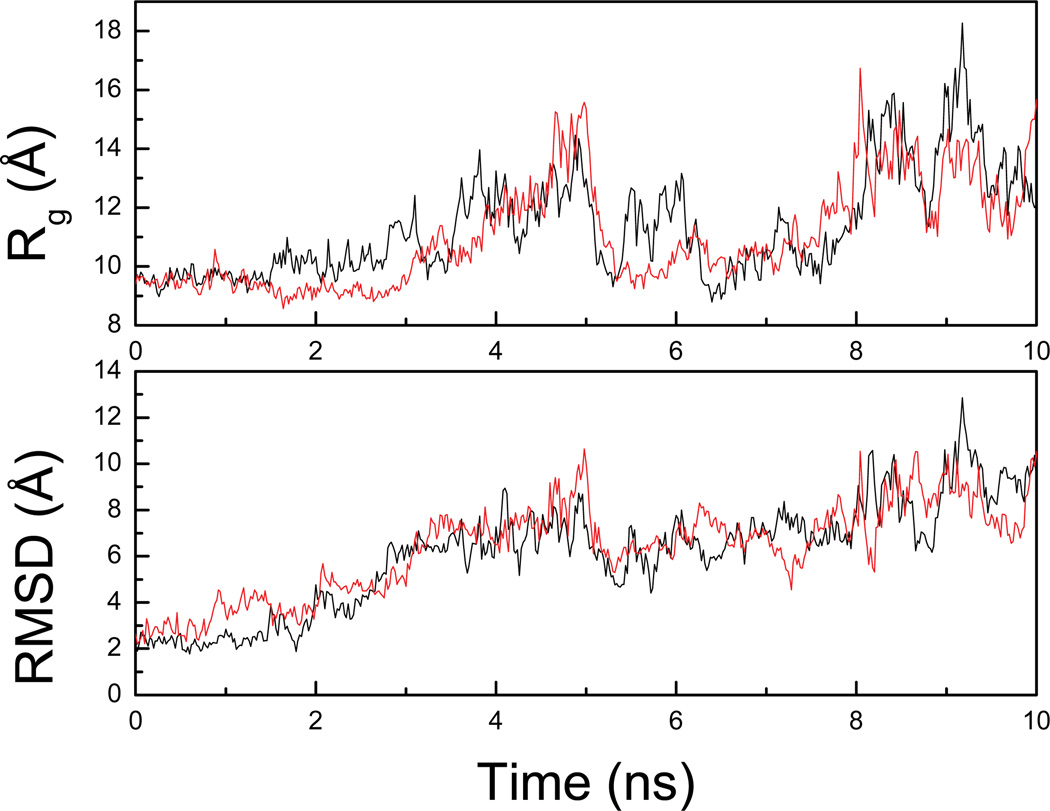
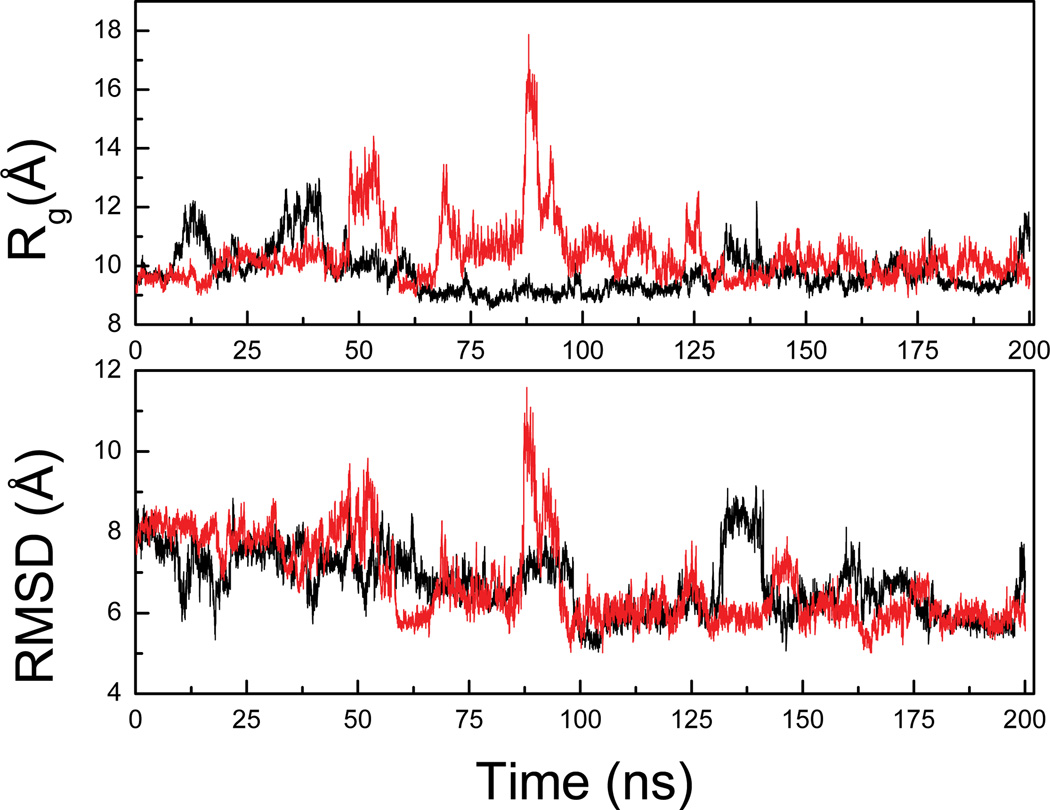
The details of the unfolding process of FSD-1 at relatively lower temperatures have been reported in a previous work ³³. Here the unfolding has been conducted at 500K which is higher than the previously reported temperatures for unfolding ³³. The elevated temperature allows better sampling of the unfolded state. Figure 3 shows the RMSD from the native structure of two of the total 10 unfolding trajectories (UTRAJ). The RMSD reached more than 4.0 Å within 1.0 ns at 500 K and up to 8–10 Å within 5 ns. During this time the unfolding of the β-hairpin took 8 place first while most of the helix retained its structure and denatured slowly. After that, the RMSD fell back to below 5.0 Å and resumed the increasing trend after 5.5 ns and eventually reached ~10Å at the end of the trajectory (10 ns). The R_g remained close to that of native (~9.5Å) up to 1.5 ns and then started to increase afterwards and reached up to ~15 Å within 5 ns when the RMSD reached ~8–10Å. A rapid collapse was observed during 5–5.5 ns when the R_g fell rapidly back to ~9.5Å, close to R_g of the native state. However, this is a completely denatured state since the corresponding RMSD is lager than 6 Å. The reduction in R_g was indicative of compact structures even in the denatured states. The R_g then fluctuated in a narrow band (between 10–12Å) up to 8 ns, and started to increase again to 17Å after 8 ns till the end of the trajectory.

Figure 3.

R_g and RMSD from two representative unfolding trajectories of the UTRAJ set at 500K.

Denatured state ensemble and early folding processes

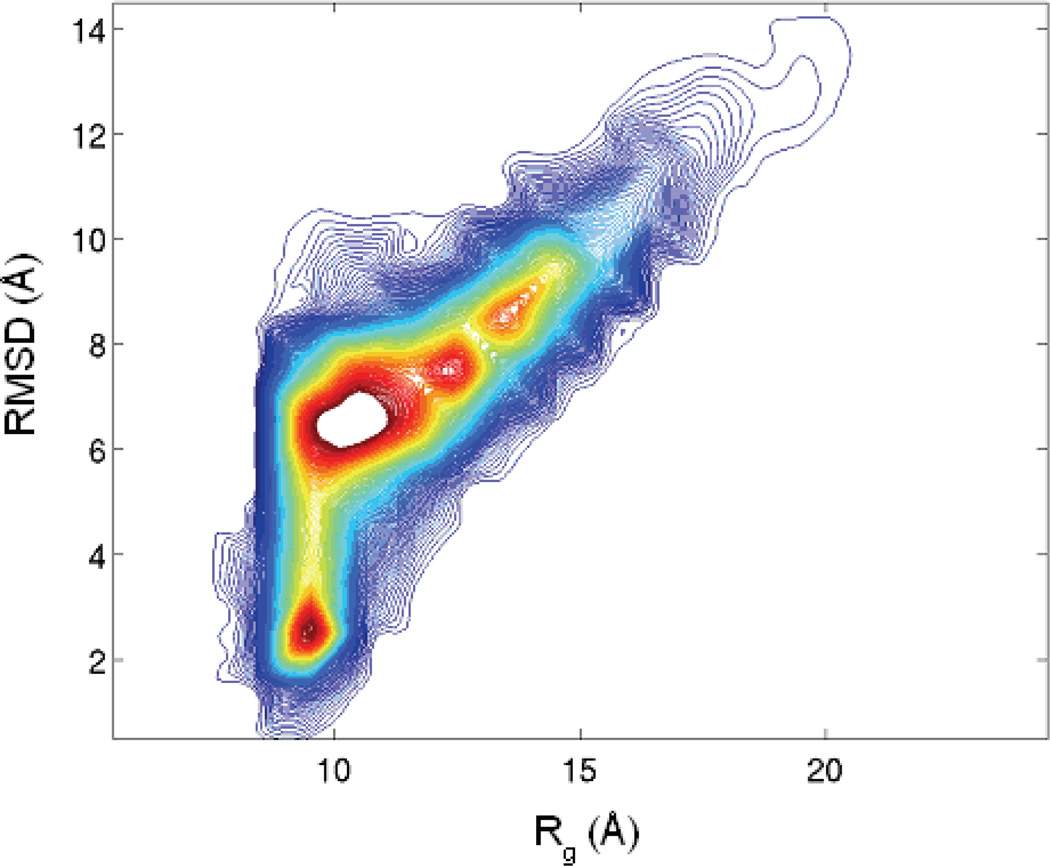
Figure 4 shows the two dimensional contour map of the population density obtained from the 10 unfolding trajectories using RMSD and R_g as the reaction coordinates. Apart from the high population around the native structures (RMSD~2.5, R_g~9.5), population in the denatured state is also high. In fact, at 500K, the most populated region is around RMSD ~7Å and R_g ~10Å which is a fully denatured state and represents the denatured state ensemble. Interestingly, although the denatured state ensemble is structurally very different than the native state, as judged by the large (~7 Å) RMSD, their R_g’s are quite similar; the native state R_g of ~9.5Å is compared to ~10Å of the most populated denatured state. This implies that the denatured state ensemble is dominated by compact structures.

Figure 4.

The 2-dimensional population contour from the unfolding trajectories (UTRAJ) at 500K. The coloring scheme is same at Fig 2.

We conducted five folding simulations (FTRAJ) at 300K starting from the extended conformations to examine the early stage folding. Figure 5 shows the RMSD from two of the five folding trajectories. The RMSD decreased to ~6Å within 100.0 ns and fluctuated around this value up to 200.0 ns when the trajectory was stopped. During the slow decrease of the RMSD, occasional sudden jump of the RMSD was also observed, e.g. between 85.0–100.0 ns in one trajectory and between 130.0–140.0 ns in the other, indicative of unfolding events. In some cases, these unfolding events were accompanied by increases in R_g, indicating that the protein moved toward extended state transiently. For example, the R_g transiently reached beyond 17 Å at around 85 ns in one trajectory when RMSD also increased. However, these transient events soon dissipated and the previous trend of the RMSD was resumed. In these two trajectories the lowest RMSD was around ~5Å. Similar events were also observed in other trajectories (data not shown).

Figure 5.

R_g and RMSD of two representative trajectories of the folding simulations (FTRAJ) at 300K.

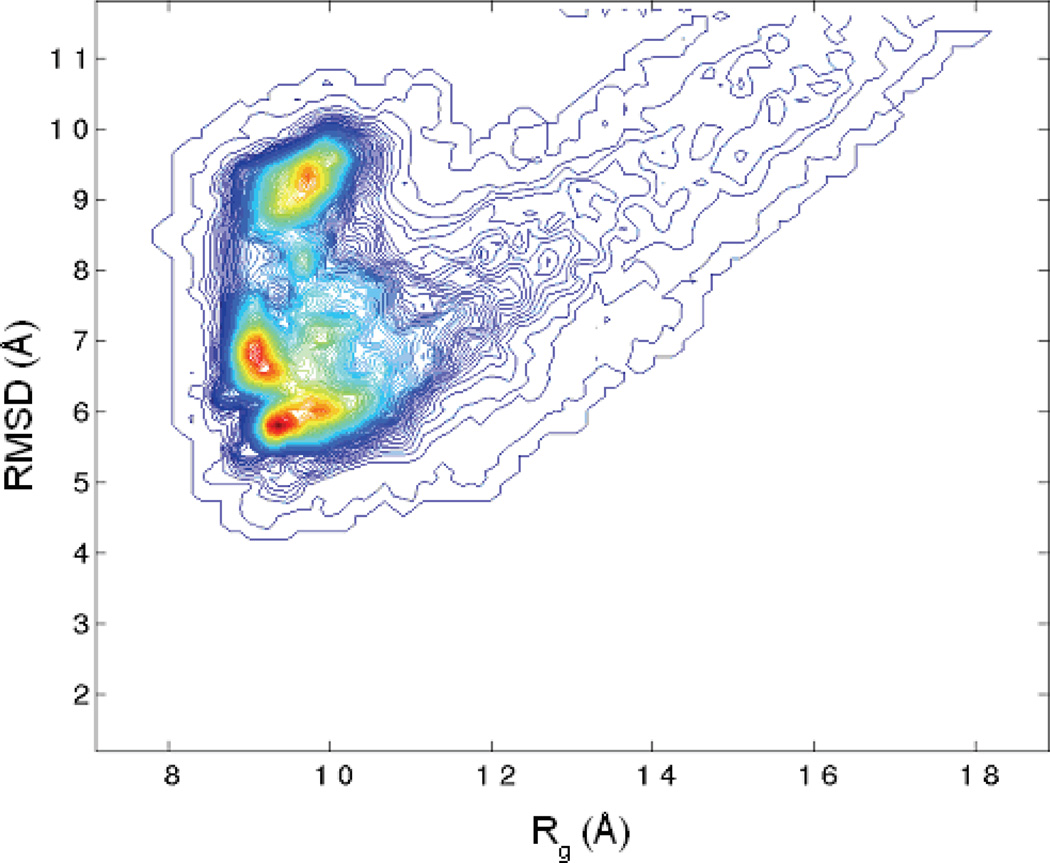
A two-dimensional distribution map, shown in Figure 6, was generated by combining the data from all the folding trajectories (FTRAJ) using the weighted histogram analysis method (WHAM) ^34,35. The most populated region was around RMSD ~5Å and Rg ~9Å, both were notably smaller than the RMSD ~7Å and R_g ~10Å observed in the unfolding simulations. The difference suggests a shift toward the compact and the native state. Presumably, such shift was due to the early folding process. Interestingly, there were additional populated regions at RMSD ~7 Å and R_g ~9.0 Å and RMSD ~9.0 Å and R_g ~9.5 Å. These regions were not observed in the 500K unfolding simulations. The difference suggests that the free energy landscape is notably smoother at the higher temperature.

Figure 6.

The 2-dimensional population distribution from the folding trajectories (FTRAJ) at 300K. The coloring scheme is same as Fig 2.

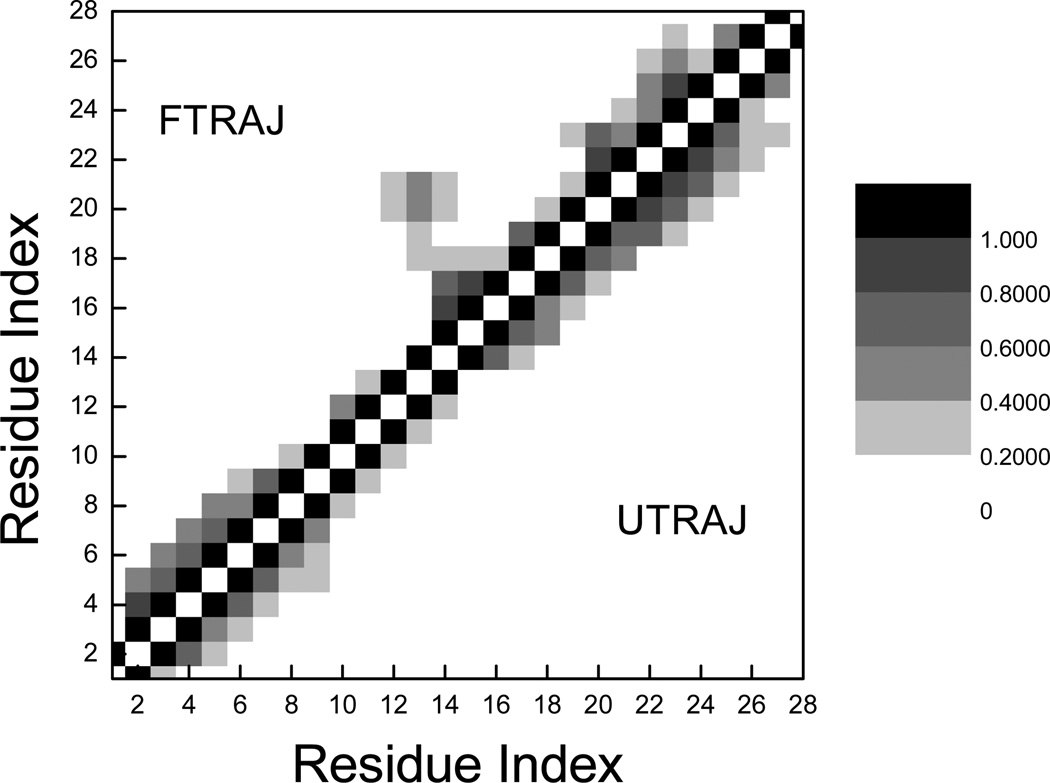
The C_α-C_α contact maps were calculated for both the unfolding (UTRAJ) and folding (FTRAJ) simulations and are shown in Figure 7 for comparison. The unfolding contact map was calculated for those snapshots that are within the general basin of the denatured state (RMSD > 5.5 Å) whereas the folding map was obtained from the second half of the trajectories (100–200ns). A rather interesting observation was the residual helical secondary structures in the denatured state, including the native helix. As for the folding map, the pattern of secondary structures resembled that of the denatured state. A notable difference was the partial formation of the non-native contacts including long-range hydrophobic contacts between F12 and F21, I22 that partially stabilized a transient β-hairpin of fragment F₁₂RNE₁₅KELRD₂₀FI. These long-range contacts were responsible for the increased contact order observed in the FTRAJ simulations (discussed later).

Figure 7.

Comparison of C_α-C_α contact maps calculated for the unfolding (UTRAJ, lower-right triangle) and folding (FTRAJ, upperleft triangle) simulations. The gray scale indicates the fractional occupancy. The cutoff distance is 6 Å.

The conformations evolved in the five folding trajectories were examined by the clustering analysis. The structures whose main chain RMSD’s were within 2.5 Å from each other were put into the same cluster. The representative structures (taken from the centre of the cluster) of the highest populated clusters from the folding trajectories are shown in Figure 8. These structures were all reasonably compact and had partial formation of the secondary structural elements, including both the native and non-native secondary structures.

Figure 8.

Representative structures of the most populated clusters in folding trajectories (FTRAJ).

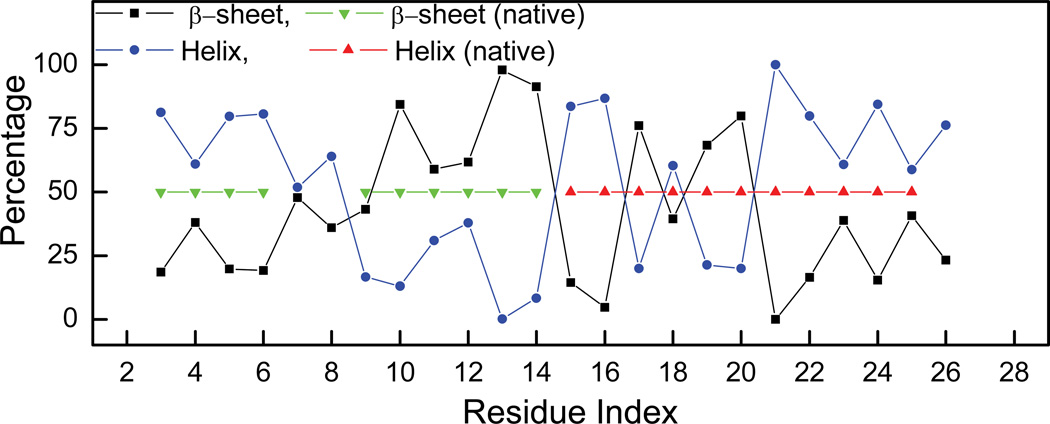
We further examined the secondary structures in the early stage folding. Figure 9 shows the secondary structures averaged over the second half (100–200ns) of the FTRAJ trajectories. The native secondary structures are also shown in the figure as green and red triangles for comparison. In comparison with the native secondary structures, the second β-strand and the loop region (R₁₀TFRN) and the C-terminal portion of the helix (F₂₁IEKFK) were mostly in their respective native conformations during the simulations. These fragments were also in their respective native secondary structures in the UTRAJ simulations (i.e., contact maps in Figure 7). Thus, residual (native) secondary structures may exist in the denatured state ensemble and are perhaps the early folding nucleus. However, the N-terminal β-strand (Y₃TAK) stayed mostly in the helical region in the early stage of folding (FTRAJ), forming a non-native helix. This was probably due to the relatively high helical propensity of Ala₅ and Lys₆. According to Chou-Fasman³⁶ scale, the helix propensities of Ala and Lys are, respectively, 1.4 and 1.2, notably higher than their β-sheet propensities (0.83 and 0.74, respectively). Thus, A₅K₆ facilitated helix nucleation in the denatured state ensemble.

Figure 9.

Average percentage helix (blue) or β-sheet (black) from the five folding trajectories (FTRAJ). The secondary structures of the native structures are shown in green (β-sheet) and red (helix).

On the other hand, although most residues of the C-terminal helix (E₁₅KELRDFIEKF₂₅) had high helix population in early folding (FTRAJ), the helix was broken in the middle primarily because of the lack of helix formation in three residues, E₁₇, R₁₉ and D₂₀. Judging from the strong helical populations of E₁₅ (84%) and E₂₃ (61%), the lack of helix population of E₁₇ was likely due to local (non-native) interactions. Indeed, a non-native salt bridge was formed between E₁₇ and R₁₉. This salt bridge was quite stable during the simulation with an occupancy rate of more than 58% when averaged over 100–200 ns of FTRAJ which was the highest occupancy rate among all salt bridges found in the same period. The observed high stability was partially due to their close proximity. Such local attractive force facilitated formation of short-range salt bridges as observed in many high-resolution protein structures³⁷. Since E₁₇ and R₁₉ are next to each other when local sequence assumes β-sheet conformation, the non-native salt bridge “locked” the local fragment into the non-native β-sheet conformation and reduced the folding rate. In summary, the early stage folding vents and the denatured state ensemble included the formation of both native and non-native secondary structures. Evidentially, the non-native ones would have to dissipate in the subsequent folding processes and could have negative impact to both folding kinetics and stability.

In an attempt to enhance the stability of FSD-1, Sarisky and Mayo examined the relevant sequences ³⁸ based on the energetic analyses of FSD-1 native structure. Here, we propose that enhancement of the stability and the folding rate could arise from substituting the key residues that help to stabilize the non-native secondary structures and salt bridges. These proposed changes are based on the analyses on the denatured state ensemble. Thus, our approach is complementary to the work of Sarisky and Mayo. Two examples are residues Ala₅ and Lys₆ that are part of the first β-strand. Because they have relatively high helical propensities, as discussed earlier, they likely facilitate formation of the non-native helix in the denatured state ensemble. A possible substitution is the K6R since Arg has almost equal propensities in helix and sheet according to Chou-Fasman scale whereas Lys has much stronger helical propensity according to the same scale. One may also contemplate substituting Ala₅ to a less helical residue (e.g., Ile). Other possible changes include E₁₇, R₁₉, and D₂₀ to stabilize the helix. Some of the likely beneficial substitutions include R19K and D20E, both of which increase the overall helical propensity. Another useful strategy may be destabilization of the E₁₇-R₁₉ non-native salt bridge.

The folding transition state ensemble

Transition state ensemble is characterized by its instability because it resides on a peak of the free energy landscape. Therefore, in simulations, the population around TSE should be much less compared to the native and the unfolded state ensembles. Hence, TSE can be identified from the unfolding simulations ^3–7 though caution should be made since the unfolding-TS and folding-TS might be slightly different from each other. In our simulations, an interesting observation from the unfolding (500K) simulations was that the native state and the denatured state ensemble were separated by a less populated region around RMSD ~3.5–5.5Å and R_g ~9.0–10.0Å, as shown in Figure 4. The low population was indicative to the presence of a barrier on the free energy landscape. This barrier was present like a crest between the highly populated troughs in the free energy landscape. The low density region corresponded to a high energy barrier which stood on the way from the denatured state to the native state and the reverse. On the other hand, the folding simulations at 300 K sampled the region RMSD ~5Å and R_g ~9Å and the folding process met resistance at around RMSD ~4.5Å and R_g~9.5Å. Thus, the region also showed the characteristics of high (free) energy barrier at the folding temperature (300K) and was close to the transition state ensemble identified from the unfolding simulations.

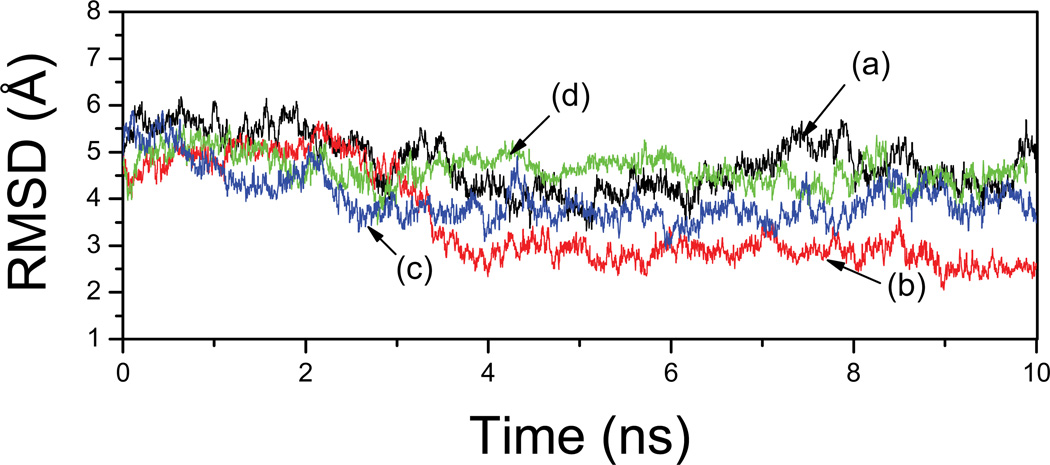
Since the position of TSE is at a maximum on the free energy surface, it is expected that the process can go to either directions (i.e., towards either the native or the denatured states) if the simulations start from the TSE. Thus, a possible validation of the proposed TSE is to conduct a series of simulations from the TSE structures. Ten simulations were performed (TSTRAJ) starting from different conformations with RMSD~3.5–5.5Å and R_g ~9.0–10.0Å selected randomly from the unfolding trajectories. Indeed, as expected, four trajectories demonstrated various degrees of decreasing RMSD (Figure 10), indicating that the protein moved toward the native structure in the trajectories, whereas others demonstrated increasing RMSD (data not shown) and the structures moved toward the denatured state. In particular, one trajectory demonstrated almost complete folding process and its RMSD started from ~4.8Å and reduced to 2.5Å by the end of 10.0 ns. Thus, the structure reached the general basin of the native structure ensemble. Such rapid folding was indicative to a down-hill process. Three other trajectories also demonstrated various degrees of decreasing RMSD (~4Å). In the remaining six trajectories (data not show), some unfolded completely and moved towards the higher values of the RMSD. In all these trajectories, the variation of R_g was small and fluctuated within the range 9Å –10Å which was similar to the native R_g (~9.5Å).

Figure 10.

RMSD of four trajectories at 300K started from unfolding-TSE (TSTRAJ). The labels (a)–(d) indicate the corresponding starting structures (a)–(d) shown in Figure 11.

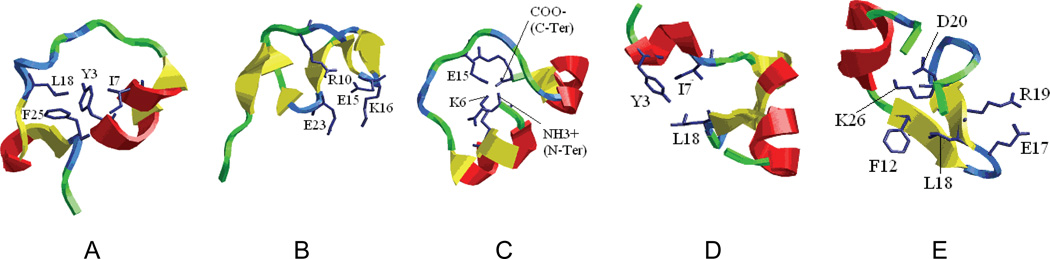
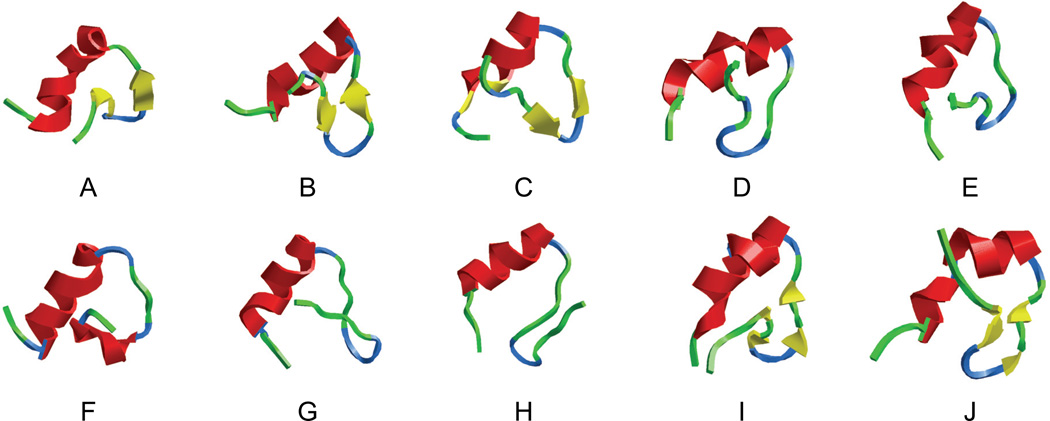
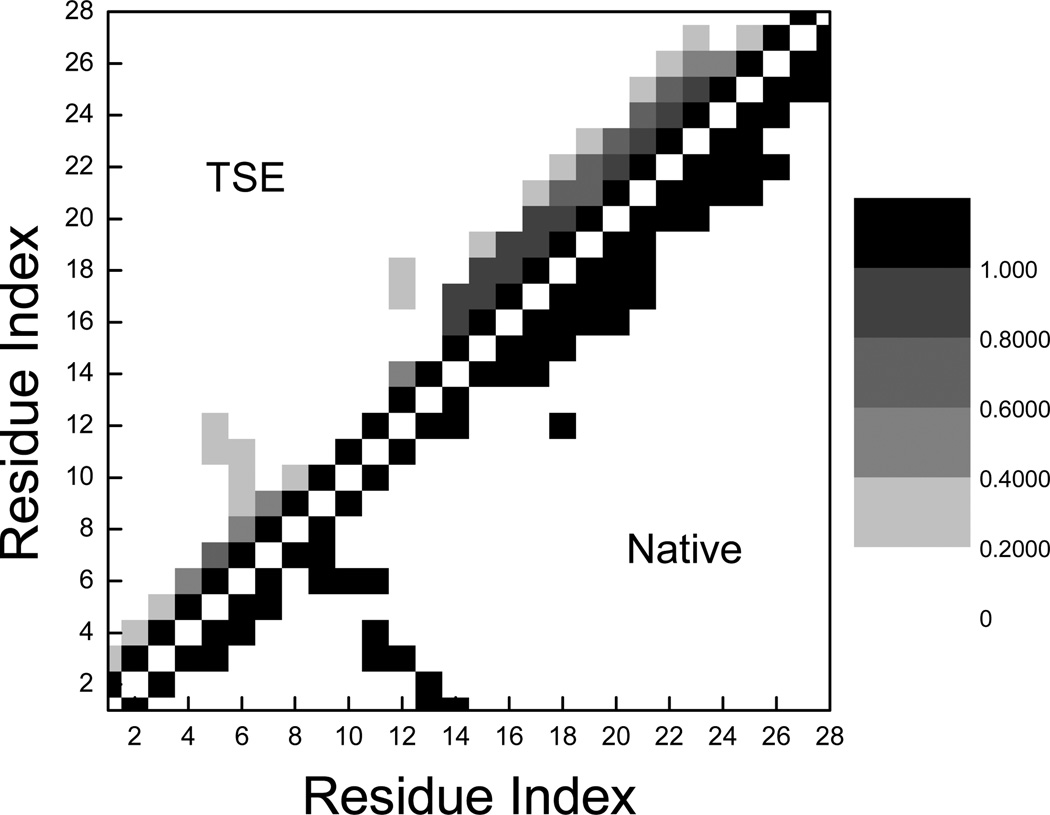
Representative structures of the TSE are shown in Figure 11. A common feature of these structures is the substantial formation of the native secondary structures. In all cases, the native helix was almost complete and the β-hairpin opened up and the hydrophobic core was partially exposed to solvent. Notable variations of the structures were observed around the β-hairpin. In most cases, the β-hairpin was partially formed and the overall topology was close to the native structure. These observations were confirmed by the residue contacts formed during the simulations. The average C_α-C_α contacts of the TSE structures are shown in Figure 12 and are compared with the native map. In addition to the near completion of the native helix, the β-hairpin also started to form, starting from the turn region. The contact map also shows that the turn was the nucleation site of the β-hairpin. Thus, improvement in the turn is likely beneficial to the overall stability and folding of the protein. Among the non-native contacts, the N-terminal β-strand showed signs of a transient helix, similar to that observed in the denatured state.

Figure 11.

Representative structures of the transition state ensemble that were used as the starting structures in ‘TSTRAJ’ simulations. Close resemblance to the native secondary structures is readily apparent.

Figure 12.

C_α-C_α contact map in the native NMR structure (lower-right triangle) and that averaged over TSE structures (upper-left triangle). The cutoff is 6.0 Å.

Discussion

The simulations reported in this herewith have been performed in both directions (folding/unfolding) of the folding reaction coordinate and have been started from different points on the conformational space and at different temperatures. The major aim of this work was to characterize the TSE of the folding process by combining all the information gathered from the simulations. We identified the high (free) energy barrier which separates the native state from the unfolded conformations.

We investigated three key areas of the free energy landscape of FSD-1. In the denatured state ensemble, there was considerable amount of residual secondary structure, albeit both the native and non-native secondary structures exist. Thus, when measured by overall secondary structure population, transition (e.g., thermal melting) between the native and denatured state ensembles is expected to be smooth. This is consistent with the experimental observation that FSD-1 has a rather smooth melting curve^24,38 when monitored using circular dichroism. In fact, experimentally, the transition, as measured by the CD signal, is marked by a wide range from ~4.0 °C to 80 °C with the middle point close to ~40 °C. The wide-range of transition also suggests a somewhat flexible native structure and broad native free energy basin. Indeed, this was observed in the simulations.

On the other hand, the structures of the transition state ensemble were characterized by near-native secondary structures and the overall near-native topology. A consistent observation was the partial formation of the β-hairpin and partial unfolding of the native hydrophobic core. This suggests that completion of the native structure is triggered by simultaneous formation of both β-hairpin and the native core in a cooperative manner. Furthermore, folding of FSD-1 is initiated by substantial formation of native (helical) secondary structures which lead to tertiary structure formation toward TSE. This is consistent with the framework models^39–41.

A notable difference between the denatured state structures and the TSE structures is the lack of formation of the overall topology in the former. Although these denatured structures are compact, and, on average, have (transient) native secondary structures, the overall topology of these structures do not resemble that of the native structure or the structures of TSE. Based on this observation, we propose that the rate-limiting step in the folding of FSD-1 is the formation of the correct topology which leads to the TSE structures.

We calculated the relative contact orders^42–44 of the representative structures observed in the simulations to obtain a qualitative assessment on the topological entropy^43–45. The relative contact orders of the early stage clusters (Figure 8) ranged from 0.134 to 0.175 and those of the TSE structures (Figure 11) were between 0.117 and 0.163. The FSD-1 native structure has a relative contact order of 0.139 which is very close to the average relative contact order of the TSE structures (0.135) and notably lower than that of the early stage structures (0.150). The higher contact orders in the early stage structures imply that there was substantial formation of non-native long-range contacts in these structures and that the native structure has favorable chain (topology) entropy.

We shall note that the denatured states were identified from our unfolding simulations at 500 K. This temperature is notably higher than the typical experimental unfolding temperatures. Thus, the structures identified from the simulations could be even “more denatured” than the ones in typical thermal denaturation experiments. For the denatured state ensemble, as expected, the average contact order was 0.100, the lowest of all states, because of lack of formation of any long-range contacts. An interesting observation was the substantial increase in the contact order in the early stage of folding in comparison to the (fully) denatured state, indicative of long-range contacts and compact structures. This was largely due to the non-specific hydrophobic collapse. For example, the persistent long-range contacts among F₁₂, F₂₁, I₂₂ observed in early stage folding was stabilized by the hydrophobic force. However, as some of these long-range contacts were non-native, they have to dissipate in the subsequent folding which led to lower contact order. The increase in chain (topology) entropy was a favorable direction which drove the protein toward the native structures. Thus, chain (topology) entropy appears to play important roles in protein folding. Interestingly, we found that the chain (or topological) entropy favored the native state in comparison to those structures found in early stage folding and was one of the driving forces to unfold some of the early stage compact structures.

Furthermore, similarity in contact orders of the native and those of the TSE structures is consistent with the observation of similar topological structures in these two states. Because of this similarity, one may be able to use the native structure to estimate the contact orders of the transition state ensemble from which the folding rates may be estimated.

Accurate identification of the folding TSE is an important step towards understanding of the folding mechanisms. In this work, we combined unfolding and folding simulations with a set of simulations that started from a small set of selected perspective TSE structures. Although the results were consistent with the notion that these were likely representative to the TSE, some cautionary notes are clearly warranted. Most notably was the small set of the selected structures in the “refolding” (TSTRAJ) simulations. Obviously, the ten simulations, regardless of where they started from, were insufficient to provide solid statistics for a vigorous identification of TSE. Thus, the conclusions based on these ten simulations were rather qualitative. Fortunately, these conclusions were also consistent with the observations based on other sets of simulations, including both folding and stability simulations. Thus, we are cautiously optimistic that the identified structures captured the main features of the TSE.

Conclusion

Three key areas of the free energy landscape of FSD-1 protein, native, transition, and denatured and their respective structural ensembles have been investigated by a combined folding and unfolding molecular dynamics simulations with explicit solvent. The native ensemble of FSD-1 rests on a relatively flat free energy basin marked by the high flexibility of the protein. The TSE was initially identified from unfolding simulations at 500 K and was examined by ten folding simulations starting from the selected structures of the ensemble. Among which, four trajectories moved closer to the native structure as judged by the main chain RMSD and one moved into the native ensemble within 10.0 ns. The TSE is about main chain RMSD 4.5 Å away from the native structure, and is characterized by substantial formation of the native secondary structures, including both α-helix and β-sheet, with partial exposure of the hydrophobic core in solvent. Residual secondary structures were observed in the denatured state ensemble obtained from the unfolding simulations. These secondary structures were also present in the early stage of folding. Thus, they are likely the folding nucleus of early stage folding. The presence of non-native secondary structures in the denatured state is consistent with the smooth melting curve observed using circular dichroism. Taken together, the results suggest that the rate-limiting step of FSD-1 folding is the development of tertiary structures and the key fragments of secondary structures. This was followed by a cooperative step in which completion of the secondary structures and packing of the hydrophobic core take place simultaneously. Analyses indicated that non-native interactions involving Ala₅, Lys₆ and Glu₁₇, Arg₁₉ were partially responsible for stabilizing the non-native structures in the denatured state ensemble. We propose that destabilization of these interactions could help to enhance the stability and folding rate of the protein.