Multiscale Simulation of Microbe Structure and Dynamics

Abstract

A multiscale mathematical and computational approach is developed that captures the hierarchical organization of a microbe. It is found that a natural perspective for understanding a microbe is in terms of a hierarchy of variables at various levels of resolution. This hierarchy starts with the N -atom description and terminates with order parameters characterizing a whole microbe. This conceptual framework is used to guide the analysis of the Liouville equation for the probability density of the positions and momenta of the N atoms constituting the microbe and its environment. Using multiscale mathematical techniques, we derive equations for the co-evolution of the order parameters and the probability density of the N-atom state. This approach yields a rigorous way to transfer information between variables on different space-time scales. It elucidates the interplay between equilibrium and far-from-equilibrium processes underlying microbial behavior. It also provides framework for using coarse-grained nanocharacterization data to guide microbial simulation. It enables a methodical search for free-energy minimizing structures, many of which are typically supported by the set of macromolecules and membranes constituting a given microbe. This suite of capabilities provides a natural framework for arriving at a fundamental understanding of microbial behavior, the analysis of nanocharacterization data, and the computer-aided design of nanostructures for biotechnical and medical purposes. Selected features of the methodology are demonstrated using our multiscale bionanosystem simulator DeductiveMultiscaleSimulator. Systems used to demonstrate the approach are structural transitions in the cowpea chlorotic mosaic virus, RNA of satellite tobacco mosaic virus, virus-like particles related to human papillomavirus, and iron-binding protein lactoferrin.

1 Background

Microbes such as viruses and bacteria are organized hierarchically. For example, a virus is constituted of atoms assembled into macromolecules which, in turn, constitute several substructures. For a nonenveloped virus, the latter are genetic material and the capsid. For an enveloped system such as dengue virus, there is an outer protein net, a lipid zone, and an inner RNA-protein complex. Accompanying this hierarchical organization is a spectrum of time and length scales. The objective of this article is to present our strategy for developing a theory that parallels the hierarchical organization of microbes with a mathematical and computational framework for efficiently modeling microbial systems.

Modern nanocharacterization experimental methodologies make the development of microbial simulation approaches timely. For example, Atomic Force Microscopy (AFM) is employed to investigate a range of biological processes from unfolding of a single molecule to nano-indentation of viruses (Brown et al., 2007; Florin et al., 1994; Roos et al., 2010). A standard AFM can scan a sample more than 10 thousand times per second, yielding an ensemble measurement that parallels a statistical mechanical approach. Thus, to model such experiments computationally, a framework is needed that addresses structures in a range of sizes from single macromolecules to viruses and bacteria, without losing information at any time or length scale.

Nanotechnical methods for characterizing macromolecular assemblies include AFM (Hinterdorfer and Dufrene, 2006), Ion Mobility – Mass Spectrometry (Bernstein et al., 2009; Ruotolo et al., 2005; Uetrecht et al., 2010), chemical labeling (Beardsley et al., 2006), and nanopore measurements (Zhou et al., 2008). While these techniques provide information on structure, they are coarse-grained in that they do not resolve all-atom conurations. X-ray and electron microscopy provide detailed structure but do not provide information on dynamics (Barthel and Thust, 2008; Gaffney and Chapman, 2007). Solid-state NMR techniques do provide an ensemble of atom-resolved structures but cannot be used to give overall structure for a macromolecular assembly (Dvinskikh et al., 2006; McDermott, 2009; Svergun and Koch, 2003). Thus, we suggest that a method which integrates multiple types of nano-characterization data with a predictive all-atom simulation approach would greatly advance the understanding of microbial systems; a preliminary approach of this type has been presented earlier (Pankavich et al., 2008).

The above and other (D’Alfonso et al., 2010; Florin et al., 1994; Goldstein et al., 2003; Lyon et al., 1998) experimental techniques can be performed under various microenvironmental conditions such as salinity and pH. These variations modulate interactions between solvent accessible parts of the microbe and host medium atoms, inducing structural and functional changes of the former. For example, viral RNA is found to be stable and facilitate encapsulation in a 2:1 electrolyte due to “tight” electrostatic binding with Mg²⁺ ions, but loses tertiary structure in a 1:1 electrolyte (Freddolino et al., 2006; Singharoy et al., 2010b). An all-atom model is often essential to correctly probe these interactions. Structural fluctuations and internal dynamics are a central feature of several biological processes. For example, in the presence of an energy barrier, the atomic fluctuations allow self-organization of lipids in membranes (Sung and Kim, 2005). Fluctuations are also important in expressing the conformational diversity of macromolecules that allows for large deformations upon drug binding (Rohs et al., 2005). Similarly, excessive fluctuations in viral epitopes appear to diminish immune response (Joshi et al., 2011) and may explain the dependence of immunogenicity on their fluctuations (Nowak, 1996). Thus, an all-atom description is necessary to account for all sources of fluctuation in simulating aforementioned processes, and hence has been the basis of traditional molecular dynamics (MD) approaches.

All-atom MD simulations of macromolecular assemblies involving more than a million atoms (such as a virus in an explicit solvation environment) require large computational capabilities and have been accomplished using more than 1000 processors for a single time-course. To simulate viruses over microseconds on such a platform would require engaging this many processors for months (assuming the usual femto-second MD timestep). This restricts traditional MD to less than 50 nm structures and hundred nano-second timescales. Hence, incorporating information about atomic processes into microbe modeling has been a challenge. Billion-atom MD simulations have been accomplished (Abraham et al., 2002; Ahmed et al., 2010; Sanbonmatsu and Tung, 2006, 2007; Schulz et al., 2009; Timothy C. Germann et al., 2005). However, these simulations neglect Coulomb interactions, bonded forces, or the rapidly fluctuating proton. All the latter are central to biomolecular structure and dynamics. Thus, such billion-atom simulations should not be viewed as the standard for microbial modeling.

Multiscale approaches have been developed to address the above computational challenges. These methods yield insights into the dynamics of a system as it simultaneously evolves across multiple scales in space and time. By the definition adopted here, a multiscale method simultaneously accounts for processes on a range of scales. This scale bridging requires development of models for various scales which are thermodynamically and structurally consistent with each other (Noid et al., 2008a). For example, the deductive multiscale methodology (Sect. 1.1) maintains the effect of all degrees of freedom while greatly accelerating simulations. The advantages and shortcomings of this and other methods are compared in Sect. 1.3.

1.1 Deductive multiscale analysis

Deductive multiscale analysis is a collection of concepts and mathematical techniques for understanding the dynamics of a complex system as derived from a primitive model cast at the finest scale of interest. In essence, it adheres to the basic program of statistical physics that started, for example, with Gibbs (Gibbs, 1981) and Liouville (McQuarrie, 1976). A goal of our studies is to retain information on all scales simultaneously and capture the dynamic cross-talk between processes on the relevant spectrum of space-time scales. For example, overall viral structure affects atomistic fluctuations. These fluctuations mediate the stability of entire structure through the free-energy driving forces, illustrating an interscale feedback underlying microbial processes.

The main steps in deductive multiscale analysis can be summarized as follows:

1. The starting point is a primitive model that is cast in terms of variables describing the systems at the shortest space-time scale. For the present case, the fine-scale description is cast in terms of the positions and momenta of all the atoms in the system. This description is a viable starting point as it contains much of the physics of biological systems and, through deductive multiscaling, results in coarser-grained model which needs minimal recalibration given an interatomic force filed (e.g., CHARMM (MacKerell et al., 2001) or AMBER (Ponder and Case, 2003)).

2. Deductive multiscaling then facilitates the identification of coarse-grained variables (order parameters) that describe the salient features of a system on longer space-time scales. For microbial simulations, these order parameters (OPs) capture overall structural information, e.g., the position, shape, size, and orientation of major components of the microbe.

3. Deductive multiscaling provides criteria for determining the completeness of the set of OPs (Sect. 2.4).

4. Rigorous Smoluchowski/Langevin equations for evolving the OPs are then derived. These equations are stochastic because the behavior of matter at the nanoscale is strongly influenced by the fluctuating states of the atomic configurations. To address this, deductive multiscaling yields the co-evolving quasi-equilibrium ensemble for fine scale (atomistic) states consistent with the instantaneous values of OPs. Thus, the all-atom description of the system is retained.

In summary, deductive multiscaling is a method for deriving equations capturing the two-way flow of information between fine- and coarse-scale variables. With this, it probes the interplay of far-from-equilibrium and equilibrium processes that underlies many microbial behaviors. For example, much of the structure of membranes and DNA or RNA corresponds to a free-energy minimizing state. In contrast, the self-assembly of proteins and genetic material into a virus, and the diffusion of molecules across a membrane or within a cell, are far-from-equilibrium processes. Deductive multiscaling provides a way to obtain the free-energy gradients that drive the afore-mentioned processes.

1.2 Multiscale analysis

As the OPs evolve slowly in time, they change the conditions determining the ensemble of all-atom configurations. Since atomistic variables change rapidly, the associated probability takes an equilibrium-like form as suggested by the Gibbs-hypothesized equivalence of long-time and thermal averages. This probability then influences the factors in the equations of OP dynamics. The resulting transfer of information from the OPs to the atomistic configurations (characterized by the quasi-equilibrium probabilities) and, in turn, back to the OPs, is summarized in Fig. 1. This provides a natural way to transfer information between descriptions at various scales that are rigorously derived from the statistical mechanics of a microbial system. This conceptual scheme has been used to derive a framework for multiscale modeling of biological systems (Cheluvaraja and Ortoleva, 2010; Singharoy et al., 2011a). Similar schemes are designed and implemented for investigating electrostatic (Singharoy et al., 2010b) and quantum (Iyengar and Ortoleva, 2008; Shreif and Ortoleva, 2010a, b) properties of nanosystems.

Fig. 1.

Interscale feedback, and the manner in which information is transferred across scales underlying the DMS computational approach. Here, OPs mediate the quasi-equilibrium probability of atomistic configurations. The latter is used in the construction of thermal-average forces and diffusion factors which underlie the Langevin dynamics of the OPs.

Our deductive multiscale approach has been implemented as DeductiveMultiscaleSimulator (DMS) software. Forces that drive the Langevin dynamics of slow variables must be computed via an ensemble method. In DMS these forces are efficiently computed via an ensemble/Monte Carlo integration method enabled by the nature of OPs (Cheluvaraja and Ortoleva, 2010; Singharoy et al., 2011a). Atomic forces are obtained from a quasi-equilibrium ensemble of all-atom structures constrained by the instantaneous values of OPs. Monte Carlo integration averaging of these forces over the ensemble is carried out to obtain the thermal average forces at every Langevin timestep. This approach has the advantage that no phenomenological relation between forces and OPs is required.

1.3 Comparison of deductive multiscaling with other methods

A variety of methods, their strengths and limitations in the context of microbial simulations, and a comparison with deductive multiscaling are briefly as follows.

1.3.1 Molecular dynamics and coarse-grained models

Traditional MD does provide all-atom structure but typically gets trapped in often biologically irrelevant free-energy minima (Chipot and Pohorille, 2007). In “coarse graining” (CG) approaches, a system is simplified computationally by clustering several subcomponents into one component; this effectively reduces the computational complexity by removing both degrees of freedom and interactions. The fundamental assumption behind such techniques is that, by eliminating unimportant degrees of freedom, one can obtain results over longer time scales than would otherwise be achievable. A variety of coarse graining methods currently exists, ranging from united-atom to elastic network models (Ding et al., 2008; Marrink et al., 2007). For example, in residue-based CG, clusters of 10–20 covalently bonded atoms are represented by one bead; it is a natural and commonly used method for coarse graining, and yields a speedup of 1–2 orders of magnitude over all-atom MD (López et al., 2009; Proctor et al., 2010). Shape-based CG uses a neural network algorithm to assign parts of a macromolecule to beads, efficiently reproducing the shape of the macromolecular assemblies with a minimal number of beads (Arkhipov et al., 2008). Interactions between beads are typically calibrated from all-atom simulations (Marrink et al., 2007; Nguyen et al., 2009), and more recently via a variational approach, multiscale coarse-graining (MSCG), that optimizes agreement of predictions to respect equilibrium probability distribution (Chu et al., 2007; Das and Andersen, 2009, 2010; Izvekov and Voth, 2005a, b; Krishna et al., 2009; Liu et al., 2007; Noid et al., 2008a; Noid et al., 2007; Noid et al., 2008b; Wang et al., 2006).

The similarity of MSCG to deductive multiscaling lies in the nature of free-energy minimizing forces that drive the CG (or OP) dynamics (Eqs. (4), (6), and (7) of Sect. 2.3 and Eqs. (22) and (9) of Ref. (Noid et al., 2008a) ). However, MSCG requires a huge initial ensemble of atomistic structures to estimate the probability distribution at an all-atom level and “self-consistently” calibrate the CG force fields according to this information. In DMS, the generation of a huge ensemble of atomic structures is replaced by the generation of quasi-equilibrium sub-ensembles that respect the instantaneous OP states. Thus, the forces are calculated on the fly during OP dynamics, and are not preconstructed from a prior set of calculations that are often inconsistent with the evolving state of the system. DMS enables simulation of the time evolution of an atomistic ensemble as the mapping from OP to all-atom configurations can be probed at any point in the trajectory.

1.3.2 Multiphysics approaches

Phenomenological coarse-grained models are often only applicable close to the reference state and require calibration with many new applications (Kamerlin et al., 2011). Semi-phenomenological multiscale coupling bridges the nanometer and mesoscopic scales by embedding a nanostructure into a continuum model; this does not capture fluctuations near the nanostructure/continuum boundary (Chang et al., 2005; Zhuang et al., 2010). The central idea behind these approaches is to use results from a model operating at one scale as input to a model operating at another. For example, in the case of proteins embedded in membranes, a continuum membrane model was coupled to a more microscopic macromolecular model using heuristic interactions between these two models which operate on different scales (Chang et al., 2005). Another way to combine models operating on different scales is to treat them separately and pass information from one level of resolution to the next (e.g., QM/MM (Warshel and Levitt, 1976)). An even more sophisticated multiscale approach allows dynamic switching between resolution levels as the immediate environment of a molecule changes (Praprotnik et al., 2009).

In conventional phenomenological approaches, one often recalibrates chosen functional dependencies of coarse-grained potentials to account for new systems with different geometries or molecular constituents. Deductive multiscaling does not require any postulated phenomenological relationships to provide the dependence of thermal average forces or diffusion factors on the OPs. Rather, these factors are calculated from all-atom configurations and interatomic forces are provided by established force-fields. This is because, by construction, OPs mediate the configurations needed to compute these factors. With this, the coarse-graining procedure and ensuing Langevin dynamics of DMS are applicable to a broad spectrum of microbial systems since the underlying all-atom interactions are provided by well-established set of force-field parameters.

1.3.3 Symmetry-constrained models

Symmetry-constrained models take advantage of the inherent symmetry of structures, such as for icosahedral viruses, to reduce the number of degrees of freedom and thereby increase computational efficiency (Phelps et al., 2000; Speelman et al., 2001; Tama and Brooks, 2002; van Vlijmen and Karplus, 2005). However, structural transitions often break this symmetry via nucleation events (Miao et al., 2010; Miao and Ortoleva, 2010), so that even if the initial and final structures of the system have the same symmetry, the dynamic pathway of transition can violate it. Thus, symmetry-constrained models often cannot be used to simulate microbial structural transitions due to their highly nonlinear, friction-dominated, symmetry-breaking character (Miao and Ortoleva, 2010).

1.3.4 Chemical kinetic self-assembly models

These models predict the time-course of populations of beginning, intermediate, and final structures (Zlotnick, 2005). They do not enable prediction of detailed molecular structure and require extensive experimental data for calibration and to determine the assembly pathway, restricting their predictive capability.

1.3.5 Langevin dynamics and projection operators

The theory of random processes started with work on Brownian motion by Einstein (Einstein, 1905), Smoluchowski (Smoluchowski, 1906), and P. Langevin (Langevin, 1908; Lemons and Gythiel, 1997). These approaches are based on the connection between frictional forces and atomistic fluctuations, and resulted in the development of the generalized Langevin equation. Langevin dynamics simulations have been employed in macromolecular studies (Allen and Tildesley, 1987) and to impose isothermal conditions on MD simulations (Pastor et al., 1988). Slow dynamics in terms of the coarse-grained variables is often described by generalized Langevin equations (Kubo, 1966; Zwanzig, 1973).

A scheme that incorporates Langevin dynamics of slow variables is described in Normal Mode Langevin simulations (NML) (Sweet et al., 2008). NML identifies the slow modes by diagonalizing a Hessian matrix and overdamps the high frequency modes near their energy minimum while respecting the subspace of low frequency normal modes. In our approach, rapidly fluctuating variables are allowed to explore a representative ensemble of configurations. Forces driving the evolution of the OPs are constructed from the ensemble of atomistic configurations predicted by our analysis to satisfy a quasi-equilibrium distribution. Hence, overdamping of rapidly fluctuating modes is avoided.

In contrast to deductive multiscaling, extended Lagrangian techniques employ fictitious masses to adjust the timescales and still allow for the adiabatic propagation of the faster (atomistic) degrees of freedom in response to the slower ones (Iyengar and Jakowski, 2005). These methods bypass explicit averaging for calculation of the driving forces either via explicit variable transformation (Zhu et al., 2002) or extended phase-space approaches (Maragliano and Vanden-Eijnden, 2006). Even though an adiabatic decoupling between the slow (OP) and fast (atomistic) variables appears naturally in deductive multiscaling (by the scaling of the Liouville operator, Sect. 2), the relative efficiency of an adiabatic relaxation scheme versus the present OP-constrained sampling scheme remains to be determined. In particular, the present scheme requires the development of a rich ensemble of atomistic configurations at each Langevin timestep, while the adiabatic scheme requires co-evolution of the slow and many [O(N)] fast variables. This issue is of critical importance for the efficiency of the simulation of systems involving 10⁶ or more atoms.

A commonly used approach for treating far-from-equilibrium systems is based on projection operators (Deutch and Oppenheim, 1987; Shea and Oppenheim, 1996, 1998). It is very general in the sense that no approximations are made in arriving at an equation for the reduced probability of a subset of variables (OPs here) (Zwanzig, 1961; Zwanzig, 2001). However, this kinetic equation requires construction of a memory function, which usually can only be accomplished via extensive MD simulations or experimental data. This is numerically expensive for N-atom problems except when the memory functions have short relaxation times (Darve et al., 2009; Izvekov and Voth, 2006; Singharoy et al., 2011a).

In our microbial modeling, the OPs of interest are much slower than the characteristic rate of atomistic fluctuations, and therefore the relaxation times are typically short relative to OP dynamics. Under these conditions, deductive multiscaling leads to the same set of Langevin equations as those from projection operators. However, deductive multiscaling is a more direct way to construct these coarse-grained equations; we do not start with the projection operators and then resort to perturbation methods for constructing memory functions. Instead, we make an ansatz on the dependence of the N-atom probability and analyze the resulting Liouville equation via multiscale perturbation techniques.

1.3.6 Space-warping and related methods for computing thermal-average quantities

A space-warping technique was used to introduce OPs for macromolecular systems (Jaqaman and Ortoleva, 2002). These OPs facilitate the use of deductive multiscaling to derive Langevin equations for their dynamics (Cheluvaraja and Ortoleva, 2010; Jaqaman and Ortoleva, 2002; Miao et al., 2010; Miao and Ortoleva, 2010; Ortoleva, 2005; Pankavich et al., 2008; Singharoy et al., 2011a). The term space-warping was also used to describe a method for achieving efficient sampling of configuration space by lowering barriers (Minary et al., 2008; Zhu et al., 2002). Integration of these methods within a deductive multiscaling context could bring additional efficiency to multiscale simulations of microbial systems but has not yet been carried out.

1.4 Practical advantages of deductive multiscaling

In light of Sect. 1.2 and 1.3, deductive multiscaling has the following practical advantages over other methods:

• the equations for the OPs are force-field based, i.e., all factors (thermal average forces and diffusivities) in these equations can be computed from factors in the N-atom model;

• the form of these equations need not be hypothesized; they are computed at each instant via an ensemble algorithm;

• the forces driving OP dynamics are not based on a phenomenological, precalibrated expression; thus, the ensemble of configurations mediated by the changing OPs is accounted for;

• Accounting for friction at the coarse-grained level allows for probing the non-inertial dynamics of the microbe; and

• an efficient algorithm for simulating the dynamics of a complex system on multiple scales is provided that simultaneously preserves the all-atom description and the overall picture captured by the OPs.

These features imply that deductive multiscaling captures the interplay between far-from-equilibrium and equilibrium processes that underlies microbial behavior.

1.5 Advances in hardware and software engineering

With computational power becoming available at very low cost, there may be a question as to why a multiscale simulation methodology is still needed. The ever-increasing capability of high-end computing platforms is enabling unprecedented scales of MD simulation, thereby enabling the modeling of system-level behavior of the large scale behavior of complex systems (Sanbonmatsu and Tung, 2007; Shaw et al., 2010). One of the driving forces for this development has been the exponentially increasing density of integrated circuits. Current petaflop computers involve thousands of multicore processors. Modern hardware advances such as GPU and FPGA computing also show promise (Herbordt et al., 2007; Stone et al., 2007; Ufimtsev and Martinez, 2008). However, planned exascale supercomputers and hybrid architectures do pose some technological challenges (e.g., CPU-GPU integration, high power consumption, and lack of scalability over heterogeneous platforms) (Dongarra et al., 2011). Even currently available homogeneous multicore architectures involve software engineering challenges. (Valiant, 2011).

Difficulties in biomolecular simulations arise due to calculations of non-bonded interactions. Algorithmic improvements to MD overcome some of these difficulties in a hardware-specific fashion. These advances have taken advantage of query search algorithms (Benetis et al., 2006; Kraemer and Seeger, 2009). Two main MD algorithms (Verlet list and linked cell) were optimized to yield an efficient identification of near-neighbor atoms for efficient computation of non-bonded forces (Allen and Tildesley, 1987; Gonnet, 2007; Mason, 2005; Petrella et al., 2003; Verlet, 1967; Wang et al., 2007; Welling and Germano, 2011; Yao et al., 2004). Extra efficiencies arising from reducing the number of minimum image force calculations have been realized (Heinz and Hünenberger, 2004; Mason, 2005; Pütz and Kolb, 1998). Additional efficiency in calculating pairwise forces has been achieved via domain decomposition implemented in parallel fashion (Pütz and Kolb, 1998; Shaw, 2005).

Hardware-specific optimizations are used wherein the neighboring particles are reordered so that they reside close to each other in memory. This optimization achieves cache hits within the hierarchical memory typical of contemporary computers, and has enabled highly efficient multi-billion atom simulations (Berendsen, 1996; Kadau et al., 2006; Meloni et al., 2007; Yao et al., 2004). However, this approach limits the use of a program to a particular computer or cluster, since it heavily relies on the architecture of the computing system. These and other hardware-specific approaches, notably those based on harnessing GPU or cell processor efficiency, often require different adjustments every time the hardware changes (Anderson et al., 2008; Liu et al., 2008). While these improvements have been impressive, billion-atom simulations as needed for microbes still remain a challenge (Sect. 4). Thus, for microbial simulations, it is timely to have a general mathematical framework that accelerates MD, is based on fundamental laws of molecular physics to minimize recalibration, and is platform-independent.

2 Materials and methods

In this section, key aspects of our deductive multiscale approach are discussed in some detail. The essence our computational algorithm is suggested in Fig. 1 and has been implemented as the DMS software.

2.1 Order parameters

OPs are coarse-grained variables characterizing the overall spatial organization of a system. A central element of our multiscale analysis is the construction of OPs describing the coarse-grained features of a microbe. An OP-mediated model captures the separation in timescales between the coherent (slow) and non-coherent (fast) degrees of freedom. In effect, OPs filter out the high frequency atomistic fluctuations from the low frequency coherent modes. This property of OPs enables them to serve as the basis of a multiscale approach for simulating microbial dynamics (Cheluvaraja and Ortoleva, 2010; Ortoleva, 2005; Pankavich et al., 2008; Singharoy et al., 2010a). A number of types of OPs have been identified through our work and an extensive set of studies on phase transitions and related phenomena. Examples and the phenomena they have been used to describe are as follows.

• Scaled coordinates: Collective and single-particle behaviors in many-particle quantum systems (Fan et al., 2010; Iyengar and Ortoleva, 2008; Ortoleva, 2005; Pankavich et al., 2009a; Shreif and Ortoleva, 2010a, b) and scaled center-of-mass coordinates for multi-atom assemblies (Cukier and Deutch, 1969; Deutch and Oppenheim, 1987; Shea and Oppenheim, 1996, 1997, 1998).

• Curvilinear coordinates: Macromolecular conformational dynamics (Shreif and Ortoleva, 2008; Tuckerman and Berne, 1991).

• Density-like variable profiles: Release of drug molecules from a nanocapsule, the dynamics of enveloped viruses (Shreif et al., 2008; Shreif et al., 2009), and liquid crystal phase transitions (Lubensky, 1973; Nemtsov, 1977; Rothman et al., 1994; Shreif et al., 2009; Zwanzig, 2001).

• Space-warping parameters: Overall size, shape, and state of deformation of viruses and other macromolecular assemblies (Cheluvaraja and Ortoleva, 2010; Jaqaman and Ortoleva, 2002; Miao et al., 2010; Miao and Ortoleva, 2010; Ortoleva, 2005; Pankavich et al., 2008; Singharoy et al., 2011a).

• Subsystem OPs: The motion and deformation of different parts of a virus (Shreif et al., 2008; Pankavich et al., 2009b).

• Hierarchical order parameters: The icosahedral or other structures of viruses (Singharoy et al., 2011b).

By definition, OPs are variables chosen to be slowly varying in time. The origins of the slowness include the following:

• inertia associated with the coherent dynamics of many atoms evolving simultaneously;

• migration over long distances;

• stochastic forces that tend to cancel;

• species population levels that track the simultaneous dynamics of many units (as in chemical and self-assembly kinetics), only a few of which change on the atomic timescale.

In the following, further discussion on structural (space-warping, subsystem, and hierarchical) OPs is presented, and deductive multiscaling is used to derive stochastic equations for their dynamics.

2.2 Structural order parameters for microbes

2.2.1 Space-warping structural order parameters

Consider a microbe described via the positions of its N constituent atoms labeled ℓ = 1, ···, N. Let the ℓ-th atom in the system be moved from its original (reference) position ${\stackrel{\rightharpoonup }{r}}_{\ell }^o$ via

$${\stackrel{\rightharpoonup }{r}}_{\ell }=\sum _k{\stackrel{\rightharpoonup }{\mathrm{\Phi }}}_k{U}_{k\ell }+{\stackrel{\rightharpoonup }{\sigma }}_{\ell },$$ (1)

where the Φ⃑_k and $U_{k\ell }\equiv U_k({\stackrel{\rightharpoonup }{r}}_{\ell }^o)$ are k-th OP and basis function respectively. For example, the use of k have been taken to be products of Legendre polynomials in the X, Y, Z Cartesian directions (Cheluvaraja and Ortoleva, 2010; Miao and Ortoleva, 2009). Through the OPs and the Eq. (1), the reference position is deformed into the instantaneous position r⃑_ℓ. Given a finite truncation of the k sum in Eq. (1), there is a residual displacement (denoted σ⃑_ℓ) for each atom.

An explicit expression for Φ⃑_k is obtained by minimizing the mass-weighted square residual with respect to the Φ⃑_k (Pankavich et al., 2008; Shreif and Ortoleva, 2008). This procedure maximizes the information content in these OPs. One obtains

$${\stackrel{\rightharpoonup }{\mathrm{\Phi }}}_k=\frac{{\displaystyle \sum _{\ell =1}^N}{m}_{\ell }{U}_{k\ell }{\stackrel{\rightharpoonup }{r}}_{\ell }}{{\mu }_k};{\mu }_k=\sum _{\ell =1}^N{m}_{\ell }{U}_{k\ell }^2,$$ (2)

where m_ℓ is the mass of atom ℓ. Inclusion of m_ℓ in Eq. (2) gives Φ⃑_k the character of a generalized center-of-mass. For example, if U_kℓ is independent of ℓ, then Φ⃑_k is proportional to the center-of-mass of the assembly. Some of the OPs defined in this way constitute a strain tensor accounting for compression-extension-rotation, while others describe more complex deformations. The μ_k serve as effective masses associated with each OP. The masses primarily decrease with increasing complexity of the basis functions. Thus, the OPs with higher k probe smaller regions in space. In summary, a model based on this set of OPs probes the structure over a diverse range of spatial scales via different orders in k. Further details on the construction of the Φ⃑_k are provided elsewhere (Cheluvaraja and Ortoleva, 2010; Jaqaman and Ortoleva, 2002; Miao and Ortoleva, 2009).

2.2.2 Subsystem decomposition

In the previous discussion, one set of OPs was introduced for the whole system. This is adequate for studying changes like uniform contraction of a virus capsid (Miao and Ortoleva, 2010) or collapse of viral RNA (Singharoy et al., 2011a), wherein the major structural changes could be described by a small set of global OPs. However, macromolecular assemblies like viruses and ribosomes are composed of several subunits organized in a complex structure that can move in opposite ways. For example, during escape of RNA from a virus, it migrates outwards while the capsid might contract. With these applications in mind, the deductive multiscale scheme developed above is extended to describe multiple OP types interacting with each other, which characterize the structure, location, and orientation of each subsystem. In this extension, a system is divided into subsystems, each of which is described by a given set of OPs (Φ⃑_ks, s = 1,2, ···). For example, a virus capsid can often be divided into pentamers and hexamers of the constituent protomers. In this case, different sets of OPs are defined for each of these subsystems. Fewer OPs can be introduced for rigid parts compared to flexible ones.

As system complexity (e.g., the number of subsystems and their internal structure) increases, one may increase the number of OPs, i.e., the range of the k sum in Eq. (1). As the number of OPs increases, smaller and smaller scale features are captured, and their characteristic timescales decrease.

2.2.3 Hierarchical order parameters

Again, consider a microbe to be an assembly of interacting subsystems, each of which has internal structure. This hierarchical structure of a microbe is reflected in the broader spectrum of length and timescales involved, adding additional complexity to the logical flow of Fig. 1. This is illustrated here via a three-level formulation. At the finest level, the system is described by the positions of the N constituent atoms. At an intermediate level, each subsystem is described via subsystem-centered OPs similar to those of Sect. 2.1.2. Then, a global set of variables is constructed from the subsystem-centered OPs to capture overall organization of the entire system. Using an approach similar to that of Eq. (1), a set of hierarchical OPs Ψ that are expressed in terms of the subsystem OPs Φ⃑_ks is introduced. For illustrative purposes here, from the set of subsystem OPs we focus on the position R⃑_s of the center of mass of each subsystem, s = 1,2, ···

$${\stackrel{\rightharpoonup }{\mathrm{\Psi }}}_K=\frac{{\displaystyle \sum _s}{M}_s{U}_{Ks}{\stackrel{\rightharpoonup }{R}}_s}{{\displaystyle \sum _s}{M}_s{U_{Ks}}^2},$$ (3)

where U_Ks is the analogue of U_kℓ in Eq. (1). Eq. (3) expresses overall structural characteristics of the assembly (Ψ⃑_K) as a function of the position of individual subsystems (R⃑_s ). Thus, r⃑_ℓ explicitly defines R⃑_s, which, in turn, yield Ψ⃑_K, reflecting the structural hierarchy of a microbe.

2.3 Stochastic equations for order parameter dynamics

The statistical description of a microbial system is provided by the probability density ρ of the N atomic positions and momenta Γ. However, this formulation masks the underlying hierarchical organization of a microbe. To address this, in our approach, ρ is hypothesized to depend on Γ both directly, and via a set of OPs, indirectly. In light of the hierarchical organization of a microbe, one way to achieve this is to include the OPs for all subsystems s = 1,2, ··· in this hypothesized dependence of ρ. With this ansatz, a multiscale analysis of the Liouville equation yields sets of coupled Langevin equations for the OPs (Pankavich et al., 2008; Pankavich et al., 2009b; Shreif et al., 2009). For the subsystem OPs of Sect. 2.1.2, one obtains

$$\frac{d{\stackrel{\rightharpoonup }{\mathrm{\Phi }}}_{ks}}{dt}=\sum _{k^{\prime }{s}^{\prime }}{\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{{\mathit{ksk}}^{\prime }{s}^{\prime }}{\stackrel{\rightharpoonup }{f}}_{k^{\prime }{s}^{\prime }}+{\stackrel{\rightharpoonup }{\xi }}_{ks},$$ (4)

where the diffusivity factors ${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{{\mathit{ksk}}^{\prime }{s}^{\prime }}$ are related to the correlation functions of OP momenta Π⃑_ks via

$${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{{\mathit{ksk}}^{\prime }{s}^{\prime }}=\frac{1}{{\mu }_{ks}{\mu }_{k^{\prime }{s}^{\prime }}}\underset{-\infty }{\overset{0}{\int }}dt\langle {\stackrel{\rightharpoonup }{\mathrm{\Pi }}}_{k^{\prime }{s}^{\prime }}(t){\stackrel{\rightharpoonup }{\mathrm{\Pi }}}_{ks}\rangle ,$$ (5)

where Π⃑_ks is the value of the OP momentum for a given N-atom configuration, Π⃑_k′s′(t) is momentum advanced in time through Newtonian mechanics, and the 〈···〉 implies thermal average over atomic configurations. The thermal-average force f⃗_ks acting on subsystem s is given by

$${\stackrel{\rightharpoonup }{f}}_{ks}=-\frac{\partial F}{\partial {\stackrel{\rightharpoonup }{\mathrm{\Phi }}}_{ks}}$$ (6)

for OP-constrained Helmholtz free-energy F, where

$$F=-\frac{1}{\beta }lnQ(\mathrm{\Phi },\beta ),$$ (7)

Q(Φ, β) is the partition function constructed from configurations consistent with the set of Φ⃑_ks (denoted Φ collectively), and β times the Boltzmann constant and absolute temperature is one. Eq. (4) has been implemented as the DMS simulator for the case of a single subsystem (Cheluvaraja and Ortoleva, 2010) and more recently for a set of interacting subsystems (Cheluvaraja and Ortoleva, 2010; Pankavich et al., 2009b). The logic of Fig. 1 serves as the schematic workflow of DMS.

In the above formalism, the thermal average forces f⃑_ks are constructed at each Langevin timestep via MonteCarlo integration and the use of interatomic force fields (e.g., CHARMM) (Vanommeslaeghe et al., 2009). This does not require any assumption on the form of the dependence of the thermal average forces on the OPs; this dependence is automatically incorporated because the ensembles used to carry out the thermal averaging are constructed for the values of the OPs at the given Langevin timestep. This formalism accounts for the full impact of fluctuations ξ⃑_ks as the random forces in the Langevin equations are constructed to be consistent with the diffusion factors of Eq. (4). Finally, equations analogous to Eq. (4) are obtained for simple (Cheluvaraja and Ortoleva, 2010) and hierarchical (Singharoy et al., 2011b) OPs.

Inherent in our deductive multiscale approach is the capability to reconstruct atomistically resolved states given the evolving coarse-grained picture. Any coarse-grained theory carries an inherent uncertainty in the fine-scale state (Ayton et al., 2007; Ortoleva, 2005). Our approach addresses this by providing the conditional probability density for the atomistic configurations given the instantaneous values of the OPs. In this sense, our approach is equivalent to an ensemble of MD simulations (Singharoy et al., 2011a). Details on ensemble generation are provided elsewhere (Cheluvaraja and Ortoleva, 2010).

2.4 Controls on accuracy

Accuracy of our multiscale simulations is controlled as follows.

2.4.1 Comparison with MD

Trajectories obtained via Langevin-quasi equilibrium ensemble co-evolution by DMS are compared with conventional all-atom MD to estimate/control errors. If performed with full electrostatics and solvated structures, MD captures physio-chemical processes without artifacts. It can be used to model experiments if simulations are carried out for sufficiently long time (Freddolino et al., 2006). A comparison of distributions of backbone dihedral angles and system energies serves as a quantitative estimate of DMS simulation errors relative to MD. Root-mean-square deviation (RMSD) calculations similarly provide error estimates. Thus, comparisons are made at the level of OP time courses and all-atom configurations by calculating RMSDs and dihedral angle distributions.

2.4.2 Comparison with experimental data

Experimental Data on the stability of various structures provide a sensitive error measure when compared with DMS simulations.

2.4.3 Computed relaxation times of correlation functions underlying diffusion factors and identification of missing OPs

OP velocity relaxation times are monitored to ensure that they are smaller than the time-scale associated with OP variation. This provides a self-consistency check for our deductive multiscaling approach. Neglect of essential OPs results in unstable simulation trajectories with attendant unphysical structures and energies and large diffusion factors. Missing OPs are identified by monitoring the extent to which atomistic motion deviates from that generated by the OPs, i.e., by tracking the growth of residuals σ⃑_ℓ for ℓ = 1, ···, N (Sect 2.2.1).

2.4.4 Re-referencing for new OP definitions

The reference structure ( ${\stackrel{\rightharpoonup }{r}}_{\ell }^o$ for ℓ = 1, ···, N) used to define OPs in Eq. (1) is updated at regular intervals to minimize errors. This ensures that OPs remain a valid coarse-grained description as the system evolves.

2.4.5 Emergent OPs

Internal consistency of DMS calculations is determined by calculating the effect of a larger set of OPs on results. As the simulation proceeds and the structure undergoes major transformations, new OPs are identified and integrated into the simulation.

2.5 Free-energy basin discovery and data-guided simulations

Our deductive multiscale approach was extended to facilitate the discovery of low free-energy states of macromolecular assemblies. This was achieved by modifying the free-energy of the system as follows. A state-counting factor Δ⁻ was introduced into our canonical partition function Q (Pankavich et al., 2008), which mediates against the states that are within any of the known free-energy basins. It uses a set of molecular descriptors (η) such as total mass, charge, and eigenvalues of the moment of inertia and electrical quadrapole moment tensors. This provides rotation-independent factors to discriminate between the known and instantaneous structures. With this, the thermal average forces responsible for OP dynamics are modified to incorporate terms that drive the system away from known low-energy configurations. The result is a partition function (and associated free-energy) given by

$$Q(\mathrm{\Phi })=\int d{\mathrm{\Gamma }}^{\ast }{\mathrm{\Delta }}^{+}\left(\mathrm{\Phi }-{\mathrm{\Phi }}^{\ast }\right){\mathrm{\Delta }}^{-}\left(\eta -{\eta }^{\ast }\right)exp\left(-\beta H^{\ast }\right),$$ (8)

where H is the total energy of the system and ^* indicates evaluation at Γ^*, the state over which integration is taken. The factor Δ⁺ is included in the calculation to only include configurations Γ^* consistent with the given values of OPs Φ. This framework enables a sequential elimination of known stable structures and thus guides the search for new ones. The above free-energy basin discovery method can also be used to guide a simulation to states consistent with nanocharacterization data (e.g., cross-section, AFM, chemical labeling). This is achieved via modification of Δ⁺ with experimental data (Pankavich et al., 2008).

3 Results and discussion

In this section, DMS simulations are presented to demonstrate various facets of our approach. Our deductive multiscale approach is shown to transfer structural information between the OPs (coarse-grained description) and the atomistic configurations (characterized by quasi-equilibrium probability densities), and vice versa. Accounting for interscale feedback is necessary for modeling the structure and dynamics of microbial systems. Bionanosystems provide ideal examples for testing our methodology. With this, microbial behavior is understood here in terms of the slow dynamics of OPs coevolved with the quasi-equilibrium probability density of rapidly fluctuating atomic configurations. The systems chosen for DMS demonstration are the cowpea chlorotic mosaic virus (CCMV) capsid, a T=1 human papillomavirus (HPV) – like particle, and the RNA of satellite tobacco mosaic virus (STMV).

3.1 CCMV capsid structural transition

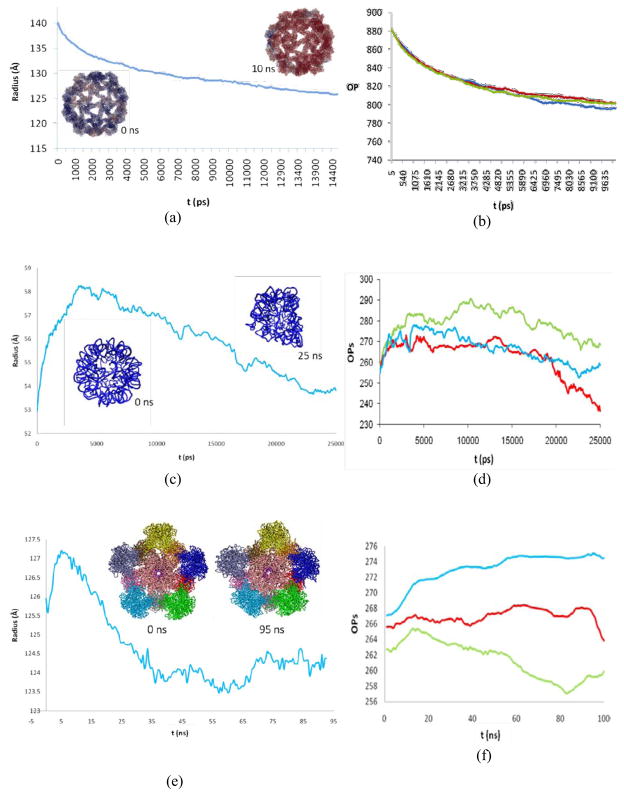
The CCMV capsid consists of 180 identical protomers organized as 12 pentamers and 20 hexamers arranged in a T=3 icosahedron, having 432,120 atoms in total. Both in vacuum and an aqueous host medium, this structure shrinks, in agreement with DMS simulations. DMS trajectory based on 27 structural OPs shows the gradual reduction in radius over time (Fig. 2(a)). About 10% decrease in radius is observed over the first 10 ns. Langevin timesteps of 80 ps were used. These steps are several orders of magnitude larger than those required for conventional MD. Since the characteristic time scale of OP evolution is much longer than that for atomic fluctuations, the Langevin timesteps can be this large. OPs are seen to filter out rapid atomistic fluctuations, reflecting the capability of microbes to achieve the coherence fundamental to biological functionality. Behavior of the OPs can be directly correlated to some overall structural parameters. For example, evolution of the CCMV radius over 10 ns is reflected in the decrease in the magnitudes of the three OPs that track compression/extension in the X, Y, and Z directions (Fig. 2(b)). At initial stage of shrinkage, these three OPs decrease in a similar way indicating that overall symmetry of the system is conserved. The capsomers undergo cooperative motions through strongly coupled long-range interactions during shrinkage (Miao and Ortoleva, 2010). However, at a later stage shrinking proceeds via a symmetry-breaking process that involves large-scale translation and rotation of pentamers and hexamers in the capsid (Miao et al., 2010; Miao and Ortoleva, 2010). As a result, the structural transition starts locally and then propagates across the capsid, i.e., it proceeds via intermediate states that are not constrained to the T=3 icosahedral symmetry of the initial and final states. This example indicates that symmetry-constrained models may be inappropriate to study the pathways and mechanisms of viral structural transition, while DMS captures this symmetry breaking pathway.

Fig. 2.

Structural transitions in CCMV (PDB ID: 1CWP) simulated via DMS. (a) Initial and final structures with radius of gyration time course. (b) Evolution of three OPs capturing compression/extension in the three Cartesian directions. (c,d) Similar evolutions for STMV RNA (PDB ID: 1A34) with initial and final structures. (e,f) The evolution of radius of gyration and the OPs for the HPV VLP (PDB ID: 1DZL) similar to (a,b). Insets in (e) show initial and final VLP structures.

3.2 STMV RNA structural transition

The 949 nucleotide RNA of STMV has been studied extensively both experimentally and theoretically (Freddolino et al., 2006; Schneemann, 2006). The shape of this RNA is confined by the STMV capsid, in which it achieves an equilibrium structure. The RNA changes its conformation depending on conditions in the microenvironment. Dynamics of capsid-free STMV RNA in 0.3 M NaCl solution was simulated using DMS. Immediately after the simulation starts, the RNA evolves towards a new equilibrium state, distinct from the capsid-confined one. It first expands, then shrinks, and ultimately fluctuates around the new equilibrium structure (Fig. 2(c)). The tertiary structure of the RNA becomes highly disrupted during 25 ns of evolution, after which the initial symmetry was completely lost (Fig. 2(c)). This is in agreement with experimental results on the free viral RNA (Schneemann, 2006). The gradual shrinkage of RNA observed in the simulations is explained on the basis of ion shielding. The cloud of Na⁺ counter-ions minimizes the repulsion between similarly charged regions in the RNA (Singharoy et al., 2011a). This electrostatic shielding stabilizes the RNA in a collapsed state. In contrast, a simulation of the RNA bound to residues 2 to 27 from the N-terminal region of capsid proteins exhibits stable STMV core particle conformations with a size distribution of ~50 Å (Day et al., 2001). Both the overall changes in shape and size of RNA, as well as the symmetry-breaking nature of its anisotropic expansion-shrinkage, are successfully tracked by the variation in the OP values in all three stages (Fig. 2(c, d)). During the initial transient stage the Langevin timestep of 40 ps was used. After 3 ns, the RNA was resolvated in a bigger box to accommodate the expansion. After an initial transient, Langevin evolution was executed using a timestep of 100 ps, reflecting the longer characteristic time for this phase. In this slower evolution regime an 11-fold efficiency relative to conventional MD was achieved. However, since a DMS simulation involves ensemble computations, its performance should be compared with many MD runs. While for each single traditional MD run the OP time-course is essentially the same as that predicted by DMS (Cheluvaraja and Ortoleva, 2010), the detailed atomistic configuration varies among members of the ensemble. In addition, a single MD run may not be representative of an ensemble of possible time-courses which, in contrast, is automatically generated using our deductive multiscale approach as implemented in DMS. For these reasons, DMS results display an additional speedup over traditional MD. In the given case this factor is equal to 168, the size of the sample used in the Monte Carlo integration to compute the thermal-average forces at each Langevin step.

3.3 HPV virus-like particles stability and fluctuations

3.3.1 Epitope behavior and immunogenicity

Epitopes are the outwardly projecting surface features of a viral capsid that play a critical role in invoking the immune response. This feature is recently utilized in the development of epitope-dressed vaccines constructed from virus-like particles (VLPs) (Jennings and Bachmann, 2009). VLPs are devoid of genetic material (RNA or DNA), but outwardly resemble the structure of the intact virus. Considering the high cost of developing vaccines, a computer-aided approach to vaccine discovery is of great interest. Since vaccine efficacy is tied to immunogenicity of VLPs, and immunogenicity may in turn be correlated with epitope behavior, study of epitopes is an important issue in developing VLP based vaccines. Epitopes may exhibit structural variation when binding to antibodies; such studies require simulations of whole VLPs while retaining small-scale details (at times to the atomic-level) in structural and dynamical variations (so as to study binding, structural transitions due to changing conditions). We demonstrate here the capability of DMS to capture such details in epitope behavior while efficiently simulating supra-million atom VLP structures (amounting to more than a million atoms). For this purpose we undertook a study of HPV VLPs, the active ingredient in vaccines developed for the prevention of cervical cancer (e.g., Gardasil^™) (Koutsky et al., 2002).

HPV VLPs are developed from the L1 major capsid protein (Brown and Garland, 2008). As more than 40 HPV types that cause genital tract disease have been identified, there is a need to expand the capabilities of current vaccines to target a broader spectrum of HPV types (Kreider et al., 1990; Smith et al., 2007; zur Hausen, 2009). When invoking immune response by HPV VLPs, type-specific antibodies are generated that are capable of neutralizing specific HPV types (Kreider et al., 1990). The specificity arises from the diversity in conformations of epitopes that bind to the antibodies. Five important epitope regions in HPV VLPs have been identified: BC, DE, EF, FG, and HI (Carter et al., 2006; Roden et al., 1997; Roth et al., 2006; Ryding et al., 2007), with FG shown to play a key role in antibody binding. A pentameric substructure of an HPV VLP shows immunogenic responses (Thönes et al., 2008) (however, less than that of a complete VLP); this has initiated interest in generating smaller size cost-effective vaccines having similar immunogenicity to that of a complete VLP.

A T=1 HPV16 VLP contains 12 pentamers of the L1 major capsid protein totaling ~400,000 atoms when unsolvated. The solvated system of this system consists of more than 2 million atoms. We simulated it and its pentameric substructures with MD and DMS to investigate structural stability and epitope behavior. The goal is to study structural and dynamical differences in epitope behavior for systems that show different immunogenicities. In particular, we studied a full T=1 HPV16 VLP, one of its isolated pentameric substructures, and a pentameric substructure with helix h4 removed from each L1 protein. Experimentally, the latter structure shows less immunogenicity than the full pentamer (Schadlich et al., 2009) (Sect. 3.3.2).

Here we focus the discussion on dihedral distribution for the epitopes in various structures, and in particular for the FG loop. The dihedral distribution for FG from MD and DMS of the h4 truncated pentamer of the HPV16 VLP shows excellent overlap (Fig. 3(a)). This indicates that DMS samples regions in the conformation space that are similar to those from conventional MD, thus validating the deductive multiscaling approach. The analysis provides a benchmark on DMS simulation accuracy as mentioned in Sect. 2.4.1. Fig. 3(b) shows a comparison between dihedral distribution for FG from the simulation of an isolated pentamer and that for the pentamer embedded in a complete HPV16 VLP. The dihedral angles of FG varied over a smaller region for the VLP relative to the pentamer. Reduced spread of dihedral distribution in the former reflects an overall reduced flexibility of a pentamer in a tightly-packed assembly relative to in an isolated one. Furthermore, FG explores different regions of configuration space in a truncated pentamer than in an intact one (Fig. 3(c)). Observed differences in dihedral distributions suggest a correlation between epitope conformations and VLP immunogenicity (Nowak, 1996), i.e., structures with larger epitope fluctuations (higher flexibility) are observed to produce lower immunogenic response. Further tests of the fluctuation-immunogenicity correlation hypothesis are in progress.

Fig. 3.

Behaviors of the FG loop in HPV VLP and substructures. (a) Comparison of MD (black) and DMS (red) generated dihedral distributions for FG in pentamer structure with helix h4 removed for 10 ns trajectories. Excellent agreement is seen, indicating the ability of DMS to capture all-atom MD features. (b) Similarly for FG in an isolated pentamer (black) and pentamer extracted from a full T=1 VLP simulation (red). The variance for a free pentamer is larger, showing that epitopes are more flexible in this structure than within a larger, tighter VLP framework. Full VLP simulation was carried out for 100 ns. The first 10 ns of this trajectory is used for comparison with that of the isolated pentamer. (c) Similarly for FG in an isolated pentamer (black) versus in a pentamer with helix h4 removed (red). The truncated pentamer shows larger flexibility, thereby affecting the epitope behavior. Both simulations were carried out for 10 ns using DMS.

The above DMS simulation of the complete VLP was carried out for 100 ns using 27 OPs. The pentameric structures are simulated for 10 ns to benchmark with MD. These studies demonstrate the ability of DMS to efficiently capture the details on structural variations. Such subtle differences are difficult to capture through coarse-grained/bead models.

3.3.2 Disassembly of truncated VLP structures

DMS was used to simulate the collapse of an HPV type 16 VLP to investigate thermal stability. Pentamers in the VLP are joined by “attacking arms” that stabilize the assembly via strong hydrophobic interactions (Bishop et al., 2007a; Bishop et al., 2007b). The C-terminal of the L1 protein consists of four helical regions h2, h3, h4, and h5 that are responsible for intra- and inter-pentameric stabilization. While h2, h3, and h5 are responsible for L1 protein folding and pentameric stability, h4 is indispensable for construction of the T=1 scaffold as it binds two separate pentamers. Helices h2, h3, and h4 were truncated from the L1 protein and the resulting structure was simulated. A 100 ns simulation of a 2 million atom system (including water and ions) was performed using DMS with the 27 OPs. A symmetry breaking collapse of the VLP was observed, in agreement with experimental data on the inability of these pentamers to self-assemble into VLP (Bishop et al., 2007a). A Langevin timestep of 125 ps was used. While the majority of the pentamers moved inwards from their initial position, others diffused outwards, resulting in a collapse and disassembly (Fig. 2(e)). Inward motion of the pentamers is facilitated by strong hydrophobic interactions between loops of neighboring pentamers. This demonstrates the role of hydrophobic interactions in generating an ensemble of intermediate structures along the assembly pathway. Phenomenological modeling studies of the assembly pathways of other viruses led to related conclusions (Hagan and Chandler, 2006). As with other examples, symmetry breaking in the temporal dynamics of the VLP is successfully captured by the OPs (Fig. 2(f)) (Miao et al., 2010; Miao and Ortoleva, 2010). Furthermore, helix truncations increase structural flexibility (leading to disassembly), enhancing disassembly and the spread in epitope dihedral distributions (not shown).

These examples represent a class of complex biological problems that can be studied with DMS due to its basis in underlying all-atom model and deductive multiscale analysis. All the stated results are consistent with those from experiments or other theoretical methods. No experimental data was used to calibrate the system (except for that already embedded in the CHARMM force field (Patel and Brooks, 2004)). To achieve the all-atom level of details over 10 – 100 ns time periods, the simulations were run on fewer than 128 processors. Traditional MD simulations would require far greater computational resources to achieve the above results. Our multiscale approach models system behavior via a set of OPs and coevolving quasi-equilibrium all-atom configuration ensembles; therefore, a broad spectrum of space-time scales is probed efficiently. With this, both the overall and the internal dynamics of a microbe are captured.

3.4 Information transfer between scales

Here we demonstrate the transfer of structural information from the all-atom to the coarse-grained description to numerically validate the logical flow of deductive multiscaling (Fig. 1) that underlies the above results. The direction and mechanism of information transfer accounted for in DMS is suggested in Fig. 1 (circles indicate the sources and targets of information transfer). The atomistic configurations constitute the ensemble used to calculate the thermal-average forces; conversely, instantaneous values of the OPs fix the probability density that weights the atomistic configurations in the ensemble. Sects. 2.2 – 2.3 describe methods of constructing the OP-constrained quasi-equilibrium ensembles of atomistic configurations and associated thermal-average forces and diffusivities which drive Langevin dynamics of OPs. Here information transfer between microscopic motions and the coarse-grained dynamics is studied numerically. There was heretofore no such study of the OP to atomistic scale transfer.

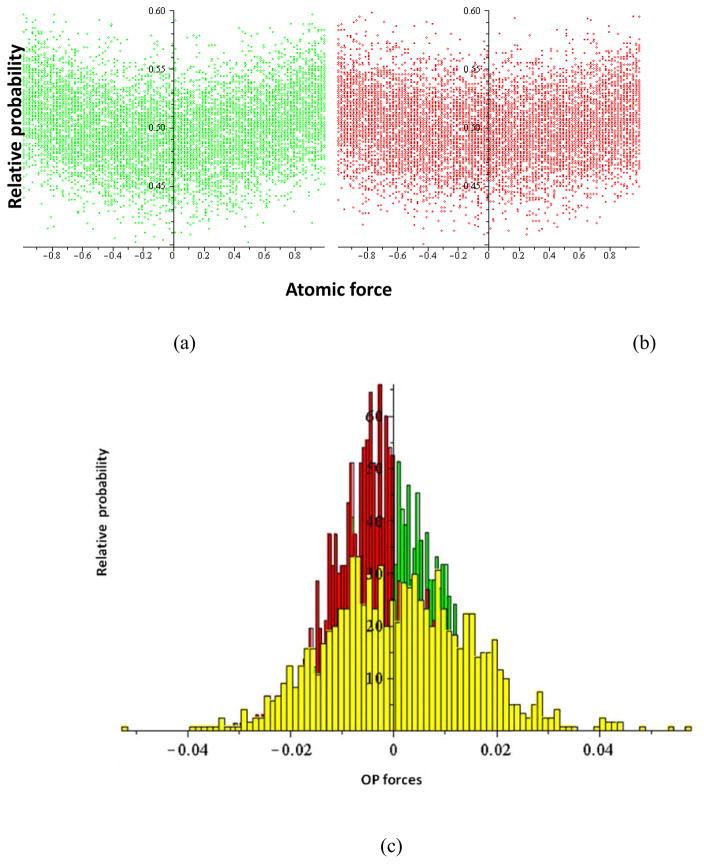
For this purpose we have investigated the OP-constrained ensembles of N-atom configurations for the STMV RNA (Sect. 3.2). Two ensembles were generated at different stages of RNA evolution (its expansion and collapse), and the corresponding probability distributions of atomic forces are plotted in Figs. 4(a–b). For each of the 100 bins constituting these two histograms, a probability of the atomic force projected on the line connecting the center of mass with each atom is shown for each of the sampled structures. While the atomistic ensembles do not show appreciable differences directly (even though the underlying structures are dramatically different, data not shown), distributions of OP forces constructed from the two ensembles (Fig. 4(c)) show a distinct shift in character as the underlying population of atomic structures changes. A peak in the distribution of OP forces in the initial structure (4 ns) shifts from a positive value to a negative at a later time (15 ns). Thus, coherency in microbial systems occurs at OP level as large atomistic fluctuations are filtered out in the process of constructing the forces driving OP dynamics. It is through the filtering enabled by the OPs that information is self-consistently transferred from the atomic to the larger-scale structural dynamics.

Fig. 4.

Histograms of atomic forces (projected along the ray from the center of mass) for the STMV RNA at (a) 4 ns and (b) 15 ns. (c) Histogram of thermal average forces driving overall extension/compression in the three Cartesian directions. Unlike for the atomic forces, the histograms of the OP forces show shift in the distribution from positive (green) to intermediate (10 ns, yellow), and finally to negative (red) values as the structure first expands and then contracts. (d, e) Linear correlation between the rate of change in the OPs and thermal average forces (obtained from ensembles at 4 ns and 15 ns, respectively) validating the DMS approach.

Next, the applicability of Langevin dynamics for evolving our structural OPs is validated. Data used for this analysis was obtained from NAMD (Phillips et al., 2005) generated trajectories of STMV RNA starting from structures obtained at 4 ns and 15 ns, as above. Eight structures are chosen at an interval of 50 ps from each trajectory. The OPs corresponding to simple compression/extension along the Z direction and corresponding thermal average forces were constructed at each of these times. Since off-diagonal terms in the diffusion matrix for the present problem are found to be smaller than the diagonal ones, a linear correlation between ΔΦ⃑_k/Δt and f⃑_k implies that the Langevin dynamics is satisfied. Fig. 4(d)–(e) validates this point. Therefore, trajectories from all-atom MD simulations demonstrate coherence in OP behavior due to the filtering of noise in the atomic forces manifest in the thermal average forces, and provide a validation of the Langevin dynamics, Eq. (4). Similar results hold for all lower-order OPs.

The present results demonstrate the capability of the present OPs to transfer information between all-atom and coarse-grained descriptions. Furthermore, these OPs are shown to evolve via Langevin dynamics, validating the logical workflow of Fig. 1.

3.5 Hierarchical order parameters

The higher order OPs (corresponding to higher k values) probe smaller regions in space (Miao and Ortoleva, 2009). Since the nonhierarchical system-wide structural OPs of Sect. 2.2.1 are expressed in terms of the all-atom configuration, OPs capturing deformations on a shorter spatial scale express much more atomic fluctuations than those addressing overall system behavior. Therefore, otherwise coherence behavior of the higher order OPs may be masked by high frequency fluctuations. Thus, the Langevin timestep needed to simulate their dynamics decreases, affecting multiscale simulation efficiency.

The hierarchical OP construction formalism introduced in Sect. 2.2.3 enables a three-level description of the microbial system that captures its structural hierarchy. By construction, these OPs provide a “double filter” of fluctuations while the nonhierarchical system-wide ones involve a single filter. The choice of subsystem centers of mass R⃑_s (s = 1,2, ···) filters some atomistic-scale fluctuations. Then the residual fluctuation in R⃑_s is re-filtered over the entire system via U_Ks to yield coherent Ψ⃑_K dynamics. Thus, slow dynamics for higher order OPs is realized (Fig. 5). In this way, hierarchical OPs allow longer Langevin timesteps and capture more structural details than can be achieved using the simple overall-system (Sect. 2.2.1) and subsystem OPs (Sect. 2.2.2).

Fig. 5.

(a) Time evolution of non-hierarchical higher order OPs (Φ). (b,c) Similar evolution for the hierarchical OPs (Ψ) demonstrating the increased coherence of the latter relative to the former.

3.6 Controls on accuracy

To assess the accuracy of the multiscale OP dynamics, comparisons are carried out with conventional MD simulations for 10 ns trajectories of capsid-free STMV RNA in 0.3 M NaCl solution. Fig. 6(a) shows the progress of the RMSD from the initial structure as a function of time; agreement of the RMSD between MD and multiscale simulation is excellent. Fig. 6(b) shows the alignment of STMV RNA structures generated from the MD and DMS simulations at the end of 10 ns. Further, OP time courses from the final 5 ns of conventional MD and DMS are shown (Fig. 6(c)). These results again validate the DMS approach, confirming that multiscale simulation generates configurations consistent with the same value of the OPs consistent with MD. Fig. 6(d) shows that the structural transition in RNA is energy driven, since the potential energy gradually decreases. Energies from the MD and DMS generated trajectories show good agreement in trend as well as quantitatively. The observed difference is within limits of the uncertainty in an MD run indicated by an ensemble MD starting from the same initial structure with different initial velocities (not shown).

Fig. 6.

Time evolution of the STMV RNA system. (a) RMSD from the initial structure for conventional MD (blue) and DMS (red) simulations. (b) Alignment of MD (blue) and DMS (red) generated pentamer structures of nucleic acid residues 1 to 150 after 10 ns of simulation. Time evolution of the (c) OPs 010Y (MD [blue]; DMS [orange]), 100X (MD [mauve]; DMS [red]) and 001Z (MD [deep-blue]; DMS [green]) showing the OP-equivalence of DMS and conventional MD. Details on the OP nomenclature are provided elsewhere (Singharoy et al., 2011a). (d) RNA potential energy via MD (red) and DMS (blue). (e) A Boltzmann average OP velocity autocorrelation function timecourse showing the absence of a long-time tail, and hence the lack of coupling to other slow variables not included in the set of Ops adopted. (f) Time evolution of the stable RNA core showing radius of gyration distribution of ~50 Å, in good agreement with experiments (Day et al., 2001).

A built-in self-consistency check in DMS is related to the relaxation times of correlation functions underlying diffusion factors. For the bionanosystems studied here, this correlation decays on a time scale much shorter than that of OP evolution (i.e., the OPs are constant over the time of autocorrelation decay). The decay period is followed by a fluctuating phase that reflects insufficient statistics for constructing long-time correlation function behavior. To illustrate this, the ensemble averaged auto-correlation function for a typical OP is plotted (Fig. 6(e)). The correlation analysis validates the completeness of the set of OPs as there is no long-time tail behavior in the correlation functions; the latter would have indicated the presence of slow variables that couple to the set of OPs used (Singharoy et al., 2011a).

Another self-consistency check is related to refreshing the reference structure. Our simulations begin with the energy-minimized and thermally equilibrated X-ray crystallographic or other all-atom structure as the reference structure. As the system evolves in time, the resulting deformation may increase some of the residuals σ⃑_ℓ of Eq. (1). This may reflect the need for a new reference structure. The reference structure transition point is chosen when the maximum residual for a structure in the constant OP ensemble becomes comparable with its RMSD from the initial reference structure, i.e., when some local change in a structure reaches the order of an overall deformation (Singharoy et al., 2011a). Increase in the residuals may indicate the presence of an improbable fluctuation in the MD generated part of the finite ensemble used for a practical computation. For these cases, a simple re-referencing is found to account for the resulting motions. However, increase in residuals may indicate the presence of coherent motions that are not accounted for by the set of OPs initially chosen. In this case, long-time tails in OP velocity autocorrelations are expected. The remedy for this difficulty is to increase the number of OPs considered. Additional OPs Φ⃑_k,new are constructed from the growing residuals via

$${\stackrel{\rightharpoonup }{\mathrm{\Phi }}}_{k,\mathit{new}}=\frac{{\displaystyle \sum _{\ell =1}^N}{m}_{\ell }{U}_{k\ell }{\stackrel{\rightharpoonup }{\sigma }}_{\ell }}{{\mu }_k}.$$ (9)

For the RNA simulation, no long-time tails in the velocity autocorrelation, or a significant population of high residual structures signifying absence of additional slow modes, were observed.

Comparison with experimental observations is also used to validate DMS. A control experiment is performed to compare the deformation in free STMV RNA versus under protein encapsulation. In agreement with experiments (Day et al., 2001), this complex is predicted to be stable with an average radius of gyration ~50 Å (Fig. 6(f)).

All the above measures ensure that DMS simulations have minimum errors or artifacts at any step, validating the DMS approach.

3.7 Discovering Free-energy Basins

The free-energy basin discovery method (Sect. 2.5) was implemented in DMS and demonstrated for the iron binding protein lactoferrin that supports multiple free-energy minimizing structures. The closed state of this protein was chosen to be the initial configuration. The Δ⁻ factor was constructed using the set of eigenvalues of the moment of inertia tensor as molecular descriptors η (Eq. (8)). These three descriptors discriminate among the basins for this molecule. With this, in 30 DMS Langevin timesteps the system was guided away from the initial state to one in the basin containing the structure with two of the three protein lobes open. A plot of the progress of the total potential energy (protein-protein and protein-water) shows that the system traverses an energy barrier separating the two basins (Fig. 7(a)). Eigenvalues of the moment of inertia tensor have distinct ranges of value before and after barrier crossing (Fig. 7(b)). This demonstrates how our formalism allows for the step-by-step discovery of basins in the free-energy landscape. In ongoing studies, Δ⁻ is further modified to incorporate nanocharacterization data such as collision cross-sections and AFM. This guides basin exploration to states that are consistent with experimental data.

Fig. 7.

Time course of (a) thermal-average protein potential energy and (b) smallest of the moment of inertia eigenvalues for lactoferrin as it changes during barrier crossing from an original free-energy basin to a new one (Sect. 2.5). Every Langevin timestep was equivalent to 50 ps.

3.8 Performance

In this section we compare the performance of DMS and other approaches. All-atom simulations (MD and quantum calculations) are computationally demanding in terms of compute load, communication speed, and memory load. Simulations are reported that successfully model multi-million to multi-billion atom systems (Abraham et al., 2002; Ahmed et al., 2010; Sanbonmatsu and Tung, 2006, 2007; Schulz et al., 2009; Germann et al., 2005). However, these studies require very sophisticated supercomputing platforms (such as CRAY or National facility supercomputers), thousands of processors, and very low latency interconnect (such as InfiniBand) (Liu et al., 2003). Thus, these applications are not achievable using readily available platforms. Moreover, for reported billion-atom simulations (Germann et al., 2005), electrostatics, bonded forces, and the rapidly fluctuating proton (all of which are essential for microbial modeling) were not included; thus, while interesting, they do not serve as a benchmark for microbial simulation. More generally, the forces, types of atoms, and various approximations/shortcuts (implicit/explicit solvent) adopted may significantly modify the CPU burden. In the case of forces, the simulations may account for Particle Mesh Ewald and truncated Coulomb, or may neglect bonded forces. If the high-frequency fluctuations of protons are neglected by excluding hydrogen, then the MD timestep can be greater (Andersen, 1983; Forester and Smith, 1998; Hess et al., 1997; Miyamoto and Kollman, 1992). Our simulations of RNA (total 500,000 atoms) have been carried on for 50 ns, and HPV16 VLP (total 2 million atoms) for 100 ns, while including all the standard biomolecular parameters such as Particle Mesh Ewald electrostatics.

Our goal is to not to develop an entire simulation package suited for only a particular application, but present a multiscale framework that is general enough to work with a spectrum of established simulation packages such as NAMD (Phillips et al., 2005) or GROMACS (Hess, 2008) so that it can be used for multitude of applications. Compared to the computational performances mentioned in the above literature, DMS achieves a great efficiency because it is capable of simulating these systems with more modest computing resources (typically 128 cores with Myrinet Interconnect) for examples described in Sect. 3. The scalability of DMS for a given size microbial system can be similar to that of the MD package (here NAMD (Phillips et al., 2005)) used for generating all-atom ensembles. Thus, simulating systems with millions or more atoms with DMS is plausible if it is achievable, but with much less efficiency, via NAMD under available compute resources.

Simulations carried out in this study were without any of the commonly used MD shortcuts. For ensemble generation, a timestep of 1 fs was used, while using SHAKE/RATTLE (Andersen, 1983; Forester and Smith, 1998; Hess et al., 1997; Miyamoto and Kollman, 1992) could have allowed for 2 fs timesteps, increasing performance two-fold. A factor of acceleration (commonly about 6) is achieved using a GPU-Infiniband platform. Another factor of acceleration can also be attained via more advanced Langevin timestepping algorithms. Since all these accelerating factors are multiplicative, the future for large system, long time simulation under DMS is promising.

4 Conclusions

Microbial systems are organized hierarchically, starting with atoms, ending with supramillion atom assemblies and micron-scale structures. This biological organization is mirrored in our multiscale mathematical framework to yield insights into the coupling of processes across scales in space and time that is the hallmark of microbial behavior. These behaviors include structural transitions and assembly/disassembly. Our results show that the hierarchical organization of a microbe implies a separation between the timescales of atomic collisions/vibrations versus that of overall structural dynamics. Microbial behaviors, as reflected in our multiscale formalism, arise through coupling of equilibrium and nonequilibrium processes.

A key to the analysis of microbial phenomena from a first-principles perspective is shown to be the identification of OPs characterizing the longer scales at which microbes are organized. As with the microbe itself, the mathematical structure of a theory of microbial behavior should be hierarchical in nature, notably in the form of very coarse-grained variables constructed from less coarse-grained ones, and similarly down to the primitive N-atom description. This parallel conceptualization leads to deeper insights into the transfer of information between the various scales of behavior, and suggests a simulation algorithm incorporating it.

When this conceptual framework is implemented as a simulator, computational efficiencies are achieved. This multiscale computational algorithm yields the co-evolution of the OPs with an ensemble of all-atom configurations. In essence, our methodology provides an integrated coarse- and fine-graining approach. Since the OPs provide incomplete information (i.e., relative to the 6N atomic positions and momenta), theory of multiscale microbial dynamics is fundamentally probabilistic in character. Thus, our theory provides both the evolution of the OPs and the co-evolving quasi-equilibrium probability distribution of the all-atom configuration.

Our multiscale approach was implemented as the DMS software. This software is used to demonstrate our multiscale framework for microbial simulation. Results not only capture key mechanistic details of structural transition at the nanometer and atomic scale, but also reveal the robustness of our algorithm. Insights obtained from these simulations include (1) the discovery of nucleation and front propagation pathways for viral structural transition, (2) counter-ion induced collapse and stabilization of the free and protein bound states in STMV RNA, (3) variations in epitope behavior from different structures of the HPV VLP, and (4) importance of hydrophobic interactions in preserving the assembly of the HPV vaccine nanoparticle.

A speed-up of ~11 fold is obtained for the nonhierarchical OPs of Sect. 2 over conventional MD simulations (Singharoy et al., 2011a). However, a direct comparison with conventional MD is not appropriate. In this study, a single DMS simulation corresponds to an ensemble of 168 conventional MD runs, thus yielding a speed-up of ~1500 relative to a single conventional MD. This efficiency results from the OP-mediated coarse-graining of all-atom dynamics that provides Langevin timesteps of 50–100 ps, and a quasi-equilibrium probability of atomistic configurations coevolves with the OPs. Such timesteps enable simulation of longer timescale microbial phenomena. The hierarchical OP formulation enhances the coherence of structural OPs and allows for a more detailed OP description of the microbial systems without significant reduction of Langevin timesteps. Finally, DMS was extended to enable the automated discovery of multiple free-energy basins using information from known basins and/or data from nanocharacterization experiments. This idea is demonstrated for exploring the closed and open conformations of lactoferrin. In addition, several measures are discussed to ensure the validity of our multiscale approach and its implementation as DMS.

The algorithm implied by our multiscale approach provides a self-consistent framework for transferring information between scales in space and time, as evidenced by several microbial simulations. We believe the DMS scheme can be further optimized and generalized to address more complex microbes such as enveloped viruses, bacteria, and eukaryotic cells. This will yield a calibration-free multiscale theory of microbial behavior.

Abbreviations

AFM

atomic force microscopy

CCMV

cowpea chlorotic mosaic virus

STMV

satellite tobacco mosaic virus

HPV

human papillomavirus

RMSD

root mean square deviation

CG

coarse-grained

MD

molecular dynamics

QM/MM

quantum mechanics/molecular mechanics

OP

order parameters

DMS

DeductiveMultiscaleSimulator