Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Jul 1.
Published in final edited form as: Magn Reson Med. 2011 Feb 24;66(1):174–179. doi: 10.1002/mrm.22773

Real-Time Motion Correction for High-Resolution Larynx Imaging

Joëlle K Barral 1, Juan M Santos 1,2, Edward J Damrose 3, Nancy J Fischbein 3,4, Dwight G Nishimura 1
PMCID: PMC3383318  NIHMSID: NIHMS382083  PMID: 21695722

Abstract

Motion—both rigid-body and non-rigid—is the main limitation to in vivo, high-resolution larynx imaging. In this work, a new real-time motion compensation algorithm is introduced. Navigator data are processed in real-time to compute the displacement information, and projections are corrected using phase-modulation in k-space. Upon automatic feedback, the system immediately reacquires the data most heavily corrupted by non-rigid motion, i.e., the data whose corresponding projections could not be properly corrected. This algorithm overcomes the shortcomings of the so-called Diminishing Variance Algorithm (DVA) by combining it with navigator-based rigid-body motion correction. Because rigid-body motion correction is performed first, continual bulk motion no longer impedes nor prevents the convergence of the algorithm. Phantom experiments show that the algorithm properly corrects for translations and reacquires data corrupted by non-rigid motion. Larynx imaging was performed on healthy volunteers, and substantial reduction of motion artifacts caused by bulk shift, swallowing, and coughing was achieved.

Keywords: Larynx imaging, Motion correction, Real time imaging, Navigators, DVA

1 Introduction

High-resolution MR imaging requires small voxels and long scan times and is therefore vulnerable to involuntary and physiologic motion. In high-resolution imaging of the larynx, motion poses an even greater challenge than in high-resolution imaging of other body areas because patients often swallow and cough during the scan, and the carotid arteries are typically within the field-of-view (FOV), causing pulsatile flow artifacts (1).

Motion can be classified into intermittent, sporadic motion (e.g., swallowing, coughing, jolting) and continuous motion (e.g., flow, bulk motion, respiration). Among the many methods that have been proposed to handle these types of motion in specific body areas, several, described below, are relevant for larynx imaging.

Different ordering schemes (spiral, elliptical) have been investigated to increase the robustness of the acquisition against sporadic motion (2, 3). These schemes acquire the center of k-space—which concentrates most of the energy—at the beginning of the scan, when the patient is most likely to stay still. Motion occurring when the outer part of k-space is being acquired, however, is also undesirable, because high frequencies are essential to obtaining a sharp image where resolution matches the prescribed voxel size.

To avoid pulsatile flow artifacts, which manifest as ghosts in the phase-encode direction, the frequency direction can be chosen in the Anterior/Posterior direction. This avoids the overlap of the ghosts from the carotid arteries with structures of interest.

The amplitude of bulk motion can be limited by physical restraints and coaching of the patient. In larynx imaging, because the cervical rotational axis is relatively far from the region-of-interest (ROI), bulk motion is well-approximated by translations, and we propose to effectively track it using Cartesian navigators (4), as has been done for high-resolution trabecular bone imaging (5).

Gating is a common approach to limiting data acquisition to a specific window of the respiratory cycle and freezing respiratory motion, which is non-rigid but quasi-periodic. Gating requires additional patient preparation, however, and might be impractical for patients with irregular breathing patterns. The Diminished Variance Algorithm (DVA) acknowledges the complexity of organ motion during respiration. It has been used to eliminate respiratory artifacts from thoracic and abdominal images (6,7). In DVA, motion is estimated in real time using navigators and, at the end of a full acquisition, the data most heavily corrupted by motion are reacquired. The motion information is then updated, and the process is repeated. DVA ignores intraview motion and assumes quasi-periodic motion. If bulk motion occurs, the position of the navigator is updated, and all the data need to be reacquired. Therefore, if continuous bulk motion happens—superimposed on the quasi-periodic pattern—the algorithm will never converge. Indeed, the reacquired data always correspond to a baseline position that has shifted since the full acquisition. This is a major limitation of DVA, especially when imaging is done outside the thoracic and abdominal areas.

To combat all the types of motion affecting larynx imaging, we propose a real-time algorithm that integrates different strategies. Navigator-based motion correction is used to correct for rigid-body motion, while data corrupted by non-rigid motion are reacquired. A full dataset is first acquired, using a sequential, spiral, elliptical, or pseudo-random trajectory. Navigators interleaved in X, Y, Z are processed in real time to obtain the displacement information. Data are corrected using phase-modulation in k-space, and the mean-square-error (MSE) between the corrected projections and the projection chosen as the reference is computed for each axis. Based on the sum over the different axes of the weighted MSE, a list of data (e.g., encodes in Cartesian imaging or interleaves in spiral imaging) that need to be reacquired is then sent to the scanner. These reacquired data replace the previously corrupted ones, and the MSE is updated. The process is repeated until satisfactory image quality is obtained and the user decides to stop the acquisition. This algorithm therefore overcomes the shortcomings of DVA by combining it with navigator-based rigid-body motion correction. Because motion correction is performed first, continuous bulk motion no longer impedes nor prevents the convergence of the algorithm.

In this article, we first present our algorithm and its implementation. We then show results from phantom scans that validate our method. Finally, we demonstrate the application of our motion-correction scheme to in vivo larynx imaging of healthy volunteers.

2 Methods

2.1 RTHawk

We implemented our algorithm within RTHawk (HeartVista, Inc., Los Altos, CA), a real-time acquisition, control, and reconstruction environment for MRI (8). This framework allows for on-the-fly changes in pulse sequence and acquisition parameters. With our 1.5 T GE scanner (GE Healthcare, Milwaukee, WI), RTHawk runs on a dual core AMD Opteron 270 4×2 GHz processor with 7 GB RAM.

Localization and shimming come as modules of RTHawk. Localization is carried out using 2D spirals running in real-time, and the plane of acquisition is chosen interactively. Shimming can be performed automatically or manually. For larynx imaging, proper shimming is important because it limits the off-resonances that are expected at the air/void interface.

2.2 Pulse sequence

We implemented a 3D Fast Large Angle Spin Echo (FLASE) sequence (9, 10). As a spin-echo sequence, FLASE is relatively immune to off-resonance effects. It is also a 3D sequence, which offers thin, contiguous slices in a reasonable scan time. Last, it provides T1-weighted contrast similar to what is obtained with the Fast Spin Echo (FSE) T1-weighted sequence of the head and neck protocol typically used for larynx imaging.

FLASE has been used with navigators interleaved between the X and Y axes—i.e., with only one navigator played every TR, either on X or on Y—for high-resolution trabecular bone imaging (5, 10). To improve motion estimation and correction by accounting for any arbitrary translation, we used navigators interleaved among the X, Y, and Z axes. The alternative would be to play the three navigators sequentially every TR, but the interleaving scheme is necessary to preserve high SNR for the navigators and comply with the duty cycle of the gradients.

2.3 Trajectory

RTHawk is given a list of gradient waveforms for each axis as well as a lookup table. The table indicates which waveform to play for each encode and each axis. We designed gradients with and without navigator for all encodes, because the order of encodes that will be reacquired is not known a priori and we want to maintain the same order for the navigators throughout the scan. The index of the waveform indicates both the encode number and the axis on which the navigator is played. A high-resolution trajectory was designed with 256 sampling points, 128 phase encodes, 32 slice encodes, 64-point navigators, a receiver bandwidth of ±32 kHz, a minimum FOV of 12 cm, and a navigator FOV equal to the image FOV.

2.4 Ordering scheme

The order of the encodes that need to be acquired is described in a table that is loaded on the fly. The navigator interleaving scheme is then added. “Dummy” views are also added (1) at the beginning of the first list of encodes to acquire, to establish steady state, and (2) at the end of each list of encodes to (re)acquire, to account for any delay in processing. A delay might indeed happen at the end of an iteration, if reconstructing the uncorrected and motion-corrected images and computing the list of encodes to reacquire during the next iteration take longer than a TR.

2.5 Reconstruction pipeline

Data received from the scanner are separated between image data, which are accumulated until a full acquisition is done, and navigator data, which are processed in real time. The first views after the “dummy” views are taken as the references (one reference per axis). The views taken as references can indeed be arbitrary provided they are not corrupted by sporadic motion, which is unlikely to happen at the very beginning of the scan. The displacements (shifts) are extracted from the navigator data using a Lucas-Kanade algorithm (11, 12). The Lucas-Kanade algorithm is a Gauss-Newton algorithm that minimizes the dissimilarity between two signals. Note that motion could be detected by other means than navigators (13, 14). A pair view/displacement is then sent to the motion-correction blocks (image and navigator). The navigator data are corrected using phase-modulation.1 The stream of both projections, without and with motion correction, is displayed (cf. Sec. 2.6). The MSE between the corrected projection and the reference is computed and sent to the block that will generate the list of encodes that need to be reacquired when a full acquisition is done.

When a full acquisition is completed, images without and with motion correction are reconstructed and displayed (cf. Sec. 2.6). Simultaneously, the list of encodes to reacquire is computed and sent to the scanner (with the addition of both “dummy” views at the end and a navigator scheme). The number N of encodes to reacquire at each iteration has been set by the user beforehand. In the current implementation, reacquiring only one encode at each iteration would imply reconstructing an uncorrected/corrected pair of images every TR, which would be inefficient. The priority criterion is defined as the sum over the different axes of the residual (MSE) between the corrected projections and the reference, divided by the energy of the reference, weighted by a power N of distance from the origin of k-space, divided by the maximum distance (we typically used N = 2) (6, 15): the list of encodes to reacquire consists of the n encodes with the largest sum of weighted MSE. Interpolation of the displacements and the residuals—necessary because navigators were interleaved among the three axes—is performed using splines (16). Once the list is sent, reacquisition starts the next TR.

The process is repeated until satisfactory image quality is obtained and the user decides to stop the acquisition.

Navigator processing needs to be performed at the incoming data rate, i.e., within a fraction of a TR. Image reconstruction and list computation should be performed as quickly as possible, but, if delays occur, the “dummy” views that have been added at the end of each list will fill the time gap and ensure that steady state is maintained. Note that these “dummy” views are only played if necessary and until the processing is done.

2.6 Graphical user interface

The graphical user interface (GUI) provides real-time interactive visual feedback. The GUI consists of two panels. The first one displays side by side the reconstructed images (without and with correction) and allows the user to interact with the scan. The second shows the projections as they are being acquired.

The parameters controlled through the GUI include image orientation and contrast, FOV, echo time (TE), TR, number of “dummy” views at the beginning of the acquisition, number of encodes to reacquire at each iteration, name of the file where the order of encodes is described, and starting and stopping of data acquisition.

2.7 Experiments

2.7.1 Phantom scans

To validate the algorithm, we performed coronal scans of an orange, using a larynx-dedicated three-coil array (17). We used the following parameters: TR/TE = 80/10 ms, FOV = 12 cm, slice thickness = 1.5 mm, sequential encodes order (slice encoding making the inner loop), matrix size = 256×128×32 (4096 encodes), n = 64 encodes reacquired per iteration (pass).

DVA

To demonstrate the performance of DVA, we simulated non-rigid motion in the following way, taking advantage of RTHawk capabilities: we started with a coronal acquisition for the first half of the full acquisition, then switched to an axial acquisition for several seconds, and then returned to the coronal acquisition until the end of the full acquisition. In this way, at the end of the full acquisition, several encodes were corrupted. In addition, we were guaranteed to be back at the original position for the rest of the scan.

Motion correction

To demonstrate the performance of the motion correction, we manually translated the table by about 1 cm towards the middle of the scan, and we brought it back to the approximated original position several seconds later.

Combined algorithm: DVA with motion correction

To demonstrate the performance of the combined algorithm, we performed the two previously described experiments in the same scan, with a slight modification (note that the orange was repositioned with respect to the previous scans): towards the middle of the scan, we switched to an axial acquisition for several seconds and returned to the coronal acquisition; we then manually translated the table by about 1 cm and left it at this new position for the rest of the scan.

2.7.2 Volunteer scans

Two healthy male volunteers were scanned. We complied with the regulations of our institution’s human ethics committee. We used the same larynx-dedicated three-coil array used in the phantom scans and the following parameters: TR/TE = 80/10 ms, FOV = 12 cm, slice thickness = 1.5 mm, sequential encodes order, matrix size = 256×128×32 (4096 encodes), n = 192 encodes reacquired per pass.

For the first scan, the first volunteer was not given any instructions. For the second scan, the second volunteer was instructed to swallow and cough intermittently at will, and he was asked to accentuate his movements when the center of k-space was being acquired. This mimics the worst-case scenario that can happen in vivo.

3 Results

For each experiment, figures show a selected slice of the 3D dataset after the full acquisition and after several additional passes. We also provide (1) the residual information after the full acquisition and (2) the displacement information corresponding to the displayed slice after the full acquisition and after several additional passes.

3.1 Phantom scans

3.1.1 DVA

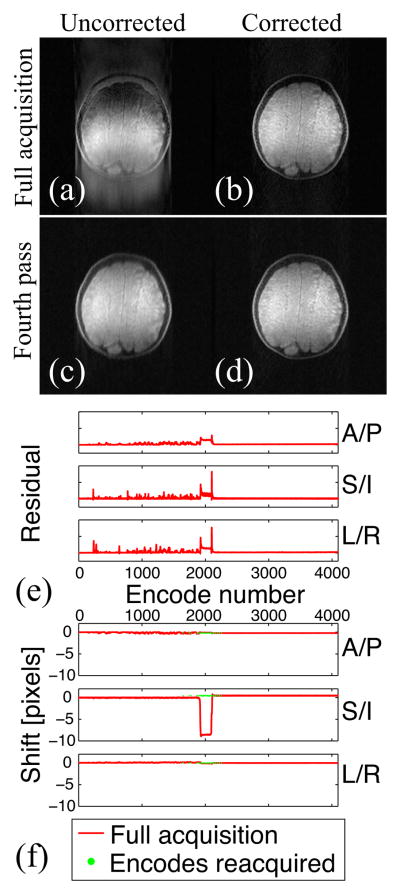
Figure 1 shows the results of the DVA experiment. As expected, the first frame (full acquisition) is corrupted by motion-like artifacts, but motion correction fails because motion was non-rigid. Once the corrupted encodes are reacquired, an image free of motion artifacts is obtained, and uncorrected and corrected images are identical. The shift information indicates that all the projections that were corrupted after the initial acquisition have been reacquired.

Figure 1.

Figure 1

Open in a new tab

Uncorrected (a, c) and motion-corrected (b, d) images after the full acquisition (a, b) and the sixth pass (c, d). A/P: Anterior/Posterior; S/I: Superior/Inferior; L/R: Left/Right. The residual information (e) confirms that, as expected, motion correction fails. The shift information (f) indicates that all corrupted projections are properly reacquired. Note that for the full acquisition the encode number matches the TR number because a sequential trajectory was used, but this is no longer the case upon reacquisition.

3.1.2 Motion correction

Figure 2 shows the results of the motion-correction experiment. Motion correction is effective, and no reacquisition is necessary. If reacquisition is performed, the uncorrected image remains blurry because the final position of the table did not perfectly match its original position.

Figure 2.

Figure 2

Open in a new tab

Uncorrected (a, c) and motion-corrected (b, d) images after the full acquisition (a, b) and the fourth pass (c, d). The residual information (e) confirms that motion correction is effective. The shift information (f) shows that the table was not brought back exactly to its original location, hence the residual blur after reacquisition (c).

3.1.3 Combined algorithm: DVA with motion correction

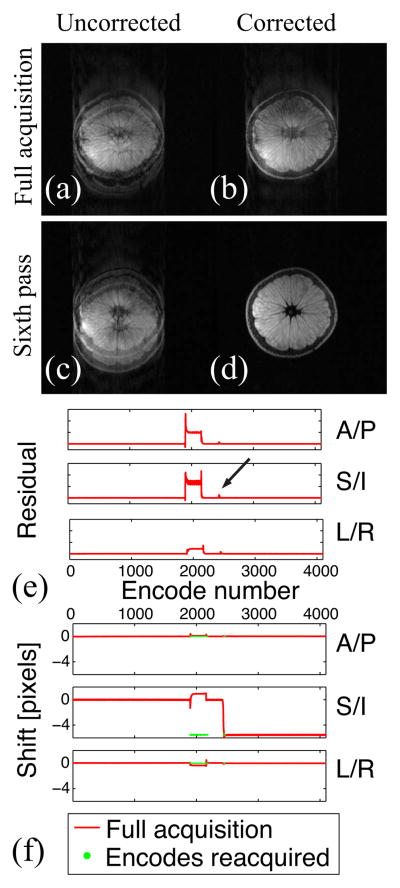
Figure 3 shows the results of the combined experiment. Motion correction successfully accounts for the translation, and the encodes corresponding to non-rigid motion are reacquired first. Once these encodes have been reacquired, the quality of the motion-corrected image is satisfactory. Neither motion-correction nor reacquisition alone but only their combination provides an image free of motion artifacts. Note that further reacquisitions would not improve the uncorrected image unless the reference were updated to account for the new table position.

Figure 3.

Figure 3

Open in a new tab

Uncorrected (a, c) and motion-corrected (b, d) images after the full acquisition (a, b) and the sixth pass (c, d). Both motion correction and reacquisition are needed to obtain an image free of motion artifacts (d). The residual information (e) confirms that motion correction successfully accounts for the translation (note the “zero” residual after the transient peak indicated by the arrow). The shift information (f) indicates that encodes corrupted by non-rigid motion are properly reacquired at the new table position.

3.2 Volunteer scans

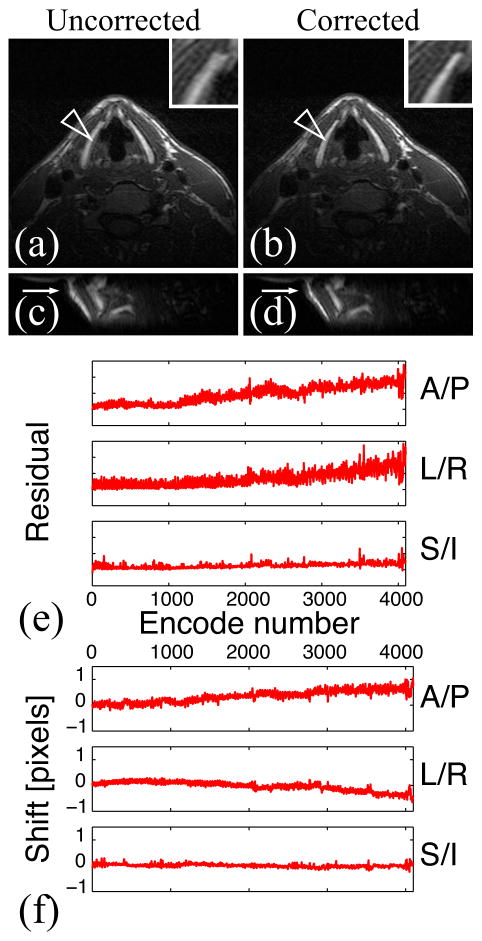
Figure 4 shows the results of the in vivo experiment in which the volunteer was not given any specific instructions. Blurring artifacts due to bulk motion are visible in the uncorrected image. As Figs. 4b and 4d show, these artifacts were successfully removed by motion correction.

Figure 4.

Figure 4

Open in a new tab

In vivo experiment: the volunteer was not given any instructions. Uncorrected (a) and motion-corrected (b) images after the full acquisition, and sagittal uncorrected (c) and corrected (d) reformatted images (resolution = 0.5×1×1.5 mm3). The residual (e) and shift (f) information show that bulk motion occurred. Motion correction improves image sharpness (arrows).

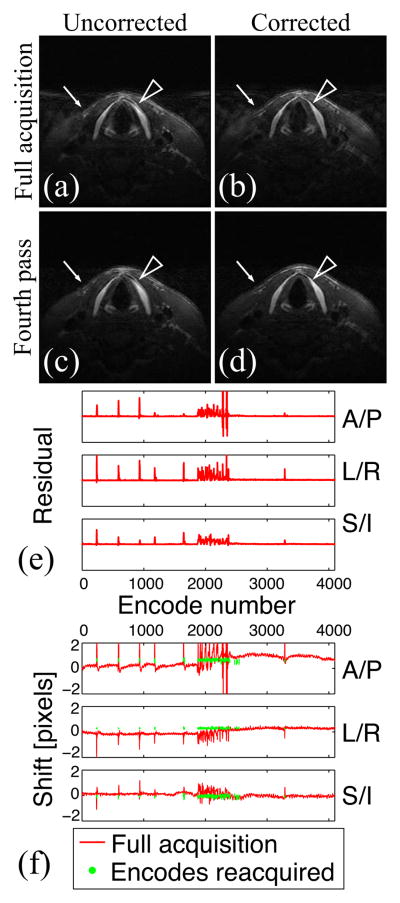
Figure 5 shows the results of the in vivo experiment in which the volunteer was asked to swallow and cough intermittently at will. As a result, blurring and ghosting artifacts, especially visible in the background, corrupt the image (Fig. 5a). Reacquisition was needed to account for this non-rigid, sporadic motion. Artifacts were greatly reduced once the corrupted encodes were reacquired (Fig. 5c). Motion correction was then needed to correct for bulk motion. A sharp depiction of thyroid cartilage and skin—otherwise blurred even after reacquisition—was then obtained (Fig. 5d). In this experiment, four passes were acquired, with 4096 encodes acquired for the full acquisition (first pass), and 192 encodes reacquired for each additional pass: only 14% of the data had to be reacquired to obtain an image free of motion artifacts.

Figure 5.

Figure 5

Open in a new tab

In vivo experiment with motion: the volunteer was asked to swallow and cough intermittently at will. Uncorrected (a, c) and motion-corrected (b, d) images after the full acquisition (a, b) and the fourth pass (c, d) (resolution = 0.5×1×1.5 mm3). The residual (e) and shift (f) information show sporadic motion. Corresponding encodes are successfully reacquired and motion artifacts are greatly reduced (background). Note that motion correction is necessary to provide a sharp depiction of the skin (arrow) and thyroid cartilage (arrowhead).

4 Discussion

Our algorithm does not rely on the cooperation of the person being scanned and inherits the robustness of DVA. As with DVA, the scan time overhead might be substantial if an image free of motion artifacts is desired, but several additional TRs are often sufficient to transform a heavily-corrupted image into a useful one. Our algorithm differs from DVA in two important ways. First, the navigators are interleaved, i.e., only one navigator, either X, Y, or Z, is played every TR. This is particularly relevant for high-resolution imaging and/or imaging of short-T2 species. The interleaving scheme makes interpolation necessary, and care is required to ensure a smooth transition upon reacquisition. Second, we integrated motion correction to account for bulk motion of the object. This is critical for high-resolution larynx imaging, where we have shown that DVA alone fails because of bulk motion. Note also that we have implemented DVA with a 3D Cartesian trajectory and 3D Cartesian navigators, whereas previous work used spiral or Cartesian trajectories with cylindrical navigators (6, 7,18). Our algorithm could also be used with radial trajectories, which by themselves show good motion properties. We demonstrated the benefits of our algorithm for larynx imaging, but the method is general and could be applied to other body areas.

Our current implementation has several limitations that could be overcome with slight modifications of the algorithm. First, even if unlikely, sporadic motion can happen at the very beginning of the scan, and the references will then be corrupted. More robust references based on a set of encodes could be used (19). Also, presently, the user decides to stop the acquisition when he/she deems image quality satisfactory. Therefore, there is no uncertainty about the outcome at the end of the scan. However, an automatic stopping criterion could be added to the algorithm, which would alleviate inter-user variability. For example, the scan could stop when all residuals are below a given threshold or when the scan has reached the maximum allotted time (6). Furthermore, in the current implementation, the encodes that are reacquired overwrite the previous ones. This might not be optimal towards the end of the scan if the new data do not improve upon the old. A condition could be added so that data are not stored unless the residual decreases. In addition, the length of the list of encodes to reacquire is currently set a priori. The time taken to reconstruct an uncorrected/corrected pair of images argues for a longer list of encodes to reacquire at each iteration. If the list is too long, however, unnecessary encodes might be reacquired. Note that even if the motion-corrected image were not systematically reconstructed, the list could not be made arbitrarily short (1 encode) for the shortest TRs, due to the processing complexity to determine the next encode to reacquire. The algorithm could be modified so that the length of the list is adapted to the residual information—e.g., by determining the number of encodes whose residual is above the threshold of the stopping criterion—at each iteration. Last, although 3D-navigators have proven useful for high-resolution imaging of the larynx, for other specific applications, some dimensions might not further improve the image, or temporal resolution might be an issue. Our implementation could be easily modified to allow specific navigator dimensions to be turned on and off (7).

Conclusion

We have presented a new algorithm for real-time motion compensation. The algorithm combines navigator-based rigid-body motion correction with a reacquisition strategy and therefore accounts for the main types of motion encountered in high-resolution MRI. We applied the algorithm to larynx imaging and demonstrated reduction of motion artifacts caused by bulk shift, swallowing, and coughing.

Acknowledgments

The authors would like to thank Michael Lustig, Todd Sachs, and Robert Schaffer for insightful discussions.

Footnotes

1

Motion correction refers to this navigator-based phase-modulation in k-space, not to the reacquisition scheme offered by DVA.

References

  • 1.Larkman DJ, Bydder M, Callaghan M, Melhem ER, Gilderdale DJ, Hajnal JV. A feasibility study of detection and correction of motion artifacts in MR imaging of the larynx using parallel imaging. Proceedings of the 10th Annual Meeting of ISMRM; Honolulu, HI. 2002. p. 75. [Google Scholar]
  • 2.Wilman AH, Riederer SJ. Performance of an elliptical centric view order for signal enhancement and motion artifact suppression in breath-hold three-dimensional gradient echo imaging. Magn Reson Med. 1997;38:793–802. doi: 10.1002/mrm.1910380516. [DOI] [PubMed] [Google Scholar]
  • 3.Bernstein MA, Shu Y, Elliott AM. RINGLET motion correction for 3D MRI acquired with the elliptical centric view order. Magn Reson Med. 2003;50:802–812. doi: 10.1002/mrm.10584. [DOI] [PubMed] [Google Scholar]
  • 4.Ehman RL, Felmlee J. Adaptive technique for high-definition MR imaging of moving structures. Magn Reson Imaging. 1989;173:255–263. doi: 10.1148/radiology.173.1.2781017. [DOI] [PubMed] [Google Scholar]
  • 5.Song HK, Wehrli FW. In vivo micro-imaging using alternating navigator echoes with applications to cancellous bone structural analysis. Magn Reson Med. 1999;41:947–953. doi: 10.1002/(sici)1522-2594(199905)41:5<947::aid-mrm14>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
  • 6.Sachs TS, Meyer CH, Irarrazabal P, Hu BS, Nishimura DG, Macovski A. The diminishing variance algorithm for real-time reduction of motion artifacts in MRI. Magn Reson Med. 1995;34:412–422. doi: 10.1002/mrm.1910340319. [DOI] [PubMed] [Google Scholar]
  • 7.Sachs TS, Meyer CH, Pauly JM, Hu BS, Nishimura DG, Macovski A. The real-time interactive 3-D-DVA for robust coronary MRA. IEEE Trans Med Imaging. 2000;19:73–79. doi: 10.1109/42.836367. [DOI] [PubMed] [Google Scholar]
  • 8.Santos JM, Wright GA, Pauly JM. Flexible real-time magnetic resonance imaging framework. Conf Proc IEEE Eng Med Biol Soc. 2004;2:1048–1051. doi: 10.1109/IEMBS.2004.1403343. [DOI] [PubMed] [Google Scholar]
  • 9.Ma J, Wehrli FW, Song HK. Fast 3D large-angle spin-echo imaging (3D FLASE) Magn Reson Med. 1996;35:903–910. doi: 10.1002/mrm.1910350619. [DOI] [PubMed] [Google Scholar]
  • 10.Magland JF, Wald MJ, Wehrli FW. Spin-echo micro-MRI of trabecular bone using improved 3D fast large-angle spin-echo (FLASE) Magn Reson Med. 2009;61:1114–1421. doi: 10.1002/mrm.21905. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Lucas BD, Kanade T. An iterative image registration technique with an application to stereo vision. Proc 7th Intl Joint Conf on Artificial Intelligence; Vancouver, BC, Canada. 1981. pp. 676–679. [Google Scholar]
  • 12.Barral JK, Lustig M, Nishimura DG. Lucas-Kanade algorithm for displacement extraction from navigators. Current Concepts of Motion Correction for MRI and MRS (ISMRM Workshop); Kitzbuhel, Austria. 2010. p. 18. http://www-mrsrl.stanford.edu/~jbarral/JoelleBarral_ISMRM10Workshop_Motion.pdf. [Google Scholar]
  • 13.Dold C, Zaitsev M, Speck O, Firle EA, Hennig J, Sakas G. Advantages and limitations of prospective head motion compensation for MRI using an optical motion tracking device. Acad Radiol. 2006;13:1093–1103. doi: 10.1016/j.acra.2006.05.010. [DOI] [PubMed] [Google Scholar]
  • 14.Buikman D, Helzel T, Roschmann P. The RF coil as a sensitive motion detector for magnetic resonance imaging. Magn Reson Imaging. 1988;6:281–289. doi: 10.1016/0730-725x(88)90403-1. [DOI] [PubMed] [Google Scholar]
  • 15.Sinkus R, Boernert P. Real-time reduction of motion artifacts using k-space weighting. Proceedings of the 5th Annual Meeting of ISMRM; Vancouver, BC. 1997. p. 1894. [Google Scholar]
  • 16.Press WH. Numerical recipes in C: the art of scientific computing. 2. Cambridge University Press; Cambridge: 1992. p. 113. [Google Scholar]
  • 17.Barral JK, Wu HH, Damrose EJ, Fischbein NJ, Nishimura DG. High-resolution larynx imaging. Proceedings of the 17th Annual Meeting of ISMRM; Honolulu, HI. 2009. p. 1318. [Google Scholar]
  • 18.Nguyen TD, Spincemaille P, Cham MD, Weinsaft JW, Prince MR, Wang Y. Free- breathing 3-dimensional steady-state free precession coronary magnetic resonance angiography: comparison of four navigator gating techniques. Magn Reson Imaging. 2009 Jul;27:807–814. doi: 10.1016/j.mri.2008.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Schaffer RW, Meyer CH, Pauly JM, Hu BS, Nishimura DG. Calculating a reference from navigators placed over the heart. Proceedings of the 10th Annual Meeting of ISMRM; Honolulu, HI. 2002. p. 2308. [Google Scholar]

RESOURCES