Testing Physical Models of Passive Membrane Permeation

Abstract

The biophysical basis of passive membrane permeability is well understood, but most methods for predicting membrane permeability in the context of drug design are based on statistical relationships that indirectly capture the key physical aspects. Here, we investigate molecular mechanics-based models of passive membrane permeability and evaluate their performance against different types of experimental data, including parallel artificial membrane permeability assays (PAMPA), cell-based assays, in vivo measurements, and other in silico predictions. The experimental data sets we use in these tests are diverse, including peptidomimetics, congeneric series, and diverse FDA approved drugs. The physical models are not specifically trained for any of these data sets; rather, input parameters are based on standard molecular mechanics force fields, such as partial charges, and an implicit solvent model. A systematic approach is taken to analyze the contribution from each component in the physics-based permeability model. A primary factor in determining rates of passive membrane permeation is the conformation-dependent free energy of desolvating the molecule, and this measure alone provides good agreement with experimental permeability measurements in many cases. Other factors that improve agreement with experimental data include deionization and estimates of entropy losses of the ligand and the membrane, which lead to size-dependence of the permeation rate.

INTRODUCTION

Permeability assessment is a crucial component in the drug development process for selecting and optimizing leads with favorable absorption, distribution, metabolism and excretion (ADME) properties. In order to avoid compounds with poor permeability or other ADME properties, a commonly adopted strategy is to comply with rules-of-thumb for ‘drug-likeness’ such as Lipinski’s Rules of Five.¹ These rules qualitatively outline the physiochemical space defined by the majority of well-absorbed drugs, which include (1) molecular weight (MW) <500, (2) number of hydrogen bond donors ≤5, (3) number of hydrogen bond acceptors ≤10, and (4) octanol-water partition coefficient (LogP_o/w) <5. Exceptions to these rules are known, and such rules do not provide quantitative measures.

Predictive quantitative models in use for drug design are primarily quantitative structure-permeability relationship (QSPR) methods that employ statistical relationships derived empirically from experimental permeability measurements and various physiochemical properties of a training set of compounds.^2–14 The development of these quantitative models has previously been reviewed elsewhere.^15,16 The QSPR approach has been widely applied in modeling oral bioavailability,¹⁷ intestinal absorption,¹⁸ skin permeation,^19,20 and brain permeability.^9,21,22 Some of the common QSPR descriptors include MW, polar surface area (PSA), partition coefficients, and hydrogen bond counts, all of which are known to correlate with rates of permeation. However, the main limitation of such an approach, like other empirical scoring models, is transferability. The performance of the model depends on the chemical similarity between the molecules of interest and the training set.¹² Empirical statistical relationship can also be difficult to interpret, for example, what modifications to a compound would most successfully improve permeability?

An alternate approach is to develop models that are more directly based on the physics of the underlying processes. In the case of intestinal permeability, for example, there are (at least) three primary processes: passive diffusion across the cellular membrane, paracellular diffusion through the cell junctions, and active transport that includes chemical influx and efflux facilitated by transporter proteins. Increasing structural knowledge of key transport proteins, such as the efflux transporter P-glycoprotein (PGP),^23,24 will undoubtedly advance predictive models of active transport mechanisms. Paracellular diffusion, which is primarily pertinent for very small and polar molecules, has been treated by others using hindered diffusion models.^25–27

Here, we consider transmembrane passive diffusion which, for many molecules, is a dominant factor in intestinal absorption, rates of crossing the blood-brain barrier, and simply entering cells, as in in vitro cell-based experiments. In the extreme, it is possible to study passive membrane permeability in all-atom detail, i.e., using molecular dynamics simulations with explicit permeant and lipid molecules.^28–36 Such simulations provided many important insights into the process and were shown to be capable of predicting relative permeability coefficients, at least for very small molecules. However, it remains difficult to predict absolute permeability by this underutilized approach, which is as yet computationally too expensive to be practically applied in drug design.^29,35 A less computationally intensive alternative is to augment QSPR models with membrane-interaction descriptors obtained from MD simulations of permeants in lipid layers, such as the membrane-interaction QSAR method developed by Hopfinger and coworkers.^37–41 Another approach is to use coarse-grained or implicit membrane models,^42–49 which in principle provide an adequate representation of the membrane environment with lower computational expense. While implicit membrane models have been employed in studies of transmembrane proteins, their application to membrane permeation remains limited.^46–48 One such example is the implicit model recently developed by Parisio and Ferrarini that accounts for the anisotropic and nonuniform membrane environment.⁴⁹

Alternatively, solubility-diffusion theory has been used as the basis for a predictive framework, in which the permeability is assessed in terms of three components: the partitioning between water and the membrane, the diffusion across the membrane, and the width of the membrane.^50,51 This theory was originated from the general permeability model for nonelectrolytes derived by Diamond et al.⁵⁰ The statistical mechanical basis of this model was developed by Xiang and Anderson, who implemented methods to describe crucial aspects of the membrane physics, such as the size selectivity and chain ordering of lipids.^52–52 A similar solubility-diffusion model was also utilized to study blood-brain barrier permeation by Seelig and coworkers, using parameters including the air/water partition coefficient and molecular shape of the permeant.^59,60 The conceptual and theoretical underpinnings of these models are described in more detail in the following section.

While these solubility-diffusion approaches are typically more computationally expensive in comparison to QSPR models and remain less commonly employed, they do offer several advantages. Such methods capture the underlying physics of the permeation process and do not require training with permeability data, and thus are expected to be more general and transferrable. By the same token, the quality of a physical model, instead of being governed by the training set data, is determined by the theoretical representation of the process. Hence, in principle, physics-based models can be systematically improved by elevating the level of theory to describe the permeation process and to calculate each of the physical contributions. Since permeability is evaluated in physically-meaningful terms, the physics-based approach also offers a mechanistic understanding of the permeation process that allows for rational modulation.

Our own contributions in this area have emphasized the importance of performing extensive conformational sampling of the permeant, particularly for larger, conformationally complex molecules such as cyclic and linear peptides. ^61–65 The free energy of desolvating the molecule, upon entering the hydrophobic interior of the membrane, is a critical parameter for accurate determination of the permeation rate. Conformationally flexible molecules can reduce this free energy cost by adopting conformations that, for example, maximize internal hydrogen bonding. Applications of this model to predict permeability of cyclic peptides and drug-like molecules resulted in good agreement with experimental data, including in prospective tests, warranting further development.^61–65

In the present work, this simple physical model was expanded to provide a more sophisticated representation of the permeation process based on solubility-diffusion theory, building on prior work. ^53,54,60 Additional attributes were incorporated in the model to account for contributions from both the permeant and the membrane that influence permeability, especially those related to the size- and shape-dependence of permeation. Along with combining these physical aspects with extensive conformational sampling, our major contribution is the systematic evaluation of different aspects of the model through a large and diverse group of experimental data sets as summarized in Table 1. The examined data ranges from in vitro measurements, which include parallel artificial membrane permeability assays (PAMPA), Caco-2 cell-based assays, and Madin-Darby canine kidney (MDCK) cell-based assays, to in vivo data, which includes percentage absorption in human (%Abs) and rat in situ perfusion assays.^66–74

Table 1.

The examined data sets and their data types.

Set	Compounds	Congeneric?	Data type (N)	Reference
Avdeef	FDA drugs	No	PAMPA (11)	66
			Caco-2 (11)
Balamine	FDA drugs	No	PAMPA (22)	67
			Caco-2 (21)
			%Abs (22)
Bermejo	Fluoroquinolones	Yes	PAMPA (16)	68
			Caco2 (14)
			Perfusion assay (16)
Di	FDA drugs	No	PAMPA (27)	69
Fujikawa	FDA drugs & small chemicals	No	PAMPA (70)	70
			Caco-2 (29)
Goodwin	Peptidomimetics	Yes	Caco-2 (12)	71
Irvine	FDA drugs	No	Caco-2 (50)	72
			MDCK (51)
			%Abs (53)
Li	Peptidomimetics	Yes	PAMPA (25)	73
			Caco-2 (25)
Whitlock	1-(2-Phenoxyphenyl) methanamines	Yes	PAMPA (8)	74

With the exception of PAMPA, all measurements involve biological membranes. The artificial membrane in PAMPA is typically composed of lipids and organic solvent, thus the assay measures strictly passive diffusion across an organic layer. The cell-based assays measure permeability across a monocellular layer. The Caco-2 and MDCK cell lines are well established models for biological processes, such as intestinal absorption or penetration across the blood brain barrier. The cellular membranes possess active transport facilitated by transport proteins and paracellular transport through cell junctions, in addition to transcellular passive permeation. Common approaches to evaluating passive permeation in these assays include using inhibiting substrate for transporter proteins, identifying possible active efflux or influx by measuring permeations in both apical-to-basolateral (A→B) and basolateral-to-apical (B→A) directions,⁷¹ measuring permeability of paracellular permeants as a control,⁷² and genetically knocking out known transporters.⁷⁵

The in vivo data examined in this study are absorption measurements in human or rat. The percentage human absorption (%Abs) refers to intestinal absorption in human. The in situ perfusion assay allows assessment of gut absorption in rat by perfusing the substance of interest through the cannulated gut of an anesthetized rat and monitoring the change in substance concentration.⁷⁶ Although the extent of drug absorption involves many properties, including solubility, passive membrane permeability is critical to the absorption process. Therefore, in vitro permeability measurements and calculated “hydrophobicity” measures, such as LogPo/w and PSA, are often utilized to predict absorption.

By evaluating the physics-based permeability model with respect to the different data types and conventional regression-based in silico models, the results highlight the generality of the approach and the ability to systematically improve the model.

THEORY

The physical models of passive membrane permeability considered here are based upon solubility-diffusion theory. The conceptual underpinnings and applications of this model have been described and reviewed in detail previously.^{50,53,54,55,60} A key concept of the theory is that membrane permeability is inversely related to the resistances presented in the permeation process, including the internal resistance of the membrane and the resistance at the water-membrane interface. If the aqueous unstirred layers and interfacial resistances are assumed to be negligible, then conceptually, the rate limiting step involves traversing a barrier region, i.e. the region of the membrane where the free energy of the molecule reaches a maximum. Molecule dynamics simulations suggest that this region, for molecules with polar groups, is located close to the middle of the membrane, where most permeants become nearly or completely desolvated.^32,54

Using these assumption, solubility-diffusion theory estimates the permeation rate based on membrane/water partition, membrane diffusion and the permeation distance. Considering the membrane as a planar barrier in the xy-plane that varies only in the z direction, i.e. any plane parallel to the membrane is homogenous, the partition coefficient between water and the membrane, K_m/w, and the diffusion coefficient in the membrane, D_m, can be expressed in terms of the membrane depth along the z-axis, z. In the steady state, the diffusional resistance of such membrane with thickness of d can be written as the reciprocal of the membrane permeability coefficient, P_m:

$$\frac{1}{P_m}={\displaystyle {\int }_0^d}\frac{\mathit{\text{dz}}}{K_{m/w}(z)D_m(z)}$$ (1)

If the rate of permeation is limited by a homogenous “barrier region”, which the partition and the diffusion coefficients can be considered to be independent to the membrane depth, then the permeation rate across the membrane depends on the thickness of the barrier region, and the integral of Eq. 1 can be simplified as Eq. 2:

$$P_m=\frac{K_{\mathit{\text{barrier}}}{D}_{\mathit{\text{barrier}}}}{{\delta }_{\mathit{\text{barrier}}}},$$ (2)

where K_barrier is the permeant’s barrier/water partition coefficient of the permeant, D_barrier is the diffusion coefficient within the barrier, and δ_barrier is the effective thickness of the rate-limiting barrier. Conceptually, this model implies that rates of permeation are dominated by the free energy cost of desolvating the molecules in the hydrophobic interior of the membrane, as well as other free energy costs of inserting a molecule in the membrane, such as the free energy cost of creating a cavity of the appropriate size and shape; the rate of diffusion in the semi-ordered membrane environment is the other major contributor.

The functional form of P_m in this work follows Eq. 2. The overall scheme of the model is outlined in Figure 1. The focus of this study is on estimating the membrane/water partition based upon an expanded physical model of interfacial transfer in which the permeant is postulated to assume a neutral “membranephilic” state from the “hydrophilic” conformational ensemble in order to partition into a size-sensitive low-dielectric barrier region. The transmembrane diffusivity is estimated by diffusion coefficient across the low dielectric barrier. The effective thickness of the barrier is treated as an intrinsic characteristic of the membrane which is, in turn, assumed to be consistent for each assay of the same study and unaffected by the permeant. Since predictions were not cross-compared between different data sets or data types, the value of δ_barrier was defined as 18 Å for a general membrane in all reported calculations.⁵⁴

Figure 1.

The proposed physical model of passive membrane permeability.

Partition coefficient estimation

Following the barrier domain model proposed by Xiang and Anderson from experimental and theoretical studies,^53,54 the lipid/water partition coefficient was estimated from the partition between water and a bulk organic solvent that resembles the membrane environment. In order to reproduce the chemical environment in the membrane, organic solvents with comparable hydrophobicity as that of the lipid membrane are employed as the model medium, such as 1,9-decadiene and 1-hexadecene.⁵⁴ As such a reference medium is isotropic in nature, the estimation is augmented by a size-dependent factor to incorporate the anisotropic property of size/shape selectivity in membrane permeation. In essence, the correction factor relates the permeant’s size to the spatial constraints in the membrane, where are different from those in a disordered organic liquid; the correction factor is formulated as the reversible work of creating a cavity to accommodate the permeant under the pressure exerted by the lipid molecules. In the present implementation, the lipid barrier/water partition coefficient, K_barrier, is computed from the partition coefficient between water and chloroform, K_c/w, and the size selectivity factor, ξ _V, as Eq. 3 below.

$$K_{\mathit{\text{barrier}}}=K_{c/w}{\xi }_V,$$ (3)

Based upon properties of both the permeant (volume) and the membrane (interior pressure within the membrane), ξ _V is defined as:

$${\xi }_V=e^{\frac{-2V_p(P_{\perp }-P_{\Vert })}{3k_{B}T}},$$ (4)

where k_B is the Boltzmann constant, T is the temperature, V_p is the volume of the permeant, P_‖ is the normal pressure, and P_⊥ is the lateral pressure exerted by the lipid molecules. In the current model, P_‖ and P_⊥ are set to 1 bar and 300 bar, respectively.⁵⁴ This factor lowers the partition coefficient exponentially as the volume of the permeant increases, thus incorporating at least a part of the observed size-dependence of membrane permeability. As shown elsewhere, differences in membrane composition, such as the addition of cholesterol, can be approximated as differences in lateral pressure.⁷⁷

In our previous model, we effectively ignored the size-dependence of permeation, a limitation that we remedy here, along with other improvements. The focus of our previous work was explicit treatment of conformational flexibility of permeants, a strength that we retain in this work. Permeability was evaluated as the conformation-dependent partition free energy between a high dielectric environment (water) and a low dielectric environment (chloroform) using a conformational search approach.^61–65 A key concept of the model was to link permeability with the structural flexibility of the permeant by allowing conformational change in response to the change of the surroundings from water to membrane. The predicted relative permeabilities were based on the lowest energy conformation in the low dielectric continuum, which we termed the low dielectric conformation (LDC). With the assumption that the desolvation penalty is proportional to the free energy cost of the partitioning, the partition free energy was calculated as the free energy of transfer of the LDC from water to chloroform, ΔG_transfer, as Eq. 5.

$$\mathrm{\Delta }{G}_{\mathit{\text{transfer}}}=E_{{\mathit{\text{CHCl}}}_3}-E_{H_{2}O},$$ (5)

where E_CHCl3 and E_H2O are, respectively, the energies of the LDC in chloroform and water. Although this simple model clearly ignores many aspects of the actual permeation process, the predicted ΔG_transfer values, namely the desolvation costs, correlated well with experimental permeability measurements for cyclic peptides and drug-like molecules.^61–65 Those promising results indicate that conformational sampling of the permeant can be important for flexible molecules, and the approximation of the lipid/water interface with implicit solvent models is reasonable in the context of the model.

Building upon this simple model and the work of others, this work presents a more sophisticated model with improved estimation of the K_barrier. Here, the permeant is assumed to retain a neutral (deionized, if possible) state, as stated by the pH partition theory,⁷⁸ and to adopt one particular “membranephilic conformation” when diffusing across the membrane. Conceptually, we utilize a thermodynamic cycle in which all the additional contributions to K_barrier concern the permeant in the water phase prior to membrane permeation, including (1) the deionization penalty, (2) the tautomerization penalty of maintaining a certain tautomeric state, and (3) the conformational change from the lowest energy conformer in water to the membranephilic conformer (Fig. 1).

Charged molecules permeate through membranes much more slowly than neutral compounds, and our model assumes that for drug-like molecules, the permeation rate is dominated by the neutral species, even if it is present at a relatively low concentration in water. The free energy cost of charge neutralization of the permeant can be assessed by first predicting the pK_a values for possible ionizable groups, followed by quantifying the free energy required to maintain a zero net charge with all ionization groups deionized, if possible, at a desired pH. Most in vitro assays are performed with the aqueous phase at pH 7.4, and so we adopted this value for the results represented here; it is straightforward to generate results for other pH’s if desired. Similarly, a tautomerization penalty is derived from possible tautomer states and their estimated relative populations. These two processes are combined as a state penalty, ΔG_state, that represents the free energy cost for the permeant to adopt a particular neutral, tautomeric form for membrane permeation.

In previous work, we emphasized the role of internal hydrogen bonds in minimizing the free energy cost of partitioning into the membrane. However, adopting such a LDC with favorable hydrogen bonds may result in internal strain in the compound as well as entropy loss relative to the ensemble of states present in water, both of which would reduce permeation rates. To estimate these effects, we assumed that each permeant has only one probable membranephilic conformation, which we identify by conformational sampling. The free energy cost corresponding to this conformational change is quantified as the conformer-focusing free energy, ΔG_cf, which reflects the cost of retaining a specific conformation. Such an approach for quantifying the conformational penalty as ΔG_cf was originally employed in the context of protein-ligand binding with the purpose of estimating the free energy cost required for the unbound ligand to adopt the bound conformation while giving up other conformational states.⁷⁹ In light of the similar scenario in our model of passive permeation, this two-state model is applied to estimate a conformational penalty of adopting the membranephilic conformation. The conformational shift to the membranephilic state is assumed to occur in water, so the calculation of ΔG_cf requires knowledge of the conformational ensemble and the corresponding energetics in water. In the simple case where the permeant has i conformational states in the high dielectric environment but only one state in the low dielectric environment, i.e. the membranephilic state, the ΔG_cf can be estimated as the following:

$$\mathrm{\Delta }{G}_{\mathit{\text{cf}}}=(E_{\mathit{\text{LDC}}(\mathit{\text{HD}})}-E_{\mathit{\text{HDC}}})+\mathit{\text{RTln}}{\displaystyle {\sum }_i}{n}_i{e}^{((E_{\mathit{\text{HD}},i}-E_{\mathit{\text{HDC}}})/\mathit{\text{RT}})},$$ (6)

where E_LDC(HD) is the energy of the sole low dielectric state in the high dielectric environment, E_HDC is the energy of the lowest energy conformer in the high dielectric environment, namely the high dielectric conformation (HDC), E_HD,i is the energy of state i in the high dielectric environment, and n_i is the degeneracy of state i. The first term in Eq. 6 is the reorganization cost obtained from the relative energy difference between the membranephilic state and the HDC in the high dielectric environment. The second term accounts for the loss of conformational states, which is quantified by the modified partition function that includes the relative energy difference between the HDC and all other conformation states in the high dielectric environment. While this approach is highly approximate, it is more rigorous than estimating the effect by rotatable bond count, which can be misleading without considering the conformational ensemble.⁸⁰ As the calculation of ΔG_cf is relatively straightforward, we tested whether this simple approximation would contribute positively to the ability to reproduce experimental permeation rates.

Combining ΔG_transfer with the state and conformational penalties, the partition free energy between chloroform and water, ΔG_c/w, and the corresponding K_c/w can be obtained from Eq. 7 and Eq. 8, respectively.

$$\mathrm{\Delta }{G}_{c/w}=\mathrm{\Delta }{G}_{\mathit{\text{transfer}}}+\mathrm{\Delta }{G}_{\mathit{\text{state}}}+\mathrm{\Delta }{G}_{\mathit{\text{cf}}}$$ (7)

$$K_{c/w}={10}^{\mathrm{\Delta }{G}_{c/w}/-2.3\mathit{\text{RT}}}$$ (8)

Finally, K_barrier can subsequently be computed from K_c/w and ξ_V as defined in Eq. 3.

An alternative method reported by Seelig et al. to estimate K_barrier from the air/water partition is examined as well.⁶⁰ The formulation of K_barrier in this approach is very similar to that of Eq. 3 from which the air/water partition is scaled by a shape-dependent insertion factor. This approach to calculating K_barrier is investigated with our physics-based model by which the air/water partition is derived from the solvation free energy and the shape is measured as the cross-sectional area of the permeant. However, relative to the barrier domain model using the chloroform/water partition as the reference state, application of this method does not result in any significant improvement in accuracy. A more detailed discussion of this approach and its performance against various experimental data is included in the Supporting Information.

Diffusion coefficient

We use a very simple assumption that the rate-limiting barrier is similar to that of the bulk solvent, and the Stokes-Einstein relation is applied to describe the diffusion across the barrier.⁵³ The size-dependent diffusion coefficient of the permeant in the barrier, D_barrier, is computed using the Stokes-Einstein equation for spherical particle:

$$D_{\mathit{\text{barrier}}}=\frac{k_{B}T}{6\pi {\eta }_m{r}_p},$$ (9)

where η_m is the membrane viscosity that is assumed to be 1 poise and r_p is the radius of the permeant. Following the spherical approximation of Eq. 9, r_p is estimate from volume of the permeant, V_p.

$$r_p={\left(\frac{3V_p}{4\pi }\right)}^{\frac{1}{3}}$$ (10)

In this work, we do not consider the rate of diffusion across the unstirred water layer, because the width of this barrier will vary significantly between assays and is difficult to estimate.

COMPUTATIONAL PROCEDURES

The overall workflow of the permeability calculation is outlined in Figure 2. The coordinates of compounds were downloaded from the PubChem database if available or prepared in Maestro.⁸¹ All downloaded 2-dimensional structures were converted to 3-dimensional structures by the Ligprep module (Schrödinger). Prior to the permeability calculations, all compounds were minimized using MacroModel (Schrödinger) with the OPLS2005 force field and the implicit water model.^82–84 Molecular descriptors and QSPR regression-based predictions were computed by QikProp (Schrödinger) for all optimized input structures.⁸⁵

Figure 2.

Computational protocol of the physics-based permeability model.

Using EPIK, the probable ionization states and tautomeric forms of the permeant were first generated along with their pK_a values, followed by the estimation of the free energy cost of neutralizing the compound at pH 7.4.^86,87 The next step was to generate conformers for each of these neutral states using the PLOP program.⁸⁸ The OPLS2005 force field parameters of the permeant were generated by the hetgrp_ffgen program (Schrödinger). A semi-exhaustive sampling in the torsional space was carried out to identify sterically allowed conformations, as described elsewhere.⁸⁸ The subsequent clustering based on Cartesian atomic coordinates identified a maximum of 400 representative conformations. A major difference between the current protocol and previously published work is that, rather than focusing only on one LDC, all low energy conformations of the permeant were processed and evaluated. Energy evaluations in chloroform and water were performed for all unique conformations with the use of the implicit solvent model.^89–91 For computational efficiency, only conformers that are within a 5 kcal/mol threshold from the lowest energy conformation in either water or chloroform were included in the final conformer ‘ensemble’. The solvent-accessible volume in water of each of the selected conformations was computed by QikProp to calculate the size-selectivity factor and diffusion coefficient. Finally, the conformer with the highest predicted permeability was selected as the membranephilic conformation. The calculation on average takes about 2–4 minutes per molecule on a single-core CPU using PRIME (Schrödinger) for conformational search and energy calculations.⁹² The Li set, which consists of flexible peptidomimetics with 11–18 rotatable bonds, is the only exception, with average CPU time of 38.6 minutes per molecule.

RESULTS

To benchmark and evaluate the computational models, we collected permeability data from the literature, which is dominated by PAMPA and cell-based assays. In many cases, the permeability studies were performed to evaluate or parameterize other methods. The general criteria we followed in selecting data sets include 1) permeability data reported from the same source (for at least one data type), 2) the dynamic range of the data spans at least 1 log unit, and 3) broad chemical diversity, including both diverse and congeneric series of drug-like (FDA approved drugs or other small molecules) and non-drug-like compounds (peptidomimetics that do not follow Lipinski’s Rules). The 9 examined data sets include 188 compounds in total from which 36 compounds have data reported in multiple sources.

For the cell-based assay data, a major concern is that the permeability measurements were polarized by facilitated transport mechanisms, which are beyond the scope of the current model. It is important to reinforce the idea that the observed permeability from these assays is a combined effect of passive permeation, facilitated transport and paracellular transport. The cellular permeation rate in the A→B direction can be considered as an additive rate of different processes:

$$P_{\text{cell},A\to B}=P_{\text{transcellular}}+P_{\text{paraceullar}}+P_{\text{active},A\to B}-P_{\text{active},B\to A},$$ (11)

where P_cell,A→B is the cellular permeability rate in the A→B direction, P_{transcellular} is the passive transcellular permeability, P_paracellular is the paracellular permeability, P_active,A→B is the active “influx” rate in A→B direction, and P_active,B→A is the active “efflux” rate in the B→A direction. Assessing passive permeability solely based on unidirectional cell-based permeability data may not be straightforward. For example, a non-PGP substrate with low passive permeability and a strong PGP substrate with high passive permeability may have similar P_cell,A→B values. In the present study, we invoke the assumption that the transmembrane or transcellular permeability is the dominant component of the overall permeation process. We identified 37 compounds in the data sets that have reported active transport with PGP or other transporters. As listed in the Supporting Information, six cell-based assay data sets, including the Avdeef, Balimane, Bermejo, Fujikawa and the two Irvine sets, have compounds with reported active transport mechanisms. Hence, in addition to the analysis with all compounds, a passive permeation subset with active transport compounds excluded was also examined for each of these sets. The following analyses and discussions for these cell-based data sets are based on the results from the passive permeation subsets. The analyses with all compounds including those with reported active transport are reported in the Supporting Information. The Caco-2 permeability measurements for the Goodwin set were obtained in the presence of a PGP substrate, verapamil, which was used to minimize the effect of facilitated transport. The reported efflux ratio also provided evidence that active transport did not take place, so we did not exclude any compounds from this data set. For the Li set, information from the original article is insufficient to identify actively transported compounds, and we did not eliminate any from this set either.

The metrics for assessing the performance of the computational predictions include 1) the correlation coefficient (r²) and the slope (m) from the linear regression model with the experimental data, and 2) the Spearman’s rank correlation coefficient (ρ), which compares the rankings by predictions and experimental data. We do not combine data sets from different papers, because there are frequently significant differences in the assay conditions and other experimental details. Some compounds appear in multiple data sets and indeed the reported permeation rates vary significantly in some cases. As a result, we focus our analysis on the ability to reproduce relative, not absolute, permeation rates. Also, few predictions with statistical insignificant ρ (p-value >0.05) are noted in the analyses. These predictions mostly show low correlation with the experimental data, or are for data sets that have either a small sample size (<10) or a relatively small dynamic range (Whitlock set).

Results for in vitro measurements

The correlation coefficients (r²) from linear regression analyses and the Spearman’s rank correlation coefficients (ρ) between the in vitro permeability data and our physics-based predicted permeabilities are summarized in Tables 2 and 3. Following the relationship stated in Eq. 8, the calculated free energy values were converted to LogK for comparisons with LogP_m and experimental data. The linear regression models for the original (LogK(ΔG_{transfer(LDC)})) and the present (LogP_m) physics-based predictions are shown in Figures 3 (PAMPA) and 4 (cell-based assays). Overall, the physics-based predictions correlate well with experimental data, producing r² >0.55 and ρ >0.70 for most data sets.

Table 2.

The correlation coefficients between PAMPA data and computational predictions. The key component(s) of each physical model is/are marked with “X”. Physics-based predictions with correlation coefficient differences (Δr² or Δρ) relative to LogK(ΔG_{transfer(LDC)}) ≥0.05 and ≤-0.05 are highlighted in green and red, respectively. QikProp predictions with correlation coefficient differences relative to LogP_m ≥0.05 (Δ|r²| or Δ|ρ|) are highlighted in light green.

	Model’s component						Correlation coefficient
Predictiona	Conf. search	Conf. ensemble	State penalty	Conf. penalty	Size selectivity	Membrane diffusion	Avdeef		Balimane		Bermejo		Di		Fujikawa		Li		Whitlock
							r2	ρ	r2	ρ	r2	ρ	r2	ρ	r2	ρ	r2	ρ	r2	ρ
LogK(ΔGtransfer(LDC))	×						0.73	0.82	0.57	0.73	0.77	0.94	0.47	0.67	0.43	0.65	0.57	0.74	0.69	0.97
LogK(ΔGtransfer)	×	×					0.73	0.83	0.57	0.75	0.80	0.95	0.49	0.68	0.43	0.63	0.52	0.71	0.62	0.89
LogK(ΔGtransfer+ΔGstate)	×	×	×				0.75	0.90	0.65	0.85	0.90	0.98	0.58	0.71	0.54	0.71	0.79	0.78	0.74	0.85
LogK(ΔGtransfer+ΔGcf)	×	×		×			0.77	0.88	0.57	0.77	0.82	0.94	0.50	0.69	0.47	0.67	0.65	0.76	0.59	0.86
LogK(ΔGc/w)	×	×	×	×			0.78	0.88	0.64	0.83	0.88	0.95	0.57	0.72	0.56	0.73	0.82	0.76	0.74	0.85
LogKbarrier	×	×	×	×	×		0.80	0.91	0.62	0.83	0.82	0.95	0.56	0.70	0.58	0.73	0.83	0.81	0.78	0.87
LogPm	×	×	×	×	×	×	0.80	0.91	0.61	0.83	0.81	0.95	0.56	0.70	0.58	0.74	0.83	0.81	0.78	0.87
MW	Physiochemical descriptor						0.11	0.33b	0.03	0.13b	0.12	0.62	0.00	−0.31b	0.19	−0.47	0.13	0.33b	0.41	−0.36b
Vol	Physiochemical descriptor						0.21	0.55b	0.10	0.23b	0.22	0.67	0.02	−0.17b	0.13	−0.41	0.15	0.32b	0.07	0.13b
PSA	Physiochemical descriptor						0.61	−0.76	0.45	−0.68	0.16	−0.72	0.45	−0.66	0.39	−0.60	0.12	−0.47	0.17	−0.66b
QPlogPo/w	QSPR regression-based model						0.86	0.92	0.52	0.72	0.65	0.81	0.53	0.75	0.18	0.33	0.12	0.36b	0.16	0.68b
LogQPPCaco	QSPR regression-based model						0.67	0.75	0.71	0.87	0.29	0.80	0.59	0.76	0.47	0.60	0.63	0.84	0.16	0.68b
LogQPPMDCK	QSPR regression-based model						0.74	0.76	0.73	0.89	0.28	0.77	0.57	0.76	0.41	0.58	0.70	0.85	0.22	0.73b
N(Total)c							11		22		16		27		70		25		8
N(QikProp-TS)d							10		15		0		14		37		0		0

^aOptimal values were determined from the refined conformational ensemble for each physics-based prediction, except for ΔG_{transfer(LDC)}, which were computed using the LDC, and for LogK_barrier, which was computed using the conformation with the optimal LogP_m value.

^bThe p-value of ρ is greater than 0.05.

^cNumber of compounds included in the analysis.

^dNumber of compounds in QikProp training sets (QPlogPo/w, QPPCaco, and QPPMDCK). The physics-based model does not use a training set.

Table 3.

The correlation coefficients between cell-based assay data and computational predictions. The key component(s) of each physical model is/are marked with “X”. Physics-based predictions with correlation coefficient differences (Δr² or Δρ) relative to LogK(ΔG_{transfer(LDC)}) ≥0.05 and ≤-0.05 are highlighted in green and red, respectively. QikProp predictions with correlation coefficient differences relative to LogP_m (Δ|r²| or Δ|ρ|) ≥0.05 are highlighted in light green.

	Model’s component						Correlation coefficient
Predictiona	Conf. search	Conf. ensemble	State penalty	Conf. penalty	Size selectivity	Membrane diffusion	Avdeef (Caco-2)		Balimane (Caco-2)		Bermejo (Caco-2)		Fujikawa (Caco-2)		Goodwin (Caco-2)		Irvine (Caco-2)		Irvine (MDCK)		Li (Caco-2)
							r2	ρ	r2	ρ	r2	ρ	r2	ρ	r2	ρ	r2	ρ	r2	ρ	r2	ρ
LogK(ΔGtransfer(LDC))	×						0.67	0.89	0.56	0.44b	0.39	0.50b	0.32	0.35b	0.83	0.89	0.59	0.77	0.68	0.83	0.49	0.61
LogK(ΔGtransfer)	×	×					0.70	0.89	0.55	0.44b	0.37	0.45b	0.33	0.35b	0.88	0.96	0.57	0.75	0.67	0.83	0.55	0.69
LogK(ΔGtransfer+cGstate)	×	×	×				0.80	0.89	0.55	0.56b	0.58	0.52b	0.35	0.43b	0.88	0.96	0.68	0.80	0.74	0.84	0.49	0.66
LogK(ΔGtransfer+cGcf)	×	×		×			0.75	0.89	0.53	0.54b	0.44	0.47b	0.30	0.30b	0.82	0.92	0.61	0.78	0.70	0.84	0.54	0.65
LogK(ΔGc/w)	×	×	×	×			0.83	0.89	0.50	0.56b	0.61	0.55b	0.32	0.41b	0.82	0.92	0.69	0.82	0.75	0.84	0.45	0.64
LogKbarrier	×	×	×	×	×		0.84	0.89	0.55	0.56b	0.59	0.55b	0.34	0.37b	0.86	0.95	0.70	0.81	0.77	0.84	0.45	0.66
LogPm	×	×	×	×	×	×	0.84	0.89	0.56	0.56b	0.59	0.55b	0.34	0.37b	0.86	0.95	0.70	0.81	0.77	0.84	0.45	0.66
MW	Physiochemical descriptor						0.00	0.14b	0.31	−0.33b	0.00	−0.01b	0.08	−0.01b	0.05	−0.23b	0.12	−0.43	0.19	−0.43	0.04	0.18b
Vol	Physiochemical descriptor						0.06	0.37b	0.13	−0.51b	0.01	−0.02b	0.00	0.02b	0.01	0.01b	0.02	−0.21b	0.05	−0.23b	0.06	0.23b
PSA	Physiochemical descriptor						0.41	−0.71b	0.59	−0.59b	0.07	−0.17b	0.34	−0.20b	0.83	−0.89	0.54	−0.79	0.63	−0.78	0.30	−0.66
QPlogPo/w	QSPR regression-based model						0.74	0.71b	0.50	0.71	0.39	0.38b	0.32	0.55	0.53	0.76	0.27	0.48	0.31	0.54	0.15	0.45
LogQPPCaco	QSPR regression-based model						0.91	0.94	0.47	0.66b	0.42	0.62	0.81	0.81	0.84	0.90	0.74	0.85	0.81	0.88	0.55	0.72
LogQPPMDCK	QSPR regression-based model						0.91	0.94	0.51	0.66b	0.32	0.47b	0.68	0.74	0.76	0.83	0.73	0.83	0.81	0.87	0.56	0.68
N(Total)c							6		9		12		20		12		31		32		25
N(QikProp-TS)d							6		7		0		12		0		31		32		0

^aOptimal values were determined from the refined conformational ensemble for each physics-based prediction, except for ΔG_{transfer(LDC)}, which were computed using the LDC, and for LogK_barrier, which was computed using the conformation with the optimal LogP_m value.

^bThe p-value of ρ is greater than 0.05.

^cNumber of compounds included in the analysis.

^dNumber of compounds in QikProp training sets (QPlogPo/w, QPPCaco, and QPPMDCK). The physics-based model does not use a training set.

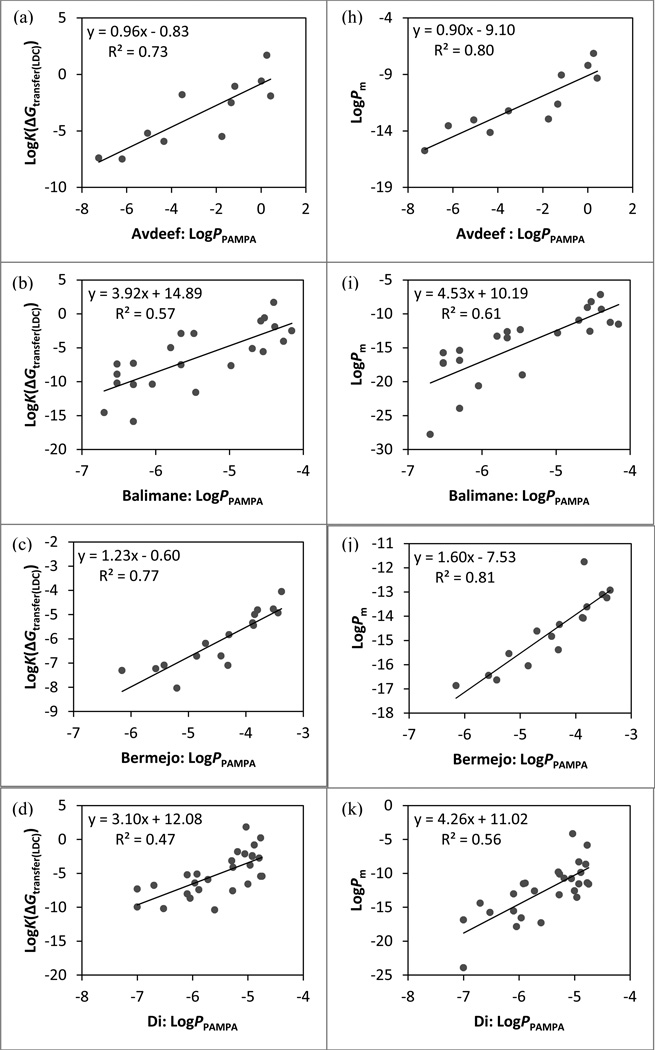
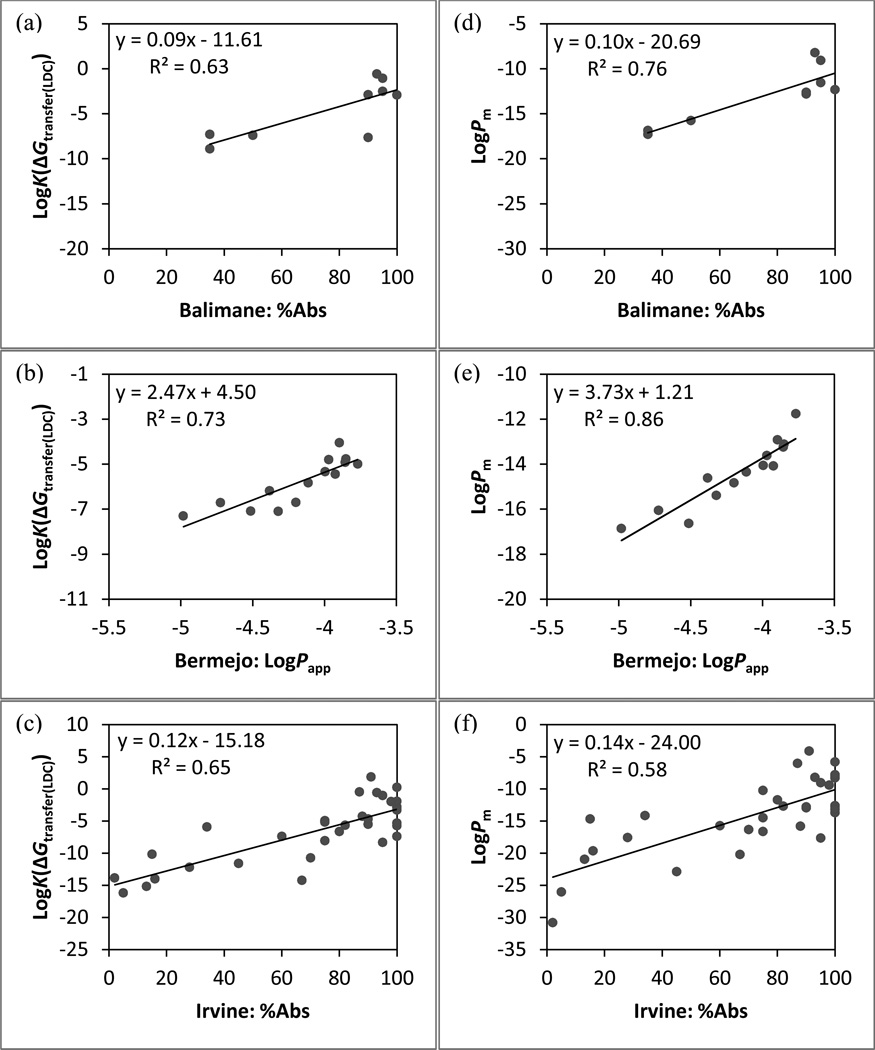
Figure 3.

The linear regression models between PAMPA data and physics-based permeability predictions. Predictions based on LogK(cG_{transfer(LDC)}): (a) Avdeef set, (b) Balimane set, (c) Bermejo set, (d) Di set, (e) Fujikawa set, (f) Li set, and (g) Whitlock set. Predictions based on LogP_m: (h) Avdeef set, (i) Balimane set, (j) Bermejo set, (k) Di set, (l) Fujikawa set, (m) Li set, and (n) Whitlock set.

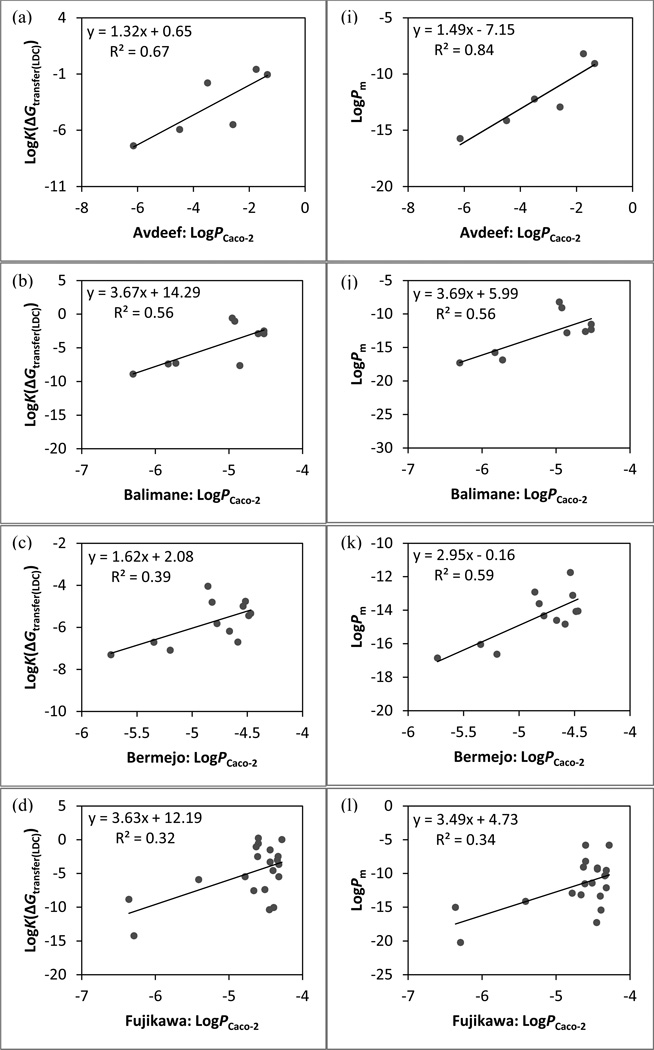
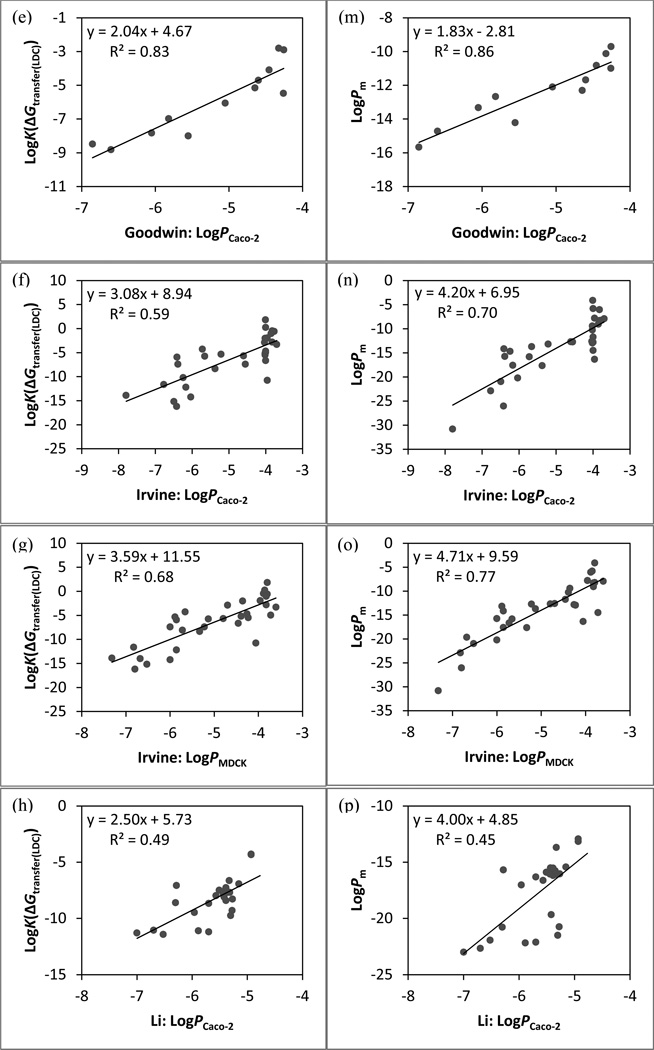
Figure 4.

The linear regression models between cell-based assay data and physics-based permeability. Predictions based on LogK(cG_{transfer(LDC)}): (a) Avdeef set (Caco-2), (b) Balimane set (Caco-2), (c) Bermejo set (Caco-2), (d) Fujikawa set (Caco-2), (e) Goodwin set (Caco-2), (f) Irvine set (Caco-2), (g) Irvine set (MDCK), and (h) Li set (Caco-2). Predictions based on LogP_m: (i) Avdeef set (Caco-2), (j) Balimane set (Caco-2), (k) Bermejo set (Caco-2), (l) Fujikawa set (Caco-2), (m) Goodwin set (Caco-2), (n) Irvine set (Caco-2), (o) Irvine set (MDCK), and (p) Li set (Caco-2).

In order to evaluate the performance of the updated method in calculating the partition free energy systematically, new components were added to the model progressively. Obtaining the free energy of transfer from the refined ensemble of low energy conformations (ΔG_transfer) instead of from the single lowest-energy conformation in low dielectric (ΔG_{transfer(LDC)}) has no significant effect on the correlation between calculations and experiments for most sets. The incorporation of either the state penalty (ΔG_transfer+ΔG_state) or the conformational penalty (ΔG_transfer+ΔG_cf) is shown to be favorable for modeling both types of in vitro permeability data. Including the ΔG_state term leads to significant improvements in r² and ρ for many data sets, reflecting the importance of accounting for neutralization of ionizable groups and tautomerization. While imposing the conformational penalty is constructive as well, the beneficial effects are noticeably smaller than that of the state penalty. We speculate that this may be due to the fact that the examined data sets contain many relatively rigid drug-like molecules for which the conformational effect is likely to be small.⁹³ As anticipated, the biggest improvement in r² by introducing the ΔG_cf term alone is seen with the PAMPA data of flexible peptidomimetics with 11–18 rotatable bonds from the Li set (Δr² = 0.13 between ΔG_transfer and ΔG_transfer+ΔG_cf). Computing the partitioning free energy with both the state and conformational penalties (ΔG_c/w) yields similar correlation coefficients as those by including ΔG_state alone for both PAMPA and cell-based data, suggesting that ΔG_state is the dominant term.

An important aspect of the physical model considered here, building on prior work, is the dependence of membrane permeation and diffusion on the size of the permeant. The results from LogK_barrier values of conformations with the highest LogP_m values illustrate that the size-selectivity term does improve r² over predictions by ΔG_c/w for more than half of the in vitro data sets. However, the resulting improvements in accuracy are relatively small for either PAMPA or cell-based data as most changes in either correlation coefficient are less than 0.05. The addition of the size-dependent diffusion coefficient is also shown to have no significant effect. Given that the diffusion coefficient is inversely proportional to the radius of the permeant and the molecular sizes within each set are not very different, the diffusion terms of any pair of molecules are thus expected to be similar.

The slopes of the linear regression models are reported in Tables 4 and 5 for the PAMPA and cell-based assays, respectively. These slopes are variable and generally greater than one. The slopes do not generally vary dramatically based on which aspects of the model are included. That is, as previously reported, the simplest model based on ΔG_{transfer(LDC)} values (conformation-dependent solvation free energy) produces linear regression models with slopes steeper than one.⁶³ It is important to note that the slopes are sensitive to the dielectric constant used for the membrane; using chloroform as the reference state, with dielectric ~4, may underestimate the effective dielectric constant of the barrier region. We cannot fully account for the variability in slope observed for the different data sets. Differences in assay conditions, such as pH, the composition of the artificial membrane, cell layer, may contribute. We speculate that entropic losses, which we cannot account for in a rigorous manner, may contribute to this variability as well (i.e. some of the series involve larger, more flexible ligands, while others have predominantly small, rigid compounds). In addition, the current model neglects the aqueous boundary layer at the water/membrane interface, which can act as another rate limiting region for passive permeation. The volume-based size-selectivity factor in the present implementation is a relatively simple approximation. Exploring other approaches, such as free-surface-area theory used to model membrane order, may also be constructive.^57,58

Table 4.

The slopes from linear regression analyses between PAMPA data and computational predictions.

	Slope of linear regression model (|m|)
Prediction	Avdeef	Balimane	Bermejo	Di	Fujikawa	Li	Whitlock
LogK(ΔGtransfer(LDC))	0.96	3.92	1.23	3.10	2.64	1.36	3.76
LogK(ΔGc/w)	0.99	4.73	1.77	4.35	3.29	2.83	5.08
LogKbarrier	0.91	4.54	1.61	4.26	3.51	2.74	5.19
LogPm	0.90	4.53	1.60	4.26	3.53	2.74	5.19
QPlogPo/w	0.45	1.41	0.86	2.11	0.64	0.29	0.66
LogQPPCaco	0.14	0.70	0.17	0.87	0.58	0.46	0.32
LogQPPMDCK	0.13	0.77	0.16	0.97	0.61	0.47	0.42

Table 5.

The slopes from linear regression analyses between cell-based assay data and computational predictions.

	Slope of linear regression model (|m|)
Prediction	Avdeef (Caco-2)	Balimane (Caco-2)	Bermejo (Caco-2)	Fujikawa (Caco-2)	Goodwin (Caco-2)	Irvine (Caco-2)	Irvine (MDCK)	Li (Caco-2)
LogK(ΔGtransfer(LDC))	1.32	3.67	1.62	3.63	2.04	3.08	3.59	2.50
LogK(ΔGc/w)	1.52	3.47	3.10	3.49	1.79	4.16	4.65	4.15
LogKbarrier	1.49	3.67	2.96	3.49	1.83	4.20	4.71	4.00
LogPm	1.49	3.69	2.95	3.49	1.83	4.20	4.71	4.00
QPlogPo/w	0.51	2.18	1.42	1.57	0.71	0.67	0.70	0.64
LogQPPCaco	0.22	0.72	0.48	0.95	0.29	0.63	0.70	0.85
LogQPPMDCK	0.24	0.76	0.39	1.02	0.20	0.66	0.74	0.82

Overall, the results suggest that the conformation-dependent free energy cost of desolvating permeants (as quantified as ΔG_transfer) is a dominant factor affecting the rate of permeation. However, other factors expected to also be important, such as charge neutralization and size-dependent effects, do appear to also contribute, in that including these terms improves correlation with in vitro measures of permeability. The P_m prediction yields higher r² and ρ values with experimental data than the previous basic model of ΔG_transfer for almost all cases, illustrating the ability to improve a physical model by incorporating description of the underlying physical processes. Further improvements may be possible in future work.

In contrast to the obvious improvements when comparing the PAMPA data, the favorable effects of the additional components to the model are less profound for the cell-based assay data but, as expected, the physical model performs better for compounds not known to be substantially affected by active transport (Supporting Information). These findings suggest that the model does capture key aspects of the permeation process across the biological membrane, albeit that many assumptions and approximations have been made to simplify the calculations required. On the other hand, many of the compounds with known active transport mechanisms are predicted as outliers by our model when compared to the cell-based data, such as occurs in the Irvine set (Supporting Information).

Results for in vivo measurements

Our focus in this study is comparison with in vitro permeability assays, but three of the studies whose data we employ also reported in vivo measurements, and we provide comparisons to those data as well. While the current permeability model does not include other cellular transport components, such as active transport and paracellular transport, the following comparisons with in vivo data are done under the simple assumption that passive transmembrane permeability is a major contributor to the absorption process. Despite being overly simplistic and approximate, such an assumption is implicit in other QSPR models of absorption and in the physiochemical principles underlying Lipinski’s Rules of Five for druglikeness, i.e. LogP_o/w <5 and the hydrogen bond donor and acceptor counts.

As with the cell-based data sets, compounds with known active transport were not included in the analyses below for the in vivo data sets and the analyses with all compounds included are reported in the Supporting Information. The correlation coefficients r² and ρ are summarized in Table 6. The linear regression models of predictions, LogK(ΔG_{transfer(LDC)}) and LogP_m, are shown in Figure 5, and the slopes of linear regression models are summarized in Table 7. Overall, these results are consistent with the previous findings from comparisons with the in vitro data. Excluding compounds with active transport yields higher r² for both Balimane and Irvine sets, while the changes in r² are minor for the Bermejo set as only two compounds are excluded (Supporting information). The physics-based predictions correlate well with the in vivo measurements, yielding r² ≥0.7 and ρ ≥0.8 for most cases except for the %Abs data from the Irvine set.

Table 6.

The correlation coefficients between PAMPA data and computational predictions. The key component(s) of each physical model is/are marked with “X”. Physics-based predictions with correlation coefficient differences (Δr² or Δρ) relative to LogK(ΔG_{transfer(LDC)}) ≥0.05 and ≤−0.05 are highlighted in green and red, respectively. The QikProp prediction with correlation coefficient difference relative to LogP_m (Δ|r²|) ≥0.05 is highlighted in light green.

	Model’s component						Correlation coefficient
Predictiona	Conf. search	Conf. ensemble	State penalty	Conf. penalty	Size selectivity	Membrane diffusion	Balimane (%Abs)		Bermejo (Papp)		Irvine (%Abs)
							r2	ρ	r2	ρ	r2	ρ
LogK(ΔGtransfer(LDC))	×						0.63	0.66c	0.73	0.87	0.65	0.74
LogK(ΔGtransfer)	×	×					0.63	0.66c	0.75	0.89	0.66	0.76
LogK(ΔG transfer+ΔGstate)	×	×	×				0.72	0.84	0.88	0.94	0.62	0.74
LogK(ΔGtransfer+ΔGcf)	×	×		×			0.65	0.76	0.78	0.91	0.63	0.74
LogK(ΔGc/w)	×	×	×	×			0.69	0.84	0.88	0.96	0.59	0.72
LogKbarrier	×	×	×	×	×		0.76	0.84	0.86	0.96	0.58	0.73
LogPm	×	×	×	×	×	×	0.76	0.84	0.86	0.96	0.58	0.73
MW	Physiochemical descriptor						0.36	−0.30b	0.01	0.34b	0.03	−0.17b
Vol	Physiochemical descriptor						0.10	−0.23b	0.07	0.41b	0.01	0.03b
PSA	Physiochemical descriptor						0.65	−0.84	0.16	−0.70	0.54	−0.59
QPlogPo/w	QSPR regression-based model						0.52	0.76	0.62	0.77	0.40	0.56
LogQPPCaco	QSPR regression-based model						0.68	0.86	0.38	0.80	0.47	0.55
LogQPPMDCK	QSPR regression-based model						0.69	0.86	0.32	0.73	0.44	0.53
QP%HOA	QSPR regression-based model						0.70	0.85	0.59	0.84	0.63	0.67
N(Total)c							9		14		33
N(QikProp-TS)d							7		0		33

^aOptimal values were determined from the refined conformational ensemble for each physics-based prediction, except for ΔG_{transfer(LDC)}, which were computed using the LDC, and for LogK_barrier, which was computed using the conformation with the optimal LogP_m value.

^bThe p-value of ρ is greater than 0.05.

^cNumber of compounds included in the analysis.

^dNumber of compounds in QikProp training sets (QPlogPo/w, QPPCaco, QPPMDCK, and QP%HOA). The physics-based model does not use a training set.

Figure 5.

The linear regression models between in vivo data and physics-based permeability predictions for all compounds. Predictions based on LogK(ΔG_{transfer(LDC)}): (a) Balimane set, (b) Bermejo set, and (c) Irvine set. Predictions based on LogP_m: (d) Balimane set, (e) Bermejo set, and (f) Irvine set.

Table 7.

The slopes from linear regression analyses between in vivo data and computational predictions.

	Slope of linear regression model (|m|)
Prediction	Balimane (%Abs)	Bermejo (Papp)	Irvine (%Abs)
LogK(ΔGtransfer(LDC))	0.09	2.46	0.12
LogK(ΔGc/w)	0.10	3.97	0.14
LogKbarrier	0.10	3.75	0.14
LogPm	0.10	3.73	0.14
QPlogPo/w	0.05	1.86	0.03
LogQPPCaco	0.02	0.47	0.02
LogQPPMDCK	0.02	0.40	0.02
QP%HOA	0.64	19.24	0.54

Relative to the basic desolvation model, the current model of P_m prediction show improved correlations with Balimane (%Abs) and Bermejo (perfusion assay) sets. No improvement is evident for the %Abs data from the Irvine set, although the physics-based predictions does give reasonable correlation with the data (r² ~0.6 and ρ ~0.7 for the passive permeation subset). Given that in vivo absorption is a complicated biological process, being able to predict absorption data at this level of accuracy with physics-based passive permeation is encouraging, especially considering that 1) no prior training with existing data was performed, and 2) there is no reason to expect a simple linear relationship between our computed values and %Abs.

To compare the performance of different approaches in predicting human absorption data, the correlation coefficients with %Abs from both experiments and predictions for the Balimane and Irvine sets are summarized in Table 8. The LogP_m model is shown to predict %Abs with accuracy comparable to PAMPA data (Balimane set), as well as cell-based assay data when excluding compounds that are actively transported (Irvine set). However, without discriminating compounds with active transport, the cell-based assays are demonstrated to have a stronger correlation with %Abs than the passive permeability prediction for both data sets, as expected.

Table 8.

The correlation coefficients between absorption data and experimental models.

		Allc		Passived
Set	Comparison	r2	ρ	r2	ρ
Balimanea	PAMPA vs. %Abs	0.67	0.77
	Caco-2 vs. %Abs	0.83	0.82	0.89	0.80
	LogPm vs. %Abs	0.68	0.82	0.76	0.84
Irvineb	Caco-2 vs. %Abs	0.40	0.54b	0.62	0.66
	MDCK vs. %Abs	0.46	0.58b	0.59	0.65
	LogPm vs. %Abs	0.24	0.50	0.58	0.73

^aRef. 67.

^bRef. 72.

^cComplete compound set.

^dPassive permeation subset.

Comparison to other computational methods

To further evaluate the utility of the physics-based permeability model, its predictive power is compared to that of common regression-based QSPR physiochemical descriptors and permeability predictions computed by QikProp, including molecular weight (MW), solvent-accessible volume (Vol), octanol/water partition coefficients (QPlogPo/w), polar surface area (PSA), predicted Caco-2 permeability (QPPCaco), predicted MDCK permeability (QPPMDCK), and predicted percentage human oral absorption (QP%HOA). The results of linear regression analyses and Spearman’s rank correlation coefficients between these descriptors and experimental data are summarized in Tables 2, 3 and 6.

For the in vitro data (Tables 2 and 3), MW and Vol show weak or no correlation with experimental data in most cases, whereas QPlogPo/w and PSA produce stronger correlations. Among all the regression-based predictions, LogQPPCaco, which was trained using many of the compounds in these data sets, yields the highest correlations for both the PAMPA and cell-based assay data, as anticipated. While QPPMDCK is optimized for MDCK data, its performance is similar to that of QPPCaco. In comparison, the physics-based LogP_m values correlate better with the PAMPA data than those by QikProp predictions for most cases, generating higher r² and ρ values. For cell-based assay data, predictions by LogP_m values are more accurate than QPlogPo/w and comparable to the QPPCaco and QPPMDCK models.

These parameterized models are, as expected, most effective in predicting sets containing FDA-approved drugs and small molecules, such as for the Avdeef, Irvine and Fujikawa sets (r² >0.7 for Caco-2 data and r² >0.8 for MDCK data), which dominate the training sets, but are less optimal for sets with congeneric series and peptidomimetic compounds, like the Bermejo and Li sets (r² <0.6 for Caco-2 data). An exception is the congeneric series of Goodwin set (LogQPPCaco: r² = 0.84) from which the Caco-2 permeabilities correlate well with the hydrophobicity of the side-chain substitutions as supported by the strong correlation with PSA (r² = 0.83). The physics-based model, on the other hand, performs considerably better in predicting relative permeabilities among congeneric series and peptidomimetic compounds. In addition, the quality of the physics-based predictions for drug-like molecules is frequently nearly as good as those given by the regression-based models that were trained specifically for this chemical space.

A notable difference between the two computational approaches is that the slopes of linear regression models with QikProp permeability predictions (QPlogPo/w, QPPCaco and QPPMDCK) are closer to 1 than those by physics-based predictions as shown in Tables 4, 5 and 7. However, the slopes of these QikProp models do vary across different data sets, and the range of slopes is similar to that of the physics-based predictions. This suggests that the slopes of the correlations between the experimental data and computational predictions may be related in part to the details of the experimental assays, and not solely due to limitations of the computational models.

DISCUSSION AND CONCLUSIONS

The performance of a physical model for passive membrane permeability was investigated by comparing its predictive power to experimental data of nine diverse compound sets, as well as regression-based in silico QSPR predictions. In general, the physics-based prediction of P_m is shown to consistently correlate well with the assorted permeability data that covers diverse chemical space. In many cases, the QSPR descriptors (PSA and QPlogPo/w) and parameterized permeability models (QPPCaco, QPPMDCK, and QP%HOA) also deliver comparable agreement with the experimental data. However, a “fair” comparison between the physics-based model and the regression-based model is not straightforward because many compounds in the examined data sets are part of the training sets for the parameterized models. Although QSPR prediction is still significantly faster than the physics-based method, the CPU time of the LogP_m calculation is short enough to be practical for many drug design applications (~15 ligands per CPU-hour). As the physics-based predictions are fundamentally different from the QSPR method, performing both types of calculation can be of value as the agreement or disagreement of the results may provide further insight into the molecule.

We wish to emphasize several other potential advantages of this “physics-based” approach. First, the performance in predicting relative permeability differences for a wide-range of data types and compounds reflects the general applicability of the molecular-mechanics based approach. Second, systematically analyzing the contributions of different components of the model provides important physical insights into the contribution of each physical component, such as the effects of ionizable groups and conformational flexibility, elucidating the underlying basis of permeability. Third, as we have shown here, a physically grounded model is systematically improvable by escalating the level of theory and methods employed. The current model can be further improved: in particular, our attempts to estimate entropic losses and the size dependence of the diffusion rate are rather crude (largely for computational expediency), possibly accounting for their limited contribution to the accuracy of the model.

On the other hand, as a future direction, we envision that components of the physics-based model presented here may be used as QSPR descriptors in order to provide a better description of the physical process than many commonly used physiochemical descriptors. That is, the “physics-based” and empirical/statistical approaches may be complementary. For example, we posit that the permeant’s polarity or hydrophilicity, which is often measured by its PSA, is better described by the solvation free energy. Similarly, molecular size and shape are likely more appropriate descriptors than molecular weight. Therefore, we envision a regression-based model using physically-meaningful terms, such as ΔG_transfer, ΔG_solv, and ΔG_cf; reweighing each component to better agree with experimental data would be possible while retaining the same functional form of the current model. One potential advantage of such a model would be the ability to estimate a confidence in the prediction that is related to the distance in chemical space between the compounds of interest and the training set.

The current physical model performs best at reproducing the PAMPA data. Considering that the artificial membrane of PAMPA is essentially two half-membrane layers sandwiching a middle organic/hydrophobic layer, the physics-based model and PAMPA both share the same approximation in mimicking the membrane with a low dielectric organic or lipophilic layer. On the other hand, passive permeation across the cell layer in the cell-based assays is more complicated. Efforts were made in the current study to filter the cell-based permeability data by excluding compounds with possible active transport mechanisms. However, factors like paracellular transport and variation in the cell monolayers are expected to also introduce noise in the comparisons. By the same token, intestinal absorption and perfusion assays include contributions from many biological events, in addition to passive permeation. The fact that the proposed model of passive permeability provides reasonable predictions that rival the accuracy of in vitro assays is promising.

Interestingly, the limitations of the physics-based permeability prediction parallel those of predicting protein/ligand interactions. While the permeability model presented in this work is demonstrated to be proficient in predicting relative permeability, calculating absolute membrane permeability would require further development and parameterization. Similarly, predicting relative binding affinity is technically less difficult, less expensive, and more accurate than computing absolute binding affinity. The slopes of the correlations between the computed values and the experimental values are also generally >1 in both cases. Another common feature between the two is that a congeneric series of similar compounds is easier to model than a diverse chemical set.

In summary, the performance of a physics-based permeability model is investigated and benchmarked against in vitro permeability data, in vivo data, and in silico predictions. Without any training against any existing data, the calculated LogP_m values are shown to correlate well with different types of experimental data from various studies, suggesting that the model does provide a reasonable physical description of passive membrane permeation. Efforts to apply the model in the context of molecular design and to develop a physical model for gut absorption are underway.