Abstract
Iron oxide nanoparticles (IONPs) are widely used as MR contrast agents because of their strong magnetic properties and broad range of applications. The contrast induced by IONPs typically depends on concentration, water accessibility, particle size, and heterogeneity of IONP distribution within the microenvironment. Although the latter could be a tool to assess local physiological effects at the molecular level, it renders IONP quantification from relaxation measurements challenging. This study aims to quantify IONP concentration using susceptibility measurements. In addition, further analysis of relaxation data is proposed to extract quantitative information about the IONP spatial distribution.
Mesenchymal stem cells were labeled with IONPs and the IONP concentration measured by mass spectroscopy. MR relaxation parameters (T1, T2, T2*) as well as magnetic susceptibility of cylindrical samples containing serial dilutions of mixtures of free and cell-internalized IONPs were measured and correlated with IONP concentration.
Unlike relaxation data, magnetic susceptibility was independent of whether IONPs were free or internalized, making it an excellent candidate for IONP quantification. Using IONP concentration derived from mass spectroscopy and measured relaxation times, free and internalized IONP fractions were accurately calculated.
Magnetic susceptibility was shown to be a robust technique to measure IONP concentration in this preliminary study. Novel imaging based susceptibility mapping techniques could prove to be valuable tools to quantify IONP concentration directly by MRI, for samples of arbitrarily shape. Combined with relaxation time mapping techniques, especially T2 and T2*, this could be an efficient way to measure both IONP concentration and the internalized IONP fraction in vivo using MRI, to gain insight into tissue function and molecular imaging paradigms.
Keywords: iron oxide nanoparticle, quantification, magnetic susceptibility, relaxation, responsive agent, cellular imaging
1. Introduction
Iron oxide nanoparticles (IONPs) have garnered a great deal of interest as MR contrast agents (CAs) because of their strong magnetic properties and broad range of applications (1–3). Although initially introduced as non specific markers, they have been shown to be effective agents for molecular and cellular imaging applications. After IONP labeling and following local or intravenous injection, cells become MRI visible and their biodistribution can be studied in vivo, providing valuable information for stem cell therapy (4,5). Remarkably, researchers have been able to track single cells in vivo using IONPs (6,7), under optimal experimental conditions. Over the last decade IONPs have also emerged as a new class of activable or responsive CAs (8–12), capable of sensing specific chemical species and enzymatic activity in vivo.
The versatility of IONPs is due to their multiple and efficient contrast mechanisms (both negative and positive contrast can be exploited (13,14)) as well as the influence of local particle distribution within a voxel on MRI contrast. As IONP distribution switches from a dispersed to a clustered state (or vice versa), and as IONPs undergo cell internalization, their relaxation properties are modified (15–18) affecting MR image contrast. This is due to a modification of the susceptibility contrast mechanism and of the water access conditions to the iron core. The T1 effect is strongly reduced when IONPs undergo cell-internalization (17). In addition, T2 and T2* relaxivity effects are modulated by a diffusion mediated contrast mechanism that depends on the size of the IONP particles or IONP clusters (16,19–21). For small IONP particles, the random motion of water protons leads to an irreversible loss of phase coherence. The signal cannot be refocused by use of spin echoes; as a result T2 and T2* are equivalents. On the other hand, large IONP particles, or clusters of multiple small particles, fulfill the static dephasing regime (SDR) theory where proton dephasing is reversible because the size of the magnetic field heterogeneities is much larger than the random walk of the water molecules during the time scale of the MR experiment. In this case R2’ defined as R2*-R2 (where R2(*) = 1/T2(*)) is large and its value predictable by theory (16,22).
Although MR contrast switching capability enables specific detection of local interaction in vivo, it complicates IONP concentration quantification at the same time. Kuhlpeter et al. (18) have recently shown that cell-internalized IONPs can be differentiated form freely distributed IONPs by using joint T2- and T2*-mapping. In their study however, IONP concentration and internalized fraction were not quantified. Indeed, in any realistic experimental setting, both dispersed and clustered IONP pools typically coexist, and IONP distribution may change with space and time; hence no single calibrated relaxivity can be used to extract IONP concentration from relaxation measurements. Although qualitative detection may be sufficient for some applications, it is ultimately desirable to quantify IONPs in molecular and cellular MRI in order to extract biologically relevant information such as the cell-homing efficiency or the local concentration of molecules of interest such as targeted receptors or enzymes.
Recent work on quantitative susceptibility mapping (23,24) has suggested that susceptibility measurements may be used for IONP quantification. In this report we study IONP samples that contain mixtures of freely dispersed IONP as well as IONP clusters contained within suspended stem cells as a model of a responsive agent for molecular and cellular imaging application. We investigate multiple MR characteristic parameters (namely T1, T2, T2* and magnetic susceptibility χ) and their ability to deliver quantitative information about the IONP content and the spatial distribution of the particles. Our aim was to determine if MRI could not only allow the quantification of IONP concentration regardless of its physical condition, but also if we could estimate the dispersed and internalized fractions.
2. Results
Our stem cell labeling technique yielded approximately 60 pg of iron/cell for an average cell viability of 93%. A histological section of labeled cells with iron staining is shown in Figure 1. The free and internalized IONP fractions used in presented experiments are summarized in Table 1.
Figure 1.
Microscopic picture of IONP labeled ERC cells after iron staining. This picture was taken from the fully internalized stock solution (i.e. after iron labeling and free iron washout) prior to placing them in gel. IONPs are visible as blue/dark clusters, showing the compartmentalization of IONPs associated with cell internalization.
Table 1.
Internalized IONP fraction. ICP-MS Control: control fractions derived from ICP-MS. Measured ri: group derived fractions using measured 100% internalized relaxivity as a reference and the corresponding relaxation mechanisms (i = 1, 2, 2* and 2’). Measured r2’ using SDR prediction: group derived fractions using SDR prediction for the 100% internalized r2’ reference. The free IONP fraction is always the complement to 100%.
| Group # | 1 (100% free) | 2 | 3 | 4 (100% internalized) |
|---|---|---|---|---|
| Intended internalized iron fraction | 0% | 33.3% | 66.7% | 100% |
|
| ||||
| ICP-MS Control | 0% | 27.0% | 72.3% | 100% |
|
| ||||
| Measured r1 | 0% | 33.2% | 81.6% | 100% |
| Measured r2 | 0% | 24.6% | 76.8% | 100% |
| Measured r2* | 0% | 27.6% | 62.8% | 100% |
| Measured r2’ | 0% | 26.9% | 65.8% | 100% |
|
| ||||
| Measured r2’ using SDR prediction | 0% | 27.0% | 68.5% | 103.4% |
The signal to noise ratio of the 2% agarose gel sample was about 104, 60 and 29 for the T1, T2 and T2* scans, respectively. MRI relaxation results are summarized in Figure 2. All samples yielded measurable T1s and T2s using the described methods. Conversely, T2*s shorter than ~ 3.5 ms could not be measured accurately because of rapid signal decay, and were not used in further analysis. Linear regression analysis correctly fitted experimental data, as evidenced by a minimum r2 value of 0.988. Consistent with previous published studies (15–18), we observed a strong dependence of all IONP relaxivities on spatial distribution. Cell internalization of IONPs strongly reduced relaxivities r1 and r2 and increased r2* and r2’. The r1 relaxivity was most affected by internalization – decreased by 15 fold, as r1 relies on close water access to the iron core as well as fast exchange with bulk water that are known to be affected by cell-internalization (25). The r2 effect, which also includes a long distance contribution through a susceptibility mechanism, was reduced by about 5 fold. Finally the r2* and r2’ effects were roughly doubled and tripled, respectively, when IONPs were internalized compared to free IONPs, consistent with a contrast regime switch related to the effective particle size (19–21).
Figure 2.
Relaxation rates and corresponding relaxivities for various fractions of free and internalized IONPs. Large relaxivity variations are observed between different groups. The coefficient of determination r2 was higher than 0.988 for all fitted curves.
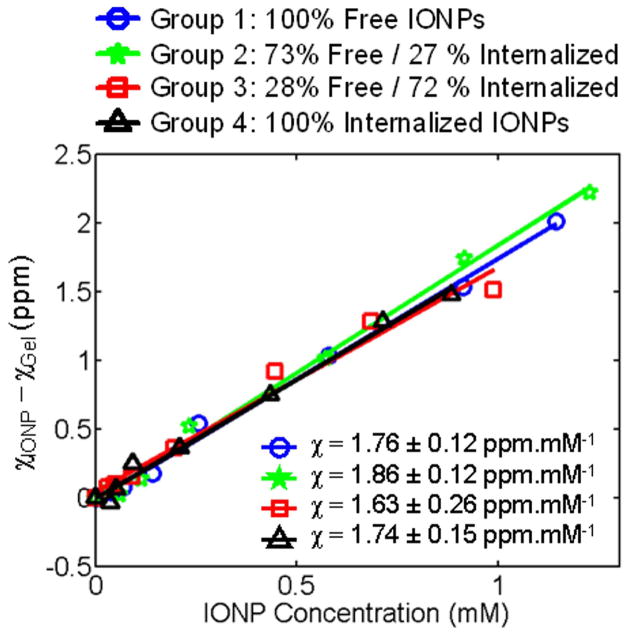
The susceptibility values of deionized water and pure vegetable oil were −8.98 ppm and −8.23 ppm, respectively, in good agreement with published data of −9.05 ppm (26) and −8.31 ppm (27), respectively. Susceptibility measurements of all IONP samples are summarized in Figure 3. For all groups r2 was higher than 0.976. Interestingly, note that magnetic susceptibility relative to iron content was similar regardless whether IONP was dispersed or internalized. The maximum variation (+/−0.12 ppm) between each group was on the order of the measurement errors. The average susceptibility among all samples was 1.77 ± 0.05 ppm.mM−1 (r2=0.994) which is in excellent agreement with published data of 1.81 ppm.mM−1 for free ferumoxides at 3T as derived from De Rochefort, et al, (23), assuming identical IONP magnetization at 1.5T as 3T. This latter assumption is justified by the magnetization curve of IONPs which exhibits a saturation plateau above ~1T (3).
Figure 3.
Magnetic susceptibility measurements for various fractions of free and internalized IONPs. The susceptibility per unit concentration is independent of IONP local distribution.
We further applied the SDR theory to the particle system under consideration (16,22). Using the average susceptibility of all samples, we estimated a local magnetic dose (LMD) of 5.31 uT.mM−1 and a SDR prediction of 573 s−1.mM−1 for r2’ (cf. Eq. 2 expressed in SI unit from ref (16)). This theoretical r2’ estimation was consistent with measured r2’ for the fully internalized group (r2’ = 586± 24 s−1.mM−1).
IONP fractions were derived on a sample basis using relaxation rate measurements and on a group basis using corresponding relaxivities. The group derived fractions are summarized in Table 1 for all four contrast mechanisms, in good agreement with the control fractions. When using the SDR prediction for r2’ the error is lower than 4% for all groups. Figure 4 displays the internalized fraction measured on each sample; they were estimated using R2’ relaxation rate measurements. We discarded the measurements of the lowest concentration samples ([IONP] < 0.05 mM) because of poor accuracy of several long T2* samples (see Discussion section and Figure 5). The remaining samples resulted in measured internalized fractions that are in agreement with the control fractions, with a maximum error of about 9 %.
Figure 4.

Internalized IONP fraction estimated from R2’ relaxation rate data. Measured fraction vs. actual fraction for various samples containing mixtures of free and internalized IONPs.
Figure 5.
Illustration of T2* decay curves measured at various locations in the samples. Background field heterogeneities mainly occur close to air/gel interfaces that intercept B0; such variations interfere with the intrinsic T2*, leading to a signal behavior different from the usual exponential decay model (e.g. vial #2), especially for long intrinsic T2* values. Conversely, the exponential model satisfactorily describes the decay curves when background field heterogeneities are low (e.g. vial #1) and for short intrinsic T2* values (e.g. vial #3).
3. Discussion
This study confirmed that relaxation time quantification is not a robust mean to assess IONP concentration by MRI since it is affected by whether IONP particles are free or clustered, as can be found when internalized by cells. Susceptibility measurements on the other hand, constitute a promising way of evaluating IONP concentration regardless of IONP microdistribution. In addition, when IONP concentration becomes known, relaxation data provide insight into the local distribution of the particles and allows an estimation of the dispersed to internalized iron fractions.
The ability to extract free and internalized IONP fractions from relaxation measurements relies on IONP concentration estimation and necessitates free and internalized reference relaxivity values. As demonstrated here, all four relaxation mechanisms could potentially be used in this perspective. However, the SDR theory correctly predicts r2’ in the case of cell-internalized IONP, for several kinds of IONP and cell lines (from this report and references (16,22)). This makes the corresponding calibration step dispensable and makes T2’ measurements particularly suited for IONP fraction quantification (more so than T1, T2 or T2* which are harder to predict by theory for internalized IONP).
Although T2* may not be considered as a meaningful parameter by some authors because of the inherent difficulties associated with its measurement, it is a very important parameter to consider for IONP characterization since it is the most sensitive relaxation parameter when IONPs are clustered (16), and is a prerequisite for T2’ measurements. Hence it is important to pay particular attention to measurement methods in order to get robust T2* estimates. When background field variations are low and small voxels are used, an exponential model is expected in the case of IONPs (13). In the present study we used isotropic 0.5 mm voxels and aimed to minimize background field variations associated with the external shape of the sample by embedding all individual syringes inside a block of agarose gel. Such an arrangement allowed us to measure T2* (84.4 ± 2.6 ms), which was on the order of T2 (84.2 ± 5.3 ms) for the syringe containing pure gel without IONP, located approximately in the middle of the block – far from any air/gel interface. However significant deviation from the exponential decay model was observed for samples located near the edge of the container (see Figure 5); these were the low concentration samples ([IONP] < 0.05 mM) and were thus not used for the internalized fraction calculations.
In addition to these large scale background field variations, other sources of magnetic field inhomogeneities may be encountered at the voxel scale and could bias the IONP fraction estimates because of their impact on T2’. Blood oxygen saturation and microbleeds for instance, have a direct impact on T2’ because of the susceptibility effects of oxy- and deoxy- haemoglobin. In this latter context, vessel network models consisting of long cylinders arranged with random orientations have allowed the extraction of quantitative blood oxygenation level from relaxation data (28,29). Accounting for these effects and extracting unbiased IONP fractions may be ultimately possible by applying the SDR theory to more complex models, which would consider both iron-loaded cells and capillary networks jointly to simulate the T2’ effect. Furthermore, water diffusion also has an impact on T2’ measurements because of partial motional averaging occurring during the inter-echo delay (τCP) of a spin echo train. τCP may be tuned to maximize T2’ variations (e.g. see Fig. 15 in (3)) for a given cell line, IONP size and internalization process since these parameters could all potentially affect the extent of water diffusion and the corresponding contrast. Understanding these confounding effects is of great interest to refine further the present method and to adapt it to specific tissue environments and experimental conditions; however this is outside the scope of the present paper. Simply note that a T1 or T2 based quantification approach may be used (see Table 1) when the T2’ approach fails, although this would require calibration of the fully internalized r1 or r2, respectively.
In the presented study, spectroscopic methods were used to extract χ and an assumption about the shape of the sample container was necessary. This approach therefore, is not directly applicable for in vivo studies. However, compared to conventional susceptometry methods such as those described in (16), frequency data were measured directly inside the solution of interest (as opposed to externally), in order to probe the local magnetic fields induced by IONPs. We expect that imaging based susceptibility mapping techniques that rely on the local phase information (23,24) will be independent of IONP distribution as well. These latter techniques would then allow the extraction of susceptibility maps, and hence potentially IONP concentration maps, for samples of arbitrary shapes. Although progress in this field have been particularly fruitful recently, implementation of susceptibility mapping is not straightforward and requires deployment of complex reconstruction algorithms that are not widely available.
The present study was simply intended as a proof of concept of the potential of multi-parametric MRI for quantification of IONP concentration and estimation of the cell-internalized fraction. The proposed methodology could be used as a non destructive control of cell labeling efficiency prior to in vivo injection, without the need of complex imaging based susceptibility mapping techniques. For direct in vivo quantification, it is not clear yet how demanding susceptibility measurements would need to be to achieve acceptable accuracy and precision, or whether novel susceptibility mapping techniques will meet these requirements. Further studies will address this question.
4. Conclusion
Our study showed that susceptibility measurements accurately estimated IONP concentration regardless whether the particles were dispersed or clustered. The measured concentration allowed the estimation of dispersed and cell-internalized IONP fractions using relaxation measurements. Novel imaging based susceptibility mapping techniques could prove to be a valuable tool to quantify IONP content in samples of arbitrary shapes and in tissues in vivo. Combined with relaxation time mapping techniques, especially T2 and T2*, this could be an efficient way to measure both IONP concentration as well as dispersed and cell-internalized IONP fractions in vivo, to gain insight into tissue function or detect and quantify molecular imaging paradigms.
5. Material and Methods
5.1. Cell labeling
Endometrial regenerative stem cells (ERCs) were supplied in flasks by Boris Minev, PhD (Moores/UCSD Cancer Center, San Diego, CA), when cells were approximately 80% confluent. Cells were labeled with ferumoxides (Feridex, Bayer HealthCare Pharmaceutical Inc., NJ, USA) by adding 100 ug Fe/mL to each flask containing 15 mL of media and then incubated for 24 hours at 37oC. The media was then aspirated and each flask was washed three times with PBS to remove free iron. Cells were then detached by adding 3 mL trypsin. Ten minutes later, trypsin activity was quenched by adding fresh media. Cells were then collected and a small sample was used for viability assessment using dye exclusion test. Finally cells were centrifuged and the supernatant was aspirated. The cell pellet was re-suspended in fresh media and placed in a dedicated vial: this was considered the fully internalized IONP stock solution. Cell counting and iron quantification were performed to assess the iron labeling efficiency.
5.2. Sample preparation
Iron concentration in cells was measured by Inductively Coupled Plasma – Mass Spectroscopy (ICP-MS) using a small sample of the internalized IONP stock solution. The amount of iron per cell was calculated by dividing total iron content in the sample by its cell count. We prepared four sample groups: 1) 100% free IONPs; 2) 67% free and 33% cell-internalized IONPs; 3) 33% free and 67% cell-internalized IONPs; and 4) 100% cell-internalized IONPs. In order to control retrospectively for actual fractions of free and cell-internalized IONPs, all samples were made from identical stock solutions of free and fully internalized ferumoxides. For each group, serial dilutions were prepared in 2% agarose gel (Type I, Sigma-Aldrich Inc., St. Louis, MO, USA) using approximate concentrations: 0, 0.03, 0.06, 0.13, 0.25, 0.5, 0.75, and 1mM of iron. Samples were stocked in 1 mL tuberculin syringes. No further cell integrity test was carried out after placing them in gel; internalized IONPs were simply assumed to keep a clustered arrangement and free IONPs to keep a dispersed one. All imaged samples were re-characterized for total iron content by ICP-MS to obtain accurate IONP concentration.
5.3. Relaxation measurements
All MR experiments were performed at room temperature on a Sigma HDx 3T scanner (GE Healthcare, Milwaukee, WI, USA). T1, T2 and T2* were measured by imaging with an inversion recovery fast spin echo sequence (TE = 9.9 ms, TR = 3 s, ETL = 8, BW = ±15.6 kHz, FOV = 13 cm, Mx = 160×160, NEX = 1, 2 mm slice thickness, and 20 inversion times TI, ranging from 50 ms to 2.5 s), a multi-echo spin echo sequence (TR = 1.5 s, BW = ±31.3 kHz, FOV = 13 cm, Mx = 160×160, NEX = 1, 2 mm slice thickness, and 8 evenly spaced TEs ranging from 6.9 ms to 55.6 ms) and a multi-echo gradient echo sequence respectively (TR = 500 ms, FA = 50o, BW = ±31.3 kHz, FOV = 13 cm, Mx = 256×256, NEX = 2, 0.5 mm slice, and 16 evenly spaced TEs ranging from 4.2 ms to 71.7 ms). The signal to noise ratio obtained on the 2% agarose gel sample was measured to provide insight into the image quality. Signal was evaluated as the mean signal intensity measured in the corresponding tube at the shortest TE for both T2 and T2* scans (i.e. multi-echo spin echo and gradient echo, respectively), and at the longest TI for the T1 scan (i.e. inversion recovery fast spin echo). The noise was evaluated as the standard deviation of the MR signal measured over a region of interest (ROI) located outside the samples; the correcting factor [2/(4-π)]1/2 was included to account for the Rice distribution of MR signal on magnitude images.
On each image, signal intensities were measured by drawing ROIs in the center of each sample. T1 quantification was performed by curve-fitting the analytical function A×|1 − B×exp(-TI/T1)| to the signal, with A, B, and T1 as free parameters. T2 and T2* were extracted by fitting [(C×exp(-TE/T2(*)))2 + D2]1/2 to the measured signal decay, with C, D, and T2(*) as free parameters. Free parameters B and D were added to the usual exponential models in order to improve the goodness of fit (13). T1 and T2(*) nonlinear least square fitting algorithms were implemented using Matlab (The MathWorks Inc., Natick, MA, USA). Finally, Corresponding relaxivities were extracted by regression analysis, using the usual linear relaxivity assumption Ri = Ri0 + ri.[IONP], where i = 1, 2, 2*.
5.4. Magnetic susceptibility measurements
In this preliminary study, magnetic susceptibility was measured using MR spectroscopy. For each sample, two slice-selective FIDs were acquired on the central slice of the elongated shape 1 mL tuberculin syringe, with its main axis oriented parallel and then perpendicular with respect to B0. Corresponding central frequencies were measured from the FIDs by Fourier transform. MR spectroscopy acquisition parameters were as follows: 5mm slice thickness selective FID with TR = 3.5 s, FA = 90o, 4096 number of readout points, BW = ±2.5 kHz, number of average = 4 and no water suppression.
For further analysis, the containers (i.e. the syringes) were assumed to be infinitely long cylinders. According to theory (30), the local magnetic field experienced by protons inside the container varies with its orientation with respect to B0 and depends on the susceptibility of the solution as well as the susceptibility of the surrounding medium, i.e. air in the present case. Assuming small susceptibility values (i.e. χ ≪ 1) and following first order analytical solutions, the parallel and perpendicular configurations yield the following resonance frequency shifts (given in ppm): δf0// ≈ δCS + χ / 3 and δf0⊥ ≈ δCS − χ / 6 + χair / 2, respectively where δCS and χ are the chemical shift (in ppm) and the susceptibility of the solution, and χair is the susceptibility of the surrounding air. χ was finally extracted from both Larmor frequency measurements as χ ≈ 2 × (δf0// − δf0⊥) + χair using a reference value of 0.36 ppm (26) for the susceptibility of air. Two extra samples were characterized using the present method (deionized water and vegetable oil) in order to control for accuracy. For all IONP samples, the background susceptibility value of a 2 % agarose gel sample was subtracted form the total measured susceptibility in order to extract the IONP contribution.
5.5. Internalized IONP fraction estimation
Using IONP concentration measurement derived from ICP-MS, relaxation data were used to estimate the internalized IONP fraction, assuming additive contribution of free and cell-internalized IONPs: ri = (1−f).rifree + f.ricell, where f is the internalized IONP fraction, 1 – f is the free IONP fraction and i = 1, 2, 2* or 2’ indicates the corresponding contrast mechanism. Internalized IONP fractions were extracted on a group basis for all four contrast mechanisms using measured free and fully internalized relaxivity value as references (i.e. rifree and ricell were measured values). For the r2’ relaxation mechanism, a group-based fraction estimation was also assessed using the SDR prediction for the reference relaxivity value of the fully internalized IONPs group (i.e. r2’cell was estimated by theory).
R2’ relaxation rate data were also considered to extract the internalized IONP fraction on a sample basis. The underlying idea was to compare the relaxation rate of a given sample with relaxation rates of 100% free and 100% internalized sample of identical concentration. Measured free group relaxivity and SDR prediction of the internalized group relaxivity were used as references.
Acknowledgments
The authors thank Dr Boris Minev (Moores/UCSD Cancer Center) for providing the ERC cells, as well as Dr Elamprakash N. Savariar (UCSD, Department of Pharmacology) for his help with ICP-MS iron measurements. This work was supported in part by the NIH ICMIC P50-CA128346, and Pfizer.
References
- 1.Corot C, Robert P, Idee JM, Port M. Recent advances in iron oxide nanocrystal technology for medical imaging. Adv Drug Deliver Rev. 2006;58(14):1471–1504. doi: 10.1016/j.addr.2006.09.013. [DOI] [PubMed] [Google Scholar]
- 2.Liu W, Frank JA. Detection and quantification of magnetically labeled cells by cellular MRI. European Journal of Radiology. 2009;70(2):258–264. doi: 10.1016/j.ejrad.2008.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Laurent S, Forge D, Port M, Roch A, Robic C, Elst LV, Muller RN. Magnetic iron oxide nanoparticles: Synthesis, stabilization, vectorization, physicochemical characterizations, and biological applications. Chemical Reviews. 2008;108(6):2064–2110. doi: 10.1021/cr068445e. [DOI] [PubMed] [Google Scholar]
- 4.Rogers WJ, Meyer CH, Kramer CM. Technology Insight: in vivo cell tracking by use of MRI. Nat Clin Pract Cardiovasc Med. 2006;3(10):554–562. doi: 10.1038/ncpcardio0659. [DOI] [PubMed] [Google Scholar]
- 5.Bulte JWM. In Vivo MRI Cell Tracking: Clinical Studies. Am J Roentgenol. 2009;193(2):314–325. doi: 10.2214/AJR.09.3107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shapiro EM, Sharer K, Skrtic S, Koretsky AP. In vivo detection of single cells by MRI. Magn Reson Med. 2006;55(2):242–249. doi: 10.1002/mrm.20718. [DOI] [PubMed] [Google Scholar]
- 7.Smirnov P, Poirier-Quinot M, Wilhelm C, Lavergne E, Ginefri JC, Combadiere B, Clement O, Darrasse L, Gazeau F. In Vivo Single Cell Detection of Tumor-Infiltrating Lymphocytes With a Clinical 1. 5 Tesla MRI System. Magn Reson Med. 2008;60(6):1292–1297. doi: 10.1002/mrm.21812. [DOI] [PubMed] [Google Scholar]
- 8.Perez JM, Josephson L, O'Loughlin T, Hogemann D, Weissleder R. Magnetic relaxation switches capable of sensing molecular interactions. Nat Biotechnol. 2002;20(8):816–820. doi: 10.1038/nbt720. [DOI] [PubMed] [Google Scholar]
- 9.Perez JM, Josephson L, Weissleder R. Use of magnetic nanoparticles as nanosensors to probe for molecular interactions. ChemBioChem. 2004;5(3):261–264. doi: 10.1002/cbic.200300730. [DOI] [PubMed] [Google Scholar]
- 10.Atanasijevic T, Shusteff M, Fam P, Jasanoff A. Calcium-sensitive MRI contrast agents based on superparamagnetic iron oxide nanoparticles and calmodulin. PNAS. 2006;103(40):14707–14712. doi: 10.1073/pnas.0606749103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Demas V, Lowery TJ. Magnetic resonance for in vitro medical diagnostics: superparamagnetic nanoparticle-based magnetic relaxation switches. New J Phys. 2011;13:24. [Google Scholar]
- 12.Tu CQ, Osborne EA, Louie AY. Activatable T (1) and T (2) Magnetic Resonance Imaging Contrast Agents. Ann Biomed Eng. 2011;39(4):1335–1348. doi: 10.1007/s10439-011-0270-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Girard OM, Du J, Agemy L, Sugahara KN, Kotamraju VR, Ruoslahti E, Bydder GM, Mattrey RF. Optimization of Iron Oxide Nanoparticle Detection Using Ultrashort Echo Time Pulse Sequences: Comparison of T1, T2*, and Synergistic T1–T2* Contrast Mechanisms. Magn Reson Med. 2011;65(6):1649–1660. doi: 10.1002/mrm.22755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liu W, Dahnke H, Jordan EK, Schaeffter T, Frank JA. In vivo MRI using positive-contrast techniques in detection of cells labeled with superparamagnetic iron oxide nanoparticles. NMR Biomed. 2008;21(3):242–250. doi: 10.1002/nbm.1187. [DOI] [PubMed] [Google Scholar]
- 15.Tanimoto A, Oshio K, Suematsu M, Pouliquen D, Stark DD. Relaxation effects of clustered particles. J Magn Reson Imaging. 2001;14(1):72–77. doi: 10.1002/jmri.1153. [DOI] [PubMed] [Google Scholar]
- 16.Bowen CV, Zhang XW, Saab G, Gareau PJ, Rutt BK. Application of the static dephasing regime theory to superparamagnetic iron-oxide loaded cells. Magn Reson Med. 2002;48(1):52–61. doi: 10.1002/mrm.10192. [DOI] [PubMed] [Google Scholar]
- 17.Billotey C, Wilhelm C, Devaud M, Bacri JC, Bittoun J, Gazeau F. Cell internalization of anionic maghemite nanoparticles: Quantitative effect on magnetic resonance imaging. Magn Reson Med. 2003;49(4):646–654. doi: 10.1002/mrm.10418. [DOI] [PubMed] [Google Scholar]
- 18.Kuhlpeter R, Dahnke H, Matuszewski L, Persigehl T, von Wallbrunn A, Allkemper T, Heindel WL, Schaeffter T, Bremer C. R2 and R2*mapping for sensing cell-bound superparamagnetic nanoparticles: In vitro and murine in vivo testing. Radiology. 2007;245(2):449–457. doi: 10.1148/radiol.2451061345. [DOI] [PubMed] [Google Scholar]
- 19.Gillis P, Moiny F, Brooks RA. On T-2-shortening by strongly magnetized spheres: A partial refocusing model. Magn Reson Med. 2002;47(2):257–263. doi: 10.1002/mrm.10059. [DOI] [PubMed] [Google Scholar]
- 20.Matsumoto Y, Jasanoff A. T-2 relaxation induced by clusters of superparamagnetic nanoparticles: Monte Carlo simulations. Magn Reson Imag. 2008;26(7):994–998. doi: 10.1016/j.mri.2008.01.039. [DOI] [PubMed] [Google Scholar]
- 21.Weisskoff RM, Zuo CS, Boxerman JL, Rosen BR. Microscopic Susceptibility Variation and Transverse Relaxation - Theory and Experiment. Magn Reson Med. 1994;31(6):601–610. doi: 10.1002/mrm.1910310605. [DOI] [PubMed] [Google Scholar]
- 22.Yablonskiy DA, Haacke EM. Theory of NMR signal behavior in magnetically inhomogeneous tissues: the static dephasing regime. Magn Reson Med. 1994;32(6):749–763. doi: 10.1002/mrm.1910320610. [DOI] [PubMed] [Google Scholar]
- 23.De Rochefort L, Brown R, Prince MR, Wang Y. Quantitative MR susceptibility mapping using piece-wise constant regularized inversion of the magnetic field. Magn Reson Med. 2008;60(4):1003–1009. doi: 10.1002/mrm.21710. [DOI] [PubMed] [Google Scholar]
- 24.de Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, Wu JL, Wang Y. Quantitative Susceptibility Map Reconstruction from MR Phase Data Using Bayesian Regularization: Validation and Application to Brain Imaging. Magn Reson Med. 2010;63(1):194–206. doi: 10.1002/mrm.22187. [DOI] [PubMed] [Google Scholar]
- 25.Terreno E, Crich SG, Belfiore S, Biancone L, Cabella C, Esposito G, Manazza AD, Aime S. Effect of the intracellular localization of a Gd-based imaging probe on the relaxation enhancement of water protons. Magn Reson Med. 2006;55(3):491–497. doi: 10.1002/mrm.20793. [DOI] [PubMed] [Google Scholar]
- 26.Schenck JF. The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds. Med Phys. 1996;23(6):815–850. doi: 10.1118/1.597854. [DOI] [PubMed] [Google Scholar]
- 27.Kuchel PW, Chapman BE, Bubb WA, Hansen PE, Durrant CJ, Hertzberg MP. Magnetic susceptibility: Solutions, emulsions, and cells. Concepts Magn Reson Part A. 2003;18A(1):56–71. [Google Scholar]
- 28.He X, Zhu M, Yablonskiy DA. Validation of oxygen extraction fraction measurement by qBOLD technique. Magn Reson Med. 2008;60(4):882–888. doi: 10.1002/mrm.21719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Christen T, Lemasson B, Pannetier N, Farion R, Segebarth C, Remy C, Barbier EL. Evaluation of a quantitative blood oxygenation level-dependent (qBOLD) approach to map local blood oxygen saturation. NMR Biomed. 24(4):393–403. doi: 10.1002/nbm.1603. [DOI] [PubMed] [Google Scholar]
- 30.Chu SCK, Xu Y, Balschi JA, Springer CS. Bulk Magnetic-Susceptibility Shifts in NMR-Studies of Compartmentalized Samples - Use of Paramagnetic Reagents. Magn Reson Med. 1990;13(2):239–262. doi: 10.1002/mrm.1910130207. [DOI] [PubMed] [Google Scholar]