Modeling Structural Coordination and Ligand Binding in Zinc Proteins with a Polarizable Potential

Abstract

As the second most abundant cation in human body, zinc is vital for the structures and functions of many proteins. Zinc-containing matrix metalloproteinases (MMPs) have been widely investigated as potential drug targets in a range of diseases ranging from cardiovascular disorders to cancers. However, it remains a challenge in theoretical studies to treat zinc in proteins with classical mechanics. In this study, we examined Zn²⁺ coordination with organic compounds and protein side chains using a polarizable atomic multipole based electrostatic model. We find that polarization effect plays a determining role in Zn²⁺ coordination geometry in both matrix metalloproteinase (MMP) complexes and in zinc-finger proteins. In addition, the relative binding free energies of selected inhibitors binding with MMP13 have been estimated and compared with experimental results. While not directly interacting with the small molecule inhibitors, the permanent and polarizing field of Zn²⁺ exerts a strong influence on the relative affinities of the ligands. The simulation results also reveal the polarization effect on binding is ligand dependent and thus difficult to be incorporated into fixed-charge models implicitly.

Introduction

One third of all proteins contain metal ions as their integral parts ¹. The metal ions in these protein complexes serve essential biological functions from organizing the secondary or tertiary structure, facilitating protein-ligand interactions, to directly participating in catalytic activities. Many metalloproteins, similar to the ion channels, recognize and associate with only specific types of ions against a solution of various ions of similar properties (e.g. charge and size). For example, calmodulin, involved in signal transduction, DNA synthesis, and cell division, undergoes significant conformational changes upon binding to Ca^{2+ 2}; protein kinases and ATPase require Mg²⁺ in coordination with ATP to facilitate phosphoryl transfer ^3,4; metalloenzymes, such as alcohol dehyrogenase, carboxypeptidase, thermolysin, and matrix metalloproteinases (MMPs), rely on Zn²⁺ for their catalytic activities ⁵. As the second most abundant cation in human body ⁶, Zn has important biological implications and is involved in survival and pathogenesis of many viruses including HIV, hepatitis, herpes simplex, Rubella and influenza^7–11.

In aqueous solution, it is well established that Zn²⁺ has a coordination number of six and forms an octahedral structure with water. When binding in the protein complexes, a tetrahedral arrangement to the surrounding amino acid residues is often observed although Zn²⁺ can also exist in a five-, or a six-coordinated complex. In protein, Zn²⁺ can serve either a catalytic role, by participating directly in chemical catalysis, or a structural role solely to maintain protein structure and stability ¹². Analysis of protein X-ray structures shows that among 126 structural proteins, a majority of the zinc sites (82%) are 4-coordinated, only 14% are 5-coordinated, and 4% are 6-coordinated; Of 147 catalytic binding proteins, 58% are 4-coordinated, 31% are 5-coordinated, and 11% are 6-coordinated ¹³. Therefore, tetrahedral coordination is dominant in proteins although a significant amount of zinc ions display higher coordination numbers. Common ligands for the zinc ion include histidine, aspartate or glutamate, and cysteine, in a variety of combinations. The flexibility in the ligand choices and coordination geometries leads to diverse Zn²⁺ binding sites in zinc metalloenzymes, rendering a range of important biological roles, such as catalytic, coactive and structural functions¹⁴.

Computational study of zinc ions embedded in a protein active site has been a long-standing challenge. While Quantum Mechanics ¹⁵ or combined Quantum Mechanics/Molecular Mechanics methods ^16,17 have been applied to investigate zinc-containing molecular systems, the computational cost of high level ab initio calculation makes it difficult to tackle complex configurational space or long-time dynamics. On the other hand, classical mechanics treatment of Zn²⁺ is problematic. The strong local electrostatic field and induction effect ¹⁸ pose challenges for the traditional fixed-charge molecular mechanics ^19–21 and quantum chemistry methods ^22,23 to model zinc ion in biomolecules.

Two types of approaches have been implemented in fixed-charge force field: non-bonded and bonded models. The non-bonded model presented by Stote and Karplus ²⁴ is widely used due to its simplicity and efficiency to investigate the structure, dynamics and energetics of zinc containing proteins. For example, Donini and Kollman reported studies on inhibitors binding to matrix metalloproteinases based on such a nonbonded description for Zn^{2+ 20}. However, it is generally believed that treating zinc metal in a non-bonded fashion leads to an overly strong preference for octahedral coordination and sometimes the zinc ion even escapes away from the coordination sphere. It has also been reported that nonbonded model is not able to properly describe the coordination number and energy at the same time ²⁵. Many have attempted to use artificial bonds between ion and ligand atoms to fix the geometry for the purpose of modeling ion-ligand interactions, which is referred to as the bonded model ^26–28. A semi-bonded model with tetrahedral charge dummies around zinc has also been proposed ²⁹. By placing four cationic dummy atoms tetrahedrally around the zinc nucleus, the orientation requirement for the zinc coordinates is imposed all the time during the simulation. The extra charge sites however give rise to unphysical permanent dipole and quadrupole moments to the Zn²⁺. These bonded or semi-bonded models and their variants methods freeze the specific zinc coordination to the surroundings, which will likely cause artifacts on the ligand conformational sampling and dynamics. The inability to model zinc has been a hindrance to understand the versatile functions of Zn²⁺ and metalloenzymes, given that the variability in Zn²⁺ coordination may be coupled with enzyme function at different stages of reaction ⁶. The lack of charge transfer and explicit polarizability can result in poor accuracy for the association energies ³⁰. Classical nonpolarizable force fields are inherently unsuitable for describing flexible zinc coordination.

Polarizable potentials hold promise as they explicitly accounts for polarization and even charge-transfer effects. SIBFA was one of the first potentials developed to model Zn interaction with organic and biological molecules by rigorously incorporating polarization, charge transfer, penetration and other effects ^31–37. Gresh reported the very first attempt to introduce explicit charge transfer energy term in Zn²⁺ modeling and this work systematically monitored the distal and angular dependencies against quantum chemistry energy decomposition in various Zn²⁺ ligand complexes ³³. A critical feature of charge transfer effect relates to its non-additive behavior in polyligated complexes, which was monitored against quantum chemistry computations by Tiraboschi et al ^36,37. The penetration effect was also introduced for Zn by Gresh and co-workers in their subsequent work ³². The applications of SIBFA to model the complexes of inhibitors to a Zn-metalloenzyme, thermolysin, were initiated early in 1997–1998 ^34,35, followed by applications to β-lactamase ^38,39, Zn-fingers ⁴⁰, and phosphomannoisomerase ^41,42. Sakharov and Lim also developed a model which reproduced the experimentally observed tetrahedral structures of Cys₂His₂ and Cys₄ Zn-binding sites in proteins ⁴³. The treatment by Sakharov and Lim simply introduced distance-dependent partial charges on Zinc without actually accounting for the second order charge-transfer effect. It is interesting to note that reduced partial charges lead to less favorable Coulombic interactions, opposite to what one expects from charge-transfer effect.

Previously we developed a polarizable multipole-based model for Zn²⁺ in water environment ¹⁸. In this study, we are extending the polarizable model to investigate zinc binding with organic molecules and proteins. Three molecules, acetate anion, methanethiol anion (CH₃S⁻), and imidazole, were selected to mimic the side chains of typical Zn²⁺-interacting ligands, Asp, Cys and His. Two zinc enzyme systems with different coordination ligands (Asp, His, Cys, water) have been examined using MD simulations (Figure 2); system A is a zinc-finger with three four-fold coordinated zinc structural sites, and System B, A matrix metalloproteinases (MMP) complex with two four-fold coordinated zinc sites, one catalytic and the other structural zinc.

Figure 2.

Crystal structures of Zinc-finger protein in complex with DNA (PDB entry:1AAY, panel a) and MMP13 protein (PDB entry:1XUD, panel b). In panel a, the DNA is shown in red cartoon, the three zinc finger motifs are illustrated in yellow, green and blue respectively. In panel b, the alpha helices are in red, beta sheets are in yellow, and the ligand is in line representation. In both panels, the zinc ions are in purple, and zinc-coordinating residues are in stick.

The Cys₂His₂-type zinc-finger protein consists of highly conserved zinc finger domains where each zinc ion is coordinated by two cysteines and two histidines. Each domain consists of two beta strands, one alpha helix and a hairpin structure. Three residues located at the alpha helices in each finger interact with three nucleotide bases of the DNA, typically making contacts with contiguous three base pair recognition sites. Such a direct recognition mode to DNA makes zinc finger proteins an ideal scaffold to design proteins that can recognize the predetermined DNA sequences specifically ⁴⁴. During the zinc-finger protein folding process, zinc ions play a crucial role by binding to the peptides first, then directing the folding and stabilizing the β-hairpin and α-helix as suggested by Li et. al. ⁴⁵.

The other Zn-containing protein investigated here is MMPs, belongs to a family of zinc-dependent endopeptidases related to the physiological homeostasis of the extracellular matrix. Abnormal expression of MMPs has been implicated in a number of pathological conditions such as metastasis, angiogenesis, osteoarthritis, rheumathoid arthritis and cardiovascular diseases. Development of selective and potent inhibitors to MMPs is a topic of considerable interest ^46–50. A number of computational studies of inhibitors binding to MMPs have been reported ^19,20,48,51. A majority of available MMP inhibitors are zinc chelating compounds containing zinc binding groups (ZBG), such as hydroxamate (CONH-O⁻), carboxylate (COO⁻), thiolate (S⁻) or phosphinate (PO₂⁻) ⁵². Unfortunately these inhibitors are often found to be biologically labile, lacking selectivity, or having toxic side effects ⁵³. Considerable efforts have also been made to develop non-zinc chelating compounds that lead to inhibitors with specificity to certain MMP subtypes ^54,55.

Computational Methods

The polarizable force field and parameterization

In AMOEBA force field, permanent atomic multipoles up to quadrupoles are used to describe electrostatic interactions. The polarization effect is explicitly accounted for by incorporating dipole induction in a self-consistent manner ⁵⁶. A buffered 14-7 potential is used to describe the repulsion-dispersion interactions between pairs of nonbonded atoms ⁵⁷. Parameters for all proteins and existing small molecules involved in this study were taken from the AMOEBA force field ⁵⁸. Previously, AMOEBA polarizable multipole based force field has been applied to study water ^59,60, monovalent and divalent ions ^18,61–63, organic molecules and peptides ^56,64,65, protein-ligand binding prediction ^66,67 and computational X-ray crystallography ^68–70 with very encouraging success. A number of independent studies on ions ^71–76 and peptides using AMOEBA also demonstrated the improvements and advantages offered by the polarizable force field ^77–80.

Zn²⁺ electrostatic parameters include a point charge (2+) and an atomic polarizability¹⁸. In AMOEBA force field, Thole damping is achieved by screening of pairwise atomic multipole interactions and is equivalent to replacing a point multipole moment with a smear charge distribution. The damping function for charges is given by functional form ⁸¹

$$u=\frac{3a}{4\pi }\text{exp}(-{\mathit{\text{au}}}^3)$$ eqn.(1)

where μ = r_ij/(α_iα_j)^1/6 is the effective distance as a function of linear separation r_ij and atomic polarizabilities of sites i (α_i) and j (α_j). The coefficient α is the dimensionless width of the smeared charge distribution and controls the damping strength. The corresponding damping functions for charge, dipole, and quadrupole interactions were reported previously⁵⁹. A single transferable isotropic polarizability for each common chemical element was derived by fitting to experimental polarizabilities of a set of representative organic molecules. Except for the aromatic atoms and atoms with formal charges (details below), the atomic polarizabilities as originally suggested by Thole were adopted in AMOEBA force field, i.e. 1.334 ų for carbon, 0.496 ų for hydrogen, 1.073 ų for nitrogen, and 0.837 ų for oxygen (Table 2). The parameters for Zn and water were published previously ¹⁸ and are used in this study.

Table 2.

AMOEBA force field parameters derived from ab initio Zn²⁺-model compound structure and interaction energy.

	polarizability(Å3)	vdw r/ε
O	0.837	1.650/0.1120
O−	1.600	1.850/0.1290
S	2.800	2.0025/0.3550
S−	4.000	2.100/0.3550
N	1.073
N(aromatic)	1.500
C	1.334
C(aromatic & COO−)	1.750
H	0.496
H(aromatic)	0.696

The ab initio calculation of molecular polarizability tensor of three model compounds was performed at the level of MP2/6-31++G(2d,2p) (See Table 1). These molecular polarizability tensor values were used to verify and refine the atomic polarizability of aromatic atoms (C, N and H) and atoms with formal charges (O− and S−). The final values of standard and adjusted atomic polarizabilities are compared in Table 2.

Table 1.

Comparison of molecular polarizabilities (ų) from ab initio quantum mechanical, AMOEBA polarizable model prediction and experimental measurement.

		ab initioa	AMOEBA	Other exp or calc.
CH3COO−	αxx	7.12	6.09	7.34b
	αyy	6.95	5.71	7.49b
	αzz	4.58	4.47	4.91b
	αtotal	6.21	5.42	6.58 b
CH3S−	αxx	6.97	5.34
	αyy	6.97	5.34
	αzz	8.42	7.14
	αtotal	7.45	5.94	4.3c; 4.4c;5.5c; 6.7c
C3N2H4 (imidazole)	αxx	8.09	9.44	9.6d
	αyy	7.97	8.81	8.6d
	αzz	4.88	5.39	6.6d
	αtotal	6.98	7.88	8.24d; 7.5e

^aCalculated at the level of MP2/6–311++G(2d,2p)

^bCalculation from Ref. ¹⁰⁴;

^cCalculation from Ref. ¹⁰⁵;

^dExperimental measurement from Ref. ¹⁰⁶;

^eRef. ¹⁰⁷;

Permanent atomic multipole parameters of the charged model compounds acetate anion (COO⁻), methanethiol anion (CH₃S⁻), and imidazole, were derived in this study from ab initio QM calculations. Specifically, the permanent multipole moments were derived using the original Distributed Multipole Analysis (DMA) method from the density matrix output at the level of MP2/6-311G** using the GDMA software ⁸², and then optimized to reproduce the ab initio QM electrostatic potential from a higher level basis set (e.g. MP2/aug-cc-pVTZ) using TINKER ⁸³.

Finally, the Zn²⁺-model compound dimer and water-model compound dimer (Figure 1) interaction energy profiles were evaluated by both AMOEBA and ab initio methods (at the level of MP2/Aug-cc-pvtz with BSSE corrections) using TINKER ⁸³ and Gaussian 03 ⁸⁴, respectively (See Supplemental Materials). Both the ab initio and AMOEBA results were compared at the same geometries, which were minima on the QM surface for different radial variations. The dimer energy was evaluated as the difference between the dimer and monomer energy values, without relaxing the monomer geometry. The missing vdW AMOEBA parameters of ionic model compounds were fitted to reproduce the ab initio dimer energy, with the electrostatic parameters fixed. The resulting parameters from the model compounds are then transferred to the side chains of the residues for the Zn protein MD simulations (Table 2).

Figure 1.

The model systems studied with QM and AMOEBA.

For the four pyrimidine dicarboxamide inhibitors in MMP complexes (Figure 6), the equilibrium bond and angle values were obtained from the QM (at the level of HF/6-31G*) optimized geometry of the ligands. The same procedure described above is used to acquire permanent atomic multipoles. The vdW, bond, angle, out-of-plane, and atomic polarizability parameters of ligands were transferred from AMOEBA protein force field. The torsion parameters for the rotational bond were fitted to ab initio conformational energy profiles. The parameterization can be automated by using poltype program⁸⁵.

Figure 6.

Pyrimidine dicarboxamide inhibitors binding with MMP-13.

MD simulation

All the MD simulations in this study were performed using PMEMD and SANDER in AMBER9 ⁸⁶ with the AMOEBA force field. TINKER ⁸³ was used to prepare the initial systems. Two independent 5-ns MD simulation for the Zinc-finger protein were performed. The starting conformation was taken from crystal structure (PDB entry: 1AAY ⁸⁷) with DNA removed. The cysteine and histidine residues in the proximity of Zn²⁺ ion were deprotonated on the Zn-bound N. Based on the crystal structure, HIS69, HIS84, HIS119, HIS123, and HIS129 are deprotonated at Nε while HIS97 is deprotonated at Nδ. The protein was placed in a periodic octahedral water box with at least 15 Å from the solute to the nearest box edge. Each simulation cell has 75 Å on each side, and it contains 9321 AMOEBA water molecules ⁵⁹ and 11 Cl⁻ counter ions, contributing to a total of 29393 atoms. Two independent 5-ns MD simulations for the MMP protein complexes were also performed starting from crystal structure (PDB entry:1XUD ⁸⁸). A similar periodic octahedral water box with 70 Å on each side was set up with 23470 atoms, including 6938 water molecules. The systems were minimized first and then heated up to 298 K gradually in 50 ps and then equilibrated for 225 ps under NPT ensemble. The subsequent 5-ns MD simulations were performed in NVT ensemble, with the density fixed at the NPT-average value and a time step of 1 fs. The temperature was maintained at 298 K using Berendsen thermostat ⁸⁹. The vdW cutoff was set to 12 Å with long-tail correction applied. In all calculations the long-range electrostatics was treated using Particle Mesh Ewald (PME) summation ^90–92. The PME real space cutoff is set to 7 Å. The PME calculation used a 90×90×90 grid and fifth-order B-spline interpolation. The induced dipoles were iterated until the root-mean-square change was below 0.01 D/atom. Atomic coordinates of the simulation system were saved every 0.5 ps.

Binding free energy calculation

The relative binding free energy of four pyrimidine dicarboxamide ligands (Figure 6) to MMP13 was calculated by alchemically transform one ligand into another in both water and solvated protein complex, respectively. A scaling factor λ is used to divide the perturbation into intermediate steps. For example, ligand 1 (λ = 0) to ligand 2 (λ =1) conversion can be expressed through 11 intermediate steps when λ = {0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0}. In both sets of simulations, the electrostatic interactions between ligand 1 and the surroundings were first perturbed to those of ligand 2 and the surroundings by scaling the electrostatic parameters of the two ligands linearly in 5~10 steps depending on the structural similarity of the ligands. Subsequently the vdW interactions between the ligand and environment were transformed from ligand 1 to 2 in 5~10 steps, followed by valence terms (e.g. changing the equilibrium bond lengths from ligand 1 to 2) in 5~10 steps if applicable. During the decoupling of the vdW interactions, soft-core modifications ⁹³ were introduced to the buffered 14-7 vdW potential function, to avoid the singularity problem at the end point:

$$U_{\mathit{\text{ij}}}={\lambda }^n{\epsilon }_{\mathit{\text{ij}}}\frac{{1.07}^7}{[\alpha {(1-\lambda )}^2+{(\rho +0.07)}^7]}\left(\frac{1.12}{\alpha {(1-\lambda )}^2+{\rho }^7+0.12}-2\right)$$ eqn.(2)

where the potential well depth ε_ij is in kcal/mol, ρ is the effective radii, $\rho =R_{\mathit{\text{ij}}}/R_{\mathit{\text{ij}}}^0$. R_ij is the actual separation between i and j in Å, and $R_{\mathit{\text{ij}}}^0$ is the minimum energy distance; α is 0.07 and λ is the scaling factor.

MD simulations were performed at each step along the alchemical pathways for 2 ns for ligands in protein complexes and 1 ns for ligands in water. Bennett Acceptance Ratio estimator (BAR) ⁹⁴ was used to compute the free energy differences between the adjacent intermediate steps:

$$\mathrm{\Delta }A{(j)}_{{\lambda }_i\to {\lambda }_{i+\mathrm{1}}}=-\mathit{\text{RT}}\text{ln}\frac{{\langle \mathrm{1}/\left[\mathrm{1}+\text{exp}((E_{{\lambda }_i}-E_{{\lambda }_{i+\mathrm{1}}}+C)/\mathit{\text{RT}})\right]\rangle }_{{\lambda }_{i+\mathrm{1}}}}{{\langle \mathrm{1}/\left[\mathrm{1}+\text{exp}((E_{{\lambda }_{i+\mathrm{1}}}-E_{{\lambda }_i}+C)/\mathit{\text{RT}})\right]\rangle }_{{\lambda }_i}}+C$$ eqn.(3)

where C is given by C=ΔA(j−1)λ_i → λ_i+1, and j is the iteration index. Here, E_λi is the total energy of the system evaluated using the simulation snapshots at λ_i, with a dipole convergence of 10⁻⁶ D. ΔA is solved iteratively until the value of (ΔA(j) − ΔA(j-1)) is less than 0.01 kcal/mol. While an induced dipole convergence (0.01 D per atom) has been used during the simulations for computational efficiency, a tighter convergence of 10⁻⁶ D per atom is applied to re-analyze the saved snapshots and compute the results. The reweighting is incorporated rigorously into the BAR formula:

$$\mathrm{\Delta }A{(j)}_{{\lambda }_i\to {\lambda }_{i+\mathrm{1}}}=-\mathit{\text{RT}}\text{ln}\frac{\frac{{\langle \left[\mathrm{1}/(\mathrm{1}+\text{exp}((E_{{\lambda }_i}-E_{{\lambda }_{i+\mathrm{1}}}+C)/\mathit{\text{RT}}))\right]\times \left[\text{exp}((E_{{\lambda }_{i+\mathrm{1}}}^{\text{'}}-E_{{\lambda }_{i+\mathrm{1}}})/\mathit{\text{RT}})\right]\rangle }_{{\lambda }_{i+\mathrm{1}}^{\text{'}}}}{{\langle \text{exp}((E_{{\lambda }_{i+\mathrm{1}}}^{\text{'}}-E_{{\lambda }_{i+\mathrm{1}}})/\mathit{\text{RT}})\rangle }_{{\lambda }_{i+\mathrm{1}}^{\text{'}}}}}{\frac{{\langle \left[\mathrm{1}/(\mathrm{1}+\text{exp}((E_{{\lambda }_{i+\mathrm{1}}}-E_{{\lambda }_i}+C)/\mathit{\text{RT}}))\right]\times \left[\text{exp}((E_{{\lambda }_i}^{\text{'}}-E_{{\lambda }_i})/\mathit{\text{RT}})\right]\rangle }_{{\lambda }_i^{\text{'}}}}{{\langle \text{exp}((E_{{\lambda }_i}^{\text{'}}-E_{{\lambda }_i})/\mathit{\text{RT}})\rangle }_{{\lambda }_i^{\text{'}}}}}+C$$ eqn.(4)

where E’_λi is the total energy of the system evaluated at λ_i using a dipole convergence of 0.01 D, while E_λi indicates the potential energy evaluated using full convergence at 10⁻⁶ D per atom. λ’ indicates the ensemble obtained using the looser dipole convergence. The re-analysis method was used and the numerical reliability was verified. The comparison between using BAR formula eqn.(3) and using reweighting BAR formula eqn.(4) is discussed in Table 5.

Table 5.

Relative binding free energies from alchemical perturbation calculations (kcal/mol). In the BAR procedure the simulation was performed using an induced-dipole convergence of 0.01 D per atom, and the free energy was evaluated with a tighter convergence (10⁻⁶) using eqn (3). The reweighting BAR introduces a rigorous reweighting due to the different polarization convergence based on eqn (4).

	BAR (eqn.(3))			Reweighting BAR (eqn.(4))			BAR with Zn charge set to 0			BAR without polarization by Zn2+			Experiment Results
	ΔGlig-wat	ΔGlig-pro	ΔΔG	ΔGlig-wat	ΔGlig-pro	ΔΔG	ΔGlig-wat	ΔGlig-pro	ΔΔG	ΔGlig-wat	ΔGlig-pro	ΔΔG	ΔΔGexpra
4→3	4.14	5.52	1.38	4.14	5.55	1.41	4.14	5.82	1.68	4.14	5.29	1.15	1.30
4→2	11.94	13.45	1.51	13.47	15.15	1.68	11.94	15.01	3.07	11.94	13.02	1.08	2.32
2→1	−10.07	−9.36	0.71	−9.77	−9.30	0.46	−10.07	−5.52	4.55	−10.07	−10.85	−0.62	1.66

^aRef ¹⁰⁰.

Results and Discussion

Dimers of Zn²⁺/water interacting with model compounds

We have first evaluated the Zn²⁺ or a water molecule interacting with each of the model compound in both QM and AMOEBA calculations. The goal is to verify and systematically improve the AMOEBA parameters, especially atomic polarizability and vdW radii, of the three model compounds acetate anion, methanthiol anion, and imidazole. The first two ionic compounds were studied for the first time using AMOEBA. The purpose of examining both water and Zn²⁺ interacting with the same model compound is to avoid any biased changes in the model compound parameters. The AMOEBA atomic multipole parameters for three model compounds were obtained from QM calculations. The atomic polarizability values were mostly transferred from AMOEBA parameter set except for few new types. For the oxygen atom in acetate anion and the sulfur in CH₃S⁻, we found that atomic polarizability values larger than those in neutral molecules are necessary to reproduce the QM and experimental molecular polarizability (Table 1 and 2). Previously we also established that the atomic polarizabilities of the aromatic C and H in benzene ring need to be greater than those of sp3 C and attached H atoms ⁶⁴ In order to reproduce QM dimer energy and minimum-energy structure, increased polarizabilities are also needed for N and attached H in imidazole. Larger atomic polarizabilities in anions and aromatic molecules are expected given the excess electrons and more diffused electron clouds. The fact that larger vdw radii are needed for anionic atoms as compared to their neutral counterparts has been reported previously ^32,33. Larger vdW radii (Table 2) than those in the neutral forms were also obtained by matching AMOEBA with the QM binding energy and geometry for both Zn²⁺-model compound and water-model compound dimers. In Table 3, the final AMOEBA results are compared with ab initio values, and the binding energy differences and structure deviations are within 10% for all dimers except for CH₃S⁻-water and the bridge configuration of CH3COO⁻ - Zn²⁺. Note that the “constraint” here is that any change in the model compound vdW parameters will affect the Zn-model compound and water-model compound simultaneously. For example, decreasing the oxygen vdW radius in CH₃COO⁻ could lead to better agreement for water-CH₃COO⁻ interaction but will also significantly overestimate the Zn²⁺-CH₃COO⁻attraction and pull them even closer than the QM distance. Similar trend were observed previously in fixed charge force fields ⁹⁵. Charge transfer effect accounts for this strongly anticooperative character in the polyligated complexes Zn²⁺ with anionic ligands ^36,37, and it should also contribute, along with polarization effects, to the increase of the Zn-ligand distances optimized by quantum chemistry. In addition, it is observed that (Table 3) AMOEBA overestimated the energy gap between “bridge” (both oxygen atoms interacting with Zn in bidentate fashion) and “external” (one oxygen forming a close interaction with Zn). The AMOEBA dimer energy for the “external” configuration is not as low as that of ab initio. It was noticed from the ab initio energy minimization of “external” dimer that the C-O bond length involving the O that binds with Zn was 1.43 Å, the other C-O bond length was only 1.18 Å. The former is essentially a single bond and the Zn²⁺ seems to have stabilized one of the "resonance" structures. Our force field has not been implemented to distinguish the two oxygens or the two C-O bonds in such cases.

Table 3.

Heterodimer binding energies (kcal/mol) and structures (Å) computed by AMOEBA and ab initio QM at different configurations (shown in Figure 1). The ab initio results were obtained at the level of MP2/Aug-cc-pvtz with BSSE unless otherwise noted.

Configuration	Ab initio		AMOEBA
	Distance	Eint	Distance	Eint
Conf.      A:	1.65(O…H)	−17.39	1.74 (O…H)	−17.81
CH3COO− - water (External)
Conf.      B:	3.18 (C...O)	−20.99	3.18 (C…O)	−22.93
CH3COO− - water (Bridge)	1.96(O1…H1)		1.96(O1…H1)
	1.96(O2…H2)		1.96(O2…H2)
Conf.      C:	1.82(O…Zn)	−409.81a	1.72(O…Zn)	−356.59
CH3COO− - Zn2+ (External)
Conf.      D:	2.25 (C…Zn)		2.10 (C…Zn)	−442.30
CH3COO− - Zn2+ (Bridge)b	1.90(O…Zn)	−425.80a	1.81(O…Zn)
Conf.  E: CH3S− - water	2.14(S…H)	−16.36	2.14 (S…H)	−21.30
Conf.  F: CH3S− - Zn2+	2.24(S..Zn)	−421.78	2.06 (S…Zn)	−391.76
Conf.      G: Imidazole - water	1.91 (N…H)	−8.20	2.11 (N…H)	−8.10
Conf.      H: Imidazole – Zn2+	1.85 (N…Zn)	−175.55	1.75 (N…Zn)	−172.25

^aat the level of B3LYP6-311G**.

^bwith C-O-Zn angle at 150º.

MD simulations of zinc proteins

We have investigated two zinc-binding proteins: (A) a zinc-finger system with three four-fold coordinated zinc structural sites, and (B) a MMP13 complex with one four-coordinated catalytic zinc binding site and another bidentate structural site. The results are presented in Figure 3–5 and are discussed below.

Figure 3.

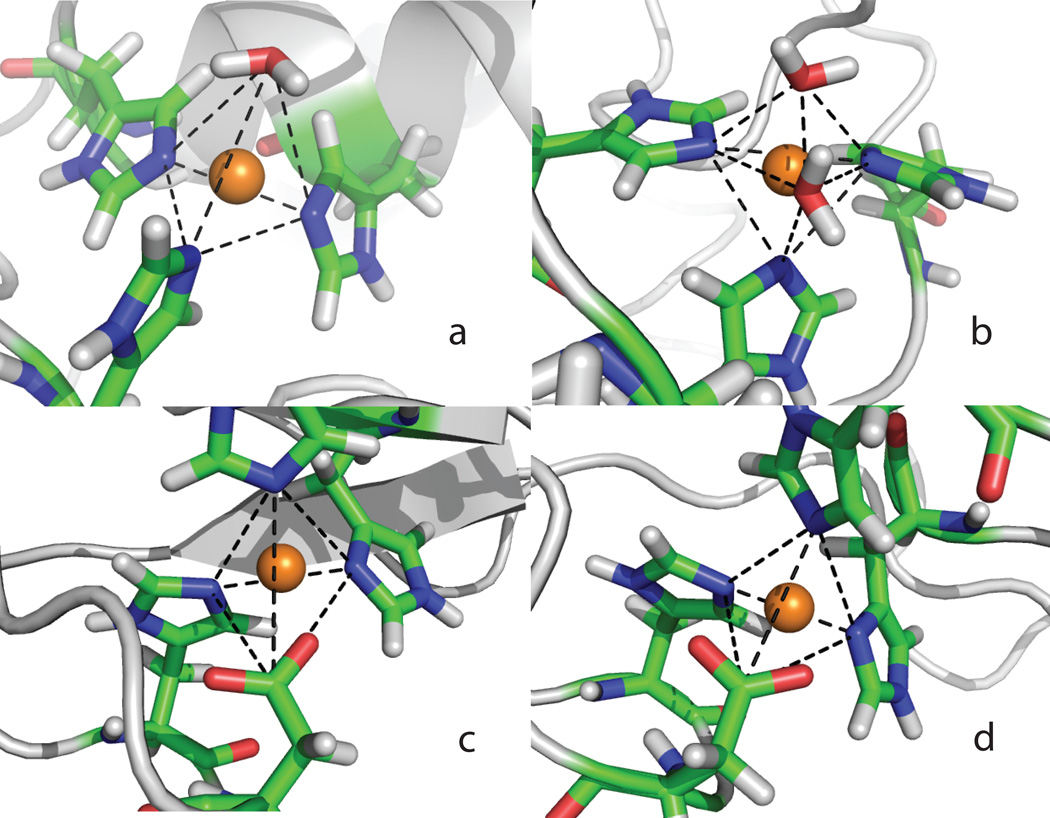
Structure comparison of the two zinc ions in the MMP13 complex (PDB entry: 1XUD): first zinc ion from the crystal structure in tetrahedron (panel a), first zinc ion from 5-ns MD simulation in trigonal bipyramidal geometry (panel b), second zinc ion from the crystal structure in bidentate tetrahedron (panel c) and second zinc ion from 5-ns MD simulation in bidentate tetrahedron (panel d).

Figure 5.

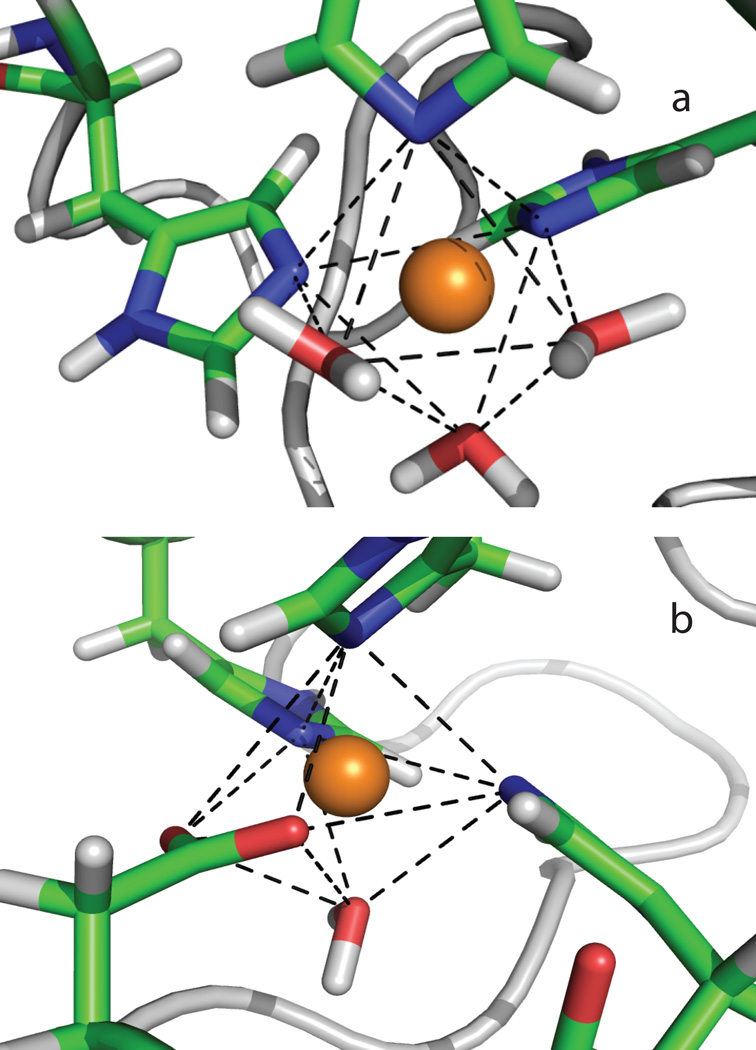
Under-polarization leads to 6-coordinated octahedral geometry for both His₃H₂O (panel a) and His₃Asp (panel b) Zn-binding sites in MMP-13. The corresponding crystal structures are shown in Figure 3.

Zn²⁺-Cys₂His₂ motif from the Zn finger simulation

Starting from the X-ray structure of a zinc-finger protein (1AAY) containing three zinc ions, two independent 5-ns simulations have been performed. As we will show later, the change of coordination (due to subtle change in atom polarizability) occurs within a few hundred picoseconds. All three zinc ions are coordinated with two histidines and two cysteines stably throughout the simulations. For all three Zn²⁺ binding sites, the root-mean-square deviations (RMSDs) of the backbone heavy atoms are 0.6 Å, 0.6 Å and 0.8 Å from the X-ray structures respectively. The average distances and angles are compared in Table 4. Overall the zinc coordination structures given by AMOEBA are in very good agreement with the corresponding crystal structures. The average Zn-S distance obtained from simulation is 2.13±0.05 Å, which is smaller than the distance of 2.25±0.07 Å observed in the crystal structure. This slight difference is considered a consequence of optimizing AMOEBA model against the ab initio calculation shown in Table 3. It is expected that implementing a charge transfer model into our AMOEBA polarizable potential can reproduce a more accurate Zn-S distance in both dimer interaction calculation and MD simulation.

Table 4.

Comparison between MD and experimental averaged Zn distances (Å) and angles (degree) in the Zn-finger motif.

		MD Simulation	X-ray
Zn-finger	Zn-S	2.13(0.05)	2.25(0.07)
	Zn-N	2.10(0.07)	2.05(0.05)
	S-Zn-S	118.5(6.6)	115.8(1.1)
	N-Zn-N	93.9(5.2)	103.1(7.3)
	S-Zn-N	106.0(5.3)	110.3(4.5)
MMP	Zn-N	2.01(0.06)	2.13(0.03)
	Zn-O1	2.19(0.09)	2.01a; 1.92(0)b
	Zn-O2	2.41(0.18)	3.22a; 2.76(0.13)b

^aX-ray structure of protein complex 1XUD.

^bX-ray structures from Zn containing protein database survey.

Zn²⁺-His₃H₂O and Zn²⁺-His₃Asp motif in MMP

We have also modeled a MMP13-ligand complex containing two zinc ions. Two independent 5 ns simulations starting from X-ray crystal structure (1XUD) have been performed. For the first Zn²⁺ ion, there are three histidines and one water coordinating to form a tetrahedral structure as shown in crystal structure (Figure 3a). The three histidine residues were well maintained during the simulation with the average Zn-N distance of 2.01±0.06 Å. The water molecules were rather fluid and attempted to enter and leave the zinc coordination sphere during the 5ns simulation. Water molecules and zinc were considered as interacting with each other if the distance between them is less than 2.2 Å. Two water molecules were observed to interact with the zinc for approximately 75% of time, contributing to a 5-coordinated trigonal bipyramidal geometry (Figure 3b), with one of the water molecule occupying the fourth ligation site as given in the crystal structure. For 25% of the simulation time, we observe the 4-coordinated tetrahedral geometry where only one water molecule was coordinating with Zn²⁺. Considering the fact that more than 30% of catalytic zinc proteins are 5-coordinated as reported in literature ¹³, this slight discrepancy seems to be reasonable and could be a realistic dynamic behavior that is not captured by the X-ray structure. In addition, a previous QM/MM study of MMP2 based on B3LYP/OPLS-AA/PB also suggested 5-coordinated with 3 HIS residues and 2 waters is the most stable structure although it was also pointed out the energy differences among different coordinations are within the accuracy of DFT methods ⁹⁶.

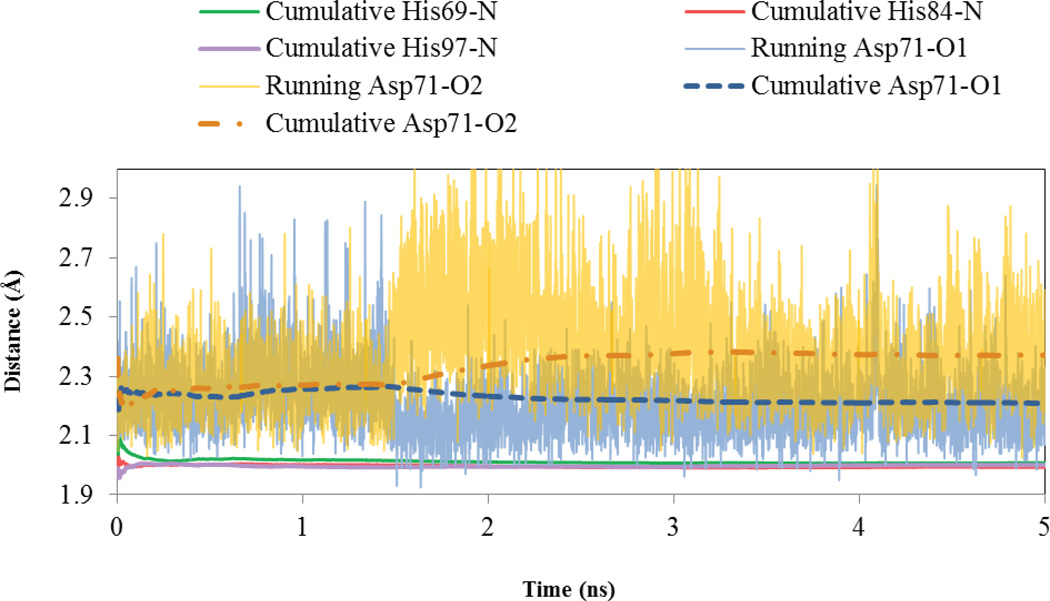
For the second zinc ion, three nitrogen atoms from the His residues plus two bidentate chelation of the Asp oxygen atoms, form a bidentate tetrahedral coordination geometry (Figure 3c) in the crystal structure. Such a bidentate tetrahedral geometry was reproduced by our simulation as shown in Figure 3d, and an alternation of the two oxygen atoms interacting with the zinc ion has been observed. During the 5-ns simulation, the average distance of Zn coordination for the closer oxygen was 2.21±0.11 Å and that for the further one was 2.38±0.17 Å as shown in Figure 4; however, during the last 3.5-ns simulation, the average distance became 2.19±0.09 Å and 2.41±0.18 Å, respectively. According to the analysis of the structural consensus of zinc coordination centers, the average distance of zinc ion and the nearer and further carboxylate oxygens is 1.92±0 Å and 2.76±0.13 Å in structural sites, and 1.99±0.06 Å and 2.58±0.28 Å in catalytic sites respectively ¹³. It is known that the conventional Coulomb scheme in the nonpolarizable force field has deficient in describing bidentate chelation of Asp/Glu residues, and our AMOEBA model shows an encouraging improvement. Nonetheless, as we discussed earlier, the inability of distinguishing the two oxygen atoms in COO⁻ by classical force fields results in an underestimation of binding energy of “external configuration” relative to the “bridge” one. Thus the population of bidentate “bridge” configurations of Zn… COO⁻ was likely overestimated by the simulation. Additional contributions such as the charge transfer and perhaps charge flow are needed in the force fields in order to capture the bidentate vs. external chelation more accurately.

Figure 4.

Interatomic distances between Zn²⁺ and its surrounding ligands during the 5ns MD simulation.

Effect of polarization on Zn²⁺ coordination geometry

We have demonstrated previously the importance of polarization effect in treating zinc hydration ¹⁸. Here we have also shown that with the induced dipole polarization, the AMOEBA model has yielded zinc coordination structures in very good agreement with the corresponding crystal structures. The Zn²⁺ parameters so far perform well in a range of different environments, from the water molecules, model compounds to protein complexes, without being “trained” on zinc enzyme complexes.

The importance of polarization effects is also revealed in this study: reduced atomic polarizabilities of the coordinating His residues would drive the coordination geometry to turn to octahedron in less than one nanosecond. The coordination number of zinc ion varies in different protein environments and with different enzyme functionalities; ion coordination numbers also play an important role in the different theories of selectivity ⁹⁷. Polarizable force field opens more possibility to describe variable zinc coordination reliably and address the different corresponding Zn enzyme functionality. It has been reported that the picture of the ion coordination given by QM/MM simulations differs somewhat from the one provided by classical MD based on nonpolarizable force fields ⁹⁸. The inclusion of polarization effects seems critical ⁹⁹.

To probe the effect of electronic polarization on the coordination geometry, we have performed two 2-ns simulations of MMP-13 complex using a different set of atomic polarizability parameters for atoms on zinc-coordinating histidine rings. The atomic polarizability values were reduced down (by ~20–30%) to those of non-aromatic elements as reported originally reported by Thole, i.e. 1.073 ų for C, 1.334 ų for N, and 0.496 ų for H. Interestingly, after ~1 ns MD simulations, the reduction in polarizability resulted in an octahedral structure for Zn²⁺ binding with (His)₃H₂O and (His)₃Asp (Figure 5), as witnessed in simulations using the fixed-charge force fields. Once the coordination turned to octahedron, it was unable to revert back in our simulations. Thus under-polarization has yielded 6-coordinated Zn-binding sites, rather than 4-coordination typically observed in experimental X-ray structures.

It has been reported that for non-polarizable force field the charge of +2 overestimates the coordination number of the zinc ions, and “+1.5” is the most appropriate for MD simulations ²⁵. However, the stabilizing effect due to charge transfer cannot be captured through the “first order” Coulombic interaction of reduced charges. It should also be noted that appropriate vdW parameters for Zn²⁺ is also important for obtaining the correct coordination of Zn-Cys₂His₂ binding site, as evidenced from earlier work by Sakharov and Lim ⁴³. In this work, we tried to separate the contribution by examining different physical properties. For example, the atomic polarizability was obtained by matching the ab initio molecular polarizability while the vdW parameters were refined using model compound dimer structures and energetics.

Binding affinity calculation for pyrimidine dicarboxamide inhibitors binding with MMP13

With the reasonable success in modeling Zn binding with model compounds and proteins, we have further evaluated the free energy of inhibitors binding to Zn-containing MMP13. Although we are interested in inhibitors that directly chelate to the catalytic zinc ion with zinc binding groups (ZBGs), here we have chosen to study the one of the earliest reported sets of non-zinc chelating inhibitors of MMP families. These four highly selective pyrimidine dicarboxamide inhibitors of MMP13 have binding free energy ranging from −7 to −11 kcal/mol, making an ideal system for evaluating our zinc model in free energy calculations (Figure 6). Generally, the non-zinc chelating inhibitors can overcome the nonselective toxicity. The zinc ion does not “directly” interact with these inhibitors but the shortest distances between the Zn ion and the inhibitor heavy atoms is only 4.7 Å. To compute the relative binding free energy among the four ligands, ligand 2 through 3 were alchemically transformed from ligand 4, and ligand 2 was transformed into ligand 1. The experimental binding free energies are based on inhibition constants determined by isothermal titration calorimetry under various assay conditions ¹⁰⁰.

The calculated relative binding free energies are in agreement with experimental measurements (Table 5) with a RMSD of 0.72 kcal/mol. The calculated relative binding free energies have been offset by experimental binding free energy of MMP13-ligand 4, and plotted in Figure 7. A correlation coefficient (R) of 0.95 between the calculated and experimental binding free energy was obtained ¹⁰⁰. Using Bar and Bar reweighting procedures gave us similar merits.

Figure 7.

Comparison of calculated and experimental relative binding free energies (kcal/mol). Ligand 4, 3, 2, and 1 can be identified from x-axis in order from left to right respectively, with the corresponding experimental binding free energies −11.05, −9.75, −8.73 and −7.07 kcal/mol.

Despite the limited data points, we observe a noticeable correlation between binding free energy and polarizability, i.e. the stronger the molecular polarizability the more favorable the binding affinity is. For ligand 1, 2, 3 and 4, the molecular polarizability values are 28.4, 29.5, 32.3, 32.4 ų, respectively, and the experimental binding affinities are −7.07, −8.73, −9.75, −11.05 kcal/mol. We have previously reported a similar trend for the trypsin-benzamidine ligands¹⁰¹.

To probe the role of the zinc electrostatics on the binding, we performed a virtual experiment where the zinc ion charge was switched off from +2 to 0. The relative binding free energies among the four inhibitors were re-evaluated by using the same MD trajectories obtained from Zn²⁺ simulations. Removing the Zn²⁺ 2+ charge led to a significant and consistent overestimation of relative binding free energy differences (Figure 7). The RMSD between experimental and calculated relative binding affinity became ~2.2 kcal/mol. It suggests that the effect of zinc charge does not “cancel” between the different inhibitors binding to MMP13. Instead, the present of Zn²⁺ seems to minimize the affinity gaps among the tested inhibitors.

We also performed an additional test where the polarization due to the zinc ion is turned off in the system but the 2+ charge on zinc was kept. The relative binding free energies were again re-evaluated using the same MD trajectories (Table 5). Compared to the “BAR” scheme with full parameters, setting Zn charge to be 0 generated less favorable relative binding free energies and turning off Zn polarization seemed to generate more favorable relative binding free energies, which is consistent with our previous study of trypsin-benzamidine binding ⁶⁶. More interestingly, neglecting the polarization effect of zinc ion led to a deviated ranking order. This suggests that the polarization effect due to the zinc ion is not systematic but inhibitor-dependent. This would make it difficult for non-polarizable force fields to capture the polarization effect implicitly, e.g. by scaling the ligand charges. The decisive role of polarization to enable for a correct ranking of competing inhibitors to a given protein targets has also been demonstrated recently, such as in the complexes of pyrrolopyrimidine inhibitors to the FAK kinase ¹⁰², and mannose phosphate/malonate surrogates to the phosphomannoisomerase Zn-metalloenzyme ¹⁰³.

Conclusion

Metal ions play indispensible roles in protein structure and function as nearly one third of all proteins contain metal ions. Understanding the Zn-protein binding, in particular the factors governing specificity and coordination geometry, is crucial for the development of novel ligands for existing Zn binding sites as well as the de novo design of new Zn-binding proteins.

Polarizable force fields hold the promise for treating metal ions in proteins in an effective way, by explicitly taking into account the polarization and potentially the charge-transfer effects. In AMOEBA polarizable potential, the polarization effect is treated via atomic dipole induction. In a previous study, we have shown that charge transfer effect in Zn²⁺ binding clusters diminishes moving from gas-phase toward the condensed-phase and to some extent can be incorporated into the dipole polarization ¹⁸. In this study we have examined Zn²⁺ interacting with common ligands in protein environment. We have refined the atomic polarizability and vdW parameters of few atom types in the His, charged Cys and Asp residue side chains by assessing their interactions with Zn²⁺ and water molecule, respectively. Extensive MD simulations of two zinc-containing enzyme systems with different coordinating ligands, including a bidentate tetrahedral binding site, has yielded reasonable zinc coordination geometry and binding distances in comparison with the X-ray crystal structures. More interestingly, we found the coordination geometry is very sensitive to the polarizabilities of the coordinating ligands. Under-polarization leads to 6-coordination instead of 4-coordination that is typically observed experimentally.

The relative binding free energies of four MMP13 inhibitors have been calculated to be in good agreement with experimental measurements. While there is a moderate separation distance between the zinc ion and the inhibitors, the 2+ net charge on zinc has a strong influence on the inhibitor relative binding affinities. The polarizing field from the zinc ion also contributes to the binding energetics but in an inhibitor–dependent way, as expected from the many-body nature of the polarization effect. The AMOEBA polarizable force field has demonstrated its capacity for accurate description of Zn-proteins interactions. The results obtained in this study encourage broader investigation of ligand binding to metalloproteins using polarizable force fields, including those directly involving metal ion at the binding site. Meanwhile, effort to include the short-range charge transfer and penetration functionalities into AMOEBA polarizable multipole model is ongoing, which is expected to further improve our ability to model complex ions-protein interactions.