Bayesian Face Recognition and Perceptual Narrowing in Face-Space

Abstract

During the first year of life, infants’ face recognition abilities are subject to “perceptual narrowing,” the end result of which is that observers lose the ability to distinguish previously discriminable faces (e.g. other-race faces) from one another. Perceptual narrowing has been reported for faces of different species and different races, in developing humans and primates. Though the phenomenon is highly robust and replicable, there have been few efforts to model the emergence of perceptual narrowing as a function of the accumulation of experience with faces during infancy. The goal of the current study is to examine how perceptual narrowing might manifest as statistical estimation in “face space,” a geometric framework for describing face recognition that has been successfully applied to adult face perception. Here, I use a computer vision algorithm for Bayesian face recognition to study how the acquisition of experience in face space and the presence of race categories affect performance for own and other-race faces. Perceptual narrowing follows from the establishment of distinct race categories, suggesting that the acquisition of category boundaries for race is a key computational mechanism in developing face expertise.

1. Introduction

Faces belonging to ethnic or racial groups that a particular observer has little experience with are generally recognized poorly. Other-race faces are remembered less accurately than own-race faces (Malpass & Kravitz, 1969) and are also subject to higher rates of matching error in explicitly perceptual tasks (Sporer, 2001). Many strongly face-specific behavioral effects are less evident during the processing of other-race faces as well, including the composite face effect (Michel, Caldara, & Rossion, 2006; Michel et al., 2006), the inversion effect (Balas & Nelson, 2010), and the part-whole effect (Tanaka, Kiefer, & Bukach, 2004).

The development of the other-race effect follows a trajectory consistent with what has been called “perceptual narrowing.” (Nelson, 2001; Scott et al., 2007; Slater et al., 2010) The key feature of perceptual narrowing across domains is the observation of broader discrimination abilities at an early age, followed by more limited discrimination abilities at older ages. In the context of the other-race effect this means that infants at a young age can successfully perform face discrimination tasks with faces belonging to many different racial groups, while older infants are typically only able to successfully discriminate between faces that belong to the racial group they have the most exposure to (Kelly et al. 2005, 2007, 2009). Perceptual narrowing of face recognition depends critically on experience, as demonstrated in an elegant primate study by Sugita (2008), in which monkeys reared without exposure to faces of any kind exhibited experience-dependent perceptual narrowing for human or monkey faces as a function of post-deprivation exposure. Similar (though necessarily less comprehensive) results have been obtained with children who experienced a significant shift in their face diet during infancy or childhood due to adoption (Bar-Haim, et al., 2006), suggesting that perceptual narrowing for other-species faces (Pascalis, De Haan, & Nelson, 2002; Pascalis et al., 2005) and other-race faces are both a function of the visual environment.

By what computational mechanisms does visual experience drive perceptual narrowing in face recognition? To date, most theoretical and computational models have been designed to account for the nature of the other-race effect in adulthood. Valentine’s “face space” framework, for example, was introduced as a conceptual model that could account for many of the basic features of mature face recognition, including (but not limited to) the other-race effect (Valentine, 1991). Briefly, face space is a geometric model of face processing in which individual faces are plotted in a multi-dimensional space spanned by perceptual and psychological axes (e.g. masculinity, mouth shape, or eye spacing) and the similarity between faces can subsequently be determined by calculating distances in this space. Within the geometric framework of Valentine’s face space, other-race faces are poorly recognized and remembered because the perceptual and psychological axes of face space are optimized to maximize variance among the majority population of faces, relegating other-race faces to a densely-packed clump of individual points that are less distinct from one another and all differ from the typical face in essentially the same way (Valentine & Endo, 1992). This basic insight is valuable, but begs the important question of what the axes of face space are and how they might be determined from the input data available to observers, both of which are key issues in understanding how perceptual narrowing might manifest during development.

Several studies that have developed and compared computational models of the adult other-race effect addressed these issues by implementing face space using Principal Components Analysis (PCA; Jolliffe, 1986) to determine the axes that best represent the variability of the image pixels across a population of human faces (Turk & Pentland, 1991). The most comprehensive analysis of PCA-based models of the other-race effect is Furl, Phillips, and O’Toole’s (2002) assessment of 13 different face recognition algorithms and their ability to reproduce the other-race effect in an old/new recognition task. The algorithms considered in this analysis included: (1) a range of different metrics for calculating distances in face-space, (2) different representational strategies for encoding face structure including raw pixels, the outputs of Gabor filters, and PCA coefficients, and (3) the use of “discriminative” techniques including Fisher’s Linear Discriminant Analysis and the use of difference images rather than raw images of faces. The most important factor that determined whether or not an algorithm successfully exhibited the other-race effect in their analysis was whether or not discriminations between faces were explicitly built into the model. That is, models that were not explicitly trained to individuate faces did not exhibit an other-race effect. Other PCA-based analyses of the other-race effect have primarily observed that other-race faces are outliers in face space relative to the majority category (Haque & Cottrell, 2002) and that consistent with Valentine’s proposal, other-race faces also tend to be more densely clumped in face space than own-race faces (Caldara & Abdi, 2006). These latter results demonstrate that the distributional properties of own-and other-race faces in PCA-based face space are consistent with Valentine’s theoretical insights regarding the other-race effect, while Furl et al.’s thorough analysis verifies that the other-race effect manifests in a specific task subject to important constraints on the encoding of face structure.

Given that the aforementioned models have offered important insights into how the other-race effect works in the mature visual system, the present study examines whether or not perceptual narrowing can be similarly understood as a by-product of accumulating experience within a Bayesian model of face recognition in face space. Specifically, I use a Bayesian algorithm for face recognition developed by Moghaddam (2002) to examine the development of the other-race effect. This model is a successful computer vision tool for face recognition and is known to exhibit the other-race effect (Furl, Phillips, & O’Toole, 2002). A key feature of this model is the use of difference images as a tool for encoding face structure: Specifically, rather than learn categories defined by raw face images, the model learns to distinguish appearance differences that arise from two images of the same person (intra-personal variation) and differences that arise from two images of different people (extra-personal variation). This strategy simplifies the recognition problem (as discussed in subsequent sections) and also is easily relatable to the behavioral tasks used to assess infant performance in face discrimination tasks. The direct analysis of the differences between faces was demonstrated to be critically important to modeling the other-race effect by Furl (2002), making Moghaddam’s model a particularly useful starting point. However, the model is not presented here as a perfect solution to face recognition nor as the sole means by which the other-race effect can be examined computationally. Instead, the model functions in the current study as a useful means of examining how quantifiable factors influence the nature of face perception in infancy. Similar models have been used to account for effects of perceptual experience on speech perception (Feldman & Griffiths, 2007) and perceptual organization (Aslin, 2011), suggesting that the approach taken here is potentially representative of a broader learning principle.

Choosing particular aspects of development and face experience to model is of paramount importance to this enterprise. How can the current model be used to characterize the differences between 6-month-old and 9-month-old face-space so that we may see if perceptual narrowing emerges naturally? I identified two aspects of infant face experience that are intuitive, supported by published data, and easily modeled within a face-space framework:

1. Older infants have seen more people than younger infants – The sheer number of unique exemplars may make relative differences in performance more evident (Humphreys & Johnson, 2007).

2. Older infants may have category-specific norms – Children and adults appear to maintain distinct norms according to gender and race (Short, Hatry, & Mondloch, 2011; Jaquet, Rhodes, & Hayward, 2007; Little et al., 2008). The emergence of these categories during infancy (see Anzures et al. (2010) for data supporting the formation of race-specific categories by 9 months) and their impact on the organization of face-space may be a critical precursor to perceptual narrowing.

There are many other aspects of visual experience and visual function that are changing during the 6 to 9-month age range, including visual acuity (Dobson & Teller, 1978), and contrast sensitivity (Peterzell, Werner, & Kaplan, 1995). Presently, I have confined myself to the aforementioned aspects of experience because they are easily incorporated into the model employed here and speak to existing theoretical proposals regarding the role of the number of points in face space (Humphreys & Johnson, 2007; Hayden et al., 2007) and the role of categories in visual recognition (Anzures et al., 2010). The current study thus does not preclude explanations based upon low-level visual development or other aspects of experience, but offers insight into whether or not the number of faces a child has seen and the presence of face categories are sufficient to induce perceptual narrowing as characterized empirically.

Both the increase in the number of exemplars expected with development and the acquisition of perceptual categories according to race are modeled in the current study by constraining the data used to train the model. Specifically, changing the character of the training data affects subsequent performance in two ways: First, with the model can be provided with an increasing number of training individuals to reflect the fact that continuing perceptual development entails the accrual of more experience with more individuals. Second, the training data can either include or exclude difference images that cross racial category boundaries (e.g. a difference image obtained by subtracting an Asian face from a White face). I suggest that this is a meaningful way to incorporate the existence of racial categories into the present model. White and Asian faces appear to be encoded by reference to distinct perceptual norms (Armann et al., 2011) which I suggest should preclude robust comparisons between individuals belonging to different categories. This is not to suggest that this is the sole means by which perceptual categories could be incorporated into a computational model of the other-race effect, only that this is one useful way to incorporate this aspect of high-level perceptual development.

Besides selecting relevant developmental variables to model, it is also important to carefully model the task used to measure the other-race effect in infancy. Perceptual narrowing in the domain of face recognition has thus far typically been observed by comparing the behavior of 6-month old infants to that of 9-month old infants in visual paired-comparison (VPC) tasks (Fantz, 1964). Infants in a typical VPC study of face recognition begin each trial by viewing a single face until they accumulate some amount of time (e.g., 20 seconds) looking at it. Next, this face is removed and the infant is presented with two faces, one of which matches the first stimulus, the other of which is typically a new individual belonging to the same category (e.g. race, species, gender) as the original stimulus. The relevant variable is the observed bias in looking time to the novel image – the presence of such a bias in the aggregate data suggests that infants could discriminate between the individuals presented at test, while its absence suggests they could not. In terms of the model under consideration here, a VPC task can be translated as follows: Can extra-personal variation (the difference between the novel face and the original image) be distinguished from intra-personal variation (the difference between the original image and the distractor)? Formulated as such, VPC performance for own-and other-race faces is relatively easy to assess using Moghaddam’s model, subject to a range of developmental variables.

I continue by describing the Moghaddam model in more detail, with an emphasis on how it was used in the current analysis as a model of VPC performance. Following this specification of the model, I report how the model performs as a function of own-vs. other-race stimuli, the number of faces used to train the model, and the category structure imposed on the data. I find that perceptual narrowing is evident in the model subject to the developmental factors considered here, and conclude by discussing the implications of the model’s behavior in relation to previous literature and directions for future research into the mechanisms of perceptual narrowing.

2. A Bayesian Model of the Visual Paired Comparison task

Moghaddam’s model of Bayesian face recognition is comprised of 4 basic steps: (1) Construct difference images of faces to model intra-and extra-personal variation separately. (2) Use Principal Components Analysis to determine low-dimensional spaces into which the training and test data can be embedded. (3) Estimate the probability density of intra-and extra-personal differences using the training data in each face-space. (4) Project the test data into both the intra-and extra-personal spaces and estimate the probability that the new data represents intra-or extra-personal variation using the estimated densities. This step makes use of the PCA components determined from the training data – there is no new estimation of principal components from the test data.

2.1 Constructing difference images

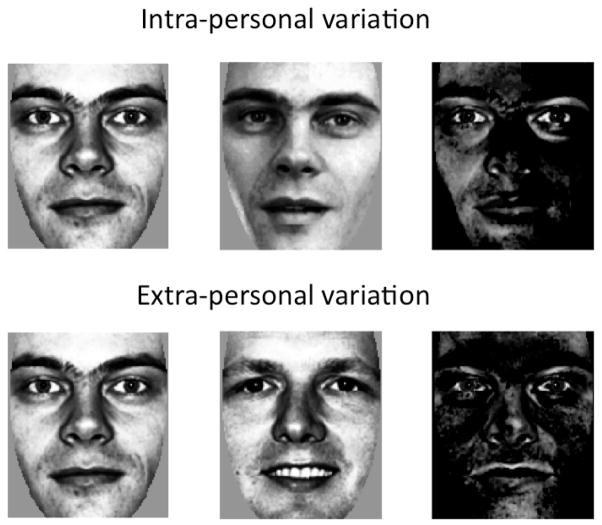
As already stated above, a unique feature of this model is the use of difference images rather than raw facial appearance to build two distinct face-spaces. Specifically, the training images are used to construct one space that captures intra-personal variation and another that captures extra-personal variation. Intra-personal variation refers to image-level differences between two images of the same person, while extra-personal variation refers to differences that exist between two different people. Both of these types of difference images are made by subtracting the corresponding pixel intensities of two images, point by point (Figure 1). For computer vision applications, the advantage of this dual estimation procedure is the reduction of the standard multi-category recognition problem (categorizing according to identity) to a simpler 2-category problem (categorizing as intra-or extra-personal variation). For the current study, this approach is well-suited to the nature of the VPC task infants perform in typical perceptual narrowing studies; infants do not report identity in looking-time tasks, but instead indicate by their behavior whether they detect extra-personal variation (a novel face).

Figure 1.

Examples of intra-personal and extra-personal difference images. In the top row, two different images of the same person are subtracted, yielding the difference image at the far right that captures intra-personal variation. In the bottom row, two images of two different individuals are subtracted, yielding an extra-personal difference image. In the model, these two classes of difference image are used to create separate face-spaces so that new difference images can be analyzed probabilistically.

2.2 Deriving intra-and extra-personal face spaces

Once intra-personal and extra-personal training data are obtained, the next step in the model is to derive a separate face space for each set of difference images. This is done by using PCA to determine a rigid rotation of the original pixel-based axes such that maximal variance in the training data is captured by each successive axis. The purpose of this step is to make it easier to estimate probability distributions for intra-and inter-personal variation. In general, face recognition models suffer from a paucity of training images (typically several hundred images) relative to the dimensionality of the data (typically thousands or tens of thousands), making it difficult or intractable to estimate the distribution of a small amount of data in a very high-dimensional space. PCA provides a principled means of reducing the dimensionality of the data so that the distribution can be estimated robustly.

In these simulations, PCA was used to determine separate 3-dimensional face spaces for intra-and extra-personal variation respectively, typically accounting for 40–50% of the variance in each category. The number 3 is not a “magic number” – we obtain consistent results for a number of PCs ranging between 2 and 5. For computer vision applications, much higher dimensionality is often used (~100 principal components), but a relatively low-dimensionality seemed prudent for the present study for several reasons. First, compared to typical computer vision applications, the present simulations made use of far fewer difference images. Second, previous models of the other-race effect have often employed very low-dimensional subspaces (Caldara & Abdi, 2006; O’Toole et al., 1991). Finally, projecting our data into a low-dimensional space facilitates the estimation of probability distributions to model the training data. Unlike some previous PCA-based models of face recognition (O’Toole et al., 1998) we do not examine principal components individually to determine which ones are most useful for discrimination, since the separate construction of intra-an extra-personal face spaces makes this goal explicit. Further, the original formulation of Moghaddam’s model (which proved very successful for face recognition) uses PCA in the same manner, leading us to use their formulation for our simulations.

2.3 Bayesian classification of the test data

Once we obtain low-dimensional face spaces that describe intra-and extra-personal variation, the training data from each class can be projected into the appropriate face space and used to estimate a probability distribution. These probability distributions can then be used to make a Bayesian decision about whether new data is more likely to be an instance of intra-or extra-personal variation. Specifically, given a candidate difference image Δ, we would like to know the probability that this image is an instance of extra-personal variation, denoted p(Ω_E|Δ). We cannot directly estimate this, however, so we use Bayes’ Law to compute the posterior probability we are interested in using probabilities that we can estimate by projecting Δ into each face space.

Specifically, we may express the posterior probability as follows:

$$p({\mathrm{\Omega }}_E\mid \mathrm{\Delta })=\frac{p({\mathrm{\Omega }}_E)p(\mathrm{\Delta }\mid {\mathrm{\Omega }}_E)}{p({\mathrm{\Omega }}_E)p(\mathrm{\Delta }\mid {\mathrm{\Omega }}_E)+p({\mathrm{\Omega }}_I)p(\mathrm{\Delta }\mid {\mathrm{\Omega }}_I)}$$

Where p(Ω_E) and p(Ω_I) represent the prior probability of extra-and intra-personal variation respectively, and p(Δ|Ω_E) and p(Δ|Ω_I) represent the likelihoods of the difference image Δ given the estimated distributions of extra-and intra-personal variation within their respective face spaces.

In the current study, we use a uniform prior, indicating no a priori bias for either extra-or intra-personal variation. This allows us to simplify the above expression for p(Ω_E|Δ) as follows:

$$p({\mathrm{\Omega }}_E\mid \mathrm{\Delta })=\frac{p(\mathrm{\Delta }\mid {\mathrm{\Omega }}_E)}{p(\mathrm{\Delta }\mid {\mathrm{\Omega }}_E)+p(\mathrm{\Delta }\mid {\mathrm{\Omega }}_I)}$$

Where the likelihood terms are calculated by using the training data to estimate the parameters (mean and covariance) of a normal distribution in each face space, such that p(Δ|Ω_I) and p(Δ|Ω_E) can be estimated as follows:

$$p(\mathrm{\Delta }\mid \mathrm{\Omega })=\frac{1}{{(2\pi )}^{k/2}{\mid {\mathrm{\sum }}_{\mathrm{\Omega }}\mid }^{1/2}}exp(-\frac{1}{2}{(\mathrm{\Delta }-{\mu }_{\mathrm{\Omega }})}^{\prime }{\mathrm{\sum }}^{-1}(\mathrm{\Delta }-{\mu }_{\mathrm{\Omega }}))$$

Where k is equal to the dimensionality of the data, and μ_Ω and Σ_Ω are the mean and covariance of the category Ω under consideration. The normal distribution is used to model the likelihood of difference vectors in the intra-and extra-personal face spaces for two reasons. First, its parameters are easily estimated from even relatively small amounts of data, making it a computationally convenient choice. Second, the original formulation of Moghaddam’s model used the same parametrization and was quite successful at face recognition. It is possible that the normal distribution is not the most accurate characterization of the true distribution of face differences, but for our purposes it is both tractable to compute and known to be effective in another domain.

With these likelihoods established, we now have all the pieces necessary to compute the probability that we want, namely p(Ω_E|Δ). For a given difference image Δ, we may now estimate this posterior probability and use it to determine a category label. For a typical computer vision application, if p(Ω_E|Δ) > 0.5, we would infer that Δ represents extra-personal variation. In the context of modeling VPC performance, I suggest that it is more relevant to compare the values of p(Ω_E|Δ) for the two difference images that can be constructed from the input. I discuss this in more detail in the following section.

The Moghaddam model as described above is the foundation for the following analysis of how developmentally-relevant variables affect VPC performance for own-and other-race faces. Given a fixed proportion of other-race faces in the set of individuals used to generate training data, I varied both the number of unique individuals included in the training set and whether or not cross-race difference images were included as training data for modeling extra-personal variation. The former manipulation makes it possible to examine the impact of simple exposure to more faces on the other-race effect, and by extension, perceptual narrowing. The latter manipulation implements the role of category formation in development, insofar as the development of distinct race categories may limit infants to modeling extra-personal variation solely within categories. In each case, I ask whether or not varying these parameters elicits model behavior consistent with perceptual narrowing.

3. Simulating Perceptual Narrowing for Own-and Other-race faces

In these simulations, I examined how the number of individuals used to generate training data (N) and the inclusion/exclusion of cross-race extra-personal difference images at training affected the ability to detect extra-personal variation in own-and other-race faces.

3.1 Stimuli

The simulations were conducted using the FERET database (Phillips et al., 1998), which has been extensively used for benchmarking computer vision algorithms for face recognition. Caucasian and Asian faces were selected for use in the current study if more than one image per individual was available that did not include facial hair, eye-glasses, or piercings. Ultimately, a total of 678 individuals (608 Caucasian, 70 Asian) were deemed suitable for further use. All images were 150×130 pixels in size and were normalized to have zero mean and unit variance. Finally, all images were cropped into a standard oval shape and aligned with one another using the position of the eyes. The oval shape used to crop faces does not fully exclude a small fraction of background pixels for some individuals, but we do not expect that this impacts our simulations. These cropped images have been used in many benchmark analyses of computer vision algorithms for face recognition where high levels of accuracy have been achieved, suggesting that these minor imperfections are not a major concern. Details of the cropping and normalization procedures can be found in the User Guide for the CSU Face Identification Evaluation System (Bolme et al., 2003). Examples of Caucasian and Asian images can be found in Figure 2.

Figure 2.

Examples of Caucasian and Asian faces used in the current study. All faces have been cropped to the same oval template and are aligned according to the position of the eyes.

3.2 Training data

The training data for each simulation was generated from N=16, 32, or 64 distinct individuals. The proportion of other-race (Asian) individuals included in the set of training individuals was fixed at 10%, in accordance with the rates of exposure to other-race faces reported by the caregivers or infants in the 6–10 month age range (Rennels, 2008). Fractional proportions of faces (e.g. 10% of 16 is 1.6 Asian faces) were rounded up to the nearest integer. Asian faces were always included as the minority category due to the small number of usable images available in the FERET database (When N=64, we are unable to select both the requisite number of training images and an independent test set of 25 faces, as described in the following section), a factor that has limited previous modeling studies as well. Intra-personal difference images were created by selecting a random pair of images for each individual in the training set and subtracting them from each other (e.g. A–B and B–A are both stored for two images A and B), yielding 2N intra-personal difference images for a training database of N individuals. Own-race extra-personal difference images were created by randomly selecting N pairs of individuals from the set of own-race faces, selecting a random picture of each individual, and subtracting these images from each other, generating 2N own-race extra-personal difference images. Other-race extra-personal training data was generated similarly, with the caveat that for small values of N, there were not sufficient extra-personal pairings of individuals to create 2N difference images. In these cases, all possible difference images were created and stored as training data. When cross-race extra-personal variation was permitted, these difference images were created by randomly selecting N pairs of individuals (one from each race), selecting a random image of each person, and subtracting these images from one another. When cross-race extra-personal differences were not included, the training set was augmented with additional extra-personal difference images drawn solely from within-race comparisons to match the number of training exemplars across conditions.

3.3 Testing the model

Test trials were conducted by simulating individual visual-paired comparisons trials using an independent test set of own-and other-race faces comprised of 25 individuals per race. In a typical VPC task, infants are familiarized with a single image of one individual (A1), and then presented with two images: one depicting the familiarized individual (A2) and one depicting someone novel (B1). In the context of the current model, this scenario presents the observer with two difference images per trial: One representing intra-personal variation (A1–A2) and one representing extra-personal variation (A1–B1). The observer’s task is to determine which one is which using their estimates of each source of image variability (Figure 3). Own-and other-race test trials were therefore conducted by generating a single intra-personal difference image (A1–A2, as above) and a single extra-personal difference image (A1–B1, as above) and evaluating p(Ω_E|Δ) for each of these test vectors. A trial was scored as “correct” if the posterior probability for the extra-personal difference image was larger than that of the intra-personal difference image. For each set of simulation values (Race=White/Asian, N=16, 32, or 64, Cross-race differences = included/excluded) I carried out 250 iterations of the model, each of which included 50 unique VPC trials. The result of each iteration was summarized via the percent correct obtained over all simulated VPC trials.

Figure 3.

A schematic view of how a single VPC trial would be carried out using the current model. The two test faces can each be compared to the original sample, leading to two difference images labeled here as Δ_intra and Δ_extra. Both of these can be analyzed using the intra-and extra-personal subspaces to determine the probability that each one represents extra-personal variation. Ideally, the true extra-personal difference image will have a larger posterior probability than the intra-personal difference.

3.4 Results

The model’s behavior was characterized in each condition by estimating 99% confidence intervals that were bootstrapped from the raw data. In Figure 4, mean performance with accompanying error bars is plotted for each condition.

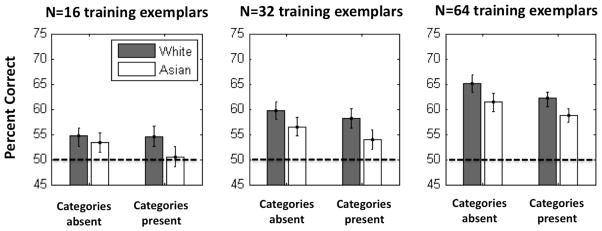
Figure 4.

Mean percent correct performance on simulated VPC trials for own-and other-race stimuli as a function of N and the presence or absence of racial categories. When categories are “absent,” cross-race difference images are included during training – when they are “present,” those differences are not included. Error bars represent 99% confidence intervals of the mean. The dashed line in each plot indicates chance performance of 50%.

There are several interesting features of the data. First, there is a clear improvement in performance as a function of the number of exemplars. Second, the other-race effect obtains consistently when racial categories are present (and cross-race difference images are excluded from training), and is less evident when racial categories are absent at training. Critically, when the number of training exemplars is low (N=16) we observe that the model exhibits behavior consistent with perceptual narrowing subject to the category structure of the training data. The absence of cross-category difference images in the training data leads to above-chance performance for own-and other-race faces that is not statistically different. That is, own-and other-race performance is approximately equal, though there is a non-significant trend favoring own-race recognition. By contrast, performance with other-race faces drops to chance levels when cross-category difference vectors are included during training, but own-race performance remains above chance.. This pattern of performance is in strong accordance with the results of perceptual narrowing in other-race and other-species face recognition tasks – In one state, the model is above-chance with both races and neither race is recognized significantly more accurately than the other, but in another the minority category can only be recognized at chance levels. This suggests that establishing category boundaries in face space may be an important precursor to perceptual narrowing. Specifically, the inclusion of cross-category data (White-Asian difference images) appears to be a critical factor governing performance in early stages of face learning, having less influence later.

To what extent are these results dependent on the 10% proportion of other-race exemplars included in the training data? The simulations were repeated with the more “extreme” case of 0% other-race faces to see if our model would still reproduce the effects observed at 10% when cross-race comparisons were not permitted (analogous simulations with cross-race comparisons included could not be run, since the exclusion of other-race faces also excludes their comparison with own-race faces). The results exhibit good numerical agreement with the data displayed in Figure 4: When N=16, confidence intervals for White/Asian accuracy were [55%–58%] and [50%–54%] respectively. For N=32, we obtained White/Asian intervals of [58–62%] and [55–59%], and for N=64, we obtained White/Asian intervals of [61–64%] and [58–61%]. These data validate the results obtained at an ecologically relevant proportion of 10% in a less-realistic, but more extreme setting where there is no other-race exposure at all. These results cannot speak to the function of cross-category comparisons however, which is a critically important feature of the model.

5. Discussion

The model demonstrates sensitivity to the developmental variables that were manipulated in the current analyses. Increasing the number of unique individuals available for training improved VPC performance for both races and allowing cross-category comparisons to be included in the training data also generally improved performance. Most importantly, the model displays a performance profile consistent with perceptual narrowing, suggesting that the formation of categories is a key mechanism underlying the emergence and nature of face expertise. This is consistent with recent empirical results demonstrating a similar relationship between categorization and the other-race effect in infancy (Anzures et al., 2010), and also with previous results obtained from adult observers (Levin, 2000) -the current model provides a computational validation of this relationship via an explicitly computational model that uses real face images.

The overall success of this model in reproducing the other-race effect reflects the importance of subordinate-level training in acquiring recognition expertise. Specifically, the model’s reliance on difference images is in good concordance with results from infants and adults suggesting that learning discriminations between individuals is an effective means of modulating other-race and other-species face processing. For example, Scott & Monesson (2010) have recently reported that picture-book training that includes individual labels can help infants maintain above-chance performance with other-species faces and objects (Scott, in press). Mere exposure to the same faces does not accomplish this, in keeping with the modeling results presented by Furl et al. (2002) and consistent with the current data. In adults, similar experiments have indicated that subordinate level training with birds (Tanaka, Curran, & Sheinberg, 2005; Scott et al., 2006) and other-race faces (Tanaka & Pierce, 2009) impacts behavioral and neural responses to new stimuli, while basic level training does not.

The model thus provides several mechanistic insights into how perceptual narrowing takes place. First, our results (and previous attempts to model the other-race effect outside of a developmental context) suggest that ongoing refinement of the observer’s estimation of what intra-and extra-personal variation look like is an important factor in the establishment of the other-race effect. The mechanism here is an increasingly specific estimate of extra-personal variation that does not apply to other-race faces well – typical other-race extra-personal variation is “unlikely” once the model has been trained on own-race variation, and is thus recognized poorly. With regard to perceptual narrowing, the key insight provided by the current results is how the presence or absence of race categories can also alter the underlying the estimate of extra-personal variation in such a way that narrowing emerges naturally. Specifically, when cross-race differences are included in the estimate of extra-personal variation, the underlying distribution is sufficiently “broad” that both own-and other-race differences can be classified at above-chance levels. When those differences are not included, the underlying distribution becomes more specific, and other-race differences between individuals are “unlikely” because the estimate of extra-personal variation has become more specific to one race. The mechanism of perceptual narrowing in this setting is therefore increased specificity in the estimate of extra-personal variation, modulated both by overall experience (number of exemplars) and by perceptual categories restricting the data used to compute this estimate.

The current model also suggests that face processing is far more plastic when few exemplars have been seen, which is also commensurate with existing literature describing the plasticity of other-race and other-species effects in infancy. Sangrigoli and de Schonen (2004) demonstrated the malleability of the other-race effect in 3-month olds, who exhibited improved performance for other-race faces after seeing a fairly small number of training exemplars. Even in early childhood, intensive experience with a new face environment appears to be sufficient to reduce or reverse the other-race effect acquired in infancy (Sangrigoli et al., 2005), though far more training examples are likely necessary. Early experience may facilitate later plasticity of own-and other-category face processing (Cassia et al., 2009) however, again highlighting the impact of experience at early stages of face learning. Overall, these results are in good agreement with the current finding that perceptual narrowing and other-category face processing is most impacted by changes in a relatively sparse face space. The current model also makes it possible to raise an interesting question that remains to be tested rigorously: How does the number of unique individuals and the proportion of other-race faces impact perceptual narrowing? Presently, we lack the data to rigorously quantify the number of unique individuals a child has seen throughout infancy. We thus do not suggest that the numbers, 16, 32, and 64 be taken as representative of what is seen during a typical infancy – similarly, other parameters in the model should not be taken as any kind of final word on what face space looks like developmentally. Nonetheless, the current model suggests that the number of other-race faces (and also potentially the proportion of other-race faces (Rennels, 2008)) does affect the time-course of perceptual narrowing. The use of a computational model such as this one makes it possible to make quantitative predictions about discrimination ability as a function of a specific number of faces and a specific set of face images.

Besides the possibility of quantifying individual experience, there are many other avenues for exploration within the context of the current model. Several parameter values within the model, including the number of PCA basis functions, were chosen to be consistent with previous modeling efforts. Further exploring the consequences of changing these parameters may provide additional insight into the computations supporting the development of the other-race effect. It is not surprising that the model will perform much more accurately as the number of basis functions and the number of exemplars increase (though it is unlikely that “ceiling performance” will be reached, especially when realistic, unconstrained face images are used), but can we learn more about continuing development as we gradually manipulate these parameters? We have already observed in our data that the other-race effect persists as N=32 and N=64, but that other-race face performance gradually increases above chance. We do not know if the rate of this increase is consistent with how the other-race develops over early childhood, or how it might compare to adult performance after extensive training with other-race faces. Second, the current model provides an interesting account of performance on other-race VPC tasks, which suggests that it may be informative to try and apply the same basic computational principles to other types of own-and other-category effects observed in infancy. In particular, infants also exhibit gender preferences that are dictated by experience. For example, novel female faces tend to be discriminated from previously seen exemplars while novel male faces are not reliably discriminated from familiarized male faces (Quinn et al., 2002). Other aspects of visual preference for male and female faces are dependent on the sex of the infant’s primary caregiver, demonstrating that early experience plays a key role in driving behavior in this context. Moreover, gender effects also appear to interact with race (Quinn et al., 2008) such that fine-tuning for face sex is only evident for own-race faces. These features of perceptual narrowing and the development of face expertise are potentially rich test domains for a general computational model of face learning in infancy.

Ideally, it would also be valuable to apply the model to a large set of faces of multiple racial categories so that non-white faces could serve as the majority category. Theoretically, one might expect that the model’s results should be symmetric with regard to which category is assigned to the majority, but there are also intriguing results suggesting that this may be more complex. Asian infants do not exhibit a perfectly symmetric time course of perceptual narrowing relative to White infants, for example (Kelly 2009). Further, White and Asian adults do not exhibit a symmetric effect of race on holistic processing (Michel et al., 2006; Tanaka, Kiefer & Bukach, 2004), which is a common behavioral marker of face expertise (Young, Hellawell, & Hay, 1987). The potential for the current model to reproduce these potential asymmetries is intriguing, but would require a larger set of faces than was available for the current study.

Finally, besides the applicability of the current model to a wider range of VPC and visual preference tasks, it may also be possible to use the model to gain insight into other observed differences between own-and other-group face processing. For example, it has recently been shown that infants’ eye movements to own-and other-race faces differ in systematic ways (Liu et al., 2011; Wheeler et al., 2011) – an effect that may also be accounted for by the developing computations that dictate how discriminative features for face recognition are encoded. Similarly, it would also be intriguing to try and empirically measure infants’ “template” for making face discriminations using classification image techniques (Gosselin & Schyns, 2001) and measure the correspondence between this behavioral template and an ideal observer based on the model. In general, the model provides a potentially useful platform for making predictions about how diverse face experience affects behavior.

Conclusion

The simulations reported here demonstrate that the emergence of the other-race effect in infancy following “perceptual narrowing” can be accounted for within a Bayesian model of face recognition. Further, within this model, the acquisition of distinct race categories is necessary for perceptual narrowing to manifest. Race categories are not sufficient, however – chance performance for other-race faces only occurs when a small number of faces have been used for training. These results provide a computational account of how perceptual narrowing occurs in the context of own-and other-race faces and suggest useful directions for further research into the mechanisms of perceptual narrowing and the development of face recognition in general.