Abstract
Parties in real-world conflicts often attempt to punish each other’s behavior. If this strategy fails to produce mutual cooperation, they may increase punishment magnitude. The present experiment investigated whether delay-reduction – potentially less harmful than magnitude increase – would generate mutual cooperation as interactions are repeated. Participants played a prisoner’s dilemma game against a computer that played a tit-for-tat strategy, cooperating after a participant cooperated, defecting after a participant defected. For half of the participants, the delay between their choice and the computer’s next choice was long relative to the delay between the computer’s choice and their next choice. For the other half, long and short delays were reversed. The tit-for-tat contingency reinforces the other player’s cooperation (by cooperating) and punishes the other player’s defection (by defecting). Both rewards and punishers are discounted by delay. Consistent with delay discounting, participants cooperated more when the delay between their choice and the computer’s cooperation (reward) or defection (punishment) was relatively short. These results suggest that, in real-world tit-for-tat conflicts, decreasing delay of reciprocation or retaliation may foster mutual cooperation as effectively as (or more effectively than) the more usual tactic of increasing magnitude of reciprocation or retaliation.
Keywords: cooperation, prisoner’s dilemma, punishment delay, punishment magnitude, reward delay, reward magnitude, tit-for-tat
Many everyday life conflicts between individuals as well as nations involve a tit-for-tat series of exchanges where one party rewards or punishes the other, the other party reciprocates in kind, the first party reciprocates in turn, and so forth. Exchanges of punishment may result in vicious Punch-and-Judy cycles – each party in turn trying to stamp out the other’s harmful behavior. Fights between individuals, tariff wars, cold wars, and real wars between nations, often result. An example from recent history is the 2008–2009 rocket exchange between Israel and Hamas (Levy, 2010). Punishment exchanges are particularly subject to escalation of intensity; Israel at first did not retaliate to Hamas’s rocket attacks, then retaliated by aerial bombardment and eventually, by invasion.
On the other hand, reward exchanges among individuals and nations are the basis of all economic activity. The main conclusion from the economic study of exchange of positive goods or rewards is that both parties benefit (Newman, 1965). We here call real-life exchanges of reward, “reciprocation” and exchanges of punishment, “retaliation.” Minimizing retaliation and maximizing reciprocation among individuals and groups is obviously a great practical concern.
Cooperation in the Prisoner’s Dilemma
Prisoner’s dilemmas and related games have been much studied by mathematicians, economists, and psychologists (for reviews, see Axelrod, 1980; Camerer, 2003; Ledyard, 1995; Rapoport, 1974; and Sally, 1995). Variables examined include common interest, relationship and communication among players, number of players, marginal payoffs, and probability of cooperation or defection. The repeated prisoner’s dilemma game (RPD game) has served as a laboratory model of both reciprocation (“mutual cooperation” in RPD terminology) and retaliation (“mutual defection”) (Axelrod, 1980). The purpose of the present experiment was to study the effect of delay between choice and outcome on reciprocation and retaliation in an RPD game.
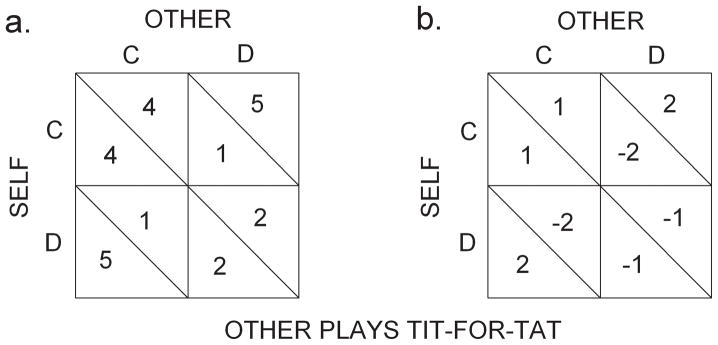
In the prisoner’s dilemma, as it is usually studied (Rapoport, 1974), two players each choose between cooperation (C) and defection (D). Figure 1a shows a typical PD reward matrix. If both cooperate (CC), each gains a moderately high reward (4 points); if both defect (DD), each gains a moderately low reward (2 points). Clearly it is better for both if both cooperate than if both defect. However, if one player cooperates and the other defects (CD or DC), the defector gains the highest reward (5 points) and the cooperator gains the lowest reward (1 point). The reward magnitudes are chosen so that on any given trial, regardless of the other player’s choice, each player gains most by defecting; if O (other) cooperates, a player, S (self), gains the highest reward by defecting; if O defects, S avoids the lowest reward by defecting. In game-theory terms, mutual defection in RPD games is the only point of “Nash equilibrium;” neither player benefits by deviating from that point. Thus, what is better for both players (“Pareto efficient”) is worse for each individually. This is the core of the dilemma. The usual result when PD games with the matrix values of Figure 1 are repeated many times (RPD) is that both players come to defect (Roth, 1995) – whereas if they had both cooperated they would have both obtained higher rewards overall.
Figure 1.
The Prisoner’s Dilemma reward matrices used with the (a) All-Gains and (b) Mixed-Outcome groups. Cooperating or defecting produced the points indicated in the top row (C) or bottom row (D), respectively. Points below each diagonal were given to the participant (Self) and points above were for the other player.
Cooperation in Social Discounting
Consider again the PD matrix of Figure 1a. S gains 1 point by defecting regardless of O’s choice; symmetrically, S loses 1 point by cooperating. Note however that if S were to cooperate, O would gain 3 points (4 rather than 1 or 5 rather than 2) regardless of what O herself chose. A player, by cooperating, loses 1 point herself but gives the other player 3 points. The question arises: Can another person’s (larger) gain compensate for one’s own (smaller) loss? In behavioral terms: Can another person’s reward (or punishment) act on one’s own behavior?
It has been argued by philosophers (e.g. Parfit, 1984), economists (e.g. Simon, 1995), as well as psychologists (Ainslie, 2001; Rachlin, 2000), that the answer to this question is yes. The effect may be quantified in terms of a social discount function (decrease in value to S of a reward to O with increasing social distance to O). Social discounting (willingness, for example, to pay $1 to give a friend $5 but to pay only 10 cents to give a distant acquaintance $5) parallels delay discounting (willingness, for example, to pay $1 now for a $5 bond payable in 10 years but only 10 cents for a $5 bond payable in 50 years). Experiments in our laboratory (Jones & Rachlin, 2006, 2009; Rachlin & Jones, 2008a, 2008b) have found S’s choice between rewards to S and rewards to O to be well described by a hyperbolic social discount function of the form:
| (1) |
where v is the value to S of reward V given to O, N is the social distance from S to O (defined as the rank order of O among the 100 people closest to S), and k is a constant varying from person to person.
Equation 1 may be used as follows to roughly estimate the value to S of the 3-point reward to O contingent on S’s cooperation in the PD game of Figure 1a: The median undergraduate puts a random fellow undergraduate at a distance equivalent to 75th place on her list of 100 closest people (N 75).FN1 The median of individual k-values (with small hypothetical amounts of money given to O) has been found to be about 0.05 (k 0.05). Suppose points are dollars (V = $3). Substituting in Equation 1 and solving, v $0.63. That is, it would be worth about 63 cents to an undergraduate to give a random other undergraduate $3. Since the cost of cooperation with the PD matrix of Figure 1a is $1, the net value of cooperating would be minus 37 cents ($0.63 minus $1); cooperation would be punished by a net loss. Assuming that the steepness of social discounting by undergraduates does not differ widely from that of the general population, people should defect in an RPD game. This is generally the case. For example, Selten and Stoecker (1986), studying choice in 25 sets of 10 repetitions of a PD game, found that mutual defection increased within each 10-game sequence. As participants gained experience with the contingencies, mutual defection developed faster and faster in each set (a pattern of learning to learn). Roth (1995) cites these results as typical of RPD games. Similarly, Brown and Rachlin (1999) found significant increases in mutual defection over repeated PD trials with matrices similar to that of Figure 1a, and players choosing sequentially (as in the present experiments).FN2
Tit-for-Tat in a Prisoner’s Dilemma
A simple strategy that players often adopt in the RPD is aptly called, “tit-for-tat” (Axelrod, 1980). Suppose O rigidly plays tit-for-tat as follows: if S cooperates on trial n, O will cooperate on trial n+1; if S defects on trial n, O will defect on trial n+1. In empirical studies of RPD games, tit-for-tat often increases mutual cooperation (Rapoport, 1974). Cooperation increases because the tit-for-tat strategy rewards cooperation and punishes defection (Rachlin, Brown, & Baker, 2000). As in the game where S and O both play freely, S’s cooperation costs S 1 point and gives O 3 points. With O rigorously playing tit-for-tat, S’s cooperation still costs 1 point but is rewarded with 3 points when O cooperates in turn. However, these 3 points are discounted by the delay between S’s cooperation and O’s reciprocation on the next trial. With the matrix of Figure 1a, and O playing tit-for-tat, S’s cooperation has 3 consequences:
A cost of 1 point to S.
A gain of 3 points by O (discounted to S by social distance).
A gain of 3 points by S (discounted by the time between S’s cooperation and O’s reciprocation on the following trial).
Since tit-for-tat makes O’s cooperation contingent on S’s cooperation, S is rewarded for cooperating; symmetrically, since tit-for-tat makes O’s defection contingent on S’s defection, S is punished for defecting. Although Consequence #2 may be insufficient to compensate for Consequence #1 (as illustrated quantitatively above), Consequence #3, applied with 100% probability if O plays tit-for-tat, may tip the balance in favor of cooperation.
In general, increases of reward or punishment parameters (magnitude, probability, and immediacy) increase behavioral change (Rachlin, 1976). Over a series of PD trials versus tit-for-tat, the average number of points per trial earned by S increases linearly with S’s own rate of cooperation (O playing tit-for-tat). S’s reward is maximized when S cooperates on 100% of the trials and decreases proportionally as defection rate increases.
Because tit-for-tat rewards cooperation and punishes defection, the effectiveness of Consequence #3 in changing behavior should increase with increases in reward or punishment parameters. In experimental tests of play versus tit-for-tat, Brown and Rachlin (1999) varied the magnitudes of reward and punishment changing the matrix from 1-2-3-4 as in Figure 1a to 1-2-5-6. With the latter matrix, defection was rewarded by 1 point (Consequence #1 remained the same) but cooperation was rewarded by a gain of 4 (rather than 3) points on the following trial (Consequences #2 and #3 increased in magnitude). With the greater rewards, participants learned to cooperate at a higher rate and to a higher asymptote. Similarly, probability of reciprocation and retaliation affect cooperation. When the tit-for-tat strategy was modified to respond probabilistically rather than one-to-one, cooperation decreased as probability decreased (Baker & Rachlin, 2001).
Escalation of Immediacy
Turning to immediacy of reward and punishment, note that the delay of reciprocation or retaliation (Consequence #3) may decrease cooperation in two ways:
Directly by discounting the value of the reward for cooperation (or of the punishment for defection) as a bond of a fixed amount is less valuable with a later maturity date.
Indirectly, by decreasing the saliency of the contingency of the reward or punishment on cooperation or defection, thus retarding learning. Modern learning theory (e.g., Gallistel & Gibbon, 2000) predicts slower learning with decreases in the salience of the contingency between behavior and consequence.
The direct and indirect effects of delay may be distinguished over a long series of trials in terms of effect on slope and asymptote of the learning curve. Such separation requires many trials with detailed individual-subject data. In this experiment, as in most real-life situations, the two effects are intertwined. For example, Komorita, Parks, and colleagues (e.g., Komorita, Hilty, & Parks, 1991; Parks & Rumble, 2001) varied delay of reciprocation separately from delay of retaliation and found less cooperation with longer delays for both. Delay in their experiments was programmed via a lag in number of trials between a participant’s choice and its consequence; a participant’s trial-n cooperation could be reciprocated by the computer on trial n+1 or trial n+2 or n+3, etc. Thus, one or more subsequent participant-choices intervened between each choice and its reciprocation or retaliation. As indicated above, salience may be degraded by increasing delay or increasing the number of intervening events between behavior and outcome. It is not possible to determine from the results of these experiments what part of any failure to cooperate was due to delay itself and what part was due to the number of subsequent choices between a given choice and its consequences (nor were the experiments intended to do so). On the other hand, in the present experiment, as in many real life conflict situations, each choice was followed (with varying delay) by reciprocation or retaliation; there was an intervening outcome but no intervening participant-choices. In Komorita and Parks’s terms, the lag in the present experiment was zero in all cases; thus, change of cooperation can be attributed to delay.
Baker and Rachlin (2002) found that pigeons could learn to consistently cooperate versus tit-for-tat when delays were bridged over with discriminative stimuli that signaled to the pigeons their own prior choice (also see Sanabria, Baker, & Rachlin, 2003). Stephens, McLinn and Stevens (2002, 2006) studied bluejays playing a prisoner’s dilemma game versus tit-for-tat. They found that cooperation levels increased when the (normally immediate) reinforcement of defection was postponed over groups of trials to coincide relatively more closely with the normally delayed but greater reinforcement of cooperation. With humans playing against each other in an RPD, grouping of choices without feedback (effectively delaying the usually immediate reward for defection) significantly increased cooperation (Brown & Rachlin, 1999). In general, when increased delay is reported to enhance cooperation in an RPD, the delay in question is that of the (normally immediate) reinforcement of defection. Bringing this smaller reward into closer temporal correspondence with the greater reward due to reciprocation of cooperation results in a choice between a larger reward for cooperation and an equally delayed smaller reward for defection; naturally the larger reward is chosen.
Delay between S’s cooperation or defection and O’s reciprocation or retaliation – the intertrial interval – is always present in an RPD. The present experiment varied the intertrial interval but did not eliminate it. Thus, individuals with steeper delay discount functions would be expected to learn to cooperate against tit-for-tat more slowly than individuals with shallower delay discount functions. That is, Consequence #3 is predicted to be less influential as delay is more steeply discounted. Indeed, this is found. With human participants playing an RPD versus tit-for-tat, Harris and Madden (2002) and Yi, Johnson, and Bickel (2005) found that participants with steeper delay discount functions (with greater sensitivity to delay) defected more in an RPG versus tit-for-tat than did participants with shallower delay discount functions.
It is often the case in real life that one party to a conflict has more power than the other to manipulate the contingencies. This occurred in the recent conflict between Israel and Hamas. Israel’s escalation of the intensity of its retaliation to Hamas’s rocket attacks was eventually effective in reducing their frequency. However, that effectiveness came at a high cost in terms of civilian casualties and international condemnation (Erlanger, 2010). Another possibility for Israel would have been to increase the certainty and reduce the delay (rather than to increase the intensity) of its response to the rocket attacks.
Overview of the Present Study
The present experiment was designed to examine in the laboratory whether delay reduction by one party rigidly playing tit-for-tat in an RPD exchange would speed up the development of mutual cooperation. We tested this expectation with the contingencies of Figure 1a as well as those of Figure 1b. In the matrix of Figure 1b, 3 points were subtracted from each reward of the matrix of Figure 1a so that defection by both players would result in a loss for both while cooperation by both players would result in a gain for both. With the contingencies of Figure 1a, punishment consisted in a reduction of gain; with those of Figure 1b, punishment consisted in an actual loss of points. Since actual losses are generally more effective in altering behavior than gain reductions (e.g., Gray & Tallman, 1987) we expected that the contingencies of Figure 1b would lead to greater cooperation than would those of Figure 1a.
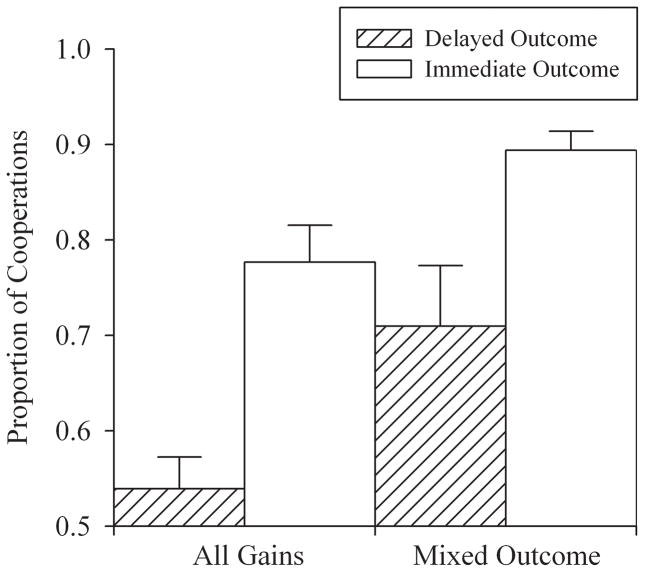
Figure 3.
Total proportion of cooperation responses for each of the four groups. Error bars indicate standard error of the mean. Note the y-axis begins at 0.5.
Method
Participants
Eighty undergraduate students (46 female, 34 male) were recruited through the psychology subject pool at the State University of New York at Stony Brook. Each participant was randomly assigned to one of the four groups (n = 20 in each) described below.
Apparatus & Instructions
Participants were tested in pairs. They were seated in adjacent cubicles separated by a pair of 1.5-meter square opaque partitions approximately 1.2 meters apart. White noise generated by an overhead fan (turned on after instructions were read) limited aural interaction. Each cubicle contained a personal computer with a 17-inch monitor and an optical mouse. The session instructions, read aloud by the experimenter to both participants simultaneously, were as follows (instructions in parentheses were given only in the Mixed-Outcome conditions described later):
You will be using the mouse to repeatedly make choices between the ‘X’ button and the ‘Y’ button at the bottom of your screen. Each time that you or the other player presses one of those buttons, you will (either) gain (or lose) points. The large numbers are the points that you will gain (or lose) and the smaller numbers are the points that the other player will gain (or lose).
At the end of this game, you will win a gift card based on the amount of points you earned. The card on the table shows how many points you need for the different value gift cards.
Please do not talk during the session.
For the Mixed-Outcome groups, an index card on the table indicated that 0 – 49 points were needed for a $5 gift card, 50 – 149 points were needed for a $10 gift card, and 150 or more points were needed for a $15 gift card. For the All-Gains groups, all of the point requirements were 600 points higher (600, 650, and 750 for $5, $10, and $15 cards).
After the instructions were read, the experimenter indicated to each participant whether they were Player A or Player B. Each computer monitor showed a grid similar to one of the top panels of Figure 1. Points for the chooser (self) were in a 72-point font whereas points for the other player were in an 18-point font. The X and Y buttons were located below the grid columns corresponding to “C” and “D” in Figure 1. The buttons were surrounded by a blue box labeled either “Player A” or “Player B” corresponding to the “SELF” label in Figure 1. Similar but inactive X and Y buttons were located on the right side of the screen (corresponding to the “Other” in Figure 1) in a Yellow box with the label “Player B” (if the participant was Player A) or “Player A” (if the participant was Player B) above the inactive buttons. For half of the participants, “X” was the cooperate button (C) and “Y” the defect button (D); for the other half, the reverse was the case. After the experimenter indicated which participant was Player A and which was Player B, he asked if there were any further questions. Questions were answered using only direct excerpts from the instructions. Participants were then instructed to press the “Start” button as the experimenter activated the overhead fan and receded from view. Pressing the “Start” button initiated the procedure described below.
Procedure
Although participants were led to believe that they were playing against each other, they actually played against a computer employing a tit-for-tat strategy. All participants made 100 choices. The participant (S) and computer (O) took turns choosing between C and D. Choices by S highlighted in blue the column above the chosen button (row C or D in Figure 1). Choices by O (always matching S’s previous choice) highlighted in yellow the C or D row. The cell where the blue column met the yellow row was highlighted in green and indicated S’s and O’s point gain or loss on that trial. Responses by the person sitting next to the participant were effectively masked by the noise of the fan.
Participants received (or lost) points immediately after each of their own choices and immediately after each of O’s choices. Each of S’s choices thus influenced the magnitudes of two outcomes – that following S’s own choice, and that following O’s next “choice” (which, again, always matched S’s previous choice). To illustrate, suppose on 5 successive trials with the matrix of Figure 1a, S chose: C–D–D–C–C. (On the first trial of each session, O is assumed to have previously chosen C.) Inserting O’s tit-for-tat choices into this sequence (in lower case): C-c-D-d-D-d-C-c-C-c. The reward amounts for S after these 10 choices (from Figure 1a) are: (C) 4, (Cc) 4, (cD) 5, (Dd) 2, (dD) 2, (Dd) 2, (dC) 1, (Cc) 4, (cC) 4, (Cc) 4. We had two reasons for programming tit-for-tat in this way. One is that, in real-world tit-for-tat exchanges the parties rarely if ever coordinate their actions to coincide. Rather, each party reacts in turn to the other’s action. Moreover, consequences for both parties (costs and benefits) often occur after both their own and the other party’s actions, not just after their own actions and, to the extent possible, we tried to model those contingencies. The second reason, as stated in the introduction, is that with this way of programming tit-for-tat, reciprocation or retaliation follows a choice without intervening participant choices; this allowed us to attribute increased cooperation to reward immediacy.
The principal variable of the experiment was the inter-trial interval. For half of the participants (Delayed-Outcome groups), the interval between their current choice and O’s next choice was longer than that between O’s prior choice and their current choice (----O-S----O-S----O-S----); for the other half (Immediate-Outcome groups), the reverse was the case (----S-O----SO----S-O----). The short delay was 1 second; the long delay was 6 seconds plus S’s most recent latency to respond (the time from choice availability to choice selection – typically less than 1 s after the first several trials). During the longer delay (S----O for the Delayed-Outcome group; O----S for the Immediate-Outcome group), the participants watched a silent video: the default visualization for Windows Media Player 10. The video began 1 second after S’s choice (for the Delayed-Outcome group) or O’s choice (Immediate-Outcome group). The purpose of the video was to eliminate discriminative stimuli during the delay period. Delay of reward or punishment does not retard learning if a discriminative stimulus is present during the delay period. This has been known in animal learning since Watson’s (1917) early experiments in which rats learned to traverse mazes just as fast when food rewards were buried under sawdust in the goal box as when the rewards were immediately accessible. Baker and Rachlin (2002) found that pigeons learned to cooperate in a PD game versus tit-for-tat only when their prior-trial choice (which determined their current-trial reward for cooperating) was signaled during the intertrial interval.
The second experimental variable was the reward and punishment matrix. Half of the participants were tested with the matrix of Figure 1a, (all gains), and half with that of Figure 1b, with both gains and losses. Each of the four conditions (Immediate-Outcome/Delayed-Outcome; All-Gains/Mixed-Outcome) was tested with a separate group of participants.
At the end of the session, all subjects were fully debriefed. None reported or evidenced any negative feelings about being led to believe that they were playing against each other rather than against themselves (from the preceding trial).
Results
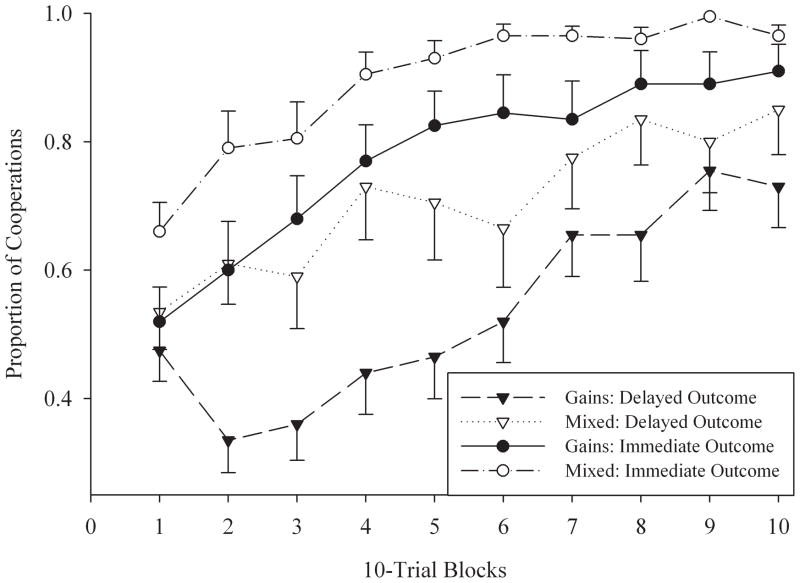
Figure 2 shows the change in proportion of cooperation responses over the course of the session, divided into ten consecutive 10-trial blocks. All four groups cooperated significantly more (and defected less) in the last 10-trial block than in the first (mixed design ANOVA with trial block as the within-subject factor: F (1, 76) = 72.89, p < .0001). Three of the four groups defected about half of the time in the initial block. Although not apparent in Figure 2, the Immediate-Outcome, Mixed-Outcome group also began by defecting about half the time (53% defections over the first 4 trials) but learned to cooperate much more quickly (66% cooperation responses in the first 10 trials; SE = 4.6%). All groups cooperated more than half of the time by the final 10-trial block (mean = 73% – 96.5%, SE = 1.7% – 7%).
Figure 2.
Proportion of cooperation responses for each of the four groups as a function of consecutive 10-trial blocks (over the course of the 100-trial session). Error bars indicate standard error of the mean. Note the y-axis begins at 0.25.
For most groups, the change in cooperation was a steady increase over the course of the session. The primary exception to this was the All-Gains, Delayed-Outcome group which showed a sharp decline in cooperation in the second block of trials before cooperation began to increase in a manner similar to the other groups. An unpaired t-test indicated a significant difference between the decrease in cooperation during the second block for this group (mean = −.14, SE = .054) compared to the increase in cooperation for the other three groups (mean = +.095, SE = .034; t (78) = 3.526, p = .0007).
Figure 3 shows the total proportion of cooperation responses for each of the four groups. Both Immediate-Outcome groups cooperated significantly more (defected less) than did the corresponding Delayed-Outcome groups; both of the Mixed-Outcome groups cooperated significantly more than the corresponding All-Gains groups. A two-way ANOVA indicated a main effect of both delay (F (1, 76) = 25.35, p < .0001) and point matrix (F (1, 76) = 11.81, p = .001). There was no significant interaction (F (1, 76) = .4, p = .53)
Discussion
Learning to cooperate
Tit-for-tat, applied with 100% probability was effective in increasing cooperation. This increase was not always immediate, as indicated by the two different learning patterns in Figure 2; the curve of the All-Gains, Delayed-Outcome group falls before rising while the other three rise directly. The All-Gains, Delayed-Outcome group also cooperated less overall than the other three groups. Since defection was immediately rewarded, and cooperation rewarded after a delay, participants in the All-Gains, Delayed-Outcome group may have first learned to defect and only later learned to cooperate.
Outcome valence
As Figure 3 shows, cooperation was generally greater (defection consequently lower) when outcomes were mixed (gains and losses) than when outcomes were all gains. Faster learning by the Mixed-Outcome groups may have been due to subjective reward magnitude rather than outcome valence per se. It is well established that losses are subjectively greater than gains of equal absolute magnitude (called “gain-loss asymmetry” by Loewenstein & Prelec, 1992). Additionally, where outcomes are all gains (as in Figure 1b), larger gains are valued proportionally less than smaller ones (called “the absolute magnitude effect” by Loewenstein and Prelec). Gain-loss asymmetry and absolute magnitude effects combined would act to increase the subjective magnitude (of reward and punishment) with mixed outcomes relative to that with all-positive outcomes.
Temporal patterning
For both All-Gains and Mixed-Outcome groups, shortening the delay between a player’s (S’s) action and the other’s (O’s) response to that action (relative to the delay between O’s action and S’s response) significantly increased S’s rate of cooperation. This was the main effect we had hypothesized on the basis of discounting of delayed rewards. With O playing tit-for-tat, the greater the delay between cooperation or defection by S and reciprocation or retaliation by O (Consequence #3), the less was both the reward to S for cooperating and the punishment for defecting, the slower cooperation was learned.
If one party to a tit-for-tat exchange has more power than the other to speed up its response (increase its immediacy), doing so may have an effect much like that obtained when one party has more power than the other to increase the magnitude of its response – the decrease of mutual defection (retaliation) and increase of mutual cooperation (reciprocation).
Conclusions
A recent New York Times Magazine article (Rosen, 2010) describes the results of a program, put in place by a judge in Hawaii in 2004, to deal with drug violators who had been sentenced to probation and then violated the terms of their probation. Previously, violators were sent to jail to serve out their original sentences (months or years). Because this punishment was so severe, probation officers would impose it only after many violations had occurred. As in the Israel-Hamas conflict, the response of the state to violations was delayed and of high magnitude. The judge, Steven Alm,
….reasoned that if the offenders knew that a probation violation would lead immediately to some certain punishment, they might shape up….Working with U.S. marshals and local police, Alm arranged for a new procedure: if offenders tested positive for drugs or missed an appointment, they would be arrested within hours and most would have a hearing within 72 hours. Those who were found to have violated probation would be sentenced to a short jail term proportionate to the severity of the violation – typically a few days. (p. 36)
In addition, all the current probationers were warned in advance that the new procedure would be imposed. It was found that, “within a six-month period, the rate of positive drug tests fell by 93 percent…compared with a fall of 14 percent for probationers in a comparison group” (p. 36). Of course it is well-known that punishment, like reward, is more effective when it is certain and when its delay is minimal (Miltenberger, 2008). But it is not usually recognized that prisoner’s dilemma games versus tit-for-tat embody reward and punishment and that to vary prisoner’s dilemma parameters is to vary the parameters of reward and punishment.FN3
We have shown that escalation of immediacy can work in the laboratory to reduce retaliation and increase reciprocation. However, despite our attempts to duplicate real-life tit-for-tat contingencies in the laboratory, there is good reason to question the direct applicability of these results. Such laboratory tests might ultimately prove to be inadequate for modeling the efficacy of delay reduction (escalation of immediacy) as a technique in tit-for-tat conflicts in more complex, real-life situations. It seems to us, however, that the costs of escalating immediacy are so low, relative to those of escalating magnitude, that this technique is worth trying.
Acknowledgments
This research was supported by grant DA02652021 from the National Institute of Drug Abuse. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Biographies
Matthew L. Locey is a post-doctoral research associate at Stony Brook University. He received a B.A. in philosophy, a B.S. in psychology, and an M.S. and PhD in behavioral pharmacology from the University of Florida. His research interests are in quantitative models of choice.
Howard Rachlin is Emeritus Distinguished Professor and Research Professor at Stony Brook University. He received a Bachelor of Mechanical Engineering degree from Cooper Union, an MA in psychology from The New School University, and a PhD in psychology from Harvard University. His research interests are in choice, self-control, and altruism in humans and non-humans.
Footnotes
Fifty Stony Brook undergraduates were given instructions similar to those given in Rachlin and Jones (2009) – asking them to imagine everyone they knew to be on a vast field in which physical distance was based on social distance. These students were then asked to assign a physical distance measure for people at various social distances (1, 10, 100) and for a randomly selected classmate. On average, a random classmate was placed at a distance corresponding to the ordinal social distance (an N-value) of 75.
Mutual defection is not inevitable in a two-player PD game. With a 1-2-9-10 matrix, rather than the 1-2-3-4 matrix used in this experiment, cooperation still loses 1 point relative to defection (2 to 1 or 10 to 9) but cooperation by S gives 8 points to O relative to O’s gain if S defects (9 to 1 or 10 to 2). An 8-point gain by O, socially discounted as in the example in the text, is worth more than the 1-point cost to S. Consequently, with the 1-2-9-10 matrix, S would be expected to cooperate. Preliminary experiments in our lab with one-shot play have found significantly more cooperation with the 1-2-9-10 matrix than with the 1-2-3-4 matrix.
In the case of drug violators, a smaller-sooner punishment imposed by the state, when effective, would replace the non-immediate and much greater harmful effects of addiction itself (bad health, social rejection, work disability).
References
- Ainslie G. Breakdown of will. New York: Cambridge University Press; 2001. [Google Scholar]
- Axelrod R. Effective choice in the Prisoner’s Dilemma. Journal of Conflict Resolution. 1980;24:3–25. [Google Scholar]
- Baker F, Rachlin H. Probability of reciprocation in repeated prisoner’s dilemma games. Journal of Behavioral Decision Making. 2001;14:51–67. [Google Scholar]
- Baker F, Rachlin H. Self-control by pigeons in the Prisoner’s Dilemma. Psychonomic Bulletin & Review. 2002;9:482–488. doi: 10.3758/bf03196303. [DOI] [PubMed] [Google Scholar]
- Brown J, Rachlin H. Self-control and social cooperation. Behavioural Processes. 1999;47:65–72. doi: 10.1016/s0376-6357(99)00054-6. [DOI] [PubMed] [Google Scholar]
- Camerer CF. Behavioral game theory: Experiments in strategic interaction. New York: Russell Sage Foundation; 2003. [Google Scholar]
- Erlanger S. French protest of Israeli raid reaches wide audience. The New York Times. 2010 January 12;:A10. [Google Scholar]
- Gallistel CR, Gibbon J. Time, rate, and conditioning. Psychological Review. 2000;107:289–344. doi: 10.1037/0033-295x.107.2.289. [DOI] [PubMed] [Google Scholar]
- Gray LN, Tallman I. Theories of choice: contingent reward and punishment applications. Social Psychology Quarterly. 1987;50:16–23. [Google Scholar]
- Harris AC, Madden GJ. Delay discounting and performance on the prisoner’s dilemma game. Psychological Record. 2002;52:429–440. [Google Scholar]
- Jones BA, Rachlin H. Social discounting. Psychological Science. 2006;17:283–286. doi: 10.1111/j.1467-9280.2006.01699.x. [DOI] [PubMed] [Google Scholar]
- Jones BA, Rachlin H. Delay, probability, and social discounting in a public goods game. Journal of the Experimental Analysis of Behavior. 2009;91:61–74. doi: 10.1901/jeab.2009.91-61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komorita SS, Hilty JA, Parks CD. Reciprocity and cooperation in social dilemmas. Journal of Conflict Resolution. 1991;35:494–518. [Google Scholar]
- Ledyard JO. Public goods: A survey of experimental research. In: Kagel JH, Roth AE, editors. The handbook of experimental economics. Princeton, NJ: Princeton University Press; 1995. pp. 111–194. [Google Scholar]
- Levy G. The punishment of Gaza. New York: Verso; 2010. [Google Scholar]
- Loewenstein G, Prelec D. Anomalies in intertemporal choice: Evidence and an interpretation. The Quarterly Journal of Economics. 1992;107:573–597. [Google Scholar]
- Newman P. The theory of exchange. Englewood Cliffs, NJ: Prentice-Hall; 1965. [Google Scholar]
- Parfit D. Reasons and persons. New York: Oxford University Press; 1984. [Google Scholar]
- Parks CD, Rumble AC. Elements of reciprocity and social value orientation. Personality and Social Psychology. 2001;27:1301–1309. [Google Scholar]
- Rachlin H. Behavior and learning. San Francisco: W.H. Freeman; 1976. [Google Scholar]
- Rachlin H. The science of self-control. Harvard University Press; 2000. [Google Scholar]
- Rachlin H, Brown J, Baker F. Reinforcement and punishment in the prisoner’s dilemma game. In: Medin D, editor. The Psychology of learning and motivation. Vol. 40. New York: Academic Press; 2000. pp. 327–364. [Google Scholar]
- Rachlin H, Jones BA. Social discounting and delay discounting. Behavioral Decision Making. 2008a;21:29–43. [Google Scholar]
- Rachlin H, Jones BA. Altruism among relatives and non-relatives. Behavioural Processes. 2008b;79:120–123. doi: 10.1016/j.beproc.2008.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rapoport A. Game theory as a theory of conflict resolution. Dordrecht, Holland: D. Reidel Publishing Company; 1974. [Google Scholar]
- Rosen J. Prisoners of parole. New York Times Magazine. 2010 January 10;:36–39. [Google Scholar]
- Roth AE. Introduction. In: Kagel JH, Roth AE, editors. The handbook of experimental economics. Princeton, NJ: Princeton University Press; 1995. pp. 3–20. [Google Scholar]
- Sally D. Conversation and cooperation in social dilemmas: a meta-analysis of experiments from 1958 to 1992. Rationality and Society. 1995;7:58–92. [Google Scholar]
- Sanabria F, Baker F, Rachlin H. Learning by pigeons playing against tit-for-tat in a free operant prisoner’s dilemma. Learning And Behavior. 2003;31:318–331. doi: 10.3758/bf03195994. [DOI] [PubMed] [Google Scholar]
- Selten R, Stoecker R. End behavior in sequences of finite prisoner’s dilemma supergames: A learning theory approach. Journal of Economic Behavior and Organization. 1986;7:47–70. [Google Scholar]
- Simon J. Interpersonal allocation continuous with intertemporal allocation. Rationality and Society. 1995;7:367–392. [Google Scholar]
- Stephens W, McLinn CM, Stevens JR. Discounting and reciprocity in an iterated prisoner’s dilemma. Science. 2002;298:2216–2218. doi: 10.1126/science.1078498. [DOI] [PubMed] [Google Scholar]
- Stephens DW, McLinn CM, Stevens JR. Effects of temporal clumping and payoff accumulation on impulsiveness and cooperation. Behavioural Processes. 2006;71:29–40. doi: 10.1016/j.beproc.2005.09.003. [DOI] [PubMed] [Google Scholar]
- Watson JB. The effect of delayed feeding upon learning. Psychobiology. 1917;1:51–59. [Google Scholar]
- Yi R, Johnson MW, Bickel WK. Relationship between cooperation in an iterated prisoners dilemma game and the discounting of hypothetical outcomes. Learning and Behavior. 2005;33:324–336. doi: 10.3758/bf03192861. [DOI] [PubMed] [Google Scholar]