Abstract
BEDAM calculations are described to predict the free energies of binding of a series of anaesthetic drugs to a recently characterized acyclic cucurbituril host. The modeling predictions, conducted as part of the SAMPL3 host-guest affinity blind challenge, are generally in good quantitative agreement with the experimental measurements. The correlation coefficient between computed and measured binding free energies is 70% with high statistical significance. Multiple conformational stereoisomers and protonation states of the guests have been considered. Better agreement is obtained with high statistical confidence under acidic modeling conditions. It is shown that this level of quantitative agreement could have not been reached without taking into account reorganization energy and configurational entropy effects. Extensive conformational variability of the host, the guests and their complexes is observed in the simulations, affecting binding free energy estimates and structural predictions. A conformational reservoir technique is introduced as part of the parallel Hamiltonian replica exchange molecular dynamics BEDAM protocol to fully capture conformational variability. It is shown that these advanced computational strategies lead to converged free energy estimates for these systems, offering the prospect of utilizing host-guest binding free energy data for force field validation and development.
1 Introduction
Molecular recognition forms the basis of many of physiochemical processes, yet quantitative models of molecular association remain incomplete. A well understood and widely accepted statistical mechanics theory of molecular association equilibria exist,[1, 2] and atomistic models and computational algorithms have reached the potential of capturing the complexities of molecular interactions. Models based on the fundamental physical and chemical principles that govern molecular association equilibria[3, 4, 5, 6, 7] have the best potential to incorporate the level of detail necessary to achieve sufficient predictive accuracy to be useful in application such as as drug development and optimization.[8]
Despite their potential, physics-based models of protein-ligand binding are not widely employed in academic and industrial research, and their effectiveness as predictive tools remains uncertain.[5, 9, 7] There are clearly many reasons that this is the case. Models of this kind are more computationally demanding and harder to set up properly than alternative empirical techniques. Furthermore the promises of early encouraging outcomes did not always live up to expectations, likely dissuading adoption by the current generation of researchers.[10] It is therefore important in this context to strive to build a body of unbiased assessments to test the limits of applicability of theories, and of the quality of models, algorithms, and computational practices with the aim of improving accuracy and reproducibility.
Host-guest systems, relatively small supramolecular complexes employed in a large variety of applications ranging from food and pharmaceutical preparations, in-situ catalysis, and nanoengineering, offer unique opportunities in this respect for the computational community. As shown by the pioneering work of Gilson and collaborators,[11, 12, 13] appropriate computational algorithms can yield converged results for these systems with moderate computational costs, thus offering the opportunity to reliably assess the robustness of force field models and the relative performance of binding free energy algorithms.
Here we assess the performance of the Binding Energy Distribution Analysis Method (BEDAM), an absolute binding free energy method we recently proposed,[14, 15] and the OPLS-AA/AGBNP2 effective potential,[16, 17] on the calculation of the standard free energies of binding of a series of anaesthetic drugs[18] to a recently characterized acyclic cu-curbituril host;[19] a dataset proposed as part of the latest SAMPL host-guest affinity blind challenge.[20] BEDAM is based on the statistical analysis of probability distributions of the effective binding energy of the complex as a function of a thermodynamic progress variable, λ, connecting the unbound and bound states of the complex. The methodology is aimed at not only providing binding affinity estimates but also at providing physical insights concerning the driving forces for or against binding. The design of BEDAM emphasizes effects such as conformational entropy and reorganization, and the contribution of multiple binding modes,[14] aspects that, while often neglected by empirical models, are shown here to be critical to achieve quantitative predictions. The BEDAM method makes use of parallel Hamiltonian replica exchange (HREMD) to enhance conformational sampling efficiency to search for the most effective binding mode, as well as to equilibrate multiple binding modes.[21] Advanced statistical reweighting techniques[22, 23] are used to optimally merge data obtained along the binding thermodynamic path. The BEDAM method is based on an implicit solvent description of the aqueous solution environment. This choice allows for a more direct estimation of the binding free energy which would otherwise require long equilibration times and two separate calculations, one for the ligand in solution and one for the ligand bound to the receptor, with explicit solvation. However, if not properly formulated and parametrized, an implicit solvation description is potentially less accurate than an explicit description and care has to be exercised to properly validate model predictions.[15]
The challenge of offering predictions without knowledge of the “right” answer gives us an unique opportunity to validate in a realistic and unbiased way the potential model and the computational protocols. Despite the unavoidable shortcomings in performing model validation with respect to experimental data when the relation between models and experimental observables is not exactly known (due to uncertainties in protonation state assignment, the physiochemical nature of the experimental reporting system, etc.), blind experiments have been very useful in various areas of computational biophysics such as in protein structure prediction,[24] hydration free energy prediction,[25] pKa prediction,[26] and protein-protein[27] and protein-ligand binding.[28] Binding free energy estimation is a complex process involving many steps from system setup and structure prediction, to conformational sampling and free energy estimation. Traditional model validations against selected and limited experimental datasets are too often affected by operational biases and parameter overfitting. Blind datasets, being unknown to the model being tested, represent excellent validation experiments for free energy models and system preparation procedures. Because all of the participants work on the same dataset, assessments such a SAMPL3 also make it possible to compare directly the strengths and weaknesses of the various approaches, offering guidance to developers on ways to improve their models and to users on how to best apply them.
2 Methods
2.1 System preparation
Computations were conducted for the complexes of host 1 with guests 1–7. The molecular models for the host and guests were prepared using the LigPrep workflow as part of the 2010 version of the Maestro program (Schrödinger, inc.). Protonation states were assigned based on a pH range of 7 ± 4. All aliphatic amine nitrogen atoms were modeled as protonated. Multiple protonation states were tested for guests 2, 3, 4 and 7. For these guests, in addition to the singly protonated forms at the aliphatic amine nitrogen, we also examined doubly charged forms protonated at the aniline (guests 2 and 4), the N-methylaniline (guest 7), and methoxypyridine (guest 3) functionalities. All of the four carboxylic functionalities of the host were modeled as deprotonated.
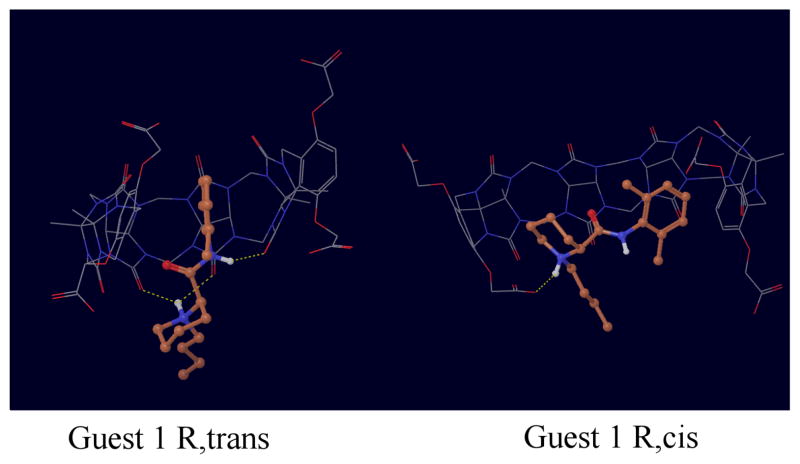
We identified two cis/trans conformational stereoisomers due to nitrogen inversion for each of the two enantiomers of guest1 (Fig. 1). Stereoisomers related by nitrogen inversion are freely interconverting in solution, and the observed binding affinity is a combination of the affinities and populations of both. However nitrogen inversion is not modeled in the calculations so that each stereoisomer must be considered separately in the calculations. Because host 1 is achiral, guest enantiomer pairs have identical binding affinities. Nevertheless we have simulated all four stereoisomers of guest 1, including enantiomer pairs, to validate the conformational sampling free energies of the computational protocol. Similarly, we have identified three conformational stereoisomers of guest 6 due to nitrogen inversion at the two aliphatic amine centers. These correspond to RR and SS enantiomers, and RS and SR di-asteroisomers that, given the plane of symmetry, correspond to a single meso compound. As for guest 1, calculations for each of the three stereoisomers of guest 6 was performed individually.
Figure 1.
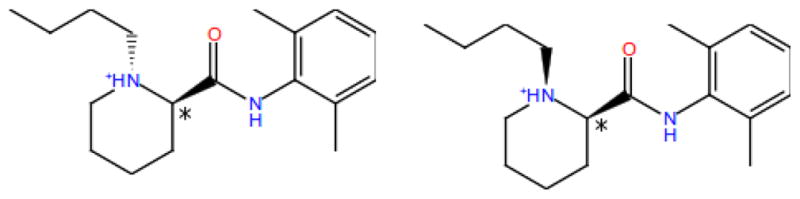
The trans (left) and cis (right) conformational isomers of the R enantiomer of guest 1.
2.2 BEDAM binding free energy protocol
The BEDAM method[14] computes the binding free energy between a receptor A and a ligand B with implicit solvation by means of the expression
| (1) |
which follows, without approximations, from a well-established statistical mechanics theory of molecular association,[1] where β = 1/kT, C∘ is the standard concentration of ligand molecules (set to C∘ = 1 M, or equivalently 1, 668 Å−3), Vsite is the volume of the binding site, and p0(u) is the probability distribution of binding energies collected in an appropriate decoupled ensemble of conformations in which the ligand is confined in the binding site while the receptor and the ligand are both interacting only with the solvent continuum and not with each other. The binding energy
| (2) |
is defined for each conformation r = (rB, rA) of the complex as the difference between the effective potential energies V (r) (here OPLS-AA/AGBNP2)[17] of the bound and separated conformations of the complex without conformational rearrangements.
BEDAM is based on biasing potentials of the form λu(r) yielding a family of λ-dependent hybrid potentials of the form
| (3) |
where
| (4) |
is the potential energy of the unbound state. It is easy to see from Eqs. (2), (3), and (4) that Vλ=1 corresponds to the effective potential energy of the bound complex and Vλ=0 corresponds to the state in which the receptor and ligand are not interacting. Intermediate values of λ trace an alchemical thermodynamic path connecting these two states. The binding free energy ΔGb is by definition the difference in free energy between these two states.
Rather than simulating each λ state independently, BEDAM employs a Hamiltonian replica exchange λ-hopping strategy whereby simulation replicas periodically attempt to exchange λ values through Monte Carlo (MC) λ-swapping moves. λ-exchanges are accepted with the Metropolis probability min[1, exp(−βΔλΔu)][14] where Δλ is the difference in λ’s being exchanged and Δu is the difference in binding energies between the replicas exchanging them. Replica exchange strategies of this kind yield superior conformational sampling and more rapid convergence rates by allowing conformational transitions to occur at the value of λ at which they are most likely to occur and to be then propagated to other states.[21]
To improve convergence of the free energy near λ = 0, in this work we employ a modified “soft-core” binding energy function of the form
| (5) |
where umax is some large positive value (set in this work as 1, 000 kcal/mol). This modified binding energy function, which is used in place of the actual binding energy function [Eq. (2)] wherever it appears, caps the maximum value of the binding energy while leaving unchanged the value of favorable binding energies.
In this work we employed multistate Bennett acceptance ratio estimator (MBAR)[23] to estimate binding energy distributions and standard binding free energies from binding energy samples obtained from the HREM simulations. Binding free energies are computed directly from the MBAR dimensionless free energies f̂λ using the relationship
| (6) |
The MBAR dimensionless free energies f̂λ = −ln Zλ are defined as the negative of the logarithm of the λ-dependent biased partition functions Zλ. In this case the dimensionless free energies are estimated by the self-consistent solution of the set of equations[23]
| (7) |
where f̂i = f̂λiujn is the nth binding energy sample from replica j, K is the number of replicas and Nj is the total number of binding energy samples from replica j. For the MBAR analysis we employed the code provided by John Chodera and Michael Shirts (http://alchemistry.org). Statistical uncertainties were obtained from the standard deviation of the binding free energies from the last five 0.5 ns blocks of binding energy data (see below).
For later use we introduce here the reorganization free energy for binding defined by the expression[2]
| (8) |
where 〈u〉1 is the average binding energy at λ = 1 and is the standard binding free energy. The former is computed from the ensemble of conformations of the complex collected at λ = 1 and is computed by difference using Eq. (8).
2.3 Conformational reservoirs
Preparatory analysis indicated that both the host and many of the guests experience extensive conformational variability when unbound in solution (see below). We therefore decided to model explicitly this conformational variability by means of conformational reservoirs, a strategy employed in other contexts[29, 30] aimed here at facilitating the identification of multiple binding modes, as well as at capturing the conformational reorganization free energy component of the binding free energy. The idea behind this approach is illustrated in Fig. 2.
Figure 2.
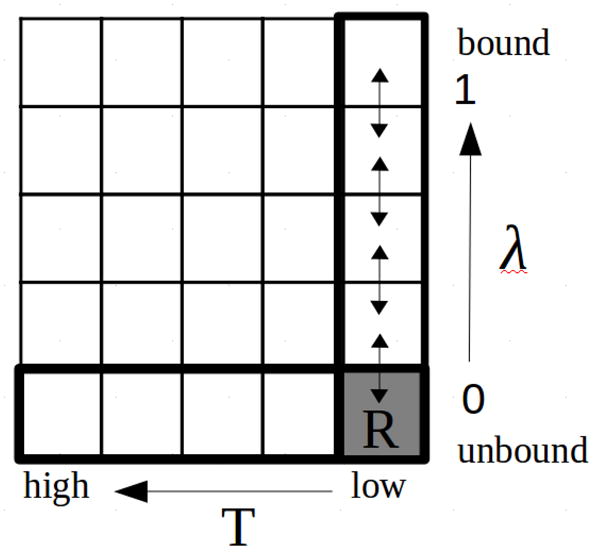
Illustration of the BEDAM calculation protocol with conformational reservoirs at λ = 0. The horizontal axis represents the temperature dimension and the vertical axis the binding progress parameter λ. The matrix of cells represents a hypothetical two-dimensional replica exchange simulation with the cells representing replicas at all possible combinations of temperatures and λ’s. In practice only the one-dimensional temperature replica exchange simulation at λ = 0 is conducted (bottom row). Conformations collected at low temperature are saved in a conformational reservoir (denoted by “R”, lower right) that takes the place of the λ = 0 replica of a conventional BEDAM Hamiltonian replica exchange calculation (right column).
We have shown[14] that the BEDAM λ-hopping replica exchange scheme, corresponding to the highlighted vertical column in Fig. 2, is very efficient at exploring intermolecular degrees of freedom, that is the position and orientation of the guest relative to the host. However, λ-hopping does not directly accelerate the exploration of intramolecular degrees of freedom, that is internal conformational rearrangements of host and guest. Temperature replica exchange is a commonly employed method to accelerate exploration of conformational space. We have shown in particular its usefulness in rapidly converging the conformational landscape of small molecules.[31] This suggests that a two-dimensional replica exchange strategy along the and temperature dimensions (Fig. 2) would be a powerful method for conformational sampling in binding free energy calculations. Diffusion along the λ variable (the vertical direction in Fig. 2) would connect the bound and unbound conformational states and accelerate the exploration of intermolecular degrees of freedom, while diffusion in the temperature direction (the horizontal direction in Fig. 2) would activate intramolecular degrees of freedom.
However, performing multi-dimensional replica exchange simulations is in many cases impractical because of complications in the design and scheduling of exchanges[32] as well as because of the need for large number of replicas. As an alternative, one can consider performing temperature replica exchange only at λ = 0 (the highlighted bottom horizontal row). At this value of λ the guest and host are uncoupled so that the two can be simulated independently. Also, it is expected that in most cases greater conformational freedom exist in the unbound state than in the bound state.
To simplify the calculations further, the temperature replica exchange runs are conducted prior to the BEDAM run. The ensemble of conformations for the guest and host collected at the experimental temperature are collected and saved in repositories referred to as conformational reservoirs.[30] The conformational reservoirs then take the place of the = 0 replica of conventional BEDAM calculations (labeled “R” in Fig. 2). λ-exchanges with the repositories follow the same acceptance rule as for the other replicas. When an exchange is requested, one conformation for the guest and one conformation of the host are selected randomly from the reservoirs. Then the two are combined by placing the guest randomly within the binding site volume. The binding energy of the resulting complex is evaluated and inserted in the Metropolis acceptance step as above. If the exchange is accepted the conformation from the reservoir is passed on to the next replica and begins to be propagated by MD and λ-exchanges as in conventional BEDAM. In the current implementation the conformation held by the replica exchanging with the reservoir disappears from the calculation rather than being added to the reservoirs.
Because the reservoir represents a canonical ensemble of conformations, overall the method is canonical, while providing greater coverage of the conformational space for the guest and the host. In addition, the method is computationally efficient because a single host reservoir is employed for calculations involving many guests.
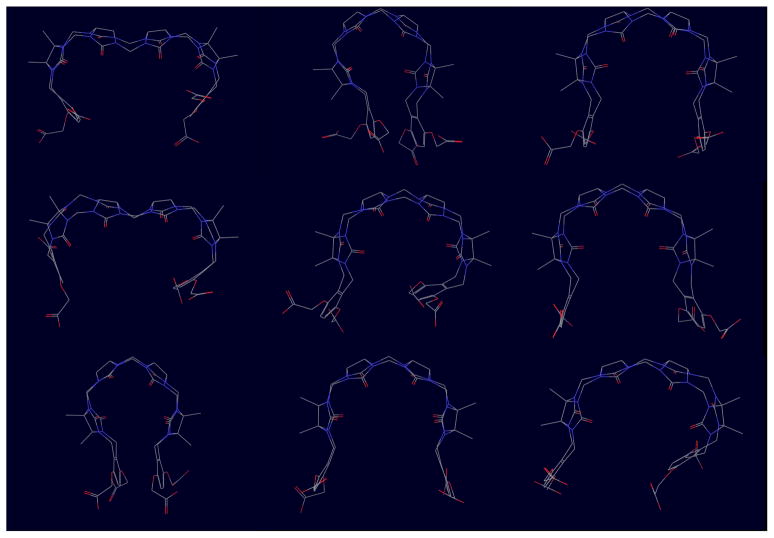
The computed conformational reservoirs for host 1 and some of the guests are illustrated in Figs. 3 and 4, respectively. Unexpectedly, the unbound host displays a variety of closed and open conformations. Wide open conformations are made possible by the formation of a kink of the methylene links between the two central ureidyl monomers (top and center left of Fig. 3). In the most compact closed conformations the o-xylylene gates are often found associated face to face (top center and bottom left), while in less closed conformations often both gates are open or one gate is turned in while the other is turned outwardly. Examples of many of these host conformations are found in the conformational ensemble of the host-guest complexes (see below). Without the extra conformational variability afforded by precomputed temperature replica exchange reservoirs these complex conformations would have been missed. Also, note that, while the host conformation provided by the SAMPL organizer displays helical chirality, the unbound ensemble of the host in the conformational reservoir consist of a nearly homogeneous racemic mixture of left-handed and right-handed helical conformations (together with other not easily characterizable open conformations). This symmetry in conformational populations is expected given the achiral nature of host 1, and this is reflected in the similar binding free energies computed for enantiomer pairs of the guests (see below).
Figure 3.
Representative conformations from the λ = 0 conformational reservoir for host 1. Closed and open conformations are shown approximately in proportion of the corresponding occurrence in the reservoir, which contains 10, 000 conformations.
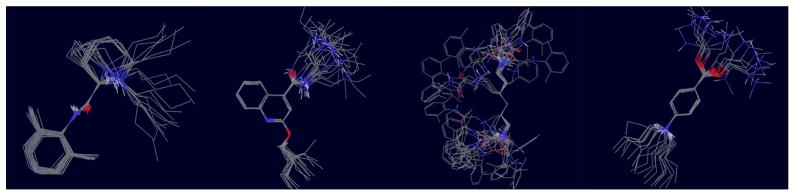
Figure 4.
Representative conformations from the λ = 0 conformational reservoirs for, from left to right, guest1 (R, trans), guest3, guest 6 (RR), and guest 7. Conformations are superimposed on conserved cores to show conformational variations of distal groups.
While some guests are relatively rigid, many, as illustrated in Fig. 4, were found to have considerable conformational variability when unbound in solution. Conformational variations are due mainly to simple rotations around single bonds. However we found that free energy barriers are often sufficiently high that it is not feasible to achieve equilibrated populations of rotamers using conventional molecular dynamics. The accelerated conformational sampling afforded by temperature replica exchange allows to overcome this obstacle.[31] As for the host, it is important to achieve an equilibrated ensemble of conformations in order to estimate correctly the reorganization free energy component of the binding free energy. A large variety of host and guest conformations also aids in the search for the most favorable configurations of the host-guest complexes.
2.4 Computational details
In our implementation BEDAM employs an effective potential in which the effect of the solvent is represented implicitly by means of the AGBNP2 implicit solvent model[17] together with the OPLS-AA[33, 34] force field for covalent and non-bonded interatomic interactions. For this work the water site AGBNP2 parametrization[17] was augmented to include two hydration sites for each ureidyl monomer pointing to the interior of the cucurbituril host. The aim of these additional hydration sites is to capture the favorable free energy of releasing confined water molecules upon binding of the guest.[35] Based on preliminary tests on β-cyclodextrin host-guest systems, the hydration strength of these water sites was set to hs = 0.4 kcal/mol.
Parallel molecular dynamics simulations were conducted with the IMPACT program.[36] The simulation temperature was set to 300K. We employed 29 intermediate steps at lambda=0, 0.001, 0.002, 0.0033, 0.0048, 0.006, 0.008, 0.01, 0.04, 0.07, 0.1, 0.15, 0.2, 0.25, 0.30, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, and 1. The binding site volume was defined as any conformation in which the center of mass of the guest was within 6 Å of the center of mass of the host. The guest was sequestered within this binding site volume by means of a flat-bottom harmonic potential. Based on this definition the volume of the binding site, Vsite, is calculated as approximately 904 Å3 and −kT ln C∘Vsite = 0.36 kcal/mol. The temperature replica exchange simulations to obtain λ = 0 conformational reservoirs utilized 8 replicas distributed between 300 and 600 K and were 20 ns in length. The collected 300 K ensembles, saved every 2 ps, constituted the conformational reservoirs used in the parallel Hamiltonian replica exchange calculations.
BEDAM calculations were performed with 5 ns of MD per replica (145 ns of MD total for each guest). The second half of the trajectory (2.5 ns) was used for data analysis. Binding energies were sampled with a frequency of 1 ps.
2.5 Prediction of experimental binding affinities
Observed experimental affinities are the result of the binding of all the chemical forms of the guest present in solution. In the present application different species differing in protonation state and stereoisomer form are potentially present for each guest. In this circumstances the observed affinity, , is given by[14, 2]
| (9) |
where P0(i) is the relative fraction of species i in solution and is the binding free energy corresponding to species i. For an acid/base equilibrium between a protonated species AH and a deprotonated species A, the corresponding populations can be computed from the pKa for the deprotonation reaction and the solution pH as
| (10) |
and
| (11) |
where
| (12) |
In this work we assumed a solution pH of 7.4. At this pH and with the assumed pKa’s (see below) the protonated forms of guests 2, 3, 4 and 7 have much lower population in solution than the singly protonated forms. It is convenient to express the effect of the small populations of the AH species in Eq. (9) in terms of ionization penalties ΔFI = −kT ln PAH that together with the computed binding free energy yields an effective binding free energy of the protonated species. We computed ionization penalties of 3.7 and 3.5 kcal/mol for the doubly protonated forms of guests 2 and 7 using the pKa values of anilinium (pKa = 4.7) and N-methylanilinium (pKa = 4.8), respectively. The same ionization penalty as for guest 2 was applied to guest 4 protonated at the aniline functionality. The doubly protonated form of guest 3 was penalized by 5.3 kcal/mol based on the pKa of 2-methoxypyridine (pKa = 3.4). In all cases (see below) one of the protonation states of the ligand had an effective binding free energy much more favorable than the other so that the contribution of the latter was negligible.
Eq. (9) was also used to predict the observed binding free energies for guest 1 and guest 6, which have multiple stereoisomers. We have not attempted to compute the relative solution populations of these conformers. The binding free energies for the two conformational stereoisomers of guest 1 (−7.8 and −5.7 kcal/mol, for the trans and cis conformers, respectively) significantly favor the trans stereoisomer. Furthermore the trans conformer has presumably also higher population in solution based on the structure (we assumed a 80% to 20% trans/cis ratio), so that the role of the other is relatively small. However an uncertainty of as much as 0.8 kcal/mol cannot be ruled out for guest 1 without proper estimation of the relative stereoisomer populations. The stereoisomers of guest 6 include two enantiomers (RR/SS) and one meso form (RS/SR). The computed binding free energies of the enantiomer pair and the meso form were similar (−9.1 and −8.5 kcal/mol, respectively). The observed binding free energy estimate for guest 6 was obtained by assuming equal populations for all stereoisomers. The binding free energies are sufficiently similar so that even large population redistribution cause small changes in the apparent binding affinity. However in this case too an uncontrolled uncertainty of as much as 0.5 kcal/mol can not be ruled out.
3 Results and Discussion
3.1 Binding free energy predictions
The predicted binding free energies for guests 1–7 with host 1 submitted to the SAMPL3 experiment are listed in Table 1. The predictions pick up correctly the strongest (guest 6) and weakest (guest 4) binders. The root mean square deviation (RM SD) between experiments and predictions is 2.46 kcal/mol. Some of this deviation is due to a systematic offset of approximately 1.6 kcal/mol, with the predictions underestimating on average affinities. While the origin of this systematic offset is uncertain, we can speculate that it can be due to overestimation of the hydration free energy of the host.
Table 1.
Experimental, , and predicted, a, binding free energies of guests 1–7 with host 1.
|
|
Chargeb |
|
ΔFIa,d |
|
||||
|---|---|---|---|---|---|---|---|---|
| guest1 | −5.84 | +1 | −7.6 ± 0.2 | 0 | −7.6 ± 0.2 | |||
| guest2 | −7.10 | +2 | −7.3 ± 0.4 | 3.7 | −3.6 ± 0.4 | |||
| guest3 | −6.80 | +1 | −5.8 ± 0.3 | 0 | −5.8 ± 0.3 | |||
| guest4 | −4.17 | +1 | −3.9 ± 0.3 | 3.7 | −0.2 ± 0.3 | |||
| guest5 | −6.06 | +1 | −6.1 ± 0.3 | 0 | −6.1 ± 0.3 | |||
| guest6 | −10.72 | +2 | −8.9 ± 0.5 | 0 | −8.9 ± 0.5 | |||
| guest7 | −7.85 | +2 | −8.7 ± 0.4 | 3.5 | −5.2 ± 0.4 | |||
|
| ||||||||
| RM SDa | 1.08 | 2.46 | ||||||
| Re (p-value)f | 0.82 (0.9%) | 0.70 (4 %) | ||||||
In kcal/mol.
Protonation state used in BEDAM calculation.
BEDAM binding free energy for indicated protonation state.
Ionization penalty.
Correlation coefficient.
Computed with a random range of binding free energies between 0 and −11 kcal/mol.
The correlation between predictions and experiments is relatively high with a correlation coefficient of 70%, moreover the gradient of the least square correlation line is close to unitary (1.14 ± 0.16). The probability that the observed correlation is due to chance (p-value) is only 4%, as obtained from the probability distribution of correlation coefficients corresponding to uniform random samples of predictions within 0 and −11 kcal/mol (that is by guessing within the highest and lowest binding free energies measured or predicted for this set). The best agreement is obtained for guest 5 with almost no deviation, while the worst agreement is observed for guest 4 (4 kcal/mol deviation), guest 2 (3.5 kcal/mol deviation), and guest 7 (2.6 kcal/mol deviation).
Interestingly, the latter three complexes were the only ones for which an ionization penalty has been applied. Omitting the ionization penalties for this compounds leads to much better agreement with the experiments (see Table 1). The RM SD is reduced to 1.08 kcal/mol (from 2.46 kcal/mol) and the correlation coefficient increases to 82% (up from 70%) with a p-value of less than 1%. The much better agreement obtained omitting ionization penalties is unlikely to be coincidental. One possibility, which was discussed and discounted at the SAMPL3 meeting, is that the measurements reflect acidic conditions —according to Eqs. (10)–(12) at acidic pH ionization penalties are reduced—either because the effective solution pH is lower than reported or the spectroscopic reporting signal is more sensitive to the protonated species. A more likely explanation is that the charge states of guests 2, 4, and 7 with neutral aniline and N-methylaniline groups, which do not require an ionization penalty correction, are, contrary to the predictions, contributing more to the observed affinities than the protonated species. However the computed binding free energies for the neutral aniline charges states of guests 2, 4, and 7 were 1.6, 2.4, and −0.8 kcal/mol, respectively, which deviate very significantly (from 7 to 9 kcal/mol) from the observed binding free energies. It is unclear whether a force field parametrization issue could be entirely responsible for deviations of this magnitude, so perhaps other as yet unappreciated contributing factors exist.
In any case, on overall these results, with or without ionization penalty corrections, are encouraging given that the model does not include adjustable parameters tuned to reproduce binding affinities of these or related systems. The fact that the predictions are within the same range of measured affinities is a remarkable result in itself, as the model computes the absolute binding free energies independently for each complex rather than estimating relative affinities from a reference compound. As shown in Table 2, entropy and reorganization energy constitute a large fraction of the binding free energy and therefore neglecting them would produce predictions of the incorrect magnitude. This highlights the fact that, in addition to host-guest interaction energy components, it is also necessary to include entropic and reorganization free energy factors in order to obtain computational predictions of magnitude commensurate with the physical system. The BEDAM method automatically includes entropic and reorganization energy effects.
Table 2.
Decomposition of the compute binding free energies from Table 1 into average binding energies, 〈u〉1 and reorganization free energy, , components.
|
|
〈u〉1a |
|
|||
|---|---|---|---|---|---|
| guest1 | −7.6 | −26.8 | 19.2 | ||
| guest2 | −7.3 | −37.9 | 30.6 | ||
| guest3 | −5.8 | −24.2 | 18.4 | ||
| guest4 | −3.9 | −22.2 | 18.3 | ||
| guest5 | −6.1 | −25.3 | 19.2 | ||
| guest6 | −8.9 | −45.0 | 36.1 | ||
| guest7 | −8.7 | −38.1 | 29.4 |
In kcal/mol.
3.2 Thermodynamic decomposition
Table 2, reports the decomposition of the computed binding free energies into the average binding energy, 〈u〉1, and the reorganization free energy . The average binding energy measures the thermodynamic driving force towards binding provided by favorable host-guest interactions. Conversely, the reorganization free energy measures configurational entropy loss and intramolecular energetic strain caused by complex formation, which, collectively, oppose binding.[2] Both contributions are much larger in magnitude than the binding free energies. The binding free energies result from a large compensation between opposing effects. Complexes with the most favorable interaction energies (−45 to −38 kcal/mol found with guests 2, 6, and 7 compared to −25 to −22 with most other guests) tend to have the highest affinities, however these variations are reflected in significantly smaller variations in binding free energies because these same complexes are also the ones with the largest reorganization free energies (from 30 to 36 kcal/mol compared to 18–19 kcal/mol for the other guests). Interestingly, this pattern mirrors the level of protonation of the guests. This indicates that the doubly protonated guests 2, 6, and 7 (see Fig. 5) can form the strongest but also more specific interactions with the host, which occur at the expense of conformational variability.
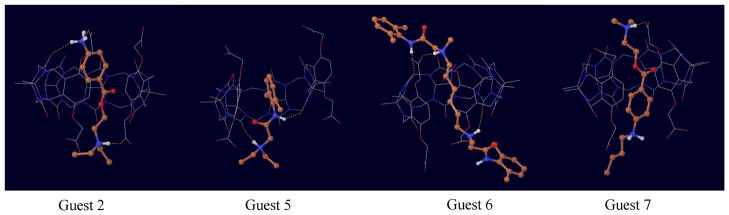
Figure 5.
Representative conformations of the complexes with guests 2, 5, 6, and 7.
3.3 Structures of the complexes
Modeling also provides structures of the host, guests, and the corresponding complexes. This information provides additional insights on the characteristics of these compounds whose solution structures are often not uniquely identifiable by spectroscopic means alone.[19, 18] The ensemble of structures of the unbound hosts and guests are illustrated in Figs. 3 and 4. The most surprising result is the large conformational variability of the host, and in particular the occurrence of wide open kinked conformations. It is unclear whether this reflects the actual behavior of the host in solution or a force field artifact. It has been pointed out at the SAMPL3 meeting that, as some have done, selecting the protonation state of the carboxylic end chains such that two are deprotonated and two are protonated, rather than all deprotonated as done here, would lead to hydrogen bonding interactions between the carboxylic group and stabilize closed conformations. In retrospect, this appears a reasonable choice although neither can be immediately supported by experimental evidence.
Most of the complexes are characterized by conformations in which the guest occupies the center of the host (Fig. 5), which is wrapped around the guest in a closed conformation. These are similar to the crystal structure of the complex of spermine with host 1.[19] Hydrophobic interactions and hydrogen bonding interactions between the amino, ammonium, and amide groups of the guests with the carboxylic groups of one of both of the rims of the host stabilize these conformations. We confirmed that in the simulations symmetric conformations of the complexes occur with approximately the same frequencies. Conversely, we observed that enantiomers (as for example for guest 1 in Fig. 6) tend to bind to helical conformations of the host with opposite chirality with approximately the same frequency. These are indications that, as further discussed below, the calculations have reached a reasonable level of convergence.
Figure 6.
Representative conformations of the complexes with the trans and cis isomers of guest 1.
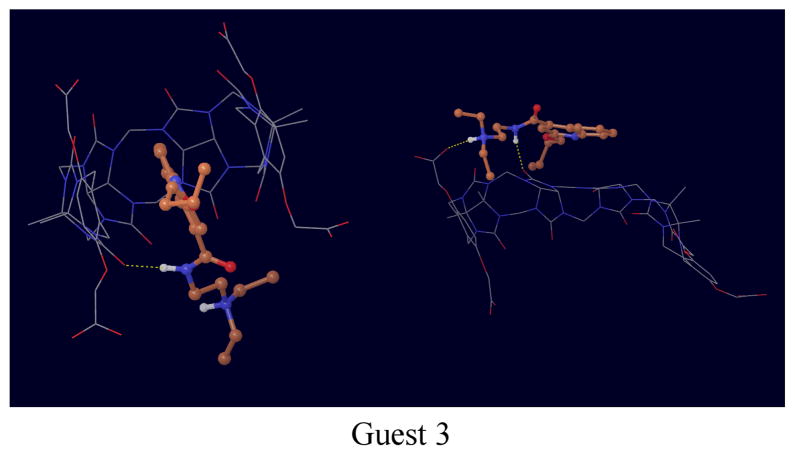
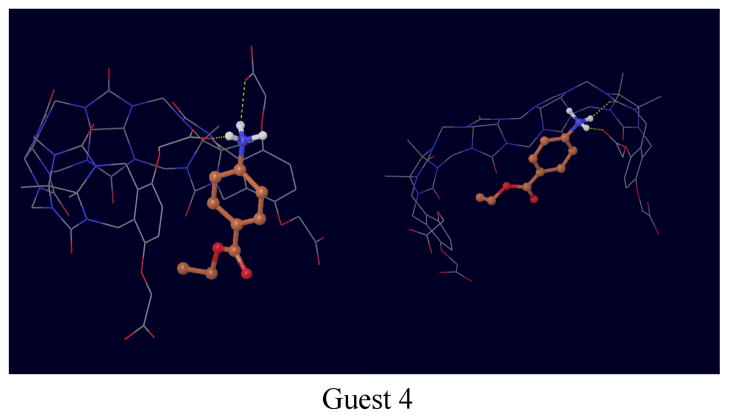
The structures of complexes with guests 1, 3 and 4 deserve particular mention. While the trans isomer of guest 1 tends to bind in the conventional through-the-cavity mode discussed above, the cis isomer (Fig. 6) sits preferentially sideways against the inner surface of the host, which wraps the guest in an open conformations. Guests 3 and 4 (Figs. 7 and 8) were observed to bind in multiple modes. In one mode the guest is sandwiched in between the o-xylylene rings and only partly occupying the middle of the host cavity. In addition to these modes, guests 3 and 4 are also seen interacting with open conformations of the host (see Figs. 7 and 8).
Figure 7.
Representative conformations of the complex with guest 3.
Figure 8.
Representative conformations of the complex with guest 4.
3.4 Convergence checks
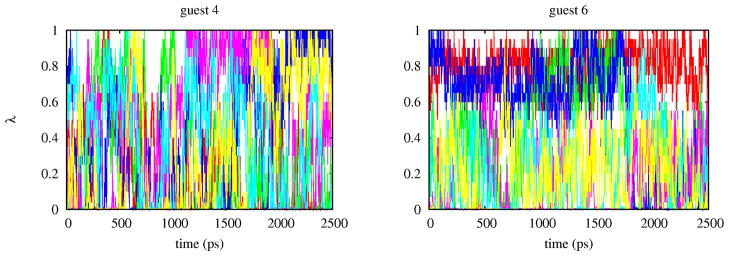
Assessing the reproducibility and level of convergence of the results is important to determine whether the predictions truly reflect the quality of the potential model rather than algorithmic or procedural elements of the calculations. We have analyzed convergence at various levels. The choice of the number of replicas and their λ assignments affects the reliability and reproducibility of the BEDAM calculations in two related ways. To estimate the binding free energy it is necessary that an unbroken sequence of overlaps between the binding energy distributions pλ(u) exist between λ = 0 (the unbound state) and λ = 1 (the bound state). So the choice of the λ-schedule must meet this minimum requirement.[37] The choice of the λ schedule also affects the acceptance ratio of λ-exchanges in the HREM conformational sampling scheme (see above). Statistically, the frequency of accepted exchanges tends to increase as overlaps between binding energy distributions are increased. It follows that monitoring the extent of diffusion in λ-space of the replicas is also equivalent to monitoring the level of overlaps between binding energy distributions and ultimately the quality of the selected λ schedule. Analysis of the HREM data shows that in all cases replicas visit a wide range of λ values, but the rate of diffusion in λ-space vary from system to system. Fig. 9 illustrates the best and worst case scenarios we observed. In both cases λ-exchanges are frequent, however while many replicas of guest 4 frequently span most values of λ between 0 and 1, replicas of guest 6 diffuse more slowly and some are confined in a limited range of λ’s.
Figure 9.
Trajectories in λ-space of six replicas of the complexes with guest 4 and guest 6. Each color represents a replica. The degree of “color mixing” represents the rate at which replicas diffuse in λ-space.
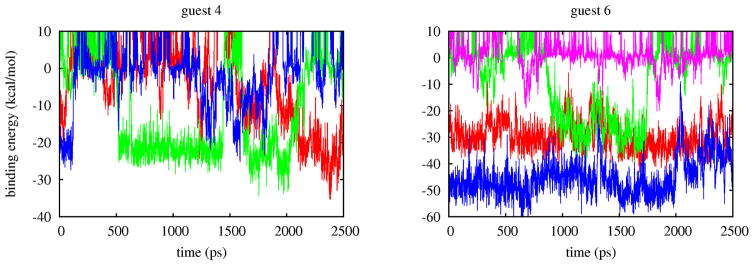
This is because, even though local λ exchanges are promoted by a larger distribution of overlaps, global diffusion of replicas in λ space also depends on the ability of replicas to undergo conformational transitions.[38] Replicas in conformations with unfavorable binding energies tend to remain at small values of whereas replicas in bound conformations with favorable binding energies tend to remain at large values of λ. The rate of occurrence of conformational transitions is illustrated in Fig. 10. Replicas of the complex with guest 4 undergo several binding/unbinding transitions during the simulation while the complex with guest 6 is characterized by multiple bound conformations which slowly interconvert among themselves and with unbound conformations. Because it is mainly tied to the occurrence of conformational transitions, this type of convergence behavior hinges on the quality of the conformational sampling algorithm and is not addressable by only adding more replicas.
Figure 10.
Trajectories of the binding energies of four replicas of the complexes with guest 4 and guest 6. Each color represents a replica. Bound conformations of guest 4 assume binding energies around −20 and −30 kcal/mol and replicas frequently transition from these to unbound conformations (binding energies greater than zero). The bound state of guest 6 is characterized by two states at −30 and −50 kcal/mol which slowly interconvert and rarely transition to unbound conformations.
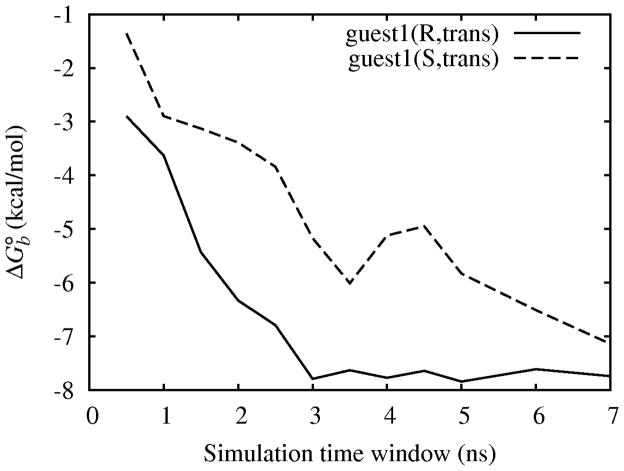
We have directly monitored convergence by analyzing the variation of computed binding free energies within a series of data windows collected at different times during the simulation. One example is shown in Fig. 11 for the trans stereoisomer of guest 1. This figure shows the computed binding free energies from windows of 0.5 ns in length containing 14, 500 time-contiguous binding energy samples as a function of simulation time. Note that these are not running averages. The profile obtained for the R enantiomer (full line) is typical of all of the guests for which we have provided predictions. After a lag phase of 1–3 ns we observe consistent results that do not change significantly as simulations progress. This indicates that the predictions are mostly free of spurious effects due to insufficient equilibration and that have converged to stable reproducible values.
Figure 11.
Variation of the BEDAM binding free energy to the host of the R and S enantiomers of the trans stereoisomer of guest 1 computed from 0.5 ns windows as a function of simulation time.
The data for the S enantiomer of guest 1 shown in Fig. 11 (dashed line) however shows a much longer lag phase in which the binding free energy slowly converges towards the same value as for the R enantiomer. The slow equilibration for the complex with the S enantiomer is explained by the fact that, while both simulations were started from the same left-handed helical host conformation provided by the SAMPL3 organizers, the initial host conformation is more compatible to binding to the R enantiomer than the S enantiomer. Strong binding to the S enantiomer requires reorganization of the host from left-handed to right-handed helical conformations. These conformations are present in the λ = 0 conformational reservoir of the host but it takes time for them to migrate to larger values of λ. As shown in Fig. 11 however, eventually the S enantiomer yields similar results as for the R enantiomer as would be expected for an achiral host. Obtaining similar values of binding free energies starting from such different starting conditions increases our confidence of the good quality of convergence provided by the BEDAM computational protocol for these systems.
4 Conclusions
As part of the SAMPL3 blind binding affinity challenge we have predicted the affinities of a series of guests to an acyclic cucurbituril host using the BEDAM binding free energy protocol. The results were found to be in reasonably good agreement with the experimental measurements. Both energetic and entropic factors have contributed to this result. Analysis of the simulation data indicates that the conformational sampling protocol based on -hopping parallel Hamiltonian replica exchange combined with temperature replica exchange reservoirs leads to reliable convergence of the binding free energies of these systems. Inconsistencies between predicted and experimental affinities is attributed in part to deficiencies of the implicit solvent effective potential employed but also to challenges regarding the chemical modeling of the molecular systems. Each guest can exist in multiple conformational stereoisomers due to nitrogen inversion, each potentially corresponding to multiple protonation states. Uncertainties exist in regard to the correct protonation state of the host as well. A full prediction of the affinities would have required estimation of relative stereoisomer and protonation state populations, which would have considerably complicated the calculations. Attempt to use experimental pKa’s has lead to unexplained inconsistencies.
Overall, participation to the SAMPL3 challenge has been an instructive experience which has provided very useful data to better understand the strengths as well as the limits of the computational protocol and the potential energy model. We intend to pursue further the study of host-guest systems as force field validation and development platforms. Unexpectedly, this experience has also highlighted the challenge of understanding and faithfully representing the nature of the chemical system under investigation so as to properly bridge modeling predictions and measurements.
Acknowledgments
This work has been supported in part by a research grant from the National Institute of Health (GM30580). The calculations reported in this work have been performed at the BioMaPS High Performance Computing Center at Rutgers University funded in part by the NIH shared instrumentation grants no. 1 S10 RR022375 and 1 S10 RR027444, and on the Lonestar4 cluster at the Texas Advanced Computing Center under TeraGrid/XSEDE National Science Foundation allocation grant no. TG-MCB100145.
References
- 1.Gilson MK, Given JA, Bush BL, McCammon JA. The statistical-thermodynamic basis for computation of binding affinities: A critical review. Biophys J. 1997;72:1047–1069. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gallicchio Emilio, Levy Ronald M. Recent Theoretical and Computational Advances for Modeling Protein-Ligand Binding Affinities. Vol. 85. Academic Press; 2011. Advances in Protein Chemistry and Structural Biology; pp. 27–80. chapter. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gilson Michael K, Zhou Huan-Xiang. Calculation of protein-ligand binding affinities. Annu Rev Biophys Biomol Struct. 2007;36:21–42. doi: 10.1146/annurev.biophys.36.040306.132550. [DOI] [PubMed] [Google Scholar]
- 4.Shirts MR, Mobley DL, Chodera JD. Alchemical free energy calculations: ready for prime time? Ann Rep Comput Chem. 2007;3:41–59. [Google Scholar]
- 5.Mobley David L, Dill Ken A. Binding of small-molecule ligands to proteins: “what you see” is not always “what you get”. Structure. 2009 Apr;17(4):489–498. doi: 10.1016/j.str.2009.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Deng Yuqing, Roux Benoît. Computations of standard binding free energies with molecular dynamics simulations. J Phys Chem B. 2009 Feb;113(8):2234–2246. doi: 10.1021/jp807701h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chodera John D, Mobley David L, Shirts Michael R, Dixon Richard W, Branson Kim, Pande Vijay S. Alchemical free energy methods for drug discovery: Progress and challenges. Curr Opin Struct Biol. 2011;21:150–160. doi: 10.1016/j.sbi.2011.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jorgensen William L. The many roles of computation in drug discovery. Science. 2004 Mar;303(5665):1813–1818. doi: 10.1126/science.1096361. [DOI] [PubMed] [Google Scholar]
- 9.Shirts MR, Mobley DL, Brown SP. Free energy calculations in structure-based drug design. Cambridge University Press; 2010. Structure Based Drug Discovery. chapter. [Google Scholar]
- 10.Chipot Christophe, Pohorille Andrew., editors. Springer Series in Chemical Physics. Springer; Berlin Heidelberg, Berlin Heidelberg: 2007. Free Energy Calculations. Theory and Applications in Chemistry and Biology. [Google Scholar]
- 11.Head Martha S, Given James A, Gilson Michael K. Mining minima: Direct computation of conformational free energy. The Journal of Physical Chemistry A. 1997 Feb;101(8):1609–1618. [Google Scholar]
- 12.Chang Chiaen A, Chen Wei, Gilson Michael K. Ligand configurational entropy and protein binding. Proc Natl Acad Sci USA. 2007 Jan;104(5):1534–1539. doi: 10.1073/pnas.0610494104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Moghaddam Sarvin, Yang Cheng, Rekharsky Mikhail, Ko Young Ho, Kim Kimoon, Inoue Yoshihisa, Gilson Michael K. New ultrahigh affinity host-guest complexes of cucurbit[7]uril with bicyclo[2.2.2]octane and adamantane guests: thermodynamic analysis and evaluation of m2 affinity calculations. J Am Chem Soc. 2011 Mar;133(10):3570–3581. doi: 10.1021/ja109904u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gallicchio Emilio, Lapelosa Mauro, Levy Ronald M. Binding energy distribution analysis method (BEDAM) for estimation of protein-ligand binding affinities. J Chem Theory Comput. 2010 Sep;6(9):2961–2977. doi: 10.1021/ct1002913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lapelosa Mauro, Gallicchio Emilio, Levy Ronald M. Conformational transitions and convergence of absolute binding free energy calculations. J Chem Theory Comput. 2012;8:47–60. doi: 10.1021/ct200684b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gallicchio E, Levy RM. AGBNP: an analytic implicit solvent model suitable for molecular dynamics simulations and high-resolution modeling. J Comput Chem. 2004;25:479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 17.Gallicchio Emilio, Paris Kristina, Levy Ronald M. The agbnp2 implicit solvation model. J Chem Theory Comput. 2009 Sep;5(9):2544–2564. doi: 10.1021/ct900234u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wyman Ian W, Macartney Donal H. Host-guest complexations of local anaesthetics by cucurbit[7]uril in aqueous solution. Org Biomol Chem. 2010 Jan;8(1):247–252. doi: 10.1039/b915694a. [DOI] [PubMed] [Google Scholar]
- 19.Ma Da, Zavalij Peter Y, Isaacs Lyle. Acyclic cucurbit[n]uril congeners are high affinity hosts. J Org Chem. 2010 Jul;75(14):4786–4795. doi: 10.1021/jo100760g. [DOI] [PubMed] [Google Scholar]
- 20.Muddana Hari S, Daniel Varnado C, Bielawski Christopher W, Urbach Adam R, Isaacs Lyle, Geballe Matthew T, Gilson Michael K. Blind prediction of host-guest binding affinities: A new sampl3 challenge. J Comp Aided Mol Design. 2012 doi: 10.1007/s10822-012-9554-1. page In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gallicchio Emilio, Levy Ronald M. Advances in all atom sampling methods for modeling protein-ligand binding affinities. Curr Opin Struct Biol. 2011 Apr;21(2):161–166. doi: 10.1016/j.sbi.2011.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gallicchio E, Andrec M, Felts AK, Levy RM. Temperature weighted histogram analysis method, replica exchange, and transition paths. J Phys Chem B. 2005;109:6722–6731. doi: 10.1021/jp045294f. [DOI] [PubMed] [Google Scholar]
- 23.Shirts Michael R, Chodera John D. Statistically optimal analysis of samples from multiple equilibrium states. J Chem Phys. 2008 Sep;129(12):124105. doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Moult John, Fidelis Krzysztof, Kryshtafovych Andriy, Rost Burkhard, Tramontano Anna. Critical assessment of methods of protein structure prediction - round viii. Proteins. 2009;77(Suppl 9):1–4. doi: 10.1002/prot.22589. [DOI] [PubMed] [Google Scholar]
- 25.Peter Guthrie J. A blind challenge for computational solvation free energies: Introduction and overview. J Phys Chem B. 2009 Apr;113(14):4501–4507. doi: 10.1021/jp806724u. [DOI] [PubMed] [Google Scholar]
- 26.Nielsen Jens E, Gunner MR, Bertrand García-Moreno E. The pka cooperative: A collaborative effort to advance structure-based calculations of pka values and electrostatic effects in proteins. Proteins. 2011;79(12):3249–3259. doi: 10.1002/prot.23194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wodak Shoshana J. From the mediterranean coast to the shores of lake ontario: Capri’s premiere on the american continent. Proteins. 2007;69(4):697–698. doi: 10.1002/prot.21805. [DOI] [PubMed] [Google Scholar]
- 28.Boyce Sarah E, Mobley David L, Rocklin Gabriel J, Graves Alan P, Dill Ken A, Shoichet Brian K. Predicting ligand binding affinity with alchemical free energy methods in a polar model binding site. J Mol Biol. 2009 Dec;394(4):747–763. doi: 10.1016/j.jmb.2009.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hagen M, Kim B, Liu P, Berne BJ. Serial replica exchange. J Phys Chem B. 2006;111:1416–1423. doi: 10.1021/jp064479e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Roitberg Adrian E, Okur Asim, Simmerling Carlos. Coupling of replica exchange simulations to a non-boltzmann structure reservoir. J Phys Chem B. 2007 Mar;111(10):2415–2418. doi: 10.1021/jp068335b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Okumura Hisashi, Gallicchio Emilio, Levy Ronald M. Conformational populations of ligand-sized molecules by replica exchange molecular dynamics and temperature reweighting. J Comput Chem. 2010;31:1357–1367. doi: 10.1002/jcc.21419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gallicchio Emilio, Levy Ronald M, Parashar Manish. Asynchronous replica exchange for molecular simulations. J Comp Chem. 2008;29(5):788–794. doi: 10.1002/jcc.20839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jorgensen WL, Maxwell DS, Tirado-Rives J. Developement and testing of the opls all-atom force field on conformational energetics and properties of organic liquids. J Am Chem Soc. 1996;118:11225–11236. [Google Scholar]
- 34.Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. Evaluation and reparameterization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J Phys Chem B. 2001;105:6474–6487. [Google Scholar]
- 35.Nguyen Crystal, Gilson Michael K, Young Tom. Structure and thermodynamics of molecular hydration via grid inhomogeneous solvation theory. 2011 doi: 10.1063/1.4733951. arXiv:1108.4876v1 [q-bio.BM] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Banks JL, Beard JS, Cao Y, Cho AE, Damm W, Farid R, Felts AK, Halgren TA, Mainz DT, Maple JR, Murphy R, Philipp DM, Repasky MP, Zhang LY, Berne BJ, Friesner RA, Gallicchio E, Levy RM. Integrated modeling program, applied chemical theory (IMPACT) J Comp Chem. 2005;26:1752–1780. doi: 10.1002/jcc.20292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pohorille Andrew, Jarzynski Christopher, Chipot Christophe. Good practices in free-energy calculations. J Phys Chem B. 2010 Aug;114(32):10235–10253. doi: 10.1021/jp102971x. [DOI] [PubMed] [Google Scholar]
- 38.Zheng Weihua, Andrec Michael, Gallicchio Emilio, Levy Ronald M. Simple continuous and discrete models for simulating replica exchange simulations of protein folding. J Phys Chem B. 2008 May;112(19):6083–6093. doi: 10.1021/jp076377+. [DOI] [PMC free article] [PubMed] [Google Scholar]