Applying propensity scores estimated in a full cohort to adjust for confounding in subgroup analyses

Abstract

A correctly-specified propensity score (PS) estimated in a cohort (“cohort PS”) should in expectation remain valid in a subgroup population. We sought to determine whether using a cohort PS can be validly applied to subgroup analyses and thus add efficiency to studies with many subgroups or restricted data. In each of 3 cohort studies we estimated a cohort PS, defined 5 subgroups, and then estimated subgroup-specific PSs. We compared difference in treatment effect estimates for subgroup analyses adjusted by cohort PSs versus subgroup-specific PSs. Then, 10M times, we simulated a population with known characteristics of confounding, subgroup size, treatment interactions, and treatment effect, and again assessed difference in point estimates. We observed that point estimates in most subgroups were substantially similar with the two methods of adjustment. In simulations, the effect estimates differed by a median of 3.4% (interquartile [IQ] range 1.3% to 10.0%). The IQ range exceeded 10% only in cases where the subgroup had <1000 patients or few outcome events. Our empirical and simulation results indicated that using a cohort PS in subgroup analyses was a feasible approach, particularly in larger subgroups.

INTRODUCTION

Propensity scores (PSs) are widely used in comparative safety and effectiveness studies to create balance among treatment groups and thereby control confounding. They have shown particular utility in pharmacoepidemiology studies conducted within healthcare utilization databases, where cohorts are large, confounding by indication is often strong,¹ and measured confounding variables frequently outnumber outcomes.² PSs have several operational advantages as well, including their fast and robust implementation³ and an easy-to-demonstrate balance of patient characteristics after matching. PSs also retain rich confounder information while assuring the anonymity of the cohort’s patients,⁴ a desired property in pooled database studies and ongoing drug safety surveillance systems.⁵

In all of these cases, investigators may wish to examine both population average treatment effects and effects within subgroups of patients, in particular patient subgroups that may be at high risk for adverse events or be more likely to benefit from treatment.⁶ However, it remains a challenge to preserve the operational advantages of PSs across a series of subgroup analyses when each subgroup analysis requires treatment group balance for valid inference. Estimating a PS in many subgroups may be impractical or even impossible in cases when full patient-level data is not available. Given this, we examine whether using a PS estimated across the entire cohort (“cohort PS”) for inference within subgroups is a valid approach.

In a two-arm study, the PS is the predicted probability of whether a patient will receive the treatment of interest or the referent treatment, estimated as function of the patients’ measured covariates.^7,8 Given a correctly-specified propensity score, it is theoretically possible to balance treatment groups in subgroup analyses using a cohort PS given that two key conditions are met.⁸ First, the cohort PS must reflect the underlying distribution of confounders; in particular, if the subgroup of interest is those patients with C₁ = 1, and C₁ is a confounder, then C₁ must be a term in the cohort PS model. Second, both the population and the subgroup must be “large enough” for large-sample theory to hold. How large the subgroup should be, and more broadly, whether the theory applies in common epidemiologic scenarios, is not a question that has been previously answered.

In this paper, we test whether in common settings, a PS estimated in a full cohort can be validly applied to subgroup analyses. We begin with an empirical analysis of three healthcare database cohort studies. We then conduct an extensive simulation analysis. In both cases, we compare the subgroup-specific treatment effect estimates resulting from the usual practice of estimating a propensity score within the subgroup versus the estimates resulting from applying a cohort PS. We characterize the situations in which applying a cohort PS to a subgroup analysis may be feasible.

METHODS

Specification of Propensity Scores

Propensity scores are the predicted probability of exposure given a certain set of measured covariates.^7,8 After stratifying by a correctly-specified propensity score, patients can be assumed to be exchangeable within strata of PS; likewise, matching on a PS should yield a cohort is balanced between treatment groups.

Let a series of variables C_i be a study’s measured confounders. A PS is commonly estimated with a logistic model:

$$\text{logit}(\text{Pr}(X))={\mathrm{\beta }}_0+{\mathrm{\beta }}_{C1}{C}_1+{\mathrm{\beta }}_{C2}{C}_2+\dots +{\mathrm{\beta }}_{\mathit{\text{Ck}}}{C}_k$$ [1]

While this is the most commonly-used PS model, it may not be correctly specified as it may lack necessary interactions. In a PS, interactions reflect clinical situations in which treatment is assigned differently within particular subgroups. Extending Equation [1], we include a C₁ by C₂ interaction:

$$\text{logit}(\text{Pr}(X))={\mathrm{\beta }}_0+{\mathrm{\beta }}_{C1}{C}_1+{\mathrm{\beta }}_{C2}{C}_2+\dots +{\mathrm{\beta }}_{\mathit{\text{Ck}}}{C}_k+{\mathrm{\beta }}_{\mathit{\text{INT}}}{C}_1{C}_2$$ [2]

Empirical Analysis

We wished to examine whether confounding adjustment using a propensity score estimated in a full cohort (“cohort PS”, or PS_COH) yielded a different treatment effect in subgroup analyses when compared to the usual practice of adjusting by a PS estimated specifically within a subgroup (“subgroup-specific PS”, or PS_SS). We performed two example studies with three cohorts of patients. We estimated PS_COH as in equation [2], and PS_SS as:

$$\text{logit}(\text{Pr}(X|C_1=1))={\mathrm{\beta }}_0^{\prime }+{\mathrm{\beta }}_{C2}^{\prime }{C}_2+\dots +{\mathrm{\beta }}_{\mathit{\text{Ck}}}^{\prime }{C}_k$$ [3]

We examined whether there was a change in estimated treatment effects after adjusting for decile of PS_SS versus adjusting for decile of PS_COH, and after matching on PS_SS versus matching on PS_COH.

Example Study 1: Non-Steroidal Anti-Inflammatory Drug (NSAID) Initiation and Risk of Severe GI Complications

We performed a study of initiation of NSAID therapy and its relation to severe gastrointestinal (GI) complications.⁹ A dichotomous exposure variable indicated class of NSAID; non-selective NSAIDs (ibuprofen, naproxen, and diclofenac) were the referent category, which we compared to Cox-2 inhibitors (coxibs; celecoxib, rofecoxib, valdecoxib). We defined outcome as the cumulative risk of a GI complication (hospitalization for GI hemorrhage or peptic ulcer disease, or claim for associated services) within 180 days of treatment initiation. The study was performed in the Pennsylvania cohort described below. The full study design has been described in other work.^10–12

Example Study 2: APM Initiation and Risk of Short-Term Mortality

In our second example, we performed a study of initiation of conventional versus atypical anti-psychotic medications (APMs) to investigate the risk of short-term mortality, often occurring as a consequence of arrhythmias.^13–17 We defined outcome as the cumulative risk of death from any cause within 180 days of treatment initiation. The study was performed twice, once each in the British Columbia and Pennsylvania cohorts described below. As above, the full study design has been described in other work.^12,18,19

British Columbia and Pennsylvania Cohorts

We studied two cohorts of patients ≥65 years who initiated treatment with the study drugs. The first cohort was drawn from participants in Pennsylvania’s Pharmaceutical Assistance Contract for the Elderly (PACE), a drug assistance program for the state’s lower-income seniors, from the years 1994 to 2003. The second cohort was drawn from all residents of British Columbia (BC) ≥ 65 years old who initiated therapy between 1996 and 2004.

Measured Patient Characteristics & Subgroups

In each cohort, we measured age and gender, and among the PA patients, race. We also measured approximately 25 important confounders identified from previous studies that were recorded in the 180 days prior to the study exposure. These included comorbidities, prior medications, and health services utilization factors, and are displayed in Supplemental Tables S1a–S1c. Drug usage was measured from pharmacy claims data, while services and diagnoses were measured from claims submitted by medical offices and hospitals. We used these measured characteristics in each cohort to create our propensity scores.

In each case, we created five subgroups: men, women, patients aged < 75, patients aged ≥ 75, and a high-risk subgroup. In the NSAID study, this high-risk subgroup were patients with a history of GI disorders. In the APM study, the high-risk subgroup were patients with a history of cerebrovascular disease, myocardial infarction (MI), or any recorded arrhythmias. We expected some effect measure modification among the groups due to variation in the baseline risk and other factors.

Statistical Analysis

We estimated propensity scores with logistic regression models in which exposure was the dependent variable and all of the studies’ measured confounders were the independent variables. We estimated the PS_COH both without interactions (equation [1]) and with interactions among key confounders and effect modifiers (equation [2]), and did the same within each subgroup to estimate PS_SS (equation [3] for the PS_SS without interactions). In the NSAID study, the models with interactions included the 13 two-way interactions among age and gender with each of: history of GI hemorrhage; prior use of warfarin, corticosteroids, or gastroprotective drugs; and Charlson score.²⁰ In the APM studies, we included all two-way interactions among age and gender with each of: history of MI, heart failure, previous nursing home residence or hospitalization, and race (in PA).

Over the entire cohort and within each subgroup, we estimated four odds ratios and their 95% confidence intervals using logistic regression: (1) unadjusted; (2) age/sex adjusted outcome models; (3) adjusted by deciles of PS_COH; and (4) by deciles of PS_SS. We then matched both on PS_COH and PS_SS, and calculated treatment effect estimates in the two matched cohorts. Finally, we did a third matched analysis in which we matched on PS_COH but only kept matched pairs in which both patients appeared in the subgroup. Matching was performed with the 1:1 Nearest Neighbor matching algorithm provided in our Pharmacoepidemiology Toolbox (http://www.hdpharmacoepi.org).

With the estimated odds ratios, we computed our primary outcome measure Δ_β̂X, defined as the difference in the observed log odds ratio in each subgroup adjusting for or matching on PS_COH versus PS_SS. We also recorded a summary measure of balance among the treatment groups, the Mahalanobis distance.²¹ Lower distances indicate better balance.

Simulation Analysis

We undertook a simulation analysis to test certain important scenarios in a controlled environment: rare outcomes, small subgroups, strong confounding, strong confounder/treatment interactions, and strong confounder/confounder interactions within the propensity score.

Simulation Framework

We began each simulation run by creating 10 dichotomous confounders (C_i) with a randomly-chosen prevalence P(C_i) of between 5 and 25%, in increments of 5%. All simulation parameters are summarized in Table 1. We then created a model of exposure (X); frequency of exposure depended on the confounders and an interaction between confounders 1 and 2:

$$\text{logit}(\text{Pr}(X))={\mathrm{\beta }}_0+{\mathrm{\beta }}_{C1}{C}_1+{\mathrm{\beta }}_{C2}{C}_2+\dots +{\mathrm{\beta }}_{C10}{C}_{10}+{\mathrm{\beta }}_{\mathit{\text{PS−INT}}}{C}_1{C}_2$$ [4]

TABLE 1.

Explanation of simulation parameters and other symbols.

Parameter	Explanation	Range of values
X	Dichotomous exposure	0 or 1
Y	Count outcome	≥0
Ci	Ten dichotomous confounders	0 or 1
P(Ci)	Prevalence of confounder i	5% to 25% in increments of 5%
β0	Baseline exposure prevalence	25% or 50%
βCi	Strength of the confounder-exposure association	log(1.5) to log(4.0) in increments of 0.5
βPS−INT	Strength of the C1 by C2 within-PS interaction	log(1.0) log(3.0) to log(5.0) in increments of 0.5
γX	Treatment effect	log(1.0) to log(5.0) in increments of 1.0
γ0	Baseline outcome rate	0.01, 0.10, 0.25 or 0.50 events per unit of person-time
γCi	Strength of the confounder-outcome association	log(1.5) to log(4.0) in increments of 0.5
γTX−INT	Strength of the C1 by treatment interaction	log(1.0) log(3.0) to log(5.0) in increments of 0.5
PSCOH	Propensity score estimated in the entire cohort	0 to 1
PSSS	Propensity score estimated in the subgroup	0 to 1
a	Number of exposed outcomes in the entire cohort	As observed
aC1=1	Number of exposed outcomes in the subgroup of C1 =1	As observed

This model reflected the true propensity for treatment.

The baseline prevalence of exposure β₀ was randomly set to either 25% or 50%. To simulate confounding from weak to strong, the β_Ci were chosen randomly with values selected from log(1.5) to log(4.0), in increments of 0.5. To simulate a combination of positive and negative confounders, half of the selected values were inverted. β_PS−INT was simulated to either be absent or strong, with a value either of log(1.0), or of log(3.0) to log(5.0) in increments of 0.5.

We then created a population of 10,000 patients with X ~ B(Pr(X)). In this population, we created a model for outcome with average event frequency (λ):

$$\text{log}(\mathrm{\lambda })={\mathrm{\gamma }}_0+{\mathrm{\gamma }}_{X}X+{\mathrm{\gamma }}_{C1}{C}_1+{\mathrm{\gamma }}_{C2}{C}_2+{\mathrm{\gamma }}_{C3}{C}_3+{\mathrm{\gamma }}_{\mathit{\text{TX−INT}}}{\mathit{\text{XC}}}_1$$ [5]

The baseline rate of the outcome γ₀ was randomly chosen from rare (0.01 or 0.10 events per unit of person-time) to frequent (0.25 or 0.50 events per unit of person-time). As above, the γ_Ci were chosen randomly like the β_Ci, and γ_TX−INT was chosen as was β_PS−INT. γ_X, the treatment effect, was chosen as log(1.0) to log(5.0), in increments of 1.0. We then simulated count outcomes (Y) with Y ~ Poisson(λ).

Statistical Analysis

In each of 10 million simulation runs, we estimated the sample propensity scores 3 ways. We first estimated PS_COH in the entire study cohort (equation [1]), and then PS_SS among our subgroup of interest, the simulated patients with C₁ = 1 (equation [3]). To test whether proper specification of the PS model was important, we further estimated a misspecified propensity score, PS_COH−MS, which did not include the within-propensity interaction term (equation [2]).

Using Poisson regression, we then estimated the rate ratio (RR) in the subgroup of patients with C₁ = 1, adjusted separately by each of the 3 propensity scores. We also estimated the RR by adjusting by the simulated population’s true propensity for treatment. As in the empirical analysis, we considered the RR adjusted by PS_SS by to be the referent standard. To reduce computation time, we entered a continuous value of the PS in the outcome model rather than using deciles or matching.²²

As in the empirical analysis, our primary outcome measure Δ_β̂X was the absolute difference in observed treatment effect β̂_X in the subgroup of interest after adjusting for PS_COH versus PS_SS. In each simulation run, we computed Δ_β̂X as well as the percent difference in the observed point estimates. Over pre-specified groups of runs, we recorded the minimum, maximum, median and the interquartile (IQ) range of these two measures. We also computed two secondary outcomes: the median differences between (1) the point estimates after adjusting for PS_COH versus the true propensity for treatment and (2) PS_SS versus the true propensity for treatment.

Finally, to distinguish which simulation parameters may have had a meaningful effect on Δ_β̂X, we ran a linear regression model in which we predicted Δ_β̂X as a function of the selected values of β₀, γ₀, P(C_1,2,3), β_Ci, γ_Ci, β_PS−INT, γ_TX−INT, and γ_X.

The simulations were run on Amazon’s Elastic Cloud Computing (Seattle, WA), and the data analyzed on a IBM Netezza (Marlborough, MA) data warehouse appliance. Tableau Software (Seattle, WA) was used for visual analysis and figures.

RESULTS

Empirical Analysis

The three empirical cohorts had n=42,565 (BC APM study), 46,659 (PA APM study), and 49,711 (NSAID study) patients (Tables S1a–S1c in the Supplement). When stratified by quintile of PS_COH, the propensity score estimated in the entire cohort, there was reasonable balance among measured patient characteristics within each quintile. As an example, in the first quintile of the NSAID cohort (Table S1a), mean age was 73.7 years among the coxib users and 73.4 years among the ns-NSAID users; in the fifth quintile, mean age was 83.3 years versus 83.5.

In the empirical analyses, Δ_β̂X, the difference in the subgroup treatment estimates, ranged from 0% to 9% (rows labeled “Difference”, Tables 2a–2c). The highest figures were observed in the British Columbia APM cohort (Table 2c) in the high-risk subgroup (8.7% difference) and age < 75 subgroup (7.7% difference). These were the two smallest subgroups in this study and had the fewest outcomes. The analyses matched on PS_COH showed larger values of Δ_β̂X; differences were generally from 0% to 15%. The analyses matched on PS_COH in which matched pairs were kept only if both patients were in the subgroup showed the largest values of Δ_β̂X; these values were generally 0% to 20%, but in one case in the NSAID study Δ_β̂X exceeded 40%. When matching on PS_COH rather than PS_SS, the Mahalanobis distance generally grew, indicating less balance between the treatment groups.

Table 2.

a. Empirical results for the NSAID study. Key within-PS interactions were included in PS models.
Model		Entire Cohort (n=49,711)	Males (n=7,854)	Females (n=41,857)	Age <75 (n=14,103)	Age ≥75 (n=35,608)	High Risk (n=12,627)a
Exposed outcomes	N	503	71	432	83	420	348
Unexposed outcomes	N	243	57	186	49	194	157
Unadjusted	OR [CI]	1.14 [0.98, 1.33]	0.92 [0.65, 1.30]	1.21 [1.02, 1.44]	1.30 [0.91, 1.86]	1.04 [0.87, 1.23]	0.91 [0.75, 1.10]
Age/sex adjusted	OR [CI]	1.08 [0.92, 1.26]	0.87 [0.61, 1.24]	1.14 [0.95, 1.35]	1.32 [0.93, 1.89]	1.02 [0.86, 1.21]	0.88 [0.73, 1.07]
Adjusted by all covariates	OR [CI]	0.87 [0.71, 1.08]	0.68 [0.42, 1.12]	0.93 [0.73, 1.17]	1.07 [0.67, 1.72]	0.83 [0.65, 1.05]	0.74 [0.53, 1.04]
PS estimated within subgroup (PSSS) "Referent Standard"
Adj. by deciles of PSSS	OR [CI]	0.93 [0.79, 1.09]	0.80 [0.55, 1.15]	0.96 [0.80, 1.15]	1.04 [0.72, 1.50]	0.91 [0.76, 1.09]	0.90 [0.74, 1.10]
	Distanceb	0.026	0.116	0.030	0.062	0.036	0.082
Matched on PSSS	N Matched	33,188	5,812	27,368	10,758	22,370	7,204
	OR [CI]	0.97 [0.81, 1.17]	0.83 [0.55, 1.27]	0.95 [0.77, 1.16]	0.98 [0.64, 1.48]	0.89 [0.73, 1.10]	0.91 [0.72, 1.14]
	Distance	0.001	0.003	0.001	0.002	0.001	0.003
PS estimated overall (PSCOH) and applied within subgroup
Adj. by deciles of PSCOH	OR [CI]	0.93 [0.79, 1.09]	0.79 [0.55, 1.13]	0.96 [0.81, 1.15]	1.01 [0.70, 1.46]	0.92 [0.77, 1.10]	0.90 [0.74, 1.09]
	Difference (%) c	0.00 (0.0%)	−0.01 (−1.4%)	0.00 (0.0%)	−0.03 (−2.7%)	0.01 (1.3%)	−0.01 (−0.7%)
	Distance	0.026	0.127	0.032	0.069	0.036	0.089
Matched on PSCOH	N Matched	33,188	5,826	27,368	10,810	22,398	7,232
	OR [CI]	0.97 [0.81, 1.17]	0.74 [0.49, 1.13]	1.03 [0.84, 1.26]	0.98 [0.64, 1.49]	0.96 [0.79, 1.18]	0.79 [0.62, 1.01]
	Difference (%)	0.00 (0.0%)	−0.09 (−11.0%)	0.08 (8.8%)	−0.00 (−0.1%)	0.07 (7.7%)	−0.11 (−12.5%)
	Distance	0.001	0.006	0.001	0.006	0.001	0.015
Matched pairs from PSCOH matches
Matched on PSCOH	N Matched	33,188	1,278	22,886	5,000	16,482	2,112
	OR [CI]	0.97 [0.81, 1.17]	1.00 [0.45, 2.24]	0.99 [0.79, 1.23]	0.52 [0.26, 1.05]	1.05 [0.83, 1.33]	0.87 [0.54, 1.39]
	Difference (%)	0.00 (0.0%)	0.17 (19.9%)	0.04 (4.4%)	−0.46 (−46.9%)	0.16 (17.7%)	−0.04 (−4.2%)
	Distance	0.001	0.024	0.001	0.014	0.002	0.036

b. Empirical results for the Pennsylvania APM study. Key within-PS interactions were included in PS models.
Model		Entire Cohort (n=46,659)	Males (n=7,841)	Females (n=38,818)	Age <75 (n=10,035)	Age ≥75 (n=36,624)	High Risk (n=29,994)a
Exposed outcomes	N	6214	1546	4668	1213	5001	4454
Unexposed outcomes	N	2061	510	1551	127	1934	1667
Unadjusted	OR [CI]	1.36 [1.29, 1.44]	1.44 [1.28, 1.61]	1.35 [1.27, 1.43]	2.26 [1.87, 2.74]	1.37 [1.29, 1.45]	1.37 [1.29, 1.46]
Age/sex adjusted	OR [CI]	1.58 [1.50, 1.67]	1.62 [1.44, 1.83]	1.57 [1.47, 1.67]	2.36 [1.95, 2.86]	1.51 [1.43, 1.61]	1.56 [1.46, 1.66]
Adjusted by all covariates	OR [CI]	1.25 [1.16, 1.33]	1.21 [1.05, 1.40]	1.25 [1.16, 1.35]	1.29 [1.02, 1.63]	1.26 [1.17, 1.36]	1.27 [1.18, 1.38]
PS estimated within subgroup (PSSS) "Referent Standard"
Adj. by deciles of PSSS	OR [CI]	1.24 [1.16, 1.33]	1.19 [1.03, 1.37]	1.27 [1.17, 1.37]	1.19 [0.94, 1.49]	1.26 [1.17, 1.35]	1.27 [1.18, 1.38]
	Distanceb	0.365	0.828	0.359	2.037	0.296	0.420
Matched on PSSS	N Matched	18,548	3,166	15,372	2,668	15,766	12,660
	OR [CI]	1.27 [1.17, 1.37]	1.18 [1.00, 1.39]	1.28 [1.17, 1.40]	1.11 [0.84, 1.47]	1.26 [1.16, 1.36]	1.26 [1.15, 1.38]
	Distance	0.004	0.017	0.005	0.024	0.004	0.005
PS estimated overall (PSCOH) and applied within subgroup
Adj. by deciles of PSCOH	OR [CI]	1.24 [1.16, 1.33]	1.18 [1.03, 1.36]	1.27 [1.17, 1.37]	1.44 [1.15, 1.81]	1.24 [1.16, 1.33]	1.26 [1.16, 1.36]
	Difference (%)c	0.00 (0.0%)	−0.01 (−0.9%)	0.00 (0.0%)	0.25 (21.3%)	−0.02 (−1.4%)	−0.02 (−1.3%)
	Distance	0.365	1.091	0.365	1.973	0.306	0.397
Matched on PSCOH	N Matched	18,548	3,164	15,402	2,700	15,848	12,674
	OR [CI]	1.27 [1.17, 1.37]	1.10 [0.93, 1.30]	1.26 [1.15, 1.38]	1.27 [0.97, 1.67]	1.24 [1.14, 1.34]	1.22 [1.12, 1.34]
	Difference (%)	0.00 (0.0%)	−0.08 (−6.5%)	−0.02 (−1.2%)	0.16 (14.7%)	−0.02 (−1.6%)	−0.03 (−2.7%)
	Distance	0.004	0.041	0.006	0.093	0.011	0.014
Matched pairs from PSCOH matches
Matched on PSCOH	N Matched	18,548	578	12,868	462	13,454	8,402
	OR [CI]	1.27 [1.17, 1.37]	1.27 [0.86, 1.89]	1.28 [1.16, 1.41]	1.28 [0.69, 2.38]	1.23 [1.13, 1.35]	1.31 [1.18, 1.47]
	Difference (%)	0.00 (0.0%)	0.10 (8.1%)	0.01 (0.5%)	0.17 (15.5%)	−0.03 (−2.1%)	0.06 (4.5%)
	Distance	0.004	0.151	0.007	0.257	0.015	0.019

c. Empirical results for the British Columbia APM study. Key within-PS interactions were included in PS models.
Model		Entire Cohort (n=42,565)	Males (n=16,790)	Females (n=25,775)	Age <75 (n=11,899)	Age ≥75 (n=30,666)	High Risk (n=6,519)a
Exposed outcomes	N	3883	2052	1831	1190	2693	619
Unexposed outcomes	N	3015	1445	1570	430	2585	568
Unadjusted	OR [CI]	2.41 [2.29, 2.54]	2.31 [2.14, 2.50]	2.37 [2.21, 2.55]	4.37 [3.88, 4.91]	2.09 [1.97, 2.22]	1.79 [1.58, 2.03]
Age/sex adjusted	OR [CI]	2.44 [2.32, 2.58]	2.41 [2.23, 2.60]	2.47 [2.29, 2.66]	4.44 [3.95, 5.00]	2.06 [1.94, 2.19]	1.84 [1.62, 2.09]
Adjusted by all covariates	OR [CI]	2.10 [1.97, 2.23]	1.96 [1.79, 2.16]	2.22 [2.04, 2.43]	2.83 [2.44, 3.27]	1.90 [1.77, 2.04]	1.60 [1.38, 1.86]
PS estimated within subgroup (PSSS) "Referent Standard"
Adj. by deciles of PSSS	OR [CI]	1.92 [1.81, 2.04]	1.80 [1.65, 1.97]	2.04 [1.88, 2.22]	2.51 [2.20, 2.86]	1.79 [1.67, 1.92]	1.53 [1.33, 1.77]
	Distanceb	0.112	0.148	0.142	0.246	0.104	0.287
Matched on PSSS	N Matched	22,358	9,074	13,234	6,558	15,612	3,670
	OR [CI]	1.89 [1.76, 2.03]	1.74 [1.58, 1.92]	2.15 [1.95, 2.38]	2.48 [2.13, 2.89]	1.72 [1.59, 1.87]	1.45 [1.23, 1.71]
	Distance	0.003	0.004	0.004	0.005	0.002	0.009
PS estimated overall (PSCOH) and applied within subgroup
Adj. by deciles of PSCOH	OR [CI]	1.92 [1.81, 2.04]	1.82 [1.67, 1.99]	2.03 [1.87, 2.21]	2.70 [2.37, 3.07]	1.76 [1.64, 1.89]	1.40 [1.21, 1.61]
	Difference (%)c	0.00 (0.0%)	0.02 (1.1%)	−0.01 (−0.5%)	0.19 (7.7%)	−0.03 (−1.7%)	−0.13 (−8.7%)
	Distance	0.112	0.151	0.136	0.304	0.127	0.382
Matched on PSCOH	N Matched	22,358	9,090	13,266	6,640	15,664	3,708
	OR [CI]	1.89 [1.76, 2.03]	1.76 [1.60, 1.95]	2.09 [1.89, 2.31]	2.55 [2.20, 2.96]	1.71 [1.58, 1.86]	1.25 [1.06, 1.47]
	Difference (%)	0.00 (0.0%)	0.02 (1.3%)	−0.06 (−2.8%)	0.08 (3.1%)	−0.01 (−0.5%)	−0.20 (−14.0%)
	Distance	0.003	0.013	0.005	0.061	0.015	0.078
Matched pairs from PSCOH matches
Matched on PSCOH	N Matched	22,358	4,140	8,182	2,492	11,382	620
	OR [CI]	1.89 [1.77, 2.03]	1.75 [1.51, 2.03]	2.08 [1.83, 2.36]	2.51 [1.95, 3.23]	1.68 [1.52, 1.84]	1.10 [0.75, 1.60]
	Difference (%)	0.01 (0.3%)	0.01 (0.6%)	−0.08 (−3.5%)	0.04 (1.5%)	−0.05 (−2.6%)	−0.35 (−24.3%)
	Distance	0.003	0.032	0.009	0.090	0.020	0.163

^aPatients with prior gastrointestinal-related diagnoses or hospitalizations.

^bMahalanobis distance between patients in the exposure and referent categories. In the decile analyses, the distance is measured within each decile and then averaged.

^cDifference between the observed odds ratio after adjusting by or matching on PS_COH versus PS_SS.

^aPatients with a history of cerebrovascular disease, myocardial infarction, or arrhythmias.

^bMahalanobis distance between patients in the exposure and referent categories. In the decile analyses, the distance is measured within each decile and then averaged.

^cDifference between the observed odds ratio after adjusting by or matching on PS_COH versus PS_SS.

^aPatients with a history of cerebrovascular disease, myocardial infarction, or arrhythmias.

^bMahalanobis distance between patients in the exposure and referent categories. In the decile analyses, the distance is measured within each decile and then averaged.

^cDifference between the observed odds ratio after adjusting by or matching on PS_COH versus PS_SS.

Values of Δ_β̂X were far larger (0% to 25%) when the propensity score did not include key interaction terms and was thus misspecified (Tables S2a–S2a).

Simulation Analysis

Over 10 million simulation runs (Table 3 and Figure 1), we observed a median difference Δ_β̂X in the log rate ratio observed after adjusting by PS_SS versus that observed after adjusting by PS_COH of 3.4%, with an IQ range of 1.3% to 10.0%. On an absolute scale the median Δ_β̂X was small (0.040, IQ range 0.018 to 0.075); if a study’s true RR were 1.00, the median Δ_β̂X would equate to an observed RR of 1.04.

Table 3.

Simulation Results: Difference in the log of the treatment effect after adjusting by PS_COH versus PS_SS.

	Number of Runs	Correctly Specified PS Models		Misspecified PS Modelsa
Grouping of Simulation Runs		Absolute Differenceb (Median [Interquartile Range])	Percent Differencec (Median [Interquartile Range])	Absolute Difference (Median [Interquartile Range])	Percent difference (Median [Interquartile Range])
All simulation runs	10,092,231	0.040 [0.018, 0.075]	3.4% [1.3%, 10.0%]	0.096 [0.041, 0.183]	8.1% [3.0%, 22.7%]
Baseline exposure prevalence (β0)
β0 = 25%	5,050,241	0.040 [0.018, 0.077]	3.4% [1.3%, 10.2%]	0.099 [0.043, 0.188]	8.3% [3.1%, 23.4%]
β0 = 50%	5,041,990	0.039 [0.018, 0.073]	3.3% [1.2%, 9.8%]	0.092 [0.040, 0.177]	7.9% [2.9%, 22.0%]
Baseline outcome event rate (γ0)
γ0 = 0.01 events per unit of person-time	2,486,731	0.043 [0.019, 0.083]	3.0% [1.1%, 8.6%]	0.102 [0.043, 0.200]	7.1% [2.4%, 19.3%]
γ0 = 0.1 events per unit of person-time	2,533,750	0.039 [0.018, 0.073]	3.5% [1.3%, 10.5%]	0.094 [0.041, 0.179]	8.5% [3.2%, 24.0%]
γ0 = 0.25 events per unit of person-time	2,493,000	0.039 [0.018, 0.072]	3.5% [1.3%, 10.6%]	0.093 [0.041, 0.177]	8.4% [3.2%, 24.1%]
γ0 = 0.50 events per unit of person-time	2,578,750	0.038 [0.017, 0.072]	3.4% [1.3%, 10.4%]	0.094 [0.041, 0.177]	8.5% [3.2%, 23.8%]
Within-PS interactions (βPS−INT)
βPS−INT = log(1.0) (No interaction)	1,669,748	0.040 [0.018, 0.075]	3.3% [1.3%, 9.6%]	0.043 [0.019, 0.080]	3.5% [1.3%, 10.3%]
βPS−INT = log(3.0)	1,682,247	0.039 [0.018, 0.074]	3.3% [1.2%, 9.6%]	0.094 [0.043, 0.168]	7.6% [3.0%, 20.7%]
βPS−INT = log(3.5)	1,705,495	0.040 [0.018, 0.074]	3.4% [1.3%, 10.0%]	0.103 [0.048, 0.184]	8.5% [3.4%, 23.7%]
βPS−INT = log(4.0)	1,673,249	0.040 [0.018, 0.075]	3.4% [1.3%, 10.2%]	0.114 [0.053, 0.203]	9.5% [3.8%, 25.9%]
βPS−INT = log(4.5)	1,670,245	0.039 [0.018, 0.074]	3.4% [1.2%, 10.2%]	0.123 [0.057, 0.219]	10.3% [4.1%, 27.7%]
βPS−INT = log(5.0)	1,691,247	0.040 [0.018, 0.075]	3.4% [1.3%, 10.2%]	0.132 [0.061, 0.234]	11.0% [4.3%, 29.7%]
Treatment interactions (βINT)
βINT = log(1.0) (No interaction)	1,679,739	0.042 [0.019, 0.079]	4.4% [1.7%, 11.4%]	0.093 [0.041, 0.179]	10.1% [3.8%, 24.9%]
βINT = log(3.0)	1,687,495	0.040 [0.018, 0.075]	3.6% [1.3%, 10.5%]	0.095 [0.041, 0.181]	8.7% [3.2%, 23.9%]
βINT = log(3.5)	1,685,249	0.040 [0.018, 0.074]	3.3% [1.2%, 10.0%]	0.095 [0.041, 0.182]	8.0% [3.0%, 22.6%]
βINT = log(4.0)	1,670,248	0.040 [0.018, 0.074]	3.2% [1.2%, 10.1%]	0.096 [0.042, 0.183]	7.8% [2.9%, 23.2%]
βINT = log(4.5)	1,704,500	0.039 [0.018, 0.073]	3.0% [1.1%, 9.3%]	0.097 [0.042, 0.186]	7.6% [2.8%, 21.8%]
βINT = log(5.0)	1,665,000	0.039 [0.018, 0.073]	2.8% [1.1%, 8.2%]	0.097 [0.042, 0.184]	6.9% [2.6%, 19.2%]
Treatment effect (βx)
βx = log(1.0) (No effect)	1,991,749	0.040 [0.018, 0.074]	3.5% [1.5%, 7.9%]	0.095 [0.041, 0.183]	8.6% [3.5%, 18.9%]
βx = log(2.0)	2,035,996	0.040 [0.018, 0.074]	3.4% [1.4%, 7.9%]	0.096 [0.042, 0.183]	8.3% [3.2%, 18.6%]
βx = log(3.0)	2,040,746	0.040 [0.018, 0.075]	3.5% [1.3%, 11.6%]	0.096 [0.041, 0.183]	8.5% [3.1%, 26.9%]
βx = log(4.0)	2,025,247	0.040 [0.018, 0.075]	3.3% [1.2%, 14.9%]	0.096 [0.042, 0.182]	8.1% [2.8%, 32.9%]
βx = log(5.0)	1,998,493	0.040 [0.018, 0.075]	2.9% [1.0%, 11.9%]	0.096 [0.042, 0.182]	7.1% [2.5%, 25.9%]
Confounder-to-exposure association (βC1)
βC1 = log(1.5)	1,651,744	0.038 [0.017, 0.070]	3.2% [1.2%, 9.7%]	0.093 [0.040, 0.178]	8.2% [3.0%, 22.7%]
βC1 = log(2.0)	1,679,998	0.038 [0.017, 0.071]	3.2% [1.2%, 9.3%]	0.095 [0.041, 0.182]	8.1% [3.0%, 21.9%]
βC1 = log(2.5)	1,696,996	0.040 [0.018, 0.074]	3.4% [1.3%, 10.1%]	0.096 [0.041, 0.182]	8.2% [3.0%, 23.2%]
βC1 = log(3.0)	1,672,995	0.040 [0.018, 0.076]	3.4% [1.3%, 10.1%]	0.097 [0.042, 0.185]	8.1% [3.0%, 22.8%]
βC1 = log(3.5)	1,687,998	0.041 [0.018, 0.077]	3.5% [1.3%, 10.4%]	0.097 [0.042, 0.186]	8.2% [3.0%, 23.4%]
βC1 = log(4.0)	1,702,500	0.042 [0.019, 0.080]	3.5% [1.3%, 10.4%]	0.096 [0.042, 0.184]	8.1% [3.0%, 22.3%]
Confounder-to-outcome association (γC1)
γC1 = log(1.5)	1,681,999	0.040 [0.018, 0.075]	3.4% [1.3%, 10.3%]	0.097 [0.042, 0.184]	8.5% [3.2%, 23.6%]
γC1 = log(2.0)	1,700,750	0.039 [0.018, 0.074]	3.3% [1.2%, 9.8%]	0.094 [0.041, 0.180]	8.1% [3.0%, 22.3%]
γC1 = log(2.5)	1,683,748	0.039 [0.018, 0.074]	3.3% [1.2%, 9.7%]	0.095 [0.042, 0.183]	8.1% [3.0%, 22.3%]
γC1 = log(3.0)	1,658,998	0.040 [0.018, 0.075]	3.4% [1.2%, 10.1%]	0.095 [0.041, 0.181]	8.1% [3.0%, 22.4%]
γC1 = log(3.5)	1,671,245	0.040 [0.018, 0.076]	3.3% [1.2%, 10.0%]	0.095 [0.041, 0.183]	8.0% [2.9%, 22.6%]
γC1 = log(4.0)	1,695,491	0.040 [0.018, 0.075]	3.4% [1.2%, 10.0%]	0.097 [0.042, 0.184]	8.1% [3.0%, 23.0%]
Expected n in C1 subgroup (Pc1)
Expected n in subgroup = 500	2,011,249	0.072 [0.033, 0.131]	5.6% [2.1%, 15.9%]	0.126 [0.056, 0.232]	9.8% [3.7%, 27.1%]
Expected n in subgroup = 1000	2,027,982	0.048 [0.022, 0.087]	3.9% [1.5%, 11.0%]	0.104 [0.046, 0.195]	8.6% [3.2%, 23.6%]
Expected n in subgroup = 1500	2,039,250	0.038 [0.017, 0.068]	3.2% [1.2%, 9.0%]	0.093 [0.041, 0.177]	8.1% [3.0%, 22.4%]
Expected n in subgroup = 2000	2,003,500	0.032 [0.015, 0.057]	2.7% [1.0%, 7.7%]	0.086 [0.037, 0.165]	7.6% [2.8%, 21.0%]
Expected n in subgroup = 2500	2,010,250	0.027 [0.013, 0.049]	2.3% [0.9%, 6.8%]	0.076 [0.033, 0.147]	6.8% [2.5%, 19.4%]
Actual n in C1 subgroup
Actual n in subgroup ≤ 500	1,029,345	0.074 [0.034, 0.133]	5.7% [2.1%, 16.2%]	0.127 [0.057, 0.234]	9.9% [3.7%, 27.3%]
500 < Actual n in subgroup ≤ 1000	2,013,071	0.058 [0.026, 0.106]	4.6% [1.7%, 13.3%]	0.114 [0.051, 0.212]	9.1% [3.4%, 25.3%]
1000 < Actual n in subgroup ≤ 1500	2,030,107	0.042 [0.020, 0.076]	3.5% [1.3%, 9.9%]	0.099 [0.044, 0.186]	8.3% [3.1%, 23.0%]
1500 < Actual n in subgroup ≤ 2000	2,020,338	0.034 [0.016, 0.062]	2.9% [1.1%, 8.3%]	0.090 [0.039, 0.171]	7.8% [2.9%, 21.7%]
2000 < Actual n in subgroup ≤ 2500	2,004,923	0.029 [0.014, 0.053]	2.5% [1.0%, 7.3%]	0.081 [0.035, 0.156]	7.2% [2.7%, 20.3%]
Actual n in subgroup > 2500	994,447	0.027 [0.012, 0.048]	2.3% [0.9%, 6.8%]	0.076 [0.032, 0.146]	6.8% [2.5%, 19.2%]
Number of exposed outcomes in full cohort (a)
a ≤ 200	2,308,579	0.044 [0.020,0.086]	5.1% [1.6%, 15.6%]	0.100 [0.043, 0.195]	11.4% [3.6%, 34.4%]
200 < a ≤ 400	1,226,072	0.040 [0.018, 0.076]	4.9% [1.7%, 16.5%]	0.095 [0.041, 0.180]	11.4% [3.9%, 36.8%]
400 < a ≤ 750	1,500,218	0.039 [0.018, 0.074]	5.0% [1.8%, 16.3%]	0.094 [0.041, 0.177]	11.9% [4.2%, 37.2%]
a > 750	5,057,362	0.038 [0.017, 0.070]	2.5% [1.0%, 5.9%]	0.094 [0.041, 0.180]	6.2% [2.5%, 14.3%]
Number of exposed outcomes in C1 subgroup (aC1 = 1)
aC1=1 ≤ 10	1,001,185	0.060 [0.026, 0.120]	5.7% [1.6%, 16.8%]	0.120 [0.051, 0.236]	11.2% [3.1%, 33.1%]
10 < aC1=1 ≤ 25	795,308	0.047 [0.021, 0.089]	5.9% [2.0%, 17.2%]	0.100 [0.044, 0.189]	12.2% [4.3%, 35.6%]
25 < aC1=1 ≤ 50	917,105	0.045 [0.020, 0.085]	5.4% [1.9%, 16.2%]	0.097 [0.043, 0.184]	11.5% [4.1%, 34.2%]
aC1=1 > 50	7,378,633	0.037 [0.017, 0.068]	2.9% [1.1%, 7.8%]	0.092 [0.040, 0.176]	7.3% [2.8%, 19.1%]

^aModels that exclude necessary interaction terms within the propensity score.

^bMedian (interquartile range) of the absolute value of the difference in the log of the observed rate ratio between models adjusted by PS_COH versus those adjusted by PS_SS.

^cMedian [interquartile range] absolute value of the percent difference in the log of the observed rate ratio between models adjusted by PS_COH versus those adjusted by PS_SS.

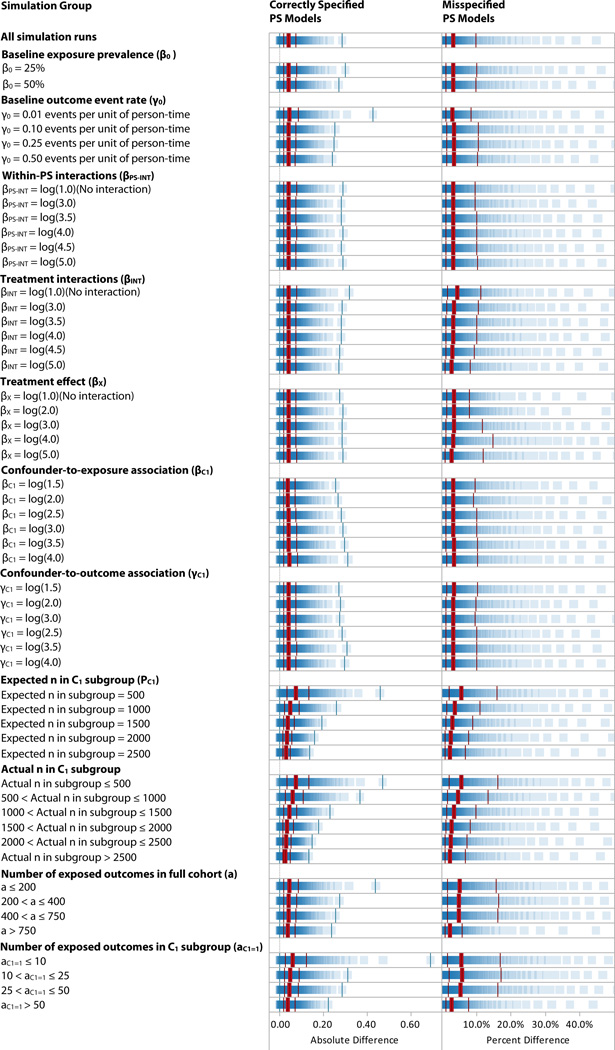
Figure 1.

Simulation Results: Difference in the log of the observed rate ratio after adjusting by PS_COH versus PS_SS. The thick bars indicate the median; the thinner bars indicate the minimum, first quartile, third quartile, and maximum.

For the correctly-specified PS models, the largest values of Δ_β̂X were in simulation runs in which the number of exposed outcomes in the subgroup was 10 to 25 (median 5.9%, IQ range 2.0% to 17.2%); the figures were similar for ≤10 outcomes and 25 to 50 outcomes, and for expected subgroup sizes of 500. With ≥50 outcomes, the upper bound of the IQ range was 7.8%. There were also relatively large median percentage differences in cases where there were ≤750 exposed outcomes in the entire cohort (approximately 5%). Simulations runs with ≥750 exposed outcomes showed the among the smallest Δ_β̂X (median 2.5%). Varying the baseline exposure prevalence (β₀), baseline outcome event rate (γ₀), strength of the treatment effect (γ_X), within-PS interaction (β_PS−INT), confounder strength (β_Ci and γ_Ci), and treatment interaction strength (γ_TX−INT) did not change the size of the difference; these differences ranged from 2% to 4% in all cases.

The misspecified PS models (Table 3 and Figure 1) showed larger differences both overall (median 8.1%, IQ range 3.0% to 22.7%) and in all specific cases. For example, in cases with 25–49 exposed outcomes in the subgroup, the median difference in the correctly-specified model was 5.4%, versus 11.5% in the misspecified models. We observed that the difference in the estimate after adjusting for PS_SS versus the known true propensity (left columns of Table S3) was generally larger than the difference after PS_COH versus adjusting for the known true propensity (right columns). Across all simulation runs, the median difference was 3.9% in the former case and 1.7% in the latter.

In the regression of the simulation parameter values on Δ_β̂X, among all simulation runs, the parameters that yielded a change in Δ_β̂X > log(1.001) were the prevalence of the C₁ subgroup indicator and γ₀, the baseline outcome rate.

DISCUSSION

Propensity score theory predicts that a PS estimated in a full cohort should remain valid within a subgroup analysis, given that the score correctly reflects the underlying propensity and that the cohort and subgroup are of sufficient size.⁸ In this paper, we examined whether this theory held true in common epidemiology and pharmacoepidemiology settings by applying both empirical and simulation approaches. In our empirical analyses of 3 cohorts of patients, we generally observed small differences (< 10%) in the log odds ratio when a the full-cohort PS was applied to a subgroup analysis. The differences were larger in cases with small subgroups or few exposed patients with outcome events. The simulation analyses confirmed and extended the empirical observations. Except when there were few outcome events, the log rate ratios we observed were substantially similar using the two propensity scores; the vast majority of simulation runs showed a small absolute difference and a <10% relative difference. Based on our observations, we believe that a propensity score estimated in a full cohort, while perhaps not ideal, can be applied to most subgroup analyses. Some caution is warranted in cases of few outcome events or small subgroups.

As expected, our observations also showed that incorrect specification of PS models often leads to biased treatment effect estimates, but specification of PS models is an issue that may be underappreciated by epidemiologists. In an informal survey of the PS literature, we found few studies that included within-PS interaction terms, even though it is easy to conceive of clinical situations in which a doctor may alter her choice of treatment based on a combination of patient factors. When we removed the interactions and thus misspecified our PS models, the difference between the models adjusted by PS_COH versus PS_SS was consistently larger. Checking that estimates do not vary as interactions are added to or removed from PS models may be a way to gauge whether the PS has been correctly specified.

Our study benefitted from making use of both actual patient data and a comprehensive simulation. However, with respect to the empirical analyses, a fuller exploration of potential within-PS interactions may have been illuminating; we chose to use strong, easily-observed covariates such as age, gender, and disease risk as a basis for interactions on the theory that these are the issues a physician would most readily consider when making treatment choices. The simulation analysis’ results may have been limited by our choice to adjust for the PS directly – rather than decile of PS or PS-matching – although in common situations, multiple studies have shown little meaningful difference in the different modeling approaches.^22,23

With the number of complex, distributed and repeated studies on the rise, particularly in the area of the comparative safety and effectiveness of medications, methods to reduce studies’ logistical and analytic challenges are key. One such question has been how to best obtain a fully-adjusted estimate in a subgroup when only a cohort-wide propensity score is available. We observed that if the cohort-wide propensity score is correctly specified, estimates of a subgroup’s treatment effect will likely be valid when the subgroup is of reasonable size and that differences, while present, were generally small. In the end, modeling the full cohort’s propensity score correctly affected validity far more meaningfully than did choice of cohort-wide or subgroup-specific score.