Computational model of a circulation current that controls electrochemical properties in the mammalian cochlea

Abstract

Sound-evoked mechanical stimuli permit endolymphatic K⁺ to enter sensory hair cells. This transduction is sensitized by an endocochlear potential (EP) of +80 mV in endolymph. After depolarizing the cells, K⁺ leaves hair cells in perilymph, and it is then circulated back to endolymph across the lateral cochlear wall. In theory, this process entails a continuous and unidirectional current carried by apical K⁺ channels and basolateral K⁺ uptake transporters in both the marginal cell and syncytial layers of the lateral wall. The transporters regulate intracellular and extracellular [K⁺], allowing the channels to form K⁺ diffusion potentials across each of the two layers. These diffusion potentials govern the EP. What remains uncertain is whether these transport mechanisms accumulating across diverse cell layers make up a continuous circulation current in the lateral wall and how this current might affect the characteristics of the endolymph. To address this question, we developed an electrophysiological model that incorporates channels and transporters of the lateral wall and channels of hair cells that derive a circulation current. The simulation replicated normal experimental EP values and reproduced experimentally measured changes in the EP and intra- and extracellular [K⁺] in the lateral wall when different transporters and channels were blocked. The model predicts that, under these different conditions, the circulation current’s contribution to the EP arises from different sources. Finally, our model also accurately simulated EP loss in a mouse model of a chloride channelopathy associated with deafness.

The mammalian cochlea is filled with two distinct extracellular solutions, perilymph and endolymph. Whereas perilymph is similar to other extracellular fluids of the body, endolymph exhibits a high [K⁺] of 150 mM and an endocochlear potential (EP) of +80 mV relative to either blood plasma or perilymph (1). The cell bodies of sensory hair cells lying on the basilar membrane are bathed in perilymph, whereas hair bundles are exposed to endolymph. Deflection of the stereocilia by acoustic stimuli results in opening of mechanoelectrical transduction (MET) channels at their tips. This process permits K⁺ to enter the hair cells, thereby depolarizing them (2). The EP sensitizes hair cells by enhancing driving force for K⁺ entry (3). K⁺ then passes through the basolateral membranes of hair cells and into the perilymph, where it is thought to be circulated back to the endolymph by K⁺ transport mechanisms in the lateral wall (Fig. 1A) (4–7). Disruption of K⁺ transport mechanisms causes deafness in mice and humans (6, 8).

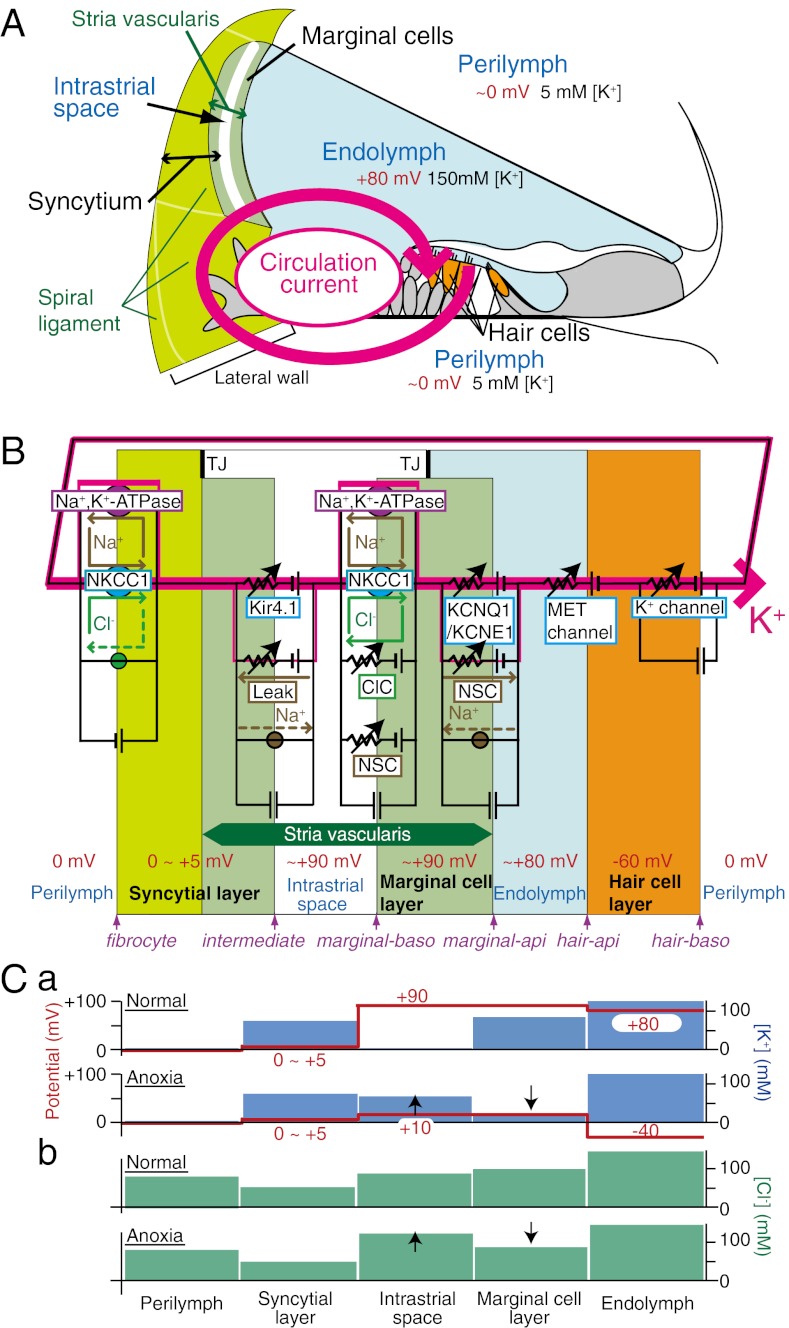
Fig. 1.

Key elements of the NHK model. (A) Structure of the cochlea and the concept underlying the circulation current. The circulation current (pink arrow) unidirectionally flows through a pathway comprising the endolymph, hair cells, perilymph, and lateral cochlear wall, and it flows back to the endolymph. In normal conditions, this flow would be carried by K⁺. (B) The electrical circuit and its components used in the modeling. The channels and transporters that are involved in driving the circulation current as well as the potential in each compartment are described. The fibrocytes belong to the spiral ligament (A). The stria vascularis contains three cell types: basal cells, intermediate cells, and marginal cells. Basal cells, which are omitted in this scheme, are apposed to the fibrocytes and intermediate cells. Note that the apical and basolateral surfaces of the syncytial layer correspond to the membranes of intermediate cells and fibrocytes, respectively. api, apical; baso, basolateral; ClC, ClC-type Cl⁻ channels; Leak, leak channels; MET, mechanoelectrical transduction; NKCC1, Na⁺, K⁺, 2 Cl⁻ cotransporter type 1; NSC, nonselective cation channels; TJ, tight junction. The circles filled with green and brown indicate the Cl⁻ and Na⁺ transporters, respectively. (C) Summary profile of [K⁺] (a; blue bars), [Cl⁻] (b; green bars), and potential (a; red lines and numbers) of the lateral wall on the basis of the experiments in the work by Nin et al. (18) and Figs. S2A and S6C. The EP primarily represents the sum of two K⁺ diffusion potentials across the apical membranes of the syncytial and marginal cell layers (C, a Upper) (18). C, a Lower shows that anoxia causes [K⁺] in the IS to increase and [K⁺] in marginal cells to decrease, modulating the two K⁺ diffusion potentials. Consequently, the EP falls to a negative value. Anoxia also changes [Cl⁻] properties (C, b). In any condition, the potential of the syncytial layer is constant. In C, a and b, up and down arrows during anoxia (Lower) indicate increase and decrease of [K⁺] or [Cl⁻], respectively, compared with normal conditions (Upper).

This net flux of K⁺, which has variously been described as the circulation current or the K⁺ cycling or K⁺ recycling pathway (4–11), might occur even in the resting state (3). In which case, such an idling current could both maintain electrochemical homeostasis within the cochlea and permit hair cells to respond rapidly to mechanical stimuli (3, 7, 12, 13). An analogous dark current exists in retinal photoreceptors (14).

The lateral cochlear wall is considered to functionally consist of two layers (Fig. 1B) (4, 5, 7, 15). One layer is a monolayer of marginal cells within the stria vascularis; the apical surfaces of these cells face the endolymph. The other layer is a syncytium that comprises intermediate and basal cells in the stria and fibrocytes in the spiral ligament. The three cell types are interconnected through gap junctions, and thus, they bear similar electrochemical properties (11). The syncytial layer exposes its basolateral surface, which contains fibrocytes, to the perilymph. The two layers sandwich numerous capillaries and an extracellular space called the intrastrial space (IS) that has fluid that shows a low [K⁺] and a potential similar to the EP (16, 17) (Fig. 1B). This positive IS potential (ISP) is a major contributor to the EP in normal conditions (16, 18).

We have recently shown that the EP largely stems from two K⁺ diffusion potentials (i.e., K⁺ equilibrium potential E_K) in the lateral wall (18, 19) (Fig. 1C, a). The first K⁺ diffusion potential dominates the ISP and is established by Ba²⁺-sensitive K⁺ channels, Kir4.1, located at the apical membranes of intermediate cells of the syncytial layer (15, 16, 20, 21). The low [K⁺] in the IS ([K⁺]_IS) is necessary for the large K⁺ diffusion potential, and it is maintained by Na⁺, K⁺-ATPases and Na⁺, K⁺, 2 Cl⁻ cotransporter type 1 (NKCC1) expressed on the basolateral membranes of the syncytial and marginal cell layers (22, 23). KCNQ1/KCNE1 K⁺ channels on the apical surfaces of marginal cells establish the second diffusion potential, and the amplitude depends on intracellular [K⁺] of marginal cells ([K⁺]_MC) (24, 25).

The work by Zidanic and Brownwell (12) measured a graded potential by serially advancing an electrode that was inserted into the perilymph. This measurement is experimental evidence for the existence of a continuous circulation current within the cochlea (13). Because the graded potential was modulated by acoustic stimuli (12), MET channels serve as the pathway for the circulation current across the hair cell layer. In the lateral wall, the pathway for the circulation current has been proposed to consist of the apical K⁺ channels and basolateral K⁺ uptake transporters in the syncytial and marginal cell layers that are crucial for the EP (4–7, 26, 27). Whether and how these separate elements in the lateral wall might assemble to drive the circulation current, however, has not yet been established. Also, the mechanisms and degree by which the circulation current contributes to the maintenance of the EP are not known. The problem is that the critical in vivo experiments that might help to elucidate the relevance of the circulation current to transporter activity regulating the EP are beyond current experimental methods.

In this study, we describe a computational approach. We assumed that the channels and transporters on each of the membranes of the lateral wall interacted and were serially connected with MET channels to form a closed-loop circuit. Our Nin–Hibino–Kurachi (NHK) model not only reproduces the electrophysiologically recorded properties within each compartment of the cochlea but also shows how the circulation current can consist of different elements and be involved in the formation of the EP under different conditions.

General Description of the Model

In our model, the circulation current and concentrations of ions in lateral wall compartments were inferred from the function of ion channels and transporters as well as morphological features of the cochlea, which included three layers and three extracellular spaces (28) (Fig. 1B). These parameters were obtained from the references tabulated in Table S1. Factors governing the activity of channels and transporters are described in SI Text. The model simulated the electrophysiological activity in a 10-μm-thick slice of the cochlea, which corresponded to the width of one row of hair cells and lateral wall cells. All simulations were carried out using the MATLAB program (Mathworks) (SI Text).

ISP and EP.

According to previous studies (16, 18), ISP and EP are defined by the relations (Eq. 1)

and (Eq. 2)

where the right-hand side terms consist of the potentials of fibrocytes (v_FC), intermediate cells (v_IM), basolateral surfaces of marginal cells (v_MB), and apical surfaces of marginal cells (v_MA). All potentials are relative to the perilymph, which is defined as 0 mV. Note that fibrocytes and intermediate cells provide the basolateral and apical surfaces of the syncytial layer, respectively, and v_FC was fixed at +3 mV in accordance with experimental data (18).

Circulation Current.

We assumed that the circulation current is established by an interplay between channels and transporters on each of the membranes of syncytial, marginal cell and hair cell layers, continuously and unidirectionally flows from endolymph to perilymph, and then returns back to endolymph across all of the six membrane compartments (Fig. 1 A and B). The membranes are, therefore, part of a closed-loop circuit that provides a pathway for the circulation current. MET channels atop the apical surface of the hair cell layer, which is assumed to have no capacitance (29), were considered the sole route for the circulation current (Fig. 1B). Thus, the circulation current, I_Cir, always equals the summed MET current, I_MET (Eq. 3):

where N_HC is the number of hair cells. The initial absolute value of the I_Cir was set to 3 nA (30).

The work by Davis (3) proposed that the amplitude of the MET current varies in proportion to the potential difference across the apical surfaces of the hair cells, v_HA. We assumed that the MET channels permeate only K⁺, which dominates the endolymph. These relations are described by (Eq. 4)

and (Eq. 5)

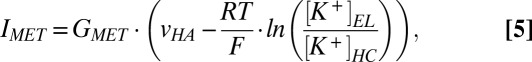where G_MET is the conductance of MET channels, v_HB is the potential of the hair cells’ basolateral surfaces, [K⁺]_EL is [K⁺] in the endolymph, [K⁺]_HC is the intracellular [K⁺] of the hair cell, R is the gas constant, T is the temperature, and F is the Faraday constant. This conductance was calculated from experimental measurements of the MET current through isolated hair cells and v_HA in the resting-state potential (30–33). Eqs. 3–5 indicate that the amplitude of the circulation current depends on the amplitude of the EP.

Membrane Potentials, Currents, and Spatial Ionic Concentrations.

I_Cir flows into a membrane, and I_M constitutes the sum of currents that pass through channels and transporters on the same membrane. At steady state, I_Cir equals I_M for all membranes. However, when either I_Cir or I_M varies relative to each other, the membrane potential, v, obeys (Eq. 6)

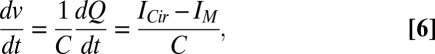where Q is the electric charge accumulated on the membrane and C is the capacitance. We used this definition to model the dynamics of membrane potentials (SI Text and Fig. S1).

Because the membrane potentials determine the EP (Eq. 2), they, in turn, modulate I_Cir (Eqs. 3–5). The potentials also directly affect the activity of channels and transporters (SI Text and Fig. S1), which further feeds back to I_M (see above). Changes in I_Cir and I_M are, therefore, cooperative and rapidly equalize. As a result, the amplitudes of I_Cir and I_M are approximately equal on the time scale of our model. In the present study, we, therefore, refer to both currents as circulation current.

In our model, the volumes of all of six extracellular and intracellular spaces of the cochlea are fixed. The [K⁺], [Na⁺], and [Cl⁻] in each space are controlled by ionic currents through the membranes (Eq. 7):

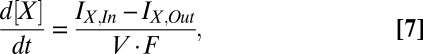where [X] is the ionic concentration, I_X,In is the inward current of X, I_X,Out is the outward current, and V is the volume of the intra-/extracellular space (Fig. S1). I_X,In and I_X,Out are the corresponding ionic currents, which are components of I_M and I_Cir. When the EP reaches a steady state, all ionic concentrations become constant (i.e., d[X]/dt = 0). In this situation, the current across any intra-/extracellular space is also constant and corresponds to I_Cir (SI Text and Fig. S1). We assumed that the Na⁺ fluxes through leak channels and nonselective cation (NSC) channels at the apical membranes of intermediate and marginal cells and the Cl⁻ flux through NKCC1 at the fibrocytes' membranes were cancelled by the fluxes of Na⁺ and Cl⁻ transporters, respectively. As a result, the net flow across membrane compartments other than the basolateral surface of the marginal cells was solely carried by K⁺ in any condition, representing a significant simplification in our model (Fig. 1B and SI Text).

In summary, Eqs. 2–7 indicate that the circulation current regulates the EP and vice versa. Furthermore, the ionic concentrations of extra-/intracellular spaces depend on the circulation current and the membrane potentials that define the EP. Accordingly, the present model proposes that the circulation current, membrane potentials, and spatial ionic concentrations are coupled.

[Cl⁻] Within the Lateral Wall.

Although Cl⁻ homeostasis in the stria vascularis seems to contribute to the EP (10), the precise [Cl⁻] of extra- and intracellular spaces of the lateral wall has not been fully elucidated. We, therefore, examined the [Cl⁻] profile by using electrodes sensitive to potential and Cl⁻ in different conditions (SI Text and Fig. S2). The measured data are summarized in Fig. 1C, b. Briefly, anoxia increased [Cl⁻] in the IS ([Cl⁻]_IS) and decreased [Cl⁻] in marginal cells ([Cl⁻]_MC), although there seems to be little gradient between these two values in normal conditions (17). This measurement was used to determine various parameters (SI Text).

Results

Simulation of Inhibition of K⁺ Transport in the Lateral Wall.

In living animals, anoxia is likely to interfere with the function of Na⁺, K⁺-ATPase in the basolateral membranes of marginal cells (22). It also seems probable that it would inhibit the concomitant transporter, NKCC1, to a similar extent (SI Text and Fig. S3). The extent of the block of these two transporters by anoxia has not been measured. Moreover, neither the volume of IS in vivo nor the conductance of basolateral NSC channels in marginal cells is known. We, thus, used estimated values (SI Text) to simulate the EP and the [K⁺] and [Cl⁻] in the IS and marginal cells under normal and anoxic conditions. When the NSC conductance and IS's volume were fixed as shown in Table S1 and the activity of both transporters was reduced to 5% of their normal value, the NHK model reasonably reproduced our experimental data (18) (Table 1, SI Text, and Figs. S2 and S4).

Table 1.

Comparison of simulated results and experimental measurement

	Simulation	Experiment	References
Guinea pigs
EP*	+74.6 mV	+78.1 ± 4.1 mV (n = 30)	17
ISP*	+83.1 mV	+80.7 ± 11.2 mV (n = 3)	16, 18
[K+]IS*	6.2 mM	4.2 ± 1.3 mM (n = 3)	18
[K+]MC*	128.1 mM	96.0 ± 12.7 mM (n = 3)	18
[Cl−]IS*	91.9 mM	92.8 ± 10.1 mM (n = 3)	Fig. S2A
[Cl−]MC*	109.2 mM	117.6 ± 21.5 mM (n = 7)	17
EP under Ba2+ block (2 min)†	+16.2 mV	+13.0 ± 2.6 mV (n = 4)	37, Fig. S6C
ISP under Ba2+ block (2 min)†	+22.0 mV	+29.6 ± 7.0 mV (n = 3)	Fig. S6C
EP under anoxia (6 min)†	−41.2 mV	−34.4 ± 10.2 mV (n = 7)	18
ISP under anoxia (6 min)†	+18.2 mV	+17.1 ± 4.3 mV (n = 3)	18
[K+]IS under anoxia (6 min)†	78.9 mM	73.5 ± 16.6 mM (n = 3)	18
[K+]MC under anoxia (6 min)†	19.0 mM	14.2 ± 8.0 mM (n = 3)	18
[Cl−]IS − [Cl−]MC under anoxia‡	29.5 mM	33.3 ± 4.8 mM (n = 3)	Fig. S2A
Barttin KO mice
EP*	+6.6 mV¶	+12.0 ± 3.1 mV (n = 14)	10

*The steady-state values in normal conditions are shown (Table S2).

^†Values for the simulations were determined at the indicated time point after the onset of anoxic or Ba²⁺ block conditions. This time point corresponded to the end point of a period of anoxic or Ba²⁺ block conditions shown in Fig. 2.

^‡The maximum difference.

^¶The conductance of ClC channels was set to 0.1 nS (Fig. 4).

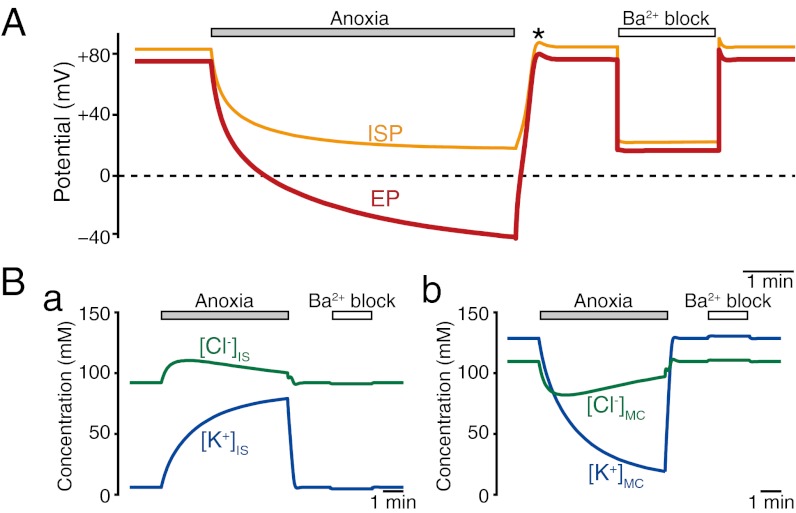
Fig. 2 illustrates the simulated electrophysiological dynamics of the endolymph, IS, and marginal cells under various conditions. The EP and ISP in normal conditions were +74.6 and +83.1 mV, respectively. Simulation of anoxia caused the EP and ISP to both decrease exponentially but with differing rates and amplitudes. Whereas the EP gradually declined with a time constant of t_1/2 = 75.3 s, the ISP decayed much more rapidly (t_1/2 = 31.9 s), nearly reaching a plateau within 3 min (Fig. 2A). At all times, the EP hyperpolarized more than the ISP. The values of the EP and ISP after 6 min of anoxia were −41.2 and +18.2 mV, respectively. Of note, similar negative EP values were recorded experimentally (34, 35) (Fig. 1C, a). On recovery from anoxia, with restoration of both transporters to full activity, both the ISP and EP recovered and briefly exhibited slight overshoots of ∼7.5 mV before returning to their initial values (18) (Fig. 2A). During this simulation of anoxia, the ion concentrations in the compartments of the lateral wall also changed dramatically (Fig. 2B). [K⁺]_IS increased from 6.2 to 78.9 mM, and [K⁺]_MC decreased from 128.1 to 19.0 mM; [Cl⁻]_IS initially increased from 91.9 to 110.6 mM but then fell by 10.3 mM, whereas [Cl⁻]_MC initially fell from 109.2 to 81.1 mM before rising by 15.5 mM. All of these behaviors of the ISP, EP, and [K⁺] and [Cl⁻] in the lateral wall were similar to experimental measurements (18) (Fig. 1C, Table 1, and Fig. S2A). [Na⁺] in the IS and inside marginal cells were also followed in the simulation, and they displayed dynamics that were symmetric to the dynamics of [K⁺] (Fig. S5A). Experimental data for [Na⁺] are not yet available.

Fig. 2.

Simulation of electrochemical properties of the lateral wall and endolymph. Traces exhibit the calculated results of the ISP (orange line in A), EP (red line in A), [K⁺] in IS and marginal cells ([K⁺]_IS and [K⁺]_MC; blue lines in B, a and b), and [Cl⁻] in the IS and marginal cells ([Cl⁻]_IS and [Cl⁻]_MC; green lines in B, a and b) in normal, anoxic, and Ba²⁺ block conditions. In this figure and subsequent figures (Fig. 3A), the initial values of all of the potentials and concentrations were steady-state values that developed over the course of 3.5 min after the start of the simulation (for the values in the initial 4 min, see Fig. S5 C and D). The asterisk in A marks the overshoots of the potentials after a period of anoxia (18).

Vascular perfusion of a Kir4.1 channel blocker, Ba²⁺, reduced the ISP and EP in a similar manner, and it affected [K⁺]_IS and [K⁺]_MC much less than anoxia (18) (Fig. S6C). To simulate the effect of Ba²⁺, we reduced the conductance of Kir4.1 channels at the apical membranes of intermediate cells by 95.5% (Fig. S6 A and B). At the onset of this condition, both the ISP and EP immediately dropped to +22.0 and +16.2 mV, respectively (Fig. 2A), consistent with experimental data (Table 1 and Fig. S6C). [K⁺]_IS and [K⁺]_MC were minimally affected (Fig. 2B). The simulated results (Fig. 2), thus, reproduce the basic feature of experimentally measured electrophysiological dynamics (18).

The successful simulation of these two experimental conditions supports the overall principles of our model. (i) There is an interplay of ion transport apparatus on each of the membranes of the lateral wall and hair cells, and these components are serially connected in a closed-loop circuit to represent the circulation current. (ii) The circulation current is coupled to all of the elements responsible for the EP, including the membrane potentials of the lateral wall and its spatial ionic concentrations.

Processes Underlying EP Reduction During Anoxia and Ba²⁺ Block.

The mechanisms by which the ISP, EP, and ionic concentrations of the lateral wall respond to anoxia and Ba²⁺ block have not yet been elucidated by experiment. We, therefore, addressed this issue in the model.

We examined the ISP and EP by first isolating their constituents: v_IM, v_MB, and v_MA (Fig. 3A). On simulated anoxia, the various potentials changed with differing kinetics. v_IM depolarized exponentially from −80.1 to −15.2 mV; the kinetics of this change seemed to bear fast and slow time constants. Whereas v_MB hyperpolarized from +3.7 mV to a peak of −8.6 mV in 1 min and then gradually returned to the initial value, v_MA monotonically depolarized from +12.2 to +57.3 mV. In contrast, simulation of Ba²⁺ block caused all potentials to change simultaneously and rapidly: v_IM depolarized from −81.5 to −19.0 mV, v_MA hyperpolarized by 2.0 mV, and v_MB depolarized by 0.8 mV.

Fig. 3.

Simulated membrane potentials and currents in the lateral wall. (A) Responses of the membrane potentials in anoxic and Ba²⁺ block conditions (solid lines) (Fig. S5C). v_MA, v_MB, and v_IM indicate the potentials across the apical and basolateral membranes of marginal cells and intermediate cells' membranes, respectively. Note that intermediate cells provide the apical surface of the syncytial layer. The purple dotted lines illustrate the change of K⁺ equilibrium potentials (E_K) across the apical membranes of marginal cells (Upper) and intermediate cells' membranes (Lower), which are calculated from [K⁺] in endolymph (Table S2) and marginal cells (Fig. 2B, b). In the IS (Fig. 2B, a) and syncytial layer (Table S2), they are calculated by the relation E_K = RT/F([K⁺]_o/[K⁺]_i), where [K⁺]_i and [K⁺]_o are intra- and extracellular [K⁺] adjacent to the membrane, respectively. (B) The behavior of the circulation current (pink). (C) The net K⁺, Na⁺, and Cl⁻ currents across the basolateral membranes of marginal cells. Each current is a sum of the respective ionic flux carried by the channels and transporters on the membranes (Fig. S7). The circulation current (pink) underlies the K⁺ current (blue) for comparison. The currents shown in this figure are derived from analysis of the data during the periods marked with the top bars in A and B.

The ISP mirrors v_IM (Eq. 1). Thus, the ISP's responses to simulations of anoxia and Ba²⁺ block result from those responses incurred by v_IM. The difference between the EP and ISP is equal to v_MB − v_MA (Eqs. 1 and 2). Throughout the duration of simulated anoxia, this difference was mainly attributable to v_MA, because its changes were considerably larger than the changes of v_MB (Fig. 3A). During simulated Ba²⁺ block, because v_MA and v_MB changed subtly, ISP and EP declined concomitantly (Fig. 2A).

Our simulations reveal possible mechanisms by which membrane potentials respond to anoxia and Ba²⁺ block. In our model, K⁺ conductance dominates the apical membranes of marginal cells and intermediate cells, whereas Cl⁻ conductance governs the basolateral surface of marginal cells (Table S1). Ionic concentrations in endolymph and the syncytial layer were nearly constant under all conditions (Table S2). Therefore, during anoxia, the drastic reactions of [K⁺] and [Cl⁻] in the IS and marginal cells (Fig. 2B) must play a central role in controlling the membrane potentials. Indeed, the K⁺ Nernst potentials (E_K) across the apical membranes of intermediate and marginal cells closely corresponded to the values of v_IM and v_MA that were simulated using the NHK model (Fig. 3A). This result agrees with our previous experimental observation that the ISP as well as the difference between the EP and marginal cells potential could be primarily described as a K⁺ diffusion potential, E_K (18, 19) (Fig. 1C, a). We found a similar relationship between E_Cl and v_MB (Fig. S5B). During Ba²⁺ block, the dynamics of spatial ionic concentrations are small, barely affecting membrane potentials (Fig. 2B). Accordingly, the behavior of v_IM clearly departed from the behavior of E_K across the apical membranes of intermediate cells (Fig. 3A). Nevertheless, in this condition, v_IM rapidly and strongly depolarized, because it is critically determined by the availability of Kir4.1 channels.

It remains unclear how anoxia alters the ionic concentrations of IS and marginal cells and why Ba²⁺ block, in contrast, evokes a relatively minimal effect. One possibility is that the circulation current responds differently during the two conditions. To test this idea, we analyzed the current across the marginal cells’ basolateral membranes, which separate these cells from the IS.

Overall, the dynamics of the circulation current always paralleled the dynamics of the EP (Figs. 2A and 3B and Eqs. 3–5). Fig. 3C elaborates the net K⁺, Na⁺, and Cl⁻ currents carried by all channels and transporters at the marginal cells’ basolateral membranes (Fig. S7). The circulation current was equal to the sum of all of these currents (General Description of the Model). In normal conditions, the membrane current was composed purely of K⁺ (Fig. 3C). At the onset of anoxia, the membrane passed far more Cl⁻ than K⁺ current. Simultaneously, Na⁺ current emerged. Consequently, whereas the Cl⁻ current was reduced to ∼0 nA in 1 min, the Na⁺ current increased to a peak of 0.72 nA around 30 s and then gradually decreased. Throughout the duration of anoxia, although the K⁺ current continued to gradually rise, its amplitude was always less than the amplitude of the circulation current. These observations indicate that a fraction of the circulation current across the marginal cells’ basolateral membranes switched from K⁺ to other ions (Fig. S7D). Consequently, K⁺ influx exceeded K⁺ efflux in the IS and vice versa in marginal cells, causing [K⁺]_IS to increase and [K⁺]_MC to decrease continuously (Fig. 2B and Fig. S1). Similarly, the additional Cl⁻ and Na⁺ currents should evoke a reaction of [Cl⁻] and [Na⁺] in the two spaces (Figs. 2B and Fig. S5). Collectively, the reduction of the EP during anoxia results from a direct modification of the profile of the circulation current.

In contrast, at the onset of Ba²⁺ block, the circulation current immediately decreased by ∼1 nA (Fig. 3B) because of its dependence on the EP (Eqs. 3–5). At the marginal cells’ basolateral membranes, K⁺ flux also reduced as much as the circulation current, but it took ∼10 s until this component reached a plateau (Fig. 3C). Thus, a small difference in amplitude between the K⁺ flux and circulation current occurred transiently, modifying [K⁺]_IS and [K⁺]_MC slightly (Fig. 2B). The charge imbalance caused by this difference was canceled by the subtle Na⁺ and Cl⁻ fluxes that emerged instantaneously (Fig. 3C). Clearly, these additional fluxes underlie the modest alternation of [Cl⁻] and [Na⁺] in the IS and marginal cells (Fig. 2B and Fig. S5).

The simulation of these two conditions shows that the involvement of the circulation current in forming the EP varies in different conditions.

Effects of Dysfunction of Cl⁻ Flow Across the Lateral Wall.

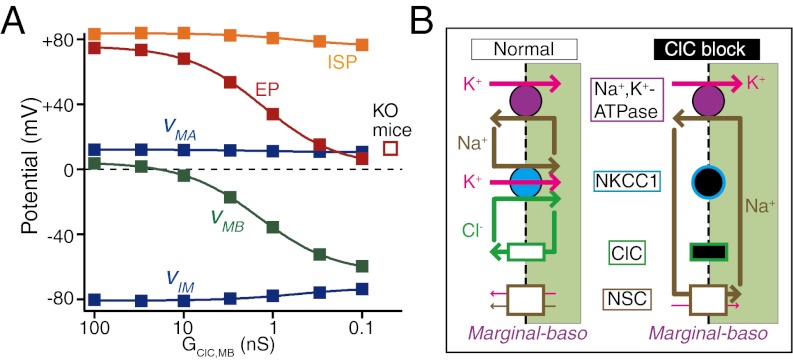
ClC-type Cl⁻ channels occur in the basolateral membranes of marginal cells. Genetic ablation of their β-subunit barttin impairs the EP and hearing in mice (9, 10). Loss-of-function mutations of the human barttin gene lead to deafness in type IV Bartter syndrome (9, 36). Therefore, Cl⁻ flow in the lateral wall contributes to the EP. We tested if our model could reproduce reduction of the EP by dysfunction of the Cl⁻ flow in the marginal cells. We decreased the conductance of ClC channels and then analyzed the steady-state potentials and ionic concentrations in the compartments of the cochlea (Fig. 4).

Fig. 4.

Effects of dysfunction of Cl⁻ flow of the lateral wall. Plotted are the steady-state values of the EP, ISP, and membrane potentials (Fig. 3A describes abbreviations) as a function of the conductance of ClC-type Cl⁻ channels (A). These potentials represent values that were predicted for a time point 18,000 s into the simulation. This ensured that all potentials represented steady-state values, therefore mimicking unperturbed values that would be measured in living animals that have varying degrees of ClC conductance. The EP measured in barttin KO mice, which lack functional ClC channels (10), is indicated by the open square. B illustrates the predicted ionic flows across the basolateral membranes of marginal cells in the normal condition (Left) and during block of ClC channels (Right). Under normal conditions, NKCC1 cancels the Cl⁻ flow through ClC channels. During block of ClC channels, Na⁺ uptake through the NKCC1 is reduced; consequently, Na⁺ inflow is rerouted from NKCC1 to NSC channels, hyperpolarizing v_MB (details in SI Text). The symbols filled with black indicate the dysfunction of the channels or transporters that is predicted to occur.

As the ClC conductance was reduced, the EP declined (Fig. 4A). When the conductance was set to 0.1% of the control (0.1 nS), the EP was +6.6 mV, which is similar to the EP measured in barttin KO mice (+12 mV) (Table 1) (10). Our model, therefore, clearly replicates the relationship between Cl⁻ homeostasis and the electrochemical properties of the lateral wall and endolymph. Of interest, the ISP remained similar to the ISP of normal conditions. An analysis of the various membrane potentials after ClC conductance reduction revealed little change in v_MA but a prominent hyperpolarization of v_MB (Fig. 4A). The latter element is, therefore, mainly responsible for the pronounced difference between the ISP and EP. Moreover, although simulated ClC channel null conditions had little effect on ionic concentrations in marginal cells (Table S2), at the basolateral surfaces, they evoked an Na⁺ influx through NSC channels that markedly increased as the ClC conductance decreased (Fig. 4B and Fig. S8). Accordingly, there was hyperpolarization of v_MB and also, reduction of the EP stem from this abnormal behavior of the Na⁺ current (Fig. 4, SI Text, and Fig. S8). Although the circulation current decreased in a manner similar to the EP, it most likely does not directly contribute to the v_MB hyperpolarization (Fig. 4B and Fig. S8). This mechanism (Fig. 4) may underlie deafness in Bartter syndrome.

Discussion

Not all of the individual elements that make up the structure and function of ion transport systems in the inner ear are known from experimental studies. We have, therefore, taken a theoretical approach to address the question of a circulation current from the endolymph to the perilymph through multiple cell layers and intercellular spaces in the lateral cochlea wall and back to the endolymph again as an element crucial for hearing. Central principles in our model are (i) channels and transporters that interact in each of the membranes of the syncytial and marginal cell layers are serially connected to MET channels in hair cells, thereby establishing a unidirectional current pathway, and (ii) the circulation current and all of the elements underlying the EP, such as the membrane potentials of the two layers of the lateral wall and their spatial ionic concentrations, are coupled (General Description of the Model). A previously described model (27) was able to predict steady-state values of the EP, but it could not address the dynamics of potentials and ionic concentrations in any compartments of the cochlea. This limitation was primarily because of the absence of spatial ionic concentrations as variables. Our model incorporated these parameters, which were allowed to vary according to ion channels and transporters (Eq. 7 and Fig. S1). In consequence, this model could reproduce both steady-state values and dynamic changes (Fig. 2 and Table 1). The principle elements and concepts underlying the model would, therefore, seem to be valid.

We show that the circulation current affects the electrochemical properties of the lateral wall and EP differently in different conditions (Fig. 3 and Fig. S7). Strikingly, during anoxia, the model predicts that the increase of [K⁺]_IS and the decrease of [K⁺]_MC—phenomena that largely account for the reduction of the EP (Fig. 1C, a) (18)—stem from a direct modification of the circulation current; its predominant charge carrier switches from K⁺ to Na⁺ and Cl⁻ at the basolateral membranes of marginal cells (Fig. 3C and Fig. S7D). In this situation, the additional Na⁺ and Cl⁻ fluxes emerge primarily through NSC and ClC channels (Fig. S7). Thus, these channels are theoretically the constituents of the pathway for the circulation current. This observation had not been suspected from experimental studies, previous models, or conceptual constructs (4–8, 11, 26, 27). However, during Ba²⁺ block, depolarization of v_IM directly reduces the EP, thereby decreasing the circulation current (Figs. 2 and 3). In this condition, modulation of the spatial ionic concentrations and membrane potentials by the circulation current seems to be only moderate, and K⁺ remains the principle charge carrier (Fig. 3 A and C and Fig. S7). Finally, our calculations reproduce the EP measured in animal models of a deaf Cl⁻ channelopathy (Fig. 4 and Fig. S8), indicating not only the robustness of our model but also, its potential use in analysis of other hearing disorders.

An idling current similar to the cochlear circulation current also seems to occur in the vestibular ampulla. The endolymph contains 150 mM [K⁺] but a potential of ∼0 mV, which is established solely by a cell layer harboring the same ion transport apparatus as the marginal cells (6). Thus, in the cochlea, the marginal cell layer may be sufficient to provide the voltage source for the circulation current. However, to maximize the hair cell sensitivity, the cochlea must additionally acquire the EP, which drives enough current through the circuit. The major source of this system is the apical K⁺ diffusion potential in the syncytial layer, which should be much larger than potential of the circulation current located in marginal cells. Consider a situation where the source of the EP was placed parallel to the circuit of the circulation current (i.e., the channels and transporters in the syncytial layer were separated from the lateral wall and directly connected to the hair cells in another circuit). In this case, the voltage supplied by the EP would be reduced rather than effectively added to the hair cells. The double cell layer of the cochlear lateral wall may serve to counter this result and serially integrate the systems of the circulation current and EP in a single circuit.