Extra twist in magnetic bubbles

In the hard disk of a computer, the memory is stored in the local direction of the magnetization of a magnetic alloy. Here, just two directions of the magnetization (e.g., parallel and antiparallel to the disk) are used. Magnets can, however, form much more complex structures. Examples are bubble domains (1), where in thin magnetic layers, a regular arrangement of magnetic bubbles is induced by small magnetic fields. In PNAS, the work by Yu et al. (2) uses EM to reveal the local orientation of the magnetization in magnetic bubbles and stripes. The magnetization shows surprising twists: instead of rotating always in one direction, it twists back and forth. Such twist may be important for the manipulation of magnetism by electric currents and electric fields.

Because magnetic fields bend the path of an electron, one can measure the local orientation of the magnetization of a thin magnetic layer by shooting electrons through it and carefully analyzing the images obtained by this method. This technique, Lorentz transmission EM, is used in the work by Yu et al. (2) to investigate how the magnetization twists in a layer of a certain magnetic material—a hexaferrite. It allows for taking pictures with nanometer resolution of the magnetization parallel to the layer. Because the amplitude of the magnetization is approximately constant, one can reconstruct the direction of the magnetization at each point in space.

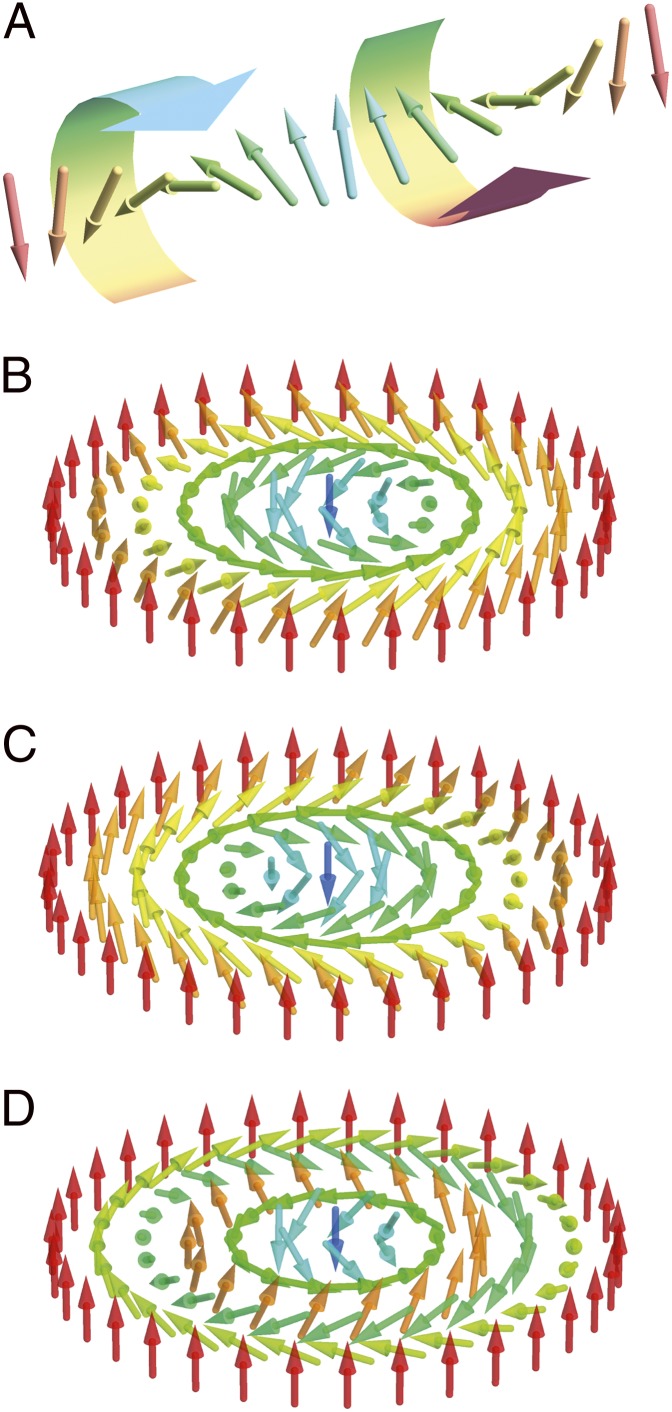
The simplest example of a magnetic structure with a rotating magnetization is a helix where the magnetization winds in one direction like the ridge of a screw. The sense of rotation, clockwise or anticlockwise when looking parallel to the helix, determines the so-called helicity. Fig. 1A shows such a helix, which first winds by 180° in one direction and then by 180° in the opposite direction. The work by Yu et al. (2) finds that such reversals of helicity occur frequently in the stripe phase of a thin magnetic layer, where dipolar forces (see below) enforce rotations of the magnetization. A small magnetic field converts the stripes into a regular array of magnetic bubbles. Fig. 1 B and C shows such bubbles where the magnetization winds smoothly from one direction in the center to the opposite direction at the edge of the figure. Models in Fig. 1 B and C differ by their helicity, and in typical bubble domains, both helicities occur with equal probability.

Fig. 1.

The work by Yu et al. (2) in PNAS reveals that changes of the helicity (i.e., the direction of rotation) are common in magnetic films. The small arrows in A show a magnetic helix with reversal of its helicity (i.e., of the direction of rotation). The helix winds first by 180° in the clockwise direction and then, by 180° in the counterclockwise direction. In small magnetic fields, magnetic bubbles form with a characteristic winding of the magnetic structure. B–D show such configurations (so-called skyrmions) schematically, where the magnetization in the center is opposite to the magnetization in the edge. B and C differ only by their helicity. In B and C, there is only one sense of rotation (i.e., one fixed helicity), whereas in D, an extra twist of the magnetization gives rise to a reversal of the helicity inside the skyrmion.

Surprisingly, the experiments in the work by Yu et al. (2) reveal that the internal structure of small magnetic bubbles can display helicity reversals. A simplified example of such a helicity reversal is shown in Fig. 1D. In contrast to the random helicity reversals within the stripe phase or the random changes of helicity from one bubble to the next, these internal twists appear in a much more regular way. The theoretical analysis shows that such extra twists are stabilized by dipolar forces between the magnetic moments (2). Such dipolar forces are, for example, familiar from the magnetic field of the earth: when moving from the equator to the magnetic North Pole, the relative orientation of the compass needle to the magnetic dipole, which gives rise to the magnetic field of the eart, changes from parallel to antiparallel. The work by Yu et al. (2) shows how such directional dependencies favor complex magnetic structures with extra twists in the magnetization.

Changes in the helicity can be fully avoided in materials where the crystal structure itself prefers one of the two helicities. Such chiral magnets [derived from the Greek χειρ (kheir) for hand] prefer either left- or right-handed helices. In a small magnetic field, they display perfectly regular arrangements of the magnetic structures shown in Fig. 1B, which are named skyrmions in this context. Furthermore, because they are not stabilized by the rather weak dipolar forces but favored more directly by the chiral atomic configuration, they can be much smaller in size (10–100 nm instead of 100–1,000 nm). First discovered in chiral magnets by neutron scattering (3), these skyrmions and the associated winding of the magnetic structure can be imaged directly using Lorentz transmission EM (4). Such magnetic structures are also interesting, because they can be manipulated by ultrasmall electric currents (5, 6). Here, the main mechanism is that the magnetic moment (the spin) of an electron moving across the magnetic structures adjusts locally to the complex magnetization pattern. By this movement, it picks up a quantum mechanical phase. The associated forces can efficiently be described by artificial electromagnetic fields, which in turn, can be used to detect the motion of the magnetic structure (6).

It is an interesting open question how the extra helicity reversals discovered in the work by Yu et al. (2) will affect the manipulation of the magnetic structure by electric fields and currents. In a recent preprint, the work by Roostaei and Nattermann (7) shows that a domain wall in a helical magnet (i.e., a plane in a 3D magnet), where the helicity is reversed (as in the middle of Fig. 1A), has rather surprising properties. On the one hand, it is very rigid, implying that forces arising from defects located close to the domain wall average out to a large extend that facilitates the motion of the domain wall. On the other hand, defects far away from the domain wall are very efficient in stopping the motion of the domain wall.

A simple analogy with the properties of screws can make this result plausible. Most screws are right-handed and can be tightened by a clockwise rotation, but for some special purposes, left-handed screws are fabricated. Now, consider a screw with a helicity reversal in its middle, where the sense of rotation of the ridge of the screw changes (Fig. 1A). Obviously, such a screw can only penetrate a piece of wood until the point is reached where the helicity is reversed. If, by some magic, it would be possible to have the whole screw inside the wood, it can be moved neither back nor forth because of the helicity reversal. Here, the forces holding the screw will not only arise from the point where the helicity is reversed but also from regions far away from this point. In analogy, the motion of a magnetic domain wall of a helix can be affected by defects located far away from the wall (7). This simple example shows how helicity reversal can dramatically affect the motion of magnetic structures and the possibility of manipulating them.