Magnetic stripes and skyrmions with helicity reversals

Abstract

It was recently realized that topological spin textures do not merely have mathematical beauty but can also give rise to unique functionalities of magnetic materials. An example is the skyrmion—a nano-sized bundle of noncoplanar spins—that by virtue of its nontrivial topology acts as a flux of magnetic field on spin-polarized electrons. Lorentz transmission electron microscopy recently emerged as a powerful tool for direct visualization of skyrmions in noncentrosymmetric helimagnets. Topologically, skyrmions are equivalent to magnetic bubbles (cylindrical domains) in ferromagnetic thin films, which were extensively explored in the 1970s for data storage applications. In this study we use Lorentz microscopy to image magnetic domain patterns in the prototypical magnetic oxide–M-type hexaferrite with a hint of scandium. Surprisingly, we find that the magnetic bubbles and stripes in the hexaferrite have a much more complex structure than the skyrmions and spirals in helimagnets, which we associate with the new degree of freedom—helicity (or vector spin chirality) describing the direction of spin rotation across the domain walls. We observe numerous random reversals of helicity in the stripe domain state. Random helicity of cylindrical domain walls coexists with the positional order of magnetic bubbles in a triangular lattice. Most unexpectedly, we observe regular helicity reversals inside skyrmions with an unusual multiple-ring structure.

Frustration of the uniform ferromagnetic order by the long-ranged dipole-dipole interactions gives rise to a wealth of intricate magnetic patterns, such as domain walls, vortices, periodic stripes, and disordered labyrinth domains (1). An applied magnetic field turns the stripe domain state into a periodic array of magnetic bubbles/skyrmions (1–4). A closely related field-induced transformation of the helical spiral into the skyrmion crystal occurs in noncentrosymmetric magnets, such as MnSi (5), Fe_1-xCo_xSi (6, 7), and FeGe (8). These examples illustrate that the mechanism of skyrmion formation for each material requires detailed studies on the magnetic anisotropy. We have listed the three main mechanisms: (i) the long-ranged magnetodipolar forces in a uniaxial-ferromagnetic-thin film with the easy axis normal to the film and (ii) the relativistic Dzyaloshinskii-Moriya (DM) interaction (9, 10) in magnets without inversion center and a weak magnetic anisotropy, to which one can add (iii) four-spin exchange interactions (11).

In spite of the common skyrmion topology, there are important differences among these three cases. First, the size ξ of the skyrmions determined by the ratio of the dipolar and exchange interactions in case (i) is typically 100 nm–1 μm, while the size of the skyrmions induced by the DM interaction is 10–100 nm. In case (iii), ξ is of the order of the crystal lattice constant (approximately 1 nm). As a result, the skyrmion crystals in cases (i) and (ii) are very “soft” and have many degrees of freedom, whereas the spin texture in case (iii) is rigid. Another important issue is helicity. The helicity of the spirals and skyrmions in case (ii) is fixed by the sign of the DM interaction, which in turn is determined by the crystal structure. In the cases of (i) and (iii), on the other hand, the two states with opposite helicities are degenerate, and hence the spontaneously chosen helicity represents an additional degree of freedom. In this paper, we provide the combined experimental and theoretical study of magnetic stripes and bubbles/skyrmions in a thin film of M-type ferrite belonging to class (i), focusing on the spin-textural richness brought about by the helicity degree of freedom.

The study of magnetic bubbles used as information bits in nonvolatile memory elements has a long history (1). The micron-sized bubbles were observed in uniaxial ferromagnets (3), garnet films (12), and amorphous alloy films (13) with the perpendicular anisotropy. The theoretical (4, 14, 15) and experimental studies (3, 12, 13) clarified the factors crucial for bubble formation, such as the quality factor Q (the ratio of the magnetic anisotropy and magnetostatic energies) and the film thickness h measured in units of the characteristic length l (the ratio of the domain wall energy per unit area and the magnetostatic energy density). Stripe domain patterns are formed in thin films of ferromagnetic materials with Q > 1. In the magnetic field applied perpendicularly to the surface of the film, the stripy pattern undergoes a transition to the hexagonal bubble lattice. The bubble size and the stripe domain width strongly depend on the film thickness and the external field. Various microscopic techniques, such as magnetic-force microscopy (16), scanning Hall microscopy (17), and Lorentz transmission electron microscopy (TEM) (3), were used to study static and dynamic properties of bubbles. Yet the details of the distribution of the magnetization in the bubble, in particular their topological properties, have not been fully unraveled. In this study, we use thin plates of Sc-doped hexagonal barium ferrite (BaFe_12-x-0.05Sc_xMg_0.05O₁₉, x = 0.16). This material, with a tunable magnetic anisotropy, was recently shown to be multiferroic (18). The relatively small quality factor Q ∼ 1 and the optimal h/l ratio help to maximize the domain wall thickness δ ∼ l/Q with respect to the bubble size or stripe width, which is important for observation of these spin textures by Lorentz microscopy. That, combined with the transport-of-intensity equation (TIE) analyses (19), makes it possible to image lateral components of magnetization.

Fig. 1 represents the room-temperature Lorentz TEM images of the 30 nm-thick (001) plate of Sc-doped M-type barium ferrite taken at different values of the magnetic field normal to the plate. The images show a large variety of magnetic domain patterns. In zero field we observe the nano-sized stripe domain state (Fig. 1A). The sharp contrast variations from dark to bright or vice versa indicate regions with maximal in-plane magnetization identified with the Bloch domain walls separating the spin-up and spin-down domains (see the local Lorentz TEM image in Fig. 2A). The ordering of magnetic stripes has many imperfections, such as stripe meandering and dislocations. As we apply magnetic field normal to the film, the transformation to the bubble (skyrmion) lattice (Fig. 1 C–E) takes place. Interestingly, the nucleation of skyrmion is facilitated by the topological defects (edge dislocation) shown in the stripe domain patterns in Fig. 1A. The stripes appear to be pinched off in a weak field generating dumbbell-shaped textures with bubble-like closed ends. Fig. 1B shows an intermediate state with coexisting stripes, dumbbells, and skyrmions. When the field exceeds 80 mT, the hexagonal skyrmion lattice is formed (Fig. 1C). The random distribution of bright and dark bubbles originates from the random helicity of their domain walls corresponding to the random winding direction of the in-plane magnetization around the skyrmion center (also called chirality), in contrast with the single-chirality skyrmions in DM helimagnets (5–8). The skyrmion size ξ decreases with increasing field, while the skyrmion lattice spacing remains practically unchanged (compare Fig. 1 C and D taken at, respectively, 100 mT and 150 mT). The bubbles first shrink retaining their shape and then completely disappear as the field exceeds 200 mT.

Fig. 1.

TEM images observed for the (001) thin plate of Sc-doped barium ferrite showing changes in magnetic domain structure produced by a magnetic field normal to the plate. (A) The stripe domains at zero field. (B) The mixed structure of stripes, dumbbells, and bubbles in a field of 80 mT. (C) The hexagonal bubble lattice with random distribution of bright/dark bubbles in 100 mT field. (D) Shrunken bubbles with the triple-circle structure in a field of 150 mT. The white or black contrast of the respective outer circle is the same as that of the innermost circle and opposite to that of the middle circle. (E) Collapse of the regular bubble lattice beginning at magnetic field of 180 mT. (F) Generation of the ferromagnetic state with uniform contrast in a field of 200 mT. The sample thickness is about 30 nm.

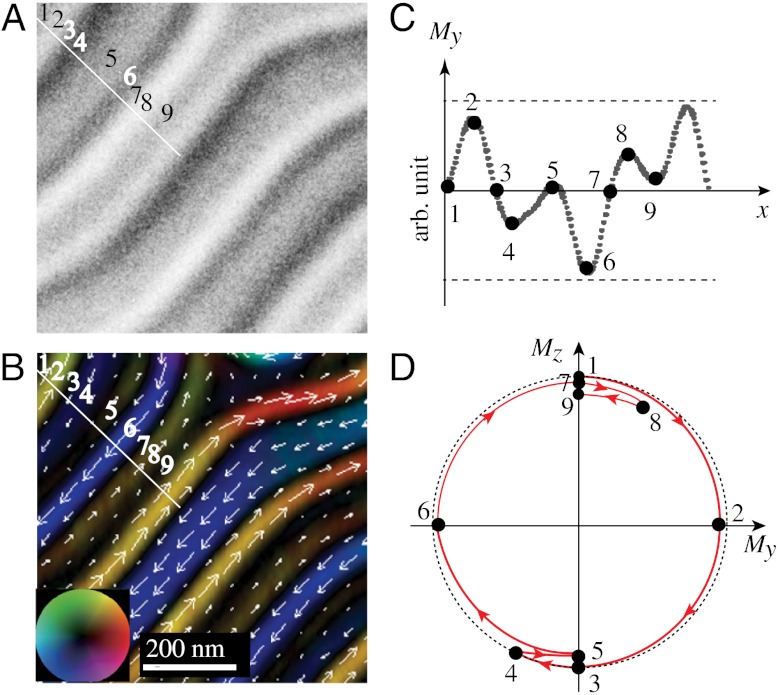
Fig. 2.

Spontaneous in-plane magnetic stripe structure of Sc-doped barium ferrite. (A and B) Lorentz TEM image (A) and the corresponding two-dimensional magnetic component maps (B). (C) The x-dependence of the lateral transverse component M_y. (D) Predicted variations of the magnetization angle θ = arctan (M_z/M_y) in the stripe structure. The numbers mark the same points in different panels. Red arrows indicate the rotation direction of the magnetization vector as x increases.

The color box in Fig. 2B displays the results of the analysis of the local Lorentz TEM images (Fig. 2A) using the TIE method (7, 8, 19, 20), which makes it possible to reconstruct the orientation and magnitude of the in-plane magnetization indicated using color vector code (see the color wheel in Fig. 2B). Black color is used for regions where no lateral component is present and magnetization is presumed to be vertical. The TIE analysis of the stripe domain state reveals unexpectedly complex patterns, very different from the periodic variation of the magnetization in the spiral state of noncentrosymmetric helimagnets (7, 8, 20). We define the ordinate x as the direction normal to the stripes (along the white straight line in Fig. 2 A and B). The estimated x-dependence of the lateral transverse component M_y is shown in Fig. 2C. In particular, at points 5 and 9, where M_y ∼ 0 and the perpendicular component of the magnetization, M_z, reaches its maximal or minimal value (we assume that (M_y)² + (M_z)² is approximately constant for this insulating magnet), the spin helicity is reversed; i.e., the derivative of the angle θ = arctan (M_z/M_y) with respect to x changes sign. The reversals also occur at the points 4 and 8, at which M_y has local minimum or maximum. In Fig. 2D, we show the conjectured x-dependence of θ in the interval between the points 1 and 9. The helicity reversals seem to occur at many random places in the stripe domain state. Similar random helicity reversals are observed everywhere in the stripe state shown in Fig. 1A.

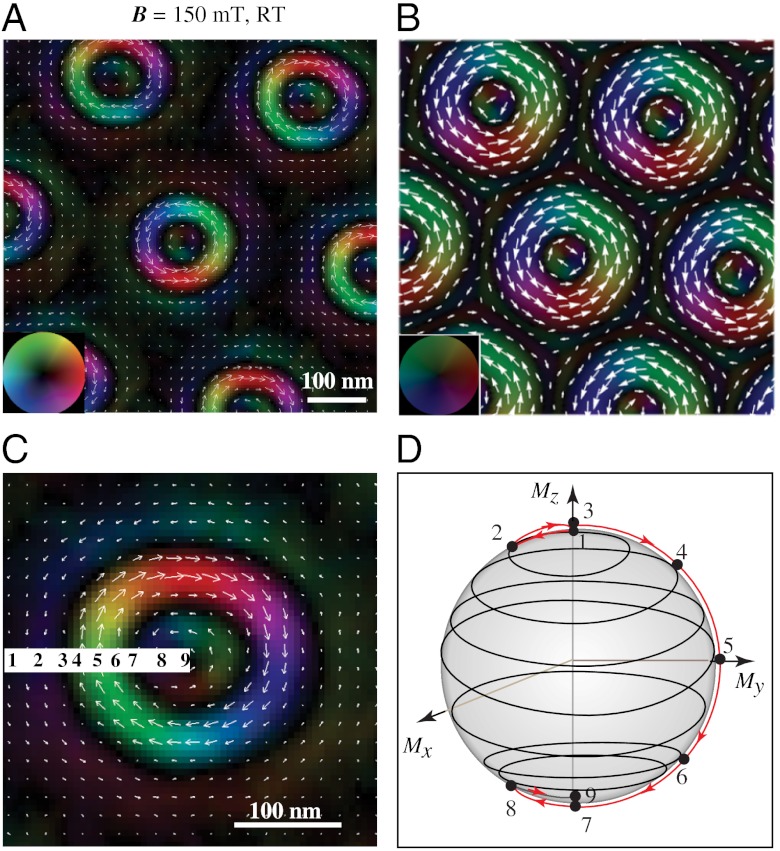
Fig. 3A shows the pattern of the lateral magnetization in the hexagonal skrymion lattice at B = 150 mT and room temperature (RT), obtained by the TIE analysis. The spin texture displays the coexistence of clockwise and counterclockwise winding spins. Each skyrmion (see the magnified image shown in Fig. 3C) is composed of three concentric rings. The winding directions in the inner and outer rings are opposite to that in the middle ring, implying helicity reversals inside the skyrmion. The magnetization is oriented downward (i.e., opposite to the applied field) at the skyrmion center and upward at its periphery. The lateral magnetization reaches maximum in the middle ring, which is brighter than the inner and outer rings. Such a topological spin texture is schematically shown in Fig. 3D, where the orientation of the magnetization vector is represented by points on a sphere. The red line with arrows shows the evolution of the magnetization vector M along the radial direction from the point 1 to point 9 in Fig. 3C. This vector undergoes the screw-like rotation from the north pole (M // +c at point 1) to the south pole (M // -c at point 9). Such a rotation differs, however, from the helical rotation characteristic of skyrmions in noncentrosymmetric magnets and conventional bubbles with the cylindrical Bloch wall and resembles more pendulum-like motion with helicity reversals occurring at points 3 and 7. The relatively small value of the in-plane magnetization in the outer and inner rings suggests that at point 3 the magnetization is oriented upward, while at point 7 it is oriented downward. Thus the net rotation angle of the magnetization vector from the periphery to the center of the bubble is π, indicating that it has the same topological charge (equal -1) as skyrmions in helimagnets. Apart from the randomness in the winding direction of skyrmions, the regularity of the helicity reversals in the triple-ring skyrmions forming a well ordered array under an applied magnetic field is markedly different from the disorder in stripe domain patterns observed at zero field.

Fig. 3.

Spin textures of room-temperature skyrmions in Sc-doped barium ferrite. (A) Triangular lattice of skyrmions with the triple-ring structure and random helicities. (B) Result of theoretical simulation of the skyrmion lattice. (C) Magnified image of the skyrmion. Color wheel and white arrows indicate the magnitude and direction of the in-plane magnetization. (D) Mapping of spin orientation in the skyrmion to the M_x-M_y-M_z sphere.

Below we shortly discuss helicity reversals from a theoretical point of view. An elegant description of the stripe domain and bubble arrays states in ferromagnetic thin films was given by Garel and Doniach (14) in the framework of Landau theory of an Ising ferromagnet with the magnetization vector normal to the film plane, supplemented with the term describing the long-range interactions between the magnetic dipoles. Because we are interested in the domain wall helicity, we extend the Garel-Doniach approach by taking into account the in-plane magnetization. We describe the magnetization of the film, M = (M_||,M_z) = (M_x,M_y,M_z), assuming the film to be sufficiently thin so that the magnetization is only a function of the in-plane coordinates, x and y: M = M(x,y); i.e., that M is independent of z.

The free energy of the model has the form

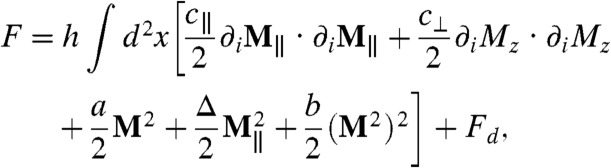[1]

where h is the film thickness, a, b, and c are the Ginzburg-Landau parameters, Δ is the easy axis magnetic anisotropy, and F_d is the magnetostatic energy. Here M_∥ describes the in-plane component of magnetization. Stripes and bubbles are only stabilized in magnets with an easy axis normal to the film plane. Positive Δ > 4π is necessary to suppress the state with a uniform in-plane magnetization. The a is a temperature-dependent coefficient of the Landau expansion changing sign at the bulk Curie temperature T_c:a(T) = α(T-T_c). The F_d has a compact expression in terms of the Fourier harmonics of the magnetization,

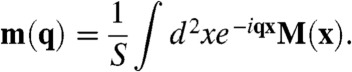[2]

(S being the film area):

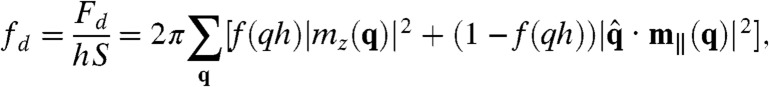[3]

where 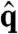is the unit in the direction of q and 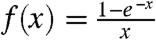. For magnetic textures varying vector slowly on the scale of the film thickness, x ≪ 1 and f(x) ≈ 1. In this limit the magnetostatic interaction is equivalent to the easy plane anisotropy, 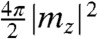. Comparing this expression with Eq. 1, we see that for the quality factor 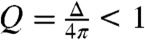, the minimal-energy spin texture is a uniform magnetic state with an in-plane magnetization, while for Q > 1 an inhomogeneous stripe domain pattern has a lower energy (the second term in the expansion, 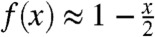, guarantees that the minimum of Eq. 1 is reached at a nonzero value of the wave vector).

For Q > 1, the in-plane magnetization appears at a lower temperature than the out-of-plane magnetization; i.e., in the stripe domain pattern appearing below the first transition temperature only M_z ≠ 0 and the transformation of collinear domain walls into Bloch walls occurs at a lower temperature, similarly to the two-stage transition in the spiral state observed in frustrated magnets (21). However, while the competing exchange interactions inducing spirals favor a single-helicity state, in the minimal-energy stripe domain state neighboring Bloch walls have opposite helicities. To understand the origin of these helicity reversals, consider magnetic stripes normal to the x-axis. From Eq. 3 it follows that the in-plane component of the magnetization, M_y(x), gives no contribution to the magnetodipolar energy, while the exchange energy is lower if M_y(x) has no zeros. The same sign of M_y corresponds to helicity reversals between the walls.

The energy minimization may not be the most important factor determining helicity of the domain walls, as the in-plane component of the magnetization and the associated energy gain due to the helicity reversals decay exponentially with the (typically large) ratio of the stripe width to the domain wall thickness. Furthermore, chirality can be reversed at defects, such as Bloch lines. In our hexaferrite films, however, Bloch lines were not observed (unless the in-plane magnetic field was applied; Fig. 4). More relevant are the topological defects in the stripe domain structure, such as disclinations or grain boundaries between stripes with different orientations, where the magnetic stripes branch off or have their end points. Because the in-plane magnetization vector rotates along the stripe edge (due to absence of Bloch lines), it has opposite orientations at the opposite sides of the stripe, so that the Bloch walls at the opposite sides have the same helicity.

Fig. 4.

Spin textures observed under magnetic fields of 80 mT with various tilt angles. (A) Stripes, dumbbells, and skyrmions with random chiralities in the normal magnetic field. (B) Mixed pattern including stripes, skyrmions, and type ∥ bubbles with Bloch lines for the tilt angle of 1.5 degree. (C) Pinched-off stripes and type ∥ bubbles with Bloch lines for the tilt angle of 2.3 degree. (D) The magnified image of (C).

The interaction with the magnetic field normal to the film plane, described by

[4]

results in the first-order transition in the state with three coexisting magnetization waves whose wave vectors q₁, q₂, and q₃ form an equilateral triangle, so that q₁ + q₂ + q₃ = 0. Such a state, favored by the quartic term in the free energy, Eq. 1, can be considered as a triangular lattice of magnetic bubbles (14). When the collinear domain wall at the boundary of the cylindrical domain transforms into a Bloch wall, the bubble turns into a skyrmion. The helicity of the Bloch wall is related to the toroidal moment of the skyrmions. The absence of long-range interactions between toroidal moments may explain the seemingly random helicities of skyrmions forming a regular triangular lattice. One can notice, however, certain short-range one-dimensional correlations between the chiralities along the basis vectors of the triangular skyrmion lattice ( Fig. 1 B–D), which are likely related to the formation of skyrmions by pinching off stripes with oriented boundaries near the topological defects.

In addition, our experiment shows multiple helicity reversals inside the stripe and cylindirical domains, which are closely related to the nonmonotonic behavior of the out-of-plane magnetization inside the domains. Such a behavior can be reproduced in numerical simulations of the extended Garel-Doniach model, in which the free energy of the skyrmion crystal was minimized on the subspace of 37 wave vectors from the reciprocal lattice (Fig. 3B). In this simulation, the out-of-plane magnetization has a “bump” in the skyrmion center, while the direction of the in-plane component of the magnetization within the single skyrmion changes its sign twice, similar to the observed double helicity reversals in skyrmions for H_z between 80 and 180 mT.

Fig. 4 shows the changes in the structure of magnetic bubbles and pinched-off stripes produced by a slight tilt of the 80 mT magnetic field off the normal direction. Fig. 4A shows bubbles with the usual skyrmion topology in the normal field. In the tilted field they transform into another type of bubbles [called type II bubbles (3)], shown in Fig. 4D, which are composed of a pair of rings with clockwise and counterclockwise winding spins (Bloch walls with opposite helicities) connected by a pair of Bloch lines. Such a bubble is topologically distinct from the skyrmion—its topological charge equals 0. As shown in Fig. 4B, at the tilt angle of 1.5 ° a large part of the skyrmions transforms into the type II bubbles, which are randomly positioned and have irregular shapes. When the tilt angle is further increased up to 2.3 ° (Fig. 4C), the skyrmions completely disappear, while the type II bubbles form regular arrays. The magnetization in the pairs of Bloch walls surrounding each cylindrical domain is largely parallel to the in-plane projection of the tilted magnetic field. Furthermore, the winding direction of spins in the peripheral regions (just outside the walls of bubbles and pinched stripes) is opposite to that in the walls, as discerned in Fig. 4C.

Also on theory grounds the long-range magnetodipolar interactions are expected to give rise to a much richer spectrum of complex magnetic patterns than the local DM interactions. We found a number of locally stable periodic spin configurations by numerically minimizing the free energy given by Eqs. 1–3 with respect to the Fourier harmonics m(q) for 91 smallest wave vectors q from the triangular lattice in the reciprocal space. The length of the basis vectors of the lattice was also optimized. Two representative examples for a = -8π, b = c_∥ = c_⊥ = 1, Δ = 4.05π (the quality factor Q = 1.0125), the film thickness h = 1.5 and zero applied magnetic field, are shown in Fig. 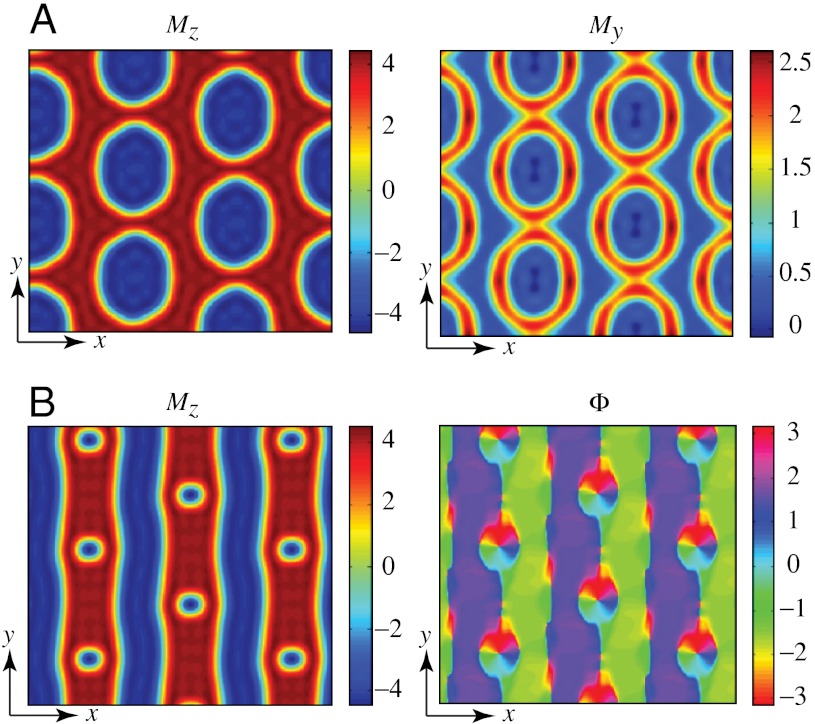5 A and B. The color plot of the out-of-plane magnetization (Fig. 5A, Left) shows that this is a bubble array state, except that bubbles are elongated along the y direction. In addition, this state has a nonzero net spontaneous magnetization along the y direction (Fig. 5A, Right). This metastable state becomes the lowest free energy state in an oblique magnetic field with both out-of-plane and in-plane components, as was observed in our experiment (see Fig. 4C). Fig. 5B Right shows another spin texture having both usual stripes and stripes with skyrmions. The angle 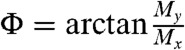describes the direction of the in-plane magnetization.

Fig. 5.

Metastable states in zero external magnetic field obtained in numerical simulations. (A) False color plot of M_z (Left) and M_y (Right) in the bubble-array state with a nonzero in-plane magnetization. (B) False color plot of M_z (Left) and the angle 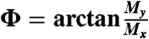, describing the direction of the in-plane magnetization (Right) for the stripes-with-bubbles state.

In conclusion, using Lorentz TEM technique we have studied the fine structure and topological properties of nano-sized magnetic domains in the thin plate of Sc-doped M-type hexaferrite at RT. The rich variety of the observed topological spin textures originates from the spin helicity reversals characteristic of domain patterns induced by magnetodipolar interactions. The in-plane magnetization profile in the stripe domain state deduced from the Lorentz TEM images suggests multiple random reversals of the spin helicity. In the magnetic field normal to the thin plate, we observe regular arrays of skyrmions with random chiralities, unusual triple-ring structure, and regular reversals of the spin helicity. Arrays of skyrmions with the multiple-ring structure and other complex magnetic patterns have also been obtained in numerical simulations based on Ginzburg-Landau theory with long-range interactions. Our results imply that thin-film ferromagnets are a fertile ground for spintronics based on manipulation of topological spin textures.

Methods

BaFe_1-x-0.05Sc_xMg_0.05O₁₉ (x = 0.16) single crystals were grown by the floating zone technique. The phase purity and compositions were checked by powder X-ray diffraction and energy dispersive X-ray spectroscopy, respectively. Bulk properties of the crystal were confirmed to be identical with those reported in the literature (18). An electron-transparent thin plate with thickness of about 30 nm was prepared by mechanical polishing and subsequent argon-ion thinning with an acceleration voltage of 4 kV at RT. The magnetic domain configurations were observed by the Lorentz TEM. The Lorentz TEM is a powerful tool to directly observe magnetic structures in FM materials with the high spatial resolution of nanometer in size. This technique is free from the external magnetic field applied normal to the thin plate and can probe the in-plane magnetization information due to the deflections of electron beam under the Lorentz forces induced by the in-plane magnetic components of the materials. On the basis of the defocused Lorentz images, the TIE analysis (7, 8, 19, 20) can give the distribution of the in-plane magnetization. The sample was positioned within the objective magnetic lens region (7, 8). To investigate the magnetic-field dependence of magnetic structures, we performed Lorentz TEM by changing the objective lens current to obtain a variable magnetic field normal to the film surface (7). When we change the lens current, the sample is subject to the magnetic field 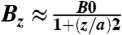, where B₀ is a field at z = 0 and a is the focal length. Both parameters are determined by objective lens current.