Global or local? Predicting secondary structure and accessibility in mRNAs

Abstract

Determining the structural properties of mRNA is key to understanding vital post-transcriptional processes. As experimental data on mRNA structure are scarce, accurate structure prediction is required to characterize RNA regulatory mechanisms. Although various structure prediction approaches are available, it is often unclear which to choose and how to set their parameters. Furthermore, no standard measure to compare predictions of local structure exists. We assessed the performance of different methods using two types of data: transcriptome-wide enzymatic probing information and a large, curated set of cis-regulatory elements. To compare the approaches, we introduced structure accuracy, a measure that is applicable to both global and local methods. Our results showed that local folding was more accurate than the classic global approach. We investigated how the locality parameters, maximum base pair span and window size, influenced the prediction performance. A span of 150 provided a reasonable balance between maximizing the number of accurately predicted base pairs, while minimizing effects of incorrect long-range predictions. We characterized the error at artificial sequence ends, which we reduced by setting the window size sufficiently greater than the maximum span. Our method, LocalFold, diminished all border effects and produced the most robust performance.

INTRODUCTION

In recent years, our perception of RNA has seen a strong shift from its role as a messenger to its roles in the regulation of a plethora of cellular processes. Here, RNA regulatory functions are often guided by its structural conformation. For example, local structures in messenger RNA (mRNA) can regulate protein gene expression. In this work, we focused on the secondary structure of mRNAs to determine and enhance the prediction performance of current computational approaches.

Many existing methods of experimental and computational structure determination concentrated on regulatory non-coding RNA (ncRNA) (1–3); notable examples are transfer RNA, ribosomal RNA, small nucleolar RNA, microRNA and small interfering RNA. In comparison, little research was dedicated to the more challenging task of elucidating the structural properties of mRNA. This is surprising, since a vast number of cis-regulatory structures (4), e.g. riboswitches (5), iron response elements (IRE) (6), internal ribosome entry sites (IRES) (7), and selenocysteine insertion sequences (SECIS) (8), are located on mRNA transcripts, predominantly in the untranslated regions. Recently, experimental approaches for transcriptome-wide enzymatic structural probing were introduced (9,10). Going beyond individual structures, more general metrics such as folding energy or accessibility were associated with translational efficiency (11,12), the viability of protein-binding sites (13,14), and the efficacy of small ncRNA target sites (15–20). These metrics were also the basis of many current algorithms for the detection of mRNA targets of small ncRNAs (15,21,22) and RNA-binding proteins (23,24).

As experimental data on mRNA structure are scarce, research into post-transcriptional regulation is greatly enhanced by the use of predicted mRNA structures. The classical algorithms for RNA secondary structure prediction are global approaches that determine the minimum free energy (MFE) structure (25) or the Boltzmann ensemble of all possible structures calculated by the partition function method (26). In global folding there is no restriction on the span of base pairs and structures are considered for the entire RNA molecule. This approach is implemented in e.g. RNAfold (27), UNAfold (formerly known as mfold) (28) and RNAstructure (29). A major challenge in global folding is the correct prediction of long-ranging base pairs (30). Furthermore, the global folding approach is cubic in time, reduced to quadratic on average for MFE predictions (31). Therefore, it is too slow for genome-wide applications. Moreover, the mRNA is translated and regulated by a plethora of molecules binding to it; these can influence its global conformation. Hence, probable local structures might be more relevant for regulatory function. Some local folding approaches have been proposed to account for these challenges: (i) Structures are kept local by restricting the maximum distance allowed between the two nucleotides that form a base pair, e.g. in RNALfold (32), Rfold (33) and Raccess (20). (ii) A window-based approach to further accommodate the uncertainty of global structure by multiple stabilizing and destabilizing factors was developed and implemented in RNAplfold (34). The runtime of all local folding algorithms is linear with respect to sequence length and they are easily applicable on a genome-wide scale.

In this work, we focused on three major unresolved problems involving the secondary structure prediction of mRNAs: (i) No comprehensive comparison of the performance of global versus local folding exists. (ii) Local approaches require the user to set additional parameters such as the base pair span and window size, which can not be easily determined from experimental data or biophysical principles. Moreover, an in-depth qualitative investigation of the locality parameters is still required. (iii) To detect cis-regulatory elements in predicted base pair probabilities, a quality measure for the stability of the structural element within a greater context is needed.

The comparison of methods requires data of high-quality structures. For benchmarking accessibility (i.e. single-strandedness of nucleotides), we used recently available transcriptome-wide structural probing data (9). This data, however, does not provide explicit information on base pairs, which is required to locate structured cis-regulatory elements. Structural information on these elements is stored in the Rfam database (2,35), which we filtered and processed to optimize structural integrity. As a result, we had two benchmarking datasets covering both aspects of secondary structure, namely base pairing and single-strandedness.

We introduced suitable measures for determining and comparing the quality of structure prediction. Subsequently, we used our benchmark datasets to perform the first comprehensive study of the qualitative differences between global and local approaches. For local folding, we assessed the two parameters of locality: the maximum base pair span and the window size. We identified optimal parameter settings for our benchmark data and analysed the relation between the parameters. We identified artefacts introduced by window borders and present a new method to reduce these effects.

Previous investigations of the locality parameters were centred around specific applications. For example, Tafer et al. evaluated effects of accessibility on the efficacy of small interfering RNA interactions (16). Folding parameters that achieved the most significant results, a window size of 80 nucleotides (nt) and a maximum base pair span of 40 nt, were subsequently used as standard values for local secondary structure predictions (14,22,24). Similar analyses were performed in (20,36). A window size that was equal to the maximum base pair span was used in (33) and it is also the default setting in RNAplfold. Our benchmark analysis showed that these previously used parameters performed poorly.

Our LocalFold method that reduces the detrimental effects of artificial window borders produced more robust mRNA secondary structure predictions on curated benchmark datasets compared to other available tools.

Availability

LocalFold, with the default parameters set to the the optimal values derived in this work, is available on www.bioinf.uni-freiburg.de/Software/LocalFold/. The dataset of mRNA cis-regulatory structures is available on http://lancelot.otago.ac.nz/CisRegRNA/.

MATERIALS AND METHODS

Secondary structure measures

Base pair span

The base pair span, bp-span, is the distance between the positions i and j of a base pair (i, j):

(1)

Accessibility

We used a position-wise accessibility pu(i) that is the probability of base_i (a nucleotide at position i in the RNA sequence) to be unpaired, i.e. single stranded. Hence, the accessibility of base_i is the complement of the sum of all base pair probabilities involving this nucleotide:

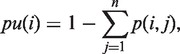(2)

where n is the length of the RNA sequence; (i, j) is a base pair between base_i and base_j; and p(i, j) is the probability for the base pair (i, j) according the the McCaskill algorithm (26). Equation 7 defines the average accessibility for window-based methods.

Available prediction algorithms for benchmarking

For benchmarking structure prediction methods, we made a careful selection of algorithms that reflect the current status of secondary structure prediction. Due to their broad usage, we concentrated on partition function-based approaches that produce probabilities or average probabilities for base pairs, given an RNA sequence (see Table 1).

Table 1.

Summary of the prediction methods and the benchmark datasets used in this work. L is the max. base pair span and W is the window size

Method	Parameters	Type	Output
RNAfold	–	Global	Base pair probabilities
Rfold	L	Local	Base pair probabilities
Raccess	L	Local	Accessibilities
RNAplfolda	L, W	Local	Average base pair probabilities and accessibilities
LocalFolda	L, W, b	Local	Average base pair probabilities and accessibilities

Dataset	Description
CisReg	2500 cis-regulatory elements in 95 Rfam families, filtered and processed in this work
YeastUnpaired	Data on the single-strandedness of single positions for 3196 Saccharomyces cervisiae mRNAs from (9)

^aWindow-based approach.

Three popular global folding methods exist: RNAfold (27), UNAfold (28) and RNAstructure (29). The individual tools each implement different features useful for RNA structure analysis, however, the method for predicting base pair probabilities is identical. We used RNAfold to represent global folding. Two types of local structure prediction algorithms exist. The first type restricts the base pair spans of the predicted structures to a maximum length. As this approach still folds the entire input sequence simultaneously and merely restricts the base pair spans of the predicted structures, we consider it to be semi-local. The second type, in addition to imposing a maximum base pair span, predicts structures in sliding windows. The results of the windows are then averaged. This window-based approach is local in the sense that each window is folded independently of the rest of the sequence. Nevertheless, a single window is folded semi-locally as before. Approaches that predict true local structures, without the use of fixed windows, currently do not exist. For the first local folding approach in which only the maximum base pair span is restricted to L, we used Rfold (33) for base pair probabilities and Raccess (20) for accessibilities. For the second approach, we used the frequently cited, local window-based approach, RNAplfold (34,37), that introduces the window size parameter W. Further details on the differences of these methods and their execution calls can be found in the Supplementary Data.

Data

CisReg: structured cis-regulatory elements

For bench-marking purposes, we curated a set of 2500 high quality, structured cis-regulatory elements (>85 000 base pairs), extracted from 95 hand-selected families from the Rfam database (2,35). This CisReg dataset is discussed in the ‘Results’ section. Additional information is given in the Supplementary Data and on the database website.

YeastUnpaired:  single strandedness

For the evaluation of the accessibility predictions we used the set of in vitro secondary structure profiles from (9). This set, referenced as YeastUnpaired in this article, consists of nucleotide-wise measurements for 3196 mRNAs from Saccharomyces cervisiae. These profiles were derived by parallel analysis of RNA structure (PARS). With PARS, the single-strandedness (as well as double-strandedness) of a set of sequences is inferred using a combination of RNase digestion and deep sequencing. Kertesz et al. report that they covered approximately 100-fold more transcribed bases than all previously published footprints combined, making this dataset uniquely suited for a comprehensive analysis of prediction performance.

Performance comparison measures

Structure accuracy

We required a measure to compare probabilities, as calculated by RNAfold (global) and Rfold/Raccess (local), to average probabilities, as calculated by RNAplfold and LocalFold (also local). This comparison is non-trivial and has not been previously addressed in the literature (to the extent of the authors' knowledge). In addition, these methods generate probabilities for individual base pairs, whereas we required a measure for a complete structure, i.e. a cis-regulatory element. Previous approaches for comparing predictions were based on individual base pairs and not on entire structures (33). In the investigation of cis-regulatory elements, however, we required a measurement for the stability of a local structured element within a greater context. More precisely, we needed to determine the accuracy of the prediction of the entire element based on individual base pair scores. In the literature, there was no consistent measure for this purpose, however, structure stability measures have been applied to global structures (38,39,40). We generalised the measure of structure accuracy to local structure prediction.

Let R be an RNA sequence, and S_l be a local structured element in R. The accuracy 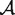is the expected overlap of a local structure S_l and a global structure S of R:

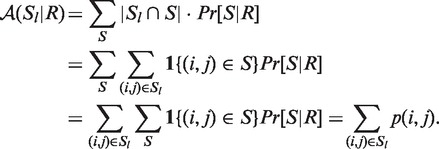(3)

1 {(i, j) ∈ S} is an indicator function that is 1 if (i, j) ∈ S and 0 otherwise.

For window-based approaches, the probability of observing a given base pair (or structure) in a window is comprised of the probability for choosing the window w and the probability of observing the base pair (structure) in w. Each window has an equal probability and the structures within each window are Boltzmann distributed as in global folding (26). For each base pair (i, j), RNAplfold averages over all windows w containing the base pair:

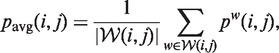(4)

where p^w(i, j) is the base pair probability of (i, j) in the window w and 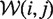is the set of all windows that include the base pair (i, j).

Regarding the accuracy of a local structure element S_l, we define 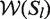to be the set of windows that contain the complete structure S_l, similar to the previous definition in the case of a base pair. Then we define the average accuracy as:

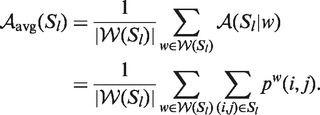If we had the same windows for each base pair in S_l, i.e. for all 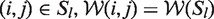, then analogously to Equation 3, we could continue with

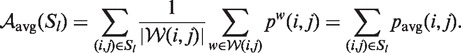(5)

Having the same set of windows for each base pair, however, could only be enforced if the location of the element was known in advance. Since this is not the case when searching for local structures, we used Equation 5 as an approximation of the average accuracy of the local structure S_l.

For the comparison of accuracies for structure elements of different sizes, we normalized them by the number of base pairs within the respective local structure S_l:

(6)

and analogously we substituted 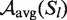with 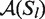for the non-averaged base pair probabilities.

Intuitively, the bp-accuracy is the mean base pair probability (or average probability) of all base pairs within the reference structure (i.e. cis-regulatory element); it measures the thermodynamic stability of the structure within its global context. The bp-accuracy, however, does not consider false positive base pair predictions. No gold standard for negative base pairing exists and it was unclear when a base pair that is not part of the local structure should be regarded as negative, or incorrect. For example, one could consider all possible conflicting base pairs, i.e. all base pairs involving one and only one base from a correct base pair, to be incorrect (in a secondary structure, a base can only be paired to one other). This is problematic for three reasons: (i) there are about 2L more incorrect than correct base pairs; (ii) a different number of negative base pairs would occur for different L values, hence, it is difficult to compare global and local folding methods; and (iii) it is unknown to which extent the mRNA folds into different conformations, or refolds. Alternative structures do exist in vivo, e.g. in riboswitches (5); some conflicting base pairs could be true variants. Kiryu et al. proposed a way to calculate specificity by considering all base pairs predicted in random sequences to be incorrect (33). Randomly designed RNA sequences, however, could also form stable structures (41).

AUC

In the case of accessibility predictions, we compared the methods according to their ability to correctly classify paired and unpaired bases. Classification performance was measured using the Receiver Operating Characteristic (ROC), summarized to the Area Under the ROC Curve (AUC). This measure is independent of the types of outputs of the different algorithms. The accessibility of a base is the complement of the sum of all base pairing probabilities that involve that base (see Equation 2), thus implicitly, the base pairing distribution is taken into account. Therefore, the performance comparisons of accessibility should indicate which method produces the more accurate base pair distributions.

LocalFold to reduce border effects of windows

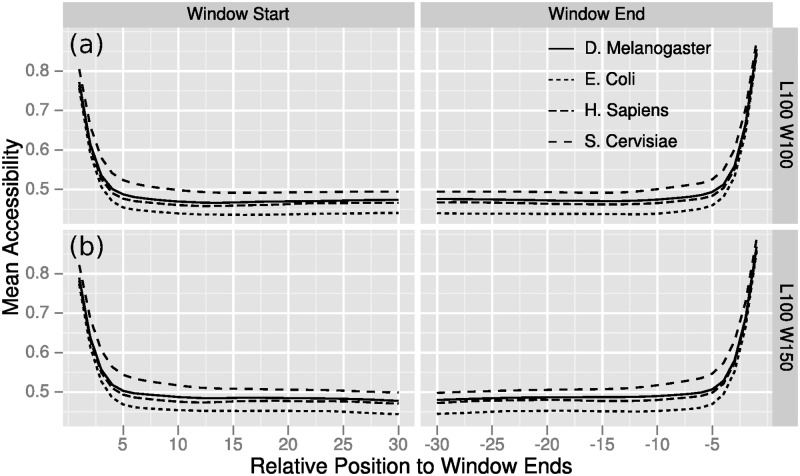
Based on our results (Figure 3), we developed a modified version of the window-based approach that ignores predictions made at window borders, since these regions result in biased probabilities.

Figure 3.

High accessibilities at window borders. Average accessibilities were computed per window position for 400 randomly chosen mRNAs from four species. Computations were done with RNAplfold, L = 100 and (a) W = 100 and (b) W = 150. Positions beyond approximately 10 nt at the window borders have equivalent average accessibilities.

For LocalFold, we modified Equation 4 so that 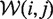contains only windows where base_i and base_j are not within the first or last b positions of the window. Window borders that coincide with the input sequence ends are exempt from the modification and are calculated as in RNAplfold.

The accessibility of base_i in a sequence of length n is calculated analogously to RNAfold, Equation 2:

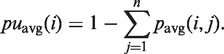(7)

The LocalFold algorithm is applicable to all parameter combinations of W, L and b satisfying W − L ≥ 2b. The LocalFold method is thus limited to a W that is sufficiently larger than L. The b parameter does not exclude any parts of the sequence; the filtering induced by b merely ignores the outliers in the averaging calculation (Equation 4). The parameters are set to W = 200, L = 150, b = 10 by default. We recommend to use b = 10, since this achieved the best result and clearly eliminated most of the bias at the borders (Figure 3). The time and space complexity stays the same as for RNAplfold (34,37).

RESULTS AND DISCUSSION

The performance of LocalFold and current methods available for folding mRNA sequences was compared using a large curated set of 2500 cis-regulatory elements (CisReg) and a position-wise structural probing dataset with the single-strandedness of over 3000 yeast mRNAs (YeastUnpaired). We developed suitable comparison measures and tests were designed to: (i) identify and elucidate the optimal degree of locality, (ii) investigate the effects of artificial window borders and sizes, and (iii) quantify the performance of each method on the two benchmark datasets. Prediction methods and datasets are summarised in Table 1. In the methods, we defined and introduced the performance measures used to compare the predicted probabilities: the bp-accuracy (Equation 6) for the CisReg dataset and the AUC for the YeastUnpaired dataset.

CisReg: a curated set of cis-regulatory elements

Their ability to detect and accurately predict known cis-regulatory elements is an important benchmark of new mRNA structure discovery methods. These known elements are characterised in several databases, of which the largest is the RNA families database (Rfam) (2,35). The latest major release (10.0) contains 1446 covariance models, mostly for non-coding RNA genes, but also for structured mRNA elements (35). Each model consists of a set of published ‘Seed’ and computationally extended ‘Full’ alignments. Sequences within the structural alignments consist of only the structured element, and usually lack the flanking sequence from the mRNA, needed to assess structure prediction.

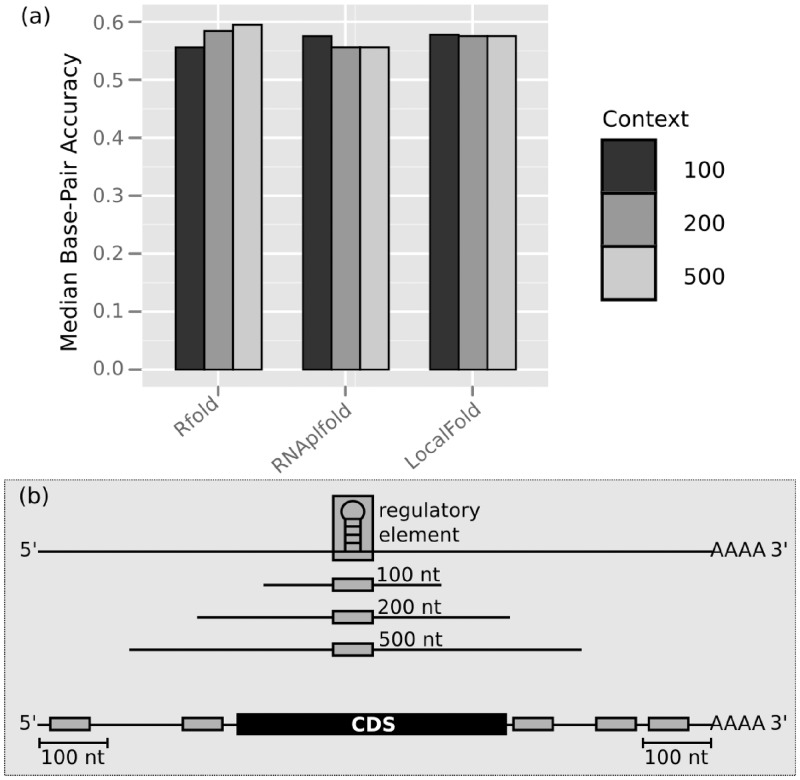
For this study, we developed a new benchmark for mRNA cis-regulatory elements. We extracted and individually re-examined a set of 95 families of cis-regulatory elements from Rfam that were correctly classified and adopted secondary structures without pseudoknots. Of these, 24 were from eukaryotic mRNAs and 71 from prokaryotic or viral genomes. The eukaryotic mRNA elements have diverse functions (e.g. mRNA localization, translation efficiency or mRNA stability) and most were located within 3′-UTRs. A large number of the genomic elements were from RNA viral genomes or from bacterial mRNAs. For each element, we extracted three different lengths of flanking sequences from the mRNAs (including coding regions and 5′-UTRs), or from the genomes when these were not available: 100, 200 and 500 nt, or otherwise to the sequence ends. Subsequently, we filtered and processed the elements to maximize structural integrity and a small proportion of sequences were excluded as they did not match sequences in the EMBL Nucleotide Sequence Database. The exact data preparation process and a redundancy analysis are provided in the Supplementary Data.

The CisReg dataset used in this study consists of 2500 individual elements (95 families) with over 85 000 base pairs and we propose it as a reference set to test future prediction algorithms. Furthermore, we provide a website for the data including additional information and statistics: http://lancelot.otago.ac.nz/CisRegRNA/.

Structure locality

Algorithms performed best for an L between 100 and 150 nt

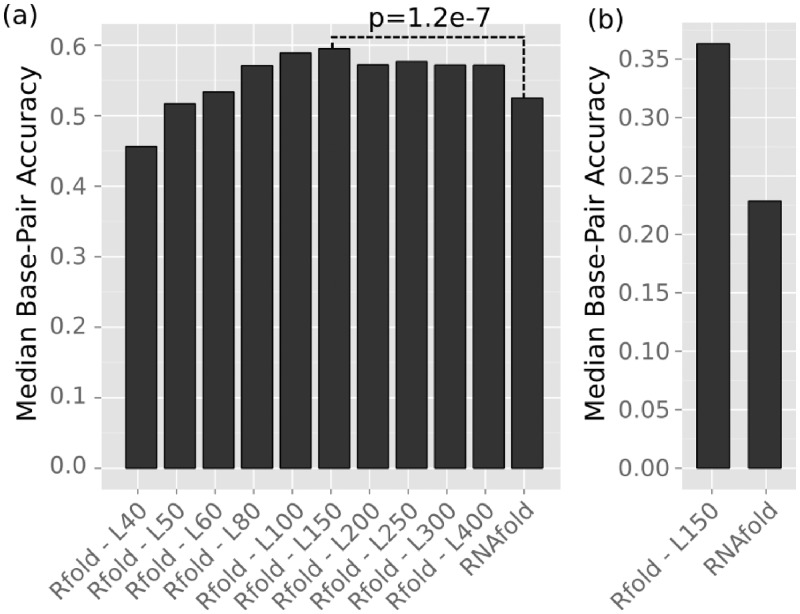
For local folding approaches, the main question was which degree of locality to use. Current methods introduced locality by restricting the maximum base pair span (bp-span, Equation 1) to L. We compared Rfold predictions with L between 40 and 400 nt to (the global) RNAfold results using the CisReg data. Local folding was represented by Rfold, because the introduction of the base pair restriction is the only conceptual difference to global folding; whereas the window-based approaches introduced the window size (W) as an additional parameter. The lowest median bp-accuracy of 0.46 was achieved using Rfold with L = 40 (Figure 1a). The accuracy increased with greater L values until a maximum of 0.59 was achieved at L = 150, after which accuracies decreased slightly to approximately 0.57. Rfold outperformed RNAfold at L ≥ 60. The difference between the bp-accuracy distributions of Rfold (L = 150) and RNAfold was significant with P = 1.2 × 10⁻⁷, two-sample Wilcoxon Rank Sum Test. The cis-regulatory structures in Figure 1a were situated within a context of up to 500 nt to either side, the folded RNA sequence was thus only approximately 1000 nt long and often not the full length mRNA. Therefore, we compared Rfold (L = 150) to RNAfold on the 179 available full-length mRNA sequences (Figure 1b). Here the median base pair accuracy of both methods was reduced, but the difference between the two methods increased: 0.13 compared to 0.07 in part (a).

Figure 1.

Comparison of global versus local folding using the methods RNAfold and Rfold. The median base pair accuracy (y-axis) is given for the CisReg dataset. (a) Comparison of RNAfold and Rfold using different L values. (b) A subset of the CisReg dataset that consists of 179 full length mRNA.

When investigating the degree of locality L suitable for the YeastUnpaired data, we observed similar results to the CisReg data, see Figure 8 (the main discussion of this figure follows later). For accessibility, Rfold outperformed RNAfold at L ≥ 50 and the performance increased up to the optimum at L = 100. L > 100 exhibited only a minor decrease in AUC, thus L was robust to larger L values. Nevertheless, the quality in prediction decreases down to the level of RNAfold for both datasets; the greater the span L, the more global the prediction becomes until it is global when L equals the sequence length.

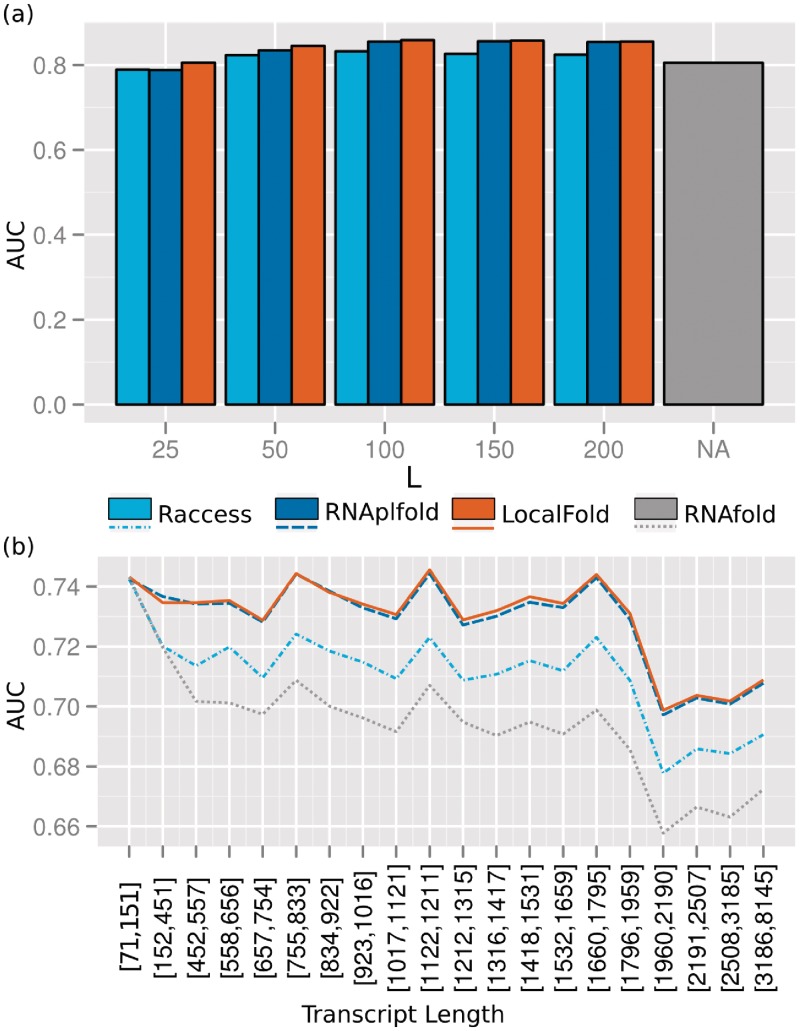
Figure 8.

Comparison of AUC values for separating high- and low scoring nucleotides of the YeastUnpaired dataset. (a) Effect of the parameter L was evaluated for W = L + 50 including only the 1% highest and lowest scoring nucleotides, respectively. (b) Using the best parameter combination (L = 100, W = 150), we show the dependency of the transcript length on the prediction quality. Here the 10% highest and lowest scoring nucleotides were included. Each interval contains roughly the same number of sequences.

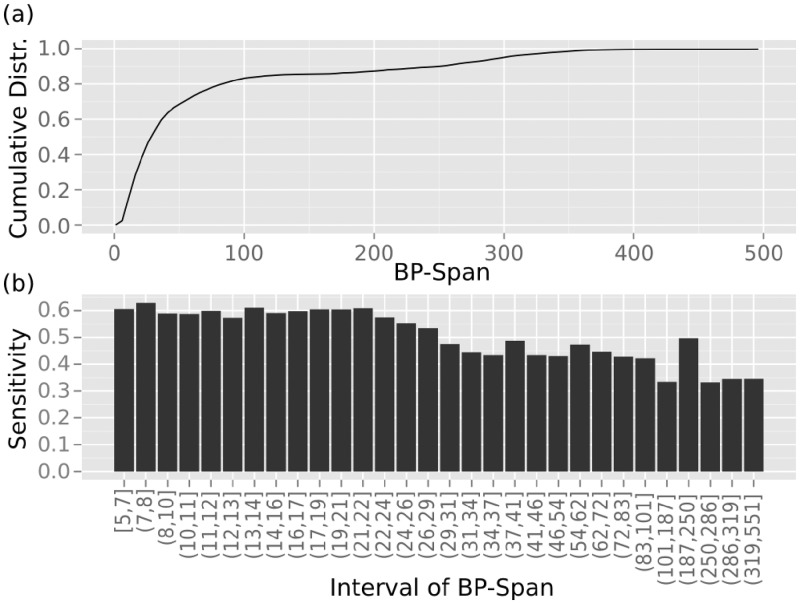
Most base pairs have short spans

Our results on the best value for L reflected the distribution of base pair spans within known structures: we observed that 83% of all base pairs had a bp-span less than 100 nt (85% ≤ 150) for all the cis-regulatory elements in the CisReg dataset (Figure 2). Thereafter, the increase in the number of base pairs with a larger span is very slow. Although we specifically chose local regulatory structures located on the mRNA, the distribution was similar to previously published data. Doshi and colleagues showed an exponential distribution for base pair spans of 496 16S rRNAs, with 75% of all base pairs with bp-span ≤ 100 nt (30). In 151 ncRNA structures from 151 seed alignments in the Rfam, 85% of the base pairs had a bp-span ≤ 100 nt (20). The latter two analyses looked at global structures that form long-range base pairs. Due to the exponential distribution of base pair spans in native RNA structures, the majority of base pairs have short spans, i.e. are local and thus smaller L values (L ≤ 100) still performed comparably well. Because of the good correlation of our results to the distribution of base pair spans, we suggest that local folding with restricted base pair spans could perform better for other classes of long RNA sequences, such as ribosomal RNA and long ncRNA. Note that although long ncRNA may be largely unstructured, local structured domains, or regulatory target sites could be located on these molecules making a structure prediction interesting. For example for determining the accessibility of miRNA target sites (42).

Figure 2.

The distribution of base pair spans and the quality of prediction with respect to span length. (a) The bp-span (x-axis) distribution for the CisReg dataset with the cumulative distribution given on the y-axis. (b) The sensitivity of base pairs (y-axis) for each base pair span interval (x-axis). The intervals were distributed such that they contain roughly an equal number of base pairs.

Base pair prediction accuracy decreased with span length

The choice of the locality parameter also depends on the prediction accuracy of base pairs with respect to their span lengths. For this evaluation we used RNAfold as it allows all base pair spans. The influence of the base pair span length on the sensitivity of the predictions is illustrated in Figure 2b. We defined sensitivity as the fraction of all true base pairs within each bp-span interval that were predicted with probability p(i, j) > 0.5. Base pairs with a probability greater than 0.5 are called high-frequency base pairs and are contained in the centroid structure (39,43,44). Base pair prediction accuracy decreased with respect to span length; this was also published in (30,45,46). The highest sensitivity of approx. 0.6 was achieved for bp-span < 30 nt, after which it dropped to 0.45, and at bp-span ≤ 100 nt the sensitivity decreased further to around 0.35 (except an outlier at 0.5). The implications of this decrease are 2-fold: (i) the current nearest neighbour energy model (47,48) is unsuited to the prediction of long-range base pairs or (ii) the multi-loop energies are incorrect (47,49,50). Our results indicated that an L = 150 represents a good balance between maximizing the number of base pairs included in the predictions and minimising the accuracy of longer base pair spans. A larger L did not increase the performance, probably due to the very few extra base pairs that could be predicted and the quality of these predictions becoming increasingly poor.

Structures are locally stable

The success of local folding approaches is based on the assumption that, in most cases, structures with short base pair spans are locally stable and do not need the global influence of long-ranging base pairs to stabilize their formation. This condition is supported by the fact that small values for L performed only slightly worse than their more global counterparts (see Figures 1 and 8). In the search for cis-regulatory elements, maximum base pair spans much smaller the real spans still predicted the local parts of the structure. The structural stability of local substructures was also stated in (30,51). These authors illustrated that in predicted sub-optimal structures, most of the rearrangement occurs in the form of long-range connections, whereas the local substructures remain the same. Moreover, Higgs et al. have shown that, due to kinetics, short-range base pairs form more quickly (52). Finally, the hierarchical evolution hypothesis, introduced in (53), could further support the initial formation of locally stable structures with short base pair spans and the subsequent addition of longer-range connections.

Window-based approaches

RNAplfold computes base pairing probabilities by averaging over subsequences, windows, of length W. On the one hand, averaging over independent windows reduces dependencies between two local structures with a distance greater than W; on the other hand, each window introduces two artificial RNA ends at the window borders. As the ends do not correspond to any real features of the RNA, this can lead to the following errors.

Window borders were biased towards higher accessibilities

To investigate a possible bias introduced by folding independent (short) subsequences, we computed the average accessibility per position of the respective windows using RNAplfold. Mean accessibilities for over 500 000 sequence windows from 400 mRNAs, selected randomly from four species, are depicted in Figure 3. Nucleotides at the window borders showed considerably higher accessibilities than nucleotides near the window centres. This effect is preserved for the full range of observed GC-contents (Supplementary Figure S2) and is not particular to mRNAs (Supplementary Figure S3). Most of the bias originated from external regions not enclosed by any base pair, as opposed to internal loops (data not shown).

Windows affected base pairing predictions

The accessibility bias towards window borders affected the probabilities of base pairs with at least one nucleotide in this region. Consequently, long-range base pairs with both nucleotides within the outer regions were affected most (Figure 4a). Two issues arise from window-based folding: (i) The number of windows in the calculation of a base pair probability is dependent on its span, i.e. probabilities of a base pair with bp-span = l occur in W − l + 1 windows. Hence, the number of windows being averaged decreases linearly with increasing bp-span. (ii) Strong secondary structures tend to form in the central part of a window, leaving the remaining unpaired bases at the window borders available to pair with each other; crossing base pairs with internal unpaired bases are not allowed in secondary structure prediction, so the ends pair up (if possible), because each additional base pair minimizes the overall free energy. In combination, when L is close to W, long-range base pairs within the borders resulted in skewed pairing probabilities, as they were not compensated by averaging over many windows.

Figure 4.

Illustration of folding-windows. Regions affected by the border effect are shaded. (a) Same window size and maximum span. Long-range base pairs can be affected by both window borders. The base pair of maximal span is part of exactly one window. (b) Window larger than maximum span. Base pairs can only be influenced by one window end. Base pairs of maximal span can be part of multiple windows.

Border effects can be reduced by the appropriate choice of window size

The negative effect of having only few windows representing long-range base pairs was mitigated by setting a suitable window size W with respect to the maximum base pair span L. When W ≥ L, base pair probabilities are averaged for at least W − L + 1 windows (Figure 4b). In Figure 5, the dot plots from RNAplfold of a cis-regulatory element exemplify the border effect on long-range base pairs. For visualization purposes, the sequences were folded with L = 70. For W = L, many base pairs with spans near L were assigned high probabilities while located in very short stems (Figure 5a). For W = L + 50, most of the long-range base pairs either disappeared or were assigned much smaller probabilities (Figure 5b). The base pair probabilities for the target structure were not influenced by the parameter settings, due to their shorter base pair spans. In our evaluations of different window sizes on both the CisReg and the YeastUnpaired datasets, W had little effect on the prediction performance as long as it was sufficiently larger than L. The current default parameter setting of RNAplfold is W = L = 70. In general, the default settings of computational tools are frequently used and in the case of RNAplfold the default, W = L, was applied in e.g. (33). Note that on the other extreme, window sizes much larger than L diminish the positive effects of the window-based approach, namely to avoid dependencies between distant local structures. When W is equal to the sequence length, the window-based approach is the same as the approach for Rfold and Raccess. Varying the window sizes from L + 50 to 3L did not influence the results significantly, however, the best results for RNAplfold were achieved using W = L + 50 (Supplementary Figures S4 and S5). For all further evaluations we set the window size to W = L + 50, which allowed each base pair to be present in at least 51 windows.

Figure 5.

Probability bias for long-ranged base pairs close to the window size and their reduced effect. We see cropped dot plots of the base pairing matrices for positions 5180-5291 of RF00435-U55047-1 in the CisReg dataset, which is a heat shock gene expression (ROSE) element. Base pairs of the target structure are marked in red. The size of each dot is relative to the probability of the base pair it represents and the nucleotides can be read by following the diagonal lines to the left and right. The incorrect long-range base pairs are much more likely when (a) W = L instead of (b) W = L + 50.

LocalFold diminished border effects

While an appropriate choice of the window size mitigated some of the adverse effects of the windowed approach, the borders still affected the accessibilities up to the 10 outer nucleotides of each folding window (Figure 3b). Therefore, we developed LocalFold that reduced these border effects and we quantified the improvement of predictions performed on our datasets. In short, the biased regions at the window borders were not considered for the computation of accessibilities or base pair probabilities. As the border effect was mostly independent of window size and maximum base pair span (data not shown), in LocalFold the first and last 10 nucleotides in each artificial window (excluding real ends of the input sequence) were removed from the calculations. Note that LocalFold only removes the bias outliers from the window average calculations and still produces probabilities for all positions of the nucleotide sequence (any length).

Performance comparison of methods

We compared the performance of the following secondary structure prediction methods applied to mRNA sequences: RNAfold (global), Rfold (restricted bp-span, base pair probabilities), Raccess (restricted bp-span, accessibilities), RNAplfold (window-based), and our method LocalFold (reduced border effects). We investigated their performance on the CisReg and the YeastUnpaired datasets, hence, we quantified their predictions of both paired and unpaired bases, respectively. For the local folding methods, we applied the best parameter combinations (for each dataset) according to the previous analyses.

Predicting cis-regulatory structures in mRNA

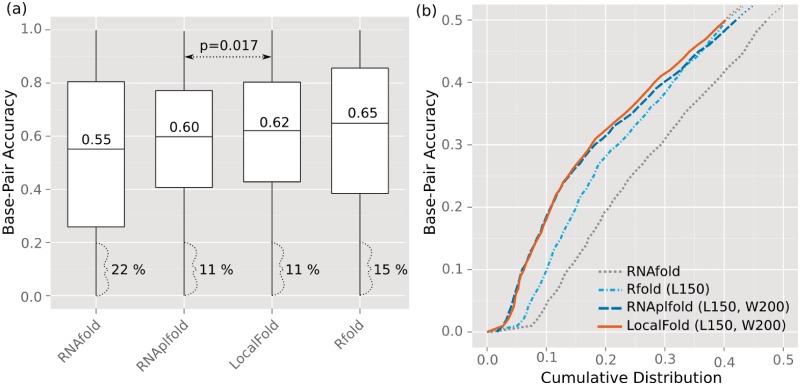
We compared the accuracies each method achieved for the base pairs of the CisReg dataset. For folding, we used sequences of up to 500 nt context to either side of the elements. Although many mRNA sequences are longer than 1000 nt, we chose this length because resource demands of RNAfold were too high for longer sequences. For the local folding methods we applied the optimal values determined previously: maximum base pair span L = 150 and window size W = 200. To fairly compare RNAfold to the local folding methods, we used a subset of the CisReg dataset in which the elements had a maximum bp-span of 150 nt. This subset included most elements (2158 out of 2500) across 90 different Rfam families. This meant L did not exclude base pairs in the dataset from being predicted. In Figure 6 we summarized the bp-accuracies (Equation 6) resulting from each method. When comparing the median bp-accuracy in part (a), it increased from 0.55 (RNAfold), through 0.6 (RNAplfold), 0.62 (LocalFold), to a maximum of 0.65 (Rfold). These accuracies indicate that the target structures were clearly predicted as illustrated in Figure 5 in which the cis-regulatory element achieved a bp-accuracy of 0.65. Although Rfold achieved the highest median bp-accuracy, the method—together with RNAfold—exhibited a much greater variation in results than the window-based approaches: RNAplfold and LocalFold. While the boxplot indicated similar distributions for the latter two approaches, the accuracies for LocalFold were significantly higher than for RNAplfold (P = 0.017, two-sided, two-sample Wilcoxon Rank Sum Test). Both window-based approaches produced the most robust predictions; LocalFold and RNAplfold made fewer predictions in the lower bp-accuracy range, i.e. they were more sensitive (Figure 6b). We considered a bp-accuracy ≤ 0.2 to mean the structure was not predicted: Rfold and RNAfold failed to predict 15 and 22%, respectively, whereas both RNAplfold and LocalFold failed in only 11% of all instances. To show that these results were not biased by redundancies in the dataset, we evaluated the median accuracy per Rfam family (Supplementary Figure S1). Albeit some exceptions, the above trends remained the same for the individual families. Only for two families with large base pair spans of 338 and 551 nt did global folding show a substantial improvement over the local folding methods.

Figure 6.

Comparison of structure prediction methods for the identification of cis-regulatory elements. Computations were performed with L = 150 and W = 200 (when applicable) on the subset of the CisReg data that have a max. base pair span of 150 nt, including 2158 elements assigned to 90 Rfam families. (a) Comparison of the achieved accuracies as boxplots. (b) Cumulative distributions of the bp-accuracy up to 0.5 (y-axis) to highlight the prediction sensitivity. Base pairs with probabilities above 0.5 are contained in the centroid structure (39,43,44) and thus a bp-accuracy above this threshold implies a well defined target structure. The P-value was calculated with a two-sample Wilcoxon Rank Sum test.

Rfold has a decreased prediction performance at sequence ends

In the investigation of different context lengths for the local folding methods, Rfold exhibited a decreased performance for smaller contexts (Figure 7); the context length was defined by the number of nucleotides to either side of the regulatory element, see part (b). Although the median bp-accuracy for Rfold was higher for the contexts of 200 and 500 nt, it performed worst for 100 nt. This, in combination with the greater variance for all Rfold predictions, indicated that the prediction of correct structures at sequence ends is poor. A similar trend was observed in (20), where the authors reported decreased prediction for the ends of sequences up to four times the maximum base pair span, i.e. a context of 600 nt for L = 150. Most cis-regulatory elements are situated within the untranslated regions (UTRs) of mRNAs and thus are frequently located at the sequence ends. Hence, poor prediction performance at sequence ends is detrimental for the prediction of cis-regulatory elements.

Figure 7.

Rfold is more sensitive to the context length and thus has increased problems predicting correct structures at sequence ends, also reported in (20). (a) A comparison of the median bp-accuracy (y-axis) achieved by the local folding methods on sequences where the regulatory element is situated within contexts 100, 200 and 500 nt (CisReg dataset). (b) When the regulatory element is located at the sequence ends, a context larger than 100 nt is often unavailable. Thus, methods performing poorly for shorter contexts are not appropriate to identify those elements.

Evaluation of accessibilities in yeast data

In the previous analysis, we inspected the accuracy at which each method predicted a given secondary structure. The extent of wrongly predicted base pairs was not explored. Here, we compared the performance of all methods on their ability to predict the accessibility of individual bases. As the accessibility of a base is defined as its probability of being unpaired, the probabilities of all possible base pairs involving this nucleotide are taken into account. Thus, wrongly predicted base pairs can have a detrimental effect on this measure. We first computed accessibilities for each folding method. For the local folding methods we used maximum base pair spans (L) between 25 and 200 nt. The window size W = L + 50 was used for the two window-based approaches. The quality of predictions for the YeastUnpaired dataset was evaluated by computing AUC values for discriminating high- and low-rated nucleotides according to the PARS score; these nucleotides achieved the clearest evidence for being paired or unpaired, respectively. Figure 8a shows the results for 1% of the highest- and 1% of the lowest-ranking nucleotides, comprising a set of approx. 80 000 measurements. In most cases, an AUC greater than 0.8 was achieved. Folding globally with RNAfold resulted in the third lowest performance, only the predictions of Raccess and RNAplfold using span L = 25 performed worse. LocalFold outperformed the other methods for all Ls. Even the worst result for LocalFold at L = 25 was significantly higher than for RNAfold (P = 8.055· 10⁻⁸, Wilcoxon Signed Rank test using AUCs derived from 1000 bootstrap samples). The best prediction result was attained by LocalFold using L = 100 with an AUC of 0.85. Larger L values resulted in comparable AUCs, hence, the prediction of accessibility was stable for different parameter settings. The fact that Raccess was clearly outperformed by the window-based approaches on the YeastUnpaired data provides further evidence that the greater variance in its base pair prediction performance (Figure 6) is detrimental.

Relative prediction performance was not influenced by transcript length

Finally, we investigated the influence of transcript lengths on the performance of the algorithms. For the analysis shown in Figure 8b, we split the data into sequence length intervals and the AUC for L = 100 was computed for each interval separately. The intervals were chosen to include roughly an equal number of sequences. We used 10% of the highest- and 10% of the lowest-ranking nucleotides so that each interval contained a sufficient number of sequences. While predictive performance fluctuated slightly for the intervals, we observed the same ranking of methods as seen in the previous analysis: global folding scored worst, the window-based approaches best. LocalFold scored marginally better than RNAplfold for most intervals and both consistently outperformed Raccess. Overall, performance dropped slightly for sequences longer than 2000 nt. The fluctuations in performance were mirrored by all methods, probably due to the quality or properties of the underlying data.

CisReg and YeastUnpaired data showed similar results

We observed similar results for both of the analysed datasets. The YeastUnpaired dataset was generated in in vitro conditions, whereas the structured cis-regulatory elements in the CisReg dataset consists of published regulatory structures with post-transcriptional functions in vivo. The fact that the results are comparable between two independent datasets supports their overall quality and highlights their validity and generality.

CONCLUSION

To benchmark the performance of mRNA secondary structure prediction, we generated a large curated set of cis-regulatory elements and introduced bp-accuracy to measure how accurately a local structure was predicted. Furthermore, we evaluated accessibility predictions using transcript-wide structural probing data. Prediction accuracy was affected by the following algorithmic assumptions and parameter combinations:

1. The optimal base pair span parameters were dataset dependent, but similar, at L = 150 for the CisReg dataset and L = 100 for the YeastUnpaired dataset. Within a range of 100–150, differences in performance were minimal. This range reflects the distribution of base pair spans for known structures.

2. The use of sliding windows allows for more locality than the mere restriction of base pairs spans. Windows, however, introduced a prediction bias at each artificial border. Windows with W = L caused unusually high base pairing probabilities of long-range base pairs. This was was resolved by setting W = L + 50.

3. Setting the larger window size (W = L + 50) did not remove the bias of high accessibilities (single strandedness) at the window borders. Therefore, LocalFold was developed to diminish this bias which resulted in a consistent improvement compared to the other methods. The greater improvement in results was observed for the CisReg data (base pairs) in comparison to the YeastUnpaired data (single-strandedness).

In addition to having much faster runtimes, we present clear quantitative and qualitative evidence that local folding methods outperformed the global approach. The advantage of local folding is that the majority of base pairs have short base pair spans and that local structure can be predicted without the stabilizing effects of long-range connections. Moreover, the reduced accuracy in the prediction of these long-range base pairs meant that local folding was better than global folding at determining secondary structure in long RNAs.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online: Supplementary methods, Supplementary Figures 1–5, and Supplementary References [54,55].

FUNDING

Deutsche Forschungsgemeinschaft (BA 2168/3-1 to R.B., BA 2168/4-2 to R.B.); Human Frontier Science Foundation (RGP0031_2009 to Ian Macara, Anne Spang and C.M.B., in part). Funding for open access charge: University of Freiburg and University of Otago.

Conflict of interest statement. None declared.