A Quantum Chemical Study of the Ground and Excited State Electronic Structures of Carbazole Oligomers with and without Triarylborane Substitutes

Abstract

Recent experimental investigation (Reitzenstein and Lambert,Macromolecules, 2009, 42, 773) indicated that the quite different optical properties of 2,7- and 3,6-linkage triarylboryl carbazole oligomers may arise from the different nature of their low-lying excited states: a low-lying delocalized within-backbone excitation in longer 2,7-linked oligomers vs a backbone-to-sidechain charge-transfer (CT) excitation independent of the polymerization length in 3,6-linked oligomers. Here in this paper, two long-range corrected functionals, CAM-B3LYP and ωB97X, are applied together with the traditional B3LYP functional in time-dependent density functional theory (TDDFT) calculations to systematically investigate the low-lying electronic excitations in both oligomers. Our calculations indicate that an extensive conjugation exists between monomer molecular orbitals in 2,7-linked oligomers, which is absent in those of 3,6-linked structures, resulting in a considerable narrowing of the HOMO-LUMO gap of their backbone moiety, while having little effect on the side-chains. CAM-B3LYP and ωB97x calculations confirm that the lowest-energy absorption is a within-backbone excitation in longer 2,7-linked oligomers as opposed to a backbone to side-chain charge transfer excitation in 2,7-linked oligmers of shorter length and 3,6-linked oligomers of any length. All these findings are consistent with the experimental findings and the qualitative energy diagram proposed by Reitzenstein and Lambert.

INTRODUCTION

For many years, carbazole (Figure 1, A) and its derivatives attracted much attention for their interesting photochemical properties, as well as high chemical and environmental stabilities.^1-6 One of the recent focuses is its potential application as an electron donor in an organic D-π-A sensitizer in dye-sensitized solar cells (DSSC)^7-11 Another fascinating advantage is its versatile reactive sites that can be substituted with a wide variety of functional groups to tune the optical and electrical properties.⁶

Figure 1.

Molecular structures of carbazole (A), triarylborane (B), 2,7-linked carbazole oligomers (C), and 3,6-linked carbazole oligomers (D), 2,7-linked triarylboryl-substituted carbazole oligomers (P1), and 3,6-linked triarylboryl-substituted carbazole oligomers (P2).

Polycarbazole is one of the widely studied blue light-emitting polymers, which are essential for the fabrication of blue light-emitting diode (LED).^12,13 When carbazoles are linked together to form oligomers or even polymers, it has at least two ways of elongation. One is through 3,6-linkage, with the formation of a non-planar structure characterized with successive nitrogen-connected benzidines, (Figure 1, D). It was well acknowledged that π-conjugation is terminated at each nitrogen atom, so that the π-conjugation is always confined within two repeating units, and accordingly, the absorption wavelength is insensitive to the degree of polymerization.^14-17 Before 2000, almost all studies on polycarbazole were focused on 3,6-polycarbazole, since that it is more feasible to be synthesized than any other isomers due to the highly activated 3,6-positions.^14,18 Another way of elongation is through 2,7-linkage, forming the planar poly(para-phenylene) resembled linear structure (Figure 1, C) , which was regarded as an extensively π-conjugated system throughout the entire polymer backbone.^19,20 It was observed that 2,7-polycarbazole showed longer electronic absorption wavelength and higher fluorescence quantum efficiency with increasing degree of polymerization,^21,22 as well as higher electron/hole mobilities along the polymer chain.^13,19,20,23 Besides 3,6-linkage and 2,7-linkage polymers, there were also a very recent report of poorly conjugated small oligomers of 1,8-linkage.²⁴

Introduction of electron donating or with-drawing substituents at 9H-position is one of the effective strategies for tuning the physical and chemical properties of polycarbazoles. When the substituent is changed from alkyl^16,19,23 to electron-donating amino-phenyls,²¹ the lowest absorption was observed to be red-shifted for 2,7-polycarbazole. In some circumstances, photo-induced charge transfer may occur between the polymer backbone and attached substituents or between different repeating units of copolymers, which may vastly change the light emitting as well as electron/hole transportation properties due to the formation of charge-transfer (CT) states.^22,25,26 Recently, Reitzenstein and Lambert synthesized 2,7-linked and 3,6-linked polycarbazole with a triarylboryl moiety (Figure 1, B) attached to the nitrogen atom of each carbazole (Figure 1, P1 and P2).²⁷ Significant improvement in the optical properties for 3,6-linked polycarbazole was reported, which were explained as originated from the formation of a CT state involving the backbone to side chain electron transfer.

Understanding of the electronic structures of the ground and excited states is essential for the explanation of the different optical properties of 3,6- and 2,7-linked polycarbazoles. In the last two to three decades, density functional theories (DFT) as well as time-dependent density functional theories (TDDFT) supplied the affordable theoretical solutions for the calculation of small to moderate size oligomers.²⁸ In general, the properties of polymers can be understood reliably from the extrapolation of properties of different sizes oligomers.^28-33 The recently developed long-range corrected density functional (LC-DFT) methods supplied a remedy for the underestimation of excitation energies for extended conjugated systems, especially for the calculation of CT states, due to the incorrect asymptotic behavior of xc-functionals in traditional DFT methods.^32,34-41

In this work, we perform DFT and TDDFT calculations on 2,7-linked and 3,6-linked carbazole oligomers as well as the triarylborane substituted derivatives, to investigate the relationship of electronic structures and the topological patterns of carbazole linkage, as well as the effect on the intramolecular charge-transfer (ICT) with increasing degree of polymerization. For TDDFT calculation, we use both CAM-B3LYP⁴⁶ and ωB97X⁴⁷ functionals. Since the CAM-B3LYP functional incorporates 65% long-range Hartree-Fock exchange, which is lower than the full 100% Hartree-Fock exchange in other LC-DFT functionals (such as ωB97X), it will also be interesting to investigate the different behaviors from CAM-B3LYP and other LC-DFT functionals in characterizing the nature of low-lying electronic excitations in such oligomers.^32,42

Computations and Discussions

All ab initio quantum chemistry calculations were run by one of the authors (S.Z.) using the Gaussian 09 program package⁴³ and the Q-Chem program package.⁴⁴ B3LYP functional⁴⁵ is used to optimize the ground-state geometries of carbazole oligomers (N ≤ 10 for unsubstituted oligomers; and N ≤ 5 for substituted oligomers). In DFT, the basis set convergence is usually fast so that 6-31G* generally gives a good balance between reliability and computational speed.³³ Once the ground-state geometry was obtained, two additional long-range corrected functionals, CAM-B3LYP⁴⁶ and ωB97X,⁴⁷ were also applied to compute the Kohn-Sham orbitals and to compute TDDFT excited states (10 lowest-lying excitations are solved).

The choice of a basis set was often a compromise between accuracy and computational speed.⁴⁰ After comparing the Pople’s 6-31G* against other basis sets ranging from 6-31G up to 6-311++G**, we find that the accuracy of the 6-31G* basis set is acceptable for computing the lowest-lying charge-transfer excitation of triarylboryl carbozole monomer, especially for a qualitative understanding of the nature of lowest-lying excitation in carbazole oligomers with an increasing degree of polymerization.

Ground-state electronic structure of unsubstituted carbazole oligomers

It was somewhat surprising that our geometry optimizations led to a non-planar structure not only for 3,6-linkage polycarbazole, but also for 2,7-linkage ones, in opposition to earlier viewpoint.²⁷ The torsion angle between the connected carbazole units is found to be insensitive to the way of linkage and to the degree of polymerization and ranges from 37° to 40° in all cases. So it becomes essential for us to look into the frontier molecular orbitals in order to understand the dissimilar photochemical properties of the two oligomers.

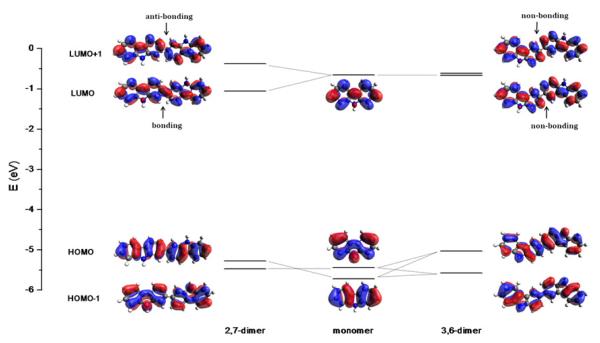
The frontier orbitals of a carbazole monomer are shown in the middle column of Figure 2. Here HOMO-1 is energetically close to HOMO: at the B3LYP/6-31G* level, the Kohn-Sham orbital energies are −0.208 (in Hartree) for HOMO-1 and −0.195 for HOMO, and both orbitals are well separated from HOMO-2 (−0.247) and LUMO (−0.023). Most importantly, the monomer HOMO has a significant contribution from nitrogen, but HOMO-1 has almost zero contribution from nitrogen. Equally importantly, the monomer LUMO has a significant contribution from 2,7-carbons, but has almost zero contribution from 3,6-carbons.

Figure 2.

Frontier orbitals of carbazole monomer, 2,7-linked dimer, and 3,6-linked dimer.

Decomposition of the frontier MOs of the dimers by projecting them into monomer MOs can reveal the bonding character between repeating units. In order to relate the dimer Kohn-Sham molecular orbitals to the monomer orbitals, the following overlap integrals are computed:

$$S_{p,q}=<{\Psi }_p^{AB}\mid {\Psi }_q^A>$$ (1)

where ${\Psi }_p^{AB}$ is the p-th Kohn-Sham molecular orbital for the dimer (AB), and ${\Psi }_q^A$ is the q-th Kohn-Sham molecular orbital for monomer A (similarly for B). These monomer molecular orbitals are obtained by running DFT calculation on either of the monomers saturated with a hydrogen link atom, but the contributions from basis functions on the hydrogen link atom are discarded in the evaluation of the overlap integrals in Eq. (1). The values of such overlap integrals are collected in Table 1 for the 2,7-linked dimer and in Table 2 for the 3,6-linked dimer.

Table 1.

Components of the frontier orbitals of the 2,7-linked carbazole dimer. AB represent the dimer, A and B represent the two monomers.

	HOMO-1(A)	HOMO(A)	LUMO(A)	HOMO-1(B)	HOMO(B)	LUMO(B)
HOMO-1(AB)	0.004	0.707	−0.001	0.004	0.706	−0.001
HOMO(AB)	−0.702	0.040	0.0 56	0.702	−0.040	−0.057
LUMO(AB)	−0.082	0.001	0.672	−0.082	0.001	0.672
LUMO+1(AB)	0.059	−0.006	0.687	−0.059	0.006	−0.687

Table 2.

Components of the frontier orbitals of the 3,6-linked carbazole dimer. AB represent the dimer, A and B represent the two monomers.

	HOMO-1(A)	HOMO(A)	LUMO(A)	HOMO-1(B)	HOMO(B)	LUMO(B)
HOMO-1(AB)	0.400	0.574	−0.001	0.400	0.574	−0.001
HOMO(AB)	−0.208	0.665	0.005	0.208	−0.665	−0.005
LUMO(AB)	−0.005	0.006	−0.701	−0.005	−0.006	0.701
LUMO+1(AB)	−0.008	0.011	0.702	−0.008	0.011	0.702

The HOMO of the 2,7-linked dimer (shown in the left column of Figure 2) is a simple combination of two monomer HOMO-1 (see Table 1 ) with little contribution from nitrogen orbitals. The HOMO of the 3,6-linked dimer (shown in the right column of Figure 2) can also be interpreted as a combination of monomer orbitals (-0.208 HOMO-1 + 0.665 HOMO from each monomer, see Table 2), so it consists of 10% monomer HOMO-1 and 90% monomer HOMOs. Since monomer HOMO-1 and HOMO are close in energy, the HOMO energies are expected to change similarly with increased oligomer length, and that is clearly seen in Figure 3 for all three functionals.

Figure 3.

HOMO and LUMO energies of (a) 2,7-linked and (b) 3,6-linked (unsubstituted) carbazole oligomers (N ≤ 10).

With both 2,7- and 3,6-linkages, dimer LUMOs are simple linear combinations of monomer LUMOs (see Table 1 and Table 2), but their energies display quite different behavior with the linkage patterns. As mentioned previously, monomer LUMO has a significant contribution from 2,7-carbons, so this allows a “bonding”-style mixing (see the middle region of the dimer LUMO in the left column of Figure 2) in the 2,7-dimer. In contrast, monomer LUMO does not cover 3,6-carbons, so the 3,6-dimer LUMO amounts to a “nonbonding” mixing of monomer LUMOs. As shown in Figure 3, the “bonding”-style mixing leads to a gradual decrease of the LUMO energy of 2,7-linked carbazole oligomers with the chain length, whereas the LUMO energy of 3,6-linked carbazole oligomers stays rather flat with the chain length.

When the functional was switched from B3LYP to long-range corrected functionals such as CAM-B3LYP and ωB97X, the percentage of long-range Hartree-Fock exact exchange increases from 0.2 to 0.65 and 1. This leads to an expected widening of the HOMO-LUMO gap, which can clearly be seen in Figure 3, but the qualitative pictures stay the same: HOMO energies follow the same trend with both linkages, whereas LUMO energies decreases only in 2,7-linked oligomers.

Ground-state electronic structures of substituted carbazole oligomers

When carbazole is substituted with triarylborane, the monomer HOMO-1 and HOMO come almost entirely from the carbazole moiety (see the middle column of Figure 4,the molecule orbitals do not show symmetrical properties since there is no symmetrical constraint on these molecules) and their energies change very little: B3LYP orbital energy stays at −0.208 for HOMO-1 and changes from −0.195 to −0.192 for HOMO. At the same time, carbazole LUMO becomes LUMO+1 (B3LYP energy: −0.022), with the new LUMO comes almost entirely from the triarylborane moiety and is noticeably lower in energy (B3LYP energy: −0.065).

Figure 4.

Frontier orbitals of triarylborylcarbazole monomer and pentamer. From bottom to the top are HOMO-1, HOMO, LUMO, and LUMO+1. Monomer is in the middle, 2,7-linked oligomer (P1) on the left and 3,6-linked oligomer (P2) on the right.

In Figure 4, the frontier orbitals for 2,7-linked and 3,6-linked substituted pentamers are also shown. Similar to the monomer, HOMO-1, HOMO and LUMO+1 are distributed on the carbazole backbone, whereas LUMO come almost entirely from the triarylborane side chains. For this reason, we can designate HOMO-1 as b-HOMO-1, HOMO as b-HOMO, LUMO as s-LUMO and LUMO+1 as b-LUMO, where “b” stands for “backbone” and “s” stands for “side chain”.

Figure 5 shows how HOMO-1, HOMO, LUMO, and LUMO+1 energies change with the chain length for both 2,7-linked carbazole oligomers (P1) and 3,6-linked carbazole oligomers (P2) with B3LYP functional. HOMO gradually increases, which is essentially the same as in the unsubstituted oligomers. LUMO (i.e., s-LUMO) stays flat for both linkages, because it comes from the side chains that are well separated in space. Most importantly, LUMO+1 (i.e., b-LUMO) follows different trends with two linkages. As in the case of unsubstituted oligomers, LUMO+1, which is distributed over the carbazole backbone, decreases gradually in energy with the chain length of 2,7-linked oligomers, whereas its energy stays flat with 3,6-linked oligomers of increasing chain length.

Figure 5.

Frontier orbital energies of (a) 2,7-linked and (b) 3,6-linked triarylborylcarbazole oligomers (N ≤ 5) with B3LYP functional. Black lines represent HOMO-1 on backbone. Red lines represent HOMO on backbone. Blue lines represent LUMO on sidechain. Green lines represent LUMO on backbone.

With long-range corrected functionals, CAM-B3LYP and ωB97X, both of which should provide a better description of charge transfer excited states, are applied, the same overall picture is obtained in Figure 6 and Figure 7. But the LUMO+1 (i.e. b-LUMO) of the 2,7-linked oligomers is now much closer to LUMO (i.e, s-LUMO). So the b-LUMO of the 2,7-linked oligomers is expected to play an important role in the lowest-energy excitations.

Figure 6.

Frontier orbital energies of (a) 2,7-linked and (b) 3,6-linked triarylborylcarbazole oligomers (N ≤ 5) with CAM-B3LYP functional. Black lines represent HOMO-1 on backbone. Red lines represent HOMO on backbone. Blue lines represent LUMO on sidechain. Green lines represent LUMO on backbone.

Figure 7.

Frontier orbital energies of (a) 2,7-linked and (b) 3,6-linked triarylborylcarbazole oligomers (N ≤ 5) with ωB97X functional. Black lines represent HOMO-1 on backbone. Red lines represent HOMO on backbone. Blue lines represent LUMO on sidechain. Green lines represent LUMO on backbone.

Excited states of triaryborylcarbazole oligomers

For low-lying excited states of triarylborylcarbazole oligomers, electrons are excited mainly from the few highest occupied molecular orbitals (including HOMO-1 and HOMO) into the first few lowest unoccupied molecular orbitals (such as LUMO and LUMO+1).

From the last subsection, it is found that both HOMO-1 and HOMO span the backbone only. The crucial question to ask is then: which unoccupied orbital(s) accepts the electron from these backbone orbitals in a low-energy excitation? If the electron fills LUMO (i.e., s-LUMO), then the electronic charge gets transferred to the side chain (triarylborane), and one has a “charge transfer” excitation – this would correspond to a low-lying CT state observed by Reitzenstein and Lambert for poly(3,6-carbazole).²⁷ If the electron fills LUMO+1 (i.e., b-LUMO), then it stays on the backbone, which we shall call it a “backbone” excitation.

To better understand the charge distribution, the Mulliken charge populations and electrostatic potential fitting (ESP) charge populations for both the ground and first excited states are computed for a carbazole monomer with a triarylborane substitute, and listed in Table 3. For the ground state, the net Mulliken charge on the carbazole moiety is −0.28, meaning that triarylborane loses some charges. With B3LYP functional, the net Mulliken charge becomes 0.53 on carbazole with the first excited state, leading to a reversal of the molecular dipole moment. So overall, the first excited state involves a net transfer of 0.83 electrons from carbazole to triarylborane. With CAM-B3LYP and ωB97X functionals, the first excited state has less charge transfer character, with a net gain flow of 0.27 and 0.13 electrons from carbazole to triarylborane, respectively. (Also contributing are excitations within the triaryloborane moiety that can clearly be seen from the monomer transition density plots in the middle column of Figure 8.) ESP population analysis leads to essentially the same picture, and the net charge flow is 0.85, 0.27, and 0.12 electrons upon excitation in the monomer. So from now on, only Mulliken charges are presented for P1 and P2 oligomers.

Table 3.

Mulliken and ESP charge populations of triarylborylcarbazole monomer

functional	changes of Mulliken charges on backbone(ground → first excited)	changes of ESP charges on backbone(ground → first excited)
B3LYP	0.81 (−0.28 → 0.53)	0.85 (−0.18 → 0.67)
CAM-B3LYP	0.27 (−0.28 → −0.01)	0.27 (−0.19 → 0.08)
ωB97X	0.13 (-0.28 → −0.15)	0.12 (−0.19 → −0.07)

Figure 8.

Transition densities of triarylborylcarbazole monomer and pentamer calculated with B3LYP, CAM-B3LYP and ωB97X functionals. Monomer densities are presented in the middle, 2,7-linked pentamer (P1) on the left and 3,6-linked pentamer (P2) on the right.

2,7-linked triaryborylcarbazole oligomers

In Table 4, we tabulated the computational results for the first excited state with significant oscillator strength for 2,7-linked triarylborylcarbazole oligomers (P1, up to pentamers). It is noteworthy that, for both 2,7-linked (Table 4) and 3,6-linked (Table 5) oligomers, LC-DFT calculations indicated small amplitudes for intra-triarylboryl local excitations, which are not listed for the compactness of the tables. With B3LYP functional, this excited state is always dominated by charge transfer excitations (HOMO to s-LUMO); but with CAM-B3LYP, this excited state already involves significant backbone excitation (HOMO to b-LUMO) for tetramer and pentamer; with ωB97X, this excited state is dominated by backbone excitations for trimer, tetramer and pentamer.

Table 4.

Lowest excited states of 2,7-linked triarylborylcarbazole oligomers (N≤5).

N	Functional	Character	E(eV)	f	amplitudes	changes of Mulliken charges on backbone(ground → first excited)
1	B3LYP	charge transfer	2.992	0.14	97%, b-HOMO→s-LUMO	0.81 (−0.28→0.53)
	CAM-B3LYP	charge transfer	3.880	0.29	56%, b-HOMO→s-LUMO	0.27 (−0.28→−0.01)
	ωB97X	charge transfer	4.244	0.32	35%, b-HOMO→s-LUMO	0.13 (−0.28→−0.15)
2	B3LYP	charge transfer	2.996	0.31	97%, b-HOMO→s-LUMO	0.80 (−0.57→0.23)
	CAM-B3LYP	charge transfer	3.848	0.65	50%, b-HOMO→s-LUMO	0.25 (−0.56→−0.43)
	ωB97X	charge transfer	4.200	0.75	31%, b-HOMO→s-LUMO	0.13 (−0.56→−0.43)
3	B3LYP	charge transfer	3.018	0.17	96%, b-HOMO→s-LUMO	0.82 (−0.85→−0.03)
	CAM-B3LYP	charge transfer	3.842	0.64	44%, b-HOMO→s-LUMO	0.21 (−0.85→−0.64)
	ωB97X	backbone	4.154	1.58	50%, b-HOMO→b-LUMO	0.06 (−0.84→−0.78)
4	B3LYP	charge transfer	3.017	0.25	94%, b-HOMO→s-LUMO	0.79 (−1.14→−0.35)
	CAM-B3LYP	backbone	3.796	2.26	52%, b-HOMO→b-LUMO	0.10 (−1.13−1.03)
	ωB97X	backbone	4.047	3.29	77%, b-HOMO→b-LUMO	0.02 (−1.12→−1.10)
5	B3LYP	charge transfer	3.005	0.34	87%, b-HOMO→s-LUMO	0.74 (−1.44→−0.70)
	CAM-B3LYP	backbone	3.777	3.67	67%, b-HOMO→b-LUMO	0.01 (−1.42→−1.41)
	ωB97X	backbone	4.018	4.40	76%, b-HOMO→b-LUMO	0.02 (−1.40→−1.38)

Table 5.

Lowest excited states of 3,6-linked triarylborylcarbazole oligomers (N≤5).

N	Functional	Character	E(eV)	f	amplitudes	changes of Mulliken charges on backbone(ground → first excited)
1	B3LYP	charge transfer	2.993	0.14	97%, b-HOMO→s-LUMO	0.81 (−0.28→0.53)
	CAM-B3LYP	charge transfer	3.880	0.51	56%, b-HOMO→s-LUMO	0.27 (−0.28→−0.01)
	ωB97X	charge transfer	4.244	0.32	35%, b-HOMO→s-LUMO	0.13 (−0.28→−0.15)
2	B3LYP	charge transfer	2.767	0.37	96%, b-HOMO→s-LUMO	0.80 (−0.56→0.24)
	CAM-B3LYP	charge transfer	3.710	0.94	61%, b-HOMO→s-LUMO	0.38 (−0.56→−0.18)
	ωB97X	charge transfer	4.083	1.07	39%, b-HOMO→s-LUMO	0.19 (−0.55→−0.36)
3	B3LYP	charge transfer	2.678	0.23	96%, b-HOMO→s-LUMO	0.85 (−0.85→0.00)
	CAM-B3LYP	charge transfer	3.761	0.92	62%, b-HOMO→s-LUMO	0.46 (−0.84→−0.38)
	ωB97X	charge transfer	4.165	1.18	29%, b-HOMO→s-LUMO	0.21 (−0.83→-0.62)
4	B3LYP	charge transfer	2.644	0.27	95%, b-HOMO→s-LUMO	0.84 (−1.14→−0.30)
	CAM-B3LYP	charge transfer	3.750	0.96	58%, b-HOMO→s-LUMO	0.43 (−1.12→−0.69)
	ωB97X	charge transfer	4.162	1.16	27%, b-HOMO→s-LUMO	0.17 (−1.11→−0.94)
5	B3LYP	charge transfer	2.634	0.22	94%, b-HOMO→s-LUMO	0.85 (−1.39→−0.54)
	CAM-B3LYP	charge transfer	3.763	0.90	53%, b-HOMO→s-LUMO	0.42 (−1.38→−0.96)
	ωB97X	charge transfer	4.177	1.47	21%, b-HOMO→s-LUMO	0.15 (−1.38→−1.23)

As far as Mulliken population is concerned, each triarylborane side chain loses about 0.28 electrons to the carbazole backbone. With B3LYP, the amount of charge transfer upon excitation changes little with chain length: 0.83 with monomer, 0.80 with dimer, 0.82 with trimer, 0.79 with tetramer and 0.74 with pentamer. The net charge transfer is much smaller with CAM-B3LYP: 0.27 with monomer, 0.25 with dimer, 0.21 with trimer, 0.10 with tetramer, and 0.01 with pentamer; and it is even smaller with ωB97X: 0.13 with monomer and dimer, 0.06 with trimer, and 0.02 with tetramer and pentamer. So from this Mulliken population analysis, we can conclude that, with long-range corrected functionals, the lowest energy excitation takes place mainly within the backbone.

The electronic excitation can be more clearly characterized by calculating the transition density, which is defined as,

$${\rho }_t\left(r\right)=\sum _{ai}{X}_{ai}{\Psi }_a\left(r\right){\Psi }_i\left(r\right),$$ (2)

where X_ai are excitation amplitudes (for a given excited state) from occupied orbitals (ψ_i) to unoccupied orbitals (ψ_a).

The transition densities for 2,7-linked triarylboryl polycarbazole pentamers are shown in the left column of Figure 8. With B3LYP, it incorrectly yields a charge transfer state spread over a couple of monomer units. With CAM-B3LYP and ωB97X, one can clearly see a delocalized backbone excitation of the oligomer, as has been suggested in a recent work.²⁷

The experimental adsorption maximum for P1 polymer is found at 363 nm (3.42 eV) with powder and films and 353 nm (3.52 eV) in dichloromethane.²⁷ In Table 4, the excitation energy with B3LYP functional fluctuates between 2.99 and 3.02 eV with the chain length. In contrast, the excitation energy steadily decreases with CAM-B3LYP (3.88 to 3.77 eV) and with ωB97X (4.24 to 4.02 eV).

3,6-linked triaryborylcarbazole oligomers

In Table 5, we collected the computational results for the first excited state with significant oscillator strength of 3,6-linked triarylborylcarbazole oligomers (P2, also up to pentamers). With B3LYP functional, this excited state is always dominated by charge transfer excitations (HOMO to s-LUMO). With CAM-B3LYP or ωB97X, no significant backbone to backbone excitations were found for this state, either.

Equally interesting are the Mulliken charges for P2 oligomers as tabulated in Table 5. With B3LYP functional, the net charge transfer is largely insensitive (between 0.80 and 0.85 electrons) to the chain length. With CAM-B3LYP, the net charge transfer actually increases first: 0.27 for monomer, 0.38 for dimer, 0.46 for trimer, 0.43 for tetramer and 0.42 for pentamer (as opposed to 0.01 for P1 pentamer). The same can be observed with the net charge transfer with ωB97X functional: 0.13 for monomer, 0.19 for dimer, 0.21 for trimer, 0.17 for tetramer and 0.15 for pentamer (as opposed to 0.02 for P1 pentamer). This also confirms that the first excited state in P2 oligomers retains significant charge transfer character.

The transition densities for 3,6-linked triarylboryl polycarbazole pentamers are shown in the right column of Figure 8. With all three functionals, it yields an excitation that is mostly localized over one monomer. This is again consistent with what has been found by Reitzenstein and Lambert.²⁷

The experimental adsorption maximum for P2 polymer is found at 379 nm (3.28 eV) with power and films and 365 nm (3.40 eV) in dichloromethane.²⁷ In Table 5, the excitation energy with B3LYP functional changes in a wrong direction: 2.99 eV for monomer, 2.77 eV for dimer, 2.68 eV for trimer, 2.64 eV for tetramer, and 2.63 eV for pentamer. With long-range corrected functionals, the excitation energy does not change much beyond dimer: 3.71 eV for dimer to 3.76 eV for pentamer with CAM-B3LYP; 4.08 eV for dimer and 4.18 eV for pentamer with ωB97X.

When putting this together, one arrives at the same qualitative energy diagram for the ground and excited states of carbazole monomer and P1 and P2 polymers, as depicted by Reitzenstein et al.²⁷ Namely, the lowest excited state involves a charge-transfer excitation for monomer and P2 oligomers, whereas it involves a backbone to backbone excitation for P1 oligomers. It is rather remarkable that the qualitatively different optical properties for long-chain polymers can be predicted with only tetramers and pentamers.

CONCLUSION

Based on the DFT and TDDFT calculations presented above, the following conclusions can be drawn:

1. backbone HOMO follows the same trend in unsubstituted or substituted 2,7-linked or 3,6-linked carbazole oligomers;

2. side-chain (triarylborane) LUMO energy does not change with chain length, regardless of linkage;

3. backbone LUMO energy of 2,7-linked oligomers decreases with the chain length due to a favorable “bonding”-type mixing of monomer LUMOs. This facilitates excitations within the backbone;

4. with 3,6-linked carbazole oligomers (N = 1 ~ 5) and with short 2,7-linked carbazole oligomers (N = 1 ~ 3), the lowest excited state involves considerable charge transfer from the backbone to the triarylborane side chain;

5. with 2,7-linked longer carbazole oligomers (such as tetramer and pentamer), the lowest excited state involves a delocalized excitation within the backbone, but only if long-range corrected functionals such as CAM-B3LYP and ωB97X are applied.

All these are in good agreement with Reitzenstein and Lambert’s experimental results and their qualitative energy diagram.²⁷

B3LYP is known to be the most popular functional in use, especially for the geometrical optimization. However, its use in excited state calculations should always be handled with caution, because B3LYP is not asymptotically correct to describe CT states.^40,41 One of the main contributions of the present work is therefore, in our opinion, perhaps the demonstration of the use of long-range corrected functionals, such as CAM-B3LYP and ωB97X, in the study of extended molecular systems (such as conjugated polymers) and/or CT excited states.

To further improve our understanding/interpretation of experimental observations, though, one has to move forward simultaneously on two fronts: on the theoretical front, two functionals (CAM-B3LYP and ωB97X) used in this work have to be compared against other long-range corrected functionals in existence, and explicit/implicit solvent models have to be adapted to work with these functionals to study solvent effects; on the technical front, the computational efficiency of TDDFT calculations need to be vastly improved, especially for the study of emission spectrum and fluorescence quenching of conjugated polymers.