Model-Free Feature Screening for Ultrahigh Dimensional Data

Abstract

With the recent explosion of scientific data of unprecedented size and complexity, feature ranking and screening are playing an increasingly important role in many scientific studies. In this article, we propose a novel feature screening procedure under a unified model framework, which covers a wide variety of commonly used parametric and semiparametric models. The new method does not require imposing a specific model structure on regression functions, and thus is particularly appealing to ultrahigh-dimensional regressions, where there are a huge number of candidate predictors but little information about the actual model forms. We demonstrate that, with the number of predictors growing at an exponential rate of the sample size, the proposed procedure possesses consistency in ranking, which is both useful in its own right and can lead to consistency in selection. The new procedure is computationally efficient and simple, and exhibits a competent empirical performance in our intensive simulations and real data analysis.

1 Introduction

High-dimensional data have frequently been collected in a large variety of areas such as biomedical imaging, functional magnetic resonance imaging, tomography, tumor classifications, and finance. In high-dimensional data, the number of variables or parameters p can be much larger than the sample size n. Such a “large p, small n” problem has imposed many challenges for statistical analysis, and calls for new statistical methodologies and theories (Donoho, 2000; Fan and Li, 2006). The sparsity principle, which assumes that only a small number of predictors contribute to the response, is frequently adopted and deemed useful in the analysis of high-dimensional data. Following this general principle, a large number of variable selection approaches have been developed in the recent literature to estimate a sparse model and select significant variables simultaneously. Examples include Lasso (Tibshirani, 1996), SCAD (Fan and Li, 2001), nonnegative garrote (Breiman, 1995), group Lasso (Yuan and Lin, 2006), adaptive Lasso (Zou, 2006), and Dantzig selector (Candes and Tao, 2007). See Fan and Lv (2010) for an overview.

While those variable selection methods have been successfully applied in many high-dimensional analysis, modern applications in areas such as genomics, proteomics, and high-frequency finance further push the dimensionality of data to an even larger scale, where p may grow exponentially with n. Such ultrahigh-dimensional data present simultaneous challenges of computational expediency, statistical accuracy and algorithm stability (Fan, Samworth and Wu, 2009). It is difficult to directly apply the aforementioned variable selection methods to those ultrahigh-dimensional statistical learning problems due to the computational complexity inherent in those methods. To address those challenges, Fan and Lv (2008) emphasized the importance of feature screening in ultrahigh-dimensional data analysis, and proposed sure independence screening (SIS) and iterated sure independence screening (ISIS) in the context of linear regression models. Furthermore, Fan, Samworth and Wu (2009) and Fan and Song (2010) extended SIS and ISIS from a linear model to a generalized linear model. Each of those proposals focuses on a specific model, and its performance is based upon the belief that the imposed working model is close to the true model.

In this article, we propose a model-free feature screening approach for ultrahigh-dimensional data. Compared with the SIS, the most distinguishable feature of our proposal is that we only impose a very general model framework instead of a specific model. It is so general that the newly proposed procedure can be viewed as a model-free screening method, and it covers a wide range of commonly used parametric and semiparametric models. This feature makes our proposed procedure particularly appealing for feature screening when there are a huge number of candidate variables, but little information suggesting that the actual model is linear or follows any other specific parametric form. This flexibility is achieved by using the newly proposed marginal utility measure that is concerned with the entire conditional distribution of the response given the predictors. In addition, our method is robust to outliers and heavy-tailed responses in that it only uses the ranks of the observed response values. Theoretically, we establish that the proposed method possesses a consistency in ranking (CIR) property. That is, in probability, our marginal utility measure always ranks an active predictor above an inactive one, and thus guarantees a clear separation between the active and inactive predictors. The CIR property can be particularly useful in some genomic studies (Choi, Shedden, Sun and Zhu, 2009) where ranking is more of a concern than selection. Moreover, it leads to consistency in selection; that is, it simultaneously selects all active predictors and excludes all inactive predictors in probability, provided an ideal cutoff of the utility measure is available. The proposed procedure is valid provided that the total number of predictors p grows slower than exp(an) for any fixed a > 0. This rate is similar to the exponential rate achieved by the SIS procedures. Given a rank of all candidate features, we further propose a combination of hard and soft thresholding strategies to obtain the cutoff point that separates the active and inactive predictors. The soft threshold is constructed by adding a series of auxiliary variables, motivated by the idea of adding pseudo variables in model selection proposed by Luo, Stefanski and Boos (2006) and Wu, Boos and Stefanski (2007). Similar to the iterative SIS procedures, we also propose an iterative version of our new screening method. This is due to the fact that the marginal utility measure may miss an active predictor that is marginally independent of the response, a phenomenon also observed in the SIS procedures. The iterative procedure is shown to resolve this issue effectively. Computationally, the proposed screening procedure does not require any complicated numerical optimization and is very simple and fast to implement.

The rest of the article is organized as follows. In Section 2, we first present our general model framework, then develop the new feature ranking and screening approach. Section 3 illustrates the finite sample performance by both Monte Carlo simulations and a real data analysis. All technical proofs are given in the Appendix.

2 A Unified Feature Screening Approach

2.1 A General Model Framework

Let Y be the response variable with support Ψ_y, and Y can be both univariate and multivariate. Let x = (X₁, · · ·, X_p)^T be a covariate vector. Here we adopt the same notation system as Fan and Lv (2008) where a boldface lower case letter denotes a vector and a boldface capital letter denotes a matrix. We first develop the notion of active predictors and inactive predictors without specifying a regression model. We consider the conditional distribution function of Y given x, denoted by F(y | x) = P(Y < y | x). Define two index sets:

• = {k : F(y | x) functionally depends on X_k for some y ∈ Ψ_y},

• = {k : F(y | x) does not functionally depend on X_k for any y ∈ Ψ_y}.

If k ∈ , X_k is referred to as an active predictor, whereas if k ∈ 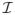, X_k is referred to as an inactive predictor. Let x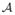, a p₁ × 1 vector, consist of all X_k with k ∈ 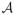. Similarly, let x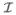, a (p − p₁) ×1 vector, consist of all inactive predictors X_k with k ∈ .

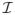Next we consider a general model framework under which we are to develop our unified screening approach. Specifically, we consider that F(y | x) depends on x only through β^Tx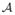 for some p₁ × K constant matrix β. In other words, we assume that

$$F(y\mid \mathbf{x})=F_0(y\mid {\mathit{\beta }}^T{\mathbf{x}}_{\mathcal{A}}),$$ (2.1)

where F₀(· | β^Tx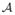) is an unknown distribution function for a given β^Tx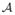. We make the following remarks. First, β may not be identifiable; what is identified is the space spanned by the columns of β. However, the identifiability of β is of no concern here because our primary goal is to identify active variables rather than to estimate β itself. Actually, our screening procedure does not require an explicit estimation of β. Second, the form of (2.1) is fairly common in a large variety of parametric and semiparametric models where the response Y depends on the predictors x through a number of linear combinations β^Tx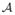. As we will show next, (2.1) covers a wide range of existing models and, in many cases, K is as small as just one, two, or three.

Before we continue the pursuit of feature screening, we examine some special cases of model (2.1) to show its generality. Note that many existing regression models for a continuous response can be written in the following form:

$$h(Y)=f_1({\mathit{\alpha }}_1^T{\mathbf{x}}_{\mathcal{A}})+{\mathit{\alpha }}_2^T{\mathbf{x}}_{\mathcal{A}}+f_2({\mathit{\alpha }}_3^T{\mathbf{x}}_{\mathcal{A}})\epsilon ,$$ (2.2)

where h(·) is a monotone function, f₂(·) is a nonnegative function, α₁, α₂, and α₃ are unknown coefficients, and it is assumed that ε is independent of x. Here h(·), f₁(·)and f₂(·) may be either known or unknown. Clearly model (2.2) is a special case of (2.1) if we choose β to be a basis of the column space spanned by α₁, α₂ and α₃. Meanwhile, it is seen that model (2.2) with h(Y) = Y includes the following special cases: the linear regression model, the partially linear model (Härdle, Liang and Gao, 2000), the single-index model (Härdle, Hall and Ichimura, 1993), and the partially linear single-index model (Carroll, Fan, Gijbels and Wand, 1997). Model (2.2) also includes the transformation regression model for a general transformation h(Y).

In survival data analysis, the response Y is the time to event of interest, and a commonly used model for Y is the accelerated failure time model:

$$log(Y)={\alpha }_0+{\mathit{\alpha }}_1^T{\mathbf{x}}_{\mathcal{A}}+\epsilon ,$$

where ε is independent of x. Different choices for the error distribution of ε lead to models that are frequently seen in survival analysis; that is, the extreme value distribution for ε yields the proportional hazards model (Cox, 1972), and the logistic distribution for ε yields the proportional odds model (Pettitt, 1982). It can again be easily verified that all those survival models are special cases of model (2.1).

Various existing models for discrete responses such as binary outcomes and count responses can be treated as a generalized partially linear single-index model (Carroll, Fan, Gijbels and Wand, 1997)

$$g_1\{E(Y\mid \mathbf{x})\}=g_2({\mathit{\alpha }}_1^T{\mathbf{x}}_{\mathcal{A}})+{\mathit{\alpha }}_2^T{\mathbf{x}}_{\mathcal{A}},$$ (2.3)

where the conditional distribution of Y given x belongs to the exponential family, g₁(·) is a link function, g₂(·) is an unknown function, and α₁ and α₂ are unknown coefficients. While model (2.3) includes the generalized linear model and the generalized single-index model as special cases, (2.3) itself is a special case of (2.1), which allows an unknown link function g₁(·) as well.

In summary, a large variety of existing models with various types of response variables can be cast into the common model framework of (2.1). As a consequence, our feature screening approach developed under (2.1) offers a unified approach that works for a wide range of existing models.

2.2 A New Screening Procedure

To facilitate presentation, we assume throughout this article that E(X_k) = 0 and var(X_k) = 1 for k = 1, …, p. Define Ω(y) = E{xF (y | x)}. It then follows by the law of iterated expectations that Ω(y) = E[xE{1(Y < y) | x}] = cov{x, 1(Y < y)}. Let Ω_k(y) be the k-th element of Ω(y), and define

$${\omega }_k=E\{{\mathrm{\Omega }}_k^2(Y)\},k=1,\dots ,p.$$ (2.4)

Then ω_k is to serve as the population quantity of our proposed marginal utility measure for predictor ranking. Intuitively, one can see that, if X_k and Y are independent, then X_k and the indicator function 1(Y < y) change independently. Consequently Ω_k(y) = 0 for any y ∈ Ψ_y and ω_k = 0. On the other hand, if X_k and Y are related, then there exists some y ∈ Ψ_y such that Ω_k(y) ≠ 0, and hence ω_k must be positive. This observation motivates us to employ the sample estimate of ω_k to rank all the predictors. We will summarize this intuitive observation more rigorously in Corollary 1 in the next section.

Given a random sample {(x_i, Y_i), i = 1, · · ·, n} from {x, Y}, we next derive a sample estimator of ω_k. For ease of presentation, we assume that the sample predictors are all standardized; that is, $n^{-1}{\sum }_{i=1}^n{X}_{ik}=0$ and $n^{-1}{\sum }_{i=1}^n{X}_{ik}^2=1$ for k = 1, · · ·, p. A natural estimator for ω_k is

$${\stackrel{\sim }{\omega }}_k=\frac{1}{n}\sum _{j=1}^n{\left\{\frac{1}{n}\sum _{i=1}^n{X}_{ik}\mathbf{1}(Y_i<Y_j)\right\}}^2,k=1,\dots ,p,$$

where X_ik denotes the k-th element of x_i. As shown in the proof of Theorem 2,

$${\widehat{\omega }}_k=\frac{n^3}{n(n-1)(n-2)}{\stackrel{\sim }{\omega }}_k$$

is a U-statistics. This enables us to directly use the theory of U-statistics to establish asymptotic property of ω̂_k. Note that ω̂_k is a scaled version of ω̃_k. They lead to the same result of feature ranking and screening.

In sum, we propose to rank all the candidate predictors X_k, k = 1, …, , p, according to ω̂_k from the largest to smallest. We then select the top ones as the active predictors. Later we will propose a thresholding rule for obtaining the cutoff value that separates the active and inactive predictors.

Before we turn to the theoretical properties of the proposed procedure, we will examine some simple settings to get more insight into our proposal. First, we consider a case where K = 1 and x ~ N_p(0, σ²I_p) with unknown σ². Note that the normality assumption on x is not necessary and will be relaxed later, to derive the measure’s properties. For ease of presentation, we write $\mathbf{x}={({\mathbf{x}}_{\mathcal{A}}^{\text{T}},{\mathbf{x}}_{\mathcal{I}}^{\text{T}})}^{\text{T}}$, and define b = (b₁, …, b_p)^T = (β^T, 0^T)^T. It follows by a direct calculation that

$$\mathbf{\Omega }(y)=E\{\mathbf{x}{F}_0(y\mid {\mathbf{b}}^{\text{T}}\mathbf{x})\}=c(y)\mathbf{b},$$

where $c(y)={\Vert \mathbf{b}\Vert }^{-1}{\int }_{-\infty }^{\infty }{vF}_0(y\mid v\Vert \mathbf{b}\Vert )\phi (v;0,{\sigma }^2)$ with φ(v; 0, σ²) being the density function of N(0, σ²) at v. Then ${\omega }_k=E\{{\mathrm{\Omega }}_k^2(Y)\}=E\{c^2(Y)\}{b}_k^2$. If E{c²(Y)} > 0, then

$$\underset{k\in \mathcal{I}}{max}{\omega }_k<\underset{k\in \mathcal{A}}{min}{\omega }_k,$$ (2.5)

and ω_k = 0 if and only if k ∈ 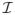. This implies that the quantity ω_k may be used for feature screening in this setting.

2.3 Theoretical Properties

The property (2.5) allows us to perform feature ranking and feature screening. To ensure this property in general, we impose the following conditions. It is interesting to note that all the conditions are placed on the distribution of x only.

• (C1)
  The following inequality condition holds uniformly for p:

  $$\frac{K^2{\lambda }_{max}\{cov({\mathbf{x}}_{\mathcal{A}},{\mathbf{x}}_{\mathcal{I}}^{\text{T}})cov({\mathbf{x}}_{\mathcal{I}},{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\}}{{\lambda }_{min}^2\{cov({\mathbf{x}}_{\mathcal{A}},{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\}}<\frac{\underset{k\in \mathcal{A}}{min}{\omega }_k}{{\lambda }_{max}\{{\mathbf{\Omega }}_{\mathcal{A}}\}},$$ (2.6)

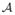  where ${\mathbf{\Omega }}_{\mathcal{A}}=E\{{\mathbf{\Omega }}_{\mathcal{A}}(Y){\mathbf{\Omega }}_{\mathcal{A}}^T(Y)\}$, Ω (y) = {Ω₁(y), · · ·, Ω_p1(y)}^T, and λ_max{B} and λ_min{B} denote the largest and smallest eigenvalues of a matrix B, respectively. Note that λ_min(B) and λ_max(B) may depend on the dimension of B. Throughout this article, when we say that “a < b holds uniformly for p”, it means that $\underset{p\to \infty }{limsup}\{a(p)-b(p)\}<0$.

• (C2)
  The linearity condition:

  $$E\{\mathbf{x}\mid {\mathit{\beta }}^{\text{T}}{\mathbf{x}}_{\mathcal{A}}\}=cov(\mathbf{x},{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\mathit{\beta }{\{cov({\mathit{\beta }}^{\text{T}}{\mathbf{x}}_{\mathcal{A}})\}}^{-1}{\mathit{\beta }}^{\text{T}}{\mathbf{x}}_{\mathcal{A}}.$$ (2.7)
• (C3)
  The moment condition: there exists a positive constant t₀ such that

  $$\underset{1\le k\le p}{max}E\{exp({tX}_k)\}<\infty ,\text{for}0<t\le t_0.$$

Condition (C1) dictates the correlations among the predictors, and is the key assumption to ensure that the proposed screening procedure works properly. We make the following remarks about this condition. First, as the dimension K of β in (2.1) increases, the condition becomes more stringent. Therefore, a model with a small K is favored by our procedure. In many commonly used models, however, K is indeed small, as partially shown in Section 2.1. Second, for the left hand side of (2.6), the numerator measures the correlation between the active predictors x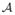 and the inactive ones x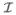, while the denominator measures the correlation among the active predictors themselves. When 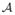x and x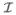 are uncorrelated, (C1) holds automatically. For the proposed screening method to work well, this condition rules out the case in which there is strong collinearity between the active and inactive predictors, or among the active predictors themselves. This is very similar to Condition 4 of Fan and Lv (2008, page 870). Third, the quantity $\underset{k\in \mathcal{A}}{min}{\omega }_k$ on the right hand side of (2.6) reflects the signal strength of individual active predictors, which in turn controls the rate of probability error in selecting the active predictors. This aspect is similar to Condition 3 of Fan and Lv (2008, page 870), which requires the contribution of an active predictor to be sufficiently large. Finally, we note that (2.6) is not scale invariant, since Σ = cov(x, x^T) is not taken into account. This is similar to the linear SIS procedure of Fan and Lv (2008), which is based upon the covariance vector cov(x, Y) alone without the term Σ. Fan and Lv (2008) imposed the concentration property (Fan and Lv, 2008, Equation (16) on page 870) that implicitly requires the marginal variances of all predictors be of the same order. In our setup, we always marginally standardize all the predictors to have sample variance equal to one.

Condition (C2) holds if x follows a normal or an elliptical distribution (Fang, Kotz and Ng, 1989). This condition was first proposed by Li (1991) and has been widely used in the dimension-reduction literature. It is remarkable though that Condition (C2) is itself weaker than both the normality and the elliptical symmetry conditions because we only require it to hold for the true value of β. Furthermore, Hall and Li (1993) showed that the linearity condition holds asymptotically if the number of predictors p diverges while the dimension K remains fixed. For this reason, we view the linearity condition as a mild assumption in ultrahigh-dimensional regressions, where p is essentially very large and grows at a fast rate towards infinity.

Condition (C3) is concerned with the moments of the predictors, which assumes that all moments of the predictors are uniformly bounded. This condition holds for a variety of distributions, including the normal distribution and the distributions with bounded support. Compared with the usual conditions imposed in the feature screening literature, (C3) relaxed the normality assumption assumed by Fan and Lv (2008), in which both x and Y | x are assumed to be normally distributed.

Next we present the theoretical properties of the proposed screening measure. The proof is given in the Appendix. It is the main theoretical foundation for our feature screening procedure.

Theorem 1

Under Conditions (C1)–(C3), the following inequality holds uniformly for p:

$$\underset{k\in \mathcal{I}}{max}{\omega }_k<\underset{k\in \mathcal{A}}{min}{\omega }_k.$$ (2.8)

The following corollary reveals that the quantity ω_k is in fact a measure of the correlation between the marginal covariate X_k and the linear combinations β^Tx.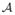

Corollary 1

Under the linearity condition (C2) and for k = 1, · · ·, p, ω_k = 0 if and only if cov(β^Tx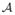, X_k) = 0.

Theorem 1 and Corollary 1 together offer more insights into the newly proposed utility measure ω_k. First, it is easy to see that, when X_k is independent of Y, ω_k = 0. On the other hand, k ∈ 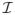alone does not necessarily imply that ω_k = 0. The quantity is zero only if X_k is uncorrelated with β^Tx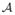. Theorem 1, however, ensures that ω_k of an inactive predictor is always smaller than ω_k of an active predictor, which is sufficient for the purpose of predictor ranking.

We next present the main theoretical result on feature ranking in terms of the utility measure ω̂_k.

Theorem 2. (Consistency in Ranking)

In addition to the conditions in Theorem 1, we further assume that p = o {exp(an)} for any fixed a > 0. Then, for any ε > 0, there exists a sufficiently small constant s_ε ∈ (0, 2/ε) such that

$$P\left(\underset{k=1,\dots ,p}{sup}\mid {\widehat{\omega }}_k-{\omega }_k\mid >\epsilon \right)\le 2pexp\{nlog(1-\epsilon s_{\epsilon }/2)/3\}.$$

In addition, if we write $\delta =\underset{k\in \mathcal{A}}{min}{\omega }_k-\underset{k\in \mathcal{I}}{min}{\omega }_k$, then there exists a sufficiently small constant s_δ/2 ∈ (0, 4/δ;) such that

$$P\left(\underset{k\in \mathcal{I}}{max}{\widehat{\omega }}_k<\underset{k\in \mathcal{A}}{min}{\widehat{\omega }}_k\right)\ge 1-4pexp\{nlog(1-\delta s_{\delta /2}/4)/3\}.$$

Note that p = o {exp(an)}. Thus, the right-hand side of the above equation approaches 1 with an exponential rate as n → ∞. Theorem 2 justifies using ω̂_k to rank the predictors, and it establishes the consistency in ranking. That is, ω̂_k always ranks an active predictor above an inactive one in probability, and so guarantees a clear separation between the active and inactive predictors. Provided an ideal cutoff is available, this property would lead to consistency in selection in the ultrahigh-dimensional setup. Next we propose a thresholding rule to obtain a cutoff value to separate the active and inactive predictors.

2.4 Thresholding Rule

The thresholding rule is based upon a combination of a soft cutoff value obtained by adding artificial auxiliary variables to the data, and a hard cutoff that retains a fixed number of predictors after ranking.

The idea of introducing auxiliary variables for thresholding was first proposed by Luo, Stefanski and Boos (2006) to tune the entry significance level in forward selection, and then extended by Wu, Boos and Stefanski (2007) to control the false selection rate of forward regression in the linear model. We adopt this idea in our setup as follows. We independently and randomly generate d auxiliary variables z ~ N_d(0, I_d) such that z is independent of both x and Y. The normality is not critical here, as we shall see later. Regard the (p + d) dimensional vector (x^T, z^T)^T as the predictors and Y as the response. We calculate ω_k for k = 1, · · ·, p + d. Since z is truly inactive by construction, we have $\underset{k\in \mathcal{A}}{min}{\omega }_k>\underset{\ell =1,\dots ,d}{max}{\omega }_{p+\ell }$ by Theorem 1, and given a random sample {(x_i, z_i, Y_i), i = 1, …, n}, it holds in probability that $\underset{k\in \mathcal{A}}{min}{\widehat{\omega }}_k>\underset{\ell =1,\dots ,d}{max}{\widehat{\omega }}_{p+\ell }$ by Theorem 2. Define $C_d=\underset{\ell =1,\dots ,d}{max}{\widehat{\omega }}_{p+\ell }$, which can be viewed as a benchmark that separates the active predictors from the inactive ones. This leads to the selection,

$${\widehat{\mathcal{A}}}_1=\{k:{\widehat{\omega }}_k>C_d\}.$$ (2.9)

We call (2.9) the soft thresholding selection.

The next theorem gives an upper bound on the probability of recruiting any inactive variables by the above soft thresholding selection. It can be viewed as an analogue of Theorem 1 of Fan, Samworth and Wu (2009), while the exchangeability condition imposed in this theorem is similar in spirit to their condition (A1). This result shows how the soft thresholding rule performs.

Theorem 3

Let r ∈ ℕ, the set of natural numbers. We assume the exchangeability condition, that is, the inactive predictors {X_j, j ∈ 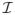} and the auxiliary variables {Z_j, j = 1, …, d} are exchangeable in the sense that both the inactive and auxiliary variables are equally likely to be recruited by the soft thresholding procedure. Then

$$P\left(\mid {\widehat{\mathcal{A}}}_1\cap \mathcal{I}\mid \ge r\right)\le {\left(1-\frac{r}{p+d}\right)}^d,$$

where |·| denotes the cardinality of a set.

An issue of practical interest in soft thresholding is the choice of number of auxiliary variables d. Intuitively, a small d value may introduce much variability, whereas a large d value requires heavier computation. Empirically, we choose d = p, and our numerical experience has suggested that this choice works quite well. Choosing an optimal d, however, is out of the scope of this paper and is a potential direction for future research.

In addition to soft thresholding, we also consider a hard thresholding rule proposed by Fan and Lv (2008), which retains a fixed number of predictors with the largest N values of ω_k’s; that is,

$${\widehat{\mathcal{A}}}_2=\{k:{\widehat{\omega }}_k>{\widehat{\omega }}_{(N)}\},$$ (2.10)

where N is usually chosen to be [n/log n] and ω̂_(N) denotes the N-th largest value among all ω̂_k’s.

In practice, the data determine whether the soft or hard thresholding comes into play. To better understand the two thresholding rules, we conducted a simulation study. The results are not reported here but in an earlier version of this paper available at the authors’ websites. We make the following observations from our simulation study. When the signal in the data is sparse (a small p₁), the hard thresholding rule often dominates the soft selection rule. On the other hand, when there are many active predictors (a large p₁), the soft thresholding becomes more dominant. While the hard thresholding is fully determined by the sample size, soft thresholding takes into account the effect of signals in the data, which is helpful when p₁ is relatively large. Consequently, we propose to combine the soft and hard thresholding, and construct the final active predictor index set as

$$\widehat{\mathcal{A}}={\widehat{\mathcal{A}}}_1\cup {\widehat{\mathcal{A}}}_2,$$ (2.11)

where the union of the two sets is taken.

2.5 Iterative Feature Screening

An inherent issue with any feature screening procedure based on a marginal utility measure is that the method may miss those predictors which are marginally unrelated but jointly related to the response. To overcome this problem, we develop an iterative version of our proposed screening method. It is similar in spirit to the family of iterative SIS methods. However, unlike iterative SIS which breaks the correlation structure among predictors through the correlation between the residuals of the response and the remaining predictors, our method computes the correlation between the original response Y and the residual of the remaining x. This is because, the residual of Y is not available in a model-free context. However, we can compute the residual of x, where the residual is defined as the projection of the remaining of x onto the orthogonal complement space of the predictors selected in the previous steps. More specifically, our iterative procedure is given as follows.

• Step 1We first apply our proposed screening procedure for y and X, where X denotes the n × p data matrix that stacks n sample observations x₁, …, x_n and y = (Y₁, …, Y_n)^T. Suppose p₍₁₎ predictors are selected, where p₍₁₎ < N = [n/log n]. We denote the set of indices of the selected predictors by 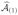, and the associated n × p₍₁₎ data matrix by X.
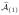• Step 2
  Let 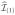denote the complement of 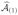, and X 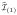denote the remaining n × (p − p₍₁₎) data matrix. Next, we define the predictor residual matrix

  $${\mathbf{X}}_r=\left\{{\mathbf{I}}_n-{\mathbf{X}}_{{\widehat{\mathcal{A}}}_1}{\left({\mathbf{X}}_{{\widehat{\mathcal{A}}}_1}^T{\mathbf{X}}_{{\widehat{\mathcal{A}}}_1}\right)}^{-1}{\mathbf{X}}_{{\widehat{\mathcal{A}}}_1}^T\right\}{\mathbf{X}}_{{\widehat{\mathcal{I}}}_{(1)}}.$$

  Apply again our proposed screening procedure for y and X_r. Suppose p₍₂₎ predictors are selected, and the resulting index set is denoted by 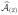. Update the total selected predictor set by ∪

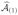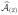
• Step 3Repeat Step 2 M − 1 times until the total selected number of predictors p₍₁₎ + … + p_(M) exceeds the pre-specified number N = [n/log n]. The final selected predictor set is ∪ … ∪ .

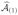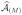For the iterative procedure, we fix the number of total selected predictors N =[n/log n]. In our simulations, we consider an M = 2 iterative procedure and choose p₍₁₎ = [N/2], which works well for our example. Some guidelines on selecting these parameters in an iterative feature screening procedure can be found in Fan, Samworth and Wu (2009).

3 Numerical Studies

3.1 General Setup

In this section we assess the finite sample performance of the proposed method and compare it with existing competitors via Monte Carlo simulations. For brevity, we refer our approach as sure independent ranking and screening (SIRS). Throughout, we set the sample size n = 200 and the total number of predictors p = 2000. We repeat each scenario 1000 times. For the soft thresholding, we set the number of auxiliary variables d = p. We generate the predictors x from a normal distribution with mean zero. Unless otherwise specified, we consider two covariance structures of x:Σ₁ = (σ_ij)_p×p with σ_ij = 0.8^|i−j|; and Σ₂ = (σ_ij)_p×p with σ_ii = 1, σ_ij = 0.4 if both i, j ∈ 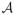or i, j ∈ 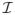, and σ_ij = 0.1 otherwise.

To evaluate the performance of the proposed method, we employ mainly two criteria. The first criterion measures accuracy of ranking the predictors (with no thresholding). For that purpose, we record the minimum number of predictors in a ranking that is required to ensure the inclusion of all the truly active predictors. We denote this number by 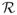. The second criterion focuses on accuracy of feature screening when applying the proposed thresholding rule to the ranked predictors. Unlike feature selection, where it is important to simultaneously achieve both a high true positive and a low false positive, feature screening is more concerned with retaining all the truly active predictors. This is because screening usually serves as a preliminary massive reduction step, and is often followed by a conventional feature selection for further refinement. For that reason, we record the proportion that all the truly active predictors are correctly identified after thresholding in 1000 repetitions, and denote this proportion by 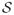. A ranking and screening procedure is deemed competent if it yields an 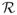value that is close to the true number of active predictors p₁, and an 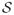value that is close to one.

3.2 Linear Models

A large number of well known variable screening and selection approaches, such as linear SIS (Fan and Lv, 2008), Lasso (Tibshirani, 1996), stepwise regression, and forward regression (Wang, 2009). We thus begin with a class of linear models. Our simulations reveal the following two key observations. First, when the model is indeed linear homoscedastic with a normal error, SIRS has a comparable performance to the model-based methods which correctly specify the model. Second, when the true model deviates from the imposed model assumptions (e.g., the variance is heteroscedastic or the error distribution is heavily tailed), our method clearly outperforms the model-based methods.

Example 1

In the first example, we consider a classical linear model with varying squared multiple correlation coefficient R², variance structure and error distribution:

$$Y=c{\mathit{\beta }}^{\text{T}}\mathbf{x}+\sigma \epsilon ,$$ (3.1)

where β = (1, 0.8, 0.6, 0.4, 0.2, 0, · · ·, 0)^T takes grid values. We consider two predictor covariances Σ₁ and Σ₂ as specified in Section 3.1. We also examine two variance structures: σ = σ₁, a constant, and σ = σ₂ = exp(γ^Tx), with γ = (0, · · ·, 0, 1, 1, 1, 0, · · ·, 0)^T and ones appear in the 20th, 21st and 22nd positions. Thus, σ₁ leads to a constant variance model, and we choose σ₁ = 6.83 for Σ₁, and σ₁ = 4.92 for Σ₂, which equals var(β^Tx) at the population level for the corresponding x. σ₂ leads to a non-constant variance model. We consider two error ε distributions, a standard normal N(0, 1), and a t-distribution with one degree of freedom that has a heavy tail. We vary the constant c in front of β^Tx to control the signal-to-noise ratio. For the constant variance model σ₁, we choose c = 0.5, 1 and 2, with the corresponding R² = 20%, 50% and 80% respectively. For the non-constant variance model σ₂, R² are all very small (< 0.01%).

We first evaluate our proposed utility measure in terms of accuracy in ranking the predictors. We also compare our method (SIRS) with another ranking procedure, linear SIS of Fan and Lv (2008). Table 1 reports the median of the 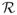values. For σ= σ₁, the number of truly actives p₁ = 5 and for σ = σ₂, p₁ = 8. It is seen that, when the model is linear, homoscedastic (σ₁), and the error follows a standard normal distribution N(0, 1), linear SIS performs the best, with the 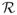measure being very close to p₁. However, the method breaks down for the heteroscedastic variance (σ₂) or the heavy-tailed error distribution (t₁). By contrast, our proposed procedure is comparable to linear SIS for the homoscedastic normal error, but is consistently superior with either the heteroscedastic variance or the heavy-tailed error distribution. Notably, our screening measure uses only the ranks of the observed response values, which partly explains why our method performs well for a heavy-tailed error (t₁). In addition, we observe that our method performs well across a wide range of signal-to-noise ratios (σ₁ with varying c), and the results for Σ₁ and Σ₂ are similar.

Table 1.

The ranking criterion 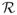for Example 1 – minimum number of predictors required to ensure the inclusion of all the truly active predictors. The numbers reported are the median of 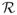out of 1000 replications.

ε	σ	Method	c = .5	c = 1	c = 2	c = .5	c = 1	c = 2
			Σ1			Σ2
N(0, 1)	σ1	SIRS	5	5	5	7	5	5
		SIS	5	5	5	6	5	5
	σ2	SIRS	9	11	18	8	9	8
		SIS	1739	1735	1646	1571	1447	1210
t1-dist	σ1	SIRS	5	5	5	5	5	5
		SIS	1358	566	31	1608	1257	337
	σ2	SIRS	10	9	12	10	9	9
		SIS	1735	1732	1757	1687	1678	1666

Next we evaluate our feature screening method with the proposed thresholding rule (2.11). We also compare with some commonly used and linear-model-based feature selection approaches, including linear SIS, Lasso, stepwise regression and forward regression. For stepwise regression, we use 0.05 as the inclusion probability and 0.10 as the exclusion probability. For Lasso and forward regression, we find that the BIC criterion proposed in the literature does not yield a satisfactory performance in our setup. Therefore, for those two methods, as well as linear SIS, we choose the same number of predictors as our proposed screening using the thresholding rule (2.11). The proportion 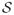is reported in Table 2, which indicates that the SIRS performs competently across different scenarios, with the proportion 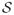close to one. As expected, SIRS outperforms other methods for error being t-distribution with one degree of freedom (i.e., the Cauchy distribution) since other methods require finite error variance. It is also expected that all the selection methods except for SIRS cannot identify the active predictors in the variance of random error. Thus, when the error is heteroscedastic, the proportions shown in Table 2 for all methods except SIRS are almost zero. To make favorable comparison toward the model-based methods when the error is heteroscedastic, we further summarize the proportion that all active predictors (X₁–X₅) contained in the regression function are correctly identified out of 1000 replications in Table 3, from which it can be seen that SIRS performs very well, while all other methods perform unsatisfactorily. This is because the random error in this case contains some very extreme values (outliers), and the SIRS is robust to the outliers because it only uses the ranks of the observed response values.

Table 2.

The selection criterion 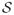for Example 1 – proportion that all the truly active predictors (X₁–X₅ for σ = σ₁ and X₁–X₅, X₂₀–X₂₂ for σ = σ₂) are correctly identified out of 1000 replications. Reported are our proposal (SIRS), linear SIS, Lasso, stepwise regression (Step) and forward regression (FR).

ε	σ	Method	c = .5	c = 1	c = 2	c = .5	c = 1	c = 2
			Σ1			Σ2
N(0, 1)	σ1	SIRS	0.953	1.000	1.000	0.778	0.998	1.000
		SIS	0.965	1.000	1.000	0.832	0.999	1.000
		Lasso	0.032	0.230	0.618	0.197	0.576	0.926
		Step	0.001	0.007	0.066	0.002	0.034	0.306
		FR	0.015	0.111	0.382	0.000	0.015	0.307
	σ2	SIRS	0.993	0.989	0.814	0.918	0.900	0.891
		SIS	0.000	0.000	0.001	0.010	0.033	0.058
		Lasso	0.000	0.000	0.000	0.000	0.000	0.001
		Step	0.000	0.000	0.000	0.000	0.000	0.000
		FR	0.000	0.000	0.000	0.000	0.000	0.000
t1-dist	σ1	SIRS	0.996	1.000	1.000	0.883	0.992	1.000
		SIS	0.052	0.231	0.513	0.014	0.118	0.357
		Lasso	0.002	0.004	0.036	0.002	0.025	0.080
		Step	0.000	0.000	0.001	0.000	0.000	0.001
		FR	0.000	0.007	0.016	0.000	0.000	0.003
	σ2	SIRS	0.932	0.990	0.974	0.844	0.895	0.887
		SIS	0.000	0.000	0.000	0.004	0.005	0.006
		Lasso	0.000	0.000	0.000	0.000	0.000	0.000
		Step	0.000	0.000	0.000	0.000	0.000	0.000
		FR	0.000	0.000	0.000	0.000	0.000	0.000

Table 3.

The selection criterion 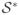for Example 1 with heteroscedastic error – proportion that all active predictors (X₁–X₅) contained in the regression function are correctly identified out of 1000 replications. Reported are linear SIS, Lasso, stepwise regression (Step) and forward regression (FR).

ε	Method	c = .5	c = 1	c = 2	c = .5	c = 1	c = 2
		Σ1			Σ2
N(0, 1)	SIRS	0.993	0.999	1.000	0.931	0.970	0.994
	SIS	0.000	0.004	0.012	0.013	0.042	0.091
	Lasso	0.000	0.000	0.000	0.000	0.000	0.008
	Step	0.000	0.000	0.000	0.000	0.000	0.000
	FR	0.000	0.000	0.000	0.000	0.000	0.000
t1-dist	SIRS	0.932	0.990	1.000	0.848	0.944	0.980
	SIS	0.000	0.000	0.000	0.004	0.005	0.007
	Lasso	0.000	0.000	0.000	0.000	0.000	0.000
	Step	0.000	0.000	0.000	0.000	0.000	0.000
	FR	0.000	0.000	0.000	0.000	0.000	0.000

Example 2

In this example, we continue to employ the linear model (3.1). In addition, we set σ = 1, c = 1 and β = (1, 1, 1, 0, · · ·, 0)^T, so that there are p₁ = 3 truly active predictors. What differs in this example is that we consider a more challenging covariance structure for the normally distributed x where cov(x) = Σ₃ = (σ_ij)_p×p with entries σ_ii = 1, i = 1, · · ·, p, and σ_ij = 0.4, i ≠ j. We note that condition (C1) is not satisfied in this setup. In addition, we generate the error ε from a t distribution with 1, 2, 3 and 30 degrees of freedom. We remark that t₁ is the Cauchy distribution, t₁ and t₂ have infinite variance, t₃ has finite variance and t₃₀ is almost indistinguishable from a standard normal distribution. As such we have a model that gradually approaches a normal distribution when the degrees of freedom increase.

Table 4 reports the ranking criterion 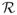and Table 5 reports the selection criterion 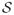. Again we observe a qualitative pattern similar to Example 1. That is, when the error is close to normal (t₃₀), the model-based SIS, Lasso, stepwise regression and forward regression perform very well, and our model-free procedure yields a comparable outcome. When the error deviates from a normal distribution (t with decreasing degrees of freedom), however, the performance of all the model-based alternatives quickly deteriorates, while our method continues to perform well.

Table 4.

The ranking criterion 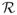for Example 2. The quintuplet in each parenthesis consists of the minimum, the first quartile, median, third quartile and maximum value of 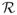out of 1000 data replications.

ε	SIRS					SIS
t1-dist	(3	4	9	28	1368)	(4	623	1126	1593	1999)
t2-dist	(3	3	3	5	680)	(3	3	7	36	1935)
t3-dist	(3	3	3	3	210)	(3	3	3	4	650)
t30-dist	(3	3	3	3	30)	(3	3	3	3	7)

Table 5.

The selection criterion 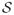for Example 2. The caption is the same as Table 2.

ε	SIRS	SIS	Lasso	Step	FR
t1-dist	0.961	0.076	0.027	0.002	0.004
t2-dist	0.997	0.913	0.849	0.640	0.647
t3-dist	0.998	0.995	0.995	0.982	0.987
t30-dist	1.000	1.000	1.000	1.000	1.000

As shown above, when the model is correctly specified (e.g., Example 1 with c = 0.5 and a normal error), or sufficiently close to the true model (as seen in the trend of Example 2 as the error degree of freedom increases), the model-based solution is more competent than our model-free solution. This is not surprising because the former is equipped with additional model information. In practice, which solution to resort to depends on the amount of knowledge and confidence of an analyst has about the model. Our approach can be used in conjunction with, rather than as an alterative to, many model-based feature screening and selection solutions.

3.3 Nonlinear Models and Discrete Response

Our next goal is to demonstrate that the proposed model-free approach offers a useful and robust procedure in the sense that it works for a large variety of different models when there is little knowledge about the underlying true model. Toward that end, we consider two sets of examples that cover a wide range of commonly used parametric and semiparametric models. The first set involves a continuous response, including the transformation model, the multiple-index model and the heteroscedastic model.

Example 3

The response is continuous. The error ε follows a standard normal distribution. β = (2 − U₁, …, 2 − U_p1, 0, …, 0)^T, β₁ = (2 − U₁, …, 2 − U_p1/2, 0, …, 0)^T, β ₂ = (0, …, 0, 2 + U_p1/2+1, …, 2 + U_p1, 0, …, 0)^T, and U_k’s follow a uniform distribution on [0, 1]. We vary the number of active predictors p₁ to reflect different sparsity levels. The predictor x follows a mean zero normal distribution with two covariances Σ₁ and Σ₂ as given in Section 3.1.

• 3.a.A transformation model: Y = exp {β^Tx/2 + ε}.
• 3.b.A multiple-index model: $Y=({\mathit{\beta }}_1^{\text{T}}\mathbf{x})+exp\{{\mathit{\beta }}_2^{\text{T}}\mathbf{x}\}+\epsilon$.
• 3.c.A heteroscedastic model: $Y=({\mathit{\beta }}_1^{\text{T}}\mathbf{x})+exp\{({\mathit{\beta }}_2^{\text{T}}\mathbf{x})+\epsilon \}$.

Table 6 reports the ranking criterion 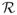and Table 7 reports the selection proportion criterion 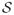after applying the thresholding rule (2.11) to the ranked predictors. For a wide range of models under investigation, 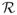is often equal or close to the actual number of truly active predictors p₁, whereas 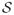is equal or close to one, indicating a very high accuracy in both ranking and selection. In addition, our method clearly outperforms the alternative approaches which assume the linear homoscedastic model while the true models are not linear homoscedastic in this example.

Table 6.

The ranking criterion 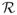for Example 3. The caption is the same as Table 4.

p1	Model	Method	Σ1					Σ2
4	3.a.	SIRS	(4	4	4	4	5)	(4	4	4	4	4)
		SIS	(4	4	4	6	690)	(4	4	4	12	1808)
	3.b.	SIRS	(4	4	4	4	5)	(4	4	4	4	4)
		SIS	(4	4	6	12	1962)	(4	4	6	60	1996)
	3.c.	SIRS	(4	4	4	4	5)	(4	4	4	4	4)
		SIS	(4	5	7	23	1739)	(4	4	25	207	1998)
8	3.a.	SIRS	(8	8	8	8	10)	(8	8	8	8	8)
		SIS	(8	25	78	214	1784)	(8	48	177	518	2000)
	3.b.	SIRS	(8	8	8	8	11)	(8	8	8	8	8)
		SIS	(8	147	458	1061	1997)	(8	99	349	825	1981)
	3.c.	SIRS	(8	8	8	8	10)	(8	8	8	8	8)
		SIS	(9	171	496	1097	1999)	(8	113	398	896	1988)
16	3.a.	SIRS	(16	16	16	16	22)	(16	16	16	16	16)
		SIS	(29	463	845	1358	2000)	(18	456	881	1310	2000)
	3.b.	SIRS	(16	16	17	18	34)	(16	16	16	16	16)
		SIS	(35	1207	1676	1881	2000)	(25	559	1019	1517	1999)
	3.c.	SIRS	(16	16	17	18	34)	(16	16	16	16	16)
		SIS	(70	1286	1705	1890	2000)	(20	560	1047	1500	2000)

Table 7.

The selection criterion 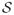for Example 3. The caption is the same as Table 2.

Model	Method	Σ1			Σ2
		p1 = 4	p1 = 8	p1 = 16	p1 = 4	p1 = 8	p1 = 16
3.a.	SIRS	1.000	1.000	1.000	1.000	1.000	1.000
	SIS	0.963	0.330	0.002	0.878	0.310	0.034
	Lasso	0.118	0.000	0.000	0.475	0.003	0.000
	Step	0.008	0.000	0.000	0.014	0.000	0.000
	FR	0.035	0.000	0.000	0.004	0.000	0.000
3.b.	SIRS	1.000	1.000	1.000	1.000	1.000	1.000
	SIS	0.868	0.084	0.001	0.741	0.191	0.025
	Lasso	0.082	0.000	0.000	0.247	0.002	0.000
	Step	0.004	0.000	0.000	0.043	0.000	0.000
	FR	0.058	0.000	0.000	0.031	0.000	0.000
3.c.	SIRS	1.000	1.000	1.000	1.000	1.000	1.000
	SIS	0.810	0.065	0.000	0.603	0.169	0.024
	Lasso	0.041	0.000	0.000	0.151	0.000	0.000
	Step	0.003	0.000	0.000	0.011	0.000	0.000
	FR	0.028	0.000	0.000	0.006	0.000	0.000

We have also examined a set of models with a discrete response, including the logistic model, the probit model, the Poisson log-linear model and the proportional hazards model (with a binary censoring indicator). Due to the space limitation, we only reported those results in an earlier version of this paper. Again, our extensive simulations show that the SIRS performs very well for the variety of discrete response models we have examined.

3.4 Iterative Screening

We next briefly examine the proposed iterative version of our marginal screening approach. The example is based upon a configuration in Fan and Lv (2008).

Example 4

We employ the linear model (3.1), with β = (5, 5, 5, −15ρ^1/2, 0, · · ·, 0)^T, c = 1, σ = 1, and ε follows a standard normal distribution. We draw x from a mean zero normal population with the covariance Σ₄ = (σ_ij)_p×p with entries σ_ii = 1, for i = 1, · · ·, p, σ_i4 = σ_4i = ρ^1/2 for i ≠ 4, and σ_ij = ρ, for i ≠ j, i ≠ 4 and j ≠ 4. That is, all predictors except for X₄ are equally correlated with correlation coefficient ρ, while X₄ has correlation ρ^1/2 with all other p − 1 predictors. By design X₄ is independent of Y, so that our method cannot pick it up except by chance, whereas X₄ is indeed an active predictor when ρ ≠ 0. We also vary the value of ρ to be 0, 0.1, 0.5 and 0.9, with a larger ρ yielding a higher collinearity.

We compare both the non-iterative and the iterative versions of our screening method. For the iterative procedure, we choose M = 2 iterations with p₍₁₎ = [N/2] and N = [n/log(n)]. This simple choice performs very well in this example. Table 8 reports the proportion criterion 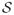, where the iterative procedure dramatically improves over its non-iterative counterpart.

Table 8.

The selection criterion 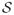for Example 4 – proportion that all the truly active predictors are correctly identified out of 1000 replications. ISIRS denotes the iterative version of the proposed SIRS method.

Method	ρ = 0	ρ = 0.1	ρ = 0.5	ρ = 0.9
ISIRS	0.925	1.000	1.000	0.940
SIRS	1.000	0.005	0.000	0.000

3.5 A Real Data Analysis

As an illustration, we apply the proposed screening method to the analysis of microarray diffuse large-B-cell lymphoma (DLBCL) data of Rosenwald et al. (2002). Given that DLBCL is the most common type of lymphoma in adults and has only about 35 to 40 percent survival rate after the standard chemotherapy, there has been continuous interest to understand the genetic factors that influence the survival outcome. The outcome in the study was the survival time of n = 240 DLBCL patients after chemotherapy. Measurements of p = 7,399 genes obtained from cDNA microarrays for each individual patient were the predictors. Given such a large number of predictors and small sample size, feature screening seems a necessary initial step as a prelude to any other sophisticated statistical modeling that does not cope well with such high dimensionality.

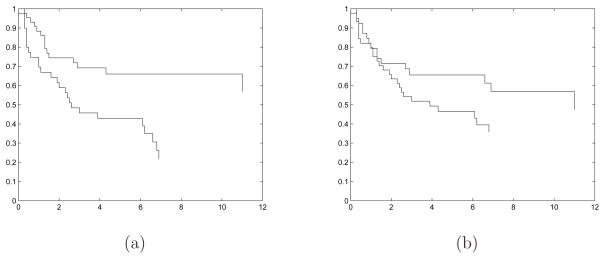
All predictors are standardized to have mean zero and variance one. We form the bivariate response consisting of the observed survival time and the censoring indicator. We use a data split of Li and Luan (2005) and Lu and Li (2008), which divides the data into a training set with n₁ = 160 patients and a testing set with 80 patients. We apply the proposed screening method to the training data. Among 200 trials of the thresholding rule (2.11), 196 times the hard thresholding rule dominates. Therefore, we choose [n₁/log(n₁)] = 31 genes in our final set. This result seems to agree with the analysis of this same data set in the literature: only a small number of genes are relevant, and according to our simulations, the hard thresholding is more dominant in this scenario. Based on those selected genes, we fit a Cox proportional hazards model. We evaluate the prediction performance of this model following the approach of Li and Luan (2005) and Lu and Li (2008). That is, we apply the screening approach and fit a Cox model for the training data. We then compute the risk scores for the testing data and divide it to a low-risk group and a high-risk group, where the cutoff value is determined by the median of the estimated scores from the training set. Figure 1(a) shows the Kaplan-Meier estimate of survival curves for the two risk groups of patients in the testing data. The two curves are well separated, with the log-rank test yielding a p-value equal to 0.0025, indicating a good prediction of the fitted model.

Figure 1.

The Kaplan-Meier estimate of survival curves for the two risk groups in the testing data. (a) is based on the proposed feature screening, and (b) is based on the univariate Cox model screening.

Both Li and Luan (2005) and Lu and Li (2008) used a univariate Cox model to screen the predictors. Applying their screening approach, while retaining as many as 31 genes, yields a subset of genes among which 12 overlap with the ones identified by our method. As a simple comparison, we also fit a Cox model based on the genes selected by their marginal screening method, and evaluate its prediction performance. Figure 1(b) is constructed in the same fashion as Figure 1(a) except that the genes are selected by the univariate Cox model. The figure shows that the two curves are less well separated, with the p-value of the log-rank test equal to 0.1489, suggesting an inferior predictive performance compared to our method.

We remark that, without any information about the appropriate model form for this data set, our model-free screening result seems more reliable compared to a model-based procedure. We also note that choosing the Cox model after screening only serves as a simple illustration in this example. More refined model building and selection could be employed after feature screening, while the model-free nature of our screening method grants full flexibility in subsequent modeling.

Biographies

Li-Ping Zhu is Associate Professor, School of Statistics and Management, Shanghai University of Finance and Economics. luz15@psu.edu. His research was supported by National Natural Science Foundation of China grant 11071077 and National Institute on Drug Abuse (NIDA) grant R21-DA024260

Lexin Li is Associate Professor, Department of Statistics, North Carolina State University, Raleigh, NC 27695-8203. li@stat.ncsu.edu. His research was supported by NSF grant DMS 0706919

Runze Li is the corresponding author and Professor, Department of Statistics and The Methodology Center, The Pennsylvania State University, University Park, PA 16802-2111. rli@stat.psu.edu. His research was supported by NSF grant DMS 0348869, National Natural Science Foundation of China grant 11028103, and National Institute on Drug Abuse (NIDA) grant P50-DA10075

Li-Xing Zhu is Chair Professor of Statistics, Department of Mathematics, Hong Kong Baptist University. lzhu@hkbu.edu.hk. His research was supported by Research Grants Council of Hong Kong grant HKBU2034/09P

Appendix: proofs

Proof of Theorem 1

Without loss of generality, we assume that the basis matrix β = (β₁, · · ·, β_K) satisfies ${\mathit{\beta }}^{\text{T}}cov({\mathbf{x}}_{\mathcal{A}},{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\mathit{\beta }={\mathbf{I}}_K$, where I_K is a K × K identity matrix. In this case, the linearity condition (2.7) is simplified as $E(X_k\mid {\mathit{\beta }}^{\text{T}}{\mathbf{x}}_{\mathcal{A}})=cov(X_k,{\mathbf{x}}_{\mathcal{A}}^{\text{T}}\mathit{\beta }){\mathit{\beta }}^{\text{T}}{\mathbf{x}}_{\mathcal{A}}$. For ease of presentation, we denote the matrix vv^T by v² for a vector v.

Consider the left hand side of (2.8). Because x is independent of Y given β^Tx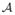 and Ỹ is an independent copy of Y, it follows that x is independent of Y and Ỹ given β^Tx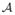. This, together with the simplified linearity condition and the law of iterated expectations, yields that

$$\begin{array}{l}E\{X_k\mathbf{1}(Y<\stackrel{\sim }{Y})\mid \stackrel{\sim }{Y}\}=E\left[E\left\{X_k\mathbf{1}(Y<\stackrel{\sim }{Y})\mid \stackrel{\sim }{Y},{\mathit{\beta }}^T{\mathbf{x}}_{\mathcal{A}}\right\}\mid \stackrel{\sim }{Y}\right]\\ =E\left[E\left(X_k\mid {\mathit{\beta }}^{\text{T}}{\mathbf{x}}_{\mathcal{A}}\right)E\left\{\mathbf{1}\left(Y<\stackrel{\sim }{Y}\right)\mid \stackrel{\sim }{Y},{\mathit{\beta }}^{\text{T}}{\mathbf{x}}_{\mathcal{A}}\right\}\mid \stackrel{\sim }{Y}\right]\\ =cov\left(X_k,{\mathbf{x}}_{\mathcal{A}}^T\mathit{\beta }\right)E\left\{{\mathit{\beta }}^T{\mathbf{x}}_{\mathcal{A}}\mathbf{1}(Y<\stackrel{\sim }{Y})\mid \stackrel{\sim }{Y}\right\}.\end{array}$$ (A.1)

Then one can obtain that

$$\begin{array}{l}\underset{k\in \mathcal{I}}{max}E\left\{E^2(X_k\mathbf{1}(Y<\stackrel{\sim }{Y})\mid \stackrel{\sim }{Y})\right\}=\underset{k\in \mathcal{I}}{max}\left(cov(X_k,{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\mathit{\beta }E\left[E^2\left\{{\mathit{\beta }}^{\text{T}}{\mathbf{x}}_{\mathcal{A}}\mathbf{1}(Y<\stackrel{\sim }{Y})\mid \stackrel{\sim }{Y}\right\}\right]{\mathit{\beta }}^{\text{T}}cov({\mathbf{x}}_{\mathcal{A}},X_k)\right)\\ \le {\lambda }_{max}\left(E\left[E^2\left\{{\mathit{\beta }}^{\text{T}}{\mathbf{x}}_{\mathcal{A}}\mathbf{1}(Y<\stackrel{\sim }{Y})\mid \stackrel{\sim }{Y}\right\}\right]\right)\underset{k\in \mathcal{I}}{max}\left\{cov(X_k,{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\mathit{\beta }{\mathit{\beta }}^{\text{T}}cov({\mathbf{x}}_{\mathcal{A}},X_k^{\text{T}})\right\}\end{array}$$ (A.2)

where the first equality follows from (C2). Then it is straightforward to verify that

$$\begin{array}{l}{\lambda }_{max}\left(E\left[E^2\left\{{\mathit{\beta }}^{\text{T}}{\mathbf{x}}_{\mathcal{A}}\mathbf{1}(Y<\stackrel{\sim }{Y})\mid \stackrel{\sim }{Y}\right\}\right]\right)\le \sum _{j=1}^{K}E\left[E^2\left\{{\mathit{\beta }}_j^{\text{T}}{\mathbf{x}}_{\mathcal{A}}\mathbf{1}(Y<\stackrel{\sim }{Y})\mid \stackrel{\sim }{Y}\right\}\right]\\ \le \sum _{j=1}^K{\lambda }_{max}\left({cov}^{-1/2}({\mathbf{x}}_{\mathcal{A}},{\mathbf{x}}_{\mathcal{A}}^{\text{T}})E\left[E^2\left\{{\mathbf{x}}_{\mathcal{A}}\mathbf{1}(Y<\stackrel{\sim }{Y})\mid \stackrel{\sim }{Y}\right\}\right]{cov}^{-1/2}({\mathbf{x}}_{\mathcal{A}},{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\right)\\ \le K{\lambda }_{max}\left\{{cov}^{-1}({\mathbf{x}}_{\mathcal{A}},{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\right\}{\lambda }_{max}\left(E\left[E^2\left\{{\mathbf{x}}_{\mathcal{A}}\mathbf{1}(Y<\stackrel{\sim }{Y})\mid \stackrel{\sim }{Y}\right\}\right]\right)\\ =K{\lambda }_{max}\left(E\left[E^2\left\{{\mathbf{x}}_{\mathcal{A}}\mathbf{1}(Y<\stackrel{\sim }{Y})\mid \stackrel{\sim }{Y}\right\}\right]\right)/{\lambda }_{min}\left\{cov({\mathbf{x}}_{\mathcal{A}},{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\right\}.\end{array}$$ (A.3)

Here the second inequality follows because ${\mathit{\beta }}^{\text{T}}cov({\mathbf{x}}_{\mathcal{A}},{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\mathit{\beta }={\mathbf{I}}_K$, and the third inequality holds due to the fact that λ_max(C^TBC) ≤ λ_max(B)λ_max(C^TC) for any matrix B ≥ 0. After some algebra, we have

$$\begin{array}{l}\underset{k\in \mathcal{I}}{max}\left\{cov(X_k,{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\mathit{\beta }{\mathit{\beta }}^{\text{T}}cov({\mathbf{x}}_{\mathcal{A}},X_k)\right\}=\sum _{j=1}^K\underset{k\in \mathcal{I}}{max}\left\{cov({\mathit{\beta }}_j^{\text{T}}{\mathbf{x}}_{\mathcal{A}},X_k)cov(X_k,{\mathbf{x}}_{\mathcal{A}}^{\text{T}}){\mathit{\beta }}_j\right\}\\ \le \sum _{j=1}^K\left\{{\mathit{\beta }}_j^{\text{T}}cov({\mathbf{x}}_{\mathcal{A}},{\mathbf{x}}_{\mathcal{I}}^{\text{T}})cov({\mathbf{x}}_{\mathcal{I}},{\mathbf{x}}_{\mathcal{A}}^{\text{T}}){\mathit{\beta }}_j\right\}\\ \le K{\lambda }_{max}\left\{cov({\mathbf{x}}_{\mathcal{A}},{\mathbf{x}}_{\mathcal{I}}^{\text{T}})cov({\mathbf{x}}_{\mathcal{I}},{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\right\}/{\lambda }_{min}\left\{cov({\mathbf{x}}_{\mathcal{A}},{\mathbf{x}}_{\mathcal{A}}^{\text{T}})\right\}.\end{array}$$ (A.4)

Then Condition (C1), together with (A.2), (A.3) and (A.4), entails (2.8).

Proof of Corollary 1

It follows from the definition in (2.4) that ω_k = 0 is equivalent to E {X_k1(Y < y) = 0 for any y ∈ Ψ_y. Because Y relates to x only through linear combinations β^Tx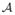, it follows that there exists some y ∈ Ψ_y such that E{β^Tx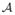1(Y < y)} ≠ 0. Consequently, (A.1) implies that E{X_k1(Y < y)} = 0 if and only if cov(β^Tx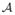, X_k) = 0, which completes of proof of Corollary 1.

Proof of Theorem 2

To enhance readability, we divide the proof into two main steps.

Step 1

We first show that, under condition (C3),

$$P\left(\underset{k=1,\dots ,p}{sup}\mid {\widehat{\omega }}_k-{\omega }_k\mid >\epsilon \right)\le 2pexp\{nlog(1-\epsilon s_{\epsilon }/2)/3\}.$$ (A.5)

Note that ω̂_k can be expressed as follows:

$$\begin{array}{l}{\widehat{\omega }}_k=\frac{2}{n(n-1)(n-2)}\sum _{j<i<l}^n\{X_{jk}{X}_{ik}\mathbf{1}(Y_j<Y_l)\mathbf{1}(Y_i<Y_l)+X_{lk}{X}_{ik}\mathbf{1}(Y_l<Y_j)\mathbf{1}(Y_i<Y_j)+X_{jk}{X}_{lk}\mathbf{1}(Y_j<Y_i)\mathbf{1}(Y_l<Y_i)\}\\ \stackrel{\text{def}}{=}\frac{6}{n(n-1)(n-2)}\sum _{j<i<l}^{n}h(X_{jk},Y_j;X_{ik},Y_i;X_{lk},Y_l).\end{array}$$

Thus, ω̂_k is a standard U-statistic. With Markov’s inequality, we can obtain that, for any 0 < t < s₀k^*, where k^* = [n/3],

$$P({\widehat{\omega }}_k-{\omega }_k\ge \epsilon )\le exp\{-t\epsilon \}exp\{-t{\omega }_k\}E[exp\{t{\widehat{\omega }}_k\}].$$

Through 5.1.6 of Serfling (1980), the U-statistic ω̂_k can be represented as an average of averages of independent and identically distributed random variables; that is, ${\widehat{\omega }}_k={(n!)}^{-1}{\displaystyle \sum _{n!}}w(X_{1k},Y_1;\dots ,X_{nk},Y_n)$, where each w(X_1k, Y₁; · · ·, X_nk, Y_n) is an average of k^* = [n/3] independent and identically distributed random variables, and ${\displaystyle \sum _{n!}}$ denotes summation over n! permutations i₁, · · ·, i_n of (1, · · ·, n). We denote that ψ_h(s) = E[exp {sh(X_jk, Y_j; X_ik, Y_i; X_lk, Y_l)}] for 0 < s < s₀. Since the exponential function is convex, it follows by Jensen’s inequality that

$$\begin{array}{l}E[exp\{t{\widehat{\omega }}_k\}]=E\left[exp\left\{t{(n!)}^{-1}\sum _{n!}w(X_{1k},Y_1;\dots ,X_{nk},Y_n)\right\}\right]\\ \le {(n!)}^{-1}\sum _{n!}E[exp\{tw(X_{1k},Y_1;\dots ,X_{nk},Y_n)\}]={\psi }_h^{k^{\ast }}(t/k^{\ast }).\end{array}$$

Combining the above two results, we obtain that

$$\begin{array}{l}P({\widehat{\omega }}_k-{\omega }_k\ge \epsilon )\le exp\{-t\epsilon \}{[exp\{-t{\omega }_k/k^{\ast }\}{\psi }_h(t/k^{\ast })]}^{k^{\ast }}\\ ={[exp\{-s\epsilon \}exp\{-s{\omega }_k\}{\psi }_h(s)]}^{k^{\ast }},\end{array}$$ (A.6)

where s = t/k^*. Note that E {h(X_jk, Y_j; X_ik, Y_i; X_lk, Y_l)} = ω_k, and with Taylor expansion, exp {sY} = 1 + sY + s²Z/2 for any generic random variable Y, where 0 < Z < Y² exp {s₁Y}, and s₁ is a constant between 0 and s. It follows that

$$exp\{-s{\omega }_k\}{\psi }_h(s)\le 1+s^2{[E\{h^4(X_{jk},Y_j;X_{ik},Y_i;X_{lk},Y_l)\}Eexp\{2s_1(h-{\omega }_k)\}]}^{1/2}/2.$$

By invoking Condition (C3), it follows that there exists a constant C (independent of n and p) such that $\underset{1\le k\le p}{max}exp\{-s{\omega }_k\}{\psi }_h(s)\le 1+{Cs}^2$; that is,

$$\underset{1\le k\le p}{max}exp\{-s{\omega }_k\}{\psi }_h(s)=1+O(s^2).$$

Recall that 0 < s = t/k^* < s₀. For a sufficiently small s, which can be achieved by selecting a sufficiently small t, we have that exp(−sε) = 1 − εs + O(s²) and therefore,

$$\underset{1\le k\le p}{max}[exp(-s\epsilon )exp(-s{\omega }_k){\psi }_h(s)]\le 1-\epsilon s/2.$$ (A.7)

Combining the results (A.6) and (A.7), we show that, for any ε > 0, there exists a sufficiently small s_ε such that $\underset{1\le k\le p}{max}\{P({\widehat{\omega }}_k-{\omega }_k\ge \epsilon )\}\le {(1-\epsilon s_{\epsilon }/2)}^{n/3}$. Here we use the notation s_ε to emphasize s depending on ε. Similarly, we can prove that $\underset{1\le k\le p}{max}\{P({\widehat{\omega }}_k-{\omega }_k\le -\epsilon )\}\le {(1-\epsilon s_{\epsilon }/2)}^{n/3}$. Therefore,

$$P\left(\underset{k=1,\dots ,p}{sup}\mid {\widehat{\omega }}_k-{\omega }_k\mid >\epsilon \right)\le 2pexp\{nlog(1-\epsilon s_{\epsilon }/2)/3\}.$$ (A.8)

This completes the proof of Step 1.

Step 2

We next show that

$$P\left(\underset{k\in \mathcal{I}}{max}{\widehat{\omega }}_k<\underset{k\in \mathcal{A}}{min}{\widehat{\omega }}_k\right)\ge 1-4pexp\{nlog(1-\delta s_{\delta /2}/4)/3\}.$$ (A.9)

Recall the assumption that $\delta =\underset{k\in \mathcal{A}}{min}{\omega }_k-\underset{k\in \mathcal{I}}{min}{\omega }_k>0$. Thus,

$$\begin{array}{l}P\left(\underset{k\in \mathcal{A}}{min}{\widehat{\omega }}_k\le \underset{k\in \mathcal{I}}{max}{\widehat{\omega }}_k\right)=P\left(\underset{k\in \mathcal{A}}{min}{\widehat{\omega }}_k-\underset{k\in \mathcal{A}}{min}{\omega }_k+\delta \le \underset{k\in \mathcal{I}}{max}{\widehat{\omega }}_k-\underset{k\in \mathcal{I}}{max}{\omega }_k\right)\\ \le P\left(\underset{k\in \mathcal{A}}{sup}\mid {\widehat{\omega }}_k-{\omega }_k\mid \ge \delta /2\right)+P\left(\underset{k\in \mathcal{I}}{sup}\mid {\widehat{\omega }}_k-{\omega }_k\mid \ge \delta /2\right).\end{array}$$ (A.10)

By using (A.8) with ε = δ/2, (A.9) holds.

Proof of Theorem 3

Denote p^* = p − | 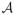|. For a fixed r ∈ ℕ, the event that | 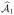∩ | ≥ r means there are at least r elements in {ω̂_k : k ∈ } greater than all values of {ω̂_k : k = p + 1, · · ·, p + d}. Because the auxiliary variables z and the inactive predictors x are equally likely to be recruited given Y, it follows that

$$P\left(\mid {\widehat{\mathcal{A}}}_1\cap \mathcal{I}\mid \ge r\right)=\frac{\frac{p^{\ast }!}{(p^{\ast }-r)!}(p^{\ast }-r+d)!}{(p^{\ast }+d)!}\le {\left(1-\frac{r}{p^{\ast }+d}\right)}^d.$$

The result of Theorem 3 follows.