Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Jun 27.
Published in final edited form as: Comput Methods Biomech Biomed Engin. 2010 Oct;13(5):605–615. doi: 10.1080/10255840903405660

Quantification of trabecular bone microdamage using the virtual internal bond model and the individual trabeculae segmentation technique

Guanhui Fang a, Baohua Ji a,*,1, X Sherry Liu b, X Edward Guo b
PMCID: PMC3384516  NIHMSID: NIHMS384426  PMID: 20077238

Abstract

Trabecular bone microdamage significantly influences the skeletal integrity and bone remodelling process. In this paper a novel constitutive model, called the virtual internal bond model (VIB), was adopted for simulating the damage behaviour of bone tissue. A unique 3D image analysis technique, named individual trabeculae segmentation, was used to analyse the effects of microarchitectures on the damage behaviours of trabecular bone. We demonstrated that the process of initiation and accumulation of microdamage in trabecular bone samples can be captured by the VIB-embedded finite-element method simulation without a separate fracture criterion. Our simulation results showed that the microdamage can occur at as early as about 0.2–0.4% apparent strain, and a large volume of microdamage was accumulated around the apparent yield strain. In addition we found that the plate-like trabeculae, especially the longitudinal ones, take crucial roles in the microdamage behaviours of trabecular bone.

Keywords: trabecular bone, microdamage, virtual internal bond model, individual trabeculae segmentation, microarchitecture

1. Introduction

Trabecular bone microdamage has significant implications in the physiology and pathology of bone tissue such as in bone remodelling, aetiology of osteoporosis and age-related fractures (Burr et al. 1997; Wachtel and Keaveny 1997; Burr 2003; Kosmopoulos and Keller 2008). While moderate levels of microdamage may play an important role in the maintenance of structural bone integrity as an important stimulus providing spatial regulation of bone-remodelling activity (Mori and Burr 1993, Nagaraja et al. 2005, Seeman 2008), excessive damage can not only reduce the elastic modulus (Liu et al. 2003) but also the strength of bone (Keaveny et al. 1994c; Burr et al. 1997; Wachtel and Keaveny 1997; Burr 2003). At present, however, how the damage initiates and accumulates in trabecular bone tissue with the increase in external loading has not yet been fully understood (Burr 2003). A quantitative study of the underlying mechanisms of this phenomenon may provide insight that can lead to the improvement of fracture risk assessment methods and to the development of therapeutic strategies to treat skeletal fragility diseases such as osteoporosis.

Many experimental studies have been dedicated to the understanding of the damage behaviours of trabecular bone. By combining the histological damage labelling technique and finite-element method (FEM) simulations, Nagaraja et al. (2005) found that damaged trabeculae possessed significantly higher local stresses and strains than did other trabeculae. Their numerical results showed that microdamage initiation occurred prior to the apparent yield of the bone samples, consistent with other studies (Keaveny et al. 1994c; Moore and Gibson 2002). Using synchrotron radiation micro-computed tomography (SRµCT), Thurner et al. (2006) studied the different failure behaviours of trabecular bone using both pre-fatigued and non-fatigued samples. They found that the fatigued sample failed in a burst-like fashion in contrast to a distinct failure band seen in the non-fatigued one. Wang and Niebur (2006) studied the microdamage propagation in trabecular bone due to changes in loading mode. They found that the propagating microcracks under mixed loading modes were, on average, longer than microcracks formed by a single-mode overload.

Theoretical and numerical methods used to model trabecular bone damage have also been developed (Guo et al. 1994; Vanrietbergen et al. 1995; Niebur et al. 2000; Moore and Gibson 2001; Yeh and Keaveny 2001; Makiyama et al. 2002; Stolken and Kinney 2003; Bevill et al. 2006; Kosmopoulos et al. 2008). Guo et al. (1994) modelled trabecular bone as a 2D hexagonal honeycomb. They assumed that the cracks in trabeculae grew according to a Paris law and trabeculae failed when the cracks reached a critical length beyond which the crack will propagate catastrophically according to the theory of fracture mechanics. Later, Makiyama et al. (2002) studied the crack growth in trabecular bone using a 3D random honeycomb, while in the work of Moore and Gibson (2001), trabecular bone was modelled by the open-cell network (rod-like structure) and closed-cell network (plate-like structure). Yeh and Keaveny (2001) used a 3D lattice model to study the roles of microdamage and microfracture in trabecular damage. In their work, a strain-based modulus reduction rule was used to simulate the microdamage formation. In addition, a strain-based microfracture criterion was applied to remove fractured trabeculae from the model once the trabeculae’s strain exceeded the critical value.

Although a lot of important progress has been made in previous studies, the underlying mechanisms of the initiation and accumulation of damage in trabecular bone still have not been fully understood because of unresolved difficulties in the numerical and experimental approaches. For instance, in previous numerical studies either ad hoc pre-microdamage had to be introduced in the model (Guo et al. 1994; Schaffner et al. 2000; Moore and Gibson 2001; Makiyama, et al. 2002) to explicitly simulate the evolution of damage, or phenomenological strain-based modulus reduction laws (Yeh and Keaveny 2001; Kosmopoulos and Keller 2008; Kosmopoulos et al. 2008) had to be adopted to implicitly model the evolution of trabecular bone damage, but the parameters in these modulus reduction laws could not be obtained from experiments. Furthermore, due to the complexity of trabecular bone architecture, it is difficult for current experimental techniques to capture the details of the damage evolution, especially the initiation, in trabecular bone (Nagaraja et al. 2005). Therefore, a physics-based numerical approach needs to be developed for studying the evolution of microdamage in trabecular bone tissue.

In this paper, a novel constitutive model, called the virtual internal bond (VIB) model (Gao and Klein 1998; Klein and Gao 1998), is introduced to explore the behaviour of microdamage in trabecular bone. Compared with previous conventional models, the VIB model has unique advantages in modelling damage and fracture of materials. It can describe the mechanical behaviours of bone tissue not only at small deformations before the initiation of microdamage, but also at large deformations during damage accumulation. In particular, separate fracture criteria are no longer necessary. Therefore, it is a natural process for the VIB model to simulate the initiation and propagation of damage in trabecular bone without a pre-assumed ad hoc crack and fracture criterion in the simulation. In addition, a novel (3D) image analysis technique, named individual trabeculae segmentation (ITS), recently developed by the co-authors of this paper for the decomposition of trabecular bone microarchitecture into individual plates and rods (Liu et al. 2006, 2008, 2009) will be adopted to examine the microdamage behaviour in individual trabecular plates and rods. The combination of these two novel approaches, i.e. the VIB model and the ITS technique, will allow a quantitative study of the micromechanics of trabecular bone microdamage.

2. Materials and methods

2.1 Specimens

Twelve cylindrical trabecular bone samples (six proximal femurs, three proximal tibiae and three third lumbar vertebrae) were obtained from fresh frozen human cadavers (six males and one female, age 44–69 years) following a previously published protocol (Keaveny et al. 1994a). Samples were cored along the superior–inferior direction in the case of vertebral bodies and along principal trabecular orientation for femurs and tibiae. The subjects were screened to exclude all possible metabolic bone diseases or bone cancers, and X-ray radiographs were taken to ensure that there was no evidence of damage or other bone pathologies. 3D high-resolution images of the central gauge with a length of 20 mm were obtained for each specimen using µCT systems (vivaCT 40, SCANCO Medical AG, Bassersdorf, Switzerland) at 21 µm resolution. A 4 mm cubical volume, which was equivalent to 190 × 190 × 190 voxels, was extracted from each specimen. The greyscale images were thresholded using a minimum between the bone and marrow peaks in the histogram (Kim et al. 2007), which has been shown to be appropriate for high-resolution µCT images.

2.2 VIB-based FEM and simulation method

The FEM model of each bone sample was constructed from each µCT image by directly converting each voxel into an eight-node brick element. Individual samples had up to 2.5 million elements. A modified version of the finite-element program Tahoe (http://tahoe.ca.sandia.gov/), in which the VIB model (Figure 1 and Appendix A1) is embedded, was used for the FEM analysis. Tahoe is a research-oriented open source platform for the development of numerical methods and material models which also supports large-scale parallel calculations. In the simulation, the value of the parameter A in Equations (A9) and (A10) (Appendix A1) was chosen as 22.5/π, so the Young’s modulus of trabecular bone tissue was 15 GPa. Parameters B and C in the bond potential were chosen as 0.015 and 90.0, respectively, to reproduce the mechanical properties of bone tissue used in the previous study where the predictions in yield properties of trabecular bone at the apparent level agreed with the experiments (Bevill et al. 2006).

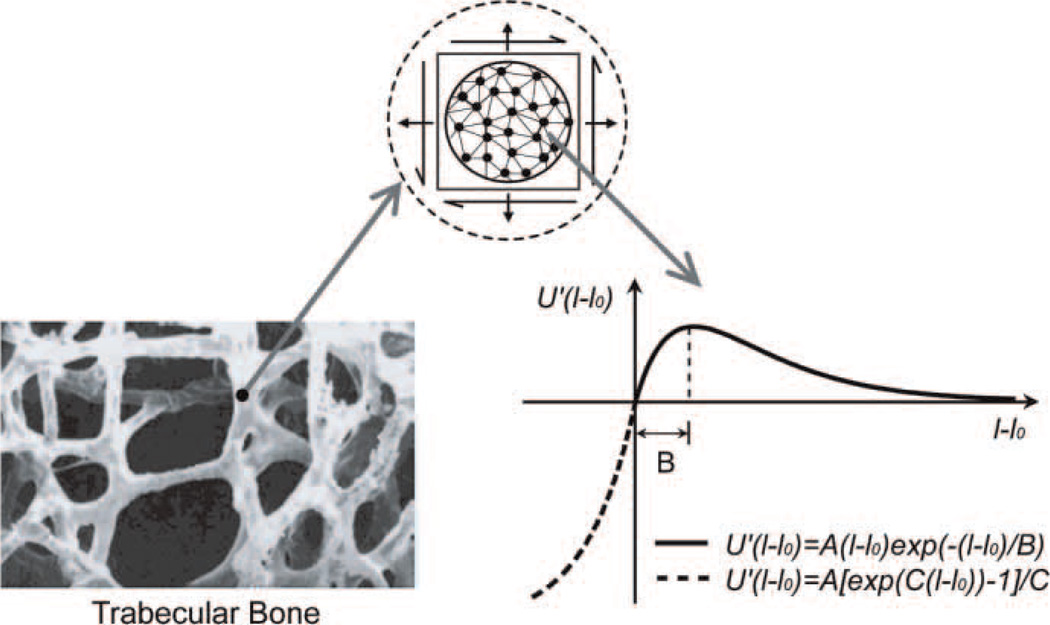
Figure 1.

Figure 1

Open in a new tab

The microstructure of trabecular bone and the virtual internal bond model. The force-extension relation of the virtual bond is used for the description of the interaction between material microstructures of bone tissue.

It is noteworthy that compared with the cohesive zone model (e.g. cohesive surface model), the VIB model is a constitutive model that describes the stress–strain behaviour of materials from zero stress level to the failure limit, which is implemented at the constitutive level. However, the cohesive zone model describes the relationship between the stress and crack opening at the crack tip with a traction–separation law, which is implemented at element level. In the simulation with the VIB model, it is not necessary to assume ad hoc fracture pathways. The microcracks can nucleate automatically as the external load is increased beyond a critical level. Although there is also no need to define a crack path, one of the disadvantages of the cohesive surface model is that it is difficult to deal with the mismatch of the mechanical properties between the cohesive surface elements and the bulk material elements. Currently, our model cannot differentiate between microcracks and diffuse damage.

Geometric non-linearity (large deformation, large displacement and large rotation) was considered in all the simulations by selecting the large deformation option. The samples were loaded by compression with the apparent strain up to 1% (however, we applied the strain up to as high as 2.5% for one sample, see Section 3.1). The top face of the sample was loaded in the axial direction (longitudinal) and the nodes on the bottom face were constrained in the axial direction (longitudinal), which produced a state of apparent uniaxial compression. The apparent elastic modulus of samples was calculated by loading the sample within the linear elastic region when the apparent strain is smaller than 0.05% (we chose 0.01% apparent strain in the calculation of elastic modulus). The apparent yield point was determined from the apparent stress–strain curve of each specimen using the 0.2% offset method. All the simulations were conducted on the Shenteng parallel supercomputer (Lenovo, SCCAS, China). Total CPU time was about 11,520 h, using 40–100 CPUs.

In the simulation, the damage information of the samples was recorded on each strain level for the analyses of the trabecular damage at different strain levels. ITS technique (see Appendix A2) was then used to analyse the damage in decomposed individual trabecular plates and rods, which allowed us to quantitatively study the influence of the microarchitecture on the damage behaviour of trabecular bone.

2.3 Statistical analyses of damage

An element (voxel) was labelled as damaged if the local stress of the element was equal to zero under the overstretching of an external load. As a result, the trabecula with the damaged element was thought of as a damaged trabecula (a single element of damage is pretty sufficient to indicate damage because the size of trabeculae is in the order of 100 µm, while the size of each voxel is 21 µm, 20% of the trabecula). We should point out that the VIB model is a non-linear hyperelastic model, a more accurate model for modelling the non-linear behaviour of materials at high strain, which can largely eliminate the artificial high stress at surface elements reported by Guldberg et al. (1998) and Charras and Guldberg (2000). In this study, the damage at very low apparent strain is mainly caused by the highly non-homogeneous deformation due to the complex structure of trabeculae instead of the discretisation in the linear elastic FEM simulations (Guldberg et al. 1998; Charras and Guldberg 2000).

The number of damaged trabecular plates or rods, (pTb.N)d or (rTb.N)d, was counted at each computing step and normalised by the total number of trabeculae within the sample to obtain the damaged number fraction (DNF) of trabecular plates or rods, (pTb.N)d/Tb.N or (rTb.N)d/Tb.N. In a similar manner, the volume of damaged bone tissue within the damaged trabecular plates or rods was calculated. Then, the volume of damaged tissue in the plates or rods, (pBV)d or (rBV)d, was normalised, respectively, by the total bone volume within the sample to calculate the damaged tissue fraction (DTF) of the trabecular plate or rod, (pBV)d/BV or (rBV)d/BV. The difference in the damage between trabecular plates and rods was then compared. In addition, the orientation (transverse, oblique and longitudinal) of the damaged trabecular plates and rods was analysed. Paired t-tests were performed first to test the difference in structural types of trabecular bone (plate and rod) in terms of the percentage of damaged number and volume at each step. Then, the difference in orientations (transverse, oblique and longitudinal) of the damaged trabecular plate and rod in terms of the yielded number and volume were tested at each loading step, respectively. All the statistical analyses were performed using Microsoft Office Excel software on a PC workstation with p ≤ 0.05 considered to be statistically significant.

3. Results

3.1 Initiation and propagation of damage

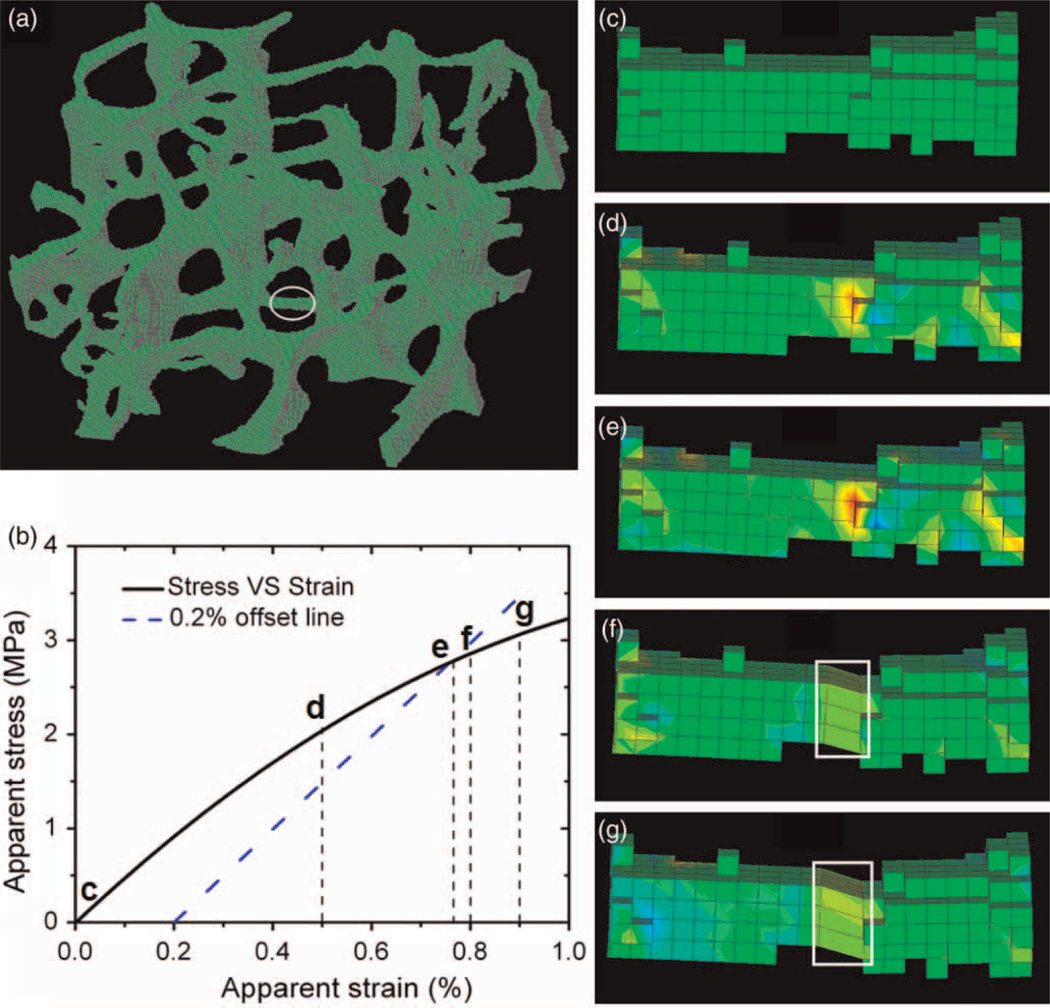
Our simulations show that the VIB-based FEM simulations can capture the details of the progression of trabecular bone damage from initiation to complete fracture. Figure 2 shows the process of fracture in a single trabecula of a sample. The local stress in the trabecula continuously develops with the increase in the applied apparent strain (Figure 2(d) and (e), where the red colour indicates high local stress). Further increase in the loading strain causes microdamage due to the overstretching of the elements with high local stress (see elements in the white box in Figure 2(f) and (g)), which results in the local stress of these elements becoming zero, i.e. these elements become microcracks. The failure of all the elements in the cross-section of the trabecula leads to a microfracture (Figure 2(g)). Figure 3 shows the microdamage initiation and evolution in a larger area of a bone sample, which is particularly loaded with up to 2.5% apparent strain as a special case in order to see more damage in the sample to demonstrate the damage evolution in the trabecular bone sample. The initiation of microdamage, i.e. the first failure in the sample, occurs at about 0.2% apparent strain. With the increase in the loading strain, more damage develops (Figure 3(a) and (b)) at an apparent strain of 0.5 and 1.0%, respectively. The damaged area is continuously enlarged with the propagation of local damage at an apparent strain of 1.5% (Figure 3(c)). Finally many localised bands of damage form at an apparent strain of 2.5% (Figure 3(d)).

Figure 2.

Figure 2

Open in a new tab

Illustrations of the evolution of the damage process in a transverse trabecular rod. (a) A 4 × 4 × 4 mm sample where the position of the transverse rod is shown in the ellipse; (b) the apparent stress and strain curve on which the typical loading points are marked corresponding to the panels (c)–(g); (c)–(g) snapshots of stress and deformation of elements in the rod at 0, 0.5, 0.77, 0.80 and 0.90% apparent strains, respectively, and green-to-red colours on the trabecula represents the magnitude of stress (S33) from low to high. The elements contained in the white box in (f) and (g) are damaged.

Figure 3.

Figure 3

Open in a new tab

Damage evolution in a local region of a trabecular bone sample at different loading strains. (a) A little damage is nucleated at 0.5% apparent strain; more damage has accumulated at (b) 1.0% apparent strain and (c) 1.5% apparent strain. (d) Catastrophic failure occurs near 2.5% apparent strain.

We find that for all of the samples, the apparent strain for the initiation of damage is in the range of 0.2–0.4% (Figure 4(a)). Furthermore, we note that some thin transverse trabeculae have been completely damaged, i.e. fractured, at much higher strain around the apparent yield point of samples (Figure 2(b) and (g)).

Figure 4.

Figure 4

Open in a new tab

(a) The apparent strain of damage initiation of trabecular bone samples. (b) The apparent yield strain of trabecular bone samples.

3.2 Apparent yield strength

There is a strong linear relationship between apparent yield strength and elastic modulus (Figure 5(a)). Moreover, we show that the apparent yield strain of all the samples is in the range of 0.7–0.9% (Figure 4(b)), and the average of the apparent yield strain is 0.79 ± 0.02%. These results agree well with previous experimental studies (Keaveny et al. 1994b; Morgan and Keaveny 2001) and numerical simulations (Hou et al. 1998; Niebur et al. 2000; Yeni and Fyhrie 2001). With linear regression correlation analysis, we get an approximate linear relationship between apparent yield strength and bone volume fraction (BV/TV) (Figure 5(b)). We find that a higher BV/TV usually results in a higher yield strength when the difference in BV/TV between two samples is large, such as for samples C316/C321 (‘/’ denotes ‘comparison with’) (Figure 5(c)). However, if two samples have similar BV/TV values, microarchitecture will determine the yield strength of the samples, such as for samples C314/320 and C324/319 (Figure 5(c)). Samples C314 and C324 have similar BV/TV values but higher yield strength than their counterparts, C320 and C319, respectively. Sometimes, the samples with lower BV/TV values have higher yield strength than those with higher BV/TV, e.g. for C322/C320 and C314/C323. We find that samples C322, C314 and C324 with higher yield strength have comparably higher axial bone volume fraction value (aBV/TV, bone volume fraction aligned along the axial direction; (Liu et al. 2008)) than their counterparts, C320, C323 and C319, respectively (see Table 1). For example, the yield stress of sample C324 is as high as 1.87 times that of C319, and the aBV/TV value of C324 is 0.1026, which is much higher than that of C319, 0.0750. Figure 5(d) shows that aBV/TV has a strong correlation with the yield strength and can describe the yield strength more specifically than BV/TV. This suggests that aBV/TV may play an important role in the strength of trabecular bone.

Figure 5.

Figure 5

Open in a new tab

(a) The linear correlation of the apparent yield strength and the apparent elastic modulus of the trabecular bone samples; (b) the linear correlation of yield strength and the bone volume fraction (BV/TV) of the bone samples; (c) A local magnification of the panel (b) at small BV/TV with the sample ID marked and (d) the linear correlation of yield strength and the axial bone volume fraction (aBV/TV).

Table 1.

The geometric parameters and mechanical properties of the samples.

Specimen ID BV/TV Yield strain (%) Yield stress (MPa) aBV/BV (%) aBV/TVa
C321 0.082 0.710 0.867 61.30 0.0503
C322 0.092 0.728 2.791 86.21 0.0793
C314 0.103 0.762 2.757 70.37 0.0725
C317 0.105 0.752 2.335 54.21 0.0740
C320 0.107 0.787 1.451 67.59 0.0580
C323 0.109 0.746 2.028 83.44 0.0737
C324 0.123 0.752 4.695 59.53 0.1026
C319 0.126 0.864 2.505 59.06 0.0750
C316 0.179 0.823 4.635 46.21 0.1057
C310 0.316 0.867 15.406 58.02 0.1460
C311 0.318 0.878 16.675 58.94 0.1845
C313 0.360 0.871 19.401 8.94 0.2122
Open in a new tab
a

aBV/TV, bone volume fraction aligned along the axial direction.

3.3 Damage analyses

In this study, we used two parameters, i.e. the damaged number fraction (DNF) and the damaged tissue fraction (DTF) (see Section 2.3 for the statistical analyses method of damage) to build the relationship between the amount of damage of the trabecular bone and the applied apparent strain, as shown in Figure 6. We can see that the DNF value of the trabecular rods and that of the trabecular plates are nearly the same at the initial stages of loading with small apparent strain (0.2–0.45%). However, with an increase in the apparent strain, many more trabecular plates are damaged than trabecular rods (Figure 6(a)). The DTF exhibits a similar trend (Figure 6(b)). This suggests that the trabecular plates play a more important role in the damage behaviour of trabecular bone at large apparent strain.

Figure 6.

Figure 6

Open in a new tab

(a) A comparison of the damaged number fraction (DNF) between trabecular plates and rods; (b) A comparison of the damage tissue fraction (DTF) between trabecular plates and rods (Mean ± SE). Asterisk indicates significantly higher damaged plate fraction than rod fraction (p < 0.05).

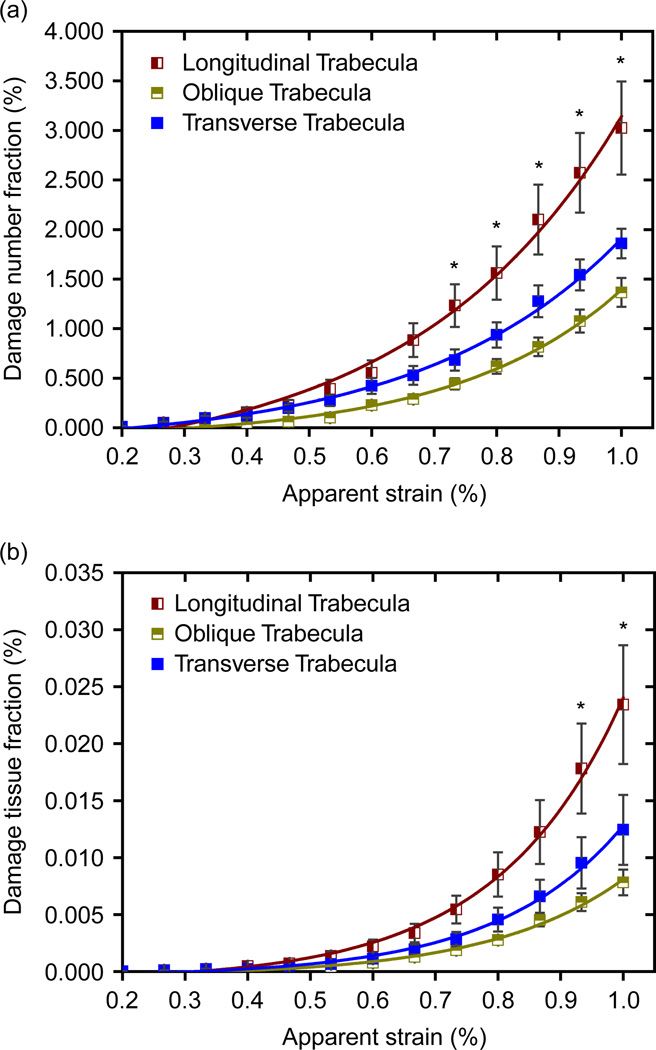
Figure 7 shows the DNF and DTF of total trabeculae in different orientations. It can be seen that the longitudinal (axial) trabeculae are most seriously damaged at high apparent strain, and the transverse trabeculae are more seriously damaged than the oblique trabeculae. This indicates that, in trabecular bone architecture, the longitudinal trabeculae play the most important role while the oblique trabeculae play the least important role, which is a strong physical basis for defining aBV/TV value as a microstructural indicator of strength of trabecular bone.

Figure 7.

Figure 7

Open in a new tab

(a) The DNF of total trabeculae in longitudinal, oblique and transverse directions. (b) The DTF of total trabeculae in longitudinal, oblique and transverse directions (mean ± SE). Asterisk indicates significantly higher damaged plate fraction than rod fraction (p < 0.05).

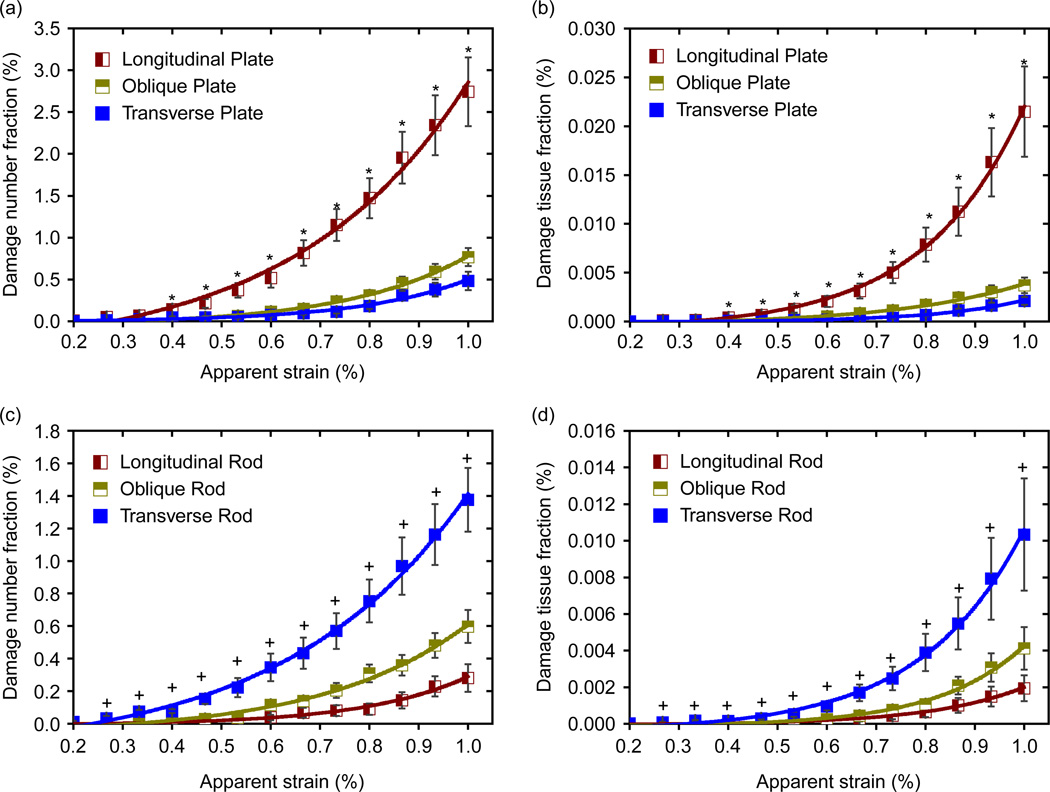
Figure 8 shows the DNF and DTF of trabecular plates and rods separately in terms of their orientation. For trabecular plates, both DNF and DTF of the longitudinal trabeculae are higher than those of the oblique and transverse trabeculae at high apparent strain (> 0.4%) (see Figure 8(a) and (b)). However, for trabecular rods, more transverse trabeculae are damaged than the oblique and longitudinal ones (Figure 8(c) and (d)). This suggests that the longitudinal trabecular plates play a more important role in the behaviour of trabecular bone damage than those plates in other directions. In contrast, the transverse trabecular rods have a more important effect on the behaviour of trabecular bone damage than those rods in other directions. This implies that the plate and rod structures have a different function in the network structure of trabecular bone. Trabecular plates act as the pillars that sustain most of the compression load of bone, while the rods act as the linkers in the network structure to transfer and distribute the load between the trabecular plates.

Figure 8.

Figure 8

Open in a new tab

(a) and (b) Comparison of DNF and DTF of trabecular plates along longitudinal, oblique and transverse directions; (c) and (d) comparison of DNF and DTF of trabecular rods along longitudinal, oblique and transverse directions (Mean ± SE). Asterisk indicates significantly higher damaged longitudinal plate fraction than either oblique or transverse plate fraction (p < 0.05). Plus indicates significantly higher damaged transverse rod than either oblique or longitudinal rod fraction (p < 0.05).

4. Discussion

In this study, we, for the first time, explicitly simulate the initiation and propagation of damage in trabecular bone using the VIB model. The main novelty of this study is that our simulations are able to capture the whole process of damage development in trabecular bone under an external load (Figures 2 and 3). Different from previous studies in which the ad hoc microdamage needed to be assumed in the simulation with explicit models or a somewhat artificial strain-based modulus reduction criterion needed to be assumed to implicitly simulate the damage, our approach can explicitly simulate the initiation and accumulation of trabecular damage automatically without any pre-defined microcrack. A unique 3D image analysis technique ITS can be used to study the effects of microarchitecture on the damage behaviour of trabecular bone. The combination of the two novel methods provides a deeper understanding of the damage mechanics of trabecular bone on both trabecular and tissue levels by directly accessing the initiation and accumulation of damage as well as the effects of the microstructural parameters on the damage behaviour of trabecular bone.

Consistent with previous studies (Yeh and Keaveny 2001; Moore and Gibson 2002; Nagaraja et al. 2005; Liu et al. 2009), our simulations show that the microdamage initiates at a very small apparent strain (Figure 4(a)), ranging from 0.2 to 0.4%; however, microfracture of trabecula occurs at a much higher apparent strain, e.g. our results show that some thin transverse trabeculae are fractured around the apparent yield strain (Figure 2). Yeh and Keaveny (2001) showed that microdamage of trabeculae began around 0.2% strain and trabecular bone fracture began near the apparent yield point of samples in their studies. Nagaraja et al. (2005) also indicated that microdamage initiation occurred at about 0.2–0.6% prior to the apparent yield when they studied the relationship between the amount of microdamage and the apparent strain of bovine trabecular bone with a combination of experiments and FEM simulations. Moore and Gibson (2002) showed that damage was initiated in the linear elastic region, but that the damage increases rapidly at the peak of the stress–strain curve.

We found that the damage behaviour has a close relationship with the yield properties of trabecular bone. Our simulations show that trabecular bone damage increases rapidly as the apparent strain approaches the yield strain (Figures 3 and 6–8). In recent studies of yield behaviour of vertebral trabecular bone, Liu et al. (2009) showed that the volume of yielded bone tissue increases rapidly near the apparent yield strain. This consistence suggests that microdamage might be the underlying mechanism of the yield behaviours of bone tissue. Liu et al. also showed that more longitudinal trabecular plates yielded than the oblique and transverse plates, whereas more transverse trabecular rods yielded than the oblique and longitudinal ones. These results are consistent with our findings about the roles of different microarchitectures in the damage behaviour of trabecular bone, i.e. the trabecular plates, especially the longitudinal ones, have a dominant role in the contribution to the damage behaviour of trabecular bone near apparent yield strain, which again demonstrates the important role that microdamage has in the yield properties of trabecular bone.

In the present study, we showed that aBV/TV is an important microstructural parameter for characterising the damage and yield behaviour of trabecular bone. The bone volume fraction, BV/TV, alone, is not sufficient for describing the damage and yield behaviour of trabecular bone. For instance, when two samples have similar BV/TVs, it is difficult to judge which one has higher yield strength (Figure 5(c)). The microarchitecture of the trabecular bone should also be considered. Previous studies (Jensen et al. 1990; Borah et al. 2000; Pothuaud et al. 2002; Liu et al. 2006, 2008, 2009) also saw the importance of microarchitecture when they studied the elastic modulus and strength of trabecular bone. Liu et al. defined the new parameter aBV/TV, called ‘axial bone volume fraction’, to characterise the microarchitecture of trabecular bone. They found that aBV/TV shows a better correlation with the axial elastic modulus when compared with BV/TV. We show that aBV/TV has a strong correlation with the yield strength of trabecular bone samples (Figure 5(d)). Furthermore, our results suggest that the longitudinal (axial) trabeculae take a dominant role in the damage behaviour of trabecular bone. The underlying mechanism is that large aBV/TV allows for more bone tissue to be sufficiently used for the stiffness and strength of trabecular bone.

Acknowledgements

This work is supported partially by grants from National Natural Science Foundation of China 10502031, 10732050 and 10872115 (BJ), a grant from National Basic Research Program of China 2004CB619304 and 2007CB936803 (BJ), the SRF for ROCS from SEM (BJ), a grant from US National Institutes of Health AR051376 (XEG) and a grant from National Natural Science Foundation of China 10628205 (XEG).

A Appendix

A1. Virtual Internal Bond model

The virtual internal bond (VIB)model developed byGao and Klein (Gao and Klein 1998; Klein and Gao 1998) is a powerful constitutive model for simulating the hyperelastic, plastic and damage behaviours of materials, especially for studying the crack nucleation, crack propagation, crack branching, etc., of materials at high local stress/strain. Recently, Gao and Ji (Gao and Ji 2003; Gao et al. 2003; Ji and Gao 2004a; Ji and Gao 2004b) have extended the VIB model to the study of the fracture strength of biological materials, including bone, teeth and nacre. The nanomechanics of the fracture of mineral crystals and the interface strength between mineral and protein of the ultrastructure of these biological materials have been investigated. A more complete discussion of the VIB model appears in Gao and Klein (1998) and Klein and Gao (1998). Here, we briefly describe the model and some of its general characteristics. The basis of the model is the so-called Cauchy–Born rule (Tadmor et al. 1996), which is a multiscale assumption about how the motion of atoms can be related to continuum deformation measures. The VIB model attempts to reproduce the behaviour of a hyperelastic or plastic solid (e.g. bone tissue) consisting of materials points, which are not necessary atoms, connected by internal cohesive bonds (Figure 1). We assume that each bond can be described by a potential energy function U(l), where l denotes the bond length, which can be expressed in terms of the right Cauchy–Green strain tensor CIJ as

l=l0ξICIJξJ (A1)

where ξI denotes the bond orientation and l0 the length of the unstretched bond and

CIJ=FiIFiJ, (A2)

FiI being the deformation gradient. The link between this discrete microstructural description and the continuum constitutive model is made via a strain energy density function. The strain energy per unit undeformed volume associated with such a network of bonds can be obtained by the Cauchy–Born rule (Tadmor et al. 1996) as

Φ(CIJ)=〈U(l)〉〈U(l0ξICIJξJ)〉. (A3)

Each bond is characterised by a spherical coordinate system (l0, θ, ϕ). For conciseness, we have adopted the notation

〈∧〉=∭(∧)D(l,θ,ϕ) sinθdl0dθdϕ (A4)

as a weighted average with respect to a bond density function, where D(l0, θ, ϕ) characterises the spatial distribution of internal bonds within the network of material particles. Equation (A4) defines the strain energy density function, which in turn defines the symmetric Piola-Kirchhoff stress tensor and the material tangent modulus CIJKL. The results are

SIJ=∂Φ∂EIJ=〈l02U′(l)lξIξJ〉 (A5)

and

CIJKL=∂2Φ∂EIJ∂EKL=〈l04(U″(l)l2−U″(l)l3)ξIξJξKξL〉 (A6)

where EIJ is the Lagrangian strain tensor which is defined as

EIJ=12(CIJ−δIJ) (A7)

For a homogeneous isotropic material, the corresponding Young’s modulus is equal to

E=2π3〈l02U″(l0)〉l0. (A8)

In this study, a modified Smith ferrante potential (Gao and Klein 1998; Klein and Gao 1998) is chosen for the VIB model, and its derivative with respect to the bond length, i.e. the bond force, is illustrated in Figure 1. When the virtual bond is extended, i.e. l = l0 ≥ 0, then

U′(l−l0)=A(l−l0) exp (−l−l0B). (A9)

However, when the virtual bond is compressed, i.e. l = l0 < 0 then

U′(l−l0)=A[ exp (C(l−l0))−1]C, (A10)

where parameter A is the slope of at U′(l − l0) at l = l0 (Figure 1) which is directly related to the elastic modulus of the material. Once the elastic modulus of the material is given, the parameter A can be calculated with Equation (A8). The parameter B is the critical stretch at which the maximum bond force is reached which can be related to the strength of materials. The parameter C is used to describe the compression behaviour of materials (Figure 1). The values of parameters B and C are determined by the criterion that the VIB model can reproduce the stress–strain curves of the materials under tension and compression, which are obtained from experimental results directly or from experiment-based numerical simulations (Bevill et al. 2006).

A2. Individual trabeculae segmentation technique

Individual trabeculae segmentation (ITS) is a novel 3D image analysis technique, which has recently been developed for decomposing trabecular bone microarchitecture into individual plates and rods (Liu et al. 2006, 2008). During the segmentation, the digital topological analyses (Liu et al. 2006, 2008, 2009), including skeletonisation (Saha et al. 1997) and topological classification (Saha and Chaudhuri 1996), were first applied to transform a trabecular bone image into a representation of one-voxel-thick skeletons of surfaces and curves. Afterwards, individual trabecular rods or plates were reconstructed back to their original volume. At the end of the procedure, the original trabecular bone image was segmented into individual trabecular rods and plates with their associated voxels. In addition, for each trabecula, an ITS-based morphological analysis was performed to identify and calculate the trabecular type and volume, respectively. The detail of this technique is described elsewhere (Liu et al. 2006, 2008, 2009). Just to mention briefly, using the ITS technique, many trabecular parameters of the sample can be taken output, such as trabecular type (plate or rod), trabecular volume fraction, trabecular thickness and trabecular orientation. These parameters were then used for the analysis of the relationship between the bone microdamage and trabecular bone microstructures.

Footnotes

Publisher's Disclaimer: Full terms and conditions of use: http://www.tandfonline.com/page/terms-and-conditions

This article may be used for research, teaching, and private study purposes. Any substantial or systematic reproduction, redistribution, reselling, loan, sub-licensing, systematic supply, or distribution in any form to anyone is expressly forbidden.

The publisher does not give any warranty express or implied or make any representation that the contents will be complete or accurate or up to date. The accuracy of any instructions, formulae, and drug doses should be independently verified with primary sources. The publisher shall not be liable for any loss, actions, claims, proceedings, demand, or costs or damages whatsoever or howsoever caused arising directly or indirectly in connection with or arising out of the use of this material.

The authors state that they have no any financial, professional and personal conflict of interests.

References

  1. Bevill G, Eswaran SK, Gupta A, Papadopoulos P, Keaveny TM. Influence of bone volume fraction and architecture on computed large-deformation failure mechanisms in human trabecular bone. Bone. 2006;39(6):1218–1225. doi: 10.1016/j.bone.2006.06.016. [DOI] [PubMed] [Google Scholar]
  2. Borah B, Dufresne TE, Cockman MD, Gross GJ, Sod EW, Myers WR, Combs KS, Higgins RE, Pierce SA, Stevens ML. Evaluation of changes in trabecular bone architecture and mechanical properties of minipig vertebrae by three-dimensional magnetic resonance microimaging and finite element modeling. J Bone Miner Res. 2000;15(9):1786–1797. doi: 10.1359/jbmr.2000.15.9.1786. [DOI] [PubMed] [Google Scholar]
  3. Burr D. Microdamage and bone strength. Osteoporos Int. 2003:S67–S72. doi: 10.1007/s00198-003-1476-2. [DOI] [PubMed] [Google Scholar]
  4. Burr DB, Forwood MR, Fyhrie DP, Martin B, Schaffler MB, Turner CH. Bone microdamage acid skeletal fragility in osteoporotic and stress fractures. J Bone Miner Res. 1997;12(1):6–15. doi: 10.1359/jbmr.1997.12.1.6. [DOI] [PubMed] [Google Scholar]
  5. Charras GT, Guldberg RE. Improving the local solution accuracy of large-scale digital image-based finite element analyses. J Biomech. 2000;33(2):255–259. doi: 10.1016/s0021-9290(99)00141-4. [DOI] [PubMed] [Google Scholar]
  6. Gao HJ, Ji BH. Modeling fracture in nanomaterials via a virtual internal bond method. Eng Fract Mech. 2003;70(14):1777–1791. [Google Scholar]
  7. Gao HJ, Klein P. Numerical simulation of crack growth in an isotropic solid with randomized internal cohesive bonds. J Mech Phys Solids. 1998;46(2):187–218. [Google Scholar]
  8. Gao HJ, Ji BH, Jager IL, Fratzl P. Materials become insensitive to flaws at nanoscale: lessons from nature. Proc Natl Acad Sci U S A. 2003;100(10):5597–5600. doi: 10.1073/pnas.0631609100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Guldberg RE, Hollister SJ, Charras GT. The accuracy of digital image-based finite element models. J Biomech Eng-Trans Asme. 1998;120(2):289–295. doi: 10.1115/1.2798314. [DOI] [PubMed] [Google Scholar]
  10. Guo XDE, McMahon TA, Keaveny TM, Hayes WC, Gibson LJ. Finite-element modeling of damage accumulation in trabecular bone under cyclic loading. J Biomech. 1994;27(2):145–155. doi: 10.1016/0021-9290(94)90203-8. [DOI] [PubMed] [Google Scholar]
  11. Hou FJ, Lang SM, Hoshaw SJ, Reimann DA, Fyhrie DP. Human vertebral body apparent and hard tissue stiffness. J Biomech. 1998;31(11):1009–1015. doi: 10.1016/s0021-9290(98)00110-9. Available: http://tahoe.ca.sandia.gov/. [DOI] [PubMed] [Google Scholar]
  12. Jensen KS, Mosekilde L, Mosekilde L. A model of vertebral trabecular bone architecture and its mechanical-properties. Bone. 1990;11(6):417–423. doi: 10.1016/8756-3282(90)90137-n. [DOI] [PubMed] [Google Scholar]
  13. Ji BH, Gao HJ. Mechanical properties of nanostructure of biological materials. J Mech Phys Solids. 2004a;52(9):1963–1990. [Google Scholar]
  14. Ji BH, Gao HJ. A study of fracture mechanisms in biological nano-composites via the virtual internal bond model. Mater Sci Eng A-Struct Mater Prop Microstruct Process. 2004b;366(1):96–103. [Google Scholar]
  15. Keaveny TM, Guo XE, Wachtel EF, Mcmahon TA, Hayes WC. Trabecular bone exhibits fully linear elastic behavior and yields at low strains. J Biomech. 1994a;27(9):1127. doi: 10.1016/0021-9290(94)90053-1. &. [DOI] [PubMed] [Google Scholar]
  16. Keaveny TM, Wachtel EF, Ford CM, Hayes WC. Differences between the tensile and compressive strengths of bovine tibial trabecular bone depend on modulus. J Biomech. 1994b;27(9):1137–1146. doi: 10.1016/0021-9290(94)90054-x. [DOI] [PubMed] [Google Scholar]
  17. Keaveny TM, Wachtel EF, Guo XE, Hayes WC. Mechanical-behavior of damaged trabecular bone. J Biomech. 1994c;27(11):1309–1318. doi: 10.1016/0021-9290(94)90040-x. [DOI] [PubMed] [Google Scholar]
  18. Kim C, Zhang H, Mikhail G, von Stechow D, Müller R, Kim H, Guo X. Effects of thresholding techniques on microCT-based finite element models of trabecular bone. J Biomech Eng. 2007;129(4):481–486. doi: 10.1115/1.2746368. [DOI] [PubMed] [Google Scholar]
  19. Klein P, Gao H. Crack nucleation and growth as strain localization in a virtual-bond continuum. Eng Fract Mech. 1998;61(1):21–48. [Google Scholar]
  20. Kosmopoulos V, Schizas C, Keller TS. Modeling the onset and propagation of bone microdamage during low-cycle trabecular fatigue. J Biomech. 2008;41(3):515–522. doi: 10.1016/j.jbiomech.2007.10.020. [DOI] [PubMed] [Google Scholar]
  21. Kosmopoulos V, Keller TS. Predicting trabecular bone microdamage initiation and accumulation using a non-linear perfect damage model. Med Eng Phys. 2008;30(6):725–732. doi: 10.1016/j.medengphy.2007.02.011. [DOI] [PubMed] [Google Scholar]
  22. Liu XG, Wang XA, Niebur GL. Effects of damage on the orthotropic material symmetry of bovine tibial trabecular bone. J Biomech. 2003;36(12):1753–1759. doi: 10.1016/s0021-9290(03)00217-3. [DOI] [PubMed] [Google Scholar]
  23. Liu XS, Sajda P, Saha PK, Wehrli FW, Guo XE. Quantification of the roles of trabecular microarchitecture and trabecular type in determining the elastic modulus of human trabecular bone. J Bone Miner Res. 2006;21(10):1608–1617. doi: 10.1359/jbmr.060716. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Liu XS, Sajda P, Saha PK, Wehrli FW, Bevill G, Keaveny TM, Guo XE. Complete volumetric decomposition of individual trabecular plates and rods and its morphological correlations with anisotropic elastic moduli in human trabecular bone. J Bone Miner Res. 2008;23(2):223–235. doi: 10.1359/JBMR.071009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Liu XS, Bevill G, Keaveny TM, Sajda P, Guo XE. Micromechanical analyses of vertebral trabecular bone based on individual trabeculae segmentation of plates and rods. J Biomech. 2009;42(3):249–256. doi: 10.1016/j.jbiomech.2008.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Makiyama AM, Vajjhala S, Gibson L. J. Analysis of crack growth in a 3D voronoi structure: a model for fatigue in low density trabecular bone. J Biomech Eng Trans Asme. 2002;124(5):512–520. doi: 10.1115/1.1503792. [DOI] [PubMed] [Google Scholar]
  27. Moore TLA, Gibson LJ. Modeling modulus reduction in bovine trabecular bone damaged in compression. J Biomech Eng Trans Asme. 2001;123(6):613–622. doi: 10.1115/1.1407828. [DOI] [PubMed] [Google Scholar]
  28. Moore TLA, Gibson LJ. Microdamage accumulation in bovine trabecular bone in uniaxial compression. J Biomech Eng Trans Asme. 2002;124(1):63–71. doi: 10.1115/1.1428745. [DOI] [PubMed] [Google Scholar]
  29. Morgan EF, Keaveny TM. Dependence of yield strain of human trabecular bone on anatomic site. J Biomech. 2001;34(5):569–577. doi: 10.1016/s0021-9290(01)00011-2. [DOI] [PubMed] [Google Scholar]
  30. Mori S, Burr DB. Increased intracortical remodeling following fatigue damage. Bone. 1993;14(2):103–109. doi: 10.1016/8756-3282(93)90235-3. [DOI] [PubMed] [Google Scholar]
  31. Nagaraja S, Couse TL, Guldberg RE. Trabecular bone microdamage and microstructural stresses under uniaxial compression. J Biomech. 2005;38(4):707–716. doi: 10.1016/j.jbiomech.2004.05.013. [DOI] [PubMed] [Google Scholar]
  32. Niebur GL, Feldstein MJ, Yuen JC, Chen TJ, Keaveny TM. High-resolution finite element models with tissue strength asymmetry accurately predict failure of trabecular bone. J Biomech. 2000;33(12):1575–1583. doi: 10.1016/s0021-9290(00)00149-4. [DOI] [PubMed] [Google Scholar]
  33. Pothuaud L, Van Rietbergen B, Mosekilde L, Beuf O, Levitz P, Benhamou CL, Majumdar S. Combination of topological parameters and bone volume fraction better predicts the mechanical properties of trabecular bone. J Biomech. 2002;35(8):1091–1099. doi: 10.1016/s0021-9290(02)00060-x. [DOI] [PubMed] [Google Scholar]
  34. Saha PK, Chaudhuri BB, Dutta D, Majumder DD. A new shape preserving parallel thinning algorithm for 3D digital images. Pattern Recognit. 1997;30(12):1939–1955. [Google Scholar]
  35. Saha PK, Chaudhuri BB. 3D digital topology under binary transformation with applications. Comput Vis Image Underst. 1996;63(3):418–429. [Google Scholar]
  36. Schaffner G, Guo XDE, Silva MJ, Gibson LJ. Modelling fatigue damage accumulation in two-dimensional voronoi honeycombs. Int J Mech Sci. 2000;42(4):645–656. [Google Scholar]
  37. Seeman E. Bone quality: the material and structural basis of bone strength. J Bone Miner Metab. 2008;26(1):1–8. doi: 10.1007/s00774-007-0793-5. [DOI] [PubMed] [Google Scholar]
  38. Stolken JS, Kinney JH. On the importance of geometric nonlinearity in finite-element simulations of trabecular bone failure. Bone. 2003;33(4):494–504. doi: 10.1016/s8756-3282(03)00214-x. [DOI] [PubMed] [Google Scholar]
  39. Tadmor EB, Ortiz M, Phillips R. Quasicontinuum analysis of defects in solids. Philos Mag A: Phys Condens Matter Struct Defects Mech Properties. 1996;73(6):1529–1563. [Google Scholar]
  40. Thurner PJ, Wyss P, Voide R, Stauber M, Stampanoni M, Sennhauser U, Muller R. Time-lapsed investigation of three-dimensional failure and damage accumulation in trabecular bone using synchrotron light. Bone. 2006;39(2):289–299. doi: 10.1016/j.bone.2006.01.147. [DOI] [PubMed] [Google Scholar]
  41. Vanrietbergen B, Weinans H, Huiskes R, Odgaard A. A new method to determine trabecular bone elastic properties and loading using micromechanical finite-element models. J Biomech. 1995;28(1):69. doi: 10.1016/0021-9290(95)80008-5. &. [DOI] [PubMed] [Google Scholar]
  42. Wachtel EF, Keaveny TM. Dependence of trabecular damage on mechanical strain. J Orthop Res. 1997;15(5):781–787. doi: 10.1002/jor.1100150522. [DOI] [PubMed] [Google Scholar]
  43. Wang XA, Niebur GL. Microdamage propagation in trabecular bone due to changes in loading mode. J Biomech. 2006;39(5):781–790. doi: 10.1016/j.jbiomech.2005.02.007. [DOI] [PubMed] [Google Scholar]
  44. Yeh OC, Keaveny TM. Relative roles of microdamage and microfracture in the mechanical behavior of trabecular bone. J Orthop Res. 2001;19(6):1001–1007. doi: 10.1016/S0736-0266(01)00053-5. [DOI] [PubMed] [Google Scholar]
  45. Yeni YN, Fyhrie DP. Finite element calculated uniaxial apparent stiffness is a consistent predictor of uniaxial apparent strength in human vertebral cancellous bone tested with different boundary conditions. J Biomech. 2001;34(12):1649–1654. doi: 10.1016/s0021-9290(01)00155-5. [DOI] [PubMed] [Google Scholar]

RESOURCES