Comparison of ISO Standard and TKR Patient Axial Force Profiles during the Stance Phase of Gait

Abstract

Preclinical endurance testing of total knee replacements (TKRs) is performed using International Organization for Standardization (ISO) load and motion protocols. The standards are based on data from normal subjects and may not sufficiently mimic in vivo implant conditions. In this study, a mathematical model was used to calculate the axial force profile of 30 TKR patients with two current implant types, 22 with NexGen and eight with Miller-Galante II Cruciate-Retaining TKRs, and statistically compare the axial force specified by the ISO standard to the TKR patients. Significant differences were found between the axial forces of both groups of TKR patients and the ISO standard at local maxima and minima points in the first half of stance. The force impulse (area under the axial force curve, representing cumulative loading) was smaller for the ISO standard than the TKR patients, but only for those with NexGen implants. Waveform analysis using the coefficient of multiple correlation showed that the ISO and TKR patient axial force profiles were similar. The combined effect of ISO standard compressive load and motion differences from TKR patients could explain some of the differences between the wear scars on retrieved tibial components and those tested in total joint simulators.

1 Introduction

Total knee replacement (TKR) is a common surgical procedure to alleviate pain and increase functional mobility in diseased or traumatized knee joints. Over 450,000 surgeries are performed annually in the United States alone [1]. A limiting factor to the service life of a TKR remains wear of the tibial polyethylene liner [2-4]. Increases in patient life expectancy and body weight, as well as the trend to perform TKR in younger, more active patients will put even higher demands on the prosthetic device in the future [5].

Preclinical endurance testing has become a standard procedure used during implant development to predict the mechanical performance of TKRs, and is required for regulatory device approval. Knee prostheses are currently tested under standardized protocols developed by the International Organization for Standardization (ISO) for simulation under either force (ISO 14243-1) or displacement (ISO 14243-3) control. Both standards specify identical axial (compressive) force patterns for an entire cycle of gait.

It is known that wear scars measured on retrieved tibial TKR components do not match those from components tested in total joint simulators [6, 7], suggesting that testing standards may not adequately reproduce in vivo conditions for TKR patients. While the primary purpose of a standard is to facilitate benchmark testing and allow comparison between laboratories, standardized testing should also make products safer and more reliable for in vivo use. Thus, an existing standard must be constantly reassessed and its usefulness re-evaluated based on new information. Recent work in our laboratory has shown that the ISO anterior-posterior force/translation and internal-external torque/rotation inputs have different magnitudes and timings compared with measurements taken from TKR patients during gait analysis [8, 9]. The TKR patients had greater knee translations and rotations with different patterning than the ISO standards. Axial contact force comparisons between the previously tested TKR patients and the ISO standards have yet to be conducted to complete the picture regarding knee simulator input.

The axial force profile defined in the ISO standards reveals three main peak forces that range from 1,887 to 2,600 N. Ideally, standard protocols for knee prosthesis testing should replicate physiological conditions of TKR patients. Accurate force magnitudes are important not only for the preclinical assessment of implant performance, but also in the implant design process, where loading of the articulating geometry must result in contact areas and stresses within material limitations. While the ISO profile was based on mathematical modeling [10-12] that used the only available data at the time, more information is now available.

In particular, direct axial force measurements have been recently published by two research groups [13-15], which can be considered as a new gold standard of expected contact forces during walking. However, these measurements are limited to a few subjects and two specific knee designs. In the current study we will determine the axial force profiles that occur during walking for a large cohort of patients implanted with current cruciate retaining TKRs [8, 9] using a validated mathematical model [16, 17]. Thus, we expand the body of existing measurements to a broader population. The purpose of this study is to characterize the axial force profile of this TKR cohort and to compare it statistically with the axial force profile specified by the ISO.

2 Methods

Thirty TKR patients were tested in the Motion Analysis Laboratory at Rush University Medical Center (Chicago, USA) under informed consent and Institutional Review Board approval. All patients had a successful primary TKR surgery with either a Miller-Galante II (MGII) or a NexGen Cruciate-Retaining implant manufactured by Zimmer, Inc. (Warsaw, IN, USA). Patients were at least 12 months post-operative and were actively being followed for post-operative care (Table 1). Patients were able to walk comfortably without aids and did not have any history of neurological disorders. The patients with NexGen implants were significantly younger and had a shorter implant in situ time compared those with MGII implants.

Table 1.

TKR patient demographics (mean ± standard deviation). Patients were implanted with either a Miller-Galante II (MGII) or a NexGen Cruciate-Retaining TKR (Zimmer Inc., Warsaw, IN). The NexGen patients were significantly younger than the MGII patients (p < 0.001) and had significantly shorter implant in situ times (p < 0.001). Despite these differences, previous studies showed that the gait patterns of the patients with either implant type were not significantly different [8, 9].

Patients	Number	Age (years)	Height (m)	Weight (N)	Male/Female	Time in situ (years)
NexGen	22	61.8 ± 6.78	1.74 ± 0.10	879 ± 200	10 M / 12 F	3.03 ± 2.20
MGII	8	76.1 ± 6.01	1.67 ± 0.05	834 ± 188	5 M / 3 F	11.6 ± 0.92
All TKRs	30	65.6 ± 9.15	1.72 ± 0.09	867 ± 195	15 M / 15 F	5.33 ± 4.32

The TKR patients underwent gait testing in a previous study to obtain their knee kinematics during level walking [8, 9]. Knee flexion-extension angles, anterior-posterior tibial translation, and internal-external tibial rotation angles were measured using the point cluster technique [18]. The knee rotations and translations were used to calculate the tibiofemoral path of contact on the surface of the tibial TKR component with previously developed software [19-21]. A multi-component force plate (Bertec, Columbus, USA) was used to record foot-ground reaction forces simultaneously with the knee kinematics during the walking trials. Inverse dynamics were used to calculate the three-dimensional external moments and intersegmental forces at the knee resulting from the action of the three-dimensional ground reaction force [22].

Knee joint kinematics, kinetics, and the tibiofemoral contact path data were inputted into a parametric knee model [16] to calculate axial force profiles through the knee during the stance phase of gait. The model uses equilibrium equations to calculate three-dimensional knee contact forces for both the medial and lateral sides of the tibial plateau. For equilibrium, external forces and moments (measured during gait analysis) are equal to internal forces and moments (from muscles, soft tissues, and contact forces). The three-dimensional contact forces have six unknown quantities, leaving only three muscle or soft tissue forces that can be calculated with the mathematical model. A classical solution to this issue is to reduce the number of muscle and soft tissue forces and obtain a determinate problem [23]. For the parametric knee model, instead of reducing the number of muscle forces, all muscles forces are allowed to vary over their physiological limits and are parametrically scaled from zero to 100 percent of their maximum possible force. Fifteen muscles crossing the knee joint were categorized into three functional groups according to their function as primary, secondary, or minor agonists in the sagittal, frontal, and transverse planes of the knee joint. At each of 100 time points during stance, the system of nine statically determinate equations were solved for six knee contact force components (three on the lateral side and three on the medial side) and three muscle group activation levels that scaled the primary, secondary, and minor agonist muscle forces. The model has been recently validated [17, 24] using published gait data and matching telemetric knee forces [25].

Knee joint axial force profiles were calculated during stance for all 90 walking trials from the 30 patients (three trials per patient). An average total (medial plus lateral) axial force profile was calculated for each patient from the three walking trials. Several comparisons were made to test if the TKR patient average total axial force profiles for both implant types were different from that specified by the ISO standards.

The similarity of the shape of the TKR and ISO axial force profiles was evaluated by calculating the adjusted coefficient of multiple determination $({\text{R}}_{\text{adj}}^2)$ (Equation 2.1).

$${\text{R}}_{\text{adj}}^2=1-\frac{\sum _{\text{m}=1}^{\text{M}}\sum _{\text{n}=1}^{\text{N}}\sum _{\text{t}=1}^{\text{T}}\frac{{\left({\text{F}}_{\text{mnt}}-{\overline{\text{F}}}_{\text{t}}\right)}^2}{\text{T}\left(\text{MN}-1\right)}}{\sum _{\text{m}=1}^{\text{M}}\sum _{\text{n}=1}^{\text{N}}\sum _{\text{t}=1}^{\text{T}}\frac{{\left({\text{F}}_{\text{mnt}}-\overline{\text{F}}\right)}^2}{\left(\text{MNT}-1\right)}}$$ (2.1)

For Equation 2.1, F_mnt was equal to the average total axial force value at the t^th time point during stance and n^th patient. Variable “m” indicated the average total axial force profile used: either the TKR profile (m=1) or the ISO profile (m=2). For m=1, the TKR patient axial forces, N was equal to 30. For m=2, the ISO axial forces, N was equal to one because one axial force profile was specified by the ISO standards. F̄_t was equal to the average overall profile at time point “t” (T=100) during stance (Equation 2.2). F̄ was equal to the grand mean of all the profiles (Equation 2.3).

$${\overline{\text{F}}}_{\text{t}}=\frac{1}{\text{MN}}\sum _{\text{m}=1}^{\text{M}}\sum _{\text{n}=1}^{\text{N}}{\text{F}}_{\text{mnt}}$$ (2.2)

$$\overline{\text{F}}=\frac{1}{\text{MNT}}\sum _{\text{m}=1}^{\text{M}}\sum _{\text{n}=1}^{\text{N}}\sum _{\text{t}=1}^T{\text{F}}_{\text{mnt}}$$ (2.3)

The ${\text{R}}_{\text{adj}}^2$ represented the amount of variability in the data that could not be attributed to differences between the TKR patients' axial forces and the ISO standard. The numerator of Equation 2.1 represented the total variation of the axial forces about each instance of time “t”. The denominator of Equation 2.1 represented the total variation about the overall mean axial force. An ${\text{R}}_{\text{adj}}^2$ of one indicated that the waveforms were similar, and an ${\text{R}}_{\text{adj}}^2$ of zero indicated that the waveforms were dissimilar. The positive square root of ${\text{R}}_{\text{adj}}^2$, the adjusted coefficient of multiple correlation (R_adj), will be reported consistent with previous literature investigating differences in gait waveforms [26].

Next, the magnitudes and timings of three local maxima and two local minima of the average total axial force profiles (Figure 1) were compared to the ISO standard axial force profile using one-sample t-tests. For the one-sample t-tests, the ISO standard axial force magnitudes and timings were assumed to be equal to the population mean and were compared with the cohort (TKR patient) mean. Comparisons between the two TKR implant types were also made using two-sample t-tests. Peak loads were investigated because they directly contribute to damage and wear on retrieved tibial plateaus [27]. Timings of the peak loads were investigated because TKR patients have differences in timings of their motions [8, 9] and, because of their disease history, are suspected to walk slower [28] than normal subjects.

Figure 1.

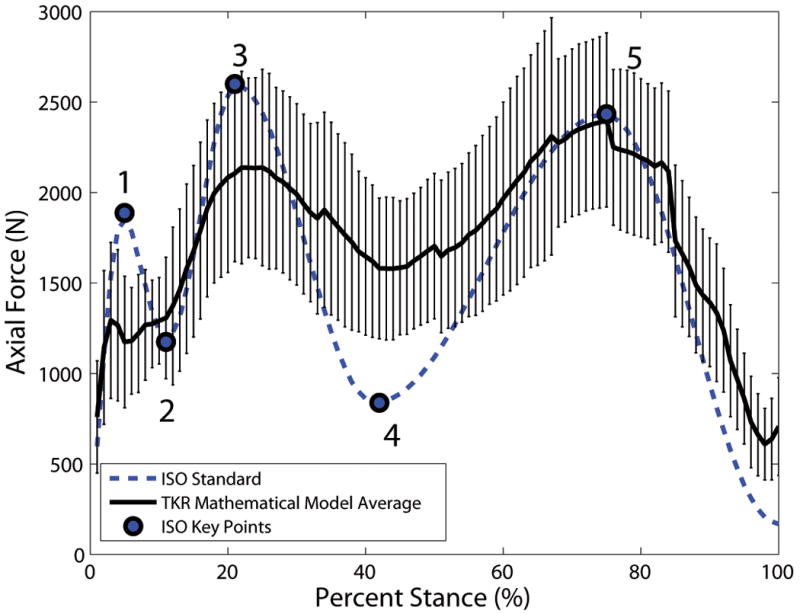
The ISO standard axial force profile (dashed line) and the TKR patient axial force profile (solid line, mean ± standard deviation) were compared at three local maxima points and two local minima points during the stance phase of gait (key points 1 through 5, shown on the ISO standard profile).

Lastly, the impulse (area under the curve) of the axial force profiles was evaluated and compared with ISO using one-sample t-tests. Force impulse was computed as an additional comparison tool because it represents the cumulative loading subjected to the polyethylene tibial plateau over a gait cycle, which could provide a surrogate measure for implant wear.

The significance level of all statistical tests was set to α≤ 0.05. In addition, to convey the estimated magnitude of the difference, descriptive statistics were used. In particular, we investigated the effects sizes and used Cohen's d, which is defined as the difference between two means divided by the standard deviation for the data [29]. Effect sizes are classified as “small” (0<d<0.35), “medium” (0.35<d<0.65), and “large” (d≥0.65). All statistical calculations were performed using SPSS (IBM SPSS, Chicago, IL).

3 Results

The shapes of the ISO standard axial profile and the TKR axial force profiles were similar. The adjusted coefficient of multiple correlation (R_adj), representing the amount of similarity between the TKR axial force profiles and the ISO standard axial force profile, was equal to 0.78 for the NexGen TKR group compared to ISO, 0.81 for the MGII TKR group compared to ISO, and 0.79 for all 30 TKR axial force profiles compared to ISO.

There were no significant differences between the magnitudes or timings of axial force key points between the NexGen and MGII TKR groups (Tables 2 through 5). The ISO standard axial force profile fell within the mean ± one standard deviation of all TKR (pooled NexGen and MGII groups) axial force profiles for three of the five key points (Figure 1). The mean TKR axial force for both implant groups was lower than the ISO standard for key points in early to mid-stance (key points 1 through 3, Figure 2, Tables 2 and 3) but higher than the ISO standard for the second local minimum contact force at mid-stance (key point 4). The TKR axial force for both groups was not significantly different from the ISO axial force for the third local maximum (key point 5). The impulse of the axial force profile (area under the curve) was greater for the NexGen patients than the ISO standard (180 ± 33.8 kN*% Stance and 156 kN*% Stance for NexGen and ISO, respectively, Figure 2, Table 2), a statistically significant difference (p = 0.004). For the group of all TKRs, the effect size was medium to large (Table 3). The impulse of the MGII axial force profile (163 ± 26.2 kN*% Stance) was not significantly different than the impulse of the ISO standard axial force profile (p = 0.49).

Table 2.

Axial forces (N) and force impulse (kN*% Stance), or area under the axial force curve, for both TKR types (NexGen and MGII) and the ISO Standard. Axial force values are given for local maxima and minima (key points, Figure 1). Values are given as mean ± standard deviation.

Patients	Force (N) at Key Points (Figure 1)					Force Impulse (kN*% Stance)
	1	2	3	4	5
NexGen	1512 ± 347	1049 ± 223	2272 ± 569	1446 ± 356	2680 ± 604	180 ± 33.8
MGII	1397 ± 330	978 ± 284	2103 ± 462	1433 ± 384	2288 ± 380	163 ± 26.2
All TKRs	1481 ± 341	1030 ± 238	2227 ± 540	1442 ± 357	2576 ± 575	175 ± 32.4
ISO	1887	1175	2600	838	2433	156

Figure 2.

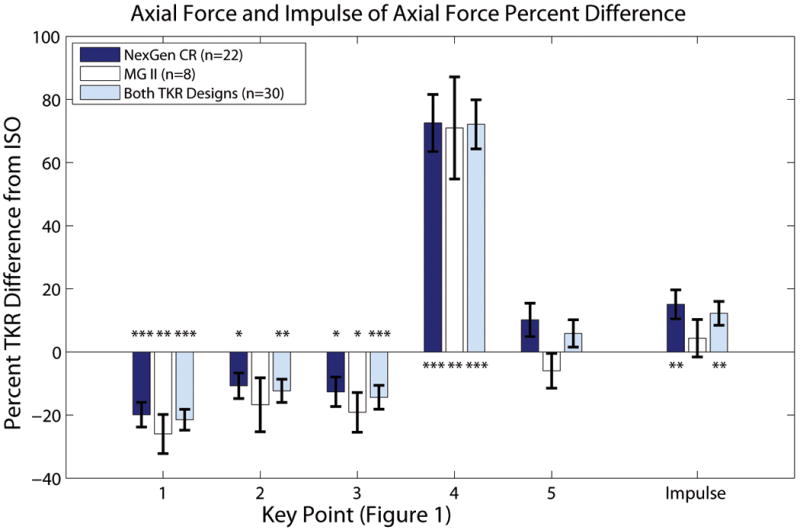
The TKR patient axial forces were significantly different from the ISO standard axial forces for the first four key points (Figure 1) during the stance phase of gait. The TKR patient impulse of the axial force profile (area under the force curve, a measure of cumulative loading) was also significantly different from the ISO profile for the NexGen patient group. Results are shown as the percent difference between the ISO and TKR values or 100 × (ISO-TKR)/ISO (mean ± standard error). The force values in Newtons are given in Table 2. Statistically significant differences from the ISO standard are indicated by asterisks: * p < 0.05, ** p < 0.01, and *** p < 0.001.

Table 3.

P values and effect sizes for the differences between the TKR patients and the ISO standard are shown for both TKR types (NexGen and MGII). Axial forces and force impulse were statistically evaluated at local maxima and minima (key points, Figure 1).

	NexGen CR (n=22)		MG II (n=8)		All TKRs (n=30)
	p value	Effect size	p value	Effect size	p value	Effect size
Key Point 1	<0.001	1.08	0.004	1.48	<0.001	1.19
Key Point 2	0.015	0.56	0.091	0.69	0.002	0.61
Key Point 3	0.013	0.58	0.019	1.08	<0.001	0.69
Key Point 4	<0.001	1.71	0.003	1.55	<0.001	1.69
Key Point 5	0.069	0.41	0.315	0.38	0.185	0.25
Impulse	0.004	0.70	0.486	0.26	0.003	0.59

The timings of axial force profile key points were also significantly different between the TKR patients and the ISO standard for key points 2 through 5 when all 30 TKR patients were pooled in the same group (Figure 3, Tables 4 and 5). Again, the effect sizes of these differences were medium to large. The NexGen TKR group had more key point timing differences with the ISO standard than the MGII group.

Figure 3.

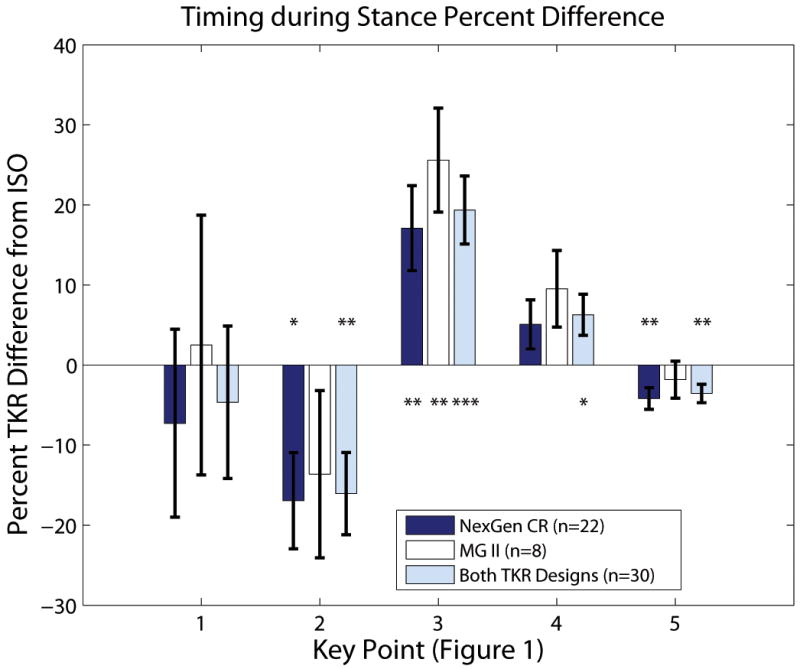
The timings of axial force maxima and minima key points (Figure 1) for the TKR patients were significantly different from the ISO standard during the stance phase of gait except for the first local maximum (key point 1). The timing differences are shown as the percent difference between the ISO and TKR values or 100 × (ISO-TKR)/ISO (mean ± standard error). Note that key point 1 was highly variable in appearance which increased the standard error. Statistically significant differences from the ISO standard are indicated by asterisks: * p < 0.05, ** p < 0.01, and *** p < 0.001.

Table 4.

Timing (% Stance) of axial force local maxima and minima (key points, Figure 1) for both TKR types (NexGen and MGII) and the ISO Standard. Values are given as mean ± standard deviation.

Patients	Timings (% Stance) of Key Points (Figure 1)
	1	2	3	4	5
NexGen	4.64 ± 2.75	9.14 ± 3.11	24.6 ± 5.23	44.1 ± 6.04	71.9 ± 4.70
MGII	5.13 ± 2.30	9.50 ± 3.25	26.4 ± 3.85	46.0 ± 5.68	73.6 ± 4.90
All TKRs	4.77 ± 2.61	9.23 ± 3.09	25.1 ± 4.90	44.6 ± 5.91	72.3 ±4.74
ISO	5	11	21	42	75

Table 5.

P values and effect sizes for the timing differences between the TKR patients and the ISO standard are shown for both TKR types (NexGen and MGII). Timing of axial force local maxima and minima were statistically evaluated at local maxima and minima (key points, Figure 1).

	NexGen CR (n=22)		MG II (n=8)		All TKRs (n=30)
	p value	Effect size	p value	Effect size	p value	Effect size
Key Point 1	0.542	0.13	0.882	0.05	0.628	0.09
Key Point 2	0.010	0.60	0.233	0.46	0.004	0.57
Key Point 3	0.004	0.69	0.006	1.40	<0.001	0.83
Key Point 4	0.112	0.35	0.087	0.70	0.021	0.45
Key Point 5	0.005	0.67	0.453	0.28	0.004	0.56

4 Discussion

The axial force profile specified by the ISO standards, although providing a standard by which TKR designs can be compared, does not result in wear characteristics that represent in vivo TKR wear [6, 7]. To determine if axial force contributes to these discrepancies, we calculated the axial forces across TKRs during the stance phase of gait using a validated mathematical model. This work represents the largest study to date (30 patients) of patient-specific TKR contact forces. Two TKR designs were evaluated and additional comparisons to the ISO standard were performed.

At first glance, the mean axial force profile from the TKR patients was surprisingly similar to the ISO standard, especially considering that the ISO standard was derived from normal subjects using one of the early mathematical knee models [10], before instrumented TKR data was available for model validation. The waveform comparison (adjusted coefficient of multiple correlation, R_adj) also suggested that the waveforms were similar, but upon further detailed analysis, differences were apparent.

The TKR axial forces were different than that specified by the ISO standard for key points located in the first half of the stance phase (key points 1 through 4) for both the NexGen and MGII TKR groups. The first local maximum (key point 1), occurring immediately after stance initiation, was subtle in appearance for the TKR patients. The axial force at midstance (key point 4) showed the greatest difference between all the TKR patients and the ISO standard; axial force was 604 N (72%) higher for the TKR patients than the ISO standard at key point 4. The maximum difference in timing occurred at key point 3 (the second local axial force maximum) where the peak occurred 4.1% Stance later for all the TKR patients than the ISO standard. The differences in magnitude and timings of peak axial loads are consistent with the differences found between TKR patients and the ISO standards for knee kinematics [8, 9]. The ISO standard underestimation of force at mid-stance (key point 4) can be explained by recent measurements of high co-activation between the quadriceps and hamstrings for TKR patients [30]. Higher levels of co-activation, indicative of increased antagonistic muscle activity, could result in higher knee joint contact force.

Because the impulse of the axial force profile represents the cumulative loading over the entire stance phase, it may be an important parameter to consider when determining what effect the axial force profile will have on wear. The impulse of the axial force profile (area under the curve) was not significantly different for the MGII group compared to the ISO standard (p = 0.486), and the effect size was equal to 0.26. For the NexGen group, the impulse of the axial force profile was significantly different from the ISO standard (p = 0.004) and had a large effect size of 0.70. When all TKR patients were treated as one group, impulse of the axial force was still significantly different from the ISO standard (p = 0.003) with a medium effect size of 0.59.

These findings are consistent with data becoming available from instrumented TKRs in which a distinct axial force peak in early stance is not always present [14, 25, 31]; in fact no evidence of a local maximum at stance initiation was seen for the measured axial force profile from five patients with instrumented TKRs during stance (Figure 4). The mean instrumented axial force was derived from walking trials from five patients (data files K1L_040707_1_24, K1L_110108_1_86, K2L_290409_1_61, K2L_290409_1_64, K2L_301107_1_67, K3R_090609_2_49, K4R_201108_1_50, K4R_201108_1_52, K5R_060809_1_51, K5R_060908_1_76) in the OrthoLoad database [32]). Kutzner et al. [15] reported a local maximum did occur just before heel strike for the five patients, but it is much lower in magnitude than that specified by the ISO standard. The instrumented TKR output at specific key points during stance and the force impulse also showed the same trends as the 30 TKR patients when compared with the ISO standard (Figure 4).

Figure 4.

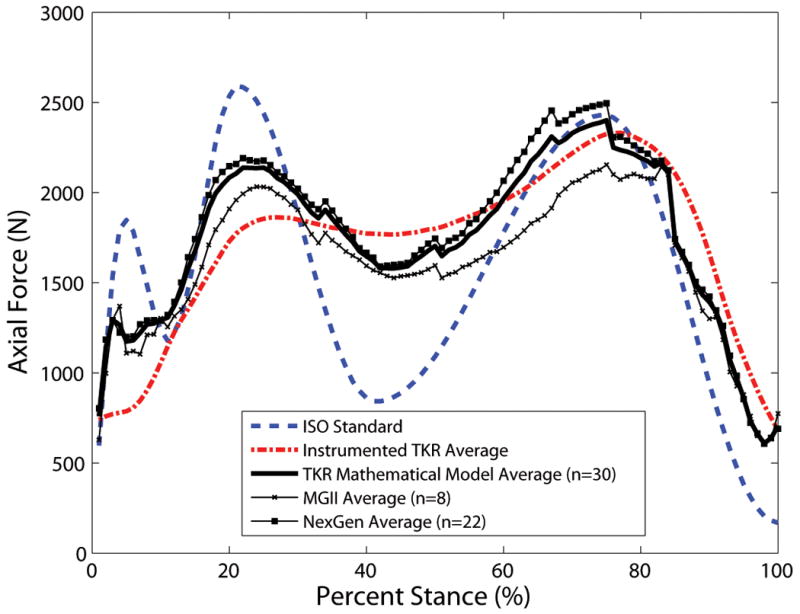
The average TKR patient axial force profile (solid lines) was similar to the mean axial force of five patients implanted with instrumented TKRs (dash dotted line). The mean instrumented axial force was derived from walking trials of five patients in the OrthoLoad database [32]. The ISO standard profile is also plotted for comparison (dashed line).

In this study the mean total axial force profiles over three level walking trials for 30 patients were compared with the ISO standard. In a previous study [17] the mean total axial force profiles from three level walking trials for four patients were compared with in vivo data from instrumented TKRs. The average difference between the instrumented and numerical global maximum axial total force was equal to -0.09 ± 0.31 body weights or 4.77 ± 11.1%. The shape of the mean total axial force profile also compared well to the in vivo data (mean coefficient of multiple correlation equal to 0.90). Hence, it is felt the approach is valid. Moreover, the force values and pattern compare very well to the telemetric data discussed above which gives further confidence into the methodology.

No statistical differences were found between the key point axial forces and timings of the NexGen and MGII TKR groups although axial force profile was lower throughout stance for the MGII TKR group than the NexGen TKR group. In addition, previous studies showed that the gait patterns of the patients with either implant type were not significantly different [8, 9]. The NexGen patients were significantly younger and had significantly shorter implant in situ times than the MGII patients. The NexGen design was introduced clinically after the MGII design, so it is not surprising that the patients enrolled in our study were younger and more recently underwent TKR surgery.

Only the stance phase of gait, and not the swing phase, is discussed in the current study. At present, our knee model is limited in calculating reliable swing phase contact forces. While the importance of swing phase load on the wear of TKR has yet to be demonstrated, it is known that loading variability during the swing phase may affect joint kinematics [33]. Thus, future studies should address swing phase loads. Because a standard axial force profile sufficient for preclinical testing should provide a reasonable description of the TKR patient population, future studies should also address axial forces for other TKR types such as cruciate substituting designs.

5 Conclusions

The differences between key points of the ISO force profile and the forces from the patient cohort showed a medium to large effect size. The combined effect of differences in compressive load and motion inputs for TKR patients and the ISO standards could explain some of the differences seen between the appearance of wear scars on retrieved tibial components compared with those tested in total joint simulators [6, 7]. This study provides axial force data for a sample of the overall TKR patient population implanted with posterior cruciate retaining and relatively unconstrained prosthesis designs. The axial force data also compared well to a different sample of patients implanted with instrumented TKRs with a more constrained design [13]. The axial force data can be used with knee joint kinematics from the same TKR patients as inputs to knee joint simulators to predict wear during level walking for cruciate-retaining TKR designs [8, 9].

Appendix

Notation

F̄	grand mean of all axial force profiles
Fmnt	axial force at time point “t” of gait trial “n” for axial force profile “m”
F̄t	average axial force profile at time point “t” during the stance phase of gait
m	index for the axial force profile (TKR, m=1; ISO, m=2)
M	total number of axial force profiles in the waveform comparison (M=2)
n	index for the gait trial number
N	total number of gait trials for waveform comparison (TKR, N=30; ISO, N=1)
t	index for time point during the stance phase of gait
T	total number time points for waveform comparison (T=100)
Radj	coefficient of multiple correlation for waveform comparison
${\text{R}}_{\text{adj}}^2$	coefficient of multiple determination for waveform comparison