Computational advances towards linking BOLD and behavior

Abstract

Traditionally, fMRI studies have focused on analyzing the mean response amplitude within a cortical area. However, the mean response is blind to many important patterns of cortical modulation, which severely limits the formulation and evaluation of linking hypotheses between neural activity, BOLD responses, and behavior. More recently, multivariate pattern classification analysis (MVPA) has been applied to fMRI data to evaluate the information content of spatially distributed activation patterns. This approach has been remarkably successful at detecting the presence of specific information in targeted brain regions, and provides an extremely flexible means of extracting that information without a precise generative model for the underlying neural activity. However, this flexibility comes at a cost: since MVPA relies on pooling information across voxels that are selective for many different stimulus attributes, it is difficult to infer how specific sub-sets of tuned neurons are modulated by an experimental manipulation. In contrast, recently developed encoding models can produce more precise estimates of feature-selective tuning functions, and can support the creation of explicit linking hypotheses between neural activity and behavior. Although these encoding models depend on strong – and often untested – assumptions about the response properties of underlying neural generators, they also provide a unique opportunity to evaluate population-level computational theories of perception and cognition that have previously been difficult to assess using either single-unit recording or conventional neuroimaging techniques.

Introduction

The field of cognitive neuroscience seeks to establish and characterize links between neural modulations and behavioral measures that index latent processes such as perception, memory, and decision making. Articulating and critically testing these linking hypotheses is far from trivial, even when neural modulations are directly measured using single-unit recording techniques (deCharms, and Zador, 2000). Sampling of individual neurons is inherently biased and caution must be exercised when generalizing beyond simple animal models, particularly when studying more abstract cognitive operations. Moreover, focusing on changes in spiking rates may not turn out to be the correct level of analysis to elucidate links between brain and behavior; perhaps lower or higher levels of analysis are more relevant (i.e. subthreshold changes in membrane potential or understanding the covariance structure of large neural populations: Cohen and Maunsell, 2009, 2010, 2011; Mitchell, and Reynolds, 2009). At the other end of the spectrum, measuring the blood oxygenation level dependent (BOLD) signal in humans using fMRI provides a non-invasive and large-scale view of cortical activation while subjects perform arbitrarily complex cognitive tasks. However, the poorly understood relationship between single-unit neural activity and the BOLD signal places a hard constraint on the specificity of linking hypotheses that can be formulated, and makes it difficult to reconcile results obtained across the two domains even when similar paradigms are employed. This failure to make mutually constraining advances stems at least in part from a general reluctance (or inability) in the neuroimaging community to explicitly state hypothesized relationships between changes in neural activity, the BOLD signal, and the cognitive state of the observer. Instead, an implicit and overly simplistic assumption has come to dominate the field: a larger BOLD response implies that a region plays a more important role in task-related information processing.

This point is not brought up to attack the utility of using fMRI as a tool for investigating links between neural activity and cognition. Instead, the general lack of stated linking hypotheses highlights the inherent limitation of available imaging technologies, and also the fact that there is no viable analysis technique that circumvents all potential shortcomings. It is becoming increasingly clear, however, that the relative paucity of fMRI studies that evaluate specific a priori hypotheses about the link between BOLD signals and behavior is a major obstacle that must be overcome if we are to start realizing the type of strong-inference that characterizes the analysis and understanding of simpler animal model circuits (e.g. Briggman & Kristan, 2008; Field, et al., 2010 for two recent examples). Following this agenda, we first provide a selective historical overview of fMRI methods that have been used over the last two decades. Then we critically discuss two complementary analysis techniques that have recently been applied to fMRI data: decoding approaches that utilize multi-voxel pattern analysis (MVPA) to infer and label stimuli or cognitive states, and complementary encoding approaches that use a priori models of neural activity to predict observed BOLD response patterns. In particular, encoding models hold promise as a means of evaluating as-yet untested ideas about the role of population codes in information processing, thus highlighting an area of inquiry for which fMRI might be well-suited to make key new discoveries. Ultimately, we argue that these new methods can be used to systematically link BOLD responses with behavior, thus placing empirical observations into a format that is more comparable with data gathered using complementary neuroscientific techniques. Although most of this review is based on studies carried out in visual cortex – primarily because so much neurophysiological data is available to constrain the interpretation of fMRI signals – the issues raised in each example should in principle generalize to other cortical areas and domains of inquiry.

Fundamental assumptions about the relationship between neural activity and the BOLD signal

The primary assumption behind all experiments seeking to understand the neural mechanisms of behavior using BOLD fMRI is that deflections in the magnitude of the BOLD signal are at least monotonically related to changes in the magnitude of underlying neural activity (Boynton, Engel, Glover, & Heeger, 1996; Heeger, Huk, Geisler, & Albrecht, 2000; Logothetis, Pauls, Augath, Trinath, & Oeltermann, 2001). However, the exact quantification of this relationship is challenging: the BOLD signal is an indirect measure of neural activity that reflects metabolic consumption and is generally thought to be most closely coupled with changes in the local field potential (LFP), suggesting a closer correspondence with increased synaptic input into a region as opposed to the spiking output (Logothetis, et al., 2001; Logothetis & Wandell, 2004b). If this account is accurate, then the locus of computation associated with a given task might be carried out in either upstream or downstream neural populations, and the output from these regions then projected into the activated ROI.

Even if we fully accept the notion that the BOLD response is driven primarily by changes in synaptic input, in some regions the majority of synaptic inputs originate from within local cortical circuits as opposed to from long-range projections (e.g. Douglas & Martin, 2007). Assuming that these local connections dominate, any measure of synaptic activity is likely to be closely coupled with spiking within that region, accounting for prior observations that the magnitude of the BOLD signal is also strongly correlated with spiking rates (Heeger, et al., 2000; Logothetis, et al., 2001; Mukamel, et al., 2005). Moreover, inhibitory activity within areas of visual cortex has been shown to decrease the magnitude of the BOLD signal, presumably by suppressing excitatory neural responses (Shmuel, Augath, Oeltermann, & Logothetis, 2006; Logothetis, 2008; Wade & Rowland, 2010).

On the other hand, at least one experiment suggests that spatially global hemodynamic responses that precede the onset of a periodic stimulus are not always correlated with changes in either LFP or spiking activity (Sirotin and Das, 2009, see also: Das & Sirotin, 2011; Handwerker & Bandettini, 2011a, 2011b; Kleinschmidt & Muller, 2010). However, this dissociation was only observed in the absence of a visual stimulus; stimulus-evoked hemodynamic activity was found to be highly correlated with changes in the LFP as well as spiking activity. Thus, the full implication of the dissociation between spiking and vascular responses provided by Sirotin and Das (2009) is not yet clear: in many instances, this dissociation may play a minimal role in influencing experimental conclusions, particularly if care is taken to remove temporal periodicity from the stimulus sequence and to remove spatially global fluctuations in the BOLD response that commonly influence all voxels.

Overall, the coupling of neural activity and the BOLD signal is likely to reflect contributions from many aspects of neural activity (e.g. synaptic activity, spiking activity, metabolic activity of glial cells supporting active neurons, etc.; Buxton, 2002). However, linking BOLD signals with changes in behavior may ultimately provide the best method for establishing fMRI as a complementary tool to other measurement modalities that have complementary strengths and weaknesses.

Univariate neuroimaging techniques

Since the advent of BOLD neuroimaging, a vast majority of studies have focused on pinpointing the anatomical loci of neural mechanisms that putatively support a particular behavior or cognitive function. This approach is very much in the neuropsychological tradition of linking focal brain damage to specific behavioral deficits, albeit using a non-invasive imaging modality applied to intact volunteer subjects. In a typical fMRI brain mapping study, two or more experimental factors are manipulated and a general linear model (GLM) is used to identify areas where the activation level associated with one task is significantly different from the activation level associated with the other(s). Ideally, the difference between the experimental conditions being compared is perfectly controlled in terms of both sensory and general cognitive demands, and only a single factor of theoretical interest is allowed to vary. Assuming that such conditions are reasonably well satisfied, the contrast between task conditions is carried out separately on the timeseries for every voxel, along with some statistical correction to account for the large number of statistical tests (often ≫ 30,000). The end result is a map of contiguous clusters of activated voxels forming a set of ROIs that are assumed to play an important role in generating behavior.

The last 20 years of research using univariate mapping techniques has produced numerous insights into the large scale networks that mediate basic cognitive functions like memory (reviewed by D’Esposito, 2007), attention (reviewed by Corbetta, Patel, & Shulman, 2008; Corbetta & Shulman, 2002; Kastner & Ungerleider, 2000; Serences and Yantis, 2006; Yantis, 2008), and decision making (reviewed by Heekeren, Marrett, & Ungerleider, 2008). Conventional univariate approaches can also provide a powerful means of dissociating cognitive operations by establishing that two experimental conditions activate distinct neural networks. Recall, for example, Brindley’s famous axiom stating that if two inputs lead to indistinguishable patterns of neural activity, then they will result in indistinguishable internal states in terms of the observer’s subjective experience (Brindley, 1960; Teller, 1984). Given the presumed functional diversity of neurons that comprise even the smallest ROI in a typical study, spatially overlapping fMRI activations should not be taken as strong evidence in support of identical neural patterns. Instead, the real strength of univariate fMRI methods lies in evaluating the inverse of this axiom: any change in the subjective state of the observer must also be accompanied by a corresponding change in the neural response produced by two inputs. Thus, even at the coarse spatial resolution afforded by fMRI, a clear dissociation in the foci of activation observed under different task conditions provides strong support for dissociable neural and cognitive mechanisms, and this is a minimum criterion for the observer distinguishing between the two inputs in a behaviorally meaningful way. Despite this ability to establish dissociations, it is also quite likely that the literature is replete with null results because the dissociation happens at a spatial scale that is impenetrable to fMRI. To some limited extent, as we review later, newer decoding and encoding techniques may help to circumvent this issue.

Limitations of univariate techniques

The main limitation of univariate methods is that different patterns of neural modulation can produce indistinguishable changes in the mean amplitude of the BOLD response, which can lead to two types of inferential error: (1) incorrectly attributing an increase in the BOLD response to a specific pattern of neural modulation, and (2) incorrectly concluding that an experimental manipulation had no influence on neural activity within a ROI. To be more concrete, consider a hypothetical experiment that measures the impact of spatial attention on neural activity in the motion selective middle-temporal (MT) area of visual cortex (see: Seidemann & Newsome, 1999; Treue & Maunsell, 1996). In this hypothetical study, two moving dot displays (or random dot kinematograms, RDKs) are presented, one on each side of fixation, and the subject has to attend to either the left stimulus or the right stimulus while maintaining central fixation. Based on single unit recording studies, we would predict that all neurons in MT with a spatial receptive field (RF) corresponding to the attended stimulus should be more active than neurons with spatial RFs located away from the attended stimulus (Boynton, 2005a; Reynolds & Heeger, 2009; Reynolds, Pasternak, & Desimone, 2000; Treue & Maunsell, 1996). Now, we can consider two models for how this increase in the activity of cells with RFs corresponding to the attended RDK might be implemented: a model where responses increase by an additive factor (Figure 1a), or a model in which responses increase by multiplicative factor (Figure 1b: note that the preponderance of data favors a hybrid of these two models with multiplicative gain dominating, but for the sake of illustration, we will present them here as competing alternatives: for more, see McAdams & Maunsell, 1999; Reynolds and Heeger, 2009). If we make the simplifying assumption that the magnitude of the BOLD signal is monotonically related to the summed neural activity within an entire ROI, then both of these models predict an increase in the BOLD signal with attention. Of course, one type of modulation might produce a slightly larger increase than the other, depending on the respective magnitude of the additive and multiplicative modulatory factors. However, without having first performed the identical experiment using single-unit recordings, there would be no principled way to distinguish these accounts based solely on the univariate measure of BOLD response amplitude measured in the ROI.

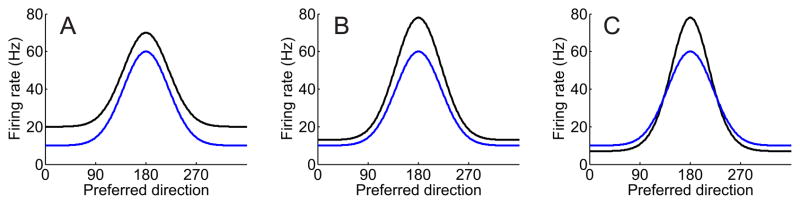
Figure 1.

Three different models of attentional modulation across a population of motion selective neurons tuned to different directions in middle temporal cortex (MT). The population response profile with attention is depicted in black, and the response profile without attention in blue. (a) model in which attention increases the response of all neurons in the population by a constant additive factor, (b) model in which attention modulates the firing rate of all neurons by a constant multiplicative gain factor, (c) model in which attention narrows the bandwidth of the population response profile by increasing the gain of neurons tuned to the attended feature, and suppressing the response of neurons tuned away from the attended feature.

Now, consider a more insidious scenario in which the subject is asked not only to deploy spatial attention to one of the two RDKs, but also to attend to the direction of motion so that they can report a brief change in direction (e.g. Martinez-Trujillo & Treue, 2004; Treue & Martinez Trujillo, 1999; Treue & Maunsell, 1999). In this situation, single-unit recording data reveal an increase in the firing rate of MT neurons that are tuned to the attended direction of motion, and a decrease in the firing rate of MT neurons tuned far away from the attended direction of motion (Figure 1c; Boynton, 2005a; Martinez-Trujillo & Treue, 2004). Under the same simplifying assumption that the BOLD response in MT is monotonically related to the summed neural activity in a ROI, a negligible change in the mean amplitude of BOLD signal should be observed with attention, as the contribution of the cells that increase their firing rates may be perfectly offset by those cells that are suppressed. As in the two models of spatial attention depicted in Figures 1a-b, the magnitude of the BOLD signal will vary depending on the exact ratio of excitation to suppression; however, univariate measures may often be blind to this type of modulation. As a result, the true nature of the underlying neural modulations – such as a narrowing of the population response profile in this case – would be obscured, despite the profound impact that such modulations have on the precision of stimulus representations in early visual areas (Kang, Shapley, & Sompolinsky, 2004; Pouget, Deneve, Ducom, & Latham, 1999; Series, Latham, & Pouget, 2004). This scenario likely generalizes far beyond the relatively orderly (or at least well-documented) realm of feature-selective tuning functions in visual cortex: any region in which there is a non-uniform modulation of firing rates across distinct neural sub-populations should be difficult to characterize or even to detect using univariate methods.

Occasionally, within the relatively limited scope of well-studied examples like the one provided in Figure 1, investigators using fMRI can gain some traction by using single-unit physiology data and computational models as additional constraints (see next section on Computational Neuroimaging). However, the problem of linking neural activity to behavior using univariate methods is greatly exacerbated when more complex tasks are used that tap into higher perceptual or cognitive mechanisms for which the neural substrates are far less informed by converging evidence from other domains (i.e. executive functions such as decision making, memory, task-switching etc). In such circumstances, univariate BOLD techniques might narrow down the number of viable hypotheses about underlying neural generators. However, a high degree of skepticism should be applied to any mechanistic claims beyond simple statements about a non-specific net increase/decrease in overall neural activity. This is not to say that such exploratory fMRI experiments aren’t worthwhile. Quite to the contrary, we argue that they are necessary to pave the way for more systematic future investigations, especially in cases where no good animal model may ever be available. We do, however, assert that advances in analysis techniques – such as the application of decoding and encoding models – are needed to move beyond general statements that focus solely on relating the mean amplitude of BOLD signals to mental operations.

Computational Neuroimaging: combining univariate approaches with quantitative models

The general approach of using quantitative models to link changes in the BOLD signal with perception and cognition was introduced by investigators such as Brian Wandell, David Heeger and others within the computational neuroimaging tradition (see Wandell, 1999 for an early review). As opposed to mapping out networks of regions using whole-brain GLM analyses, computational neuroimaging focuses on examining parametric modulations within specific brain regions for which strong BOLD/behavior linking hypotheses can be formulated based on previous psychophysics and single-unit recording studies. For example, Boynton, Demb, Glover, & Heeger (1999) measured the amplitude of the BOLD signal in primary visual cortex as a function of stimulus contrast, and were able to link the resulting BOLD contrast response function (CRF) to an analogous psychophysical measure of perceptual sensitivity within the same observers. Importantly, the same computational model that linked changes in stimulus contrast to behavioral performance also accounted for the BOLD contrast response function, thus forming a precise quantitative mapping between the BOLD signal and perception. It is impressive that models originally developed to explain single-unit data and psychophysics can also be used to account for systematic changes in the BOLD signal, as such demonstrations suggest that even though the BOLD signal is an indirect measure, it nevertheless provides a meaningful assay of neural activity. This is particularly true when investigators are able to use rigorous computational models that are grounded in quantitative psychophysics and single-unit physiology to constrain the interpretation of their results.

Furthermore, given appropriate linking propositions and experimental designs, computational neuroimaging has the potential to provide insights into information processing in the brain at a level that so far has been outside the ambit of single-unit recording. Current recording methods do not typically provide direct information about computations involving large and disparate neural populations spread across a cortical region, or about inter-region communication and synergistic computation. In contrast, though the BOLD signal lacks the spatial resolution of single-unit recording, this limitation confers an advantage in assessing large scale changes in cortical activation. Computational neuroimaging techniques exploit this advantage in a principled and rigorous manner, and thus set the stage for the development of new analysis tools that more effectively utilize fine-grained information available in the BOLD signal.

Decoding using multi-voxel pattern analysis (MVPA)

Over a decade ago now, James Haxby and his coworkers published an influential study that demonstrated how the category of an object that a subject was viewing could be decoded based on the spatially distributed activation pattern across all voxels in inferior-temporal visual cortex (a region comprised of many smaller regions such as the lateral occipital complex, fusiform gyrus, parahippocampal gyrus, and early ventral visual areas such as human V4; Haxby, et al., 2001). The insight that Haxby and his coworkers shared was that the standard approach of aggregating responses into a single univariate amplitude estimate was discarding a large amount of useful information that was contained in the multivariate pattern of activation across all voxels (Cox & Savoy, 2003; De Martino, et al., 2008; Formisano, De Martino, & Valente, 2008; Haynes & Rees, 2006; Kriegeskorte & Bandettini, 2007a, 2007b; Kriegeskorte, Goebel, & Bandettini, 2006; Norman, Polyn, Detre, & Haxby, 2006; O’Toole, et al., 2007; Pereira, Mitchell, & Botvinick, 2009). Some years later, Kamitani and Tong (Kamitani & Tong, 2005, 2006, see also: Haynes & Rees, 2005) further advanced this general idea by showing that precise inferences could be made about not just an object category but also about the specific visual feature that a subject was viewing (e.g. a specific orientation or direction of motion) based solely on activation patterns recorded from a single visual area (as opposed to the pattern across a large collection of functionally diverse visual areas, as in Haxby et al., 2001).

In general, MVPA techniques involve training a linear classifier or decoder (via a machine learning algorithm such as a Support Vector Machine, or SVM: Vapnik, 1995) to map multi-voxel activation patterns onto specific stimulus labels (e.g. faces versus houses, 45° grating versus a 135° grating orientation, etc). Given that experiments using the spatially distributed response patterns across large swaths of cortex to decode object categories or syntactic categories have been reviewed extensively in the past (see Norman et al., 2006), we focus here on the application of MVPA to decode basic stimulus features using response patterns within a single cortical area or an ROI (e.g. decoding different orientations based on activation patterns across primary visual cortex, or area V1).

MVPA techniques treat each voxel in an ROI as an independent dimension in a multidimensional space, thus the vector of BOLD responses from N voxels associated with a particular stimulus would form a point in an N dimensional space Rⁿ. Ideally, multiple responses collected from repeated presentations of the same stimulus will result in a cluster of data-points that lie close to each other in Rⁿ (Figure 3a shows a simple conception of this representation assuming only a 3 dimensional space corresponding the response pattern across 3 voxels). More generally, given a set of response vectors V_a associated with stimulus type A and another set V_b associated with stimulus type B, a linear classifier can be constructed using a support vector machine (or one of many other alternatives) that will compute a N−1 dimensional hyperplane L in the N dimensional space Rⁿ that will attempt to divide Rⁿ into two regions; one containing mostly responses associated with stimulus type A and the other containing mostly responses for stimulus type B. Given this linear classifier L, a new stimulus can be assigned to either category A or B by simply computing the side of plane L where the new data-point lies. Critically, the hyperplane L must be constructed using data that is independent of the data that is to be labeled or decoded: if this strict condition of independence is not adhered to, then the points in Rⁿ that are being labeled will influence the shape of the hyperplane L, resulting in a circular analysis that is guaranteed to produce above-chance decoding accuracy. Therefore, the first step in performing a decoding analysis using MVPA is to separate all available data into a ‘training set’ that is used to construct the hyperplane L, and an independent ‘test set’ that is used to evaluate the ability of the classifier to accurately label new data points. This process is referred to as cross-validation, and is critical for evaluating the reliability of the information contained in the spatially distributed pattern of responses across voxels (see Kriegeskorte et al., 2009).

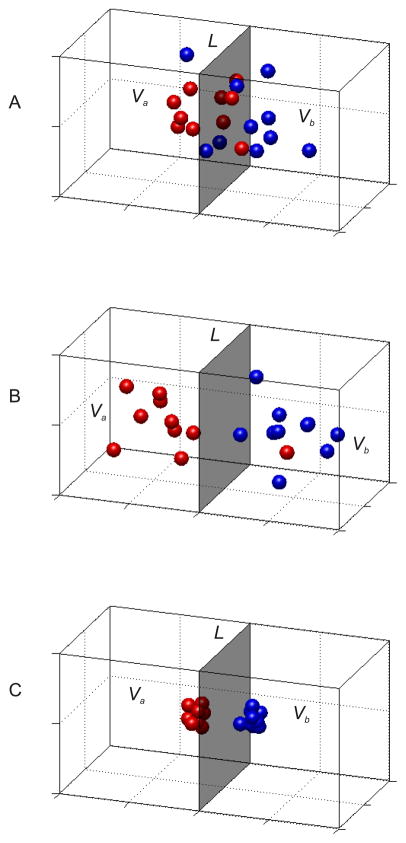
Figure 3.

(a) Each point in the 3-dimensional space represents a response vector across three hypothetical voxels in response to either stimulus A (Va, in red), or stimulus B (Vb, in blue). The grey shaded region represents a classifier plane (L) that was computed based on data from an independent training set. (b) Same as (a), but the mean distance between the cluster centers has been increased, which in turn should improve the probability of successful classification. (c) Same as in (a,b) except the variance of each cluster is smaller, which will also increase the probability of successful classification.

If no reproducible information is present, the data points in Rⁿ from the test set will be distributed randomly with respect to the hyperplane L, resulting in chance decoding accuracy. If, on the other hand, there is a reliable activation pattern associated with repeated presentations of each stimulus feature, then test data points in Rⁿ will tend to cluster with points in Rⁿ generated by the same stimulus type in the training set, and labeling these points based on hyperplane L will result in above chance accuracy. This general approach can be extended beyond the case of two stimulus classes by training multiple classifiers to discriminate one stimulus from all others and then using a max rule to assign the stimulus label based on the classifier with the highest selectivity (see discussion of Figure 5 below).

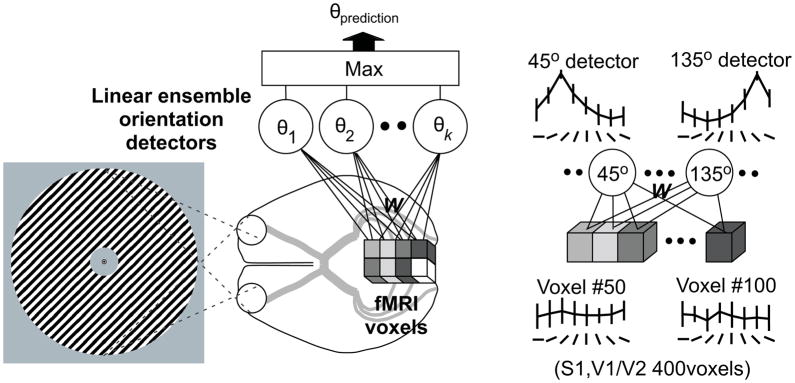
Figure 5.

(a) Each cube depicts an input fMRI activity pattern in a voxel measured while a subject viewed gratings of a given orientation. The circles represent ‘linear ensemble orientation detectors’, each of which combines the weights (W) for each voxel such that the output of each detector becomes largest for its ‘preferred orientation’ (T_i). The classifier then guesses that the subject was viewing the preferred orientation of the detector with the highest value. (b) The output from two orientation detectors (tuned to 45° and 135°, respectively) showing highly selective response profiles that are the result of the optimal pooling of information across many weakly selective voxels. Figure used with permission from F. Tong, and reprinted from Figure 1 of Kamitani and Tong (2005).

The application of MVPA to decode basic stimulus features in an ROI is usually assumed to rely on an uneven distribution of feature-selective neural populations within a voxel (Boynton, 2005b; Haynes & Rees, 2005; Kamitani & Tong, 2005; Swisher, et al., 2010). For example, if the distribution of orientation-selective columns within a given voxel in primary visual cortex (V1) is heterogeneous, then this biased distribution should give rise to a small but reliable shift in the response pattern across all voxels in response to stimuli rendered in different orientations (Figure 2a,b). If this spatially distributed response pattern varies enough as a function of the stimulus evoking the response, then relatively simple machine learning algorithms can pool the information from all voxels to decode the feature value that a subject was viewing at any given moment in time. Thus, the critical methodological advance here is simple but elegant: computing the average response across many voxels provides little feature-selective information, whereas modeling fMRI data in a multi-variate fashion permits successful decoding of specific feature values.

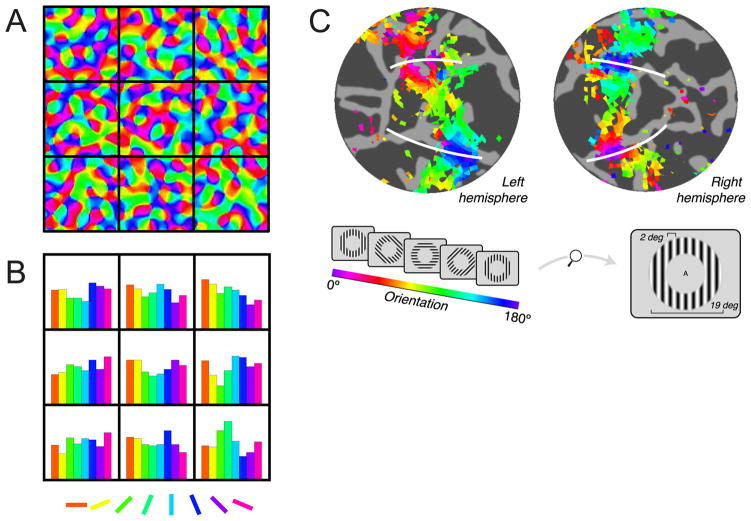
Figure 2.

(a) Synthetic orientation tuning map in primary visual cortex generated by band-pass filtering random orientation values. The black squares represent superimposed 3 × 3 mm fMRI voxels. (b) Histograms showing the distribution of orientation selectivity inside each voxel to each of the eight orientations. Aggregating the signal across many such biased voxels could potentially support orientation decoding (Panels a,b adapted with permission from G. Boynton, 2005, his Figure 1). (c) White lines depict the ventral and dorsal boundaries of human V1 (projected onto a computationally flattened cortical sheet), and each color represents areas that respond most strongly to a particular orientation (inset). The systematic orientation map across V1 – along with additional analyses – indicates that decoding might be supported by large scale feature-maps (panel c adapted with permission from J. Freeman et al., 2011, their Figure 1).

While there is little debate that MVPA methods can provide more information about subtle modulation patterns, several recent studies have challenged the notion that successful within-area decoding using MVPA is primarily driven by small biases in the within-voxel distribution of feature-selective neurons (Kamitani and Tong, 2005; Swisher et al., 2010; Boynton, 2005). One recent study reported a large-scale and systematic map of orientation across V1, and further demonstrated that this map was both necessary and sufficient for accurate decoding (Freeman, Brouwer, Heeger, & Merriam, 2011, Figure 2c). This result suggests that successful pattern-based decoding does not rely on sub-voxel anisotropies in the distribution of cortical columns, but instead on the existence of neighboring clusters of voxels that systematically differ in their orientation selectivity. Another study demonstrated that pattern classification algorithms rely heavily on feature-selective responses recorded near large draining veins (Gardner, 2010). However, the draining vein account is potentially consistent with either the sub-voxel anisotropy account or the ‘coarse map’ account, as it is not clear if the veins pool signals from like-tuned neurons that are randomly distributed or whether the veins are themselves organized into a systematic large-scale map. Finally, a recent study paradoxically found that spatially smoothing fMRI data actually improves the decoding ability of MVPA techniques, even though spatial smoothing should intuitively attenuate the precision of voxel level feature-selectivity (Op de Beeck, 2010). However, given that coarse maps contain information at both high and low spatial frequencies, this result does not clearly establish the spatial scale of information that enables MVPA. In the end, resolving these contrasting notions regarding the physiological causes underlying MVPA is certainly important; however, as long as decoding techniques can effectively distinguish between changes in perceptual or cognitive states in situations where univariate approaches would fail, MPVA offers many clear advantages.

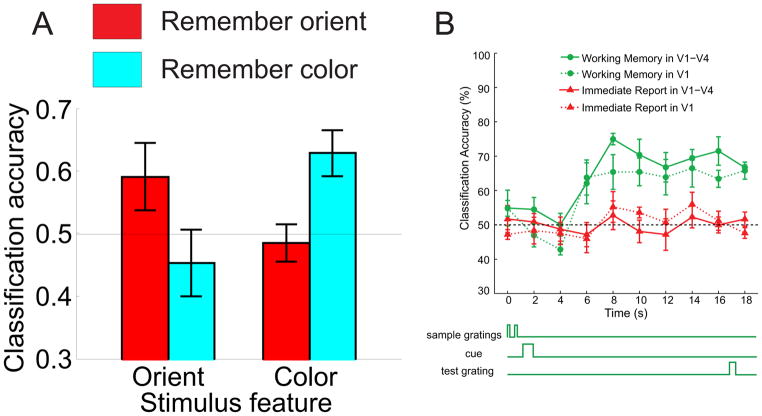
One recent set of studies that highlights the utility of MVPA focused on decoding the contents of working memory (WM) as subjects remembered basic features such as the orientation or color of a sample item across a delay period (Serences, Ester, Vogel, & Awh, 2009; Harrison & Tong, 2009). Both of these studies sought to test the ‘sensory-recruitment’ hypothesis, which states that information in WM is maintained via sustained activity in the same neural populations that encode the initial sensory input. For example, neurons in visual cortex that are responsive to a statically presented object also show a sustained increase in activity across a memory delay period, both in humans and in non-human primates (Awh & Jonides, 2001; D’Esposito, 2007; Pasternak & Greenlee, 2005; Postle, 2006). In contrast to this account, a recent investigation used univariate measures of the BOLD response to assess the role of V1 in supporting WM for basic object properties such as orientation and spatial frequency that are known to be encoded in this region (Offen, Schluppeck, & Heeger, 2009). They observed that even though overall response amplitudes in V1 increased during sustained deployments of spatial attention, activation levels during the retention interval of a WM task were indistinguishable from those observed during epochs of passive fixation. Although the observation that response amplitude fell back to baseline levels during the retention period appears to contradict the sensory-recruitment model of WM, Offen et al. (2009) noted that an area involved in WM storage may not necessarily undergo a sustained increase in the mean amplitude. For example, recall the scenario presented in Figure 1c in which feature-based attention led to the simultaneous amplification and suppression of different neural populations. Assuming that this type of feature-selective response profile supports perception (Jazayeri & Movshon, 2006; Paradiso, 1988; Pouget, Dayan, & Zemel, 2003; Sanger, 1996), the sensory recruitment hypothesis holds that a similar profile should be maintained throughout the WM delay period. However, a univariate measure of the BOLD response may not be sensitive as the contribution of neurons that are more active during the delay period may cancel out the contribution of neurons that are suppressed (Heeger & Ress, 2002; Logothetis, et al., 2001; Logothetis & Wandell, 2004a; Shmuel, et al., 2006). Thus, the lack of a sustained amplitude increase across orientation-selective neurons in V1 does not necessarily constitute evidence against the sensory-recruitment hypothesis.

Although interpreting the functional significance of changes in response magnitude can be complex in scenarios such as the one outlined above, MVPA does not rely only on a change in mean amplitude across all voxels within an ROI, but is also sensitive to changes in the spatially distributed activation pattern. Therefore, MVPA could in principle decode subtle changes in the response profile across a region such as V1 during the maintenance of information in WM. This general pattern of results was borne out: Serences et al. (2009) and Harrison and Tong (2009) failed to observe a sustained increase in amplitude in primary visual cortex during the delay period (replicating Offen et al, 2009), even though MVPA revealed that V1 maintained stimulus-specific representations during the same temporal interval (Figures 4a,b; see also Ester, Serences, & Awh, 2009). Moreover, MVPA revealed that WM does not recruit all sensory neurons that are active upon the presentation of the sample item, but only those populations that selectively encode relevant aspects of a multi-featured object (Serences, Ester, et al., 2009). These two experiments thus provide a case study in which MVPA revealed insights into the representational basis of a cognitive operation (WM) that may have been missed using traditional univariate approaches.

Figure 4.

(a) Subjects were instructed to remember either the orientation or the color of a sample stimulus, and then to retain only this relevant information across a 10s delay period. Bar-graph depicts classification accuracy (using the mean response across the delay period as input to the classifier) as a function of the stimulus feature (color or orientation) being classified and whether the subject was instructed to remember orientation or color during the scan used as the basis for classification. The horizontal lines highlight the level of chance performance. Classification accuracy was only significantly higher than chance for the relevant feature that the subject was instructed to remember. (b) Timecourse (see schematic) of classification accuracy in a study where subjects either had to remember the orientation of a stimulus across a delay period, or they had to perform an immediate report control task (i.e. a task with no WM requirements). These data show significant memory related classification in both V1 and across other early visual areas V1-V4 when the data were combined. Panel (a) used with permission from Serences et al. (2009), their Figure 3a, and panel (b) used with permission from F. Tong, adapted from Harrison and Tong (2009), their Figure S5.

In addition to simply labeling stimulus or task categories based on observed patterns of activation, decoding approaches can also be used to reconstruct a representation of the physical stimulus set presented during an experiment. Miyawaki, et al. (2008) trained a classifier to identify contrast intensities at multiple points in a 10×10 binary image array, and then used the weights assigned to each voxel to reconstruct a literal representation of the image the subject was viewing during a separate test phase (see also: Ganesh, Burdet, Haruno, & Kawato, 2008; Naselaris, Prenger, Kay, Oliver, & Gallant, 2009 for similar experiemnts on stimulus ‘reconstruction’ using different methodological approaches). This ability to accurately reconstruct internal representations of a stimulus is an exciting application of MVPA and related decoding techniques and holds great promise for clinical applications such as restoring sight and creating effective neural prostheses for people with limited mobility (see: Andersen, Hwang, & Mulliken, 2010; Haynes, 2009; Hochberg, et al., 2006; Weil & Rees, 2010).

Limitations of MVPA

Although MVPA is an elegant tool that is flexible enough for a wide range of experimental designs and research questions, this flexibility reduces the precision of the inferences that can be supported. The foremost issue is that an observation of increased classification accuracy does not clearly reveal how or why that increase occurred. For instance, the hypothetical observation that selective attention increases classification accuracy for decoding 45° from 135° oriented stimuli could arise in many different ways. It could mean that the centers of the activation cluster move farther away from the classifying plane L (see Figure 3b). Alternatively, spatial attention might decrease the variability of population responses so that activation clusters become more tightly grouped (Figure 3c). Any mixture of these two contributing factors would give rise to an increase in classification accuracy. Thus, an increase in classification accuracy only demonstrates that the representations became more separable; we learn nothing directly about what underlying neural changes gave rise to the increased separability. Although typically not reported, this issue can sometimes be addressed by computing additional metrics such as the variance (covariance) of the clusters and the mean distance between clusters, particularly when the number of classes is relatively small. When possible, such measurements may reveal important additional insights about how a manipulation impacted the representation of information in a ROI, thus heightening the inferential power of MVPA.

While such additional steps can be often be taken to determine why a classifier performed better in one scenario compared to another, a more subtle variant of the this issue can arise if seeking an even deeper understanding of the link between classifier performance and specific patterns of neural modulation. For example, the data shown in Figure 1b of Kamitani and Tong (2005; our Figure 5b) resembles a response profile that was recorded across a set of feature-selective neural populations, much as expected from a population of orientation selective cells in V1 whose responses have been sorted based on the preferred feature of each neuron (i.e. a population response profile, as shown in Figures 1a–c). However, the data in Figure 5b depict the output of a ‘linear ensemble orientation detector’ that was generated using a SVM to assign a weight to each voxel so as to maximize the response of each detector to its preferred feature value. Each detector pools the weighted activity across all voxels in a visual area to derive a response function that indicates the probability that the preferred orientation is present (as shown in Figure 5b, which demonstrates the output of a detector optimized for 45° stimuli). The classifier then ‘guesses’ that the observer is viewing the orientation associated with the maximally active detector. Thus, the MVPA approach estimates the stimulus label based on a weighted sum of input values across every voxel in the ROI, which is optimal in a statistical sense because it makes use of all the available information. On the other hand, the same optimal process of aggregating inputs from all voxels prevents direct inferences about how the tuning profiles of the underlying voxels (and by inference the tuning characteristics of different neural populations) are modulated. Thus, MVPA approaches are an extremely powerful tool for determining if there is a difference between activation patterns evoked by experimental conditions. However, the reliance on a weighted pooling of information across many voxels obscures information about exactly how the pattern of underlying neural activity changes as a function of task demands.

This distinction is very important when seeking to answer many questions in computational neuroscience. For example, again consider the situations outlined in Figures 1a–c, where three different patterns of attentional modulation are depicted. Using MVPA, you might see that different stimulus features – in this case different orientations – were more easily classifiable with attention compared to without attention [this is almost certainly true in the right two panels showing multiplicative gain and bandwidth reduction, and possible in the left panel showing an additive modulation, but only given specific assumptions about neural/BOLD noise distributions, see e.g. (Saproo & Serences, 2010)]. However, one would not be able to distinguish which of these three types of attentional modulation was occurring based solely on the observation of increased classification accuracy. In the next section we describe approaches that directly model the response profile across tuned populations of underlying neurons. In cases where generating such models is tenable, they may be able to help investigators understand how an experimental manipulation influences specific subpopulations of neurons, which is critical for testing theoretical accounts of how cortical circuits carry out complex computations.

Encoding models of BOLD responses

In contrast to the decoding approach employed by MVPA studies, forward encoding models take the opposite approach by adopting a set of a priori assumptions about the important features or stimulus labels that can be distinguished using hemodynamic signals within an ROI (Dumoulin & Wandell, 2008; Gourtzelidis, et al., 2005; Kay & Gallant, 2009; Kay, Naselaris, Prenger, & Gallant, 2008; Mitchell, et al., 2008; Naselaris, et al., 2009; Schonwiesner & Zatorre, 2009; Thirion, et al., 2006; reviewed in Naselaris, et al., 2011). The features or labels in the model are then used to predict the pattern of BOLD responses (whereas decoding approaches try to infer these labels based on observed patterns of activity). In this basic sense, most traditional univariate analysis approaches to fMRI use simple encoding models where a GLM is used to estimate the mapping between a set of stimulus or task conditions and the amplitude of the response in each voxel. More recently encoding models have been extended to encompass far more complex descriptions of stimulus space that are typically guided and constrained by existing neurophysiological data (e.g. Carandini, et al., 2005; David & Gallant, 2005; Ringach, Hawken, & Shapley, 1997; Theunissen, Sen, & Doupe, 2000; Wu, David, & Gallant, 2006). For example, Kay et al. (2008) used a mosaic of phase-shifted Gabor filters (these were the features or labels in the model) rendered in different orientations and spatial frequencies to predict the responses of voxels in visual cortex to images of natural scenes. The set of features used to model BOLD activation is typically referred to as a basis set, and in this instance the encoding model was grounded by the known properties of single neurons in these early visual areas (Carandini, et al., 2005). A weight was then assigned to each Gabor filter so as to best account for the response of each voxel to a large set of natural images. After estimating the weight that maps each Gabor filter to the stimulus set, they showed subjects a set of novel images and were able to predict the exact stimulus that the subject viewed with extremely high accuracy based on the output pattern of their encoding model (see also: Naselaris, et al., 2009).

This example highlights one major advantage of encoding models over their complementary decoding counterparts: researchers can test one or more very specific models of an underlying neural architecture to determine which basis set best accounts for the observed data and, more importantly, which basis set best generalizes beyond the training data to accurately characterize novel inputs. This is a major conceptual advance, as until recently, evaluating specific implementations of neural models was not commonly carried out in human neuroimaging work. Finally, these encoding model approaches have the distinct and important advantage that they make explicit the set of assumptions that are used to link neural activity to changes in the BOLD response. While being explicit by no means ensures that a given model is correct, it does ensure that (1) the model is unambiguously stated in mathematical terms, and (2) that it is more likely to be testable, a feature lacking in many prior fMRI investigations.

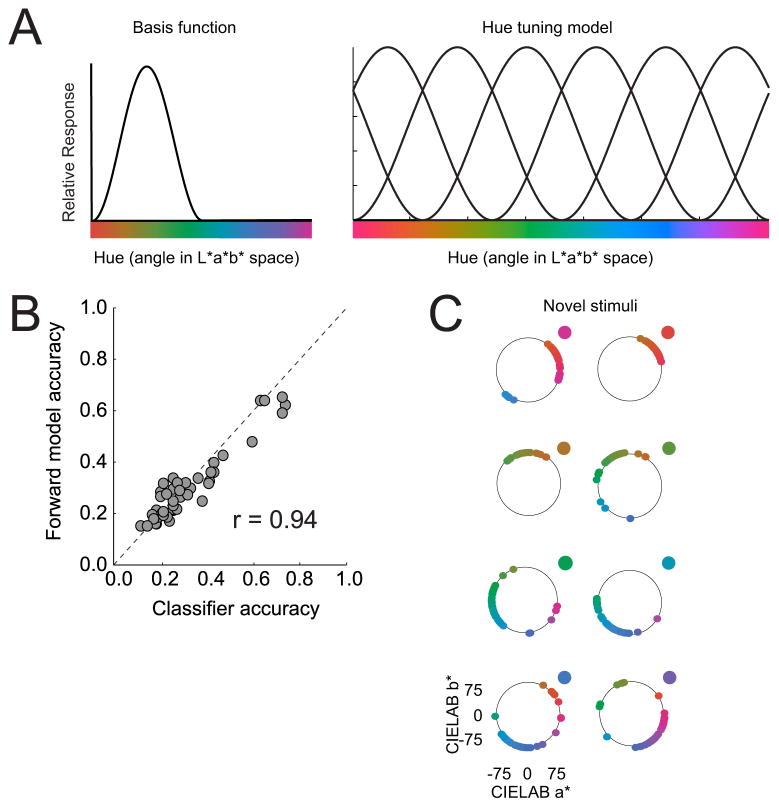
To illustrate the utility of this approach, we focus on a recent report that used a relatively simple basis set to evaluate the response of different color selective neural populations, or ‘color channels’ in V1, V2, V3, V4 and VO1 (Brouwer & Heeger, 2009). The encoding model approach described here is based on the same principles that are thought to support within-area MVPA, and thus can operate if there is a measurable feature-selective bias either within voxels or across an ROI (Boynton, 2005b; Freeman, et al., 2011; Kamitani & Tong, 2005). However, instead of using MVPA to predict the most likely color that a subject viewed on each trial, Brouwer and Heeger (2009) instead determined the response magnitude in each of six hypothetical color channels (see Figure 6) that best accounts for the observed fluctuations in the BOLD signal.

Figure 6.

(a) Graphic depiction of forward encoding model used by Brouwer and Heeger (2009). The response of each voxel is modeled as the sum of weighted responses across six hypothetical color channels, where each color channel is modeled as a half-wave rectified and squared sinusoidal function. See text for more details. Panel (a) reprinted with permission from Brouwer and Heeger (2009). (b) The decoding accuracy using forward model channel responses was virtually equivalent to that obtained using a standard MVPA classifier. (c) Most importantly, however, the encoding model presented in (a) could even reconstruct color stimuli that were not part of the training set. Each point of color on the circle represents a reconstructed color for one run where the novel color was the color dot outside the circle.

To perform this analysis, Brouwer and Heeger (2009) first split the data into two sets (training and test sets), just as is done in a typical decoding study. Adopting their terminology and formulations, let m be the number of voxels in a given visual area, n₁ be the number of observations (trials) in the training set, n₂ be the number of trials in the test set, and k be the number of hypothetical color channels, which taken together covered the entire CIE hue spectrum,. Let B₁ (m x n₁ matrix) be the training set, and B₂ (m x n₂ matrix) be the test set. The weight (W, m x k) assigned to each color channel was computed based on data from the training set using a linear model of the form:

$$B_1={WC}_1.$$ (1)

where the ordinary least-squares estimate of W is computed as:

$$\widehat{W}=B_1{C}_1^T{(C_1{C}_1^T)}^{-1}.$$ (2)

The channel responses (C₂ k x n₂) were then estimated for the test data (B₂) using the weights estimated in (2):

$$\widehat{C_2}={(\widehat{W^T}\widehat{W})}^{-1}\widehat{W^T}{B}_2.$$ (3)

Note that the first steps in this computation (eq. 1–2) are akin to a traditional univariate GLM in which each voxel gets a weight for each of several features or stimulus labels (in this case, one weight for each color channel). However, eq. 3 implements a multivariate computation because the channel responses estimated on each trial (in C₂) are constrained by the estimated weights assigned to each voxel and by the vector of responses observed across all voxels on a given trial in the test set. Thus, one key feature of this approach is that a set of estimated channel responses can be obtained on a trial-by-trial basis as so long as the number of voxels is greater than the number of channels. If there are fewer voxels than channels, then unique channel response estimates cannot be derived as the number of variables being estimated exceeds the number of available measurements.

Using this formulation, Brouwer & Heeger (2009) demonstrated that the vector of channel responses was precise enough to support above chance decoding accuracy in many visual areas, and that this performance matched that of a standard linear discriminant MVPA classifier (Figure 6b). More importantly, their forward model was able to reconstruct novel color stimuli that were not part of the training set, thereby validating the underlying model in a way that simple linear classifiers cannot (see figure 6c). In a subsequent study, Brouwer and Heeger (2010) used a similar forward model to study orientation selective response profiles in V1 and were able to accurately characterize responses to complex combinations of superimposed oriented gratings (i.e. ‘plaids’) based on a model trained using pure oriented gratings.

If at least some of the assumptions described above about the coupling of neural activity and the BOLD response are accepted, this method may provide a critical tool for evaluating competing theoretical models of how various cognitive factors influence neural activity in early sensory cortices. For instance, by examining the average pattern of direction-selective channel responses in a hypothetical space- or feature-based attention experiment, it should be possible to distinguish the three models of modulation shown in Figures 1a–c. In addition, the fact that channel responses can be estimated on a trial-by-trial basis also opens the door to more complex analyses such as evaluating the predictive relationship between channel responses and behavioral performance on a trial-by-trial basis using either logistic regression (in the case of task accuracy) or simple correlation (in the case of reaction time).

Alternatively, more sophisticated metrics, such as those derived from information theory, can be applied to trial-by-trial channel responses. The field of information theory concerns itself with the quantitative evaluation of the quality of different codes and with the development of optimal codes that maximize information transfer over noisy channels (Shannon, 1948). There is growing evidence that populations of neurons communicate via neural codes, and the communication medium between neural populations emulates a noisy channel (Doya, Ishii, Pouget, & Rao, 2007; Rieke, Warland, de Ruyter van Steveninck, & Bialek, 1999). Therefore, information theory is an important tool to evaluate the efficacy of neural coding, and in turn to generate and test models of various sensory and perceptual phenomena. For instance, mutual information (MI) evaluates the coupling between two variables without making assumptions about the order of the correlation or the underlying response distributions, and can be used to index the relationship between channel responses and stimulus features, channel responses and behavior, or channel responses across multiple cortical regions that are thought to synergistically encode sensory information (Chai, Walther, Beck, & Fei-Fei, 2009; Saproo & Serences, 2011). These types of information-based metrics, coupled with the ability to estimate the response of feature-selective channels on a trial-by-trial basis, may prove to be an invaluable future tool in evaluating theoretical principles of sensory encoding that are currently difficult to test using standard single-unit recording techniques.

Limitations of encoding models and comparison with decoding approaches

The main challenge of the encoding approach lies in generating a model that accurately characterizes neural activity within a ROI, particularly when examining higher cognitive functions that have not been subjected to intense psychophysical or single-unit physiology studies. However, the general approach provides a technique for developing multiple models – even in the absence of prior neurophysiological data as a guide – and then testing these models in at least two ways. The most intuitive first-pass test is to determine how much variance in the dependent measure (the BOLD response) is captured by the model. If the basis functions have no meaningful relationship to the true generative mechanism that created the data, then the fit of the model will be poor. Maximizing basic metrics that reflect goodness-of-fit is therefore a reasonable first step in optimizing the general form of the basis functions in the encoding model. Second, in order to evaluate inferential power, the parameter estimates associated with an encoding model should be used to characterize or label novel stimuli that were not part of the training set (as in Kay et al., 2008; Brouwer and Heeger, 2009). In turn, adjusting the model to maximize generalizability is another form of optimization that can be used to identify the best model that fully characterizes the functional properties of a given ROI (see also: Naselaris, et al., 2011). Encoding models can thus be applied to experimental domains that are constrained by existing physiological observations, as well as to more adventurous domains where existing data is sparse and the studies are completely exploratory in nature. Of course, during this process of iteratively testing and generating new models, care must be taken to avoid circularity. In addition, given the speculative mapping between neural activity and the BOLD response, any deviations away from extant models that are grounded in neurophysiology must be carefully evaluated using other methods. The use of encoding models does however form a principled method for developing new hypotheses about the functional characteristics of a ROI and for inspiring additional studies that will be mutually constraining.

Given the strong a priori assumptions that are involved in generating and evaluating an encoding model, this approach is also generally not very powerful when performing whole-brain exploratory analyses, because it is highly unlikely that one basis set would accurately capture the functional role of more than a few cortical regions. Instead, a more efficient approach might be to use MVPA as an initial tool for exploratory analysis, as it is ideally suited for this purpose precisely because no assumptions are made about the specific relationship between underlying neural activity and BOLD responses in a ROI (so long as there is some relationship). This type of exploratory MVPA has gained prominence in recent years (see Esterman, Chiu, Tamber-Rosenau, & Yantis, 2009; Kriegeskorte & Bandettini, 2007a; Kriegeskorte, et al., 2006; Serences & Boynton, 2007; Soon, Brass, Heinze, & Haynes, 2008 for some recent examples). Furthermore, the proportion of information carried by different ROIs can be estimated by computing the decrease in classification accuracy when a given ROI is removed and not allowed to contribute to training/testing the classifier, thus providing a metric that quantifies the relative importance of different nodes in a functional network (see e.g.: Hampton, Bossaerts, & O’Doherty, 2006; Pessoa & Padmala, 2007). In turn, once a region has been identified as carrying some type of important information about an experimental manipulation using MVPA, encoding models can be developed and used to evaluate a plethora of feasible generative neural models that might underlie the computational architecture of a given ROI. In this way, decoding and encoding approaches can be used in a complementary manner to first identify and then to characterize the specific contribution of nodes in a distributed network so as to better support linking propositions between BOLD responses and behavior.

Concluding remarks

Beginning with the advent of computational neuroimaging in the late 1990’s, a great deal of progress has been made with respect to testing quantitative models of perception and cognition using non-invasive methods such as fMRI. The recent explosion of MVPA and forward encoding approaches holds great promise, as these new tools have the potential to more precisely evaluate the information content of single ROIs as well as large-scale networks, and to refine our understanding of how the computational units within these networks interact to support cognition. These decoding and encoding techniques are complementary rather than competing: decoding models provide a more flexible method for establishing the presence of task-related information and for identifying important cortical regions, and encoding models provide a hypothesis-driven approach that is capable, in principle, of completely characterizing the functional significance of a ROI (Naselaris, et al., 2011). This coupling of analysis techniques may thus provide a means of exploiting the whole-brain scanning capability of fMRI while simultaneously enabling the application of strong-inference based model testing.