Ultrasound Attenuation Measurements using a Reference Phantom with a Sound Speed Mismatch

Abstract

Ultrasonic attenuation may be measured accurately with clinical systems and array transducers by using reference phantom methods (RPM) to account for diffraction and other system dependencies on echo signals. Assumptions with the RPM are that the speeds of sound in the sample (c_sam) and in the reference medium (c_ref) are the same and that they match the speed assumed in the system beamformer (c_bf). This work assesses the accuracy of attenuation measurements by the RPM when these assumptions are not met. Attenuation was measured for two homogeneous phantoms, one with a speed of sound of 1500m/s and the other with a sound speed of 1580m/s. Both have an attenuation coefficient approximately equal to that of the reference, in which the speed of sound is 1540m/s. Echo signals from the samples and the reference were acquired from a Siemens S2000 scanner with a 9L4 linear array transducer. Separate acquisitions were obtained with c_bf at its default value of 1540m/s, and when it was set at values matching the speeds of sound of the phantoms. Simulations were also performed using conditions matching those of the experiment. RPM measured attenuation coefficients exhibited spatially-dependent biases when c_sam differed from c_bf and c_ref. Mean errors of 19% were seen for simulated data, with the maximum errors in attenuation measurements occurring for regions of interest near the transmit focus. Biases were minimized (mean error with simulated data was 5.6%) using c_bf that matched c_sam, and assuring that power spectra used for attenuation computations in the sample are from precisely the same depth as those from the reference. Setting the transmit focus well beyond the depth range used to compute attenuation values minimized the bias.

I. INTRODUCTION

Ultrasound is widely recognized as a convenient and efficient diagnostic tool. B-mode ultrasound imaging primarily displays tissue characteristics by intensity modulating the display according to the amplitudes of echo signals. However, brightness contrast on B-mode images also depends on system settings and operator controls. Thus tissue characteristics presented in conventional ultrasound B-mode images are interpreted relatively and subjectively.

Quantitative ultrasound has been introduced to supplement these qualitative evaluations by providing absolute and objective measurements of tissue characteristics. For example, attenuation levels of tissues are judged qualitatively on B-mode images by their degree of shadowing or on the basis of penetration depth. When measured quantitatively, attenuation has shown potential to characterize the degree of diffuse disease and remove some of the subjectivity when describing focal lesions. Measurements of ultrasound attenuation have been used to differentiate fatty liver from normal liver^1,2,3 and benign tumors from malignant ones⁴ in the liver. Other researchers have suggested that ultrasound attenuation has diagnostic value in bone disease,^5,6 in predicting the condition of the cervix during pregnancy,⁷ and in differential diagnosis of breast masses.^8,9 Attenuation values have also been utilized to detect and characterize thermal lesions in ablation therapy.¹⁰

Attenuation can be estimated from echo data derived from clinical ultrasound systems that provide unprocessed, radiofrequency (RF) echo signals.^11,12 To do so, however, system dependent factors affecting the echo signal, such as frequency dependent sensitivity of the transducer-pulser-receiver system and beam focusing patterns must be accounted for. Use of a reference phantom is a straightforward way to eliminate these system dependent factors. With the reference phantom method¹³ (RPM), one computes the ratio of echo signal power spectra from the tissue to power spectra derived at the same depth from a well-characterized reference medium. The slope of the power spectra ratio as a function of depth yields the attenuation coefficient of the tissue. The RPM provides accurate attenuation values over homogeneous tissue regions,¹⁴ and it has been utilized successfully to measure attenuation in human liver with fatty infiltration or with cirrhosis,^15,16 and to monitor changes in canine livers resulting from glucocorticoid administration.¹⁶

Accounting for diffraction effects on the echo signal with the RPM requires that the speed of sound in the reference media (c_ref), must be approximately the same as that of the sample (c_sam).¹³ Exact guidelines for how close the sound speeds need to be were not presented by Yao.¹³ However, Tu¹⁷ reported that a difference in speeds of sound of 2.1% resulted in substantial artifacts on attenuation coefficient images computed using the RPM with an array transducer. Chen¹⁸ studied degradation of resolution in phantoms whose sound speeds differed from that used in the beamformer (c_bf) of an array system. Although Chen directed his work towards spatial resolution considerations, his simulations point to mismatches in focal patterns when transmitting into media having different sound speeds, and the mismatches could lead to artifacts when applying the RPM for determining attenuation. Omari et al.¹⁹ report that a hybrid technique for estimating attenuation, normalizing the echo signal power spectra from a region of interest (ROI) to the power spectrum from a reference phantom and then evaluating changes in the center frequency with depth, may be less prone to errors than the RPM when there are sound speed differences between the tissue and reference media. Omari et al.¹⁹ did not study depth dependencies of attenuation estimates, one of the problems vividly brought out by Tu’s¹⁷ work.

The goal of this paper is to investigate effects of sound speed mismatches on attenuation estimates done using the RPM. Emphasis is given to results at different distances from the transducer as well as with different transmit focal depths. The work is applied to array transducers with electronic beamforming. We evaluate results for tissue mimicking phantoms in which the sound speed is lower or higher than that of the reference phantom. Possible improvements in estimation accuracy are considered for cases in which the sound speed used in the system beamformer matches that of the media scanned and where steps are taken to precisely match depths in the reference and sample from which power spectra are computed and compared. Both experimental and simulation results are presented.

II. METHODS

Reference phantom method

For the convenience of the reader, a brief review of the RPM for estimating attenuation and backscatter levels is provided. Assuming the Born approximation, Yao et al.¹³ have shown that for uniform samples, the ratio of the echo signal power spectra from a sample to that from a reference medium can be described as:

$$\frac{S_{sam}(f,z)}{S_{ref}(f,z)}=\frac{G_{sam}(f,z)D_{sam}(f,z)}{G_{ref}(f,z)D_{ref}(f,z)}\frac{BS{C}_{sam}\left(f\right)\text{exp}(-4{\alpha }_{sam}\left(f\right)z)}{BS{C}_{ref}\left(f\right)\text{exp}(-4{\alpha }_{ref}\left(f\right)z)}$$ (1)

where f denotes frequency and z represents the depth of the ROI. S(f,z) is the power spectrum of the backscattered echo signal. The subscripts sam and ref denote the sample and reference medium respectively. G(f,z) represents the signal transduction and processing in the system. D(f,z) accounts for diffraction effects. BSC(f) represents the backscatter coefficient in the medium and exp(-4α(f)z) represents the total attenuation between the transducer surface and the depth of interest, and α(f) is the attenuation coefficient in the medium. Power spectra typically are computed by averaging periodograms within windowed regions whose axial extent might be, say 4mm. It is assumed that any differences in attenuation between the sample and reference phantom over these short signal segments do not affect computations of acoustic properties.

There are three depth-dependent parameters in Eq. (1): G(f,z), D(f,z), and exp(-4α(f)z). The RPM makes two additional assumptions related to these parameters: (a) the sound speed within the reference medium is approximately the same as that of the sample; and (b) for array systems, the sound speed used in the system’s beamformer is the same as that of the sample and reference medium. With these two assumptions, Eq. (1) can be simplified to:

$$\frac{S_{sam}(f,z)}{S_{ref}(f,z)}=\frac{BS{C}_{sam}\left(f\right)}{BS{C}_{ref}\left(f\right)}\text{exp}(-4({\alpha }_{sam}\left(f\right)-{\alpha }_{ref}\left(f\right))z)$$ (2)

For an ROI with constant backscatter properties, the RPM estimates the attenuation of the sample using:

$${\alpha }_{sam}\left(f\right)=-\frac{\text{ln}\left(\frac{S_{sam}(f,z)}{S_{ref}(f,z)}\right){\mid }_{z2}-\text{ln}\left(\frac{S_{sam}(f,z)}{S_{ref}(f,z)}\right){\mid }_{z1}}{4(z_2-z_1)}+{\alpha }_{ref}\left(f\right)$$ (3)

where z₂ and z₁ are depths in the ROI and z₂>z₁.

Experimental phantoms

Three tissue-mimicking homogeneous phantoms with different sound speeds were utilized. The phantoms consist of 15cm × 5cm × 15cm water-based agarose gel media housed in rectangular 9mm thick acrylic boxes. One 5cm × 15cm surface on each phantom is bounded with a 25μm thick Saran-Wrap® (Dow Chemical, Midland MI, USA) scanning window. The phantoms were made with 5-43μm diameter glass bead scatterers spatially randomly distributed in the gel, at a concentration of about 400 beads/mm³. In constructing the phantoms, molten agar was prepared by mixing dry agarose powder into an n-propanol water mixture, where the n-propanol concentration was chosen to provide sound speed values of approximately 1500m/s, 1540m/s, and 1580m/s in the different phantoms. Graphite powder (32g per liter of molten gel) was added to provide approximately 0.5dB/cm-MHz ultrasound attenuation in each phantom. Phantoms were rotated at 1rpm during congealing to prevent gravitational settling of particles.

The acoustic properties of the phantoms were measured using 2.5cm thick, 7.6cm diameter test samples produced at the time of construction of each phantom. Four pairs of unfocused single element transducers were used to span the 2.5-10MHz frequency range, and a narrowband substitution method²⁰ was applied for both attenuation and sound speed measurements. Sound speed values were determined only at 2.5MHz since dispersion (over the analysis frequency range) is negligible in these materials. Attenuation coefficients were fit to a power law of the form α(f) = α_o fⁿ where α_o and n are constants; resulting values for α_o and n are shown in table 1. Measured speeds of sound also are presented in table 1. The slope of attenuation coefficient vs. frequency are shown at 5MHz, the approximate center frequency of echo signal power spectra obtained over the ROIs in the samples and reference phantom.

Table 1.

Sound speed and attenuation measurements of three phantoms

	1500m/s Phantom	1540m/s Phantom	1580m/s Phantom
Sound speed	1499m/s	1539m/s	1581m/s
α o	0.433dB/cm	0.491dB/cm	0.524dB/cm
n	1.179	1.114	1.085
Slope of Attenuation Coefficient vs. Frequency at 5MHz	0.559dB/cm-MHz	0.573dB/cm-MHz	0.591dB/cm-MHz

Clinical scanner data collection

RF echo data were collected using a Siemens Acuson S2000 system (Siemens Medical Solutions USA, Inc., Malvern, PA) with a 9L4, 192 element linear array transducer driven at a center frequency of 6MHz. The Axius Direct ultrasound research interface on the system was used to acquire frames of RF echo data at a 40MHz sampling frequency.¹² Each frame consisted of signals from 456 acoustic beam lines. Ten frames were acquired from each phantom, each representing data from an 8.5cm (axial) by 3.8cm (lateral) field of view, with an elevational translation or a rotation of the transducer between each frame to obtain statistically independent echo data. However the scan window of the phantoms was quite narrow (5cm) so the ten frames of RF data recorded during each experiment may have been partially correlated. The same control settings, including time-gain compensation, overall gain, and transmit focal distance were used for each phantom. Separate experiments were done with transmit focal distances of 2cm, 3cm, 4cm, 5cm, and 7cm, in each experiment recording both sample and reference phantom data using the same control settings. The research interface allowed the sound speed assumed in the beamformer to be varied from the default value of 1540m/s. Data from the 1500m/s and 1580m/s phantoms were recorded setting the beamformer sound speed either at 1540m/s or equal to the sound speed of the scanned phantom.

For comparison, the experimental conditions were simulated using a frequency domain B-mode imaging model developed in our laboratory.²¹ The computational model assumes a spatially random distribution of scatterers within a medium of specified attenuation coefficient and sound speed. The program incorporates transmit focusing and dynamic receive beamforming with any desired sound speed.¹⁸ Three homogeneous numerical phantoms with attenuation coefficients and sound speeds matching those of the physical phantoms were simulated. Each numerical phantom contained scatterers at a concentration of 10 scatterers/mm³ and each of these simulated phantoms had a backscatter coefficient equal to 2×10⁻⁶f³ cm⁻¹sr⁻¹, where f is the frequency in MHz. The numerical phantoms were 8cm (axial) by 4cm (lateral) by 1cm (elevational). Sound speeds of the numerical phantoms were set to 1500m/s, 1540m/s, and 1580m/s, which were within one standard deviation of measured values of sound speeds of the physical phantoms.

To enable close comparison between simulation and experiment, the measured attenuation values at 5MHz shown in table 1 were applied to the simulated phantoms. The simulated transducer mimicked a Siemens 9L4 linear array transducer. This probe has 192 elements whose sizes are 0.18mm (lateral) by 10mm (elevational) with a center to center element spacing of 0.2mm. Using the simulated phantoms, a single frame of RF echo data for 200 closely spaced acoustic beam lines was generated over the 8cm by 4cm region that was simulated. The aperture of the transducer was adjusted to keep a constant F-number of 2 during dynamic receive focusing. Although the clinical array transducer in the experiment has a mechanical lens providing a fixed elevational focus, the simulated transducer did not use elevational focusing. A Gaussian-shaped pulse with a center frequency of 6MHz and a 70% bandwidth was assumed in the model.

Four data acquisition and analysis cases

Experimentally, the 1500m/s and the 1580m/s phantoms were used as “samples” while the 1540m/s phantom served as the reference. RPM attenuation estimations were studied for four conditions, or cases, as described in table 2.

Table 2.

Four data acquisition and analysis cases by the variations of the beamformer sound speed, c_bf, and the depth calculation sound speed c_z

Case	Beamformer sound speed, cbf	Depth calculation sound speed, cz
Case I	1540m/s	1540m/s
Case II	1540m/s	Uses each phantom’s sound speed
Case III	Match to each phantom’s sound speed	1540m/s
Case IV	Match to each phantom’s sound speed	Uses each phantom’s sound speed

Attenuation estimation

A ROI extending from 1-6cm axially and 1-3cm in width was selected from the simulated data. The near field data from the experiment suffered from ring-down and other artifacts associated with the transducer-to-phantom surface, so the ROI in the experimental data was restricted to 1.5-6cm (0.5cm shorter than the ROI used in simulations). Except for this minor adjustment, the simulated data closely mimicked the experiment.

Power spectra in the sample and reference were calculated using Welch’s method.²² In this method, a segment of data spanning a depth of several millimeters axially and several A-lines laterally are processed by first applying a Hann gating window axially to the RF data, computing the Chirp Z transform,²³ and then averaging laterally to produce the echo signal power spectrum over the specific “analysis window.” This process is repeated on multiple, overlapping data segments over the entire ROI. The size of the power spectrum analysis windows used was 4mm (axially, 5.19μs duration using 1540m/s) by 4mm (laterally, 48 acoustic scan lines for experimental data, and 40 scan lines for simulated data). Analysis windows were allowed to overlap by 75% both axially and laterally. The ratios of the power spectra from the sample to those of the reference phantom at the same depth were grouped in 8mm segments in the axial direction, and the logarithm of the ratios were fit to a straight line using a least-squares fitting routine. The slope of this line was used to estimate the attenuation coefficient (neper/cm) as shown in Eq. (3). This was done over the frequency range of 5-6MHz and 4-8MHz for experimental data and simulations, respectively. The frequency range used for the experimental data was limited to the 5-6MHz bandwidth to minimize any errors that would be caused by the slightly nonlinear frequency dependent attenuation in the phantoms, noted in table 1. However, the range used for the simulated data, where attenuation was modeled as being proportional to frequency, was 4-8MHz to enable a greater number of independent estimates of the slope of attenuation coefficient vs. frequency. The slopes of attenuation coefficient vs. frequency were obtained by converting to dB/cm and then dividing by the frequency in MHz. The slopes of attenuation coefficient vs. frequency were obtained over the entire depth from which data were acquired.

Attenuation values were obtained with the transmit focus at 2cm, 3cm, 4cm, 5cm, and 7cm for both sample phantoms. Attenuation estimates from the same depth were averaged laterally over the ROI.

Biases of RPM results with respect to the laboratory measurements were quantified using an absolute percent error, defined as:

$$Absolutepercenterror\left(z\right)=\frac{\mid {\alpha }_{estimated}\left(z\right)-{\alpha }_{known}\left(z\right)\mid }{{\alpha }_{know}\left(z\right)}\times 100$$

where α_estimated (z) and α_known(z) are the estimated attenuation coefficients using the RPM and the laboratory measurements, respectively.

III. RESULTS

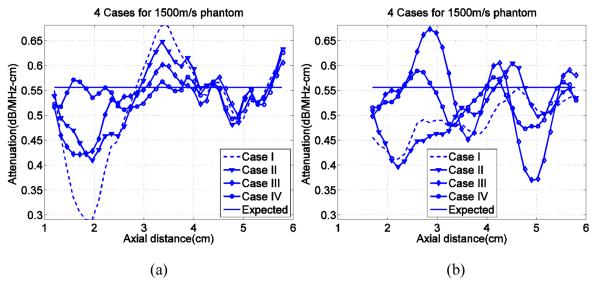
Attenuation coefficient slopes vs. depth obtained from simulated and experimental data with the transmit focus at 2cm are presented in figure 1 for the 1500m/s phantom and in figure 2 for the1580m/s phantom. The horizontal line in each plot indicates the expected slope of attenuation coefficient vs. frequency at 5MHz based on through transmission measurements made on test samples. As can be seen in figure 1, without accounting for differences in speeds of sound in the sample, beam former, and reference (Case I) significant deviations from the expected attenuation values are found, particularly near the 2cm transmit focus simulation data. This bias is reduced somewhat with partial corrections, either by precisely matching the depths from which echo signal power spectra for the sample and reference are computed (Case II) or by applying a beam former sound speed that accurately matched the sound speed of the sample or the reference media when data were acquired (Case III). The smallest deviations from expected values occurred for results from simulated echo data in Case IV, where both corrections schemes are applied.

FIG. 1.

Slopes of attenuation coefficient vs. frequency over the ROI with a 2cm transmit focal distance, for all four experimental cases (Cases I, II, III, IV) shown on each graph. Subplot (a) is from simulated data while subplot (b) shows results from experiments. The sound speed in the sample is 1500m/s and that in the reference phantom is 1540m/s. The model attenuation coefficients in the sample and reference phantom are 0.559dB/cm-MHz and 0.573dB/cm-MHz respectively (horizontal line).

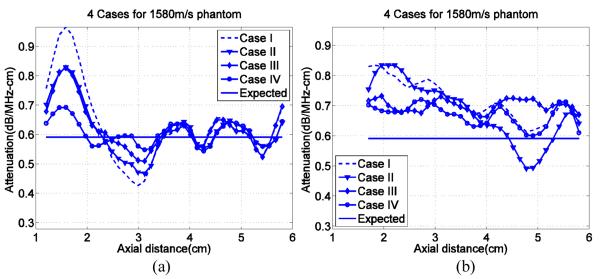
FIG. 2.

Slopes of attenuation coefficient vs. frequency over the ROI with a 2cm transmit focal distance, for all four experimental cases (Cases I, II, III, IV) shown on each graph. Subplot (a) is from simulated data while subplot (b) shows results from experiments. The sound speed in the sample is 1580m/s and that in the reference phantom is 1540m/s. The model attenuation coefficients in the sample and reference phantom are 0.591dB/cm-MHz and 0.573dB/cm-MHz respectively (horizontal line).

Similar trends in the results from the 1580m/s sample phantom are observed in figure 2 for the different Cases. Notice in this example, the large bias in results at the 2cm transmit focal depth are in the opposite direction as that for the 1500m/s case due to the opposite sound speed difference between the sample and reference. The significant improvements observed for Case IV again are observed.

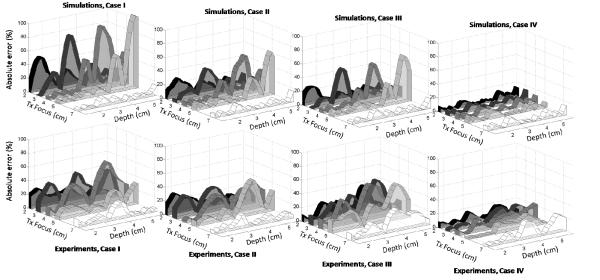
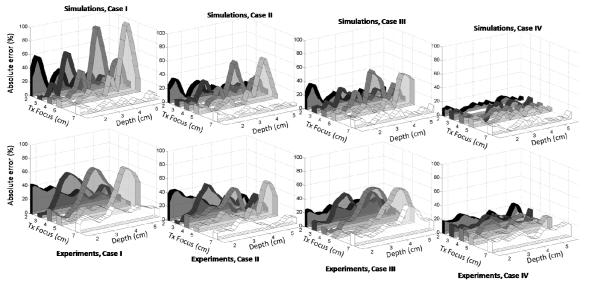
The absolute percent errors for the different data acquisition and analysis cases are summarized in table 2 and presented in figure 3 for the 1500m/s phantom and in figure 4 for the 1580m/s phantom. In each figure, the top row of plots presents results from simulations and the bottom row shows experimental results. Each sub plot includes five curves to display results for each of the five different transmit focus locations.

FIG. 3.

Absolute percent error of slopes of attenuation coefficient vs. frequency from Cases I, II, III, and IV ( from left to right), derived from simulation (top row) and experimental (bottom row) data, where c_sam = 1500m/s and c_ref = 1540m/s: Case I, where no corrections are applied, i.e. c_bf = 1540m/s for both sample and reference and z_sam ≠ z_ref ; Case II, where c_bf = 1540m/s for both sample and reference but z_sam = z_ref; Case III, where c_bf matches each of c_sam and c_ref but no depth correction is applied, z_sam ≠ z_ref ; Case IV, where c_bf matches each of c_sam and c_ref AND sound speed corrections are used to match distances, z_sam = z_ref. The transmit focus settings were 2cm, 3cm, 4cm, 5cm, and 7cm. The model attenuation coefficients in the sample and reference phantom are 0.559dB/cm-MHz and 0.573dB/cm-MHz, respectively.

FIG.4.

Absolute percent error of slopes of attenuation coefficient vs. frequency from Cases I, II, III, and IV (from left to right) derived from simulation (top row) and experimental (bottom row) data, where c_sam = 1580m/s and c_ref = 1540m/s: the Case conditions are outlined the figure 3 caption. The transmit focus settings were 2cm, 3cm, 4cm, 5cm, and 7cm. The model attenuation coefficients in the sample and reference phantom are 0.591dB/cm-MHz and 0.573dB/cm-MHz, respectively.

As can be seen in all Case I results from simulations (upper rows in figures 3 and 4), a significant bias in the estimated attenuation results occurs near the transmit focus. The bias is larger at deeper transmit focus settings, except for the 7cm focus setting. Experimental data from the two sample phantoms are presented in the lower rows in figures 3 and 4. The general trend in the experimental data follows that seen with simulations (the bias is the greatest near the transmit focal depth and it is reduced by applying the corrections outlined in table 2). Results from both simulation and experiment where the sound speed used in the beam former and the sound speed assumed in the depth calibration matched the sound speed of the sample (Case IV) exhibits the smallest fluctuation in attenuation estimates over the ROI for all focal depth settings. The experimental results exhibited less variation among the four Cases than the simulation results, possibly because of lower statistical fluctuations in the power spectral density estimates (multiple independent frames were used for computing the attenuation for experimental data).

The attenuation coefficient was generally underestimated for the 1500m/s phantom and overestimated for the 1580m/s phantom when no corrections were applied. The mean error in simulated data, obtained by averaging over depth and considering all transmit focus locations, was −4.3% for the 1500m/s phantom and 5.0% for the 1580m/s phantom.

Interestingly, no significant difference among the four analysis cases was observed when using the 7cm transmit focus location. Evidently, when the transmit focal zone is significantly deeper than the transducer aperture length and its location is beyond the ROI, the errors caused by mismatched sound speeds in the reference and sample are smaller than for the shallow transmit focus conditions. Focusing effects over the ROI are much more gradual for the 7cm depth than for the other transmit focal depths, and that apparently minimizes the attenuation estimate bias errors.

IV. DISCUSSION

The RPM provides accurate estimates of attenuation and backscatter coefficients using clinical ultrasound equipment when the speed of sound in the reference closely matches that of the sample. The focus of this paper was on the accuracy of the method when the sound speed in the reference media, used to account for system dependencies on the data, differs from the sound speed in the sample.

Three observations are noted. First, for either a sample having a sound speed of 1500m/s or 1580m/s, where the reference phantom’s sound speed is 1540m/s, a bias existed in the attenuation estimates, particularly near the transmit focus location. Secondly, this bias near the transmit focus tended to be larger (the maximum error was higher) at deeper focus settings. Finally, the polarity of the bias near the transmit focus location was in opposite directions for the 1500m/s sample results compared to those for the 1580m/s sample.

A possible explanation of these observations is the difference in spatial power distribution between the sample and reference phantoms caused by the difference in the location of the focus accompanying the difference in speeds of sound in the sample and reference media. To visualize these power distribution differences, another set of simulations was done. Most conditions were the same as those applied in simulations described above, with the sample having either a 1500m/s or a 1580m/s sound speed, the reference phantom having a sound speed of 1540m/s, and the linear array dimensions matching those of the transducer used in the experiment. However, now the sample and reference media had identical attenuation properties, 0.6dB/cm-MHz.

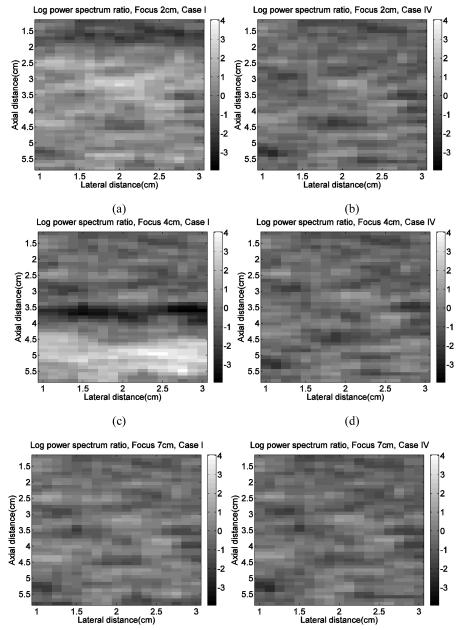
Power spectra were calculated from the sample and reference echo data applying both Cases I and IV as described in table 2. Then the log of the ratio of the power from the sample to that from the reference was obtained by integrating echo signal power spectra over the 4-8MHz frequency range. These power ratios were computed over the whole ROI and displayed as images. Results are shown in figure 5 for Case I (left column) and Case IV (right column) and are presented for transmit focus locations of 2cm, 4cm, and 7cm.

FIG.5.

Images from simulations depicting ratios of integrated echo signal power spectra from a sample to that from corresponding locations in a reference phantom. The sample and reference phantom have identical attenuation and backscatter coefficients, but c_sam = 1500m/s and c_ref = 1540m/s. The ratio values are expressed in dB. (a) Case I with transmit focus at 2cm (b) Case IV with transmit focus at 2cm (c) Case I with transmit focus at 4cm (d) Case IV with transmit focus at 4cm (e) Case I with transmit focus at 7cm (f) Case IV with transmit focus at 7cm.

Comparing the left column (Case I) with the right column (Case IV), since the sample and reference have the same attenuation and backscatter coefficients for this simulation, the expected log ratio is 0dB throughout the image. The log ratio in Case IV exhibited a consistent pattern throughout the depth range, closer to 0dB than that in Case I. Figure 5(a), and (c) depict a clear bias near the transmit focus location, resulting in a banding of the imaged sample-to-reference phantom power spectra ratios. The banding is more prominent in figure 5(c), where the transmit focal depth is deeper, than in figure 5(a). The banding disappears for Case IV where the speed of sound assumed in the beam former closely matches that in the reference or sample media and actual sound speeds in the sample and reference are used to assure that power spectra ratios are from precisely the same depth.

The banding near the transmit focus location is caused by the slight mismatch of the locations of the focal peak in the signals from the sample and those from the reference media. The actual focal depth in the 1500m/s phantom is slightly deeper than that in the reference medium whose speed of sound is 1540m/s and slightly shallower in the 1580m/s phantom.¹⁸ Beyond the focus, the energy in the beam spreads gradually, further weakening the received signal. The beam energy spread occurs more rapidly with depth when the focal depth is closer to the transducer, as in the 1580m/s sample, than when it is deeper (1500m/s sample). This is consistent with the observation that the average attenuation coefficients were underestimated by 4.3% for the 1500m/s sample but overestimated by 5.0% for the 1580m/s sample. This also explains why the bias trends near the transmit focus location in the 1500m/s phantom and 1580m/s phantom are in opposite directions.

The effects of a mismatch in the sound speed in the sample and reference media is not necessarily peculiar to the RPM, but likely occurs for any attenuation estimation method where power spectra ratios of sample to reference are employed to eliminate system dependent factors. Thus, methods where system calibrations are done using planar reflectors in water, for example, should be evaluated in a similar fashion.

Generally, when estimating attenuation coefficients in tissues, the sound speed in the sample will not be known exactly. Some ultrasound imaging instruments vary the beamformer sound speed depending on the tissue scanned, and use of such a feature to match the beamformer sounds speed to that of the tissue may enable better estimates of parameters determined using a reference phantom. Another possibility is to use instruments that provide sound speed optimization routines, either through automated methods²⁴ or by allowing the operator the choice of selecting the most appropriate beamformer sound speed, when doing attenuation estimations such as these. Future studies will investigate the ability of these algorithms to supply accurate values for correcting the RPM following our Case IV approach.

Compared to examples shown in figures 5(a), 5(c) and 5(e), horizontal banding is minimized in figure 5(e) where the transmit focus is at 7cm. This is consistent with results in figures 3 and 4, where errors caused by different sound speed values in the sample and reference phantom appear to be lowest when the transmit focal zone is beyond the ROI for which attenuation coefficients are determined. With the transmit focus well beyond the ROI, evidently focusing differences in the sample and reference are not as significant. Alternatively, applying more weakly focused transmissions might also minimize the focal zone bias errors. These conditions will be explored more thoroughly in future reports.

In figures 3 and 4, the experimental results exhibited higher pecent errors than simulation results for Case IV. One possible cause is the existence of electronic system noise in the RF data from the experiment. The simulated RF data did not include random noise which was present in the expemental data. Another possible cause for higher (apparent) errors in attenuation estimates from backscattered echo data is the linear dependence on frequency assumed from the narrowband substitution method. Attenuation in the simulated data had a linear frequency dependence. Finally elevational focusing in the clinical imaging system could have played a role in addition to electronic focusing in the image plane. Since this elevational focusing was done mechanically, the diffraction difference in the sample and reference caused by this focusing and sound speed mistmatch is as not accounted for in Case IV. Elevational focusing was not used in the simulations.

Finally, when comparing the attenuation estimate bias error for experimental and simulation data, the trends in the bias as a function of spatial position and sound speed difference are the same, even though there is a lack of exact agreement between these results. The differences between experiment and simulation might be caused by small differences between numerical and physical phantoms, the latter also having uncertainties associated with the values of attenuation vs. frequency. Moreover, the model did not attempt to simulate the precise frequency reponse of the system nor exact details of the transducer’s elevational focusing. Its purpose was to probe whether the experimental observations were reasonable. Further, there are statistical fluctuations in the RF echo signals, and corresponding power spectra, that would require very large numbers of observations to obtain true expectation values (and thereby obtain “best estimates”). Real phantoms have finite sizes, which limit the number of statistically uncorrelated RF echo signals available. With that in mind, similar trends in attenuation estimate bias from experimental and simulated data was all that was expected from this study. However, trends in bias error from both experiments (physical phantoms, transducers, etc.) and simulations (where few approximations are made) provided insight into the sources of these bias errors.

V. CONCLUSIONS

Differences between the speed of sound in a sample and that assumed in the beamformer, as well as between the sound speed of a sample and that of reference medium, cause biases in RPM attenuation measurements. With array systems, the bias is greatest near the transmit focus location. Biases are reduced or eliminated by matching the sound speed assumed in the beamformer to that of the medium and taking care to match power spectra in the sample and reference from precisely the same depth. If the sound speed of the sample is unknown, setting the transmit focus location further from the ROI minimizes biases in attenuation estimates.