Ultrasonic Attenuation and Backscatter Coefficient Estimates of Rodent-Tumor-Mimicking Structures: Comparison of Results among Clinical Scanners

Abstract

In vivo estimations of the frequency-dependent acoustic attenuation (α) and backscatter (η) coefficients using radio frequency (RF) echoes acquired with clinical ultrasound systems must be independent of the data acquisition setup and the estimation procedures. In a recent in vivo assessment of these parameters in rodent mammary tumors, overall agreement was observed among α and η estimates using data from four clinical imaging systems. In some cases, particularly in highly attenuating heterogeneous tumors, multi-system variability was observed. This paper compares α and η estimates of a well-characterized rodent-tumor-mimicking homogeneous phantom scanned using 7 transducers with the same four clinical imaging systems: a Siemens Acuson S2000, an Ultrasonix RP, a Zonare Z.one, and a VisualSonics Vevo2100. α and η estimates of lesion-mimicking spheres in the phantom were independently assessed by three research groups, who analyzed their system’s RF echo signals. Imaging-system-based estimates of α and η of both lesion-mimicking spheres were comparable to through-transmission laboratory estimates and to predictions using Faran’s theory, respectively. A few notable variations in results among the clinical systems were observed, but the average and maximum percent difference between α estimates and laboratory-assessed values was 11% and 29%, respectively. Excluding a single outlier dataset, the average and maximum average difference between η estimates for the clinical systems and values predicted from scattering theory was 16% and 33%, respectively. These results were an improvement over previous inter-laboratory comparisons of attenuation and backscatter estimates. Although the standardization of our estimation methodologies can be further improved, this study validates our results from previous rodent breast-tumor model studies.

INTRODUCTION

Ultrasound scanning has been used in combination with other imaging modalities in the detection and differential diagnosis of masses. Nevertheless, the commonly assessed sonographic features in ultrasound images, such as relative echogenicity of different tissues, are not highly specific by themselves.¹

The development of a particular disease often affects the regional cellular microenvironment, resulting in the tissue microstructure (glands, collagen bundles in connective tissue) suffering modifications in its mechanical properties.¹ In some cases, these properties can be characterized in vivo by a spectral analysis of the reflected and scattered components of radio frequency (RF) echoes detected by an ultrasound system.^1,2 This RF echo information, which is usually neglected when constructing conventional envelope-based B-mode images, could improve the objectivity of the scan evaluation, and thus aid in the diagnosis and treatment evaluation of different diseases. This analysis is referred to here as Quantitative Ultrasound (QUS).^3,4

An estimation of acoustic attenuation and backscatter coefficients is central for the assessment of many QUS parameters. These parameters have been estimated in the past to characterize as well as to differentiate between healthy and diseased tissues such as in the liver, kidney, breast, and thyroid.^1,5–11 The attenuation coefficient, α, refers to the spatial rate of sound beam attenuation, usually quantified in decibels per centimeter at a specific frequency, f, while the backscatter coefficient, η, is defined as the differential scattering cross section per unit volume for a scattering angle of 180 degrees.^12,13 Estimates of α and η are expected to be independent of the system and signal processing techniques because they are inherent acoustic properties of tissue.^14,15

In recent years, our laboratories have jointly focused on demonstrating the feasibility of obtaining accurate and precise estimates of various QUS parameters. Recent studies involved multi-system comparisons of scanner-based α and η estimates from in vivo spontaneous rat mammary fibroadenomas and implanted carcinomas.^14,15 General agreement was observed between attenuation values computed among four different systems, though the attenuation coefficients with clinical systems were significantly higher than those reported from laboratory measurements using single-element transducers.¹⁰ Root-mean-square errors among η estimates from the four clinical imaging systems over the 4–5MHz range were as low as 5% for a fibroadenoma, but up to 330% for a carcinoma, although the frequency dependence of η exhibited much better agreement. These differences were attributed mainly to spatial variations in properties of the masses, i.e., no single system scanned the exact same location of the tumor and at the exact orientation as another system. However, some of the variability might also be caused by differences in accounting for attenuation in masses as well as by other system- and analysis-dependent factors.^14,15 Therefore, an essential step in the analysis of a multi-system study is to investigate the level of agreement independently of possible sample-related heterogeneity in the acquired data.

The goal of the present work was to assess scanner-based α and η estimates of well-characterized and homogeneous rodent-tumor-mimicking structures contained in a phantom designed to mimic conditions under which tumors in small mammals are often present and scanned. The intent was to determine whether the unusual geometry of the rodent tumor protruding above the body wall was causing our measurements (with all imaging systems) to be biased high. These estimates were generated by processing RF echoes from the phantom scanned with different clinical systems, emulating the data acquisition conditions and signal processing methodology used in the in vivo rodent-tumor characterization experiment cited above.^14,15 In this paper, estimates from four ultrasound imaging systems are compared to laboratory characterization of the acoustic properties of the rodent-tumor-mimicking structures as well as to predictions from Faran’s scattering theory for spherical scatterers.¹⁶

METHODS

Phantom design

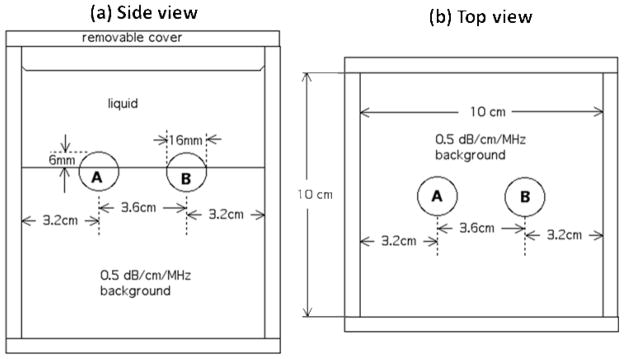
The phantom emulates experimental conditions during rodent-lesion scanning,^14,15 including a liquid path between the transducer and subject, a lesion protruding from the subject body forming a convex surface, and relatively high levels of ultrasound attenuation within the lesion compared to levels previously reported for such tumors.^10,14,15 Following this idea, the phantom consists of three macroscopically uniform sections: two lesion-mimicking 1.6cm diameter spherical inclusions (referred to as Sphere A and Sphere B, see fig. 1) protruding from a background (third section) in the shape of a rectangular parallelepiped. The phantom was fabricated using techniques reported previously.¹⁷ The phantom is immersed in a solution of water, propylene glycol and Liquid Germall Plus® (a preservative) and enclosed in an acrylic box.

FIG. 1.

Side view (a) and top view (b) of the custom-made, rodent-lesion mimicking phantom.

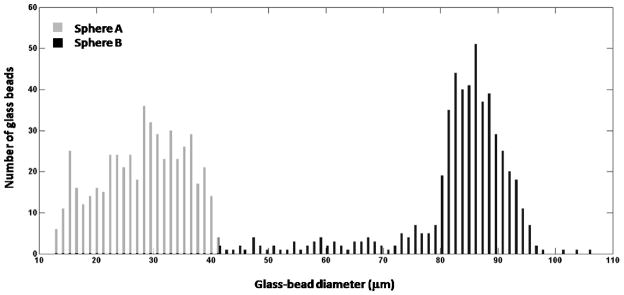
All three sections were composed of mixtures of water, agar, propylene glycol, and Liquid Germall Plus® as well as of different concentrations of graphite powder and different size distributions of glass-bead scatterers. Graphite powder concentrations were selected to achieve different levels of attenuation in each section. Attenuation coefficients were measured using substitution techniques, as described below. The glass bead scatterer size distribution (figure 2) for each phantom section was determined by measuring the diameter of 500 glass beads using a calibrated optical microscope. The density (measured as described in a previous publication¹⁸) and the glass-bead mass concentration per unit volume of the agar/graphite mixture in Sphere A and Sphere B, as well as in the surrounding background material, are presented in table 1. The beads produce acoustic scattering and are spatially randomly distributed within each section. The different scatterer size distributions produce different frequency-dependent backscatter.

FIG. 2.

Glass-bead-diameter distributions of Sphere A and Sphere B determined by measuring the diameter of 500 glass beads for each distribution using a calibrated optical microscope.

TABLE 1.

Physical characteristics of the three sections in the phantom

	Density (g/cm3)	Glass beads mass (g) per unit volume (L) of agar/graphite
Background (reference)	1.03	4.8g/1.2L
Sphere A	1.07	1.6g/0.4L
Sphere B	1.11	1.6g/0.4L

Figure 3 shows ultrasound B-mode images of (a) Sphere A and (b) Sphere B of the phantom, as well as (c) a spontaneous mammary fibroadenoma in a live rat.¹⁵ The three images were acquired with the same system and transducer (Siemens S2000, 9L4, described below) as well as acquisition parameters. As can be observed, the experimental conditions and the gray-scale appearance of the rodent tumor are similar to those for the inclusions.

FIG. 3.

B-mode images of (a) Sphere A, (b) Sphere B, and (c) a spontaneous mammary fibroadenoma in a rat.¹⁵ The three images were acquired with the 9L4 linear array transducer of the Siemens S2000 system under the same scanning parameters.

Acoustic properties of the phantom

2.5cm thick test samples, formed of the materials making up each section of the phantom and poured at the time of its fabrication, were used in laboratory measurements of the attenuation coefficient α and speed of sound c of the three sections. Laboratory measurements of these properties were generated by applying a through-transmission narrow-band substitution technique,¹⁹ involving the transmission of 30-cycle acoustic pulses of different frequencies (2.5, 5, 7.5, and 10MHz) through the sample immersed in water. Pulses were emitted by a single-element unfocused transducer, traversed the sample, and reached a corresponding receiving transducer, whose signal was read by a digital oscilloscope (500MHz, Model LT342, LeCroy, Chestnut Ridge, NY). The amplitude change and temporal shift of the detected waveforms compared to waveforms recorded in the absence of the sample were used to determine the attenuation and the speed of sound of the material in the sample, respectively.¹⁹ In the case of the speed of sound c, dispersion was neglected, and the average ± one standard deviation among values of the speed of sound determined at each transducer’s operation frequency is reported in table 2. A power law fit was applied to the measured attenuation coefficient α (in dB/cm) as function of frequency

TABLE 2.

Acoustic properties of the phantom. Speed of sound c in m/s (average ± one standard deviation from four measurements), attenuation coefficient α in dB/cm at 2.5MHz, parameters from a power fit and a linear fit to α versus frequency.

	c (m/s)	α ( 2.5MHz) (dB/cm)	Power fit α=α0fn		Linear fit α=α0f
			α0(dB/cm-MHzn)	n	α0(dB/cm-MHz)
Background (reference)	1544± 1	1.06	0.36	1.17	0.51
Sphere A	1538± 3	2.51	0.97	1.02	1.02
Sphere B	1531± 2	3.57	1.33	1.08	1.58

$$\alpha (f)={\alpha }_0{f}^n$$ (1)

to estimate the constant α₀ (dB/cm-MHzⁿ) and the exponent n. Because the values of n were close to 1, a linear fit was also applied to the data. The values from the linear fit were used for comparison with scanner-based α₀ estimates as well as for attenuation compensation during the estimation of the backscatter coefficients from clinical imaging systems, described below. The results from these fits are presented in table 2.

Test samples were also used in laboratory measurements of backscatter coefficients for the phantom components. These were performed using a broadband pulse-echo, planar reflector method and single-element focused transducers.²⁰ The test samples and the transducer were immersed in a tank of degassed water at room temperature. The transducer was coupled to a computer-driven pulser-receiver (Model 5800, Panametrics, GE Inspection Technologies, Lewiston, PA). After placing the test sample at the focal plane of the transducer, a set of RF echoes was acquired by automatically moving the transducer (using an Aerotech Undex 11 motor displacer, GE Inspection Technologies, Lewiston, PA) in a plane parallel to the surface of the test sample in a raster fashion over 40mm × 40mm, at steps of 4mm. The RF signals were gated to consider only echoes from within the sample near the focal distance of the transducer. Echo signals from a planar quartz reflector, with its reflecting surface perpendicular to the pulse trajectory, were also acquired to account for the transmit-receive frequency response of the transducer-pulser-receiver system. Assuming a long duration gate, the backscatter coefficient is given by the ratio of the square modulus of the Fourier transform of the gated RF signal averaged over all the collected signals, divided by a term that accounts for the system’s frequency response, the shape of the gating function, and the transducer field integrated over the test sample volume.²⁰ The procedure was performed using transducers with center frequencies of 3.5, 5.0, 7.5, and 10MHz to span the 2.4 to 12.9MHz range.

Data collection with clinical systems

The participating laboratories were aware of the attenuation properties of Sphere A and Sphere B as well as of the attenuation and backscatter properties of the background material surrounding them. However, the laboratories were blind to the backscatter properties of Sphere A and Sphere B. Each section was scanned with four clinical ultrasound systems: a Siemens Acuson S2000 (Siemens Medical Solutions USA, Inc, Malvern, PA) with 9L4 and 18L6 linear array transducers operated at 6 and 10MHz nominal excitation frequencies by the group from the University of Wisconsin-Madison (UW); an Ultrasonix RP system (Ultrasonix Medical Corporation, Richmond, British Columbia, Canada) with L9-4/38 and L14-5/38 linear array transducers operated at 5 and 7.5MHz nominal center frequencies by the group from the University of Illinois at Urbana-Champaign (UIUC); a Zonare Z.one scanner (Zonare Medical Systems, Inc, Mountain View, CA) with L8-3 and L14-5sp linear array transducers operated at 7 and 10MHz nominal center frequency by the group from Iowa State University (ISU); and a VisualSonics Vevo2100 (VisualSonics Inc., Toronto, Ontario, Canada) with a MS200 transducer operated at a 15MHz nominal center frequency also by the UIUC group. The scanners are equipped with research interfaces that supply either raw RF echo data or, in the case of the VisualSonics, quadrature data that permits accurate power spectral density estimation. Data collection with all four systems took place during one scanning session at UIUC. RF echoes from five different image planes of each section of the phantom were obtained by rotating the transducer about an axis defined by the central acoustic scan line of the image. The degree of correlation among the image planes was not tested, however. During analysis, the background material of the phantom was used as a reference. Thus, RF data from all three sections scanned by each transducer were acquired using identical operator control settings and the same transducer-to-section distance.

Attenuation estimation

RF data from each system were processed following the spectral slope algorithm.²¹ The general steps are the following: The spherical inclusion was identified in the B-mode image of each of the two-dimensional frames, and a region of interest (ROI) was defined within it. The ROI was subdivided into “α-estimation blocks” whose sizes are shown in table 3. An estimate of the attenuation coefficient was then obtained for each of these blocks. To do this, a block was further divided into a number of spectral estimation windows. Tapered segments of the RF echoes corresponding to each spectral estimation window were used to compute the power spectra from the sample and the reference. Windows were allowed to overlap both axially and laterally. The difference in depth dependence of the ratio of the sample to the reference power spectra was used to quantify the attenuation coefficient within each α-estimation block. The size, tapering function, and amount of overlap between spectral windows and α-attenuation blocks varied among systems, as presented in table 3.

TABLE 3.

Parameters used in the estimation of the attenuation coefficient (AL=acoustic line)

	Ultrasonix	VisualSonics	Siemens	Zonare
Spectral window size (axial × lateral)	15–20λ × 30–60AL		4mm × 4mm	2.46mm × 4.8mm
Tapering function	Rectangular		Hann	Rectangular
Spectral window overlap	85% axially		75% axially	50% axially
α-estimation block size	30–40λ axially, 30–60AL laterally		8mm axially, 6mm laterally	7.38mm axially, 4.8mm laterally
α-estimation block overlap	50% axially, 0% laterally		0%, 0% (only 1 block)	99% axially, 99% laterally (round to nearest window/AL)
Signal processing bandwidth	3–7MHz (L9-4), 4–8MHz (L14-5)	7.5–12.5MHz	3–10MHz	3–9.75MHz
Bandwidth selection criterion	−12dB	−6dB	15dB above noise floor	−20dB

Backscatter coefficient estimations

The general procedure to estimate each spherical inclusion’s η as a function of frequency from the RF data was the reference phantom method, using the phantom background (its laboratory-measured attenuation [table 2] and backscatter coefficients) as reference.^21,22 The following steps were performed:

1. A ROI was defined within the spherical inclusion based on the B-mode image of each acquired image plane. Multiple estimates of the power spectra from the sample and reference RF echoes were obtained within the ROI by placing a spectral analysis window at different locations within it. The specific window sizes, window overlap and bandwidth used for each system are listed in table 4. Note that the analysis parameters were set independently by each research group. Each group utilized criteria based on experience with the data collected by their own imaging system.

2. The frequency-dependent η was estimated by applying the reference phantom method to the power spectra of the segmented RF echoes within the ROI. Neglecting multiple scattering and based on the fact that the speed of sound of the tumor-mimicking spherical inclusions and that of the reference phantom are similar (as shown in table 2),^21,23 the backscatter coefficient of the sample (spherical inclusion) η_sample is obtained as follows:

   $${\eta }_{\mathit{sample}}(f,z)={\eta }_{\mathit{ref}}(f,z)\frac{S_{\mathit{sample}}(f,z)}{S_{\mathit{ref}}(f,z)}exp\left[4\underset{0}{\overset{z_w}{\int }}\left({\alpha }_{\mathit{sample}}(f,z)-{\alpha }_{\mathit{ref}}(f,z)\right)dz\right]$$ (2)

   where η_ref and α_ref are the laboratory-measured attenuation and backscatter coefficients of the reference, and S_sample and S_ref are the echo signal power spectra from the sample and the reference phantom from a particular spectral analysis window. The exponential term corresponds to the compensation for the attenuation caused by structures above the spectral analysis window, which is at a depth z_w from the transducer.

3. Backscatter coefficient estimates from each transducer were averaged over all spectral analysis windows within a ROI, and over the ROIs across different planes.

TABLE 4.

Parameters used in the estimation of the backscatter coefficient.

	Ultrasonix	VisualSonics	Siemens	Zonare
Spectral window size (axial ×lateral)	15λ × 15λ	15λ× 15λ	4mm × 4mm	2.46mm × 4.8mm
Tapering function	Rectangular	Rectangular	Hann	Rectangular
Spectral window overlap	85%	75%	75%	99%
Signal processing bandwidth (MHz)	L9-4: 3–6, L14-5: 3–8.6	8–12.2	9L4: 4–10 18L6: 4–12	L8-3: 3.1–7.2 L14-5: 4.4–9.5
Bandwidth selection criterion	−12dB	−6dB	15dB above noise floor	−20dB

Analysis of η estimates from each imaging system for the inclusions involved determining the level of agreement with theoretical predictions, which are calculated using the number density distribution of the glass beads and Faran’s theory for spherical scatterers.¹⁷ The theory requires the size and properties of the glass beads as input parameters. Analysis also involved computing the variation of the estimates among different systems (including laboratory estimates), and assessing the similarity of the frequency dependence of the backscatter coefficient. To perform this analysis, the following quantities were defined:

1. Percentage Difference with respect to Faran (%D_Faran): We computed the absolute value of the difference between the η_system(f) estimate from the clinical imaging system and the Faran prediction η_Faran(f) at the same frequency, normalized over the predicted value. This is expressed as

   $$\%D_{\text{Faran}}(f)=\frac{\left|{\eta }_{\text{System}}(f)-{\eta }_{\text{Faran}}(f)\right|}{{\eta }_{\text{Faran}}(f)}\times 100.$$ (3)
2. Percentage Difference with respect to the mean of η estimates from all systems (%D_Mean): This is defined as the absolute difference between the η estimate from an individual system and the mean computed from the results of all systems at the same frequency, normalized over the mean. That is,

   $$\%D_{\text{Mean}}(f)=\frac{\left|{\eta }_{\text{System}}(f)-{\eta }_{\text{Mean}}(f)\right|}{{\eta }_{\text{Mean}}(f)}\times 100.$$ (4)
3. Effective Scatterer Diameter²⁴: This was estimated through the minimization of the squared difference between the logarithms of the estimated backscatter coefficient and a theoretical model η_T(f) (in this case using Faran’s theory, updating the assumed scatterer diameter at each iteration of the minimization procedure) over a selected bandwidth.²³

   $$\widehat{d}=argmin\frac{1}{N}\sum _{f=f_1}^{f_N}{\left[10log\left[\frac{\eta (f)}{{\eta }_T(f;d)}\right]-\overline{10log\left[\frac{\eta (f)}{{\eta }_T(f;d)}\right]}\right]}^2.$$ (5)
   Diameter search ranges were 15 to 55μm for Sphere A, and 55 to 100μm for Sphere B. Once the effective scatterer diameter was estimated, the similarity between η_T assuming the estimated effective scatterer diameter and the estimated η_System was quantified by computing the mean squared error, where the mean is taken over the N frequency points included in the analysis bandwidth:

   $$\text{MSE}({\eta }_{\text{system}},\widehat{d})=\frac{1}{N}\sum _{f=f_1}^{f_N}{\left[{\eta }_{\text{system}}(f)-{\eta }_T(f;\widehat{d})\right]}^2.$$ (6)

Due to the variability of transducer bandwidths and processing methods, the frequency bandwidths used for the η estimation varied among transducers as well as among systems. To perform the analysis of the fractional differences, overlapping sections of those bandwidths were selected. Two overlapping regions were identified: a low-frequency region from 4.9 to 6MHz (including estimates from all systems except the VisualSonics MS200), and a high-frequency region from 8 to 12MHz (including estimates from the 10MHz single-element transducer, Siemens 18L6 and VisualSonics MS200). Then, η estimates from each system at the frequency points of the most coarsely sampled η estimate (Zonare 14L5 in the low-frequency region, and 10MHz single-element transducer in the high-frequency region) were obtained using linear interpolation from the original estimates. This procedure allowed us to have η estimates from all the systems within each overlapping region at the same frequency points.

The first [Eq. (3)] of the three quantities defined above [Eqs. (3)–(5)] aims at quantifying the discrepancy of each system’s η estimates with respect to Faran predictions, while the second one quantifies the variations with respect to the average trend of the experimental estimates. To simplify the analysis, the mean and standard deviations of the fractional differences over the low- and high-frequency ranges were computed. The third quantity is an approximate evaluation of the agreement among η estimates from the imaging system by assessing the effective scatterer diameter, which depends mainly on the frequency dependence of the backscatter coefficient. The estimation of the scatterer diameters was performed using the interpolated η estimates within the low-frequency and high-frequency ranges defined above.

RESULTS

Table 5 presents the estimates of α₀ [Eq. (1)] assuming linear dependence on frequency (n=1) for all scanners, as well as the laboratory estimates (presented also in table 2). As observed, most of the estimates from clinical systems are in agreement with laboratory estimates. The average and maximum differences between systems with respect to the value from the laboratory measurement for Sphere A (1.02dB/cm-MHz) were 9% and 18%, respectively. The average and maximum differences for Sphere B (1.58dB/cm-MHz) were 12% and 29%. In general, Sphere B estimates had larger differences with respect to the expected value. Furthermore, with the exception of one system, transducers with a higher nominal frequency range led to larger fractional differences.

TABLE 5.

Laboratory and scanner-based estimates of the slope of the attenuation coefficient versus frequency α₀ [Eq. (1)] assuming linear dependence on frequency (n=1) for the spherical inclusions in the rodent phantom. Uncertainties indicate one standard deviation of attenuation results obtained from different frames.

Scanning system	α0 (dB/cm-MHz)
	Sphere A	Sphere B
Laboratory	1.02	1.58
Siemens 9L4	1.00±0.05	1.66±0.07
Siemens 18L6	1.04±0.09	1.78±0.03
Ultrasonix L9-4	1.19±0.44	1.14±0.67
Ultrasonix L14-5	0.92±0.46	1.21±1.09
VisualSonics MS200	0.91±0.16	1.65±0.16
Zonare L8-3	0.98±0.08	1.66±0.13
Zonare L14-5sp	0.84±0.39	1.46±0.32

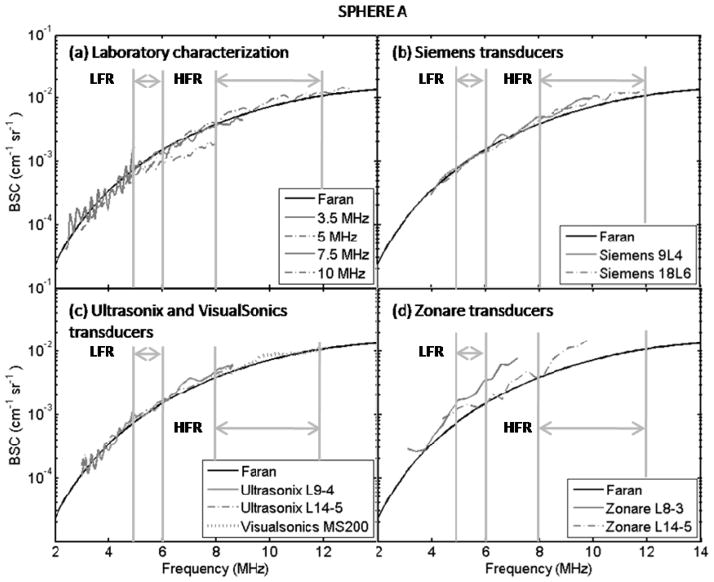
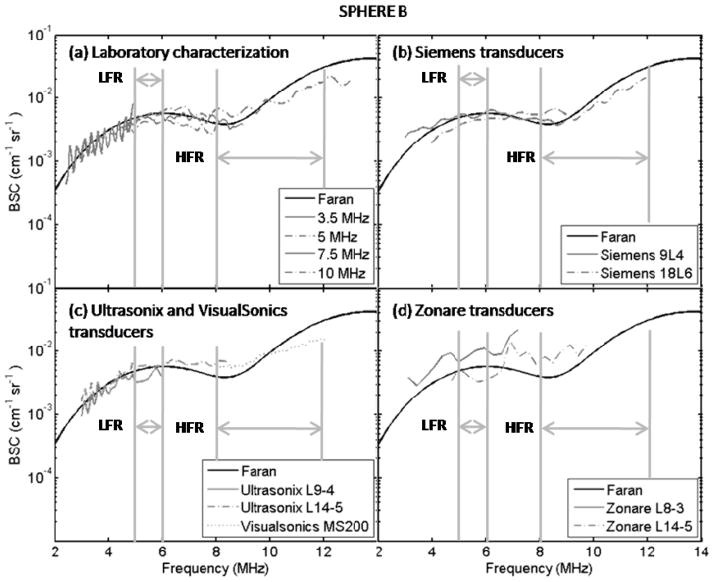
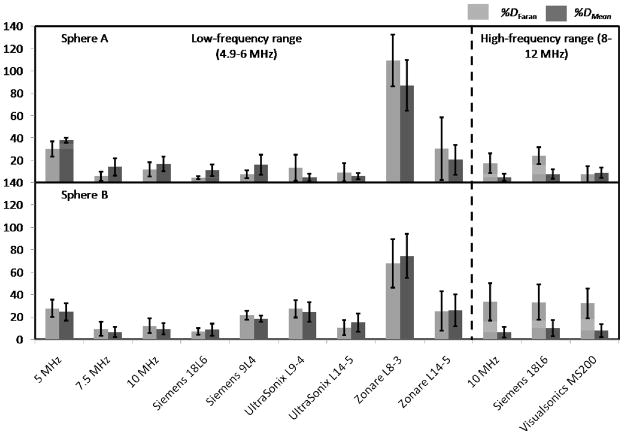
Figures 4 and 5 show backscatter coefficient vs. frequency results for the imaging systems from spherical inclusions A and B, respectively. Also shown are backscatter coefficients based on Faran predictions and those from the single-element transducer laboratory system. Figure 6 presents the mean (over frequency) values of the percentage differences with respect to Faran predictions (lightly shaded bars) and to the mean of the experimental estimates (dark bars) for each imaging system’s backscatter coefficient. These were computed using Eqs. (3) and (4), respectively. Error bars indicate standard deviations among different frequency points. The number of frequency points used for the percentage difference calculations were 6 and 45 in the low- and high-frequency ranges, respectively. In general all the percentage differences, both with respect to Faran’s theory predictions and to the mean from all systems’ results, were comparable, the only exception being the L8-3 transducer on the Zonare system. Excluding results from the Zonare, %D_Faran and %D_Mean of estimates η for Sphere A and Sphere B were computed among systems. The average, minimum, and maximum values among these systems are presented in table 6.

FIG. 4.

Experimental estimates and theoretical predictions of the backscatter coefficient of Sphere A as function of frequency. (a) Laboratory characterization using single element transducers, (b) Siemens transducers, (c) Ultrasonix and VisualSonics transducers, and (d) Zonare transducers. Vertical bars indicate the low-frequency analysis range (LWR) and the high-frequency range (HWR).

FIG. 5.

Experimental estimates and theoretical predictions of the backscatter coefficient of Sphere B as function of frequency. (a) Laboratory characterization using single element transducers, (b) Siemens transducers, (c) Ultrasonix and VisualSonics transducers, and (d) Zonare transducers. Vertical bars indicate the low-frequency analysis range (LWR) and the high-frequency range (HWR).

FIG. 6.

Percentage differences between individual system estimates of backscatter coefficients, computed with respect to Faran predictions (%D_Faran) [Eq. (3)] and the mean backscatter coefficient from all systems (%D_Mean) [Eq. (4)]. Upper panel: Sphere A. Lower panel: Sphere B. Error bars indicate 1 standard deviation.

TABLE 6.

%D _Faran and %D_Mean of η estimates for Sphere A and Sphere B among all imaging systems and single-element transducers excluding the L8-3 transducer from Zonare system (average, minimum, and maximum values).

	Sphere A		Sphere B
	%DFaran	%DMean	%DFaran	%DMean
Low-frequency range (4.9–6MHz)
Average	14	16	18	17
Minimum	5	5	7	7
Maximum	31	38	28	26
High-frequency range (8–12MHz)
Average	16	7	33	8
Minimum	8	5	32	6
Maximum	24	9	33	10

Results from the estimation of the effective scatterer diameter and the corresponding mean square error between the experimental backscatter coefficient and Faran theory predictions using the estimated effective scatterer diameter are presented in table 7. For reference, the estimated effective scatterer diameter using the predicted backscatter coefficients shown in figures 4 and 5 is also presented; here values of 35.2 and 34.7μm are obtained for Sphere A in the low- and high-frequency ranges, respectively, and of 85.9 and 85.2μm for Sphere B for these same frequency ranges. Multi-system values for the mean ± one standard deviation of the estimated scatterer diameters within Sphere A and Sphere B were 45±12μm and 79±8μm in the low-frequency range, and 35±1μm and 77±1μm in the high-frequency range, respectively. With the exception of the value for Sphere A in the low-frequency range, these values are close to the upper and lower nominal limits of the expected scatterer diameter distributions in Sphere A and Sphere B, respectively. The standard deviation is related to differences in the frequency dependence of the estimated backscatter coefficient among systems. In general, larger deviations from the mean estimated scatterer diameter as well as larger values of the mean square error with respect to the Faran model used in the estimation corresponded to those systems that also exhibited the largest percentage differences of the estimated backscatter coefficient, reported in figure 6. In addition, better agreement among systems was obtained in the high-frequency range. Dashed lines are presented in table 7 in the cases where no convergence between the experimental backscatter coefficient and the theoretical model was obtained within the diameter search range.

TABLE 7.

Effective scatterer diameters (d) for glass beads in Sphere A and Sphere B from backscatter coefficients measured by the different clinical systems. Also shown are mean square errors (MSE) for each system, with respect to the Faran’s theory model, assuming the estimated effective scatterer diameter. Dashed lines are assigned when no convergence was obtained in the minimization algorithm within the diameter search range.

System	Sphere A		Sphere B
	d (μm)	MSE (10−3)	d (μm)	MSE (10−3)
Low-frequency range (4.9–6MHz)
From ηFaran†	35.2	0.18	85.9	0.13
5.0MHz	---	---	74.8	1.43
7.5MHz	48.6	1.77	79.8	0.63
10MHz	---	---	71.5	0.42
Siemens 9L4	49.7	1.87	88.3	0.38
Siemens 18L6	27.8	0.37	79.1	1.24
Ultrasonix L9-4	53.6	2.20	83.6	1.65
Ultrasonix L14-5	---	---	90.3	0.59
Zonare L8-3	---	---	65.8	4.49
Zonare L14-5	---	---
High-frequency range (8–12MHz)
From ηFaran†	34.7	0.94	85.2	0.95
10MHz	35.9	0.59	76.7	2.99
Siemens 18L6	34.4	1.17	77.9	2.52
VisualSonics MS200	36.0	1.07	76.6	3.30

^†Effective scatterer size was estimated using η_Faran based on glass-bead distributions (Fig. 2) and concentrations.

DISCUSSION

This study compares results of attenuation and backscatter coefficient estimates for components of a phantom designed to emulate challenges when performing QUS assessments of rodent tumors using clinical imaging systems. A total of eight linear array transducers from four systems were used to estimate the attenuation and the backscatter coefficient of the rodent tumor mimicking spheres in the phantom.

Most estimates of the attenuation coefficient generated using pulse-echo data from these systems were within 29% of narrowband through-transmission measurement values. The maximum discrepancy (29%) was measured for the highly attenuating Sphere B. A possible explanation for this finding is the considerable loss of SNR for RF signals from this mass. At 9MHz, the signal loss in Sphere B would be 14.2dB over 1cm (the diameter of the sphere is 1.6cm), which is more than 70% of the noise rejection level of 20dB. This suggests that in highly attenuating structures, there is a tradeoff in the slope-based estimation methods between the ability to resolve the rate of decrease of the signal over depth and the increasing influence of noise in the estimates.

Results for the backscatter coefficients were, in general, consistent with predictions from Faran’s theory for the microscopic scatterers distributed in the phantom sections. The percentage differences between measured results and predictions, %D_Faran, and with respect to the mean estimate from all the systems, %D_Mean, were similar among most systems indicating that the level of agreement among different systems and with laboratory measured values of the backscatter coefficient is comparable to the overall agreement with predictions. The largest percentage differences (not considering results from the Zonare L8-3 transducer) were about 33% with respect to predictions and corresponded to η estimates for Sphere B in the high-frequency range. Interestingly, in this range the variability among systems was relatively small. This indicates that the results in this bandwidth may have been biased, which agrees with the observed underestimation at high frequencies in figure 5. A possible explanation of this result is the important loss of signal/noise caused by the high levels of attenuation at high frequencies.

In order to compare the frequency dependence of the backscatter coefficient derived from the different systems, we chose to fit each system’s backscatter coefficient vs. frequency estimates to a scattering model (Faran’s theory), yielding an “effective scatterer diameter”²⁴ In experiments on soft tissues, such as the rodent mammary tumor study reported by Wirtzfeld et al,¹⁵ or for studies of scattering in other organs^{6–8; 24–29} scattering is modeled as occurring from a (spatially) continuously varying acoustic impedance distribution where the spatial correlation function is represented with Gaussian or exponential functions (since there is usually insufficient information to support the use of a more sophisticated correlation function model). The use of these models partially reflects uncertainty of the scattering sources in tissues, a topic that still needs further investigation. However, in simple test media composed of glass sphere-in-gel, many investigators^13,24 have demonstrated that glass scattering can be modeled accurately using Faran’s equations. Although each of the tumor mimicking spheres contains a range of scatterer diameters, as shown in figure 2, the effective scatterer diameter resulting from this analysis provides another means to assess levels of agreement among results for the different systems. Except for Sphere A in the low-frequency range, reasonable agreement was obtained among the scatterer diameter estimates from different transducers. This discrepancy is likely due to the relatively small “ka” (product of the wave number and scatterer radius) for these scatterers at this frequency (ka = 0.39 for 35μm-diameter scatterers at 5.5MHz); it has been shown that scatterer diameter estimation is ineffective for ka < 0.6 (below which all scatterers behave as Rayleigh scatterers.²⁹) In the high-frequency range, estimated scatterer diameters for Sphere B were consistently smaller than the effective scatterer diameter predicted with Faran’s theory for the distribution of scatterer diameters. This agrees with the observed underestimation of the backscatter coefficient over 10–12MHz in figure 5, which caused the estimated η to vary more slowly with frequency than predicted from Faran’s theory using the actual scatterer sizes. The two different mean sizes in the spheres offer a reasonable contrast for this assessment and, in general, the scatterer diameter values obtained were consistent with the glass bead diameter distributions in each of the phantom’s spherical inclusions. The effective scatterer diameter values depend on the variation of backscatter coefficient with frequency, so in these determinations magnitude of the backscatter coefficients are less important. In addition, a smaller multi-system standard deviation in scatterer diameter estimates was obtained in the high-frequency range, which was derived from backscatter coefficient estimates from those transducers with higher frequency capabilities. These findings corroborate Insana and Hall’s assertion that effective scatterer diameter estimates improve, in most cases, with increasing signal bandwidth²⁹ and with Gerig et al.’s statement about the possibility of reducing the variance of scatter diameter estimates by using high-frequency transducers.² It is important to emphasize that a complete scatterer diameter analysis would require obtaining estimates at different locations within the region of interest in one frame and across independent frames to quantify the variance of each system’s estimate. In our case, the estimation was performed using the final estimate of the backscatter coefficient from each system to make a comparison of the slope of the backscatter coefficient vs. frequency.

Although the best attempt was made to standardize experimental procedures, some factors such as the variations in the location of the transducer over the sphere, differences in the frequency response of each of the transducers, or inclusion of (unnoticed) reverberations and clutter in the sample and/or reference RF data might have caused the small variations among estimates of the backscatter coefficient from imaging systems. Other factors contributing to estimate variance might have been differences in the system settings such as transmit power, gain and digitization methods, as well as the use of high transmit power that may lead to harmonic components in the detected signal, which up to now has not been strongly considered as a source of error in these measurements. Regardless of these factors, the overall agreement of the estimates of the backscatter coefficient is encouraging.

Differences in data processing techniques among different laboratories include variations in the location and size of the ROIs within the sample and the reference, variation in the spectral window size used to compute the power spectra as well as in the overlapping ratio of the sliding spectral analysis window, and different bandwidth selection criteria. As a first attempt to test the effect of the variability of these different RF echo signal processing parameters on attenuation estimates, the Siemens S2000 RF echo signal data (originally processed by the UW group) were reanalyzed by the UIUC group using their specific data analysis approaches. Their resultant α₀ estimates were 0.95dB/cm-MHz for Sphere A and 1.71dB/cm-MHz for Sphere B, which are within the ranges shown in table 5 determined by the UW group. Therefore, in this case the different signal processing techniques did not result in major variability in attenuation estimates when processing the same data set. We are completing a graphical user interface that will allow analyzing RF data acquired from various imaging systems with a choice of signal processing method. The graphical user interface will facilitate testing data analysis strategies more thoroughly.

In spite of these variations, the overall ability of our laboratories to reproduce the frequency dependence of the backscatter coefficient from these samples is very encouraging.^14,15,30 In addition, we emphasize that in this study, the variability in the estimation of the attenuation coefficient is not related to backscatter coefficient variability because laboratory-estimated attenuation values were used by all groups during attenuation compensation instead of each group’s slope estimates.

As a reference, we compared our results to those from the multi-system study performed by Wear et al.³⁰ Estimates of the attenuation coefficient from their phantoms A and B, with known attenuation properties (approximate slopes of 0.4 and 0.7dB/cm-MHz, respectively) were within 0.15 and 0.2dB/cm-MHz, which represent 38% and 29% of the expected values, respectively. In comparison, the maximum discrepancy of attenuation values found in this study was 29%, even though the spherical inclusions had considerably higher attenuation coefficients than the Wear et al. samples. Regarding the backscatter coefficients, Sphere A had a magnitude and frequency dependence similar to that in Wear et al.’s Phantom B, while Sphere B in this study exhibited backscatter coefficient data similar to their Phantom A (as shown in Wear et al.’s fig. 4). In the first case (Sphere A vs. Wear et al.’s Phantom B), multi-system variability between both studies was comparable. In the second case (Sphere B vs. Wear et al.’s Phantom A), inter-system variability from Wear et al. was larger (about two orders of magnitude) than the results from the present study. Possible reasons for the larger discrepancies found in the previous study might be larger variability in data acquisition procedures (the phantoms were scanned at each laboratory instead of performing a joint scanning session), differences in a₀ and η estimation methods (each laboratory used their own estimation methods and reference phantoms or reflectors), more complex phantoms, and possibly lower signal to noise systems than those used here.³⁰ Therefore, the improved standardization of the procedures performed for the present study, particularly using the same sample and reference phantoms and scanning both of them during the same scanning session, helped in achieving better agreement among different groups.

It should be noted that although our results are sorted by measurement systems and transducers, this is not to suggest that specific errors, or particularly accurate results, are due to inherent properties of any of the systems. Rather, currently, QUS results still require understanding the limitations on accuracy imposed by algorithms, by system control settings, and by instrumentation specifications such as bandwidth. We are encouraged by the agreement exhibited among the results reported in this paper. Experiments of this type are important because they help uncover sources of error in QUS measurements and processing procedures, thereby leading to improved accuracy of the estimates. In the final analysis this will lead to improvements in medical ultrasound diagnoses.

One shortcoming of the present experiment may be in precisely representing any effects of speed of sound variations that may have been present in the in vivo experiment. The presence of a water-alcohol solution path between the transducer and the phantom sections instead of pure water as in the in vivo experiments might have led to two differences between the phantom and the in vivo scenarios. In the in vivo case, the 22°C water path had a speed of sound of 1490m/s, while in the phantom case the water-alcohol solution used to avoid damage of the phantom had a speed of sound of 1535m/s, which closely approaches the speed of sound in the phantom sections as shown in table 2. Therefore, any possible refraction effects would have been reduced in the phantom experiment. Second, a difference in the speed of sound of water and tissue in the in vivo experiments might have led to errors in the diffraction correction implicit in the reference phantom method used to estimate the attenuation and the backscatter coefficients. In spite of these differences, the two spherical inclusions of the phantom successfully resembled the shape as well as the attenuation and echogenicity of rodent tumors, as the B-mode images in fig. 3 show.

Another shortcoming of this work is the lack of correlation between the error analysis in this study and the parameter estimation requirements for the specific task of breast tissue classification based on QUS analysis. While the studies reported here were necessary to reduce the suspicion of estimate bias in the inter-laboratory rodent tumor study,^14,15 this work does not provide estimates of the differences between QUS parameter values for various breast tissues. This work also does not yet provide guidance for the maximum QUS parameter estimate variance that would allow confident tissue classification. This work does, however, provide confidence that the parameter values estimated in our animal model work are accurate and can be used to guide studies in human subjects. Even with that, clinical trials with human subjects are necessary to investigate the utility of these techniques.

CONCLUSIONS

The present study has evaluated the accuracy of estimates of the backscatter coefficient and attenuation coefficient by various research groups using different clinical ultrasound equipment and scanning procedures set up for studying a preclinical tumor model. Most systems and transducers estimated attenuation coefficients within one standard deviation of the known value. When the known attenuation coefficient was used in the estimation of the backscatter coefficient, most systems correctly characterized the effective diameter of scatterers as long as ka exceeded 0.6. Although there is still room for improvement regarding methodology standardization for some systems, the present results validate our procedures and encourage their further application in the characterization of in vivo lesions. In addition, this study shows the importance of performing methodology evaluations using well characterized phantoms that emulate subject scanning conditions to make progress in Quantitative Ultrasound.