Plant–soil feedbacks provide an additional explanation for diversity–productivity relationships

Abstract

Plant–soil feedbacks (PSFs) have gained attention for their role in plant community dynamics, but their role in productivity has been overlooked. We developed and tested a biomass-specific, multi-species model to examine the role of PSFs in diversity–productivity relationships. The model predicts a negative relationship between PSFs and overyielding: plants with negative PSFs grow more in communities than in monoculture (i.e. overyield), and plants with positive PSFs grow less in communities than in monoculture (i.e. underyield). This effect is predicted to increase with diversity and saturate at low species richness because the proportion of ‘self-cultivated’ soils rapidly decreases as species are added to a community. Results in a set of glasshouse experiments supported model predictions. We found that PSFs measured in one experiment were negatively correlated with overyielding in three-species plant communities measured in a separate experiment. Furthermore, when parametrized with our experimental PSF data, our model successfully predicted species-level overyielding and underyielding. The model was less effective at predicting community-level overyielding and underyielding, although this appeared to reflect large differences between communities with or without nitrogen-fixing plants. Results provide conceptual and experimental support for the role of PSFs in diversity–productivity relationships.

1. Introduction

Plant productivity often increases with species diversity [1–4]. This relationship represents an important link between community and ecosystem ecology. The ability of more diverse communities to exploit a wider range of resources than less diverse communities (i.e. complementarity) and the greater likelihood that a diverse community will contain a highly productive species than a less diverse community (i.e. sampling effect) both provide explanations for why more diverse communities may be more productive than less diverse communities. However, considerable variation in diversity–productivity relationships remains unexplained by these mechanisms, prompting the suggestion that other mechanisms might also be important [5,6]. Recently, it has been suggested that soil pathogens may be one of these mechanisms [7–9].

Schnitzer et al. [7] and Maron et al. [8] reported that fungal pathogens decrease plant growth more in low-diversity than high-diversity systems, and that this can cause a positive relationship between diversity and productivity. This plant–pathogen relationship provides a strong additional explanation for overyielding (i.e. greater growth of a plant species in a community than in a monoculture), but it is unlikely to explain underyielding (i.e. lesser growth of a plant species in a community than in a monoculture [10–12]). However, a conceptual model that includes both negative (e.g. pathogen-driven) and positive (e.g. mycorrhizal) plant–soil interactions has the potential to explain both overyielding and underyielding [1,2,13].

By measuring plant growth on self-cultivated (‘self’) and non-self-cultivated (‘other’) soils, plant–soil feedback (PSF) research provides an effective way of understanding the net effect of a soil community on plant growth (i.e. both positive and negative plant–soil interactions [14–17]). There is extensive conceptual and empirical support for the role of PSFs in processes of plant community development such as succession, invasion, abundance, persistence and diversity [14,16,18]. However, one problem for understanding the role of PSFs in diversity–productivity relationships is that current PSF models simulate plant proportional abundance, not plant biomass [15,16,18]. As a result, current PSF models do not provide insight into plant productivity. A second problem is that current models are limited to two- and three-species systems and so do not allow insight across a range of diversities [14,16–18]. Finally, PSF models have not been parameterized and tested, so their importance to plant productivity and community development remains largely untested (but see Kulmatiski et al. [18]).

Our goal was to explore the effect of PSFs on plant productivity. We used both conceptual and experimental approaches to do this. First, we developed a biomass-explicit, multi-species PSF model. We ran the model using a wide range of assigned PSF values for plant communities with 2–16 species. This allowed us to regress predicted plant community biomass (i.e. overyielding) against assigned PSF values across a range of species richness, and thus describe a hypothetical relationship between PSFs and overyielding. We then used data from PSF and overyielding experiments conducted in a glasshouse to provide experimental tests of model predictions. First, to explore the general relationship between PSF and overyielding, measurements of overyielding from one experiment were regressed against measurements of PSFs from a second experiment. Finally, to test whether our PSF model could use PSF data to predict overyielding, we parametrized our model with data from the PSF experiment and compared model predictions with results from the overyielding experiment.

2. Material and methods

(a). Model development

Similar to previous modelling approaches, our PSF model is based on three premises. Each plant species cultivates a soil type. The growth of each soil type is a function of the abundance and the growth of the plant that cultivates it. Finally, each plant grows at a rate that is specific to each soil type [18].

More specifically, we model plant growth exponentially, where the growth rate is a function of the proportional abundances of each soil type. However, in contrast to previous continuous-time models [14,16–18], we use a discrete-time approach that provides specific estimates of plant and soil-type biomass (e.g. A and SA; table 1) and is easily implemented in a spreadsheet. Therefore, the growth of plant biomass A at time t is given by A_{t+ 1} = (1 + a_t)A_t, where a_t = (α_APA_t + β_APB_t + γ_APC…) and PA is the proportion of soil type A (e.g. PA_t = SA_t/(SA_t + SB_t + SC_t…)). Parameter definitions are given in table 1.

Table 1.

Parameters definitions for our plant–soil feedback model.

parameter	definition
A, B, … I	plant name
A, B, … I	mass of each plant type
At, Bt, … It	mass of each plant type at time t
at	growth rate of plant A at time t
αA, βA, … ,IA	plant A's growth rate on each soil type
Cix	biomass of species i in community x
Cx	biomass of community x
Dix	species-level overyielding of species i in community x
Dx	community-level overyielding of community x
PAtx	proportion of soil type A at time t in community x
MCi	monoculture biomass of plant i on ‘control’ soils
MOix	mean monoculture biomass of plant i on the ‘other’ soils found in community x
MSi	monoculture biomass of plant i on ‘self’ soils
C-PSFx	community-level plant–soil feedback value of community x
SAt + SBt + … SIt	mass of soil types A through I at time t
S-PSFix	species-level plant–soil feedback value for species i in community x
μ	conversion factor for microbial biomass growth rates

Similarly, growth for a particular soil type is assumed exponential, and the growth rate is a function of the biomass of the plant creating that soil type (i.e. SA_{t +1} = (1 + μa_tA_t)SA_t; table 1). Soil-type biomass is typically assumed to represent microbial biomass [15] and by setting the parameter μ to 5, we assume that microbial growth rates are greater than plant growth rates, consistent with previous work [18]. When parameterized with the same data, this model produces quantitatively similar results to the ordinary differential equation model of a three-species plant community described elsewhere [18].

(b). Calculating plant–soil feedbacks and overyielding

We were interested in PSF values at the species and community levels (S-PSF and C-PSF, respectively). S-PSF values were calculated as S-PSF_ix = (MS_i – MO_ix)/max(MS_i, MO_ix) (table 1 [19–21]). Note that because MO_ix values are unique to each plant community, each species will have a unique S-PSF value for each community in which it is growing. This and the log-ratio calculation of PSF both have the advantage that they produce values that are symmetrical around zero and bounded by ±1 [20]. However, the calculation used here has the advantage that all PSF values represent a proportional increase or decrease in biomass [19–21]. Inasmuch, the calculation used here produces easily interpretable, biologically relevant values. C-PSF values for community x reflect the weighted mean of S-PSF values from a community, where the weights are the proportion of plant i in community x (i.e. C-PSF_x = S-PSF_Ax × MC_A/(MC_A + MC_B + MC_C + …) + S-PSF_Bx × MC_B / (MC_A + MC_B + MC_C + …) + S-PSF_Cx × MC_C / (MC_A + MC_B + MC_C + …)).

Species-level overyielding, D_ix, was also calculated to represent proportional changes in biomass to allow a direct comparison with PSF values. More specifically, for species i in community x, D_ix = (C_ix – MC_i)/max(C_ix, MC_i) (table 1). This overyielding calculation creates an index with similar properties to S-PSF, with a proportional increase or decrease in biomass, symmetrical around zero and bounded by ±1 [21]. This overyielding calculation has been criticized because it does not allow interpretation across a range of environments [22], but this was not a concern for this study, where the calculation was used to analyse theoretical model dynamics with competitively equivalent species (see below) and experimental results from a single glasshouse experiment. Community-level overyielding was calculated as D_x = [C_x – (MC_a + MC_b + MC_c…)]/max[C_x, (MC_a + MC_b + MC_c…)] (table 1).

(c). Modelled plant–soil feedback effects on overyielding

To illustrate model dynamics, we performed model simulations using a wide range of hypothetical plant growth rates on ‘self’ and ‘other’ soil types (i.e. PSF values). More specifically, the model was run for every tenth of an S-PSF value from −0.9 to +0.9, and for each species richness level between 2 and 16 species. S-PSF values were attained by assigning the same final biomass and S-PSF value to all plants in the community (electronic supplementary material, appendix A). For example, all plants in a community with 10 species could be assigned a final biomass of 1.0 (e.g. 1 g) on ‘other’ soils and 0.5 on ‘self’ soils. This would result in each species, and the whole community, realizing a −0.5 PSF. This approach of assigning the same PSF value to all species isolated the effects of species richness and PSF on overyielding from the idiosyncrasies of the many potential within-community interactions (e.g. species B was a strong competitor with a weak negative PSF relative to species C). A convenient consequence of running the model with species that realize the same final biomass value and the same S-PSF value is that species- and community-level PSF values are equivalent (i.e. a community composed of species only with −0.5 PSFs will have a community-level PSF value of −0.5).

All plants were assumed to start growth as seed (0.002 g). The model was run for 40 time steps, so time-step-specific growth rates were calculated as (⁴⁰√F/I) − 1, where F is final biomass and I is initial biomass (i.e. 0.002 g). All model runs with negative PSF values used final plant biomass on ‘self’ soil values of less than one (e.g. 0.5 g) and plant biomass on ‘other’ soil values of one (i.e. 1 g; electronic supplementary material, appendix A). All model runs with positive PSF values used final plant biomass on ‘self’ soil values of one and plant biomass on ‘other’ soil values of less than one (e.g. 0.5 g; electronic supplementary material, appendix A). These values were chosen because they were similar to plant biomasses observed in our glasshouse experiment.

Thus, PSF values were effectively model input, and model output was community-specific plant species’ biomasses, which were used to calculate overyielding. More specifically, hypothetical model predictions of plant biomass in communities were used to estimate C_ix. A simple exponential growth model based on growth rates of plants on ‘control’ soils was used to estimate plant biomass in monoculture, MC_i (as in [18]). Finally, MC_i was divided by the initial proportion of the species in the community so that C and M values both describe plant growth in similar soil volumes.

(d). Testing model predictions with experimental data

Two approaches were used to test model predictions with experimental data. First, to test for a general relationship between PSF and overyielding, measurements of overyielding in three-species communities were regressed against measurements of PSFs from a second experiment. Second, to test whether our PSF model could use PSF data to predict overyielding, we parametrized our model with data from the PSF experiment and compared model predictions with results from the overyielding experiment.

(e). Plant–soil feedback experiment

In the PSF experiment, a standard two-phase ‘self’ versus ‘other’ approach was used [19,20,23]. S-PSFs were determined for eight plant species; four were native and four were non-native to the Intermountain West, USA (i.e. where soils used in the experiment were collected). S-PSFs were determined in a split-factorial design, where all native plants were grown on all native plant-cultivated soils, and all non-native plants were grown on all non-native plant-cultivated soils (table 2). Native and non-native plant communities were treated separately in the experiments because both community types are abundant in the study region, yet the two community types typically do not overlap [24].

Table 2.

Species combinations in the six experimental plant communities.

community	species 1	species 2	species 3
native 1	Hesperostipa comata	Koeleria cristata	Lupinus sericeusa
native 2	H. comata	K. cristata	Pseudoroegneria spicata
non-native 1	Agropyron cristatum	Bromus tectorum	Centaurea diffusa
non-native 2	A. cristatum	B. tectorum	Medicago sativaa

^aNitrogen-fixing species.

In phase I of the PSF experiment, 480 pots (20 cm height) were filled with 1 litre of a sterilized growth medium (a mixture of 7 : 1 sand and peat moss) that was inoculated with 50 ml field soil or 5 per cent by volume. Five germinated seeds from each of the eight target species were planted into each of 60 randomized replicate pots. After one month, each pot was weeded to include the three largest individuals. Plants were grown for three months, then harvested. Growth at the end of phase I was used as MC_i values when weighting C-PSF values. At the beginning of phase II, 16 ml of Hoagland solution was added to each pot to compensate for nutrients lost as a result of plant harvesting, minimize plant–nutrient feedbacks and isolate plant–microbe feedbacks [23]. In phase II, five germinated seeds from each plant species were planted in 60 pots: 15 with ‘self’ soils and 15 with soils from each of the other three species from the same origin (table 2). After one month in phase II, each pot was weeded to include the three largest individuals. After three months in phase II, above-ground biomass was harvested, dried to constant weight at 70°C and weighed. Final biomass values were used to calculate species- and community-level PSFs using the calculations described earlier. This design allowed the calculation of 12 species-level PSFs (i.e. for three non-native species growing in each of two non-native communities, and for three native species growing in each of two native communities) and four community-level PSFs that were relevant to the overyielding experiment (table 2).

(f). Overyielding experiment

In the overyielding experiment, five germinated seeds from each of the eight target species were grown in eight replicate 1-litre pots with control (uncultivated) soils to determine plant growth in monoculture (i.e. MC_i). After one month, pots were weeded to include only the three largest individual of each species. Second, the four target communities (table 2) were grown in 15 replicate pots in each of six soil types. Different soil types were used to provide inference on plant community growth in a range of soil types. More specifically, 360 pots were filled with 3 litres of inoculated growth medium and planted with 60 replicates of each of four monocultures or two communities: monocultures (Agropyron cristatum, Centaurea diffusa, Lupinus sericeus, Pseudoroegneria spicata) and communities (native 2 and non-native 2; table 2). After three months, vegetation was clipped from these pots, the pots were treated with 48 ml Hoagland solution, and each of the four target communities was planted into these soils, producing 24 community–soil type combinations. After three months, the biomass values of each species in each community were used to calculate overyielding. This design allowed the calculation of overyielding for each of three plant species in each of 24 plant community–soil type combinations (i.e. native 1, native 2, non-native 1 and non-native 2 on six soil types), resulting in 72 species-level overyielding values and 24 community-level overyielding values.

For these experiments, soils and seeds were collected from a shrub-steppe ecosystem in Winthrop, WA, USA (48°29′ N, 120°07′ W; for a more detailed site description, see [24]). Glasshouse experiments were conducted at the USDA-ARS Forage and Range Research Laboratory in Logan, UT, USA.

3. Results

(a). Theoretical model results

Regardless of community diversity, the PSF model predicts that plant species and communities with negative PSF values overyield (figure 1). The model also predicts that plant species and communities with positive PSFs underyield (figure 1). The slope of this relationship increased from −0.66 to −0.97 as community richness increased from 2 to 16 species. Plotting overyielding as a function of species richness for several community-level PSF values showed that overyielding effects caused by PSF saturate at low species richness (figure 2).

Figure 1.

Community-level overyielding predicted as a function of community-level plant–soil feedback in 2- (solid line), 3- (dotted line) and 16-species (dashed line) communities. Positive and negative PSFs and overyielding are standardized to reflect proportional changes in biomass.

Figure 2.

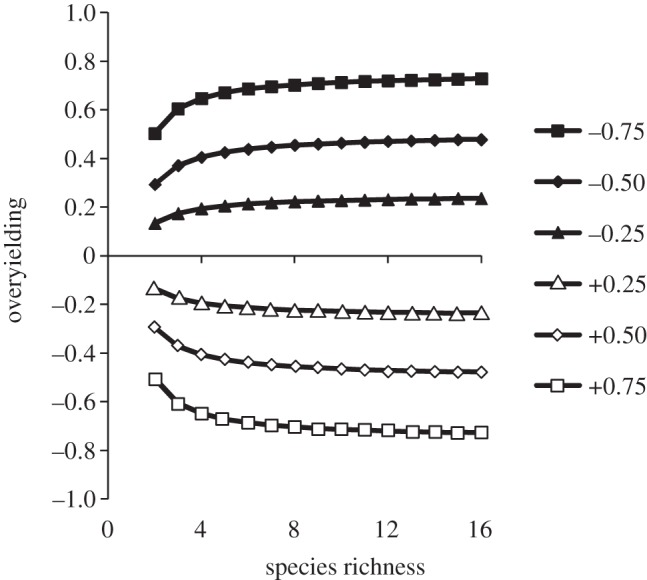
Model predictions of community-level overyielding as a function of species richness for six community-level plant–soil feedback values (ranging from −0.75 to +0.75). Overyielding is standardized to reflect proportional changes in biomass.

(b). Experiment results

Half of the S-PSF values (electronic supplementary material, appendices B and C; figure 3) and three of four C-PSF values (figure 4) were negative. S-PSF values ranged from −0.30 to +0.16, and C-PSF values ranged from −0.18 to 0.15 (electronic supplementary material, appendix B). Most species (46 of 72 tests) produced more biomass in communities than would be predicted from monocultures (i.e. overyielded; figure 3; electronic supplementary material, appendices B and D). Roughly half (13 of 24) of the community–soil type combinations produced more biomass than would be predicted from monocultures (i.e. underyielded; figure 4). However, a clear difference was seen between communities with or without nitrogen-fixing plants. Specifically, 11 of 12 overyielding values for communities without nitrogen-fixing plants were positive, and 10 of 12 overyielding values for communities with nitrogen-fixing plants were negative.

Figure 3.

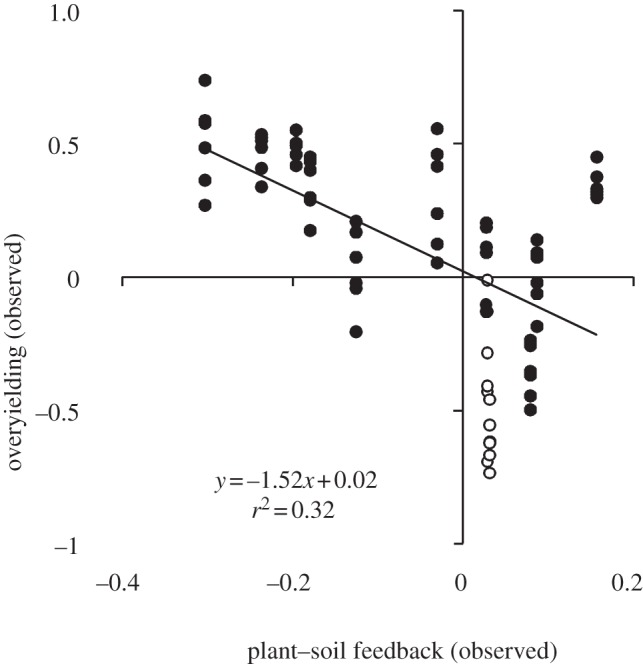
Observed species-level overyielding as a function of measured species-level plant–soil feedback. Each point represents the mean value for each of three species grown in each of 24 community–soil type combinations, for a total of 72 values. Open and filled circles represent data from nitrogen-fixing plants and non-nitrogen-fixing plants, respectively.

Figure 4.

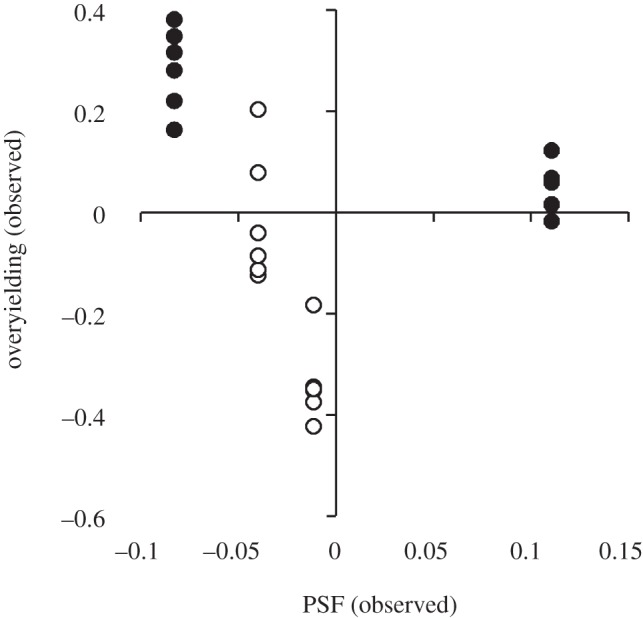
Observed community-level overyielding as a function of observed community-level plant–soil feedback (PSF). Community-level PSF and overyielding were calculated as the mean of community-specific species-level PSFs and species-level overyielding, respectively. Each point represents the mean value from one of 24 plant community–soil type combinations. Open and filled circles represent data from communities with and without nitrogen-fixing plants, respectively.

Species-level overyielding was negatively correlated with species-level PSF both with (figure 3; F_1,70 = 33.34, p < 0.001) and without results from nitrogen-fixing plants (F_1,58 = 28.64, p < 0.001, slope = −1.1, r² = 0.33). The negative relationship between PSFs and overyielding was driven more by native (F_1,34 = 39.12, p < 0.001, slope = −1.8, r² = 0.54) than non-native species (F_1,34 =3.69, p = 0.06, slope = −0.97, r² = 0.10). Community-level overyielding was not correlated with C-PSF (figure 4; F_1,22 = 1.04, p = 0.32). The lack of a correlation, however, was obviously driven by differences in the response of nitrogen- and non-nitrogen-fixing species. In a post hoc test, community-level overyielding was negatively correlated with community level PSF for nitrogen-fixing (figure 4; F_1,10 = 27.00, p < 0.001) and non-nitrogen-fixing communities (figure 4; F_1,10 = 38.30, p < 0.001) when analysed independently. Inference from these post hoc tests, however, is limited because only two communities were available for nitrogen- and non-nitrogen-fixing communities.

(c). Testing a parametrized model

Model predictions of species-level overyielding were positively correlated with species-level measurements of overyielding (figure 5; F_1,70 = 18.67, p < 0.001); however, there was a negative correlation between predicted community-level overyielding and observed overyielding (figure 6; F_1,22 = 7.29, p = 0.01). This relationship was obviously driven by differences in the response of nitrogen- and non-nitrogen-fixing species. In a post hoc test, there was a positive correlation between predicted community-level overyielding and observed overyielding for nitrogen-fixing (figure 4b; F_1,10 = 27.60, p < 0.001) and non-nitrogen-fixing species (figure 6; F_1,10 = 38.11, p < 0.001) when analysed independently, although, again, inference from these tests is limited.

Figure 5.

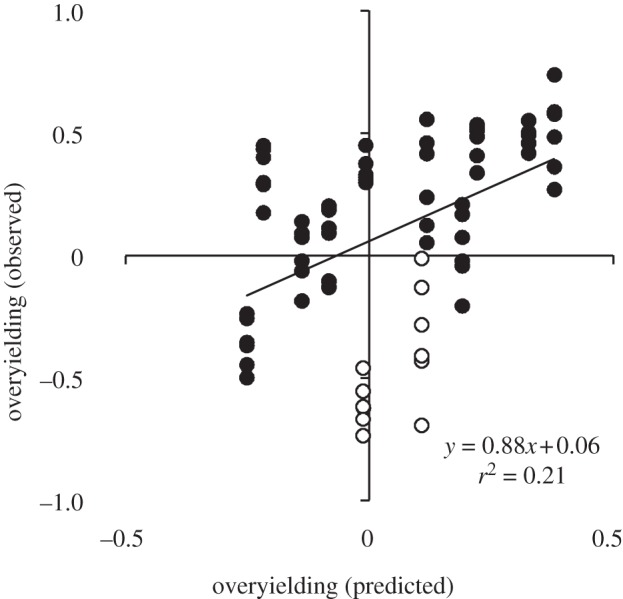
Observed species-level overyielding as a function of species-level overyielding predicted from a three-species PSF model. The model was parametrized with an independent dataset, as described in the text. Each point represents the mean value for each of three species grown in each of 24 community–soil type combinations, for a total of 72 values. Open and filled circles represent data nitrogen-fixing plants and non-nitrogen-fixing plants, respectively.

Figure 6.

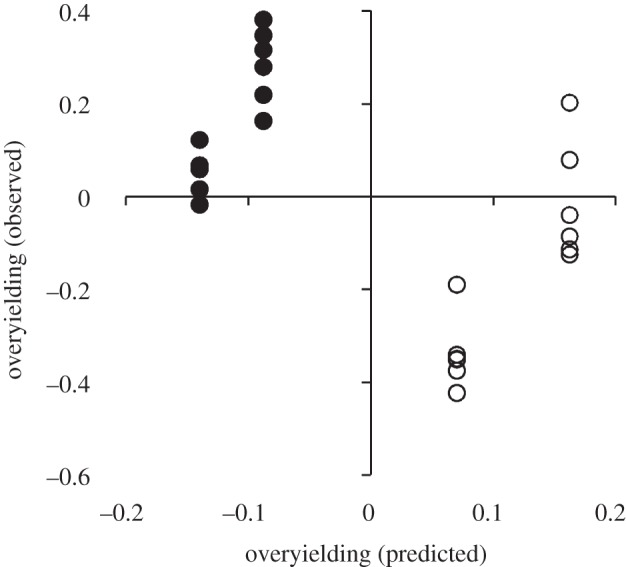
Observed plant community overyielding as a function of community-level overyielding predicted from a three-species plant–soil feedback (PSF) model. The model was parametrized with an independent dataset, as described in the text. Community-level PSF and overyielding were calculated as the mean of community-specific species-level PSFs and species-level overyielding, respectively. Each point represents the mean value from 24 plant community–soil type combinations. Open and filled circles represent data from communities with and without nitrogen-fixing plants, respectively.

4. Discussion

Using a PSF conceptual model, we explored the role of PSFs on diversity–productivity relationships. Our model predicts that plant species and communities with positive PSFs should underyield, and species and communities with negative PSFs should overyield. More specifically, our model predicts that as species richness increases, the relationship between PSFs and overyielding approaches a value of −1 : 1. This prediction is consistent with PSF values (−0.6; [25]) and overyielding values (0.7; [10,11]) reported in the literature [4,26,27], although this observation may be confounded by many experimental and plant growth factors. Model predictions were also supported by our experimental data showing (i) a negative correlation between species-level PSFs and species-level overyielding, and (ii) a positive correlation between observed and predicted species-level overyielding values. Community-level results were more difficult to interpret because our experiments included data from only two nitrogen-fixing communities and two non-nitrogen-fixing communities, and these two community types demonstrated different productivity responses. However, taken as a whole, hypothetical and experimental results suggested that PSFs may help explain why some species underyield and why other species overyield in communities, although testing with a larger number of communities is needed.

Essentially, the mechanism we are proposing to explain how PSFs influence the diversity–productivity pattern is intuitive. Our model assumes that plants in monoculture grow on 100 per cent ‘self’ soils. Plants in two-species communities grow in 50 per cent ‘self’ soils, whereas plants in three-species communities grow in 33 per cent ‘self’ soils, and so on, with plants in 16-species communities growing in 6 per cent ‘self’ soils. While the exact nature of the relationship between plant roots and different soil types may not be this simple, it is probable that the effect of ‘self’ soil diminishes with increasing diversity, and saturates at low levels of diversity, as predicted by our model. A prediction of our model is that a plant with a positive PSF will attain the greatest biomass in monoculture (i.e. where it realizes the greatest exposure to ‘self’ soil) and a plant with a negative PSF will attain the greatest biomass in the most diverse communities (i.e. where it realizes the least exposure to ‘self’ soils [7,8]). As diversity increases, this mechanism results in a diminishing decrease in growth for plants with positive PSFs (i.e. results in underyielding) and results in a diminishing increase in growth for species with negative PSFs (i.e. results in overyielding). Model results for communities with negative PSFs (figure 2) were surprisingly similar to diversity–productivity relationships measured in previous studies [3,4,6].

Species with the greatest growth rates in monocultures are often not the strongest competitors in communities [27,28]. Traditionally, this underyielding has been assumed to reflect inherent trade-offs between fast growth and nutrient-use efficiency [29]. Our results suggest that positive PSFs may provide an additional explanation for underyielding and therefore some of the unexplained variation in species-level productivity responses to increasing diversity. More specifically, species with positive PSFs realize their greatest growth rates in monoculture because they only grow well on beneficial, ‘self’ soils.

While much variability remained unexplained, species-level PSF-overyielding relationships observed in our experiments were close to the theoretical prediction (i.e. slope of −1), especially for the non-nitrogen-fixing species. Community-level relationships were less clear. There was no pattern between community-level PSFs and community-level overyielding when data from all community types were analysed; however, post hoc tests of data from nitrogen-fixing and non-nitrogen-fixing communities both individually supported model predictions. Unfortunately, only two communities of each type were used in this study, so our inference to a wide range of nitrogen-fixing or non-nitrogen-fixing communities is limited. We suggest that nitrogen-fixing species underyielded more than predicted by our PSF model because nitrogen-fixing species are likely to continuously facilitate the growth of competitors while the two-phase PSF approach measures only the legacy effect of nitrogen fixation [18]. Future studies with a larger number of nitrogen-fixing and non-nitrogen-fixing communities measured under field conditions will be needed to better test the role of PSFs on overyielding.

Several simplifying assumptions were made in our model. Density-dependent growth, competitive interactions, spatial effects, nutrient drawdown, niche partitioning, herbivory, plant life-history traits and dispersal effects were all ignored. These factors have been found to be important in previous models [14–18] suggesting that incorporating the biomass-explicit consideration of PSFs presented here with these other factors may greatly improve understanding of plant community development [30–32]. Multi-factor experiments that assess the relative importance of these different factors will be especially important.

Model analyses suggested new factors to be considered in future PSF models. Our model assumed that each plant interacts with the soils created by all other species. This becomes less and less likely as species diversity increases because a single plant's roots are likely to forage in the rhizosphere of one to several other species, but are unlikely to forage in the rhizospheres of 15 other species. This was not a problem in this study because (i) theoretical analyses of model dynamics were explored assuming that all ‘other’ species have the same effect on a target plant (electronic supplementary material, appendix A), and (ii) our experimental tests included only data from three-species communities in which root contact was likely to be extensive among all plants. Future studies can address this problem by using a spatially explicit modelling approach that limits root contact among adjacent individuals. Our model also relied on exponential growth rates for both plants and soils. These growth rates produced reasonable biomass estimates for three-month simulations, but longer-term simulations will require that some form of density dependence or carrying capacity be included. Finally, our model assumed that soil microbial communities respond immediately to plant growth, although this response may be slow in field soils [33].

PSFs have rapidly gained attention as an important mechanism of plant community development. We have adapted the PSF concept to provide insight into plant productivity–diversity relationships. Our conceptual model and experimental results demonstrate how PSFs may provide an additional explanation for diversity–productivity relationships. There are various other explanations for under- and overyielding, and without studying the relative importance of each of these (ideally in a field setting where plant productivity is allowed to equilibrate), we cannot yet determine the relative importance of PSFs in this process. Future research should integrate PSFs with other explanations of the diversity–productivity relationship to improve understanding of this central concept in ecology.