Testing the independent species’ arrangement assertion made by theories of stochastic geometry of biodiversity

Abstract

The assertion that the spatial location of different species is independent of each other is fundamental in major ecological theories such as neutral theory that describes a stochastic geometry of biodiversity. However, this assertion has rarely been tested. Here we use techniques of spatial point pattern analysis to conduct a comprehensive test of the independence assertion by analysing data from three large forest plots with different species richness: a species-rich tropical forest at Barro Colorado Island (Panama), a tropical forest in Sinharaja (Sri Lanka), and a temperate forest in Changbaishan (China). We hypothesize that stochastic dilution effects owing to increasing species richness overpower signals of species associations, thereby yielding approximate species independence. Indeed, the proportion of species pairs showing: (i) no significant interspecific association increased with species richness, (ii) segregation decreased with species richness, and (iii) small-scale interspecific interaction decreased with species richness. This suggests that independence may indeed be a good approximation in the limit of very species-rich communities. Our findings are a step towards a better understanding of factors governing species-rich communities and we propose a hypothesis to explain why species placement in species-rich communities approximates independence.

1. Introduction

One of the principal goals of ecology is to understand the processes and mechanisms that control the distribution, abundance and coexistence of species [1,2]. Classical theoretical ecology predicts that two species competing for the same resources cannot stably coexist (the exclusion principle by Gause [3]). However, for reasons that are poorly understood the number of competing species often exceeds the number of limiting resources [4]. The best-known examples are the high diversity of species in tropical forests and coral reefs [5] and the paradox of the plankton [4,6]. In tropical forests, several hundreds of tree species can be found within small areas [7] and, for example, up to 300 tree species per hectare have been recorded in the Amazonia [8].

For more than 90 years or so, major efforts have been made in field and theoretical ecology to resolve this paradox [5,9–13], and about 10 years ago investigations of this issue had gained considerable momentum and new directions since Stephen Hubbell revived neutral theory in community ecology [5]. Surprisingly, neutral models have been remarkably successful at reproducing several empirically observed macroscopic patterns for communities with organisms at the same trophic level such as tropical forests, grassland, shrubland, birds, groups of insects, fishes, marine Diatomea or coral reefs, although they ‘contradict almost everything that ecologists have to come to understand about species diversity and its maintenance in communities’ [14]. Recently, McGill [15] synthesized six theories of biodiversity that produce, based on a few underlying principles, macroscopic community patterns such as species-area curves (SARs), species-abundance distributions (SADs) and decay of similarity of distance. He showed that these theories use the same three rules or assertions to describe a stochastic geometry of biodiversity, namely: (i) intraspecific clustering, (ii) the species abundance distribution shows typically many rare and few common species (i.e. a hollow curve distribution), and (iii) interspecific individuals are placed without regard to individuals of other species. McGill [15] argued that these three rules appear sufficient for explaining several macroscopic community patterns.

Empirical evidence in support of McGill's assertion (iii) of independent species placement is, however, lacking although models assuming no species interactions are successful in predicting diversity patterns [5,15–17]. By contrast, there is good empirical evidence that most tropical tree species show intraspecific aggregation [16–18] and that species-rich communities contain usually many rare and a few common species [5,19].

The assertion that species are placed independently is also in apparent contradiction to the vast literature in ecology devoted to the study of species interactions [10,20]. However, evidence for the importance of species interactions stems mostly from species-poor communities [21], whereas the few studies that explored the full array of spatial species interactions in fully mapped species-rich communities found that only a few species pairs showed detectable spatial interactions [20,22–24].

The question arises as to whether the effect of species interactions in species-rich communities may be overpowered by stochastic effects [20,22]. For example, Hubbell and Foster [25] noted that in species-rich forests two individuals of the same species may share only a few common species among their nearest neighbours. In the Barro Colorado Island (BCI) forest the 20 nearest neighbours of a given tree comprised on average 14 different tree species [26]. Individuals of a given species are therefore often exposed to considerably different biotic neighbourhoods. This suggests that pairwise interactions may be weak on average, despite the existence of a few stronger interactions [15,20,22,27]. On evolutionary timescales, such diverse and unpredictable local assemblages of competitors around individual plants would not allow directional specialization, but species may instead converge on similar life-history strategies that are competitively equivalent [26]. The hypothesis of diffuse coevolution of functionally similar species that may produce ecological equivalence among species traits is a cornerstone of the neutral theory [5,26].

One way of assessing the evidence for species interactions in plants is to analyse their spatial patterns [22–24,28,29]. Because plants cannot move and mainly interact with their close neighbours [28], their spacing may conserve an imprint of neighbourhood interactions that could be detected using point pattern analysis [21,22,24]. This approach is promising because the intraspecific spacing of plants is also closely related with potential coexistence mechanisms [30]. For example, intraspecific clustering and interspecific segregation may retard competitive exclusion because the relative importance of interspecific versus intraspecific competition is reduced [29–31]. Analysis of the bivariate spatial patterns of all pairs of species allows testing if the interspecific arrangement of species is indeed independent as assumed by assertion (iii) [20,22–24]. However, such analyses are challenging because they require complete mapping of large plots of a species-rich community and because of difficulties in teasing apart two major, yet contrasting factors that can cause non-independence: habitat association may mediate positive or negative association and direct species interactions such as competition or facilitation [21–23].

In this study, we use spatial point pattern analysis [28,32,33] to test the assertion of species independence with data from three forests of different species richness including a 50 ha plot of neotropical forest at BCI, Panama (more than 300 species of trees and shrubs), a 25 ha plot of tropical forest in Sinharaja, Sri Lanka (more than 200 species) and a 25 ha plot temperate forest in Changbaishan (CBS), China (52 species). Because habitat association and species interactions may occur simultaneously, we conduct one analysis studying their joint effects and one analysis studying selectively species interactions. In analysis 1 we therefore analyse pairwise interspecific association patterns among large trees (greater than 10 cm diameter at breast height (dbh)) with respect to overall spatial patterning (potentially caused by habitat association and species interactions). This analysis explores how trees of a given species j are distributed within local neighbourhoods of the trees of a focal species i and therefore how frequently different species meet and have the opportunity to interact. In analysis 2, we approximately factor out larger-scale effects of the environment and analyse selectively small-scale interspecies interactions. This analysis explores how trees of species j behaved when they were close to trees of species i and therefore if they were arranged closer or further away than expected by the local density of species j. For all three forests, the methodology presented by Wiegand et al. [22] and Wang et al. [21] was used. This allows us to synthesize the results for three forests with different species richness.

We expect that species-rich forest communities should approximate species independence more closely than species-poorer communities. Our general hypothesis is that stochastic effects dilute species associations in highly diverse communities. This is because the density of individual species decreases with increasing richness, which lowers the probability that a species j tree is among the nearest neighbours of a species i [20,22,25,26]. As a result of the low rate at which individuals of two species meet, the statistical tests will detect fewer significant effects. Consequently, the occurrence of species associations or interactions in spatial patterns should decrease with increasing species richness. With respect to overall spatial patterning (i.e. habitat and interactions, analysis 1) it follows from our general hypothesis that the proportion of species pairs with ‘no association’ should increase with species richness (specific hypothesis H1a) and that the proportion of species pairs showing segregation should decrease with species richness (specific hypothesis H1b). The latter implies that the coexistence mechanism of intraspecific aggregation and interspecific segregation [30] should be more important in communities with fewer species. With respect to species interactions (analysis 2) it follows from our general hypothesis that the proportion of species pairs with non-significant interspecific small-scale interactions should increase with species richness (specific hypothesis H2). In this comparative study we found strong support for our hypotheses.

2. Methods

(a). Study sites

We collated data on spatial distributions of tree species from three forest plots. The 50 ha plot on BCI [34], Panama (9°10′ N, 79°51′ W) has a moist, lowland, tropical climate, with rainfall 2500 mm yr⁻¹, a strong 3.5 month dry season and a year-round mean daily temperature of 27°C. Elevation ranges from 120 to 155 m. The plot is described in detail by Hubbell and Foster [35], and for details of census methods see Condit [36]. The 25 ha plot at Sinharaja (06°24′ N, 80°24′ E) is a tropical forest without a distinct dry season, and annual rainfall averaged 5016 mm yr⁻¹, with a range from 4087 to 5907 mm. Annual daily maximum and minimum temperatures were 24.7°C and 20.4°C, respectively. Elevation ranges from 424 to 575 m above mean sea level and includes a valley lying between two slopes. Details of the plot are provided in Gunatilleke et al. [37]. The 25 ha plot CBS, China (42°23′ N, 128°05′ E) is located in broadleaved Korean pine (Pinus koraiensis) mixed forest and has a temperate continental climate with long cold winters and warm summers, approximately 700 mm rain yr⁻¹ which mostly falls from June to September (490–500 mm). Elevation ranges from 791.8 to 809.5 m, and the mean annual temperature is 2.9°C, with a mean January temperature of −13.7°C and a mean July temperature of 19.6°C. The plot is described in detail by Wang et al. [21]. Additional information on the plots is provided in the electronic supplementary material, table A1.

In the present analyses, we used data from the 1995 BCI census [38] and the 1996 Sinharaja census and restricted our analysis to the 62 and 46 species which had more than 70 individuals with dbh larger than 10 cm, respectively. For species with fewer individuals, stochastic effects become too large for the purpose of our study. To be consistent with Wang et al. [21] we included in the analysis of the CBS plot 15 species which had more than 50 individuals with dbh greater than 10 cm.

(b). Spatial pattern analysis

We used three summary statistics applicable to completely mapped bivariate point patterns, the K-function K₁₂(r) [39,40], the pair correlation function g₁₂(r) [32,41] and the cumulative nearest neighbour distribution function D₁₂(r) that gives the probability that the nearest species 2 neighbour of an individual of species 1 is located within distance r [33]. The quantity λ₂K₁₂(r) can be interpreted as the number of species 2 plants within distance r from species 1 plants where λ₂ is the density of species 2 plants in the study area (=the number of plants of pattern 2 divided by the area of the study plot). The pair correlation function is related to the derivative of the K-function, i.e. dK₁₂(r)/dr = g₁₂(r)2πr [33], and λ₂g₁₂(r) can be interpreted as the density of species 2 plants at distances (r−dr/2,r + dr/2) from species 1 plants, where dr is the ‘ring width’. We also calculated an index of local dominance [23], L_f(r), which is the average proportion of conspecific individuals within given neighbourhoods with radius r of the individuals of the focal species f.

We followed the implementation of the three statistics using the software Programita [22,32], which can be requested from the first author. We selected for all analyses a spatial resolution of 2 m, and for analysis 2 a ring width of dr = 6 m. This is a sufficiently fine resolution compared with the dimensions of the plots (1000 × 500 m² and 500 × 500 m²) and sufficiently fine to answer our questions [21,22].

(c). Analysis 1. Categorization of overall species–species associations

To categorize the possibly heterogeneous species–species associations, we used a two-dimensional classification scheme [21,22] based on the K-function K₁₂(r) and the nearest neighbour distribution function D₁₂(r) (see electronic supplementary material, appendix A). This allowed us to quantify how the trees of a given species 2 were distributed within local neighbourhoods of the trees of a focal species 1, irrespective of whether spacing was caused by external effects of the environment, by internal effects of species interactions or by intraspecific clustering.

To distinguish the different types of spatial associations (figure 1) from those that may arise purely by chance, we compared the observed bivariate point patterns with a null model in which the locations of the focal species remained unchanged, but trees of species 2 were distributed randomly and independently of the locations of species 1 (i.e. a homogeneous Poisson process [32]). The expectations of the summary statistics under the null model yield K₁₂(r) = πr² and D₁₂(r) = (1−exp(−λ₂πr²)). The two axes of the classification scheme [21,22] were defined as:

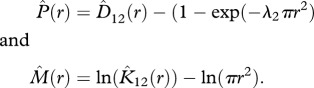2.1

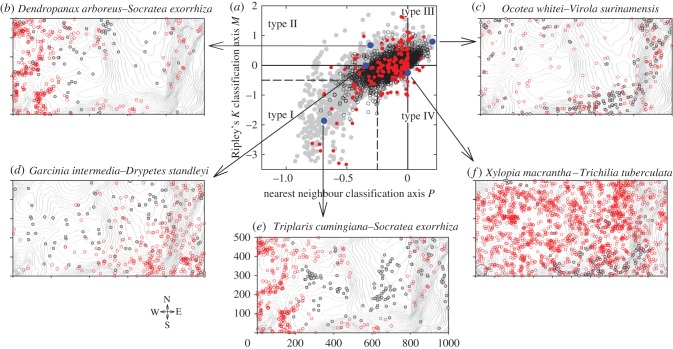
Figure 1.

Classification of association patterns at the BCI 1000 × 500 m² forest dynamics plot. (a) Allocation of the associations of the 3782 species–species pairs based on the classification axes defined in equation (2.1) (black open circles) compared with those found at the Sinharaja forest (Sri Lanka; grey dots) and the CBS plot (China; red dots). The axis P is positive (negative) if there are on average more (less) stems of species 2 at distance r_L = 30 m from species 1 stems than expected, and the axis M is positive (negative) if the probability that a stem of species 1 has its nearest species 2 neighbour within distance r_L is larger (smaller) than expected. The blue dots locate the four examples shown in panels (b–f). The dashed line indicates the area of strong segregation. (b) Example of type II association with partial overlap; black circles: species 1; red circles: species 2. (c) Example of type III association with mixing. (d) Example of a transition between type I and type II association. (e) Example of type I association with strong segregation. (f) Example of a type IV association, which is only possible because of a strong second-order effect of pattern 1.

We subtracted the theoretical values under the null model to move the null expectation onto the origin of the scheme and log-transformed the K-function to weight positive or negative departures from the null model in the same way [22]. The hat symbol indicates the observed value.

The two-axis scheme allows for the identification of four fundamental types of bivariate association: type I: ‘segregation’ [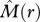 < 0 and 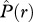< 0] where individuals of species 2 occur on average less frequently within species 1 neighbourhoods than expected by chance alone; type II: ‘partial overlap’ [i.e. 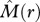> 0 and 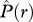< 0], where some neighbourhoods of species 1 contain more individuals of species 2 and others less; type III: ‘mixing’ [i.e. 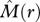> 0 and 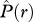> 0] where individuals of species 2 occur on average more frequently within species 1 neighbourhoods; and type IV: [ 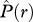> 0, 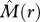< 0], which can only arise if strong second-order effects occur. Species pairs that show for a given neighbourhood r non-significant effects in both summary statistics are classified as ‘no association’ type and will be located close to the origin of the scheme. Further details of the scheme can be found in the electronic supplementary material, appendix A.

(d). Analysis 2. Small-scale species–species interactions

In analysis 1, two species may show significant effects even if they do not show direct interactions. This may happen if the two species occupy only subareas A1 and A2 of the study plot [22]. For example, imagine that species 1 and 2 both exist only in half of the landscape (A1) and assume that they are both independently distributed in A1. Analysis 1 would indicate strong mixing because they are more closely associated in the data than they would be if we moved species 2 to be in random positions on the landscape. However, we can approximately factor out this effect if we move species 2 only locally. In this case the resulting large-scale pattern will look similar to the observed large-scale pattern, and it is unlikely that a significant effect will be detected [32]. This null model leaves the density λ₂(x) of species 2 approximately unchanged, but displacement of species 2 within local neighbourhoods with radius R removes potential signals of small-scale interactions at scales r < R. Thus, under approximate separation of scales [21], we can selectively study the small-scale interactions by using a null model which randomizes the data conditionally on the observed larger-scale pattern [22,32].

Technically, we implemented this null model as a heterogeneous Poisson process [32] for the second species (the individuals of the focal species remain unchanged) and we selected a value of R = 30 m (for a justification, see the electronic supplementary material, appendix A and Wang et al. [21]). The non-cumulative pair correlation function g₁₂(r) is the appropriate summary statistic here because it allows for a more direct quantification of scale-dependent interactions than the cumulative K-function where, for instance, the effect of repulsion at smaller distances is only gradually diluted out by independence at larger distances [28,32]. However, for easier comparison between analyses 1 and 2 we present results based on the K-function (see the electronic supplementary material, appendix B). We tested all pairs of species, i.e. species 1 versus species 2 and species 2 versus species 1 since we cannot assume that the interaction would be symmetric.

(e). Significance tests

The empirical summary statistics were compared with those generated by 199 simulations of the homogeneous or heterogeneous Poisson null model. The overall fit of the null model was then determined with a goodness-of-fit test [42] which reduces the scale-dependent information contained in a summary statistic (over an appropriate distance interval) into a single test statistic u_i. The u_i were calculated for the observed data (i = 0) and for the data created by the i = 1, …, 199 simulations of the null model. If the rank of u₀ among all u_i was larger than 195 or 190, the data showed a significant departure from the null model with error rate α = 0.025 or 0.05, respectively [33,42].

In analysis 1, we tested over the 2–50 m distance interval. A significant departure from the null model occurred if at least one of the two summary statistics was significant with a 2.5 per cent error rate (this yields for two summary statistics an error rate of ≈5%). To stabilize the variance, we used the transformation L₁₂(r) = (K₁₂(r)/π)^0.5−r instead of K₁₂(r) [28,33]. In analysis 2, the goodness-of-fit test was conducted with the pair correlation function over the 2–30 m distance interval with a 5 per cent error rate. To obtain an overview of changes in spatial association structure with neighbourhood size r, we counted in both analyses the proportions of the different association or interaction types separately for each value of r (see the electronic supplementary material, appendix A).

3. Results

(a). Analysis 1. Categorization of overall species–species associations

Figure 1a shows the resulting association types of species pairs for 30 m neighbourhoods for BCI (black dots), Sinharaja (grey dots) and CBS (red dots). Figure 1b–f show for illustrative purposes the tree positions of five species pairs that correspond to extreme cases in the BCI classification scheme. The first observation is that the three schemes have a similar structure, but that of Sinharaja shows more extreme cases of segregation or mixing than BCI. This observation is also valid for other neighbourhoods (figure A1 in the electronic supplementary material). The scheme of the CBS forest shows (similarly to that of the Sinharaja forest) more extreme cases of segregation than that of the BCI forest. To quantify the proportion of species pairs with strong segregation we defined all cases where P < −0.25 and M < −0.5 (dashed lines in figure 1a) as strong segregation. We found that 3.2, 25.7 and 12.4 per cent of all species pairs at BCI, Sinharaja and CBS, respectively, showed strong segregation.

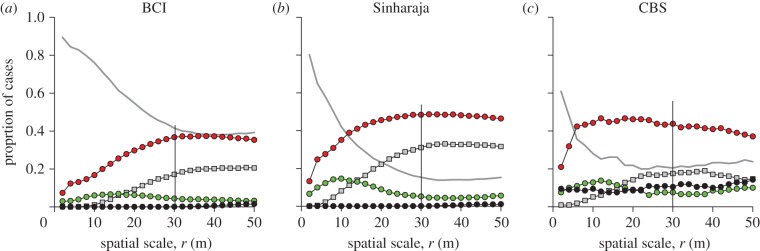
All three forests showed a qualitatively similar pattern (figure 2): the proportion of the no association type decreased with neighbourhood size, that of segregation and partial overlap increased and the proportion of mixing peaked at neighbourhoods of approximately 10 m. However, when comparing the patterns among forests we found interesting quantitative differences related with species richness. The importance of the no association type increased for smaller neighbourhoods with species richness (figure 3a). This is in agreement with our specific hypothesis H1a. Whereas the no association type dominates the species association patterns up to neighbourhoods of say 30 m at BCI, it does so at the Sinharaja and CBS forests only up to 10 and 4 m, respectively. For larger neighbourhoods (i.e. greater than 30 m), the Sinharaja plot shows a low proportion of the no association type of approximately 14 per cent, CBS 23 per cent and BCI 38 per cent (figure 2). It is also worth noting that the importance of segregation decreases with species richness (our specific hypothesis H1b; figure 3b) and that the proportion of species associations showing mixing has similar patterns in all three forests with peaks at the 10 m neighbourhood (figure 2).

Figure 2.

Assessment of overall interspecific association patterns at the three forests in dependence on the neighbourhood scale r. Illustrated are the proportion of species pairs showing the four association types and the type with no significant association. The grey line indicates no effect; closed red circles, segregation; closed squares, partial overlap; closed green circles, mixing; closed black circles, type IV.

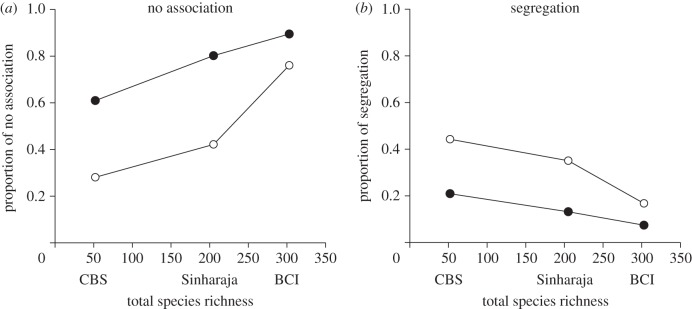
Figure 3.

Overall association patterns in relation to total species richness of the three forests. (a) Proportion of species pairs showing the no association type at 2 m (closed circles) and 10 m neighbourhoods (open circles). (b) Proportion of species pairs showing segregation at 2 m neighbourhoods (closed circles) and 10 m neighbourhoods (open circles).

Only one species at the BCI forest yielded at 10 m neighbourhoods a local dominance index greater than 0.2, but only because this species (Gustavia superba) showed an unusually high local density in a disturbed area at the northern border of the plot. All other species at BCI showed a local dominance index of less than 0.16. At Sinharaja, four species showed a local dominance index of between 0.2 and 0.34. When plotting the dominance indices over relative dominance rank (electronic supplementary material, figure A2) we find that the dominance indices at the species-richest BCI plot are lowest, followed by the Sinharaja plot with lower species richness and that the dominance indices at the species-poor CBS plot were larger when compared with that of the two tropical forests.

(b). Analysis 2. Small-scale species–species interactions

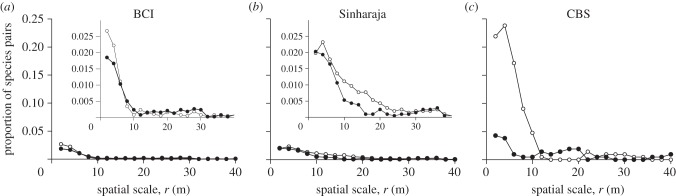
The goodness-of-fit test detected for the BCI data in 5.3 per cent of all cases (202 species pairs) significantly departs from the heterogeneous Poisson null model at scales 0–30 m. This result is similar to the 5.8 per cent found at Sinharaja (120 pairs), but quite different from the 30 per cent found at the CBS forest (64 pairs). Thus, detectable small-scale interspecific interactions are rare in the spatial pattern of the two tropical forests, but more common at the temperate forest. We also found that almost all significant spatial interactions between species pairs at BCI occurred at small scales of less than 10 m with a sharp decline in its frequency for scales greater than 2 m (inset figure 4a). Interestingly, negative effects disappeared already at scales greater than 5 m which indicates that our assumption of separation of scales was met. If there were, in reality, no separation of scales, then the frequency of significant effects should disappear only at 30 m [21].

Figure 4.

Analysis of species pairs for which the pair correlation function g₁₂(r) showed for scales 0–30 m a significant departure from the null model as indicated by the goodness-of-fit test (i.e. rank >190). Shown are for each distance r the proportion of cases where the g₁₂(r) was below the simulation envelopes (i.e. repulsion; open circles) and above the simulation envelopes (i.e. attraction; closed circles). For better clarity, the small inset graphs in (a) and (b) show the proportion with higher resolution.

The results of the BCI forest are qualitatively similar to that obtained at Sinharaja (figure 4a,b): positive and negative associations at small scales occur at both forests with similar proportion (i.e. 0.02) and quickly disappear with increasing scale. However, the temperate CBS forest yielded substantially different results with negative interactions dominating at small scales of less than 10 m (figure 4c). The K-function detected fewer significant departures from the null model and, owing to its cumulative nature, scale effects were somewhat obscured (electronic supplementary material, figure A3). Comparing across the three forests shows accordance with specific hypothesis H2, that the proportion of non-significant small-scale interactions increased with increasing species richness although no differences were found for the two species-richer tropical forests.

However, the above results do not mean that species interactions were always weak. We found that there were some species with significantly more interactions than expected by random allocation of interactions and some with fewer interactions (electronic supplementary material, appendix B). We also found that significant interspecific associations and interactions did not primarily depend on the sample sizes although, as expected, significant effects tended to be more frequent for larger sample sizes and the correlation between the number of individuals and the rank of the goodness-of-fit test was stronger for species-poorer forests (electronic supplementary material, appendix C).

4. Discussion

In this study, we analysed thousands of bivariate spatial patterns of tree and shrub species at three fully mapped 25–50 ha forest plots. Our main objective was to test the assertion of independence in the interspecific arrangement of species which is fundamental in six major theories that describe a stochastic geometry of biodiversity [15]. We conducted two sets of analyses. In analysis 1, we explored how frequently individuals of species pairs meet and have the opportunity to interact, and in analysis 2, we explored how trees of a species pair interacted when they met. Our results are in accord with our general hypothesis that stochastic effects associated with higher species richness dilute species associations in highly diverse communities, making them weak on average [15,22,26].

(a). Analysis of overall patterning

The strongest interactions between plants occur between those that are close together in space. Because the interspecific spacing of plants is closely related with coexistence mechanisms [29–31], it is of basic interest to find out how individuals of different species are arranged with respect to each other [22]. If the spatial arrangement of species is independent, individuals of species j co-occur within a neighbourhood of species i at a frequency no different from that expected by chance alone. This makes the identity of the nearest neighbours of individual plants less predictable if species richness is higher.

We found that larger trees (i.e. greater than 10 cm dbh) at the BCI forest, which hosts in total more than 300 species of trees and shrubs, showed in more than 80 per cent of all cases no detectable spatial association at a 6 m neighbourhood. However, this is likely to be a conservative estimate because the homogeneous Poisson null model does not consider the observed clustering and because we included only species with more than 70 individuals. For species with fewer individuals, significant effects will be even less detectable. Thus, our analysis for the BCI data supports the assertion of independent spatial arrangement of species, at least at small neighbourhoods of several metres where trees typically interact.

Notably, the proportion of species pairs that showed at smaller scale (i.e. 6 m) the no association type decreased with species richness from 82 per cent at BCI to 58 per cent at Sinharaja and 36 per cent at the temperate CBS plot. This result is compatible with the dilution effect of species richness [20,27]. At larger neighbourhoods of say greater than 30 m, however, species associations were dominated by segregation. This is understandable because in larger neighbourhoods stochastic effects become weaker because a given plant at BCI, Sinharaja and CBS has now on average 118, 189 and 116 neighbours within 30 m, respectively, compared with 4.8, 7.6 and 4.7 neighbours within 6 m, respectively. Species clustering (assertion (i)) now produces a detectable signal of segregation or partial overlap and substantially reduces the cases of no association. These effects are presumably owing to first-order habitat effects or effects of dispersal limitation.

The different proportions of the no association type at larger neighbourhoods of greater than 40 m in the two tropical forests (38% of all species pairs at BCI versus 14% at Sinharaja) may be a result of heterogeneity of the physical environment, which can produce negative association patterns between species if the two species show dissimilar habitat associations. The Sinharaja plot shows strong species–habitat association [37], whereas the BCI plot shows a relatively low degree of species–habitat association [43,44]. However, direct comparison of the species pairs in our scheme showed also that the higher habitat structuring at the Sinharaja plot increased the strength of the different association patterns such as segregation (electronic supplementary material, figure A1). Habitat structuring may not be the main reason for the large proportion of segregation observed at the CBS forest because this plot has weak topographic structuring. The signal of segregation was also enhanced by the high proportion of species pairs (more than 20%; figure 4c) that showed repulsive interactions that were probably caused by competitive interactions [21]. However, it is difficult here to discern between segregation patterns that are caused by direct negative interaction between species or edaphic effects because soil patchiness could have also determined the segregation pattern at the CBS forest [45].

If conspecifics tend to form clusters that are segregated from clusters of other species, the importance of intraspecific competition is increased relative to interspecific competition and coexistence may be enhanced [10,30]. Whereas recent studies in species-poor systems showed that such an interspecific segregation effect may indeed lead to dominance of intraspecific competition over interspecific competition [29], our results (electronic supplementary material, figure A2) suggest that intraspecific aggregation in species-rich communities may not be strong enough to yield local dominance. This is in agreement with our specific hypothesis H1b and illustrates the dilution effect of species richness with respect to the coexistence mechanism of intraspecific clustering and interspecific segregation [29–31]. Higher species richness means that fewer species will reach the high local dominance required for benefiting from this coexistence mechanism.

(b). Analysis of species interactions

The spatial patterns of the larger trees at the three forest plots are the outcome of different processes and mechanisms during regeneration and growth. After approximately factoring out the larger-scale effects of the environment, we found that for the two tropical forests there are significant small-scale interactions only for a few species pairs. This suggests that the spatial patterns of larger trees showed equilibrated spatial patterns [22]. Similarly, Volkov et al. [27] found that the collective effects of the pairwise interspecific interaction strengths of the 20 most abundant species at BCI were weak compared with the intraspecific interactions.

However, a low proportion of small-scale interspecific interactions does not mean that certain species may not maintain numerous interactions with other species. The distribution function of the number of significant interactions per species was close to but not fully random and contained some species with more interactions to other species than expected by chance (electronic supplementary material, figure A4). To our surprise, we found for the BCI forest (electronic supplementary material, figure A4a) and the Sinharaja forest (electronic supplementary material, figure A4b) almost the same distribution function.

When putting together the results of the three forests (figure 4), we find that the importance of negative small-scale interspecific interactions decreases with species richness. They are relatively unimportant at the two tropical forests; however, the CBS forest showed significant negative effects in approximately one-fourth of all cases, which are probably caused by competitive interactions (see above). These results are in agreement with the specific hypothesis H2 that the occurrence of small-scale interactions between species would be diluted by stochastic effects in species-rich systems. At the species-poorer CBS forest, significant small-scale effects were more likely if the two species were more abundant (electronic supplementary material, appendix C) because more direct encounters between heterospecific individuals will occur. This is also in accordance with recent studies in ecological networks that suggest the strong impact of abundance on interaction strength (e.g. the ‘abundance-asymmetry hypothesis’ [46]). Consequently, the interaction strength at the diverse BCI and Sinharaja forests depended only weakly on abundances (electronic supplementary material, appendix C). Similar results have been obtained for other species-rich plant communities [20,24].

In conclusion, our study suggests that the independent assertion may be indeed a possible approximation in the limit of very species-rich communities envisaged by stochastic geometry theories of biodiversity. However, our results also suggest that this assertion may break down in communities with lower species richness. What remains for future research is to find out if the observed departures from independence are large enough to cause problems for the biodiversity theories summarized by McGill [15]. The general hypothesis on species dilution formulated here constitutes an important contribution towards the understanding of the factors governing species-rich communities. It is based on arguments of stochastic geometry related with the probability of intraspecific species encounters and suggests a mechanism that can explain why species placement in species-rich communities cannot be distinguished from independence. Clearly, our support for the species dilution hypotheses is based only on data of three forests and we cannot exclude the possibility that it is caused by idiosyncrasies of the different forests rather than by a general rule. To further test these hypotheses, it is necessary to conduct studies with the methodology used here for additional forest plots and plots of other vegetation types.