Spider orb webs rely on radial threads to absorb prey kinetic energy

Abstract

The kinetic energy of flying insect prey is a formidable challenge for orb-weaving spiders. These spiders construct two-dimensional, round webs from a combination of stiff, strong radial silk and highly elastic, glue-coated capture spirals. Orb webs must first stop the flight of insect prey and then retain those insects long enough to be subdued by the spiders. Consequently, spider silks rank among the toughest known biomaterials. The large number of silk threads composing a web suggests that aerodynamic dissipation may also play an important role in stopping prey. Here, we quantify energy dissipation in orb webs spun by diverse species of spiders using data derived from high-speed videos of web deformation under prey impact. By integrating video data with material testing of silks, we compare the relative contributions of radial silk, the capture spiral and aerodynamic dissipation. Radial silk dominated energy absorption in all webs, with the potential to account for approximately 100 per cent of the work of stopping prey in larger webs. The most generous estimates for the roles of capture spirals and aerodynamic dissipation show that they rarely contribute more than 30 per cent and 10 per cent of the total work of stopping prey, respectively, and then only for smaller orb webs. The reliance of spider orb webs upon internal energy absorption by radial threads for prey capture suggests that the material properties of the capture spirals are largely unconstrained by the selective pressures of stopping prey and can instead evolve freely in response to alternative functional constraints such as adhering to prey.

1. Introduction

More than 3000 species of spiders rely on silk orb webs to capture flying insect prey [1,2]. The ability of orb webs to stop insects in midflight helps make these spiders dominant predators of insects in many ecosystems [3,4]. Orb webs are spun from some of the toughest known biological materials—spider silks, which can exceed even synthetic fibres such as Kevlar in their capacity to absorb energy without breaking [5–7]. The exceptional performances of the dragline silk, which composes the supporting radial threads and frames of orb webs, and the elastic capture spiral silk are hypothesized to result from strong selection of their role in absorbing the tremendous kinetic energy of flying insect prey. However, these silks are combined together into complex, composite structures—orb webs, which undergo strong deformation during prey impact. Thus, the work performed by an orb web during prey capture may be determined not only by the intrinsic material properties of silk threads, but also by how those threads are interconnected and even by the aerodynamic drag of the web moving through the air [8,9]. While many studies measure and compare the material properties of discrete spider silk threads [8,10–12], the actual process by which orb webs absorb prey energy is largely uninvestigated [9,13].

As the threads in an orb web are stretched by an insect, the kinetic energy of flight is transferred to the silk. Some of that energy is stored in the molecular deformation of the silk and will be returned to the insect as the web oscillates. However, much of the energy is permanently removed from the prey through viscous dissipation as flight energy is converted to heat [7]. The fraction of energy lost to viscous dissipation within a silk fibre as the thread is stretched is the damping capacity (or hysteresis) of the silk and is critical for preventing insects from ‘catapulting’ back out of the web after prey impact [7,14]. In contrast to other energy absorbing, tough biomaterials like rubber or mammalian hamstring that lose less than 5 per cent of energy in a cycle, spider silks exhibit damping capacities as high as 70 per cent [7,14]. This suggests that internal dissipation of energy by silk threads may dominate the prey-stopping function of orb webs.

However, spider silk stretches substantially during prey strikes so that aerodynamic damping could account for a significant proportion of the energy dissipated by orb webs [14]. Reynolds number (Re) describes the ratio of inertial to viscous force on an object moving through a fluid, such as air [15]. Spider silk moves through the air during prey impact at velocities of up to 5 m s^–1, so that its interaction with the air occurs at intermediate Re numbers typically defined as Re ∼ 1 [15]. At intermediate Re numbers, the drag force on an object moving through fluid is taken from empirical measurements, because the importance of inertial and viscous forces complicates an analytical solution. Aerodynamic drag on spider silk is supported by the ‘ballooning’ of juvenile spiders as they float through the air on silk threads [16]. However, the importance of aerodynamic dissipation for the function of orb webs is unclear, with some studies suggesting that it is crucial for stopping flying insects [9] while others ignore aerodynamic dissipation entirely when describing web mechanics [17–19].

Energy dissipation by orb webs can be partitioned into three components: (i) internal dissipation within the radial silk, (ii) internal dissipation within the capture spiral silk, and (iii) aerodynamic drag as the web moves or oscillates during prey impact. Our study is the first to quantify and compare the importance of each of the three potential routes for viscous dissipation of flight energy during prey capture. In particular, we test the hypothesis that orb webs depend upon aerodynamic dissipation as a vital component for stopping flying insects. We also consider how energy dissipation is partitioned among these three routes for different sizes of orb webs and its implications for the evolution of spider orb webs.

2. Methods

2.1. Spiders

We collected penultimate and adult female spiders at the University of Akron's Field Station at the Bath Nature Preserve, OH and nearby localities. Spiders were housed in either 40 × 40 × 10 cm or 80 × 80 × 20 cm screen cages with removable Plexiglass sides, depending upon the spider's size [20]. Spiders were held in a 23°C room and misted with tap water daily. Humidifiers were used to keep humidity above 60 per cent to stimulate web spinning and ensure that the glue droplets of the capture spiral were well hydrated, maximizing their stickiness [21]. Only freshly spun orb webs were included in the study. Eight orb webs were analysed in detail to determine how prey energy was dissipated by webs, one web each from Argiope aurantia, Neoscona domiciliorum, Araneus trifolium, Araneus bicentenarius, Larinioides cornutus and Verrucosa arenata, and two webs from two different individual Argiope trifasciata (table 1). Adult spiders in these species spin threads and webs that are sufficiently large (more than 19 cm width) to be measured in our study, although significantly smaller, ‘miniature’ orb webs are common in nature [2].

Table 1.

Spider taxa and energy parameters of reconstructed impacts. Web diameter is the horizontal span of the web. Uncertainty intervals are computed using the method of propagation of error.

taxa	body weight (mg)	projectile weight (mg)	relative impact energy (μJ mg−1)	projectile mass/spider mass	energy absorbed by radials ± uncertainty (μJ)	energy absorbed by spirals ± uncertainty (μJ)	energy absorbed by aerodynamic drag ± uncertainty (μJ)	web diameter (cm)	total input energy (μJ)
Araneus bicentenarius	800	30	0.04	0.04	28 ± 65	1.7 ± 1.8	1.2 ± 0.5	29	40
Araneus trifolium	1270	98	0.18	0.08	207 ± 244	11 ± 10	9 ± 1	21	180
Argiope aurantia	375	500	3.2	1.33	1067 ± 497	60 ± 30	85 ± 13	19	1245
Argiope trifasciata	100	30	0.38	0.30	32 ± 31	1.5 ± 1.9	4 ± 0.6	27	19
Argiope trifasciata	172	98	3.3	0.57	526 ± 365	9 ± 4	39 ± 1.9	25	466
Larinioides cornutusa	121	500	7.2	4.13	421 ± 310	214 ± 107	241 ± 3.7	33	1707
Neoscona sp.	50	30	3.4	0.60	80 ± 75	88 ± 76	4 ± 0.7	20	33
Verrucosa arenataa	56	30	0.4	0.54	9 ± 15	7.5 ± 8.6	3.2 ± 0.2	21	43

^aBreaking impacts.

An additional 45 orb webs from 45 individual spiders of seven species were examined to study how the numbers of threads contacting prey affected capture. These webs included a Metepeira species, in addition to those listed above (table 2).

Table 2.

Descriptive statistics for an escaping 300 mg projectile. The energy absorbed by webs during impact by this relatively high energy projectile was measured by tracking the deceleration of the projectile in 500 fps video. Energy measurements were taken from a total of 45 different webs spun by different spiders, and regressed against the number of spiral and radial threads contacted during the impact (figure 8).

taxa	n (number of webs)	body weight (mg) mean ± s.d.	total energy absorbed (μJ) mean ± s.d.
Metepeira sp.	6	130 ± 20	545 ± 220
Verrucosa arenata	3	56 ± 1	759 ± 960
Larinioides cornutus	29	144 ± 66	718 ± 443
Argiope trifasciata	3	136 ± 1	1919 ± 948
Neoscona domiciliorum	1	47 ± 0	835 ± 0
Araneus trifolium	2	1162 ± 153	1161 ± 977
Araneus bicentenarius	1	800 ± 0	133 ± 0
all groups	45	183 ± 226	787 ± 591

2.2. Projectiles simulating flying prey

We used rectangular blocks of balsam wood to simulate insect prey because their densities allowed us to make projectiles of similar sizes and masses as real insects. Blocks of 30, 98, 300 or 500 mg balsam wood were launched into the middle of the capture areas of orb webs with velocities between 1 and 3 m s^–1 using a spring actuated ‘gun’ constructed from PVC pipe. Projectiles were fired at a distance of 0.5 m from the webs so that ‘prey’ impacted webs with kinetic energies very similar to typical insect prey of spiders, such as flies (30 μJ) and large grasshoppers (1100 μJ) [22]. A range of prey sizes relative to spider masses were used in order to measure web performance under both easy and extreme conditions. For example, the relative size of prey versus spider body mass varied from just 4 per cent of the spider mass for an Araneus bicentenarius web up to a 500 mg prey that was 400 per cent the mass of the Larinioides cornutus web builder.

2.3. Imaging methods

Images were captured using a single Fastech Troubleshooter 1268 × 1024 pixel camera (17150 Via Del Campo Suite 301, San Diego, CA, USA) at 500 fps. The camera was fitted with a 15 f lens and positioned at a 45° angle to the web at a distance of 2 m. Webs were then back-illuminated using two 250 W lights positioned at 90° from each other, about 20 cm from the webs, and just out of the frame of view. A 15 × 15 cm Rosco Roscolux Super Heat Shield was placed between each light and the web. ProAnalyst motion analysis software (Xcitex, Inc., Cambridge, MA, USA) was then used to digitize up to 64 silk junctions between capture spirals and radial threads.

2.4. Web discretization

The prey position was tracked beginning at 16 frames (32 µs) before contact with silk. To track web motion after impact, we digitized up to 64 points (figures 1–3), representing the inner, middle and outermost capture spiral junctions with each radius in the web. The autotracking feature of ProAnalyst then measured the position of each point for every subsequent frame of video. This marking scheme designated two regions within each radius—an inner and outer segment, whose extensions could be tracked independently over time. It also defined inner, mid and outer sectors of capture silk, with the length of each row of capture spiral within a sector defined by the distance between the adjacent radial threads. Because not all the capture spiral junctions were tracked, we approximated the behaviour of some capture spiral threads within a sector from their nearest tracked neighbour. To do this, the number of rows of capture spiral within a sector was calculated as one-third of the total rows of capture spiral:

2.1

Figure 2.

Web of Araneus trifolium (body weight 1270 mg, web width 21 cm) broken by a 300 mg balsam wood projectile. Note the high displacement of threads around the local area of impact when compared with the rest of the web. Frames are separated by 10 ms.

Figure 1.

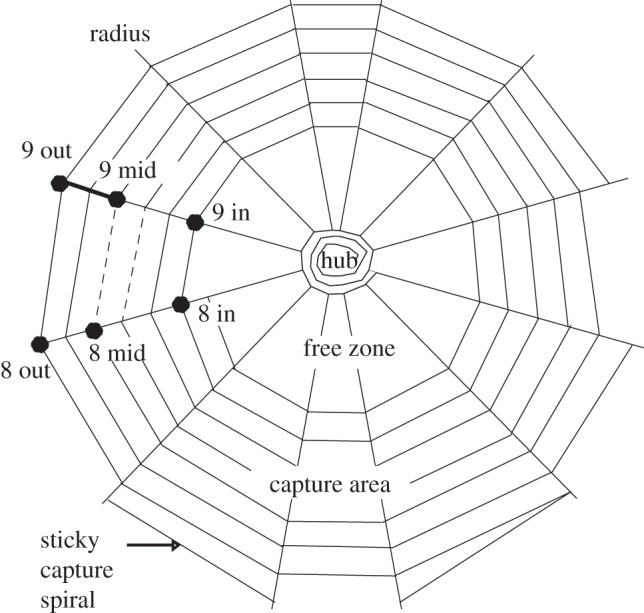
Discretization of web segments in a simplified spider orb web. The inner, middle and outermost junctions with the capture spiral were designated for each radius. Only points from 08.00 h inside to 09.00 h outside are depicted here. The radial segment 9 mid–9 out is illustrated in bold and the spiral segment group 8 mid–9 mid is illustrated with two dotted lines. The load of a single spiral segment is multiplied twofold in this simplified web because it represents two of the six total rows of the capture spiral. Actual webs used in the study had many more rows of capture spiral than this, with up to 39 rows in Argiope trifasciata. Radii are approximately three orders of magnitude stiffer than capture spirals and are therefore stretched to much lower extensions during most impacts.

Figure 3.

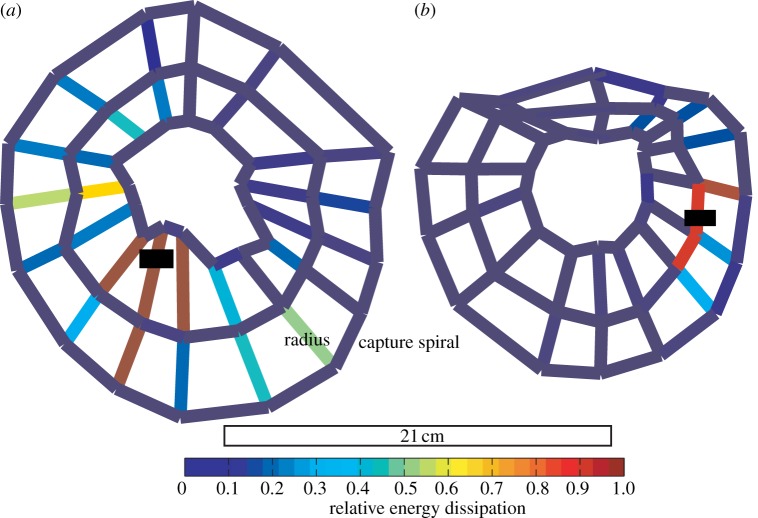
Energy absorption colour scale is normalized to the web region absorbing the highest energy. Aerodynamic dissipation for each segment was less than 0.1 relative energy, and is therefore not depicted. The inner-, middle and outer-most rows of capture spiral are summarized together. (a) Large web of A. trifolium (21 cm wide, spider weight 1270 mg) catching a balsam block (98 mg) shows that radii far from the impact site absorbed significant energy. (b) A slightly smaller web of Verrucosa arenata (21 cm wide, spider weight 56 mg) slowing, but not stopping, a balsam wood block (30 mg) shows that radial and capture spiral silk absorbed equivalent amounts of energy, with little role played by aerodynamic drag. The block broke through the web but was slowed from 2 to 0.3 m s⁻¹.

The total length of capture spiral within each discrete region was then calculated as

2.2

where S_li, the single spiral segment length (m), was computed as the distance between the two adjacent radial thread points that defined that spiral sector. In conclusion, our digitization constructed a digital web ‘skeleton’ that directly measured some of the threads and approximated the remaining threads (figure 3).

2.5. Spatial calibration

Orb webs are approximately planar structures that are distorted into conical shapes during insect impact. We used a single video camera and performed spatial calibration in two planes: parallel and perpendicular to the web plane. Neither calibration correctly captured all of the motion of the points on the three-dimensional cone, but instead provided exact measurements only for points in the specified calibration plane and then approximated the rest of the points.

A planar grid with 2.54 cm squares served as the calibration object. Perspective transformation was accomplished internally by ProAnalyst. First, the two-dimensional space was calibrated in the plane parallel to the web surface. This calibrated all motion in that two-dimensional space, assuming no motion out of this plane. Perpendicular plane calibration was also accomplished within ProAnalyst. This perspective calibration quantified motion of those points residing entirely on the plane perpendicular to the web surface and that intersected the web hub. In order to quantify the error introduced by the single plane assumption, we compared the strain values from each calibration. The difference in velocities, strains and segmental distances between these calibrations provided measures of spatial uncertainty owing to the calibration error (see electronic supplementary material) [23]. Together, the experimental error in measuring each of these variables produces a range in the energy that we compute to be absorbed by the web. We used the most extreme differences between estimates to calculate the maximum error in our measures of thread displacement.

2.6. Kinetic energy of projectiles

The pre-impact kinetic energy (KE_initial) of each projectile was calculated from the projectile's positions in the video frames for 16 frames prior to impact. Projectiles were launched at the web so that flight trajectories deviated from the normal vector of the web by less than 10° horizontally. The plane of the flight trajectory was parallel to the perpendicular calibration plane. Total energy input to the web was calculated as the sum of the changes in kinetic and gravitational potential energies in this calibration plane as the prey came to rest in the web. Gravitational energy change was computed from the difference in height between initial impact and rest.

2.7. Tensile testing of silk threads

Internal energy absorption by the radial and capture spiral silks was calculated by combining the video-derived strain data with mechanical testing data on energy absorption and damping by the capture spiral and radial silk. Tensile tests were performed using a Nano Bionix test system (Agilent Technologies, TN, USA), previously described in Blackledge et al. [24]. Our goal was to measure the load (i.e. force) versus strain curve at various relevant extension–retraction cycles, in order to characterize the work performed by threads within the capture areas of webs as they stretched to different distances [14]. Damping capacity, or the fraction of energy lost in viscous dissipation within the silk in a loading–unloading cycle, was calculated from the area under the load–strain curve during each extension–relaxation cycle [14]. It was important to separate the amount of energy lost versus stored during thread extension because prey oscillate in webs, repeatedly straining and then relaxing threads. Damping capacity was measured for three capture spirals and three radial threads from each web. The median tensile strength fibre was then chosen as representative of the performance of the rest of the fibres in the web for the reconstruction of energy absorption.

2.8. Modelling energy absorbed by thread strain

Internal silk strain energy was estimated separately for capture spiral and radial threads. For the capture spiral, the load measured for a single thread was multiplied by the number of capture spiral rows in that discretized region to compute the total load for that region. Strain energy for a time increment (frame interval of 0.002 s) was set to zero except when a thread segment was extending at positive strain beyond the native tension necessary to hold a stationary web taut. Energy dissipation owing to silk strain was then summed across web regions for each time increment separately for each silk type.

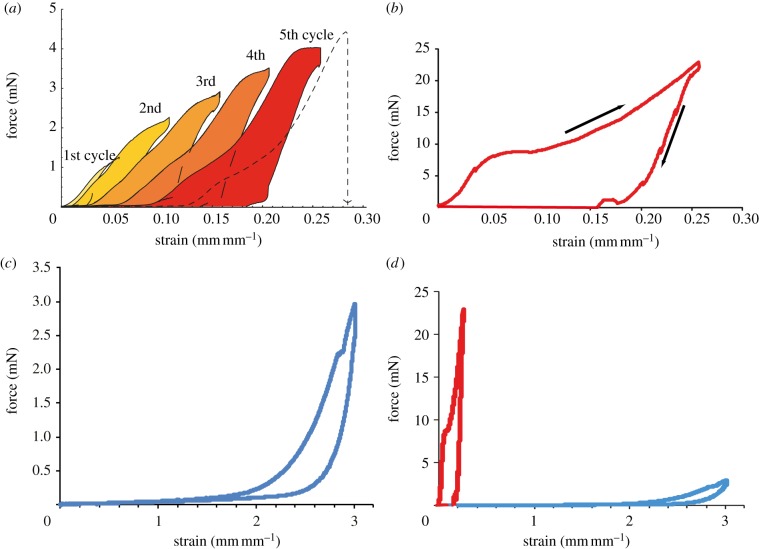
Damping capacity of 0.50 ± 0.30% was measured for both capture spiral and radial threads close to breaking strains (figure 4b,c) such that we used a damping capacity of 0.5 for all webs to reconstruct energy dissipation [14]. We measured much lower dampening capacities in silk at low strain, but they were associated with such low force that they were largely irrelevant to the overall calculation of impact energy absorption. For instance, damping capacity was less than 0.2 for radial threads stretched less than 5 per cent strain, and were subject to proportionally large experimental error owing to the low forces involved. Capture spiral threads exhibited nearly perfect elastic energy return (0 damping capacity) at strains less than 20 per cent (figure 4c). At higher strains (greater than 100%), the damping capacity of capture spiral silk was equivalent to radial threads. Thus, 0.50 of the loading energy was assumed to be lost instantaneously at each increasing strain increment for all webs. Variation in the loading force curve across spiders was far more significant for computing energy absorption than was the small variation in damping capacity (e.g. 20 times increase in radial thread energy absorption was computed using high loading force radial threads instead of low-force threads compared with only four times increase in radial thread energy absorption when modelling 70% instead of 20% damping).

Figure 4.

(a) Damping capacity testing of a single thread of radial silk. A radial thread from a Larinioides web is strained and relaxed in 5% strain increments, with energy damping indicated by the shading under each stress–strain curve. The thread was first pulled to 5%, followed by 10%, then 15%, and so on until break. The dotted line indicates the final cycle where the radius broke. The force at a given strain in subsequent stretch cycles was always lower than the previous cycle. (b) Radial thread tensile test from an Araneus web. Radius load climbs rapidly with extension, and typically breaks at approximately 0.3 engineering strain (30% extension). The force versus strain was fitted with a third-order polynomial for the loading region of the curve (top arrow). Energy absorbed by the thread is the area inside the loading and unloading curves. (c) Capture spiral thread tensile test from the same web as (b). (d) The loading cycles of (b) and (c) shown to scale. Radii are much stiffer than capture spiral, and hence absorb significant energy at very small strains. Both radii (red line) and capture spiral (blue line) are shown in cycles close to breaking strain.

The energy (R) dissipated by radius segment j at each time increment i was calculated as

2.3

where H_R is the damping capacity of 0.5, ΔL_R the incremental change in length and F_R the instantaneous load on the thread segment.

2.8.1. Aerodynamic drag estimation

The ratio of inertial to viscous force on an object moving through a fluid defines the Reynolds number (Re). Spider silk moves through the air during prey impact at velocities resulting in an intermediate Re. For example, maximum speeds of targeted flying insects are about 3 m s^–1 and maximum diameters of threads are 6 µm, producing a maximal Re of approximately 1:

2.4

for spiral segment j in time increment i, where u = speed of thread, d = thread diameter (between 1 and 6 µm), and γ is the kinematic viscosity of air at room temperature, 16 × 10^–6 m² s^–1.

Empirical formulae for the drag coefficient (C_d) on a cylinder moving normal to flow are derived from wind or water tunnel experiments at intermediate Re [25]. Such studies show that C_d is a function of Re and the classic approximation by Tritton is [25]

2.5

The velocity of each thread of the discretized web was input to Tritton's approximation to derive a drag coefficient appropriate for that thread in that time interval. Drag force (D) on spiral j in time increment i was calculated as

2.6

where u is the speed of thread, ρ the density of the fluid, d the diameter of the thread, S_l is the spiral length associated with that discretized web point and C_d the drag coefficient [25]. Note that thread diameter (d) cancels with the thread diameter implicit in C_d. Thus, drag force is independent of thread diameter, as noted in the study of Lin et al. [9].

Total length of capture spiral silk in discrete region j was computed as

2.7

where S_li is the single spiral segment length (m), and S_n the average number of capture spirals within the region.

The energy dissipation by aerodynamics (A) on region j in time increment i was calculated as

2.8

where the increment of the capture spiral region displacement in the calibration plane was calculated as

2.9

where f is the camera frame rate of 500 frames s^–1.

The dissipation owing to air resistance was then summed across web regions at each time increment, and a cumulative sum then taken over time to estimate the total aerodynamic dissipation.

By conservation of energy, total energy dissipated by the web should be equivalent to the total change in projectile energy, both for successful capture events and for escapes at the moment projectiles lost contact with the silk. We refer to the total change in projectile energy as the total energy input to the web and define the total absorbed energy as the sum of the energy dissipated internally by radial threads, internally by capture spirals and through aerodynamic drag. The congruence of the independent measures of energy input and energy absorption served as a check on the assumptions intrinsic to the dissipation calculations (electronic supplementary material, figure S9). Oscillations decay so that after two oscillations, negligible energy remains, although the web can visibly oscillate more than six times.

Spider weight correlates highly with the total silk volume used in a web [20], which itself strongly influences prey capture. Therefore, in order to standardize impact energy and to rank impacts by ‘ease of capture’, we divided the total absorbed energy by the spider weight. Hereafter, we refer to this parameter as relative impact energy. While this ignores variation in silk toughness across species, the simplification is justified in that silk toughness varies fourfold across species, while spider weight varies by 25-fold in the current study, so that it plays a significantly greater role in determining inter-individual variation in our experiment. The energy absorbed by each of the three dissipation routes was divided by the total input energy to derive a fraction of total work. We then asked, using a univariate linear regression, whether any of these work fractions changed with relative impact energy or spider body weight [26].

Finally, we calculated two parameters to measure how the contribution of capture spiral silk and radial silk to stopping projectiles varied across the entire orb web surface. The first parameter, ‘fraction of web at high strain’, measured the area of web containing silk stretched to our pre-defined high level of strain, where energy damping becomes significant. We defined high strain for radial threads as greater than 5 per cent because this meant that the silk had clearly yielded, thereby influencing its future performance in the web and resulting in significant damping. High strain for capture spiral was defined as strain greater than 20 per cent. This was near the strain in which the recovery force was not equivalent to the extension force, and therefore damping capacity became measurable. The second parameter, ‘90 per cent energy threshold’, measured the minimal area of the web accounting for 90 per cent of the total energy dissipation. Each of these parameters was computed separately for radial and spiral silk. The discretized segments meeting each criterion were normalized by total number of segments in the web, creating a ratio that was essentially the length of highly strained silk to the total length of silk in the web. We then asked whether any of the ‘area’ parameters for each of the silk types changed with relative impact energy by using univariate linear regression [26].

2.9. Influence of thread contact area

Finally, we measured the details of how threads contacted prey blocks related to energy absorption for a larger set of web impacts (table 2). The total energy input to orb webs from a 300 mg block was measured by the change in mechanical energy of the projectile. The goal here was to relate the number of radial and capture spiral threads directly in contact with the block to the performance of the web, in terms of energy removed by the web. While about half of the projectiles were caught by the web, these events can underestimate potential performance of the web. Therefore, we selected only breaking impacts for this analysis because they represent events where webs clearly performed to their maximum potential. We used a multiple regression technique to ask whether radial and/or capture spiral thread contact number had predictive value for the log-transformed energy absorbance [26]. The multiple regression technique was able to quantify the effect of one type of thread contact while controlling for the other thread type.

3. Results

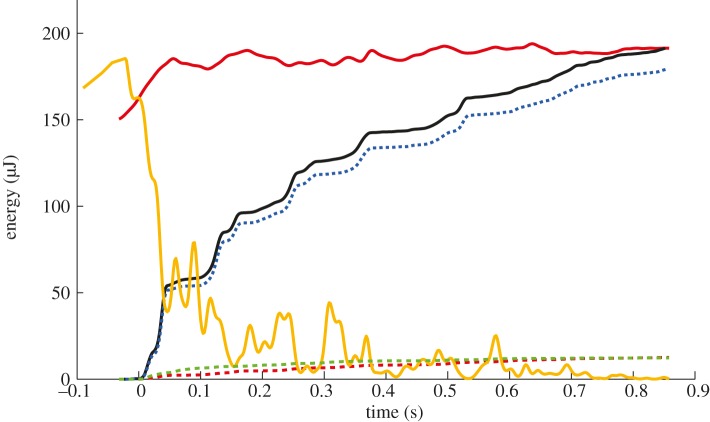
As an insect was decelerated by an orb web, its kinetic and gravitational energies were transferred along three routes—internal strain energies of the radial and capture spiral silks within the web and to the air around the moving threads. For many impacts, most of this transfer occurred within 0.1 s, even though the prey oscillated as it was brought to rest. Approximately 50 per cent of the remaining prey energy was absorbed at each subsequent oscillation (figure 5). For most impacts, internal dissipation by capture spirals and aerodynamic dampening was negligible compared with internal dissipation by radii. Radial threads could account for 100 per cent of the absorbed prey energy in six of eight trials (figure 6a,b), when measurement error was propagated to predict maximal radii dissipation. The capture spiral potentially accounted for 100 per cent of the work in only one instance. Aerodynamic damping never accounted for more than 30 per cent of the work, even under the most generous assumptions. Error propagation produced very large uncertainty intervals for some energy routes (figure 6) so that radii energy absorption intervals were often large enough that more energy was predicted to be absorbed than was originally available. This condition applies to the range greater than 1 on the y-axis (figure 6). For the internal capture spiral dissipation and aerodynamic dissipation, the upper uncertainty never overlapped with 100 per cent, indicating that those routes were always insufficient to account for web function. Our goal here was not to predict the precise energy dissipated through each route, but rather to show the potential of each route to account for spider orb web function.

Figure 5.

Energy budget for a web of A. trifolium (spider weight 1270 mg) capturing a 98 mg projectile that impacted with about 180 μJ of kinetic energy. Impact is at time 0 s, and several oscillations are shown as the prey comes to rest in the web. The time-dependent energy input was calculated as the sum of kinetic energy and gravitational potential energy change as the prey came to rest in the web. Total energy absorption was calculated as the sum of the three routes of energy dissipation after the prey came to rest—dissipation through radii, dissipation through the capture spiral and aerodynamic damping. Red solid line, total energy input; yellow solid line, prey kinetic energy; black solid line, total energy absorbed; blue dashed line, radii internal; red dashed line, capture spiral internal; green dashed line, aerodynamic.

Figure 6.

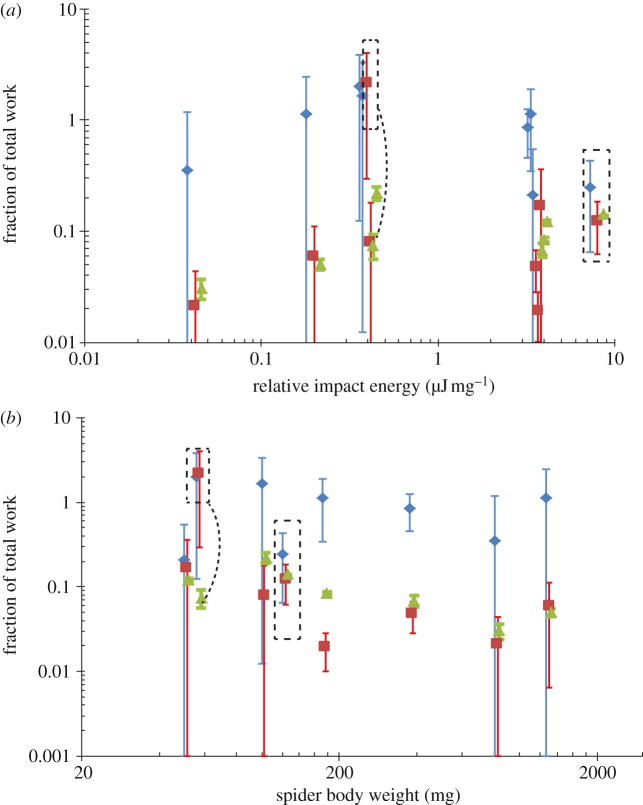
(a) Partitioning of the relative work of prey stopping by orb webs. The fraction of work performed by each route was independent of relative impact energy (aerodynamic damping F = 2.99, p = 0.17, radii F = 1.37, p = 0.29, capture spiral silk F = 0.13, p = 0.73). Fraction of work was calculated as the total energy absorbed by that specific route divided by the total energy input to the web. Relative impact energy was calculated as (total energy absorbed (μJ)/spider body weight (mg)) to account for differences in web sizes. Relative impact energy is a measure of the ‘difficulty’ of the catch. Symbols indicate the mean and bars indicate the confidence intervals of each estimate as calculated from propagation of error, with the capture spiral and aerodynamic bars shifted slightly to the right, respectively, so as not to overlap. Internal dissipation by radii was sufficient to account for all energy absorption in six of eight trials, indicated by a fraction of work that included unity (1) in the confidence interval for that estimate. Boxes and dotted line indicate the two impacts in which the projectile broke through the web. (b) Fraction of work by each of the three energy dissipation routes did not depend on spider body weight (radii F = 0.08, p = 0.78, capture spiral F = 0.69, p = 0.44, aerodynamic F = 0.46, p = 0.53). Capture spiral and aerodynamic work were only important in some smaller spiders. However, aerodynamic work was always rather low, and never exceeded 30% of total energy input to the web. Blue diamond, radii; red square, capture spiral; green triangle, aerodynamic dissipation.

The fraction of work performed by the various energy dissipation routes did not depend on relative impact energy (aerodynamic route, n sample size = 8, F statistic = 2.99, p probability = 0.17; dissipation in radial threads F = 1.37, p = 0.29; dissipation in spiral threads F = 0.13, p = 0.73; figure 6a) or on spider body weight (aerodynamic F = 0.46, p = 0.53; radial F = 0.08, p = 0.78; spiral F = 0.69, p = 0.44; figure 6b). Capture spirals and aerodynamic damping only played a significant role in webs spun by relatively small species of spiders (Neoscona domiciliorum, Larinioides cornutus, and Verrucosa arenata; figure 6b).

Fraction of highly strained radial threads did not depend on relative impact energy (fraction regressed onto log relative impact energy, y = 0.31 + 0.18x, n = 8, r = 0.56, p = 0.14) but fraction of high-strained capture spiral threads did increase (y = 0.18 + 0.17x, n = 8, r = 0.82, p = 0.01; figure 7a). The fraction of the capture spiral in the orb web strained beyond 20 per cent (i.e. contributing measurably to energy transfer) increased from about 3 per cent up to 50 per cent as the relative work performed by webs increased (figure 7a). The area of orb web recruited for 90 per cent of the total energy dissipated decreased with relative energy of impact for radial threads (fraction regressed onto log relative impact energy, y = 0.36 − 0.15x, n = 8, r = −0.73, p = 0.04). However, the area of the orb accounting for 90 per cent of the energy dissipated by capture spirals did not change with relative energy of impact (y = 0.28 + 0.028x, n = 8, r = 0.23, p = 0.59; figure 7b). Webs typically used about 30 per cent of their silk to absorb 90 per cent of prey energy (figures 3 and 7b), with radial threads far from the impact site absorbing significant energy (figure 3a,b).

Figure 7.

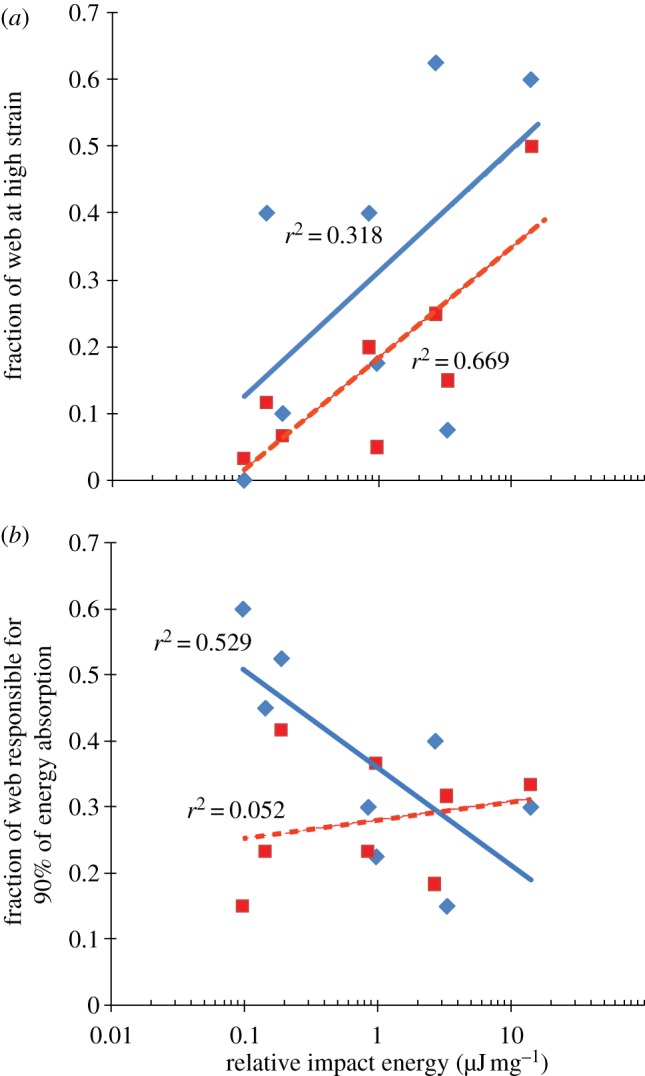
Two measures of web surface area recruitment. The x-axis can be interpreted as the relative difficulty of prey capture. (a) Proportion of silk reaching high strain during prey impact. High strain was defined as 5% for radial silk and 20% for capture spiral because this approximated the minimal strain at which significant energy damping occurs. The total fraction of silk pulled to high strain under prey impact was independent of relative impact energy for radial threads (y = 0.31 + 0.18x, n = 8, r = 0.56, p = 0.14) but increased for capture spiral threads (y = 0.18 +0.17x, n = 8, r = 0.82, p = 0.01). The ratios were calculated as the total number of segments of each type of silk pulled to high strain divided by the total number of segments of each type of silk. (b) Web area required to absorb prey energy. The y-axis indicates the minimal area of the web required for 90% of the total work performed by a particular type of silk and is a measure of how well the impact was distributed through the web. The fraction of web area recruited decreased with relative impact energy for radii (blue diamonds: y = 0.36 − 0.15x, n = 8, r = −0.73, p = 0.04) but not for capture spirals (red squares: y = 0.28 + 0.028x, n = 8, r = 0.23, p = 0.59). Between 20 and 40% of capture spirals and radii are recruited for difficult prey. The lower energy of easy prey is broadly distributed among the radii of a web while the increased energy of difficult impacts is concentrated in a smaller area of the web. Radii are recruited at greater distances from the impact site than are capture spirals.

In a separate dataset in which 45 escaping projectiles were tracked, the total work performed by the orb web increased with the number of radial threads contacting the projectile but total work was independent of the number of capture spiral rows (multiple regression of natural log of absorbed energy onto number of radial and capture spiral threads, n = 45 webs, radii F = 6.7, p = 0.01, capture spiral F = 0.7, p = 0.41; table 2 and figure 8).

Figure 8.

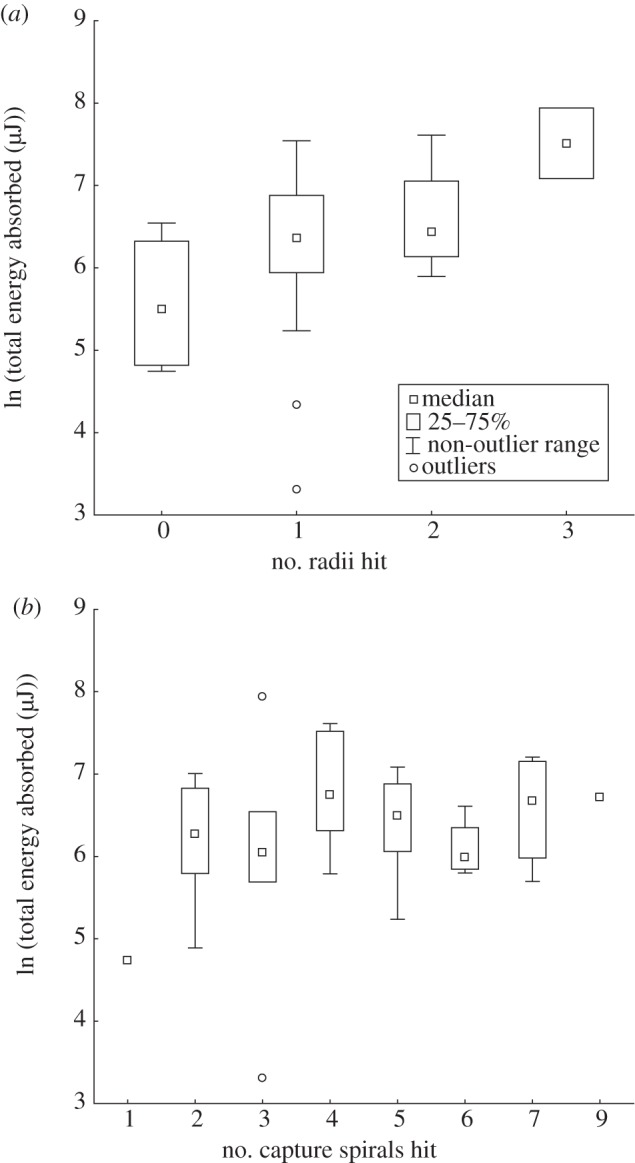
(a) The energy absorbed by webs increased with increasing number of radii that were in direct contact with a 300 mg balsam block projectile. Forty-five breaking (escape) events were analysed (p = 0.01, multiple regression of natural log of absorbed energy onto both spiral and radial thread number). The number of contacting threads varied owing to orientation of projectile, differences in impact location on the web and differences in thread density. The analysis of escape events ensured that webs were functioning at a maximal capacity. (b) The energy absorbed by webs did not change with the number of spiral threads in direct contact with the projectile as it broke through the web (p = 0.41, multiple regression).

4. Discussion

Spider orb webs evolved under selection to dissipate the tremendous kinetic energy of flying insects [2,20]. Consequently, the silk threads used to spin those webs are among the strongest and toughest known biomaterials [2]. Spider silk threads are also very thin, ranging from tens of nanometres up to a few micrometres in diameter, resulting in intermediate Reynolds numbers. Prior modelling argued that aerodynamic damping played a crucial role in energy absorption by orb webs [9], but did not directly quantify damping in realistic prey capture scenarios. Subsequently, other studies argued against a significant role for aerodynamic work performed by orb webs [19,27], but again without empirical measurement. We directly measured the strain of silk in whole orb webs during simulated prey impacts and calculated the work performed internally by both the radial threads and the capture spiral silks, as well as the work done by aerodynamic resistance to silk motion. We found that both aerodynamic damping and the capture spiral silk usually play only a minor role in energy dissipation during prey capture. Orb webs instead rely upon internal dissipation of prey energy by radial silk for up to 98 per cent of the work of stopping flying insects (figures 5 and 6). Further evidence for the primary importance of radial silk compared with capture spirals comes from the increase in web performance as more radial threads, but not capture spiral rows, contact prey (figure 8).

Orb webs are not simply passive sieves that strain insects from the air [28–30]. Instead, multiple threads within webs work together in absorbing prey energy and adhering to insects. Thus, the degree to which web architecture facilitates recruitment of additional silk during prey impact may be as important as the material properties of individual threads for energy absorption. We quantified silk recruitment for each prey impact, defined as radial threads that clearly extended past yield (5% strain) or capture spiral that stretched at least 20 per cent (where energy damping became measureable) to determine the fraction of silk in a web involved in energy dissipation. For radial silk, the area of web recruited during prey impact varied widely and was unrelated to relative impact energy (figure 7a). However, the recruitment of the capture spiral increased from less than 10 per cent for ‘easy’ captures of slower, lighter projectiles in larger spiders’ webs to up to 50 per cent under the highest energy impacts (figure 7a). In contrast, the fraction of radial silk responsible for 90 per cent of the work of stopping prey decreased under more challenging impacts, from 60 to 20 per cent (figure 7b). This means that as more kinetic energy is imparted to orb webs by increasingly larger or faster prey, orb webs depend more on the radial silk in the local area of impact. Work becomes increasingly concentrated in webs under higher impact due in part to the nonlinear material properties of radial silk, wherein it initially softens after yield but then stiffens substantially prior to failure [13]. In contrast, the fraction of capture spiral silk responsible for 90 per cent of all the work performed by the capture spiral remained constant at 20–40%, regardless of relative impact energy (figure 7b). In summary, while large amounts of silk are strained during extreme prey impacts, less of that silk is responsible for the bulk of the work. While this could indicate a failure of orb webs to effectively distribute energy under more difficult prey impacts, it could also be interpreted as a mechanism to enhance the robustness of the structure [13] because partial, damaged orb webs can continue to function as very effective traps (A. T. Sensenig 2009, unpublished data).

Both aerodynamic damping and internal energy dissipation by the capture spiral play a larger role for some smaller orb webs spun by Verrucosa arenata, Neoscona domiciliorum and Larinioides cornutus (figures 3 and 6b). The use of relatively small, immature spiders in prior studies may partially explain the report of significant aerodynamic effects [9]. Several factors may explain why dissipation through capture spirals and aerodynamic damping are more important for smaller orb webs. The architectures of smaller webs enhance these two routes because smaller species of spiders, and even smaller individuals within a species, typically spin webs with larger numbers of radial threads and more rows of capture spiral [20,31]. This may allow radial threads to distribute energy more effectively to numerous rows of capture spirals. The higher numbers of threads overall in the web may also then provide proportionally greater aerodynamic drag. Non-intuitively, however, the drag does not change as a result of silk diameter owing to the inverse dependence of the drag coefficient on diameter in the intermediate Re regime. The material properties of silk also vary with spider size. The capture spirals of smaller spiders are also stiffer, increasing their contribution to dissipating prey energy at lower extensions [20]. Regardless of the mechanism, our data suggest changes in how orb webs function across both ontogenetic and evolutionary shifts in spider body size. In particular, large spiders spin webs that are capable of capturing prey by relying almost entirely on radial silk to absorb impact energy.

The material properties of capture spiral silks contrast strongly with the major ampullate silks that comprise the supporting radial threads. Capture spiral silks are highly compliant and up to an order of magnitude more extensible than radial silk [32,33]. Yet, capture spiral silks achieve similarly impressive toughness, suggesting that they too have been shaped by selection for energy dissipation during prey impact [12,20]. However, we found little evidence for a significant role of capture spirals in energy dissipation during most prey impacts, especially for larger spiders’ webs. At best, capture spirals account for only 20 per cent of total energy dissipation at spider sizes larger than 100 mg. Thus, we argue that the material properties of capture spiral silk may have evolved primarily under selection for adhering to and retaining prey. For instance, high extensibility facilitates adhesion of capture spiral at both the whole thread [34] and individual glue droplet levels [35]. Moreover, there is a close evolutionary relationship between capture spiral extensibility and stickiness [36]. We even suggest that the prey-retaining function of the capture spiral may select for properties that decrease its contribution to energy absorption during prey impact. For example, low stiffness promotes wrapping of struggling prey, so that more spirals can be incorporated in the wrapping [32]. But, that low stiffness also means that capture spiral silk contributes little to energy dissipation until it is extended to strains well beyond those typical of prey impacts.

Orb webs overcome the daunting challenge of stopping the flight of insects by using a combination of different silks that are among the toughest known materials [32]. Despite the small diameters of these silk threads, and their correspondingly low Re, aerodynamic damping plays only a minor role in prey energy absorption for many orb webs. The elastic capture spiral of orb webs is also so compliant that it also usually dissipates little energy. Instead, orb webs rely primarily upon major ampullate silk in radial threads to dissipate most of the prey's flight energy, particularly for larger webs. This suggests that the material properties of capture spiral silk are ‘freed’ to respond to selection on alternative functions, in particular how the capture spiral retains prey through adhesion long enough to be subdued by spiders. While increasingly larger amounts of silk in orb webs become strained under higher energy prey impacts, most of the prey's energy is still dissipated by a relatively constant fraction of silk (approx. 30% of the total web), suggesting that orb webs may have evolved in part to maintain their functionality even under moderate to high levels of damage. Our findings provide new insight into how orb webs function and help identify different mechanistic pathways by which natural selection has operated on the evolutionary diversification of the spider silk toolkit.