Broiler chickens can benefit from machine learning: support vector machine analysis of observational epidemiological data

Abstract

Machine-learning algorithms pervade our daily lives. In epidemiology, supervised machine learning has the potential for classification, diagnosis and risk factor identification. Here, we report the use of support vector machine learning to identify the features associated with hock burn on commercial broiler farms, using routinely collected farm management data. These data lend themselves to analysis using machine-learning techniques. Hock burn, dermatitis of the skin over the hock, is an important indicator of broiler health and welfare. Remarkably, this classifier can predict the occurrence of high hock burn prevalence with accuracy of 0.78 on unseen data, as measured by the area under the receiver operating characteristic curve. We also compare the results with those obtained by standard multi-variable logistic regression and suggest that this technique provides new insights into the data. This novel application of a machine-learning algorithm, embedded in poultry management systems could offer significant improvements in broiler health and welfare worldwide.

1. Introduction

Broiler farmers have used data as an aid to health and production management for over 40 years [1,2]. Food and water consumption, growth and mortality have been used to construct standard production curves to monitor and improve performance. Daily flock data are plotted graphically on broiler house ‘door charts’ and deviations used as early indicators of flock health and welfare [3].

Increasingly, these and other sensor-recorded data are being collected electronically, giving birth to the concept of precision livestock farming [4]. Broiler flocks generate large datasets. In 1 year, a farm may generate data from 50–100 lifetime cohorts, representing 1.5–3 million birds. This is because birds have a short life span and are housed in large numbers on farms that have multiple houses operating ‘all in–all out’ systems in which the time between depopulation and restocking is short.

These datasets lend themselves to the application of machine-learning techniques [5,6]. Machine-learning algorithms are routine in diverse aspects of daily life, from recognition of handwritten post or zip codes on envelopes [7], to online purchasing suggestions, where products of interest are tailored to an individual's purchasing pattern [8]. The key feature of these algorithms is that they can learn to classify data from examples. This is particularly valuable when it is not possible to suggest a set of ‘simple’ rules describing the relationship between predictor and the outcome variables.

A form of artificial intelligence, two broad categories of machine learning are recognized, unsupervised and supervised [9]. Unsupervised methods are used to identify novel patterns within data. They are used when a priori knowledge about the structure of the data is not available, for example, in genomics [10], social network analysis [11] and astronomy [12].

Supervised methods are used when there is some knowledge of the data structure, presented in the form of classification examples or precedents. These examples are used to train the classifier. When training is complete, the classifier can extrapolate learned dependencies between predictor and outcome variables (commonly known as features and targets, respectively, in machine learning) to the new data. The quality of the classifier can be measured by the proportion of correctly classified test samples, i.e. those not included in the training set (testing accuracy). Supervised methods can be used to predict both continuous and categorical outcomes. In the latter case, they are known as classifiers [5,6].

The attraction of these classifiers to epidemiologists is in identifying risk factors for disease. In addition to their applicability to large datasets, machine-learning algorithms can respond to changes in feature characteristics. This is particularly important in broiler farming where innovations in genetics, nutrition and environmental control are common. Changes in environment, for example, may alter the relationship of a particular exposure with disease.

Machine-learning techniques have been applied to epidemiology, in the form of neural networks, but these are not in widespread use [13,14]. One of the major reasons is overfitting, i.e. the loss of classification accuracy on new data caused by very close fit to the training data. This results in poor generalization (i.e. performance on unseen datasets). The design and the use of neural networks also require considerable experience and the results can be difficult to interpret.

Support vector machines (SVMs) are a set of supervised learning algorithms, which overcome these problems. First introduced by Vapnik [15], they represent one of the most important developments in machine learning. They generalize well in high-dimensional space, even with a small number of training samples and can work well with noisy data [16,17]. In addition to classification, SVMs can be used to estimate how different features affect classification results, and identify those important in decision-making. Several efficient high-quality implementations of SVM algorithms exist, facilitating their practical application [18].

SVMs are based on a statistical-learning technique known as structural risk minimization [15,19–23]. An SVM uses a multi-dimensional plane, known as a hyperplane, to separate two classes of points in space (figure 1). The position and the orientation of the hyperplane are adjusted to maximize the distance (margin) between the plane and the nearest data points in both classes (H-H in figure 1). Non-optimal separators A-A and B-B are also shown.

Figure 1.

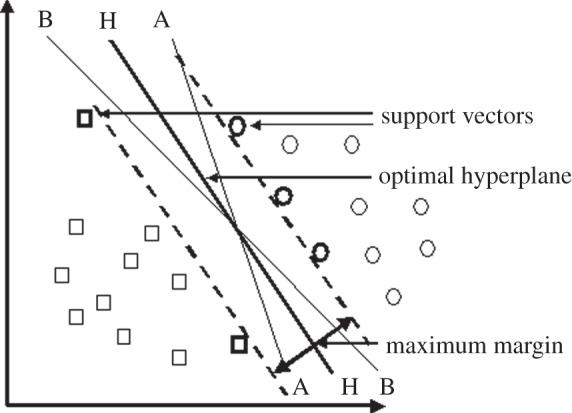
The principle of support vector machines.

The data points closest to the margin are called the support vectors, giving the technique its name.

In reality, data are rarely completely separable by a linear classifier. In figure 2, data points in bold lie on the wrong side of the classifier. The aim is to maximize the margin, while minimizing classification errors. This is achieved by introducing slack variables, the distances by which points lie on the wrong sides of the margin, and a regularization parameter, which controls the trade-off between the margin position and misclassification.

Figure 2.

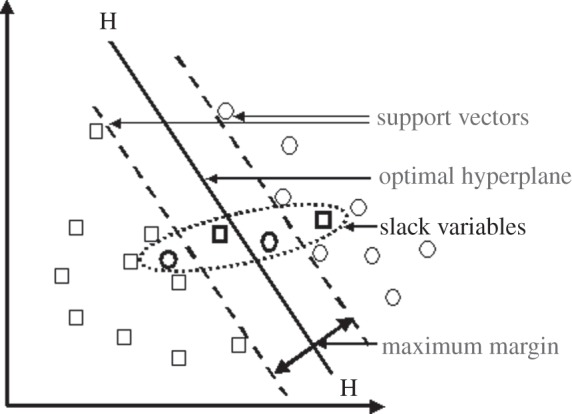
Incompletely separable data and slack variables. These correspond to the points that lie either on the wrong side of hyperplane, or in the margin.

A description of the mathematical derivation of the optimal hyperplane formula given a set of l data points (vectors) x = (x1, x2, … , xn) belonging to two classes C1 and C2 is provided in the electronic supplementary material.

The problem of a nonlinear classifier is addressed by nonlinear transformation of the inputs into high-dimensional feature space, in which the probability of linear separation is high. This transformation of input data into high-dimensional feature space is achieved using kernel functions. For further details on SVM, we refer the reader to Cristianini & Shawe-Taylor [22].

SVM has been used for the verification and recognition of faces [16,24], speech [25,26], handwriting [27,28] and such diverse events as goal detection in football matches and financial forecasting [29–31]. In life sciences, SVM has been applied to gene expression [32,33], proteomics [34,35] and disease diagnosis [36,37].

In 2005, we reported the first use of SVM for feature selection in observational epidemiology. This preliminary application was to identify risk factors for wet litter, a change in physical properties of the bedding seen in broiler houses [38,39], from a small cross-sectional dataset [40]. The risk factors identified compared favourably with those found using logistic regression (LR). This concordance between LR and SVM has been confirmed in subsequent studies [41–43]. Here, we provide a more detailed description of the use of SVM using a large set of routinely collected data to identify the risk factors for hock burn in broiler chickens. As part of the validation process, we compare the results with those obtained using multi-variable LR with and without random effects.

Hock burn is a dermatitis, which may occur on the legs of broiler chickens [44,45]. It is a major welfare problem of meat birds [45,46].

2. Material and methods

2.1. Study design

We built 20 SVM models by using 10 random splits of the data into test and training halves. A multi-variable LR model was developed using the whole dataset and the results were compared with summary data from all the SVM classifiers.

2.2. Data

Routine production data were obtained, as Excel spreadsheets, from a large UK broiler company. These data described management and processing of 5900 broiler chicken flocks produced in 442 houses over a period of 3.5 years (January 2005–August 2008). Details of the variables recorded are shown in table 1.

Table 1.

Variables measured as part of routine production.

house	management	mortality	abattoir processing
floor area	placement date	weekly numbers	rejections and downgrades (%)
	number of birds placed	culls per week	hock burn (%)
	number and age category of parent flocks	in transit
	bird sex
	rearing system (Standard or Freedom Food (RSPCA 2008))
	daily water consumption
	average weekly weight

2.3. Case definition

Hock burn was defined as an area of brown or black discoloration greater than 5 mm diameter observed on one or both hocks after slaughter. All birds were slaughtered at one abattoir and two operatives recorded hock burn. Hock burn was recorded in a sample of 500 birds from each lorry load. This was increased to 1000 if hock burn prevalence in the first sample was above 5 per cent. As each flock was represented by a variable number of lorry loads or consignments, the flock prevalence was calculated as a weighted average of hock burn prevalence in each consignment.

Flocks with a high level of hock burn were identified as those above the 75th percentile of flock prevalence and a binary variable for ‘high’ and ‘low’ flock prevalence of hock burn was created.

2.4. Data processing

Data cleaning and the creation of new variables are described elsewhere [47]. Briefly, stocking density (birds m⁻²) and weight density (g m⁻²) were calculated from the floor area, number of birds placed, weekly mortality and average weekly weight. The number of weekly deaths and culls was converted to percentages using the number of birds present at the start of the week as denominator.

Duplicate records and those with missing values were removed. Outliers, which fell beyond three standard deviations of the mean, were examined and removed. Variables with missing values in more than 20 per cent of the records were also removed. Daily water consumption values, which showed an implausible step up or down, were adjusted using an average of values from the preceding and the following day. Where two such water consumption values occurred in sequence, they were removed. Variables with a correlation coefficient above 0.8 were identified and one variable was excluded.

After processing, the total number of variables and records was 45 and 6912, respectively (1728 cases and 5184 controls).

Data were normalized by subtraction of the mean and division by the standard deviation.

2.5. Test and training data

Test and training data were created by randomly dividing the data into two halves. This was repeated 10 times. The hierarchical structure was retained in each half of the data. This was done by taking each (farm, flock date) duplet, and randomly distributing the observations belonging to it into either of the two halves. Any duplet with less than four observations was excluded from analysis (356 records). Each observation related to a single flock, house and processing date.

2.6. Support vector machine classifiers

SVM classifiers with linear kernels were built by using the open source LIBSVM library [48]. LIBSVM implements SVM with different kernels and uses one of the most efficient and fast SVM training procedures developed to date. It comes as a standalone application, as well as a variety of packages for different computing environments, including R and Matlab.

2.7. Recursive feature elimination

Recursive feature elimination (RFE) [33] was used to identify the most accurate parsimonious classifier. The RFE algorithm works by building an SVM classifier using all the variables, and then removing the variable (x_i), with the smallest absolute coefficient (w_i), from the training and testing datasets. The classifier is then rebuilt and tested using the new training and testing sets. This is repeated sequentially until the most parsimonious accurate classifier is obtained. This was identified using receiver operating characteristic (ROC) curves. These ROC curves were built by varying parameter b as shown in the electronic supplementary material, equation S1. Training and testing accuracy was estimated from the area under the ROC curves (AUC). A precipitous drop in classifier AUC to 50 per cent was used as the cut-off point. The classifier included all the non-excluded variables and the one excluded prior to the drop in AUC.

2.8. Logistic regression

Univariable and multi-variable LR models were built using Egret [49] and Stata [50]. Initial variable screening was performed using univariable LR, retaining variables with p < 0.25. Multi-variable models were built manually and by automated procedures using forward stepwise and backwards elimination. Variables were ordered by their univariable coefficients and p-values for manual model building. They were retained in the model if their p-value was less than 0.05. When the final model was obtained, variables which were important features in the SVM classifier but which were excluded from the LR model were offered to the model. None was retained. This was done as a final check of the robustness of the apparent differences in variable selection by the two methods. Models developed manually were checked using automated forward stepwise and backwards elimination techniques.

2.9. Validation of models

Validation of SVM classifiers was based on their predictive accuracy using training and testing data, using the AUC as a measure [51]. Models were also evaluated by the risk factors identified, and their relative importance to classifier outcome (based on the absolute magnitude of each coefficient). SVM models were compared with LR models. The predictive accuracy of the LR classifier on the whole data was calculated from the AUC using the lroc command in Stata [50]. The AUC for the SVM classifier was obtained by varying the classification threshold over a range that rendered sensitivity of the classifier between 0 and 100 per cent.

3. Results

 SVM classifiers incorporating all 45 variables predicted hock burn occurrence in test data with a mean AUC of 0.77 (s.d. 0.005). After RFE, the classifiers retained between 16 and 25 variables (mean 21 (s.d. 2.6)) with no loss of accuracy (figure 3). The AUC was 0.78 (s.d. 0.007).

Figure 3.

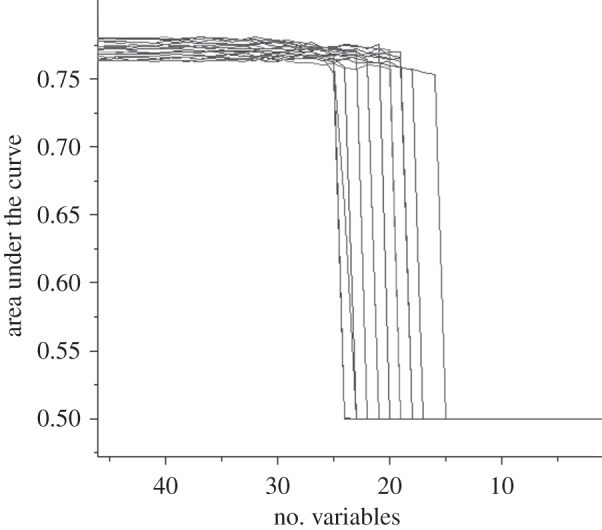
The change in area under the ROC curve (AUC) with the exclusion of variables by SVM–RFE.

The importance of individual variables was assessed from their consistent presence, ranking position and size of coefficients after RFE (table 2).

Table 2.

Frequency, rank and coefficients of features included in SVM after recursive feature elimination.

overall rank	variable	classifier frequency	median rank	IQR	mean coefficient	s.d.
1	weight density: two weeks (g m−2)	18	1	1–1	0.4845	0.1327
2	stocking density at placement (birds m−2)	18	2	2–2	−0.5405	0.1337
3	average weight: two weeks (g)	18	3	3–3	−0.4009	0.0947
4	August placement	17	4	4–5	−0.1718	0.0763
5	water consumption: five weeks (l per 1000 birds)	18	6	4.3–7	0.3068	0.0980
6	July placement	17	8.5	6–11.8	−0.1829	0.0770
7	standard rearing system	18	9	9–11	0.2260	0.0865
8	May placement	16	9	6–18	−0.1335	0.0486
9	average weight at slaughter (g)	18	9.5	6–12	0.3716	0.1067
10	June placement	14	9.5	7.3–17.3	−0.1237	0.0505
11	April placement	15	10.5	9.3–19.8	−0.1214	0.0502
12	water consumption: two weeks (l per 1000 birds)	16	14	12–16	−0.1135	0.0415
13	male birds reared separately	17	14.5	13–18.5	−0.1197	0.0459
14	December placement	15	14.5	11.3–18	0.1311	0.0580
15	March placement	14	16	13.3–21.3	−0.1113	0.0435
16	days taken to depopulate house	14	16.5	14.3–20.5	−0.1064	0.0457
17	use of automatic water meter	18	17	16–18	−0.1146	0.0448
18	stocking density: five weeks (birds m−2)	16	17	16–17	0.1222	0.0507
19	November placement	13	18.5	14.3–20.8	0.1233	0.0929
20	water consumption: four weeks (l per 1000 birds)	13	18.5	13–21	0.1180	0.0359
21	water consumption last 3 days (l per 1000 birds)	5	20.3	23.5–28.5	−0.0538	0.0704
22	female birds reared separately	8	22.5	20–27.3	0.0643	0.0308
23	October placement	7	24	16.3–25	0.1491	0.0650
24	January placement	5	24	15.3–30	0.1336	0.0483
25	percentage culled during first week	4	26.5	25–30	0.0764	0.0259

The final LR model, built manually using forward stepwise and backward elimination techniques, also had an AUC of 0.78. It identified 22 of the 25 variables selected by SVM and RFE. However, the two top-ranked variables selected by RFE were missing from the LR model. Attempts to force these variables back into the final model failed (table 3).

Table 3.

Logistic regression model of hock burn.

variable	coefficient	s.e.	OR	95% CI	p-value
average weight at slaughter (g)	0.7916	0.039	2.2068	2.045–2.382	<0.001
standard rearing system	0.2763	0.0482	1.3183	1.199–1.449	<0.001
December placement	0.2507	0.0335	1.2849	1.203–1.372	<0.001
water consumption: five weeks (l per 1000 birds)	0.5721	0.0523	1.772	1.599–1.963	<0.001
July placement	−0.468	0.0477	0.6263	0.57–0.688	<0.001
number of days to depopulate house	−0.1982	0.0406	0.8202	0.758–0.888	<0.001
August placement	−0.3778	0.0429	0.6854	0.63–0.746	<0.001
November placement	0.1703	0.0326	1.1856	1.112–1.264	<0.001
October placement	0.1203	0.0334	1.1279	1.056–1.204	<0.001
January placement	0.1039	0.0348	1.1095	1.036–1.188	0.003
use of an automatic water meter	−0.2025	0.0304	0.8167	0.769–0.867	<0.001
male birds reared separately	−0.1851	0.0414	0.8311	0.766–0.901	<0.001
water consumption: two weeks (l per 1000 birds)	−0.2	0.0411	0.8187	0.755–0.888	<0.001
female birds reared separately	0.1485	0.0323	1.1601	1.089–1.236	<0.001
May placement	−0.2378	0.0381	0.7883	0.732–0.849	<0.001
April placement	−0.2154	0.0374	0.8062	0.749–0.868	<0.001
March placement	−0.2134	0.0377	0.8078	0.75–0.87	<0.001
June placement	−0.1751	0.0364	0.8394	0.782–0.902	<0.001
percentage culled during first week	0.1104	0.0301	1.1168	1.053–1.185	<0.001
water consumption: last 3 days (l per 1000 birds)	−0.1182	0.0349	0.8885	0.83–0.951	<0.001
stocking density at five weeks (birds m−2)	0.1195	0.047	1.1269	1.028–1.236	0.011
water consumption: four weeks (l per 1000 birds)	0.1398	0.0586	1.1501	1.025–1.29	0.017
average weight at two weeks (g)	−0.0746	0.0384	0.9281	0.861–1.001	0.052

Comparison of the ranking and coefficients of the variables in the SVM classifier and the LR model showed that although quantitatively different, the direction of the effect was the same in all cases and 14 of the 22 common variables were within two rankings of each other (table 4).

Table 4.

Variable ranking and coefficients in SVM–RFE compared with an LR model of hock burn. (NI, not included; (1), (2) top-ranked variables in SVM.)

variable	SVM rank	LR rank	difference in rank	SVM coefficient	LR coefficient
weight density at two weeks (g m−2)	(1)	NI	NI	0.4845	NI
stocking density: placement (birds m−2)	(2)	NI	NI	−0.5405	NI
average weight at two weeks (g)	1	23	−22	−0.4009	−0.0746
August placement	2	4	−2	−0.1718	−0.3778
water consumption: five weeks (l per 1000)	3	2	1	0.3068	0.5721
July placement	4	3	1	−0.1829	−0.468
standard rearing system	5	5	0	0.226	0.2763
May placement	6	7	−1	−0.1335	−0.2378
average weight at slaughter (g)	7	1	6	0.3716	0.7916
June placement	8	14	−6	−0.1237	−0.1751
April placement	9	8	1	−0.1214	−0.2154
water consumption: two weeks (l per 1000)	10	11	−1	−0.1135	−0.2
December placement	11	6	5	0.1311	0.2507
male birds reared separately	12	13	−1	−0.1197	−0.1851
March placement	13	9	4	−0.1113	−0.2134
number of days to depopulate house	14	12	2	−0.1064	−0.1982
stocking density: five weeks (birds m−2)	15	19	−4	0.1222	0.1195
use of an automatic water meter	16	10	6	−0.1146	−0.2025
November placement	17	15	2	0.1233	0.1703
water consumption: four weeks (l per 1000)	18	17	1	0.118	0.1398
water consumption: last 3 days (l per 1000)	19	20	−1	−0.0538	−0.1182
female birds reared separately	20	16	4	0.0643	0.1485
October placement	21	18	3	0.1491	0.1203
January placement	22	22	0	0.1336	0.1039
percentage culled during first week	23	21	2	0.0764	0.1104

Six variables stood out as being frequently included in the classifiers, having consistently high rankings and relatively large coefficients (standard rearing system, stocking density at placement, average weight at two weeks, weight density at two weeks, water consumption at five weeks, and average weight at slaughter). Stocking density at placement and weight density at two weeks were absent and average weight at two weeks had a low ranking in the LR models (table 4).

The month of placement was an important risk factor for hock burn. Some months (July and August) were included consistently with little variation in rank. September was always absent.

The ranking and inclusion frequency of other months varied. More detailed examination showed that this was because there were two types of classifier. One included spring and summer months (March–June). These showed a negative association with hock burn. The other incorporated winter months (November–February), which were positively associated with the disease (table 5). Spring and summer months were selected on 13 occasions and winter months on five.

Table 5.

The pattern and ranking of months included in classifiers with summer and winter patterns.

	summer pattern (13)		winter pattern (5)
placement month	median ranka	IQR	median rankb	IQR
Jan	25	24–26	13	12–13
Feb	31	30–32	14	10–27
Mar	14	11–17	25	24–27
Apr	10	8–11	26	23–28
May	7	6–10	23	21–24
Jun	8	7–10	25	24–25
Jul	7	6–9	14	10–15
Aug	4	4–5	7	5–19
Sep	41	39–43	42	41–42
Oct	24	24–26	11	11–12
Nov	20	18–22	9	8–11
Dec	18	14–19	8	6–8

^aValues in italics show the spring and summer months.

^bValues in italics show the winter months.

The remaining six variables, which were consistently selected by RFE, were low ranking with relatively small coefficients. Four (water consumption at two weeks, male birds reared separately, days taken to depopulate house, use of automatic water meter) were associated with a decreased risk of hock burn. Two were associated with an increased risk: stocking density at five weeks and water consumption at four weeks.

4. Discussion

The use of SVM on routine broiler production data created a classifier which predicted high hock burn prevalence in unseen data with an accuracy of 0.78, as measured by area under the ROC curve. AUC values between 0.7 and 0.8 reflect acceptable discrimination, while AUC values between 0.8 and 0.9 suggest excellent discrimination [52].

This is remarkable, as none of the data was collected for this purpose, i.e. the selection of features was not hypothesis driven.

The original classifier comprised 45 features. Although there is no need to reduce the number of features for predictive classification, the identification and the ranking of the most important features are important for practical preventive medicine. RFE is one method of doing this. The choice of end point in this process can be rather subjective. To avoid this, the final classifier was chosen as the feature set obtained immediately prior to the large reduction in classifier AUC to 0.5.

RFE resulted in a reduction in number of features with no loss of accuracy. In 18 instances, the AUC was 0.78 (s.d. 0.007). In the remaining two cases, the classifier AUC was 0.5 prior to RFE. This classifier failure associated with particular data splits has been observed previously [53]. Although the AUC of the classifiers produced by using SVM–RFE on random data splits was similar, there were differences in the number of features included and their ranking. The sensitivity of RFE to different data splits is well recognized [33] and it is common procedure to identify the important variables by their frequency of inclusion and average ranking [5,51], the method adopted here.

The top ranking features (weight density at two weeks, stocking density at placement, average weight at two weeks, August placement and water consumption at five weeks) were consistently included and highly ranked in all SVM–RFE classifiers. One of the major reasons for the variation in ranking was the way in which the month of placement was included in the classifier. On 13 occasions, the classifier selected the months June to March and on five occasions, the months November to February. This may be explained by the relationship between month of placement and the hock burn prevalence seen in this study (figure 4) and reported elsewhere [54].

Figure 4.

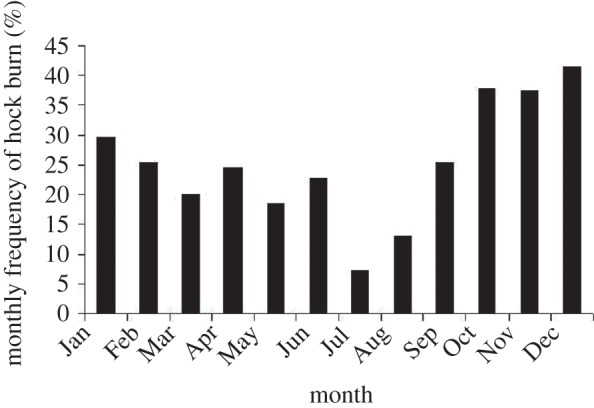
The seasonal pattern of hock burn.

Autumn and winter months (October–December) are associated with an increased risk of hock burn and spring and summer a decreased risk. In some cases, spring and summer months were included in the classifier, and their coefficients were negative. Conversely, some classifiers included autumn and winter months and their coefficients were positive. The prevalence of hock burn was lowest in July and August, and these months were consistently included and highly ranked in all classifiers (figure 4 and table 2). This provides an interesting example of the way in which seasonal prevalence is handled by SVM–RFE.

This study shows that SVM learning is a useful technique for analysing observational epidemiological data. SVM has been successfully used in several disciplines [24,31,33], but its uptake as method of identifying risk factors in observational epidemiology has been slow. Since our preliminary study in 2005 [40], there have been few published reports of its use [41–43].

The use of new analytical methods requires the target audience to be exposed to that technique. Additionally, there must be evidence that the new technique is as good as or better than existing methods. This takes time. For example, epidemiologists adopted the use of LR 10–15 years after it was first described [55]. A similar time period has elapsed since the description of SVM [15]. One of the aims of this paper is to introduce SVM to a wider audience and to provide evidence that it performs at least as well as existing methods. For this reason, we have included a comparison with LR. In doing this, we have ignored the hierarchical structure of the data although this is reported elsewhere [47].

There were many similarities between the features selected by SVM–RFE and those variables remaining in the LR. Twenty-three of the features identified by the SVM classifier were common to the LR model. The direction of effect was identical in all cases and 14 of the variables common to the SVM–RFE and LR models were ranked within two places of each other. The AUC of the LR model was similar at 0.78.

The failure of LR to identify ‘weight density at two weeks’ and ‘stocking density at placement’ as important risk factors is particularly interesting, as they are the two most consistently highly ranked features identified by SVM–RFE. This is not an effect of the structure of the data as it was also seen when the data were analysed using hierarchical LR [47].

Previously, we have shown that when data collected at either two or three weeks of age are analysed separately, ‘weight density at two weeks’ and ‘stocking density at placement’ are important predictors of hock burn. When the complete data are analysed by LR, weight density at two weeks and weight at two weeks are replaced by weight at five weeks. In contrast, SVM–RFE includes both the features related to weight at two weeks and weight at five weeks in the classifier. The reason for this is unclear, but it does suggest that SVM–RFE may provide an alternative, if not greater, insight into the data. SVM does not rely on any restrictive assumptions about the distribution and independence of data, and has proved robust for a broad range of complex datasets. In contrast, LR assumes that variables are statistically independent and fits the data to a logistic curve. This may give SVM different discriminating powers for classification.

Hock burn is defined as a contact dermatitis of the plantar surface of the hocks of broiler chickens [44]. It is important because it is an indicator of poor welfare [45,46] and is visible on processed birds. An SVM–RFE classifier built using routinely collected data identified several risk factors (average weight at slaughter, flock placement month), which have been identified in previous studies [38,56,57] providing additional evidence to support the validity of the method.

Risk factors for hock burn, which can be measured at two weeks, are examples of ‘lead welfare indicators’ [58]. Their identification offers an opportunity of intervention in real time to mitigate the risk of disease in high-risk flocks.

The use of SVM to analyse observational data in epidemiology is at an early stage of development. There are some challenges ahead in making this technique accessible to epidemiologists. These include the interpretation of coefficients with respect to the concept of odds ratios and p-values, and the introduction of techniques to deal with hierarchical data.

Machine-learning algorithms lend themselves to the development of expert management systems. This is exciting because by embedding such algorithms in data management systems used by poultry farmers, they could adapt to interventions or changes in management, by relearning from new data to produce a new classifier and new interventions. This has enormous potential for the improvement of poultry health and welfare.