Leg stiffness of sprinters using running-specific prostheses

Abstract

Running-specific prostheses (RSF) are designed to replicate the spring-like nature of biological legs (bioL) during running. However, it is not clear how these devices affect whole leg stiffness characteristics or running dynamics over a range of speeds. We used a simple spring–mass model to examine running mechanics across a range of speeds, in unilateral and bilateral transtibial amputees and performance-matched controls. We found significant differences between the affected leg (AL) of unilateral amputees and both ALs of bilateral amputees compared with the bioL of non-amputees for nearly every variable measured. Leg stiffness remained constant or increased with speed in bioL, but decreased with speed in legs with RSPs. The decrease in leg stiffness in legs with RSPs was mainly owing to a combination of lower peak ground reaction forces and increased leg compression with increasing speeds. Leg stiffness is an important parameter affecting contact time and the force exerted on the ground. It is likely that the fixed stiffness of the prosthesis coupled with differences in the limb posture required to run with the prosthesis limits the ability to modulate whole leg stiffness and the ability to apply high vertical ground reaction forces during sprinting.

1. Introduction

Recently, Paralympic athletes have achieved remarkable sprint-running performances using modern running-specific prostheses (RSPs). RSPs are essentially J-shaped carbon fibre leaf springs that are attached to a socket, which surrounds the residual lower limb of a person with an amputation. Recent studies have shown that athletes with transtibial amputations using an RSP exert smaller vertical ground reaction forces and have prolonged contact times in their affected leg (AL) compared with their unaffected leg (UL) and to the biological legs (bioL) of non-amputees [1,2]. These differences suggest that leg spring properties are also different between legs. While RSPs have been engineered to behave like springs, to our knowledge, no studies have analysed the overall leg spring properties of runners using these devices.

Human running can be fundamentally described as a bouncing movement in which each leg acts like a spring. Despite the underlying complex neuromuscular dynamics, simple spring–mass models have been able to describe the mechanics of running and other bouncing gaits remarkably well [3–7]. The simplest spring–mass model comprises a massless linear leg spring attached to a point mass representing the centre of mass (CoM) of the entire body. When hopping or running in place, the stiffness of the leg spring is an important parameter for determining CoM mechanics [8] (figure 1). However, during the stance phase of forward running, the leg sweeps through an arc and the combination of leg stiffness, the angle swept by the leg, and landing velocity determine the path of the CoM and the ground reaction forces [7]. The combination of leg stiffness and sweep angle also determine contact time, an important variable that influences maximum running speed [9].

Figure 1.

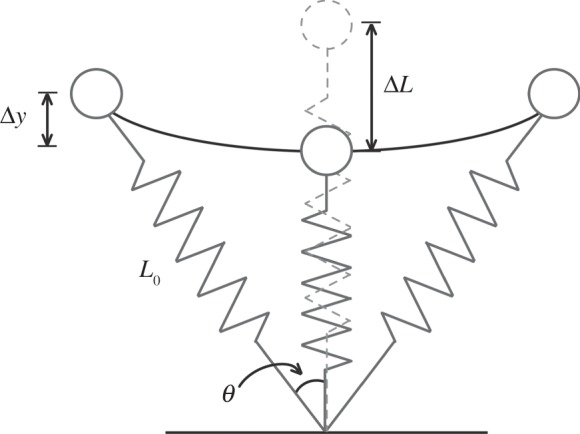
A schematic of a simple spring–mass model used to characterize the overall biomechanics of bouncing gaits such as running and sprinting. This model represents the body's mass as a point mass and the leg as a massless linear spring. At the initial point of ground contact, the leg spring is uncompressed and equals a length denoted by L₀. During the stance phase, the leg spring is compressed, and reaches maximal leg compression (ΔL) at approximately mid-stance. The CoM is displaced vertically (Δy), and horizontally, where one-half the angle swept by the leg spring during ground contact is denoted as θ.

In general, vertical stiffness and leg stiffness have been used to describe the bouncing motion of running. Vertical stiffness (k_vert) is the ratio of peak vertical force and vertical CoM displacement during the stance phase. Vertical stiffness has been predicted to increase with faster speeds and with decreased contact times [7,10]. Several studies have confirmed this in humans [11–14] and other animals [6]. Leg stiffness (k_leg) is the ratio of peak vertical force and the change in length of the leg spring. Unlike k_vert, k_leg depends on a combination of variables including the angle swept by the leg during the stance phase and contact length (L_c), the forward distance moved by the CoM during stance. Because multiple possible combinations of these variables can result in a given speed, there is no explicit prediction for how k_leg should change with speed. But empirically, human studies have shown that k_leg is independent of speed over slow to moderate speed ranges of 2–7 m s⁻¹ [6,13,14]. However, little is known about k_leg at sprinting speeds. A recent review suggests that k_leg may increase at speeds faster than approximately 5 m s⁻¹ [15].

In this study, we compared the running biomechanics of athletes with unilateral transtibial amputations, bilateral transtibial amputations and non-amputees (with two bioL). Our aim was to determine how well a residual limb plus an RSP (AL) mechanically emulates the overall spring–mass characteristics of a bioL. We tested the general null hypothesis that leg mechanical behaviour would not differ between affected and fully bioL. More specifically, we hypothesized that the leg stiffness, k_leg, of affected and bioL would be the same across the entire range of running and sprinting speeds.

2. Methods

2.1. Subjects

Eight elite Paralympic sprinters (six with a unilateral transtibial amputation and two with bilateral transtibial amputations) and 12 sprinters of similar ability without amputations (table 1) gave informed written consent prior to participation. Each participant with an amputation used his/her own sprint-specific RSP (table 1). Data from one athlete with bilateral amputations were collected in conjunction with a previous study (for details, see [2]). Data from all other athletes were collected during experiments conducted at the Biomechanics Laboratory of the Orthopedic Specialty Hospital in Salt Lake City, UT, USA.

Table 1.

Anthropometric variables and treadmill top speeds for each subject. Total mass includes RSP mass. Leg lengths equal the distance from the greater trochanter to the floor. AL length was determined when the prosthesis was not compressed.

unilateral amputees	sex (M/F)	age (yrs)	height (m)	mass (kg)	UL (m)	AL (m)	RSP (model)	RSP mass (kg)	top speed (m s−1)
1	F	35	1.68	66.1	0.955	0.985	Cheetah	1.7	7.0
2	F	23	1.69	62.9	0.895	0.950	Sprinter	1.2	8.4
3	M	36	1.84	79.9	0.985	1.030	Cheetah	1.6	9.0
4	M	27	1.75	69.3	0.930	0.970	Cheetah	1.5	9.3
5	M	29	1.87	109.1	0.985	1.065	C-Sprint	1.4	9.5
6	M	25	1.85	71.0	1.005	1.025	Cheetah	1.2	9.7
bilateral amputees	sex	age	height	mass	AL, R	AL, L	RSP	RSP mass	top speed
7	M	20	1.75	67.7	0.995	1.005	Cheetah	1.7	8.9
8	M	21	1.86	80.0	1.036	1.043	Cheetah	1.8	10.8
non-amputees	sex	age	height	mass	bioL, R	bioL, L			top speed
1	F	16	1.70	59.5	0.900	0.900			7.0
2	F	18	1.70	56.4	0.885	0.890			7.6
3	F	28	1.74	60.9	0.952	0.945			8.2
4	M	16	1.82	70.7	0.950	0.955			9.0
5	M	19	1.88	89.1	0.990	1.000			9.0
6	M	40	1.69	88.6	0.885	0.890			9.0
7	M	21	1.84	75.0	1.000	1.000			9.0
8	M	16	1.75	69.1	0.920	0.935			9.0
9	M	18	1.79	76.8	0.910	0.915			9.1
10	M	17	1.80	78.2	0.960	0.940			9.2
11	M	18	1.80	73.2	0.905	0.915			9.3
12	M	18	1.85	84.1	0.985	0.980			9.4

2.2. Experimental protocol

We measured each subject's height, mass, prosthesis mass and standing leg lengths. Leg length was defined as the vertical distance from the greater trochanter to the floor during standing. The AL length measurements were made while the leg plus prosthesis was unloaded. Following a warm-up period, subjects performed a series of discrete, constant speed running trials on a custom, high-speed, three-dimensional force-sensing treadmill (Athletic Republic, Park City, UT, USA) recording at 2400 Hz. The treadmill was set at a given speed for each trial. To begin the trial, subjects lowered themselves from handrails onto the moving treadmill belt, data were collected for at least 10 strides, and then subjects grabbed the handrails and stepped off the treadmill. Subjects started the series of trials at 3 m s⁻¹ and the speed for each subsequent trial was increased by 1 m s⁻¹ until subjects approached top speed. Then, smaller speed increments were employed until subjects reached their top speed. Top speed was determined when subjects put forth a maximal effort but could not maintain their position on the treadmill [16]. Subjects were given as much time between trials as needed to recover fully.

We selected a minimum of eight consecutive strides (eight steps per leg) for analysis from each trial. To isolate individual steps, we used a custom-written Matlab routine (MathWorks Inc.) to detect the instants of touch-down and toe-off from the raw vertical GRF data based on a 10 N threshold. To determine peak vertical GRF, we filtered the raw GRF data with a recursive 50 point moving average filter. We selected the window size that minimized both signal distortion and noise following the residual analysis described by Winter [17].

2.3. Leg spring stiffness

To calculate vertical stiffness and leg stiffness, we used a previously described spring mass model (for details, see [6,7]). Briefly, vertical stiffness (k_vert) was calculated as the ratio of peak vertical force (vGRF_peak) and maximal vertical CoM displacement (Δy)

2.1

Vertical CoM displacement was calculated by twice integrating the CoM acceleration with respect to time [18].

Leg stiffness (k_leg) was calculated as the ratio of peak vertical force (vGRF_peak) and maximum change in length of the virtual leg spring (ΔL)[6]:

2.2

Maximum displacement of the virtual leg spring (ΔL) was calculated following Farley et al. [6] using the length of the leg spring at touch-down, which was estimated to be equal to the standing leg length (L₀), and half of the angle swept by the leg spring while the foot was on the ground (θ):

3.1

In order to account for differences in the athletes’ sizes, k_vert and k_leg were made dimensionless by multiplying each by the ratio of L_o and body weight (BW), forming K_vert and K_leg, respectively:

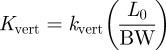2.4

and

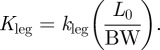2.5

2.4. Groucho number

We used the Groucho number (Gr), a dimensionless variable, to characterize hard or soft running styles [10]. A low Groucho number (i.e. less than 1) indicates a more compliant ‘softer’ running gait, whereas a higher Groucho number is associated with stiffer running. We calculated the Gr as:

2.6

where Fr_vert is the dimensionless vertical Froude number. The vertical Froude number was calculated as:

2.7

where v is the vertical landing velocity and g is the acceleration owing to gravity.

2.5. Statistics

We used a model I regression analysis to determine the relationship between variables of interest and running speed. Significance levels were set to p < 0.05. We determined significant differences between legs by comparing the 95% confidence limits.

3. Results

The results of our study do not support the null hypothesis. Using a simple spring–mass model to examine the overall running mechanics across a range of speeds, we found significant differences between the AL of unilateral transtibial amputees and both affected legs (BL) of bilateral transtibial amputees compared with the bioL of non-amputees for nearly every variable measured. We also found significant differences between the unaffected bioL of unilateral amputees and the bioL of non-amputees (figure 2).

Figure 2.

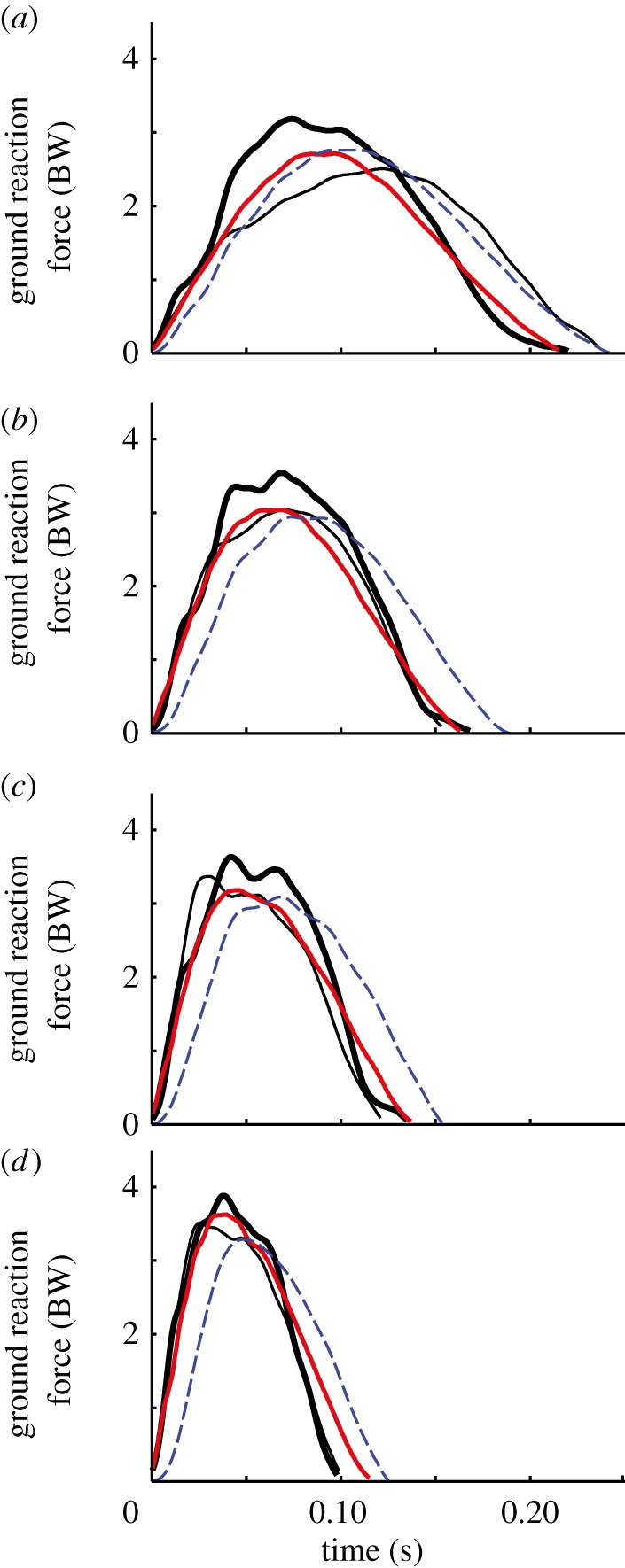
Representative vertical ground reaction forces from a non-amputee (bioL), the unaffected leg (UL) and affected leg (AL) of a unilateral amputee and a bilateral amputee (BL) running at four different speeds ((a) 3 m s⁻¹; (b) 5 m s⁻¹; (c) 7 m s⁻¹; (d) 9 m s⁻¹). Peak forces were higher in bioL and tended to be higher in UL, compared with AL and BL subjects. Thick black line, bioL; thin line, UL; red solid line, AL; blue dashed line, BL. (Online version in colour.)

3.1. Stiffness

Our specific hypothesis, that leg stiffness would not differ among runners with and without RSPs, was not supported. Leg stiffness for legs without amputations was constant or increased with speed, whereas stiffness for legs with RSPs decreased with speed. Non-amputee subjects increased dimensionless bioL leg stiffness (K_leg) by 29 per cent with increasing speeds, particularly at speeds greater than 6 m s⁻¹ (p < 0.001). Subjects with a unilateral amputation did not change UL leg stiffness (p = 0.385; figure 3a); however, AL leg stiffness had a 17 per cent decrease with increasing speed (p = 0.034). Bilateral amputees also had a significant decrease in K_leg (19%) with increasing speed (p = 0.017). The slope of the relationship between K_leg and speed was not significantly different between AL and BL subjects (figure 3b). At slow speeds (less than 5 m s⁻¹), all of our subjects had similar K_leg values; however, owing to the differing slopes, at a top speed of 9.5 m s⁻¹ ALs with RSPs (AL and BL) had a leg stiffness that was on average 27 per cent than lower than bioL (bioL and UL). Dimensionless vertical stiffness (K_vert) increased significantly with speed for all of the subject groups in our study (figure 3c,d). However, non-amputees increased bioL K_vert with speed to a significantly greater extent than athletes with amputations.

Figure 3.

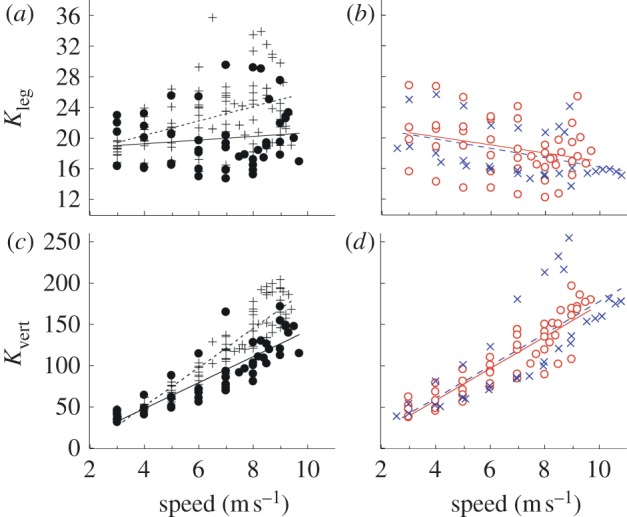
Average dimensionless leg stiffness (K_leg) and vertical stiffness (K_vert) across speed. (a) Non-amputees (bioL) increased K_leg with increasing speed; whereas subjects with a unilateral amputation did not change leg stiffness in their UL. (b) K_leg decreased with increasing speed in the AL of unilateral amputees and bilateral amputees (BL). (c,d) All subjects increased K_vert with increasing speed; however, non-amputees increased vertical stiffness to a greater extent than subjects with an amputation. The linear fit equations for K_leg were bioL: K_leg = 0.93x + 16.64, R² = 0.192, p < 0.001; UL: K_leg = 0.24x + 18.36, R² = 0.016, p = 0.385; AL: K_leg = −0.53x + 22.26, R² = 0.092, p = 0.034; BL: K_leg = −0.60x + 22.28, R² = 0.182, p = 0.017. The linear fit equations for K_vert were bioL: K_vert = 23.72x − 44.49, R² = 0.889, p < 0.001; UL: K_vert = 16.00x − 17.00, R² = 0.740, p < 0.001; AL: K_vert = 19.63x − 22.12, R² = 0.810, p < 0.001; BL: K_vert = 19.15x − 14.06, R² = 0.583, p < 0.001. Plus symbols with dashed line, bioL; open circles with solid line, AL; filled circles with solid line, UL; crosses with dashed line, BL. (Online version in colour.)

3.2. Ground reaction forces and leg compression

We calculated K_leg from peak vertical ground reaction force and virtual leg length change. Peak vertical ground reaction forces (vGRF_peak) increased with speed to a significantly greater extent in bioL (bioL and UL; figure 4a) compared with the ALs of amputees (AL and BL; figure 4b). The relationships between vGRF_peak and speed were significant (p < 0.001) and similar for bioL and UL (slopes: 0.144 and 0.134, respectively). However, vGRF_peak for the UL of unilateral amputees were significantly greater than those for the bioL of non-amputees at all speeds. vGRF_peak of ALs (AL and BL) also significantly increased with speed (p < 0.001); though the slopes were significantly less than for the biological limbs (bioL and UL). As a result, at 9.5 m s⁻¹, vGRF_peak was on average 18 per cent lower for ALs compared with bioL. The relationship between the magnitudes of vGRF_peak and speed were similar for AL and BL. The maximal change in virtual leg length (ΔL) was independent of running speed for bioL and UL (p = 0.93 and 0.42, respectively; figure 4c); however, the ΔL increased significantly for AL and BL (p < 0.001; figure 4d). Therefore, at 9.5 m s⁻¹, ΔL was 16 per cent greater in ALs compared with bioL.

Figure 4.

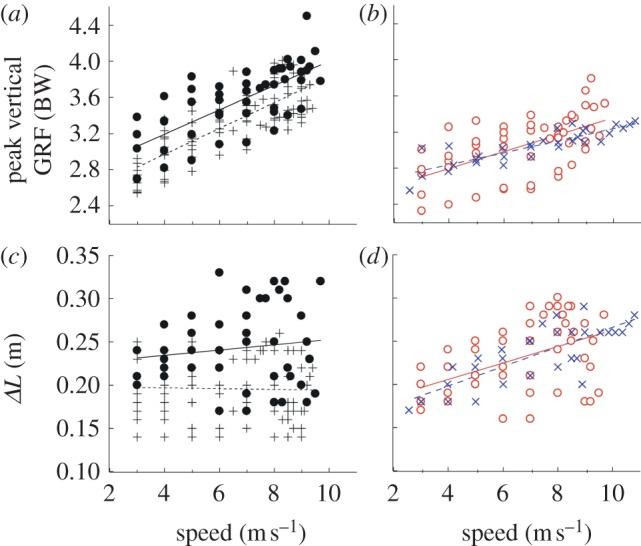
Average peak vertical ground reaction force (vGRF_peak) and (c,d) leg compression (ΔL) across speed. (a,b) Non-amputees (bioL) increased vGRF_peak at faster speeds. Subjects with a unilateral amputation increased vGRF_peak to a greater extent in their UL than in their AL. Subjects with bilateral amputations (BL) increased vGRF_peak with speed by a similar magnitude as unilateral AL, which was less than non-amputees and unilateral UL. (c,d) Non-amputees (bioL) did not change leg compression across velocity. Subjects with a unilateral amputation did not change leg compression in their UL, but increased leg compression with their AL at faster speeds. Subjects with bilateral amputations (BL) also increased leg compression at faster speeds. The linear fit equations for vGRF_peak were bioL: vGRF_peak = 0.144x + 2.40, R² = 0.615, p < 0.001; UL: vGRF_peak = 0.135x + 2.66, R² = 0.528, p < 0.001; AL: vGRF_peak = 0.094x + 2.42, R² = 0.341, p < 0.001; BL: vGRF_peak = 0.067x + 2.57, R² = 0.745, p < 0.001. The linear fit equations for ΔL were bioL: ΔL = 0 x + 0.196, R² = 0, p = 0.934; UL: ΔL = 0.003x + 0.226, R² = 0.014, p = 0.421; AL: ΔL = 0.009x + 0.172, R² = 0.206, p = 0.001; BL: ΔL = 0.012 x + 0.150, R² = 0.660, p < 0.001. (a,c) Crosses with dashed line, bioL; (a,c) circles with filled line, UL; (b,d) open circles with solid line, AL; crosses with solid line, BL. (Online version in colour.)

3.3. Leg sweep angle and landing velocity

Virtual leg length is a function of the half angle (θ) swept by the leg when the foot is on the ground. All subjects increased the leg sweep half angle with increasing speeds (p < 0.001; figure 5a,b). However, non-amputees did not increase θ as greatly with speed as the athletes with amputations. The slopes of the relationships between θ and speed were significantly lower for non-amputees compared with athletes with unilateral and bilateral amputations; whereas there were no significant differences between the legs of athletes with amputations. At a top running speed of 9.5 m s⁻¹, θ on average was not different between bioL (bioL and UL) and ALs (AL and BL); however, θ was 14 per cent lower in bioL compared with UL, AL and BL.

Figure 5.

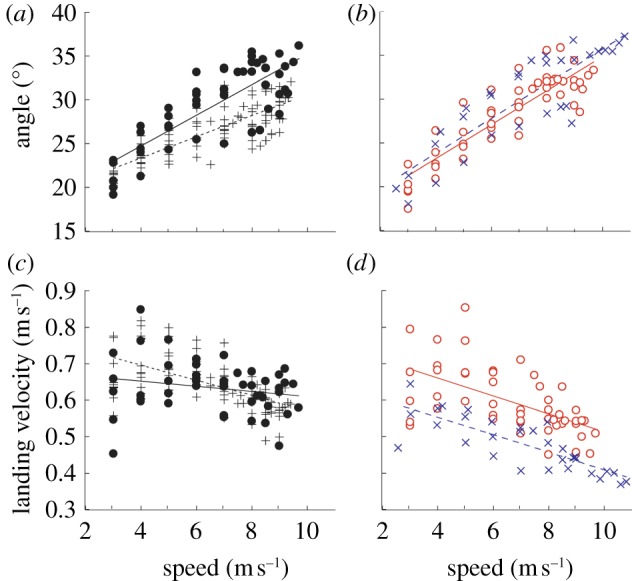
Half angle swept (θ) and landing velocity (v_land) across speed. (a,b) All subjects increased θ at faster speeds. The increase in θ was not as substantial in non-amputees (bioL) compared with all other conditions across speed. (c,d) v_land decreased across velocity for all conditions. The linear fit equations for θ were bioL: θ = 1.21x + 18.53, R² = 0.639, p < 0.001; UL: θ = 1.75x + 17.75, R² = 0.642, p < 0.001; AL: θ = 1.93x + 15.51, R² = 0.777, p < 0.001; BL: θ = 1.98x + 15.92, R² = 0.752, p < 0.001. The linear fit equations for v_land were bioL: v_land = −0.021x + 0.779, R² = 0.359, p < 0.001; UL: v_land = −0.025x + 0.759, R² = 0.333, p = 0.154; AL: v_land = −0.007x + 0.680, R² = 0.043, p < 0.001; BL: v_land = −0.024x + 0.649, R² = 0.651, p < 0.001. (a,c) Crosses with dashed line, bioL; filled circles with continuous line, UL. (b,d) open circles with solid line, AL; crosses with solid line, BL. (Online version in colour.)

The vertical landing velocity of the CoM at landing decreased significantly with speed for non-amputees and athletes with bilateral amputations (p < 0.001; figure 5c,d). Vertical landing velocity also decreased significantly with speed in the AL (p < 0.001) but was independent of speed in the UL (p = 0.154) of athletes with a unilateral amputation. The slopes between landing velocity and speed were not significantly different among bioL, UL and BL. At 9.5 m s⁻¹, vertical landing velocity was 6 per cent lower on average for ALs compared with bioL.

3.4. Groucho number

Analysis of the Groucho number showed that ALs using RSPs used softer modes of running than bioL at faster speeds (greater than 6 m s⁻¹). The Groucho number increased significantly with speed for all legs (p < 0.001; figure 6). However, the slopes of the increase were significantly greater for bioL (BioL and UL) compared with ALs with RSPs (AL and BL). There were no significant differences in the slope between BioL and UL (figure 6a) or between AL and BL (figure 6b). At a top speed of 9.5 m s⁻¹, the Groucho number was 28 per cent lower on average for ALs compared with bioL.

Figure 6.

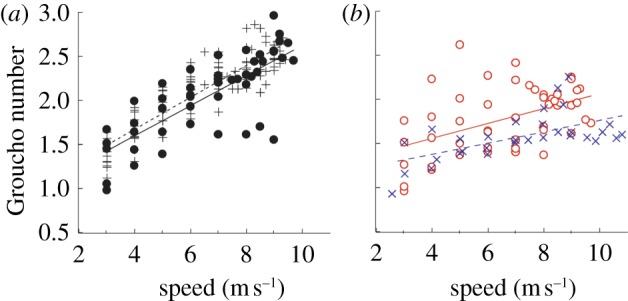
The dimensionless Groucho number across speed. The Groucho number increased with speed for in all subjects; however, the slopes were significantly greater for biological legs (bioL and UL) compared with legs with running-specific prostheses (AL and BL). Lower Groucho numbers indicate running with a ‘softer’ gait. The linear fit equations for Grouch number were bioL: Gr = 0.180x + 0.954, R² = 0.771, p < 0.001; UL: Gr = 0.170x + 0.920, R² = 0.593, p < 0.001; AL: Gr = 0.084x + 1.224, p = 0.001, R² = 0.227; BL: Gr = 0.064x + 1.124, R² = 0.339, p < 0.001. (a) Crosses with dashed line, bioL; filled circles with dashed line, UL. (b) Open circles with solid line, AL; crosses with dashed line, BL. (Online version in colour.)

4. Discussion

The goal of our study was to examine the overall spring–mass mechanics of running by athletes with transtibial amputation using RSPs relative to performance-matched non-amputees. While RSPs have been designed to emulate the natural spring-like behaviour of bioL, we found that whole body CoM mechanics differed significantly between athletes with an amputation and non-amputee athletes. Using a simple spring–mass model, we found that the dimensionless virtual leg stiffness, K_leg, either increased or remained constant across speed in bioL but decreased in legs with RSPs. K_leg is a function of both peak vertical force (vGRF_peak) and virtual leg compression (ΔL). Consistent with previous studies of amputee running [1,2], the legs using RSPs (AL and BL) had significantly lower vGRF_peak, and vGRF_peak increased less with speed compared with bioL. At the fastest running speed recorded for all study groups (9.5 m s⁻¹), vGRF_peak was 18 per cent lower for ALs compared with bioL. However, unlike bioL, ΔL increased with speed for legs with RSPs, which consequently produced the observed decrease in K_leg. Consistent with these differences in leg stiffness, the Groucho number increased less with speed for legs with RSPs compared with bioL and thus was 28 per cent lower at the fastest speeds. The Groucho number is a dimensionless parameter that can be used to differentiate between hard and soft running gaits, where lower Groucho numbers indicate softer running. Our results for Groucho number also show that the mechanics of running differ between bioL and ALs with RSPs and that using RSPs results in a softer running gait.

Previous studies of bioL have reported K_leg to be independent of running speed over slow to moderate speeds [6,12,14], because both peak vertical ground reaction force (vGRF) and peak leg compression (ΔL) increase proportionally at these speeds. The increase in ΔL is predominantly owing to an increase in the leg angle at foot contact and the resulting half angle swept. In our study, examining a range of speeds from 3 m s⁻¹ up to top speed, we found that K_leg increased in non-amputees, especially at speeds greater than 6 m s⁻¹. This was because while vGRF_peak increased, ΔL remained independent of speed. Similar to previous studies, we saw an increase in the half angle swept; however, we also saw an equal decrease in the vertical displacement of the CoM. It is important to note that the K_leg values reported here are normalized by BW and leg length and are therefore dimensionless. This normalization results in numerically similar, but slightly higher values than k_leg data which are reported in the literature as kN m⁻¹ [14]. The variability in K_leg evident in figure 3 indicates that there are multiple mechanical solutions to run at a given speed, even in runners with two bioL (figure 3a). However, in general, sprinters with RSPs use different strategies than athletes with two bioL to achieve faster speeds.

For non-amputee runners, the vertical CoM displacement is reduced at faster speeds [7]. In our study, the reduction in vertical CoM displacement with speed was nearly equal to the increase in ΔL that results from increased leg angles. The difference between our study and previous work can be partially explained by the change in vertical landing velocity that occurs at speeds greater than 6 m s⁻¹. In the simulations of McMahon & Cheng [7], vertical landing velocity was typically held constant. However, He et al. [14] showed that vertical landing velocity increased when running speed increased from 2 to 4 m s⁻¹ and then plateaued from 4 to 6 m s⁻¹. Vertical landing velocity in our study showed a similar pattern as He et al. increasing when running speed increased from 3 to 6 m s⁻¹. Above 6 m s⁻¹, vertical landing velocity decreased sharply with running speed. Vertical landing velocity plays an important role in determining the vertical displacement of the CoM during stance, with higher landing velocities resulting in greater CoM displacement. The UL of unilateral amputees had a similar pattern to non-amputees (decreasing above 6 m s⁻¹) for vertical landing velocity. However, the unilateral UL had a 45 per cent greater increase in θ than the non-amputees, which produced a trend towards increasing ΔL and therefore K_leg was independent of speed.

In a classic study of the effects of leg stiffness on running mechanics, McMahon et al. [10] coined the term ‘Groucho running’ to refer to running with bent knees, which reduced vertical stiffness by up to 82 per cent and resulted in lower peak vertical ground reaction forces. While McMahon and co-workers only focused on a single, relatively slow running speed, they showed that deeper knee flexion produced dimensionless Groucho numbers that went from approximately 1 during normal running to almost zero. In our study, we show that the Groucho number increases with speed for all conditions, but was 28 per cent lower for legs with RSPs at the higher speeds (figure 6), indicating that at high speeds, amputee athletes are using a more compliant sprinting mode. However, unlike Groucho running, this soft running mode is mainly owing to lower vertical Froude number (dimensionless value for vertical landing velocity) rather than a substantial decrease in vertical stiffness.

While the spring–mass model provides valuable information about the overall mechanics of a running system, it provides little insight into the mechanisms that underlie the calculated values. The spring-like behaviour of the virtual leg results from the coordinated effort of neuromuscular control, muscle activation, passive elastic tendons and ligaments and passive elastic RSPs when present. And, while previous studies have not shown a change in K_leg with running speed, studies have shown that K_leg can be altered in response to changes in stride frequencies [19] or surface stiffness [20]. Studies of human hopping indicate that leg stiffness is primarily modulated by changes in joint stiffness at the ankle [21,22]. However, studies examining joint stiffness over a range of running speeds suggest that ankle stiffness changes little and knee stiffness increases with speed [11,23]. The amputee athletes in our study do not have an ankle joint that could modulate stiffness. Further, a study examining joint moments during fast running by two athletes with unilateral amputation showed that knee moments differ substantially between UL and AL legs [24]. However, that study did not examine joint dynamics over a range of speeds. While the mechanisms underlying changes in K_leg with speed, especially at very fast speeds, remain somewhat unclear, differences in modulation by either the ankle or the knee may explain the differences observed between amputees and non-amputees in the present study.

While we made every attempt to minimize confounding factors in our study, there were a number of potential limitations. Our protocol of progressively increasing speed with each trial was the most practical but could have induced fatigue. To minimize the effects of fatigue, we allowed subjects to rest for at least 5 min between each trial and longer if they felt it was needed. Further, the trials at the faster speeds were very short. Because of this, we do not feel that fatigue had a significant impact on sprinting mechanics in this study. Another limitation of our study was that all amputee subjects ran using their own RSPs. It was not possible to control for exact amputation level, experience with RSP and brand/model of RSP. However, all of the RSPs comprise a passive-elastic carbon fibre leaf spring and had essentially the same function. These differences among amputee subjects may have contributed to the relatively high variation seen in the data, but did not appear to influence the overall trends in the data. Finally, there were only two bilateral amputees included in our study, making the analysis of the BL data difficult to interpret. However, these individuals are among the few bilateral amputees in the world capable of running at these sprint speeds and their data represent a unique dataset. Given the possible differences associated with control, balance and symmetry between unilateral and bilateral amputee sprinters, we feel it is imperative to include the BL group despite the low sample size.

The RSPs used by our subjects are of a fixed stiffness and thus cannot be modulated as a biological ankle can be in response to changing speed. Further, examining the force displacement curves for each condition (figure 7) suggests that for non-amputees, leg stiffness not only changes with speed, but also changes during the stance phase. At the fastest speeds, peak force is reached before peak leg compression and thus the loading stiffness is greater than the unloading stiffness. Consistent with previous studies [25], loading stiffness increased with speed for bioL. However, for legs with RSPs, loading stiffness was independent of speed. It is likely that the legs with RSPs are not able to modulate leg stiffness during stance because the fixed stiffness of the RSP dominates overall leg stiffness. Further research is required to determine how variable stiffness during stance contributes to ground reaction force development.

Figure 7.

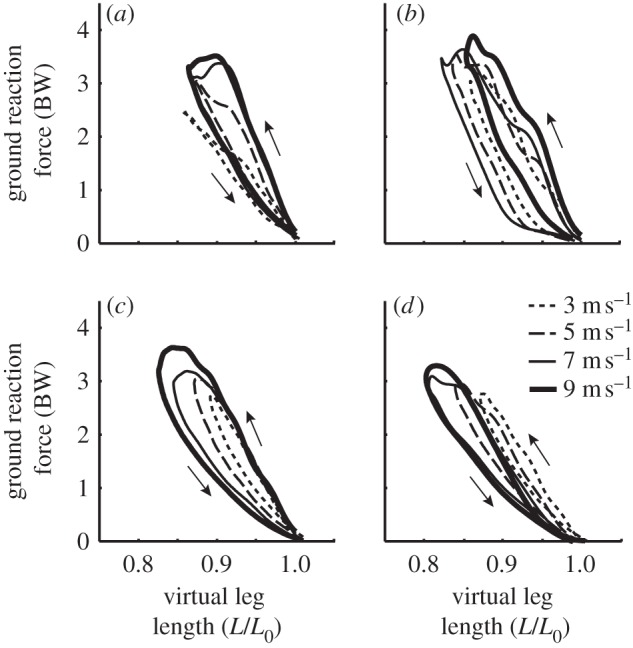
Representative force–length plots from a (a) non-amputee (bioL), (b) the UL and (c) AL of a unilateral amputee and a bilateral amputee (BL) running at four different speeds (d). Loading stiffness (upward arrow) tended to increase with speed in bioL (bioL and UL), but was independent of speed in legs with running-specific prostheses (AL and BL).

RSPs are designed to model the spring-like nature of bioL. And, despite the significant differences observed in this study, RSPs do enable athletes with lower limb amputations to run with near biological mechanics. It remains to be seen what neuromuscular adaptations are required to control these devices or how improvements in design might facilitate an even better match to biological running. It is clear that the biological ankle joint is not simply a linear spring and the mechanics of this joint during sprinting are the product of passive tissue properties, nonlinear muscle properties and active muscle control. Therefore, it is likely that a more active device or material that has an adaptive stiffness could better emulate biological ankle mechanics during sprinting. Future work using more detailed analyses and computational approaches will provide insight on how to design RSPs for better control and more biological performance.

5. Conclusions

Leg stiffness is an important parameter associated with contact time and foot–ground force. Here, we show that leg stiffness differs significantly between bioL and legs using an RSP. Non-amputee athletes and the UL of unilateral amputee athletes either maintain or increase leg stiffness with increasing speed. However, leg stiffness decreases with speed for the AL of unilateral amputees and both legs of bilateral amputees. It is likely that the fixed stiffness of the prosthesis coupled with differences in limb posture required to run with the prosthesis limits the ability to modulate whole leg stiffness. Further, it is likely that the inability to maintain or increase leg stiffness across speeds substantially limits the ability to apply high vertical ground reaction forces during sprinting. The inability to modulate RSP stiffness also likely impairs the ability to accelerate and reach maximum speed. Thus, an RSP that allows for stiffness adjustments within stance or from step to step might allow users to attain even better sprinting performance.