Glial progenitor cell recruitment drives aggressive glioma growth: mathematical and experimental modelling

Abstract

Currently available glioma treatments remain unsuccessful at prolonging disease-free remission. Recent evidence suggests that tumour recruitment of glial progenitor cells by platelet-derived growth factor (PDGF) may play a role in the development and progression of these tumours. Building upon our recent experimental results and previous proliferation–invasion (PI) reaction–diffusion model, in this study, we created a proliferation–invasion–recruitment (PIR) model that includes a mechanism for progenitor cell recruitment, wherein paracrine PDGF signalling stimulates migration and proliferation of progenitors derived from the local brain environment. Parametrizing this mathematical model with data obtained from the PDGF-driven rat glioma model, we explored the consequences of recruitment, using the PIR model to compare the effects of high versus low PDGF secretion rates on tumour growth and invasion dynamics. The mathematical model predicts correlation between high levels of recruitment and both increased radial velocity of expansion on magnetic resonance imaging and less diffusely invasive edges. Thus, the PIR model predicts that PDGF levels correlate with tumour aggressiveness, and results are consistent with both human and experimental data, demonstrating that the effects of progenitor cell recruitment provide a novel mechanism to explain the variability in the rates of proliferation and dispersion observed in human gliomas.

1. Introduction

Gliomas are incurable primary brain tumours noted for their ability to invade neighbouring brain tissue, giving rise to diffusely infiltrative lesions that extend beyond the boundaries of radiographically identifiable tumour. Relatively little work has focused on the leading edge behaviour of human tumours in vivo, primarily owing to the lack of tools to explore these areas of low-density invasion through imaging or even histopathology. Given the dominant, perhaps defining, role of these diffusely infiltrating cells in the malignant character of gliomas, in addition to emerging data from work in animal models of glioma [1–3], we propose that the interactions of these diffuse cells with the surrounding tissue are key to understand how gliomas initiate, form, progress, and become fatal.

As with many other cancers, gliomas are rich in growth factors, setting up for autocrine and paracrine signalling loops between tumour cells and the non-neoplastic cells in the local environment [1,2,4]. Tumour-induced angiogenesis is a particularly relevant example in which an assortment of growth factors (including VEGF, PDGF and others) stimulates local vasculature, via paracrine signalling, to expand through vascular cell recruitment [3,5–8]. In addition to those directly related to angiogenesis, a variety of growth factors has been found to be over-expressed in gliomas [5] with their level of over-expression generally increasing with grade [5]. Specifically, Majumdar et al. [9] found that expression of PDGF in human gliomas increased with grade [3].

Animal studies have shown that injecting PDGF-expressing retrovirus into the brains of neonatal or adult rodents will induce the formation of gliomas [9] and retroviruses that express higher levels of PDGF drive the formation of more rapidly growing and higher grade gliomas with robust vascular proliferation and necrosis [1,4,10–12]. Our PDGF-induced animal model exhibits tumour growth that is very consistent (allowing us to collect the dynamic data needed to parametrize our model), and further, it recapitulates the infiltration patterns and histological features seen in human glioblastoma multiforme (GBM), in contrast to most xenograft models and C6 glioma cell line models [13]. Most remarkably, tumours induced by high levels of PDGF are primarily composed of recruited uninfected glial progenitors that have been stimulated to proliferate via paracrine PDGF signalling. More recently, Lopez et al. [14] have shown that, when implanted into adult nude rat brains, human primary glioma cells, freshly isolated from glioblastoma specimens, can recruit and stimulate the massive expansion of rodent-derived glial progenitors, providing proof that human glioma cells also have the capacity to recruit progenitors via paracrine signalling [1]. However, the effect that progenitor cell recruitment has on the overall dynamics of glioma growth is not known. To address this question, we have developed a novel mathematical model (the proliferation–invasion–recruitment (PIR) model) to explore the consequences of cellular recruitment, focusing on the role of PDGF paracrine signal interacting with glial progenitors, since the recruitment effects of this particular factor have been well-characterized [14].

Human gliomas show a range of growth patterns—ranging from well-circumscribed, highly vascularized tumours to diffusely infiltrating lesions with little or no vascular proliferation [1,4,14], and little is known about the cellular mechanisms or growth dynamics that give rise to these different histological patterns. Our prior mathematical modelling work focused on the proliferative and migratory contributions of cancer cells to tumour growth, for which the key components are net rates of cellular proliferation and invasion (PI)/migration. This PI model has been applied to human glioma patients and has revealed that these different patterns can be well explained by varying only these net rates of glioma cell motility and proliferation [15]. Further, the PI model has been shown to be predictive of prognosis [16], treatment outcome [17] and disease distribution observed on autopsy [18,19], making the PI model a good base upon which to introduce greater levels of biological complexity, such as glial progenitor recruitment.

Given the evidence in the animal models of Swanson & Alvord [20], and given that human glioma cells can recruit progenitors [1,13], it is likely that recruitment is playing a role in human gliomas, though this role and its relevance to the human disease are unclear. Extending the framework of the PI model to investigate the consequences of recruitment enables us to bridge micro- and macroscopic spatial scales, and connect the effects of the cellular-level phenomenon with observations at the magnetic resonance imaging (MRI) level (often the only means available to follow glioma in clinic). Through the PI model, we have demonstrated the existence of a range of net proliferation and diffusion rates in human gliomas [16], which have been treated as intrinsic features of individual patients' tumour cells. In this present study, we set out to examine and characterize the extent to which adding paracrine-driven recruitment to our established PI model would change the observed growth dynamics, and whether this new PIR model could provide an explanation for the differences in the observed range of net growth parameters (refer to the Quick Guide for PIR model information). Experimental estimations of the model parameters, including observed proliferation and diffusion rates, and validation of the model predictions are provided by the PDGF-driven rat glioma model described in Assanah and co-workers [1,14].

1.1. Proliferation–invasion–recruitment model

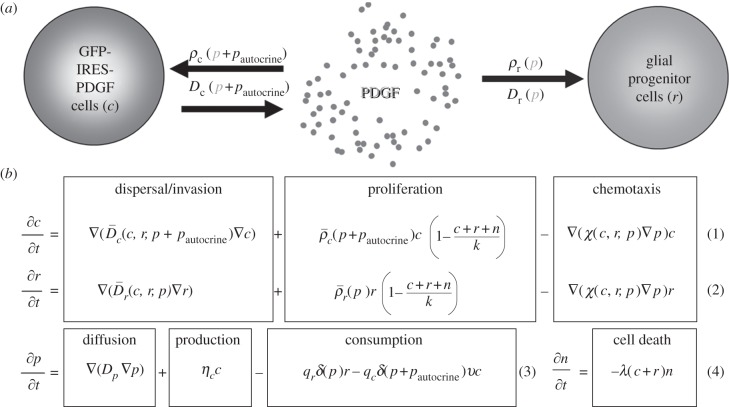
To explore the role of progenitor cell recruitment in the PDGF-driven glioma models (as we have schematized in figure 1a), we have pursued a bio-mathematical modelling strategy that follows the same formalism and retains the key characteristics of our PI model that has been successfully applied to human and experimental data. These key characteristics include an extensive diffuse invasion pattern and a linear radial expansion pattern seen on imaging (over extended periods of time). We have extended this bio-mathematical model to include interactions with the environment, specifically the effects of paracrine PDGF stimulation on the glial progenitor population that is widely distributed throughout the brain. The PIR model provides a tool to examine the effects of paracrine PDGF signalling (figure 1b) on both the composition and dynamics of glioma growth and invasion.

Figure 1.

PIR model. (a) Model schematic. The flow chart shows the main components of our model: c represents the population of glial progenitor cells that are infected with the PDGF-expressing retrovirus, r represents the glial progenitors that are recruited and do not have the retroviral infection, and p represents the free PDGF in the extracellular space (ECS). An injection of the retrovirus initiates the c population [4,21]. These cells secrete p at rate η_c into the ECS, and p is, in turn, taken up and consumed by the c and r populations at rates q_c and q_r, respectively. Uptake of p by c and r results in increased net cellular proliferation (ρ_c and ρ_r) and dispersal (D_c and D_r) in a dose-dependent manner. In addition to the paracrine stimulation from p, the infected cells experience autocrine PDGF stimulation in concentration p_autocrine. (b) Model equations. The equations for the infected (c) and uninfected ‘recruitable’ (r) progenitor cells account for the movement and growth of the respective cell populations. Their net rates of migration and proliferation, D and ρ, respectively, depend on the local concentration of PDGF (p) and the population density, at a given time point, of their own cell type, c or r (equation 1 and 2). Logistic scaling of the net proliferation terms in these equations reflects the limits contact inhibition imposes on cell division when the total population approaches the maximum possible density in the tissue. Equation 3 accounts for the secretion of PDGF (p) into the extracellular environment at rate η_c, and loss of p owing to consumption by the c and r progenitor cells at rates q_c and q_r, respectively, which are scaled by the percentage of PDGF receptors that are activated (δ), and, for infected progenitors only, the percentage of receptors that are not already in use for autocrine signalling, but rather are available for binding-free PDGF, ν. The final equation for the remaining ‘normal’ brain cells (n) (which includes, but is not restricted to, neurons and other white matter cells) reflects their proportionate decrease in local density (via cell death, which may consist of either apoptosis or necrosis) as those of c and r increase and fill up/compete for the available space (equation 4). Note that we do not model the dead cells. (Further details of model development, including values of parameters and initial conditions, may be found in the electronic supplementary material.)

In developing the model, we assume the following about the recruitment process: first, progenitors infected with a retrovirus that coexpresses PDGF-B-HA and GFP, separated by an internal ribosomal entry site (PDGF-IRES-GFP), secrete PDGF. Then, PDGF can diffuse a short distance into the local environment before binding to PDGF receptors (see electronic supplementary material for details on parameterization of PDGF diffusion rate and other model parameters). PDGFRα + glial progenitor cells (including both infected and uninfected PDGFRa + cells) bind and consume the available free PDGF, experiencing paracrine stimulation. The PDGF acts as a motogen (D_c, and D_r) and mitogen (ρ_c and ρ_r) for the retrovirally transformed (c) and recruitable (r) glial progenitor cells, respectively, in a dose-dependent fashion [1]. In addition, the retrovirally transformed, PDGF-secreting, glial progenitors experience autocrine stimulation by PDGF at a base level (p_autocrine) above and beyond the free PDGF (p) available to them in the environment, up to receptor saturation. For modelling purposes, p_autocrine is a constant, to enable us to focus specifically on the effect of paracrine signalling changes in PDGF (p). Recruited glial progenitors remain dependent on paracrine PDGF stimulation, such that those which have migrated into regions of lower PDGF concentration will show a corresponding decrease in migration (D_r) and proliferation (ρ_r).

2. Results

2.1. Time-lapse microscopy provides a direct measure of cell dispersion (D_c,r) and proliferaiton (ρ_c,r)

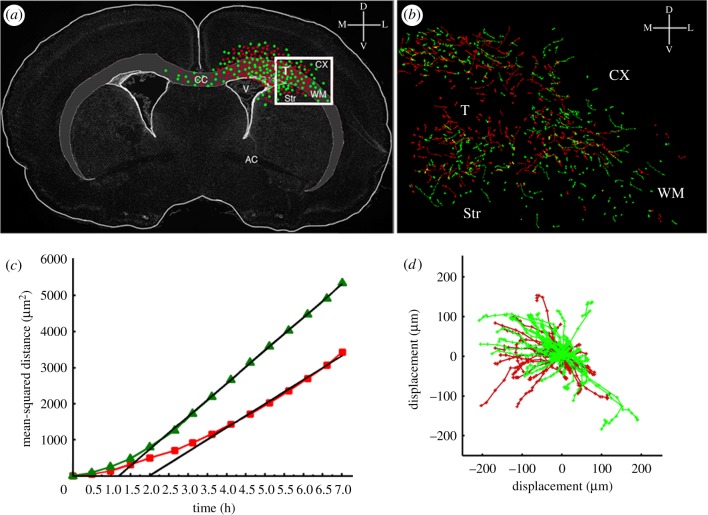
Estimates of the dispersal parameters (D_c and D_r) of PDGF-secreting and recruited progenitors were obtained from analysis of time-lapse microscopy of these progenitors migrating in acute slice cultures. Focusing on the migration at the infiltrative edge of the tumour (where there is no necrosis), we plotted individual cell tracks to a common origin (figure 2d), and the mean-squared distances (MSDs) travelled by the two progenitor types (retrovirally transformed (c) and recruitable (r) progenitors) were calculated and plotted against time (figure 2c). The slope of the MSD versus time provides an estimate of the equivalent diffusion coefficient D for each progenitor cell population [4,22–24].

Figure 2.

Tracking the migration of PDGF expressing and recruited progenitors by time-lapse microscopy. Three hundred microlitre thick slice cultures were generated at 10 days post-co-injection with PDGF-expressing retrovirus and control retrovirus and two colour time-lapse microscopy was performed for 7 h to monitor the migration of PDGF-expressing progenitors and recruited progenitors. The migratory paths of individual cells were tracked using METAMORPH image analysis system. (a) A schematic of the coronal brain slice showing the tumour location and the distribution of PDGF-expressing progenitor cells (green dots) and recruited progenitor cells (red dots). The box represents the region of the slice that was filmed by time-lapse microscopy (T, tumour; CX, cortex; WM, white matter; CC, corpus callosum; Str, striatum). (b) The green and red lines represent the migratory paths of PDGF-expressing progenitor cells (green lines) and recruited progenitors (red lines). (c) Mean-squared distance travelled by the PDGF-expressing progenitors (green lines) and recruited progenitors (red lines). (d) Windrose plot showing the tracks of cells from (b) plotted with a common origin.

Time-lapse microscopy was also effective for obtaining the proliferation rate parameter. This analysis showed that approximately 2 per cent of progenitors at the infiltrative margins of the tumour underwent mitosis every hour (giving a cell cycle time of approx. 50 h). In vitro studies have shown that PDGF-stimulated glial progenitors can proliferate with cell cycle times as fast as 10–20 h [25]. Since our observations were made at the invading edge of the tumour for clearer visualization of individual cells and cellular proliferation rate is dose-responsive to local PDGF levels [26], we have assumed that the longer cycle time is likely owing to the decreased PDGF level in this region. The overall result of having such a dose–response relationship is that we have effective proliferation rates that are slower at lower PDGF concentrations and reach maximal proliferation rates only at saturating levels of PDGF, provided there is sufficient space. Details regarding the modelling of PDGF responsiveness to simulate local proliferation and diffusion rates are in the electronic supplementary material, figures S1 and S2, as are those on the parametrization of the proliferation dose–response curve of PDGF (electronic supplementary material, figure S3).

2.2. Radial expansion rates observed on magnetic resonance imaging and predicted by the proliferation–invasion–recruitment model are consistent with human data

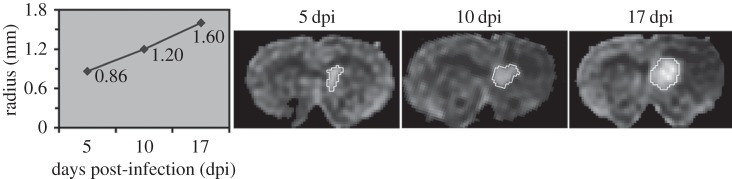
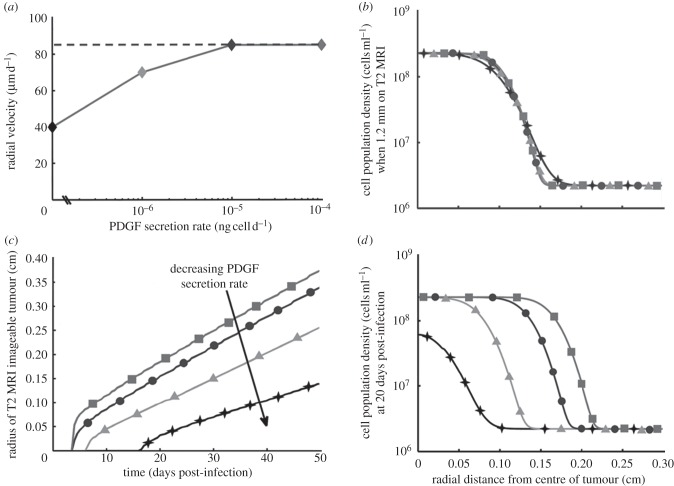
Gliomas do not have a well-defined outer ‘edge’ because they are governed by diffusive growth processes [22,23]. Thus, to look at overall tumour expansion in the model in comparison with that observed from imaging studies, we fix a cellular density to approximate the edge of the visible portion of the tumour on an MRI scan. We used c + r + n = 0.16K for approximating T2, and 0.80K for approximating T1gd MRI modalities, as done previously in our simulations of human GBM [15]. Radial velocity measured from human glioblastoma serial MRI examinations varies from 2 to 7 cm yr⁻¹ for the majority of patients, with outliers ranging from immeasurably/imperceptibly slow to very fast (10+ cm yr⁻¹) among different patients, with those patients that have more than two measurement time points maintaining an approximately linear radial expansion [16]. Given these data, we compared the human radial velocities to those obtained from serial MRI examinations of the rat brain and PIR model-simulated velocity. Serial MRI data were available for one rat; measurement indicated a linear radial velocity of 62 μm d⁻¹, which is equivalent to 2.3 cm yr⁻¹, for this individual (figure 3). PIR model simulations yield linear radial velocities as well (figure 4c), with those simulated tumours which have no recruitment growing at a rate of about 40 μm d⁻¹ after initial appearance on MRI, and those with high levels of recruitment approaching an apparent max rate of 85 μm d⁻¹ (figure 4a). Converting to the centimetre per year units used in comparing human glioma velocities, these are = 1.464 and 3.11 cm yr⁻¹, respectively. Although, these velocities are quite fast relative to the size of the rat brain, and thus likely account for their mortality by about day 20, they are on the low end of the human velocity range [16,27]. These results suggest that differences in the degree to which glioma cells stimulate migration and proliferation of non-neoplastic glia in the surrounding brain tissue can explain the differences in glioma growth rates that have been observed in the human disease.

Figure 3.

Serial FLAIR MRIs showing growth of PDGF-IRES-GFP-induced rat tumour with a linear radial expansion rate of approximately 62 μm d⁻¹ (or 2.3 cm yr⁻¹), which is consistent with the velocities observed in humans [1].

Figure 4.

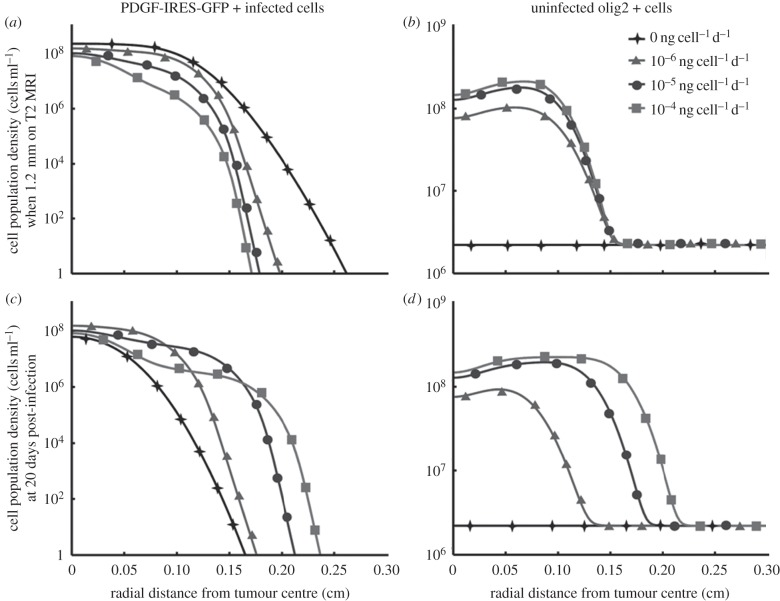
Variations in net PDGF secretion rate alter tumour growth pattern and rate. (a)  Radial velocity here is the rate of radial tumour growth on simulated MRI. The dashed grey line (at approx. 85 mm d⁻¹) indicates the observed threshold of maximum radial velocity attained for model simulations. A PDGF secretion rate of 0 ng cell⁻¹ d⁻¹ indicates that no recruitment can happen; and we supposed secretion rates could possibly be several orders higher (going up to 10⁻⁴ ng cell⁻¹ d⁻¹) than the accumulation of 10⁻⁷ ng cell⁻¹ d⁻¹ secretion into the media that was measured experimentally using confluent PDGF-IRES-GFP+ progenitor cells over 24 h [1]. Note that all of these radial velocity values, when converted to centimetre per year, occupy the lower ranges of radial velocity observed in human glioma patients, as described in the results. Thus, our data indicate that recruitment does not lead to infinitely increasing radial growth, but rather, is consistent with human GBM dynamics. (b)  When the simulated tumours reach a certain fixed size on MRI, the slope of the true edge of the tumour varies with the rate of PDGF secretion. Increased secretion results in a steeper edge, indicating a somewhat less infiltrative edge at higher levels of paracrine PDGF signalling. While this is subtle, the ‘edge’ of the tumour (that is, the region spanning the point from where the cell density drops from its highest level to the point it reaches its lowest) spans a full 1.5 mm for the tumour with no paracrine PDGF signalling, while that of the highest paracrine signalling spans only 0.75 mm, cutting this region in half. Additionally, this gradient of cell density falls in the middle of our observations in human gliomas, constituting a substantial proportion of the overall tumour radius. (c) Plot of the T2 MR-imageable tumour radius versus time shows that within 3 days of initial appearance on T2 MRI, tumours reach and maintain linear radial expansion, regardless of the degree of recruitment taking place in these tumours. (d)  Looking at the same set of tumours as in (b)  at a fixed time (20 days) post-infection, the tumours with higher net rates of PDGF secretion grew much more within that time, extending the tumour radius further at all densities above the baseline olig2+ glial progenitors in the brain. Note that in both figures (b) and (d), the constant population densities outside the tumour region corresponds to the normal density of glial progenitors outside the influence of paracrine PDGF (this value and its derivation can be found in electronic supplementary material, table S1 of parameter values and initial conditions, and in the electronic supplementary material text, respectively). Filled diamonds with solid line, 0 ng cell⁻¹ d⁻¹; filled triangles with solid line, 10⁻⁶ ng cell⁻¹ d⁻¹; filled circles with solid line, 10⁻⁵ ng cell⁻¹ d⁻¹; filled squares with solid line, 10⁻⁴ ng cell⁻¹ d⁻¹.

2.3. Paracrine platelet-derived growth factor-mediated recruitment creates a less diffusely infiltrating lesion

Comparing the distribution of cell densities across the tumour radius at a fixed time (20 days post-infection, figure 4c) demonstrated that tumour size is larger for tumours with more recruitment (i.e. higher values of η_c), with the smallest tumour being the case of no paracrine PDGF signal, as expected. However, comparing the distribution of tumour cell densities across the tumour radius for a fixed size on simulated T2 MRI (see electronic supplementary material, for details on MRI simulation) revealed surprising effects on the overall growth pattern. As PDGF secretion rate increases, the slope of the cell density versus tumour curves at the edge of the tumour become markedly steeper, resulting in a more circumscribed, less diffusely infiltrative growth pattern (figure 4b,d). Thus, the model predicts that gliomas with more robust paracrine stimulation of the non-neoplastic glia will develop a more rapidly growing, but less invasive tumour. That is, it has a steeper invasive profile, a result that was not intuitively obvious prior to the mathematical model, which formalizes the consequences of recruitment and specific cell–cell interaction on overall tumour growth.

2.4. Paracrine platelet-derived growth factor signalling affects the distribution and growth patterns of infected glial progenitors and recruited glial progenitors differently

The difference in infiltration of tumour cells at the leading edge in response to variation in PDGF secretion rate, among tumours of fixed size on MRI, is most robust for the PDGF-expressing cells (figure 5a,b). According to the model simulations, higher rates of PDGF secretion (and greater recruitment) result in a smaller margin of diffusing retrovirus-infected progenitors. Specifically, adding recruitment to the PI model results in a steeper cell density distribution (figure 4a,d) that grows more slowly (figure 4a,c). The difference in total tumour radius (including the infiltrating edge) between PI simulations having no PDGF secretion (no recruitment) and the highest rate of secretion (highest recruitment) is 1 mm, or 10 per cent of the approximately 1 cm rat brain radius (figure 5a). The distribution of uninfected glial progenitors responds differently to changes in PDGF secretion rate. High levels of PDGF secretion cause more recruitment, increasing the density of these recruited progenitors at the centre of the tumour, but do not alter the radius of this recruited population distribution, which remains constant for a fixed observed tumour size on MRI (figure 5b). Given that external PDGF secretion is required for recruitment to take place in this model, there is no change in uninfected glial progenitor density in tumours with no paracrine signalling component.

Figure 5.

Distributions of cell population densities versus the radial distance from the centre of the tumour at different levels of recruitment via PDGF secretion. (a,c) Data for the PDGF-IRES-GFP+ (infected) progenitors and (b,d) data for the uninfected olig2+ (recruited) progenitors. The top row shows the cell densities at the time at which the tumour radius is 1.2 mm on T2 MRI (fixed size on MRI), while the bottom row shows these at 20 days post-infection (fixed time). The legend in (b) applies to all plots and shows the rate of PDGF secretion by the PDGF-IRES-GFP+ infected progenitors, such that the increasing trend runs from the low value at 0 ng cell⁻¹ d⁻¹ to the high value, 10⁻⁴ ng cell⁻¹ d⁻¹. Note that the plots for uninfected olig2+ progenitor cells (b,d) have constant population densities for the tumours with no secretion of PDGF. This is because without free PDGF available to circulate in paracrine signalling loops, no recruitment can take place, causing these recruitable cells to remain at their usual density in healthy brain matter. (This value and its derivation can be found in electronic supplementary material, table S1 of parameter values and initial conditions, and in the electronic supplementary material text, respectively.) See main text for further details regarding these results.

At a fixed time post-infection, higher levels of PDGF secretion cause a drop in infected cell density just beyond the centre (figure 5c) that corresponds to an increase in uninfected progenitors in the same region (figure 5d). Thus, according to the model, recruitment causes a region of tumour to ‘fill-up’ (become more hypercellular) at a faster rate than it would via proliferation of PDGF-IRES-GFP-infected progenitors alone. For a fixed time, both the infected and recruited glial progenitor populations (figure 5c,d, respectively) have a larger radius of infiltration, indicating that both cell types have increased proliferation and migration rates owing to increased PDGF secretion. This is expected, since both populations are responsive to paracrine PDGF stimulation.

2.5. Proliferation–invasion–recruitment model confirmation via simulation of fluorescent micrographs

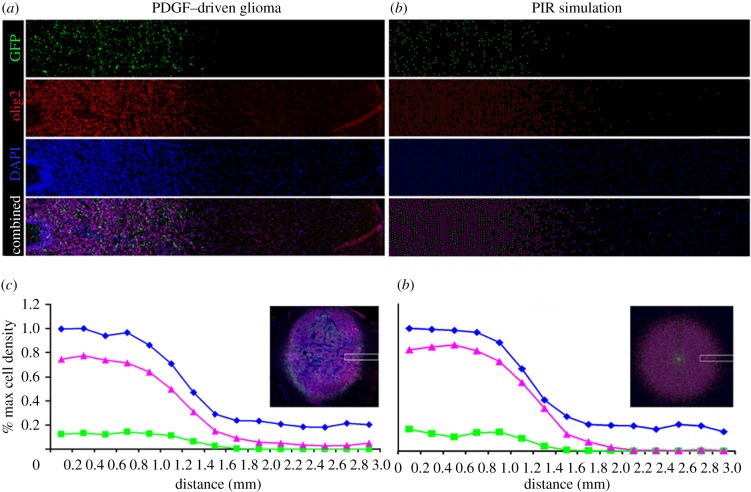
In figure 6, we used the PIR model to generate simulations and render them as discretized approximations of fluorescence microscopy of tumour cross sections (details are in the electronic supplementary material), which we then compared with actual fluorescence microscopy images and data. Using our parameter estimates, we found good agreement between the experimental cell density curve and the model simulation. We calculated the Pearson product-moment correlation coefficients between curves of similar cell type to be 0.988 for infected progenitors, 0.998 for recruited progenitors and 0.997 for the normal cells, all of which correspond to p-values of less than 0.0001, with 14 d.f.

Figure 6.

Fluorescent micrograph compared with PIR simulation. The colour separated micrographs on the left side show the distribution and abundance of PDGF-expressing progenitor cells (green), olig2+ glial progenitors (red) and the total DAPI+ nuclei (blue) within a 3 × 0.5 mm strip at the infiltrative edge of PDGF-driven glioma. The corresponding images on the right side show the distribution and abundance of cells in a corresponding region of a simulated tumour generated by the PIR model (again, PDGF-expressing progenitors are green, all progenitors red, and all cell nuclei, blue). The graphs on the bottom show the actual (c) and simulated (d) percent measurements of each cell population within the 3 mm strip at the tumour's edge. The insets show the entire PDGF-driven tumour (a) and simulation (b) indicating the region of the tumour and simulation from which the strips were taken (white boxes).

3. Discussion

Our combined experimental and mathematical investigations revealed that the addition of a PDGF-mediated recruitment mechanism to the PI model, with two populations of tumour cells, results in simulated and observed growth dynamics that are consistent with observations of human gliomas. Both the radial expansion velocities and the linear pattern of growth seen at the threshold of MRI-detectability in model simulations are similar to those observed in human serial MRI studies [16]. In combination, these two results provide additional support to our hypothesis that glial progenitor recruitment plays a role in the progression of human gliomas. Moreover, as with the PI model, the PIR mathematical model makes predictions of tumour cell density and distribution that extend beyond the boundaries detected by MRI.

As a result of recruitment, simulations of tumours varying only the PDGF secretion rate (the mechanism for recruitment) show a wide range of growth patterns. Under conditions with little or no PDGF secretion, simulated tumours exhibited significantly slower yet more diffusely infiltrative growth, reminiscent of gliomatosis cerebri. In contrast, under conditions with high levels of PDGF secretion tumours expanded more rapidly and had increased hypercellularity towards the infiltrative edge (figure 4c,d). Moreover, analysis of human gliomas shows that PDGF levels correlate with tumour grade (higher grade tumours express higher levels of PDGF) [16,19,27], and animal model studies using PDGF-expressing retrovirus have also shown that higher levels of PDGF will drive faster growing tumours [6]. Thus, while it is presently not well understood why some gliomas are aggressive and grow rapidly, whereas others grow slowly and do not progress for many years, our results demonstrate that differences in the levels of paracrine PDGF stimulation of recruited glial progenitors provide a possible cause for the observed differences in growth dynamics among human glioma patients [6,13].

In silico, high levels of PDGF secretion, in combination with recruited cell dependence on PDGF, give a more circumscribed tumour with a cell density gradient that is steeper than without recruitment (figures 4b,d and 5a–d). Additionally, the PDGF-driven increase in migration/invasion appears to contribute to increases in the rate of the radial expansion of the overall tumour (figure 4a,b). Because both the extent and the rate of tumour invasion are indicative of patient prognosis ([16] and [27], respectively), we hypothesize that more aggressive gliomas are more likely to involve significant recruitment, with greater growth factor upregulation, leading to the steeper invasive profile, greater heterogeneity and faster time course to death associated with higher grade gliomas and GBM.

Given the results of this study, we expect that blocking PDGF signalling would lead to slower growth in gliomas that express PDGF and PDGFR, both through slowing the proliferation and migration of tumour cells, as well as through inhibiting progenitor cell recruitment. The PIR model suggests that small-molecule-targeted therapies which affect paracrine signalling pathways (but not autocrine) would lead to more slowly growing tumours with a more diffuse overall tumour growth pattern (though it would not stop tumour growth, only alter it, since autocrine effects would allow for some proliferation of the infected progenitor cells). Furthermore, this could extend to other paracrine signalling pathways in the glioma microenvironment. Already, clinical trials have shown that treating GBMs with the VEGF-inhibitor Avastin can give rise to recurrence with a very diffusely invasive growth pattern [28]. Together, these results suggest that inhibition of secreted growth factors, such as PDGF or VEGF, can have significant effects on the patterns and dynamics of tumour growth, but will not be sufficient to stop it. However, combining these with other types of therapy, such as inhibitors of glioma cell migration, may have more profound effects on overall tumour growth and survival. Mathematical models, such as the PIR model, can provide a powerful tool to interpret and predict the effects of such combination therapies.

In this context, it should be further noted that recent work by Fomchenko et al. [29] has demonstrated that recruited cells can acquire genetic alterations and become tumorigenic in their own right [30]. In future studies, modelling, such as that presented here could be used to better understand and predict how such complex interactions with the microenvironment can affect the overall growth of the tumour. While the relevance of the PDGF-induced animal model to the human disease is not entirely clear, the PIR model or similar tools that allow for dynamic insight into the interaction of tumour cells with the environment may be critical to developing effective treatment strategies for glioma patients. Future refinements we intend to pursue that would help in this endeavour include adding hypoxia and angiogenesis, and developing a treatment model to fully understand the role of paracrine signalling inhibitors on the tumour microenvironment. Coupled to this, we would like to explore the outcome of fitting the PI model to the MRI data from the rodent model of recruitment, to look for patterns that may predict whether recruitment might be happening in a subset of human glioma patients.

4. Methods

To build the model, we extended the PI model [29] to include recruitment. Note that the PIR model becomes the PI model when recruitment is taken away. Setting PDGF secretion rate η_c to 0 results in a static population of uninfected progenitor cells (r), and the equation for the infected cells, c, with proliferation and invasion terms, becomes the original PI equation. The p remains at its 0 initial condition, reflecting that there is no paracrine PDGF, and causing the population of uninfected progenitors, r, to remain at baseline. The n equation simply continues to keep track of the non-progenitor cells (i.e. those normally present cells that we do not consider to be contributing to the tumour in the model), though we have not done this in the original PI model. (Detailed model equations are provided in the electronic supplementary material.)

One of the most critical steps in bio-mathematical model development is the inclusion of parameters for which values already exist or can be obtained, in order to ensure that the model has immediate applicability. While the methods of model creation in terms of equations are included in the Quick Guide, we present here our methods for obtaining some of the model parameters experimentally, as this was also necessary to complete our model and enabled us to make accurate simulations. (Electronic supplementary material, table S1 of parameters and their values, and additional details on parametrization of the bio-mathematical model, can be found in the electronic supplementary material.)

The experimental brain tumours were generated by infecting glial progenitors with PDGF-expressing retrovirus and control retrovirus, as previous described (Assanah et al. [1,4]). The two retroviruses express different fluorescent reporters, allowing us to simultaneously monitor the behaviour of PDGF-expressing glial progenitor cells (shown as green in figure 2) and recruited glial progenitors (shown as red in figure 2). The tumours that formed were composed of a mixed population of red and green cells, and immunohistochemical analysis showed that both populations express PDGFRa (data not shown). At 10 days post-injection, animals were anaesthetized with ketamine–xylazine, decapitated and 300 μm thick coronal brain sections were taken at the level of the injection site and maintained in a serum-free medium for the duration of the experiment. Time-lapse microscopy was performed on these acute brain slices using Nikon TE2000 inverted fluorescent microscope equipped with a stage mounted incubator, a digital camera. Images were captured every 3 min. The migratory paths of individual red and green cells were tracked over the course of 7 h using METAMORPH image analysis system (molecular devices), as described in the earlier study [16–20]. We also used time-lapse microscopy to directly monitor the mitotic activity of red and green cells in the acute slices of the PDGF-driven brain tumours. Proliferation rates were determined by counting the number of tracked cells that underwent mitosis during the course of the time-lapse experiment. As is the case with the analysis of cell migration, the analysis of cell proliferation was limited to cells at the infiltrative margins of the tumour, where the density of retrovirus-labelled cells was low enough to allow for clear visualization of individual dividing cells.

MRI analysis was performed at 5, 10 and 17 post-infection. Prior to imaging the animals were anaesthetized and immobilized in a Plexiglas frame and T2 flair images were collected from an MRI unit with a 1.5 T magnet.