Virtual experiments, physical validation: dental morphology at the intersection of experiment and theory

Abstract

Computational models such as finite-element analysis offer biologists a means of exploring the structural mechanics of biological systems that cannot be directly observed. Validated against experimental data, a model can be manipulated to perform virtual experiments, testing variables that are hard to control in physical experiments. The relationship between tooth form and the ability to break down prey is key to understanding the evolution of dentition. Recent experimental work has quantified how tooth shape promotes fracture in biological materials. We present a validated finite-element model derived from physical compression experiments. The model shows close agreement with strain patterns observed in photoelastic test materials and reaction forces measured during these experiments. We use the model to measure strain energy within the test material when different tooth shapes are used. Results show that notched blades deform materials for less strain energy cost than straight blades, giving insights into the energetic relationship between tooth form and prey materials. We identify a hypothetical ‘optimal’ blade angle that minimizes strain energy costs and test alternative prey materials via virtual experiments. Using experimental data and computational models offers an integrative approach to understand the mechanics of tooth morphology.

1. Introduction

Finite-element analysis (FEA) is a mathematical modelling technique originally developed in engineering to estimate stresses and strains in modelled structures under user-determined loadings [1]. It has been employed in the field of evolutionary biology to address questions of how form affects function in complex biological structures [2]. While a majority of FEA studies in biology have focused on the structural profile of a single specimen or feature, an increasing number have begun to use the digital nature of the models to alter aspects of morphology and run further tests. This can be as simple as removing features such as sutures in the skull [3,4] or altering the shape of the model specimen based on morphometric analyses [5–7]. These virtual experiments allow for specific hypotheses of morphology to be tested without the constraints and difficulties of physical experimentation; however, they leave open the possibility for these studies to deviate from biological reality.

All models are, by definition, simplifications of realty. The key is in understanding where the assumptions are being made, and what variables are being removed for the sake of the model. Studies have been devoted to the validation of FE models using both experimental and sensitivity analyses [8–10]. A few recent FEA studies have begun to eschew the use of complex models based on scan data altogether in favour of basic ‘hypothetical’ models, which represent specific aspects of morphology [11–13]. These ‘hypothetical’ models allow precise shifts in morphological structure to be tested for functional consequences, while holding other morphological variables that are not of interest constant. While some of these studies have focused on comparing the FE models to experimental data [11,12], others have focused on creating virtual experiments of form and function [13]. In this study, our aim is to combine these ideas by creating an FE model that is both validated against experimental data and allows for a broad range of virtual experimentation to understand the relationship between form, function and structure.

The biological system we are focusing on is the processing of soft foods by teeth, as previously explored experimentally [14,15]. The evolution of food processing, the ability to physically break food down into ingestible pieces, is an important development in the history of vertebrate life, allowing animals to eat larger food items, including prey larger than their mouth opening. Various qualitative descriptors (tearing, crushing and cutting) have often been used to denote different methods of food processing, but these descriptions do not lend themselves to precise comparative analyses. Recent experimental and theoretical work on fracture mechanics in foodstuffs has begun to quantify the relationship between the material properties of food items (such as brittleness and toughness) and the morphologies of the dental tools that are most efficient at processing the food [14,16,17].

The majority of experimental work and almost all theoretical work performed on dental shape and food processing has focused on the cracking of hard or brittle foods such as nuts or seeds with blunt tools (see [11,12,18]; for a review, see [19]). Less focus has been given to the cutting of tough and/or extensible foods (animal tissues or fibrous plant materials) with bladed structures [14–16,20–22] (for a review, see [23]). There is a significant volume of literature concerning FE modelling of cutting in industry [24] including studies of the reaction of soft biological tissues to cutting dynamics [25,26] and measures of sharpness in scalpel blades [27,28]. However, FEA and modelling methods have yet to be applied to studies of dental function in regards to cutting despite the prevalence of bladed edges among both modern and fossil jawed vertebrates. The first definitive appearance of bladed dentitions in jawed vertebrates is in the Early Devonian (400 million years ago) [29]. Blades are also ecologically important, as animal and plant tissues are a major component of vertebrate diets. Therefore, understanding the relationship between dental form and the cutting of extensible/tough foods is important to understand the origin and subsequent evolution of jaws and teeth.

Recent experimental work on the biomechanics of cutting biological tissues has used work to fracture, a measure of energy, as the metric to determine feeding efficiency [14,15]. Energy is the basic currency of biology; however, not all energy taken in during feeding is gained by the animal. It takes energy to physically break down food (mastication); therefore some of the energy absorbed by the animal's gut must pay off this food processing cost. The net energy gained via feeding is less than that actually absorbed by the animal's gut [30]. For some animals, the cost of feeding can be quite high, particularly if it requires a prolonged mastication phase, such as in ruminants [30]. If a particular dental design reduces the work required to break down the food material, it will allow the animal to process food for a lower cost. This is a simplification of the energetics of feeding and mastication, but the feeding efficiency can certainly be improved by a reduction of work during cutting.

FEA provides tools that allow for further exploration of the energetics of the system through the estimation of strain energy within the material during loading. Strain energy is a measure of the work expended in deforming a structure a certain amount for a given load [31]. Prior to the onset of separation (fracture or cutting), the energy applied to the food by an animal primarily goes towards deformation. A more efficient dental shape will take less work input to create an equivalent amount of deformation in the food prior to fracture. By calculating strain energy in the food for different dental designs in a series of FE models (virtual experiments), the energetics of food processing can be more fully explored.

Here, we focus on a specific aspect of bladed tooth design that has received a good deal of experimental analysis: bladed notches [14,15]. A bladed notch is defined here as two non-parallel bladed edges that converge at a point such that they create a ‘valley’. This morphology is seen in numerous animal groups including the carnassial teeth of carnivorous mammals [17,21,32], sharks with closely packed bladed teeth [19,33], and the beaks of edentate animals such as turtles [34] and birds. It has been hypothesized that notched blades trap soft, easily deformable materials such as animal muscle and skin. This restricts the material from heavily deforming or shifting position between the blades and blunting fracture growth [16]. Experimental analyses using bladed notches showed that this morphology reduces the energy required during cutting to fully fragment soft, malleable materials [14,15].

The specific aim of this paper is to explore the effects of dental design on strain energy in foods; specifically, how much strain energy is expended to deform the prey materials prior to initiating effective cutting. These results will give insight into how efficiently different blade designs deform the material during feeding. To achieve this, we devise a FEA that mimics the results from experimental compressions tests using well-defined materials in a double guillotine testing device. The results of the validated FE model will be used to calculate and compare strain energy values between different dental designs that cannot be directly measured experimentally. The validated model will also allow for virtual experimentation to explore the relationship between prey materials and the form and function of teeth.

2. Material and methods

2.1. Guillotine testing device

Our physical experiments derive from previous work testing the effects of blade design on the energetics of fracture in biological tissues [14,15]. The double guillotine testing device used here is the same as used in those studies, so only a brief description is provided here. The central components of the double guillotine are a pair of blade tools orientated in opposition to each other. The bottom blade tool is mounted onto a platform situated on top of a force transducer (LC703-100; Omegadyne, Inc., Sunbury, OH, USA). This transducer is mounted onto a large stable box base that houses an AC induction motor and gearbox (Parvalux, SD18M, Bournemouth, UK). The upper tool is mounted onto a separate platform attached to a large screw (SKF, 20 mm diameter, 3 mm pitch), which runs down through a hole in the box and is attached to the motor. The screw is driven by the motor and moves the upper platform and attached blade up and down relative to the base. An LDS sensor (HS50 Linear Displacement Sensor; Vishay Measurements Group UK Ltd, Basingstoke, UK) is attached to the mobile platform with its core rod set against the stable base and records the displacement of the platform during experiments. Both the force transducer and LDS are connected to a scanner (Vishay 5000 series 5100B), which converts their signals into force and displacement (calibrated manually).

The tools used for this study are made from blocks of high-quality tool steel (RS Components Ltd, Corby, UK). All of the tools were sharpened and have a rake angle of 30°. Previous studies performed using the double guillotine device were focused on complete separation of test materials during cutting experiments [14,15]. However, our interest here is comparing the experimental results with an FE model designed to explore deformation in prey prior to actual cutting. Therefore, these physical experiments are designed to compress the test material without actual cutting occurring. This was tested beforehand to determine what loads could be applied without separation occurring. The steel tools were mounted into the guillotine and oriented directly opposed to each other (figure 1a). In the previous cutting studies, the tools were oriented to pass each other with no friction; however, since the experiments in this study were set to never actually cut the test material, clearance between tools was not of concern.

Figure 1.

Comparison of the physical experiments and computational model design. (a) Double guillotine testing device shown with a 2 cm wide, 1 cm deep cylinder of a photoelastic resin of known material properties. (b) FE model replicating the physical experiment. The meshed portion represents the photoleastic material, while the orange analytically rigid shapes represent the steel blades. The yellow RP points are reference points used by the model to control movement of the various parts. (c–f) Blade tools used for the physical experiments. (c) Straight edge tool. (d) Blade tool set at a 120° notch angle. (e) Blade tool set at a 90° notch angle. (f) Blade tool set at a 60° notch angle. All blades have a 30° rake angle. (g) Close-up of the mesh of the FE model, illustrating the adaptive nature of the mesh, with a higher density of elements along the region where contact between blade object and mesh is made.

Four distinct combinations of paired bladed tools are used in this study: (i) a pair of tools with straight edges (figure 1c) is mounted on both the upper and lower platforms to act as a null case. Three tools that have V-shaped bladed edges at (ii) 120°, (iii) 90° and (iv) 60° (figure 1d–f) are mounted on the upper platform and each paired with the straight-edge blade on the lower platform. These V-shaped tools approximate the sort of V-shaped notched blade seen in the carnassials of carnivorous mammals [17,21,32]. In general, the steel tools are likely to be much sharper than biological tooth structures, although this may not necessarily be true as measurements on small mammals have shown tooth sharpness of the order of 10 µm [35]. Certain fossil groups (conodonts) may show even lower values for radius of curvature (D. Jones 2011, personal communication). Regardless of the comparative sharpness, the goal of this study is to test the notch angle alone, so we have simplified the rest of the morphology accordingly. Further, while the bladed tools do resemble carnassial blades, carnassial blades are not generally paired with straight blades. The occlusion of carnassial blades is actually quite complex [36], and again beyond the scope of this analysis to test. Experimental tests comparing a notched and straight blade combination to two opposing notched blades show very little difference in work to fracture [15]. Further experiments were done with two flat plates instead of blades to further test for agreement between the experiments and model.

2.2. Photoelastic tests

We used photoelastic resin (PSM-4, Vishay Measurements Group, photoelastic division) in order to visualize strain patterns during the experiments [37,38]. A photoelastic resin is a birefringent material designed to interact with polarized light (where all waves are oriented in the same plane) to illuminate strain patterns within the resin as a series of interference colours. Photoelastic materials have been used in biological studies to measure forces produced by insect walking [38,39], strains in the substrate during earthworm burrowing [40] and internal strains of materials during cutting experiments [14].

The interference colours in a photoelastic material are a function of both the magnitude of the strain present in the material as well as the thickness of the piece of material. All test pieces were of equal size and shape: 2 cm diameter circles 1 cm deep (figure 1a) in order to ensure that interference colours were comparable across tests. The double guillotine was set up in a dark room with a focused light source set right behind the test material, which was situated between the blade tools. The photoelastic material was initially set such that the upper blade just barely made contact but with a force reading of zero. This ensured it remained in place prior to the compression experiments. A polarizing filter (Optolite linear polarizer, Instrument Plastics Ltd, Maidenhead, UK) was placed between the material and light source. Photos were taken of the material during testing using a Nikon D70 SLR camera with a Nikkor 18–55 mm lens and a polarizing filter (Hoya Pro1 Digital Filter, Tokin Co. Ltd, Japan). The reaction force experienced by the lower blade as the upper blade compressed the photoelastic material was measured by the force transducer. Force recordings were taken at 1 mm and 2 mm of depression of the upper blade (while the lower blade was held rigid) and a photo was taken.

2.3. Guillotine finite-element model

FEA is a numerical technique for solving complex mathematical problems through the use of linear differential equations [1]. The basic analysis involves a complex structural model divided into discrete subsections of finite size referred to as elements. Each element represents a system with linear algebraic equations that model the response of the element to loads. Elements are bonded to each other at nodes which transfer displacement owing to loading from one element to the next, allowing the overall deformation of the complex structure to be calculated. For a further review of FEA in biology and palaeobiology, see [2].

The goal of our FE model was to recreate the double guillotine experiments. The CAD feature of the commercial FEA software package Abaqus v. 6.7 (Simula, UK) was used to construct a virtual multi-body model of the same dimensions as the experiment (figure 1b). The blade tools are modelled as analytically rigid objects with notched tools created from two ridged objects joined at the vertex of the notch and set at a given angle (i.e. 120° or 60°). The thickness of the bladed tools matches that of the tools in the experiment (1 cm) and the cutting edge of the shape is filleted with a radius of curvature of 1 µm. Another configuration was made using two rigid objects with flat surfaces for comparisons with similar experiments to further validate the model. The photoleastic material is modelled as a cylindrical-meshed object with dimensions equivalent to those of the test material in the physical experiment (2 cm wide cross section and 1 cm tall). The test material is meshed using linear eight-node hexahedral (linear) elements of varying size. Since this is a multi-body model where the blade shapes make contact with the meshed test material, it is necessary for the mesh at the points of contact to be dense enough that the filleted edge does not simply slip between nodes. Therefore, we used a manual adaptive meshing technique where the mesh was extremely dense at the point of blade contact and much coarser away from this area (figure 1g). This was accomplished by dividing the surfaces of the test material with partition lines and seeding (defining the number of nodes per line) each portion of the object separately. At its most dense, the mesh is seeded at less than a micrometre.

When dealing with contact analyses such as this, there is the possibility of large displacements and deformations in the mesh that can adversely affect the model's ability to resolve certain measures such as maximum principal strain. To help counteract this, we used the large-displacement formulation (NLGEOM) for element calculations [41]. However, exceptionally large distortions in elements can still cause problems, so we further examined our models for overly distorted elements (electronic supplementary material). To further test that our models have a high enough resolution to solve for various maximum stress–strain values, we re-ran several models with quadratic elements (20 node bricks), which have more nodes per element and offer greater overall resolution to the results. We did not use quadratic elements for all the models initially, owing to excessive computational time involved (100+ hours per model).

The photoelastic resin used as the test material in the experiments is a hyperelastic material. Hyperelasticity is the ability of a material to undergo large elastic deformations at small forces without losing its original properties [42]. Unlike linearly elastic materials, which assume linear stress–strain relationships at small deformations, hyperelastic materials show nonlinear behaviour and thus cannot be defined by a single Young's modulus. Furthermore, the measured Poisson's ratio of the resin is 0.5, meaning that it is essentially incompressible (no matter the deformation, the volume of the material is conserved). In the Abaqus software, hyperelastic materials are described in terms of strain energy potential, which defines the strain energy stored in the material per unit volume at a given point of deformation [41]. In FEAs, this strain energy needs to be modelled for hyperelastic materials using a strain energy potential of a specific form. Several such forms exist; however, choosing which to use for a given study can often be arbitrary [43]. If experimental test data are available for the material, it is possible to fit the various models to the data and determine which model most accurately reflects the experimental results. We measured the stress–strain relationship of the photoelastic resin using a miniature computer-controlled materials testing machine (Minimat 2000, Rheometric Inc., Piscataway, NJ, USA). The uniaxial stress–strain data were input directly into Abaqus (see electronic supplementary material). The software program then compares the experimental data to a series of strain energy functions and selects the best fit. When only one type of experimental data is available, the Marlow form (see electronic supplementary material) is generally recommended, as this form can reproduce the experimental data exactly and provide good estimates of other behaviours [43,44]. When we input the test data into Abaqus, the Marlow form was indeed the best fit to the experiment data. Abaqus uses the Marlow model for strain energy potential based on the input stress–strain data in order to define how the test material will behave in the FE model and calculates strain energy as part of the standard output of the model. Details of the mathematical form of the Marlow model and test data are provided in the electronic supplementary material.

The three different components of the model (upper and lower blade tools and test material) were assembled in Abaqus such that the test material was situated between blade tools in the same configuration as the physical experiments (figure 1a,b). The bottom blade is completely constrained from any sort of movement, while the upper blades are allowed movement along the y-axis (vertical) only. The test material is constrained solely by the blade object and a set of spring elements attached to the centre of each circular face. Spring elements are capable of modelling restraints to rigid body motion. In this case, they prevent initial rigid body motion of the test material as the blade initiates compression. The springs in the model are set to a stiffness (force per relative displacement) of 10 Pa. This value was an arbitrary decision, but kept low so as not to unduly affect the results. The spring elements are only in place to prevent initial movement of the test material when the blades first make contact. The interaction between the blade edges and the test material is defined as a tangential and frictionless contact surface. While most FE models are loaded by a user-defined force or pressure, we have initiated load here via vertical displacement of the upper blades. This allows us to mimic the known displacement of the experiment and compare resulting force values for validation. During the ‘load’ step, the upper blade is moved downward a set distance (1 mm and 2 mm). The resulting strains and forces can then be calculated for a given vertical displacement. Four models are used which match the four experimental set-ups performed.

2.4. Analysis comparing experimental and modelling data

The FE models were all solved using a direct linear equation solver within Abaqus/CAE v. 6.7. The results obtained from the experiments and the FE models are compared both qualitatively and quantitatively. The strain patterns seen using photoelastic material in the experiments are compared with logarithmic strain (LE) patterns observed in the FE model. LEs are used when hyperelastic materials are modelled. The resulting forces measured by the force transducer during the experiments for a given displacement of the upper blades are compared with vertical reaction forces calculated by the FEA for the bottom blade object.

Once the model is validated against the experimental results, it can be used to calculate the strain energy and compare this variable between the four blade set-ups. As previously noted, total strain energy can be directly related to the energy expenditure of an animal during mastication. This is important for an animal trying to gain the most net energy from feeding. We compared the total strain energy within the test material at a standard level of deformation (represented by a set maximum LE) for all of the different blade configurations in order to establish how much work was required in the system to deform the material at a given amount. For ductile materials, such as our hyperelastic resin, stress is generally the criterion used for judging critical failure. However, we are not interested in the failure as much as the amount of energy required to produce a set amount of deformation, so strain is the better criterion for this study.

2.5. Virtual experiments

Once the model is validated for the hyperelastic test material and the four basic tool designs have been compared, it is also possible to test tool designs that have not been tested with physical experiments. So long as the basic set-up and the majority of the variables remain the same, it is possible to vary, in a controlled manner, single variables one at a time, such as tool shape or test material, and see how this variation affects the energetics of the system. We explored these possibilities by altering two variables: tool shape and material properties.

After the basic four tool shapes were tested in the FE model, it was apparent that there might be an optimal blade angle that could minimize the strain energy in the system for a given maximum principal strain. A further set of six blade tools were made in Abaqus' CAD modelling V-shaped bladed notches with angles of 170°, 160°, 150°, 153°, 155° and 157°. By performing the same modelling experiments with these new tools, it is possible to focus in on an optimal blade design.

Tooth shape is heavily influenced by the material properties of the types of food being consumed [16]. Given that, it is reasonable to assume that an ‘optimal’ tooth design for one type of material will not necessarily be optimal for another material. When the wide range of tooth designs found in nature is considered, this assertion seems especially pertinent. Our FE model allows for any number of different materials to be subjected to the same tests to observe differences in strain energy patterns across tool types. To explore this, we ran more tests using an alternative material in our model. For an alternative material, we used material properties derived from uniaxial tests on asparagus: a plant material previously used for experimental tests [15]. For the sake of the model, the asparagus was treated as a linearly elastic material with data from the uniaxial compressive tests (using the same equipment as for the photoelastic resin) used to estimate a Young's modulus (132.5 kPa) and Poisson's ratio (0.2). Treating asparagus as linearly elastic is a simplification, but it allowed us to compare how different materials would react to the various blade configurations. The material should not be considered equivalent to actual asparagus. We ran all of the models again using this material and estimated the ‘optimal’ notch angle for deforming this plant material as opposed to the hyperelastic material originally used.

3. Results

3.1. Experimental results

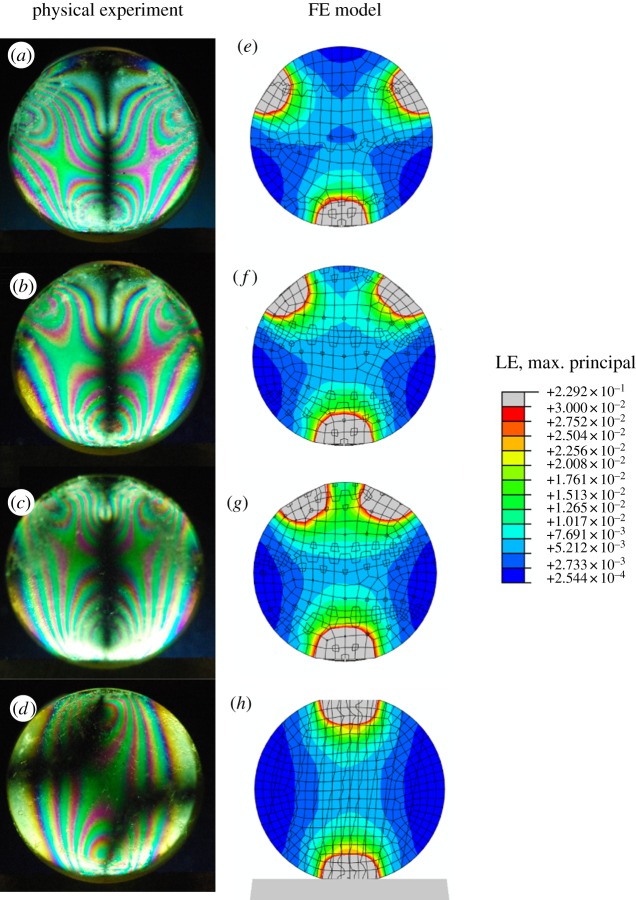
Figure 2 shows the interference colours produced on identical pieces of photoelastic material by the different blade shapes in the guillotine. When two straight blades are used (no notch), there are two centres of high strain localized at the contact points. Unsurprisingly, when a notched blade is used and there are three points of contact, there are three regions of high strain. The black line seen running down the middle of the notched blade configurations (figure 2) is due to an artefact of polarized light. Regions where the strain orientations in the material are aligned with the orientation of the polarizing filters (seen here as perfectly vertical or horizontal strain) will result in a lack of interference colours. In the paired straight blade configuration, there is a pair of dark regions created by the same effect. Table 1 shows the force values measured during testing on the photoelastic materials. More acute-angled blades result in lower forces being produced for an equivalent amount of vertical displacement, which matches previous patterns seen in biological tissues [14,15].

Figure 2.

Comparison of strain pattern results from the computational FE model and physical experiments using photoleastic test materials. The photoleastic images show strain patterns within the material during physical testing using the four blade configurations: (a) 60° notch, (b) 90° notch, (c) 120° notch, (d) straight blades. The FE results are LE values when various modelled blade configurations are used: (e) 60° notch, (f) 90° notch, (g) 120° notch, (h) straight blades. The strain scale is shown in the legend. There is a close match in strain patterns between the physical test and computational model. The black lines in the experimental images (a–d) are artefacts of the orientation of the polarizing filter. All test pieces are 2 cm in diameter.

Table 1.

Force validation between experiment and model.

	experimental force (N)	force from model (N)
flat surfacea	29.58	30.00
straight blades	15.14	15.00
120° notched blade	18.74	18.79
90° notched blade	15.80	15.92
60° notched blade	11.50	11.60

^aFlat surface refers to experiments and models run without bladed edges, but simple flat surfaces.

3.2. Model validation

Figure 2 also shows the LE patterns seen in the FE model based on our guillotine experiments. The blade displacement is set to 2 mm for both experiment and model. Since the FE models are not transparent, a section through the middle is shown in order to see the strain patterns in the plane along which the blade is contacting the meshed object (figure 1b). LE patterns in the model closely match strain patterns in the experiment, showing the same local regions of high strain. Table 1 shows the vertical reaction forces calculated on the lower analytically rigid blade object for the FE model compared with the forces measured during the experiments. The very close match indicates that the FE model is replicating the experiment to a significant degree, and strain patterns calculated for the model are realistic. Models run with 20 node brick quadratic elements show the same reaction forces. The absolute stress–strain values found with the quadratic models are higher, but the strain patterns and relative strain energy results reported below are the same regardless of whether linear or quadratic elements are used.

3.3. Strain energy and optimization

Table 2 shows a comparison of force and strain energy between the FE models representing the different blade set-ups when compressing the hyperelastic resin material. Strain energy is measured for a given value of maximum LE of 0.3 within the model. For this maximum LE value, the straight blade model shows the highest total strain energy. The notched blade values are all lower; however, the more obtuse notch (120°) shows a lower strain energy value compared with 90° and 60°. A further set of FE models were used with 150°, 153°, 155°, 157°, 160° and 170° notched blades. Strain energy hits a low point at a notch angle of 153°.

Table 2.

Strain energy comparison when maximum LE reaches 0.3.

	displacement (mm)	force (N)	strain energy (J)
straight blades	1.44	9.235	0.00527
170° notch	1.18	7.424	0.00357
160° notch	1.11	7.511	0.00336
157° notch	1.21	7.605	0.00333
155° notch	1.17	7.526	0.00329
153° notch	1.12	7.382	0.00319
150° notch	1.08	7.611	0.00334
120° notch	1.12	7.674	0.00346
90° notch	1.28	7.755	0.00381
60° notch	1.56	7.726	0.00460

Table 3 shows a similar comparison of force and strain energy across blade designs when compressing the theoretical asparagus material (linearly elastic). In this case, we were able to use the maximum tensile strain as our constant variable as we were dealing with linearly elastic materials. The maximum strain used was 0.15 owing to certain models not achieving a maximum tensile strain of 0.3. Unlike with the hyperelastic material, the most acute angled notch shows the lowest strain energy values.

Table 3.

Strain energy comparison with linear elastic materials when maximum tensile strain reaches 0.15.

	displacement (mm)	force (N)	strain energy (J)
straight blades	1.80	0.254	0.000169
120° notch	1.44	0.216	0.000117
90° notch	1.64	0.214	0.000129
60° notch	1.68	0.158	0.000096

4. Discussion

We present here a validated FE model mimicking a series of physical experiments in order to explore how bladed dental design can affect the underlying energetics and mechanics of mastication. By validating the model against a physical experiment, we can treat the numeric results from the model as realistic and compare various metrics that are nearly impossible to measure in experiments (such as internal strain energy). The validated model also allows us to create ‘simulated’ experiments, where individual aspects of the model are altered in a controlled manner to view their effects on the variables of interest. This allows us to identify potential ‘optimized’ blade designs for deforming a given material prior to the onset of cutting and exploring the relationship between material properties and blade design.

Reaction forces calculated from the FE model closely match in both direction and magnitude similar forces measured during experiments, indicating a very close match between the theoretical model and physical reality. The strain patterns seen in both the model and physical experiments also show close agreement (figure 2). Numerically validating the strain between the experiments and the model is unfeasible; however, the agreement in reaction forces and resolution of the strain results allow for numerical comparisons between models to be made (see electronic supplementary material  for full discussion). FE validation is a growing practice in biology, and numerous studies have shown that the amount of assumptions inherent in most biological FE studies results in a fair amount of disagreement in absolute values between experimental and theoretical results [45]. However, by creating an experimental design with both simple shapes and test materials with well-defined properties, it is possible to obtain very close agreement between the model and the experiment. Once a validated model is obtained, it is possible to calculate variables such as strain energy.

Strain energy is the amount of work being done to deform a given volume of material (assuming no losses) and therefore can be seen as an indication of the efficiency of a system [46]. Strain energy has generally been used to assess the structural efficiency of an object undergoing loads. These structures are often hard or brittle. However, the ability to measure strain energy in a model offers a way to address the efficiency in tools that attempt to create separation (via cutting) in softer, more deformable materials. During cutting, a certain amount of the work done goes towards providing the energy for new surfaces, the rest goes towards deformation of the bulk material [47,48]. Prior to actual separation, the work being done by the tools in deforming the material will be stored as strain energy. A blade configuration which can minimize the work necessary to create this deformation will cause the animal to expend less overall energy during mastication. Our computational model shows that using a notched blade reduces the total strain energy absorbed by the material for a given strain value: it takes less energy to deform the given volume of material. This supports previous experimental results, which showed that a notched blade could cut various biological materials for less overall work than straight blades [14,15].

One surprising result from our work is that although notched blades do show reduced strain energy compared with straight blades, the 120° notch shows lower strain energy than the two more acute angles (90° and 60°) (table 2). Based on this result, we can hypothesize that there must be a certain ‘optimal’ notch angle where the total strain energy is lowest for a given deformation somewhere between 180° and 90°. By altering the validated model, we were able to test this hypothesis as shown in table 2. Strain energy continues to decrease as the angle of the notch becomes wider until the angle is 153°, when the strain energy increases again. We can, therefore, hypothesize that an angle between 150° and 155° would be most efficient when deforming hyperelastic materials such as the resin used in this experiment.

Some basic physics may shed light on this result. Using vector mathematics, it is possible to resolve the normal force and displacement at the points of contact between the notched blade and the material (see supplementary material for full discussion). In this case, the displacement normal to the surface at the points of contact is the vertical displacement multiplied by sin(θ/2), where θ is the angle of the notched blade (electronic supplementary material, figure S3). The normal force at the point of contact is similarly given by F/2 multiplied by sin(θ/2), where F is the vertical force applied to the blade. The work done at the points of contact to deform the material is the normal force times the normal displacement, which is proportional to sin(θ/2) to the second power (see electronic supplementary material for the mathematical explanation). However, the stress at the point of contact is only proportional to sin(θ/2). The consequence of this is that as a more acute notch angle is used, both the work done and stress at the point of contact decrease, but the former will decrease faster. Therefore, there should be a specific angle where sufficient stress is created for a minimum amount of work. This is obviously an oversimplification of the problem, as it treats the system in two dimensions only and ignores complications such as the hyperelastic nature of the material (this is a primary reason for FE modelling, to explore systems that are too complicated to address by hand). However, these considerations do help put the FE results in a context and offer a possible explanation.

How does this ‘optimal’ notch angle we determined compare with actual biological tooth structures? A brief survey of carnassial blades found in the mammal collection of the City Museum in Bristol and the Natural History Museum in London illustrates a wide range of notch angles ranging from 90 to 100° in hypercarnivores like lions (Panthera leo) and tigers (Panthera tigris) up to obtuse angles such as 147° in the spotted hyena (Crocuta crocuta) and 150° in the domestic dog (Canis lupus familiaris) (P. S. L. Anderson & T. Baird 2010, unpublished data). Taxa that spend more time chewing on bones (hyenas and dogs) appear to have more obtuse angles in their carnassials than the obvious hypercarnivores (lions and tigers). There is some sense to this, as bone is a stiffer, hyperelastic material, and while not really all that similar to the resin used here, it is likely to be closer to it than soft, malleable flesh. These are only a few isolated examples and further work needs to be done looking for trends in carnassial shape to compare with our mechanical models.

The above optimization does not match expectations from previous experimental studies [14], which showed that the more acute angles would generally result in lower energy expenditure. This is likely to be due to variation between the material modelled in the FEA (hyperelastic resin) and the biological tissues used in previous experiments (extensible soft tissues such as fish muscle). However, the nature of our theoretical model lets us alter the material properties of the food item and therefore test to see if different materials might result in different ‘optimal’ designs. Our tests on a linearly elastic material patterned after an easily obtainable food item (asparagus) show a different pattern from the hyperelastic materials (compare tables 2 and 3). With the asparagus material, the most acute angled notch does show the lowest strain energy. The pattern with intermediate angles (90° and 120°) is more complicated, but overall different from the hyperelastic materials. Generally, the most acute angles seen among the mammal data are 80–90° in certain hypercarnivores. However, one specimen of the American mink (Neovison vison) does show 65° on its upper carnassials. Again, this is circumstantial data and a more rigorous analysis is required to fully compare data with model. These virtual experiments do illustrate how the specific material properties of a food item can dictate what the most efficient tooth design might be.

A strength of combining experimental and theoretical methods is the ability to gain insights and data beyond what either can provide by itself. Experimental studies offer a test of reality: how something will react under a given set of conditions. However, they are constrained by what can actually be controlled in a physical setting with real materials, which can be especially difficult with biological materials. Theoretical modelling allows us to control for all variables and set up the system precisely as we want it, creating virtual experiments not limited by physical materials and costs. However, it is easy for theoretical analyses to stray far from reality. Researchers can ground-truth numerical models (such as an FEA) using experimental data. Then they can explore aspects of biological systems not easily observed in an experiment (internal strain energies) and set up virtual experiments grounded in biological reality. Our combination of cutting experiments and FE models will allow us to create a theoretical framework for exploring the relationship between cutting mechanics, dental morphology and prey material.