A Fast Hybrid Algorithm Combining Regularized Motion Tracking and Predictive Search for Reducing the Occurrence of Large Displacement Errors

Abstract

A hybrid approach that inherits both the robustness of the regularized motion tracking approach and the efficiency of the predictive search approach is reported. The basic idea is to use regularized speckle tracking to obtain high quality seeds in an explorative search that can be used in the subsequent intelligent predictive search.

The performance of the hybrid speckle tracking algorithm was compared with three published speckle tracking methods using in vivo breast lesion data. We found that the hybrid algorithm provided higher displacement quality metric values, lower root mean squared errors compared to a locally smoothed displacement field, and higher improvement ratios compared to the classic block-matching algorithm. On the basis of these comparisons, we concluded that the hybrid method can further enhance the accuracy of speckle tracking compared to its real-time counterparts, at the expense of slightly higher computational demand.

I. Introduction

Elasticity imaging is a method for assessing stiffness of tissue. Changes in stiffness often correlate with pathological changes and can be an indicator of many diseases, such as cancer and cardiovascular disease [1]. The approaches to elasticity imaging vary widely but typically involve the use of medical imaging technologies – mainly high resolution ultrasound and magnetic resonance (MR) – to track local tissue deformation as summarized in several review articles [2-4]. Among these approaches, real-time ultrasonic strain imaging is gaining popularity. Clinical studies of breast lesions [5-9] and thyroid nodules [10] showed this modality may help differentiate benign from malignant masses. Particularly, multi-institution studies of breast strain imaging [5, 7-9] demonstrated that this modality has the potential to significantly reduce benign biopsies by measuring the lesion size difference between the B-mode and the strain images.Promising work done by Rubin and colleagues also exhibited that strain imaging was remarkably accurate at estimating the age of deep vein thrombus in rats [11] and humans [12].

Unfortunately, tracking speckle motion between de-correlated echo signals using pure correlation-based algorithms suffers from large “peak hopping” errors [13]. These “peak hopping” errors occur when echo signals are de-correlated and the magnitude of a random correlation peak may exceed the magnitude of the “true” correlation peak corresponding to the correct speckle motion. There are two main approaches in the literature for reducing the occurrence of these large tracking errors: motion regularization [14-17] and predictive search [18-21].

To use motion regularization, speckle tracking was modeled as an optimization problem using an energy function combining the correlation coefficient and speckle motion continuity. Since speckle motion corresponding to primary correlation peaks preserves at least local motion continuity, and false displacement estimates corresponding to “peak hopping errors” don’t, regularized speckle tracking can effectively eliminate the majority of “peak hopping” errors [14-17]. The basic assumption of the predictive search strategy [18-21] is that an initial explorative search can first be applied at selected/pre-determined locations and then certain prediction strategies will be employed to advance the estimation process from one point to its neighbors (e.g. as simple as a row-to-row prediction [18]). Starting with a correct prediction, the predictive search will not only improve computational efficiency but also reduce the possibility of “peak-hopping” errors by limiting the search range to as small as one radiofrequency (RF) sample in each direction. The downside of the predictive search is that cascade effects (i.e. displacement estimate errors providing incorrect guidance and creating downstream errors through bad predictions) might take place if prediction errors are not appropriately identified and eliminated. Recently, Chen and colleagues introduced a remarkably simple but very effective strategy [21]. Their approach is to ensure that the highest quality initial displacement estimate vectors (hereafter referred as to seeds) obtained from the explorative search carry priority in guiding subsequent speckle tracking.

The objective of this study is to explore the feasibility of combining the regularized speckle tracking method with the predictive search strategy. Our basic idea is to use a regularized speckle tracking method to obtain high quality seeds in an explorative search that can be used in the subsequent intelligent predictive search based on Chen’s approach [21]. We hypothesized that high quality initial seeds could improve the outcome of predictive search. To demonstrate the usefulness of this hybrid algorithm, its performance was quantitatively compared against three other published speckle tracking methods using in vivo breast lesion data. The first method is, to date, the most sophisticated predictive search method [21], hereafter referred as to “Chen’s Method”. The second method, referred to as the “lateral-guidance” method, uses regularized speckle tracking for the central column of the region of interest (ROI) followed by predictive search utilizing displacement vectors obtained along the central column [14, 16]. The last one of these three speckle tracking methods, referred to as the “multi-grid” method [16], uses regularized speckle tracking on an evenly-spaced coarse grid with a global motion continuity assumption rather than only along the central column of the ROI.

Two metrics, namely, the displacement quality metric (DQM; [22]) and the root mean squared error (RMSE) between the estimated displacements and locally fitted surfaces [23] were chosen to compare the performance among all four speckle tracking algorithms using pathologically-confirmed breast tumor data, as described below.

II.Methods and Materials

A. The Hybrid Method of Speckle Tracking

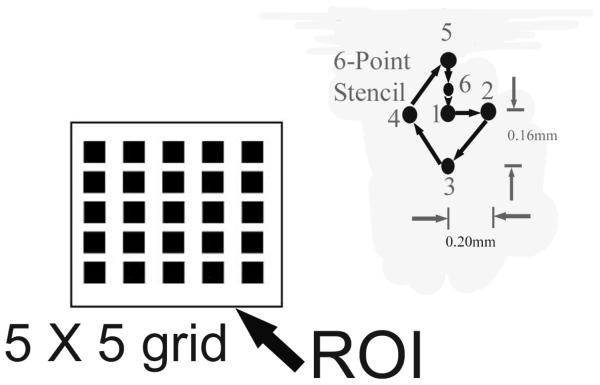
The hybrid method is a two-step speckle tracking algorithm combining both regularized motion tracking and predictive search. The first step (i.e. “pre-processing” step) performs regularized searches [16] with relatively large 2D (approx. 0.5mm [axial] long by 1mm [lateral] wide) tracking kernels at a coarse (typically 5mm spacing) 5 by 5 grid, as shown in Fig. 1. To determine a displacement vector for each point on this grid, instead of selecting the highest correlation value for each search region, as in the classic block matching algorithm, regularized speckle tracking was performed on a small (approximately two beam line wide [0.40-mm] and 1.5 wavelengths @ 7.2 MHz [0.32-mm]) 6-point diamond-shaped stencil centered at the point (also shown in Fig. 1). More specifically, a variant of the classic block-matching algorithm was used to determine 6 displacement vectors for each diamond-shaped stencil simultaneously. Given a search region for each point at the stencil (e.g. K by L), the cost associated with each possible solution in the solution space can be calculated as follows,

$$COST={\iint }_{\Omega }(\alpha E_c+\Phi \left(E_s\right))d\Omega$$ (1)

where α is an adaptively chosen scale factor, E_c is a measure of speckle similarity and E_s is a measure of motion smoothness that is minimized with high motion continuity. In this study, we set α to unity for all data investigated and normalized cross correlations were used to measure speckle similarity E_C. All calculated cost values (see Eqn. (1)) are stored in a matrix and the Viterbi algorithm [24] is then used to efficiently identify 6 displacement vectors based on the combination of signal correlation and motion continuity. Arrows connecting all points on the diamond-shaped stencil in Fig. 1 illustrate the direction of the Viterbi tracking. It is worth noting that the smoothness constraint E_S in Eqn. (1) is imposed by a finite difference scheme along the Viterbi tracking direction. More details of this method can be found in [16].

Figure 1.

Illustrations of the initial 5 by 5 search grid and the 6-point diamond-shaped search stencil.

Since the size of the 6-point diamond-shaped stencil is small, it is reasonable to enforce local motion continuity. Consequently, we defined the first quality test to require that the displacement vector at the starting point of the stencil (Point 1 in Fig. 1) differs from the displacement vector at the ending point of the stencil (Point 6 in Fig. 1) by a half (RF echo) sample spacing or less. Of note, the Points 1 and 6 are only separated by 4 RF echo samples (approximately 0.08 mm given 40 MHz sampling frequency) as shown in Fig. 1. We also require that the displacement vector at the center of the stencil (Point 1 in Fig. 1) will result in a correlation value of 0.7 or higher between the pre- and motion-compensated post-deformation RF data. If both tests are passed, the displacement vector at the center of the stencil (Point 1 in Fig. 1) will be marked as a “trusted seed” and assigned to that point on the coarse grid. These trusted seeds will be used for predictive search in the second step.

In the second step (“predictive search” step), we follow the predictive search strategy developed by Chen and colleagues [21]. The principle of their approach is to ensure that the seed with the highest correlation value (on a list of all estimated values) will be used for the predictive search of its immediate neighbors. Interested readers are referred to the flowchart (i.e. Fig. 2 in [21]) for more details. However, we have made two important modifications to their strategy. First, because Chen et al. used a “brute-force” search to generate their initial seeds, the reliability of their seeds is unknown. Therefore, their initial seeds are replaceable during any subsequent predictive search. In the hybrid algorithm, as described above, our initial “trusted” seeds are obtained by more sophisticated regularized speckle tracking and have passed two quality tests. We mark these initial “trusted” seeds as irreplaceable during the predictive search. Second, we exclude all displacement vectors with correlation values less than 0.4 from being used for predictions. This modification sometimes results in “voids” in the displacement vector field that typically correspond to the presence of significant echo de-correlation in those sub-regions. We fill in these “voids” using “interpolated” or “extrapolated” values from its immediate neighbors. The other three motion tracking methods (“Chen’s methods” [21], “lateral-guidance,” [14, 16] and “multi-grid” [16]) are reported in the literature. All four speckle tracking methods were implemented in this study as variants of the classic block matching algorithm. Thus, we can use the same tracking parameters (e.g. kernel size, spacing, etc.) for the performance comparison.

Figure 2.

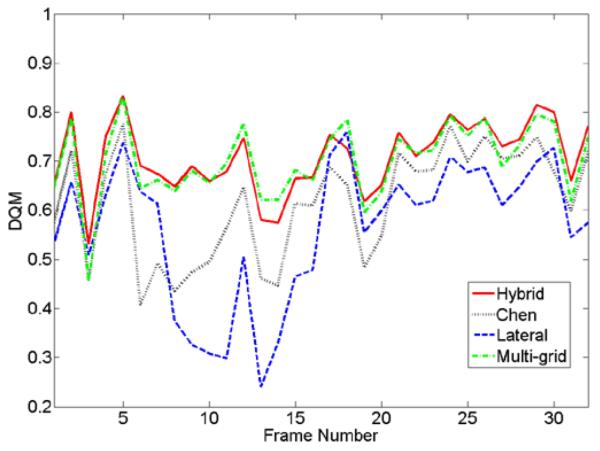
A plot of estimated DQM values for a sequence of strain images obtained from an in vivo atypical breast fibroadenoma using the hybrid, Chen’s, “lateral-guidance” and “multi-grid” tracking methods. The corresponding B-mode and strain images are shown in Movie 1.

B. Data Acquisition for in vivo Breast and Thyroid Cancers

From an archived database of ultrasound scans of human breast lesions, 5 RF echo data sets (approximately 500 echo frames) were arbitrarily selected to include both benign and malignant tumors. In data investigated, five patients were all female; ages ranged between 20 and 83 with a mean of 46 years of age. Approval for the human subject study was obtained from the appropriate Institutional Review Boards and the study was also compliant with the US Health Insurance Portability and Accountability Act. Pathology of each tumor was determined by either percutaneous or excisional biopsy. In vivo breast scanning was performed by clinicians using identical equipment (i.e. Siemens SONOLINE Elegra ultrasound scanners equipped with high frequency linear array transducers [VFX13-5 or 7.5L40], Siemens Healthcare USA Inc., Mountain View, CA). The detailed protocol for data acquisition can be found in our early work by Hall, et al. [25].

C. Data Analysis

All strain imaging examples presented in this paper were estimated off-line by the four methods described above with a small tracking kernel (0.9mm (lateral) × 0.3mm (axial)) used to estimate displacements and a 1.6mm linear regression window used to estimate strains [26]. The tracking kernel size and the length of linear regression window were empirically chosen so that resultant strain images could have good spatial resolution while maintaining good image quality. To achieve various levels of signal decorrelation between a pair of pre- and post-deformation RF echo data, echo frames were paired to obtain nominally 0.25-2% frame-average strain through retrospective processing [27, 28].

Two metrics were chosen to compare the performance among the four speckle tracking algorithms. The first metric is the “displacement quality metric” (DQM) method [22]. The DQM is the product of the normalized cross correlation among the pre-deformation and motion-compensated post-deformation RF echo fields (a measure of motion tracking accuracy applied to the entire region of interest) and the cross correlation between two consecutive motion-compensated strain images (a measure of strain image consistency) [22]. By applying the displacement estimates to the deformed data and remapping to the coordinates of the pre-deformation data, we register two RF echo fields with apparent deformations. A higher NCC value between two registered echo fields implies that the apparent deformation between these two ultrasound fields is more accurately compensated for (the displacement estimates are more accurate). For small frame-to-frame deformations (e.g. 1%), the local strain is a surrogate measure of local tissue stiffness corrupted by noise. Thus, high NCC between two consecutive strain images means relatively low noise in both strain images, thereby suggesting better strain image quality. By using the normalized correlation coefficient, all DQM values lie between 0 and 1, with 1 indicating the best result.

The second metric adopted to compare performance is a surrogate of noise level among local displacement estimates. Assuming, as a first approximation, that the tissue behaves as a continuum [1], the resultant displacement field from an external compression using an ultrasound transducer should result in a nearly continuous function. Therefore, all estimated axial displacement data points can be regarded as a smooth surface (in 2D) that is corrupted with additive noise. More specifically, we first locally fitted estimated axial (parallel to the acoustic beam direction) displacements using a first-order polynomial model (i.e. a plane 0.26 mm [axial; approximately one wavelength @ 7.2 MHz] by 1.8 mm [lateral; approximately one acoustic beam width for Siemens VFX13-5]). The selection of the plane size above will include an adequate number of points for robust surface fitting. We then used the root mean squared error (RMSE) between the local ultrasonically-measured and locally-fitted (planar) surface of axial displacements as an indicator of the noise artifacts present in the measured displacement field. A similar noise analysis method was used by Chen and Varghese [23].

During freehand scanning of breast lesions investigated here, sinusoidal (compress/release) cyclic deformation was used [25]. In all 5 breast lesions tested, acquired data contained more than one cycle. During data processing, we first adaptively selected RF frame pairs to achieve different frame-average strains [27, 28] and then estimated DQM and RMSE values from these resultant strain or displacement images.

We also calculated the normalized correlation coefficients (NCC) between the pre- and the motion-compensated post-deformation RF echo fields for all four methods plus the classic block-matching algorithm. We defined an “improvement ratio” in terms of motion tracking accuracy for each method, as the estimated NCC value for a specific method investigated in this study divided by the NCC value using the classic block-matching algorithm for the same pair of RF echo fields with the exact same set of processing parameters and compared those “improvement factors”.

All four algorithms were implemented on a Windows-based dual-CPU (1.8-GHz) workstation (DELL Precision 390, DELL Inc., TX, USA) equipped with 2-Gbytes of memory using ANSI C and MEX interface to Matlab (Mathworks Inc., MA, USA). Of note, Chen’s Method was implemented based on their publication [21] with an initial search grid of 7 by 11. The “restarting” mechanism described in [21] was not implemented because the lack of objective criteria for making such a determination. For all comparisons in Section III below, the same pairs of echo fields and strain processing parameters (kernel size, separation, etc.) were used to process data with all four speckle tracking algorithms.

III. Results

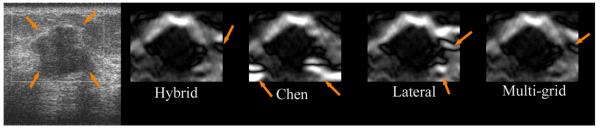
Figure 2 shows the DQM values estimated from an in vivo atypical fibroadenoma (approximately 1% frame-average strain) plotted with respect to the corresponding frame numbers for all four methods. All calculations of the frame-average axial strains in this study were based on the hybrid speckle tracking method. It is clear that the hybrid method and the “multi-grid” method were able to track motion more reliably (more consistent DQM values and visual perception) than other two algorithms (“lateral-guidance” and “Chen’s method”). In particular, a long subsequence (i.e. 18 frames vs. 10 and 10 frames, respectively) of consecutive “good” (DQM>0.6) strain images can be obtained using the hybrid method as compared to both the “lateral-guidance” and the Chen’s methods. The strain image sequence corresponding to Fig. 2 is shown in Movie 1. Representative strain images from the in vivo atypical breast fibroadenoma using these four algorithms are displayed side by side in Fig. 3 where the frame-average axial strain is approximately 1%.

Figure 3.

B-mode (far left) and strain images estimated from an in vivo atypical fibroadenoma breast lesion. Arrows in the B-mode image point to the breast lesion, while arrows in each strain image point to suspicious motion tracking errors. All strain images were 8 bit images scaled from 0 to 5% strain. The frame-average strain estimated by the hybrid method was 1%. The region of interest (ROI) where motion tracking was performed is indicated by the white box on the B-mode image.

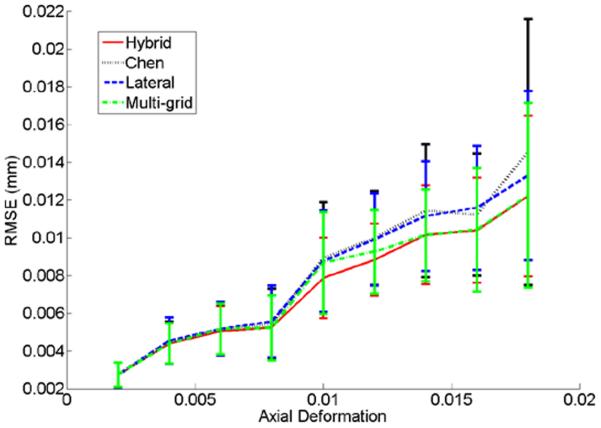
The estimated DQM and RSME values were plotted with respect to different axial deformation for all 5 breast lesions in Figs. 4(a) and (b), respectively. Each subplot in Fig. 4 was generated from approximately 1000 frame pairs of RF data. Figure 5 shows the improvement ratios for the four guided search algorithms with respect to the base line (i.e. the NCC values obtained from the classic unguided block-matching algorithm) for the same 5 breast lesions.

Figure 4.

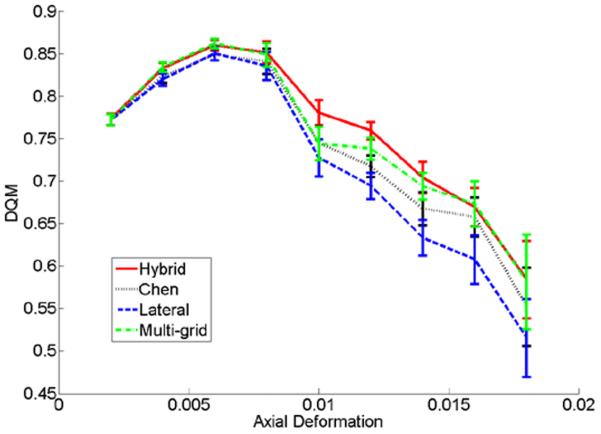
Plots of estimated (a) DQM and (b) RSME values with respect to frame-averaged axial strains using the hybrid, Chen’s, “lateral-guidance” and “multi-grid” tracking methods. Results were obtained from approximately 1000 pairs of RF echo fields among 5 in vivo breast lesions. Error bars in both plots represent standard errors.

Figure 5.

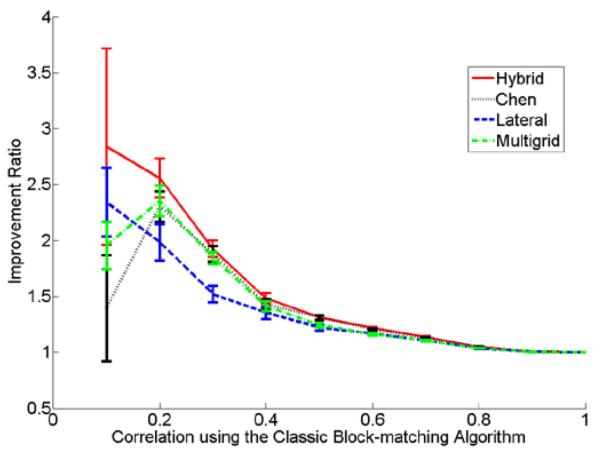
A plot demonstrating improvement ratios using the hybrid, Chen’s, “lateral-guidance” and “multi-grid” tracking methods. This plot was obtained using approximately 1000 pairs of RF echo frames from 5 different in vivo breast lesions. Error bars represent standard errors.

IV. Discussions

Four speckle tracking methods that were all modified from the classical block-matching algorithm were tested using in vivo breast ultrasound echo data. We found that all four algorithms were heuristic in nature. Consequently, they might fail (see Figs. 2 and Movie 1) from time to time. However, our overall results demonstrated that the hybrid method performed better (higher DQM values, lower RMSE values and more consistent strain images in longer sequences) than the Chen’s method [21] and our previously-developed “lateral-guidance” method. Although the performance of the hybrid method is comparable to the “multi-grid” method, our estimates suggest that the hybrid method could have a projected frame rate of 15 frames/second over a 3-cm × 3-cm ROI and with 1% axial strain, whereas the “multi-grid” method is only a near real-time algorithm (approximately 2 frames/second under the same conditions) [16]. The projected frame rate using the “lateral guidance” method and the Chen’s method under the same condition are slightly higher (15~20 frames/second). It is worth noting that the “multi-grid” approach explicitly constrains motion continuity so that displacement data obtained by this approach may have the least amount of “large displacement errors”. Consequently, strain image sequences appeared smoother (less “de-correlation” error or flashing) as compared to these produced by the hybrid method. However, more quantitative metrics such as DQM and RSME indicate both methods are comparable.

Visually, in Movie 1 as well as in the example displayed in Fig. 3, resultant strain images from the “lateral-guidance” and the Chen’s methods had higher noise. This is consistent with lower mean DQM values and higher RMSE values (see Table 2) among strain images obtained using the “lateral-guidance” and Chen’s methods.

Table 2.

A summary of mean DQM and RSME values (± standard deviation) obtained from the RF echo sequence displayed in Movie 1 (in vivo breast fibroadenoma shown in Fig. 3). M1-M4 denote the hybrid, Chen’s, the “lateral-guidance” and the “multi-grid” methods, respectively

	Breast Fibroadenoma
	DQM	RMSE (micrometer)
M1	0.71 ± 0.07	9.5 ± 1.5
M2	0.61 ± 0.11	11.3 ± 2.3
M3	0.56 ± 0.14	11.4 ± 3.1
M4	0.70 ± 0.08	9.9 ± 1.5

Consistent with our visual assessment, estimated DQM and RSME values shown in Figs. 4(a) and (b) demonstrated that the improvements (i.e. higher DQM values and lower RMSE values) provided by the hybrid method over the other two real-time methods (i.e. the “lateral-guidance” and the Chen’s methods). It is worth noting that these improvements were more distinct among in vivo thyroid data (data not shown but investigated following identical procedures as described in this paper) where tissue motion is more complex.

Overall, the hybrid method had the highest improvement ratios for nearly all data points in Fig. 5. Consistent with our experience, the improvement ratio quickly dropped to one, when signals were highly correlated and a simple classic block-matching algorithm could provide accurate displacement estimates. Interestingly, when signals were highly de-correlated (e.g. less than 0.4) and motion was complex (in and around thyroid lesions), the pure predictive search approach (i.e. the Chen’s method) provided the lowest improvement ratios. This should be expected because predictions solely based on correlations may be “sub-optimal” once the RF echo signals are highly de-correlated. It is fair to say that severe signal de-correlation (e.g. < 0.4) presents an extremely challenging condition for all four methods, but such conditions are encountered clinically.

Similar to the work reported in this paper, a follow-up paper published by Chen et al. [29] (hereafter referred as to Chen’s modified approach) proposes a method to improve the “seeding” methodology and thereby reducing “error propagation” that could happen during “predictive search”. However, the fundamental difference is that our core idea is to effectively combining regularized tracking to improve the “seeding”, while Chen’s approach used a heuristic multi-level approach.

The greatest similarity among these approaches is that during the second level (L2) search of Chen’s modified approach, they used a concentric ring pattern for “seeding”. This pattern might be similar to our 6-point stencil pattern, but there are fundamental differences. Specifically, they state “Instead, a tracking strategy is used to propagate displacement estimates from one window to the next, with the search at each window confined to a narrow range centred around the estimate propagated from its neighbor (or from the parent L1 window in the case of the initial nine L2 windows.” However, motion continuity at the L2 level (concentric windows around each L1 window) was not explicitly enforced. Interestingly, their lateral displacements were not sufficiently accurate for the purpose of multi-level motion recovery. Hence, the authors proposed to use a thin-plate-spline filter at the L2 level to remove some large errors prior to the motion tracking at the finest resolution. In other words, it is evident that “motion smoothness” was not explicitly included in the motion tracking process. Unlike Chen’s modified approach, the “stencil method” reported here is fundamentally different because we construct a closed loop so that motion continuity can be rigorously enforced using regularization and the consistency checking.

Furthermore, we attempted to enforce local motion continuity (i.e. Eqn. (1)) onto a small region of interest (on the order of acoustic pulses) by constructing a closed loop (i.e. 6-point stencil). Removal of the global motion continuity assumption is advantageous and should help to broaden the applications of ultrasound elasticity imaging in organ systems where tissue/organ interfaces are present.

Our future studies will try to test this algorithm with internal organs (e.g. uterine and kidney) where more complex and potentially discontinuous motion is presented. Although the block-matching algorithm was selected as the first attempt to combine the regularized speckle tracking [16] with Chen’s quality-guided search strategy [21], this hybrid method could feasibly be integrated with other correlation-based motion estimation algorithms and adapted to 3D for volumetric strain imaging [30].

V. Conclusions

Compared to other guided-search block matching algorithms we use, the hybrid speckle tracking algorithm provided higher DQM values, lower RMS errors compared to a locally smoothed displacement field, and higher improvement ratios compared to an unguided block-matching algorithm than the other algorithms tested. The algorithm provides performance, for these three metrics, comparable to a “multi-grid” approach [16] but can be computed nearly 8 times faster on common desktop computers.

Supplementary Material

1

Movie 1: B-mode (far left) and strain images of the in vivo breast fibroadenoma shown in Fig. 3, obtained by using four different tracking algorithms: 1) hybrid (middle left), 2) Chen’s (middle), 3) “lateral-guidance” (middle right) and 4) “multi-grid” (far right) tracking methods.

Table 1.

The estimated DQM and RMSE values for the in vivo breast fibroadenoma strain images shown in Fig. 3. M1-M4 denote the hybrid, Chen’s, the “lateral-guidance” and the “multi-grid” methods, respectively

	Fig. 5
	M1	M2	M3	M4
DQM	0.80	0.67	0.72	0.78
RMSE (micrometer)	1.56	0.79	1.53	1.60