Abstract
We develop methodology for a multistage-decision problem with flexible number of stages in which the rewards are survival times that are subject to censoring. We present a novel Q-learning algorithm that is adjusted for censored data and allows a flexible number of stages. We provide finite sample bounds on the generalization error of the policy learned by the algorithm, and show that when the optimal Q-function belongs to the approximation space, the expected survival time for policies obtained by the algorithm converges to that of the optimal policy. We simulate a multistage clinical trial with flexible number of stages and apply the proposed censored-Q-learning algorithm to find individualized treatment regimens. The methodology presented in this paper has implications in the design of personalized medicine trials in cancer and in other life-threatening diseases.
Keywords and phrases: Q-learning, reinforcement learning, survival analysis, generalization error
1. Introduction
In medical research, dynamic treatment regimes are increasingly used to choose effective treatments for individual patients with long-term patient care. A dynamic treatment regime (or similarly, policy) is a set of decision rules for how the treatment should be chosen at each decision time-point, depending on both the patient’s medical history up to the current time-point and the previous treatments. Note that although the same set of decision rules are applied to all patients, the choice of treatment at a given time-point may differ, depending on the patient’s medical state. Moreover, the patient’s treatment plan is not known at the beginning of a dynamic regime, since it may depend on subsequent time-varying variables that may be influenced by earlier treatments and response to treatment. An optimal treatment regime is a set of treatment choices that maximizes the mean response of some clinical outcome at the end of the final time interval (see, for example, Murphy, 2003; Robins, 2004; Moodie et al., 2007).
We consider the problem of finding treatment regimes that lead to longer survival times, where the number of treatments is flexible and where the data is subject to censoring. This type of framework is natural for cancer applications, where the initiation of the next line of therapy depends on the disease progression and thus the number of treatments is flexible. In addition, data are subject to censoring since patients can drop out during the trial. For example, in advanced non-small cell lung cancer (NSCLC), patients receive one to three treatment lines. The timing of the second and third lines of treatment is determined by the disease progression and by the ability of patients to tolerate therapy (Stinchcombe and Socinski, 2008; Krzakowski et al., 2010). We focus on mean survival time restricted to a specific interval, since in a limited-time study, censoring prevents reliable estimation of the unrestricted mean survival time (see discussion in Karrison, 1997; Zucker, 1998; Chen and Tsiatis, 2001, see also Wahed and Tsiatis, 2006 in the context of sequential decision problems and see Robins et al., 2008 for an alternative approach).
Finding an optimal policy for survival data poses many statistical challenges. We enumerate four. First, one needs to incorporate information accrued over time into the decision rule. Second, one needs to avoid treatments which appear optimal in the short term but may lead to poor final outcome in the long run. Third, the data is subject to censoring since some of the patients may be lost to follow-up and the final outcome of those who reached the end of the study alive is unknown. Fourth, the number of decision points (i.e., treatments) and the timing of these decision points can be different for different patients. This follows since the number of treatments and duration between treatments may depend on the medical condition of the patient. In addition, in the case of patient’s death, treatment is stopped. The first two challenges are shared with general multistage decision optimization (Lavori and Dawson, 2004; Moodie et al., 2007). The latter two arise naturally in the context of optimizing survival time, but are applicable to other scenarios as well. Developing valid methodology for estimating dynamic treatment regimes in this flexible timing set-up is crucial for applications in cancer and in other diseases where such structure is the norm and appropriate existing methods are unavailable.
One of the primary tools used in developing dynamic treatment regimes is Q-learning (Murphy et al., 2006; Zhao et al., 2009; Laber et al., 2010; Zhao et al., 2010). Q-learning (Watkins, 1989; Watkins and Dayan, 1992), which is reviewed in Section 2, is a reinforcement learning algorithm. Since we do not assume that the problem is Markovian, we present a version of Q-learning that uses backward recursion. The backward recursion used by Q-learning addresses the first two challenges posed above: It enables both accrual of information and incorporation of long-term treatment effects. However, when the number of stages is flexible, and censoring is introduced, it is not clear how to implement backward recursion. Indeed, finding the optimal treatment at the last stage is not well defined, since the number of stages is patient-dependent. Also, it is not clear how to utilize the information regarding censored patients.
In this paper we present a novel Q-learning algorithm that takes into account the censored nature of the observations using inverse-probability-of-censoring weighting (see, Robins et al., 1994, see also Wahed and Tsiatis, 2006; Robins et al., 2008 in the context of sequential decision problems). We provide finite sample bounds on the generalization error of the policy learned by the algorithm, i.e., bounds on the average difference in expected survival time between the optimal dynamic treatment regime and the dynamic treatment regime obtained by the proposed Q-learning algorithm. We also present a simulation study of a sequential-multiple-assignment randomized trial (SMART) (see Murphy, 2005a, and references therein) with flexible number of stages depending on disease progression and failure event timing. We demonstrate that the censored-Q-learning algorithm proposed here can find treatment strategies tailored to each patient which are better than any fixed-treatment sequence. We also demonstrate the result from ignoring censored observations.
One general contribution of the paper is the development of a methodology for solving backward recursion when the number and timing of stages is flexible. As mentioned previously, this is crucial for applications but has not been addressed previously. In Section 4 we present an auxiliary multistage decision problem that has a fixed number of stages. Since the number of stages is fixed for the auxiliary problem, backward recursion can be used in order to estimate the decision policy. We then show how to translate the original problem to the auxiliary one and obtain the surprising conclusion that results obtained for the auxiliary problem can be translated into results regarding the original problem with flexible number and timing of stages.
An additional contribution of the paper is the universal consistency proof for the algorithm performance. Universal consistency of an algorithm means that for every distribution function on the sample space, the expected loss of the function learned by the algorithm converges in probability to the infimum over all measurable functions of the expected loss (see, for example, Steinwart and Chirstmann, 2008 ). In Section 6 we prove that when the optimal Q-functions belong to the corresponding approximation spaces considered by the algorithm, the algorithm is universally consistent. The proof presented here is algorithm-specific, but the tools used in the proof are widely applicable for universal consistency proofs when the data are subject to censoring (see, for example, Goldberg et al., 2011 ). While other learning algorithms were suggested for survival data (see, for example, Biganzoli et al., 1998; Shivaswamy et al., 2007; Shim and Hwang, 2009, see also Zhao et al., 2010 in the context of a multistage decision problem), we are not aware of any other universal consistency proof for survival data.
The paper is organized as follows. In Section 2 we review the Q-learning algorithm and discuss the challenges for adapting the Q-leaning methodology for a framework with flexible number of stages and censored data. We also review existing methods for finding optimal policies. Definitions and notation are presented in Section 3. The auxiliary problem is presented in Section 4. The censored-Q-learning algorithm is presented in Section 5. The main theoretical results are presented in Section 6. In Section 7 we present a multistage-randomized-trial simulation study. Concluding remarks appear in Section 8. Supplementary proofs are provided in Appendix A. A description of and link to the code and data sets used in Section 7 appear in Supplement A
2. Q-learning
2.1. Reinforcement Learning
Reinforcement learning is a methodology for solving multistage decision problems. It involves recording sequences of actions, statistically estimating the relationship between these actions and their consequences and then choosing a policy (i.e., a set of decision rules) that approximates the most desirable consequence based on the statistical estimation. A detailed introduction to reinforcement learning can be found in Sutton and Barto (1998).
In the medical context of long-term patient care, the reinforcement learning setting can be described as follows. For each patient, the stages correspond to clinical decision points in the course of the patient’s treatment. At these decision points, actions (e.g., treatments) are chosen, and the state of the patient is recorded. As a consequence of a patient’s treatment, the patient receives a (random) numerical reward.
More formally, consider a multistage decision problem with T decision points. Let St be the (random) state of the patient at stage t ∈ {1, …, T +1}and let St = {S1,…, St} be the vector of all states up to and including stage t. Similarly, let At be the action chosen in stage t, and let At = {A1, …, At} be the vector of all actions up to and including stage t. We use the corresponding lower case to denote a realization of these random variables and random vectors. Let the random reward be denoted Rt = r(St, At, St+1), where r is a (unknown) time-dependent deterministic function of all states up to stage t+1 and all past actions up to stage t. A trajectory is defined as a realization of (ST+1, AT, RT). Note that we do not assume that the problem is Markovian. In the medical context example, a trajectory is a record of all the patient covariates at the different decision points, the treatments that were given, and the medical outcome in numerical terms.
We define a policy, or similarly, a dynamic treatment regime, to be a set of decision rules. More formally, define a policy π to be a sequence of deterministic decision rules, {π1, …, πT}, where for every pair (st, at−1), the output of the t-th decision rule, πt(st, at−1), is an action. Our goal is to find a policy that maximizes the expected sum of rewards. The Bellman equation (Bellman, 1957) characterizes the optimal policy π* as one that satisfies the following recursive relation:
| (1) |
where the value function
| (2) |
is the expected cumulative sum of rewards from stage t + 1 to stage T, where the history up to stage t + 1 is given by {st+1, at}, and when using the optimal policy π* thereafter.
Finding a policy that leads to a high expected cumulative reward is the main goal of reinforcement learning. Naively, one could learn the transition distribution functions and the reward function using the observed trajectories, and then solve the Bellman equation recursively. However, this approach is inefficient both computationally and memory-wise. In the following section, we introduce the Q-learning algorithm, which requires less memory and less computation.
2.2. Q-learning
Q-learning (Watkins, 1989) is an algorithm for solving reinforcement learning problems. It is claimed by Sutton and Barto to be one of the most important breakthroughs in reinforcement learning (Sutton and Barto, 1998, Section 6.5). Q-learning uses backward recursion to compute the Bellman equation without the need to know the full dynamics of the process.
More formally, we define the optimal time-dependent Q-function
Note that , and thus
| (3) |
In order to estimate the optimal policy, one first estimates the Q-functions backwards through time t = T, T − 1, …, 1 and obtains a sequence of estimators {Q̂T …, Q̂1}. The estimated policy is given by
| (4) |
In the next section we discuss the difficulties in applying the Q-learning methodology when trajectories are subject to censoring and the number of stages is flexible.
2.3. Challenges With Flexible Number of Stages and Censoring
As discussed in the introduction, our goal is to develop a Q-learning algorithm that can handle a flexible number of stages and that takes into account the censored nature of the observations. We face two main challenges. First, recall that the estimation of the Q-functions in (3) is done recursively, starting from the last stage backward. Thus, when the number of stages is flexible, it is not clear how to perform the base step of the recursion. Second, due to censoring, some of the trajectories may be incomplete. Incorporating the data of a censored trajectory is problematic: even when the number of stages is fixed, the known number of stages for a censored trajectory may be less than the number of stages in the multistage problem. Moreover, the reward is not known for the stage at which censoring occurs.
2.4. Review of Existing Approaches
Finding optimal policies or optimal treatment regimes has been discussed extensively in other work. We discuss shortly some additional work that is related to the approach taken here. However, we are not aware of any other existing approaches that address simultaneously both censoring and flexible number of stages.
The approach closest to our proposal is the censored-Q-learning algorithm of Zhao et al. (2010). Zhao et al. considered a Q-learning algorithm for censored data based on support vector regression adjusted for censoring with fixed number of stages. A simulation study was performed to demonstrate the algorithm’s performance; however, the theoretical properties of this algorithm were not evaluated.
A general approach for finding optimal polices that uses backward recursion was studied by Murphy (2003) and Robins (2004) in the semiparametric context, and by Murphy (2005b) in the nonparametric context. These works do not treat flexible number of stages or censoring, and cannot be applied to the framework considered here without some adjustments.
Another approach for finding optimal policies was studied by Orellana et al. (2010), (see also Laan and Petersen, 2007; Robins et al., 2008). Orellana et al. consider dynamic regime marginal structural mean models (Robins, 1999). In this approach, for each regime, one considers all trajectories that comply to the regime up to some point. The trajectories are then censored at the first time-point at which they do not comply to the regime. The contribution of the non-compliant trajectories is redistributed among compliant trajectories that have the same covariate and treatment history, using the inverse-probability-of-censoring weighting. Advantages and disadvantages of this approach compared to the backward recursion approach mentioned above are discussed in Robins et al. (2008, Section 5). We note that it is assumed in their approach that the length of each stage is fixed, an assumption we do not require.
This general issue is also related to the analysis of two-stage randomized trials involving right-censored data studied in a series of papers including Lunceford et al. (2002); Wahed and Tsiatis (2006); Wahed (2009); Miyahara and Wahed (2010). The authors use inverse-probability-of-censoring to correct for censoring. See also Thall et al. (2007) that considers analysis of two-stage randomized trials with interval censoring. However, the main focus of these works is in finding the best regime from a finite number of optional regimes, as opposed to the individualized-treatment policies addressed in our proposal.
3. Preliminaries
In this section we present definitions and notation which will be used in the paper.
Let T be the maximal number of decision time-points for a given multistage time-dependent decision problem. Note that the number of stages for different observations can be different. For each t = 1,…,T, the state St is the pair St = (Zt, Rt−1), where Zt is either a vector of covariates describing the state of the patient at beginning of stage t or Zt = ∅. Zt = ∅ indicates that a failure event happened during the t-th stage which has therefore reached a terminal state. Rt−1 is the length of the interval between decision time-points t − 1 and t, where we denote R0 ≡ 0. Although in the usual Q-learning context
is the sum of rewards up to and including stage t, in our context it is more useful to think of this sum as the total survival time up to and include stage t. Let At be an action chosen at decision time t, where At takes its values in a finite discrete space
 .
.
The model assumes that observations are subject to censoring. Let C be a censoring variable and let SC(x) = P (C ≥ x) be its survival function. We assume that censoring is independent of both covariates and failure time. We assume that C takes its values in the segment [0, τ] where τ < ∞ and that SC(τ) > Kmin > 0. Let δt be an indicator with δt = 1 if no censoring event happened before the t + 1-th decision time-point. Note that δt−1 = 0 ⇒ δt = 0.
Remark 3.1
Note that for a censoring variable, we define the survival function SC(x) as P (C ≥ x) rather than the usual P(C > x). This is because given a failure time x, we are interested in the probability P(C ≥ x). However, to avoid complications that are not of interest to the main results of this paper, we assume that the probability of simultaneous failure and censoring is zero (see, for example, Satten and Datta, 2001).
The inclusion of failure times in the model affects the trajectory structure. Usually, a trajectory is defined as a (2T +1)-length sequence {S1, A1, S2, …, AT, ST+1}. However, in our context, if a failure event occurs before decision-time-point T, the trajectory will not be of full length. Denote by T̄ the (random) number of stages for the individual (T̄ ≤ T). Due to the censoring, the trajectories themselves are not necessarily fully observed. Assume that a censoring event occurred during stage t. Note that this means that δt−1 = 1 while δt = 0 and that . In this case the observed trajectories have the following structure: {S1, A1, S2, …, At} and C is also observed.
We now discuss the distribution of the observed trajectories. Assume that n trajectories are sampled at random according to a fixed distribution de-noted by P0. The distribution P0 is composed of the unknown distribution of each St conditional on (St−1, At−1) (denoted by {f1, …, fT}) and an exploration policy that generates the actions. Denote the exploration policy by p = {p1, …, pT} where the probability that action a is taken given history {St, At−1} is pt(a|St, At−1). We assume that pt(a|st, at−1) ≥ L−1 for every action a ∈
 and for each possible value (st, at−1), where L ≥ 1 is a constant. The likelihood (under P0) of the trajectory {s1, a1, s2, …, at, st̄+1} is
and for each possible value (st, at−1), where L ≥ 1 is a constant. The likelihood (under P0) of the trajectory {s1, a1, s2, …, at, st̄+1} is
We denote expectations with respect to the distribution P0 by E0. The survival time with respect to the distribution P0 is denoted by . We assume that G(τ) > Gmin > 0, i.e., that there is a positive probability that the survival time is greater than τ.
We define policy π to be a sequence of deterministic decision rules, {π1, …, πT}, where for every non-terminating pair (st, at−1), the output of the t-th decision rule, πt(st, at−1), is an action. Let the distribution P0,π denote the distribution of a trajectory for which the policy π is used to generate the actions. The likelihood (under P0, π) of the trajectory, {s1, a1, s2, …, at, st̄+1} is
Our goal is to find a policy that maximizes the expected rewards. Since with probability one C ≤ τ, the maximum observed survival time is less than or equal to τ. Thus we try to maximize the truncated-by-τ expected survival time. Formally, we look for a policy π̂ that approximates the maximum over all deterministic policies of the following expectation:
where E0,π is the expectation with respect to P0,π and a ∧ b = min{a, b}.
4. The Auxiliary Problem
In this section we construct an auxiliary Q-learning model for our original problem. The modified trajectories of the construction are of fixed length T, and the modified sum of rewards is less than or equal to τ. We then show how results obtained for the auxiliary problem can be translated into results regarding the original problem.
For the auxiliary problem, we complete all trajectories to full length in the following way. Assume that a failure time occurred at stage t < T. In that case the trajectory up to St+1 is already defined. Write
for 1 ≤ j ≤ t + 1 and
for 1 ≤ j ≤ t. For all t + 1 < j ≤ T + 1 set Sj = (∅, 0) and for all t + 1 ≤ j ≤ T draw Aj uniformly from
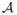 .
.
We also modify trajectories with overall survival time greater than τ in the following way. Assume that t is the first index for which
. For all j ≤ t, write
and
. Write
and assign
and thus the modified state
. If t < T, then for all t + 1 < j ≤ T + 1 set Sj = (∅, 0) and for all t + 1 ≤ j ≤ T draw
uniformly from
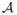 . The modified trajectory is given by the sequence {
}. Note that trajectories with fewer than 2T + 1 entries and for which
are modified twice.
. The modified trajectory is given by the sequence {
}. Note that trajectories with fewer than 2T + 1 entries and for which
are modified twice.
The n modified trajectories are distributed according to the fixed distribution P which can be obtained from P0. This distribution is composed of the unknown distribution of each conditional on ( ), denoted by { }, and exploration policy p′. The conditional distribution equals f1, and for 2 ≤ t ≤ T + 1,
| (5) |
where
and 1A is 1 if A is true and is 0 otherwise. The exploration policy p′ agrees with p on every pair (St, At−1) for which Zt ≠ ∅ and draws At uniformly from
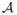 whenever Zt = ∅. The likelihood (under P) of the modified trajectory, {
}, is
whenever Zt = ∅. The likelihood (under P) of the modified trajectory, {
}, is
Denote expectations with respect to the distribution P by E.
Let π be a policy for the original problem. We define a version of the policy π′ for the auxiliary problem in the following way. For any state (
) for which
, the same action is chosen. For any state (
) for which
, a fixed action at ∈
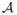 is chosen, w.o.l.g., let ao be chosen. For the auxiliary problem, we say that two policies
and
are equivalent if
for every (
) for which
. We denote both the original policy and any modified version of it by π whenever it is clear from the context which policy is considered. Similarly, we omit the prime from states and actions in the auxiliary problem whenever there is no reason for confusion.
is chosen, w.o.l.g., let ao be chosen. For the auxiliary problem, we say that two policies
and
are equivalent if
for every (
) for which
. We denote both the original policy and any modified version of it by π whenever it is clear from the context which policy is considered. Similarly, we omit the prime from states and actions in the auxiliary problem whenever there is no reason for confusion.
Let Pπ be the distribution in the auxiliary problem where actions are chosen according to π. The likelihood under Pπ of the trajectory {s1, a1, s2, …, aT, sT+1} is
Denote expectations with respect to the distribution Pπ by Eπ.
We now define the value functions and the Q-functions for policies in the auxiliary model. For any auxiliary policy π define its corresponding value function Vπ. Given an initial state s1, Vπ(s1) is the expected truncated-by-τ survival time when the initial state is s1 and the actions are chosen according to the policy π. Formally where the truncation takes place since the expectation is taken with respect to the distribution of the modified trajectories. The stage-t value function for the auxiliary policy π, Vπ,t(st, at−1), is the expected (truncated) remaining survival time from the t-th decision time-point, given the trajectory (st, at−1), and when following the policy π thereafter. Note, that given st, the survival time up to the beginning of stage t is known, and thus truncation ensures that the overall survival time is less than or equal to τ. Formally .
The stage-t Q-function for the auxiliary policy π is the expected remaining (truncated) survival time, given that the state is (st, at−1), that at is chosen at stage t, and that π is followed thereafter. Formally,
The optimal value function and the optimal Q-function are define by (2) and (3), respectively.
The following lemma relates the values of the value function Vπ in the auxiliary problem to the expected truncated-by-τ survival time for a policy π in the original problem.
Lemma 4.1
Let Π be the collection of all policies in the original problem. Then for all π ∈ Π, the following equalities hold true:
| (6) |
| (7) |
Proof
We start by decomposing the expectations depending on both the terminal stage and whether the sum of rewards is greater than or equal to τ.
Define
Denote
and similarly .
Note that
| (8) |
and
| (9) |
Note that
| (10) |
where the first equality follows from (5) and the second follows since there is a one to one correspondence between trajectories in Ft and , and by construction, for each such trajectory in we have and
Similarly we show that . Denote by Ĝt the set of all sequences (st, at) which are the beginning part of some trajectory in Gt. Note that
| (11) |
where the second equality follows from (5) and the third equality follows from the construction of .
The first assertion of the lemma, namely, equation (6), follows by substituting the right hand side of the equalities (10) and (11) in (8) for each t and comparing to (9).
The second assertion, (7), is proven by maximizing both sides of (6) over all policies. Note that the maximization is taken over two different sets since each policy in the original problem has an equivalent class of polices in the auxiliary problem. However, since Vπ is the same for all policies in the same equivalence class, the result follows.
5. The Censored-Q-Learning Algorithm
We now present the proposed censored-Q-learning algorithm. As discussed before, we are looking for a policy π̂ that approximates the maximum over all deterministic policies of the following expectation:
We find this policy in three steps. First, we map our problem to the corresponding auxiliary problem. Then we approximate the functions { } using backward recursion based on (3) and obtain the functions {Q̂1, …, Q̂T}. Finally, we define π̂ by maximizing Q̂t(st, (at−1, at)) over all possible actions at.
Let {
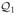 , …,
, …,
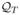 } be the approximation spaces for the Q-functions. We assume that Qt(st, at) = 0 whenever zt = ∅. In other words, if a failure occurred before the t-th-time-point, Qt equals zero.
} be the approximation spaces for the Q-functions. We assume that Qt(st, at) = 0 whenever zt = ∅. In other words, if a failure occurred before the t-th-time-point, Qt equals zero.
Note that by (3), the optimal t-stage Q-function equals the conditional expectation of given (st, at). Thus
Ideally, we could compute the functions Q̂t using backward recursion in the following way:
where
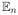 is the empirical expectation. The problem is that Rt may be censored and thus unknown.
is the empirical expectation. The problem is that Rt may be censored and thus unknown.
Note that and thus
since St includes the information regarding R1, …, Rt−1 and C is independent of the covariates and actions.
Thus, for every function Qt ∈
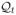 ,
,
| (12) |
Since is the minimizer of the first expression in the above sequence of equalities, it also minimize the last expression. Thus, we suggest to choose Q̂t recursively as follows:
| (13) |
where we define Q̂T+1 ≡ 0, and ŜC is the Kaplan-Meier estimator of the survival function of the censoring variable SC. Note that by Remark 3.1, the Kaplan-Meier estimator at x needs to estimate P(C ≥ x) rather than P(C > x). This can be done by taking left a continuous version of the Kaplan-Meier estimator that interchanges the roles of failure and censoring events for estimation (see Satten and Datta, 2001).
We define the policies π̂t using the approximated Q-functions Q̂t as follows:
6. Theoretical Results
Let {
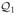 , …,
, …,
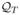 } be the approximation spaces for the minimization problems (13). Note that we do not assume that the problem is Markovian, but, instead, we assume that each Qt is a function of all the history up to and including stage t. Hence the spaces
} be the approximation spaces for the minimization problems (13). Note that we do not assume that the problem is Markovian, but, instead, we assume that each Qt is a function of all the history up to and including stage t. Hence the spaces
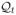 can be different over t.
can be different over t.
We assume that the absolute values of the functions in the spaces {
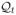 }t are bounded by some constant M. Moreover, we need to bound the complexity of the spaces {
}t are bounded by some constant M. Moreover, we need to bound the complexity of the spaces {
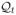 }t. We choose to use uniform entropy as the complexity measure (see van der Vaart and Wellner, 1996). This enables us to obtain exponential bounds on the difference between the true and empirical expectation of the loss function that involves a random component, namely, the Kaplan-Meier estimator, as in (13) (see Lemma A.6 ). This is different from Murphy (2005b) who uses the covering number as a measure of complexity (Anthony and Bartlett, 1999, pg 148) for the squared error loss function.
}t. We choose to use uniform entropy as the complexity measure (see van der Vaart and Wellner, 1996). This enables us to obtain exponential bounds on the difference between the true and empirical expectation of the loss function that involves a random component, namely, the Kaplan-Meier estimator, as in (13) (see Lemma A.6 ). This is different from Murphy (2005b) who uses the covering number as a measure of complexity (Anthony and Bartlett, 1999, pg 148) for the squared error loss function.
For every ε > 0 and measure P, we denote the covering number of
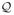 by N(ε,
by N(ε,
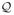 , L2(P )), where N (ε,
, L2(P )), where N (ε,
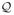 , L2(P )) is the minimal number of closed L2(P)-balls of radius ε required to cover
, L2(P )) is the minimal number of closed L2(P)-balls of radius ε required to cover
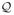 . The uniform covering number of
. The uniform covering number of
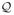 is defined as supP N (εM,
is defined as supP N (εM,
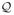 , L2(P )) where the supremum is taken over all finitely discrete probability measures P on
, L2(P )) where the supremum is taken over all finitely discrete probability measures P on
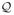 . The log of the uniform covering number is called the uniform entropy (van der Vaart and Wellner, 1996, page 84). We assume the following uniform entropy bound for the spaces {
. The log of the uniform covering number is called the uniform entropy (van der Vaart and Wellner, 1996, page 84). We assume the following uniform entropy bound for the spaces {
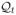 }:
}:
| (14) |
for all 0 < ε ≤ 1 and some constants 0 < W < 2 and D < ∞, where the supremum is taken over all finitely discrete probability measures, and M is the uniform bound defined above.
In the following, we prove a finite sample bound on the difference between the expected truncated survival times of an optimal policy and the policy π̂ obtained by the algorithm. As a corollary we obtain that the difference converges to zero under certain conditions.
The proof of the theorem consists of the following steps. First we use Lemma 4.1 to map the original problem to the corresponding auxiliary one. Second, for the auxiliary problem, we adapt arguments given in Murphy (2005b) to bound the difference between the expected value of the learned policy and the expected value of the optimal policy using error terms that involve expectations of both the learned and optimal Q-functions. Third, we bound these error terms by decomposing them to terms that arise due to the difference between the empirical and true expectation, terms that arise due the differences between the estimated and true censoring distribution, and terms that related to the empirical difference between the estimated and optimal Q-function. Fourth, and finally, we obtain a finite sample bound which depends on the complexity of the spaces {
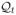 }, the deviation of the Kaplan-Meier estimator from the censoring distribution, and the size of the empirical errors in (13).
}, the deviation of the Kaplan-Meier estimator from the censoring distribution, and the size of the empirical errors in (13).
Theorem 6.1
Let {
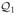 , …,
, …,
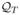 } be the approximation spaces for the Q-functions. Assume that the uniform entropy bound (14) holds. Assume that n trajectories are sampled according to P0. Let π̂ be defined by (4).
} be the approximation spaces for the Q-functions. Assume that the uniform entropy bound (14) holds. Assume that n trajectories are sampled according to P0. Let π̂ be defined by (4).
Then for any 0 < η < 1, we have with probability at least 1 − η, over the random sample of trajectories,
| (15) |
for all n that satisfies
where
and where M1 = (2M + τ)2, Co is the constant that appears in Bitouzé et al. (1999, Eq. 1), Ca, Cb, and U are the constants that appear in Lemma A.6, and for some αo small enough such that U + αo < 2.
Before we begin the proof of Theorem 6.1, we note that the bound (15) cannot be used in practice to perform structural risk minimization (see, for example, Vapnik, 1999) for two reasons. First, the bound itself is too loose (see also Murphy, 2005b, Theorem 1, Remark 4). Second, the constants, such as Ca and Cb, are not given, and are model dependent. Interestingly, a bound on Co was established recently by Wellner (2007). However, this bound is large and simulations suggest that it is not tight. The bound (15) can, however, be used to derive asymptotic rates (Steinwart and Chirstmann, 2008, Chapter 6). Moreover, when the functions
are in
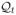 , we obtain universal consistency, as stated in the following corollary:
, we obtain universal consistency, as stated in the following corollary:
Corollary 6.2
Assume that the conditions of Theorem 6.1 hold. Assume also that for every t, . Then
Proof of Corollary 6.2
Note that for every t, Q̂t is the minimizer of
Hence, the second expression in the right hand side of (15) equals zero, and the result follows.
Proof of Theorem 6.1
By Lemma 4.1,
where the expectation on the right hand side of the equality is with respect to the modified distribution P.
By Lemma 2 of Murphy (2005b) and Remark 2 that follows, for every state so ∈
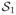 ,
,
Applying Jensen’s inequality, we obtain
| (16) |
We wish to obtain a bound on the expression using the expressions , where
for any pair of function Qt and Qt+1. To obtain this bound we follow the line of arguments that leads to the bound in Eq. 13 in the proof of Theorem 1 of Murphy (2005b). The bound (19) obtained here is tighter since only the special case of in the second Err function is considered. To simplify the following expressions, we write Qt instead of Qt(St, At) whenever no confusion could occur.
For each t,
| (17) |
where the second to the last equality follows since
Using the Cauchy-Schwarz inequality for the second expression of (17), we obtain
Note that
| (18) |
where the first inequality follows since (maxa h(a) −maxa h′(a))2 ≤ maxa(h(a) −h′(a))2 and where L is the constant that appears in the definition of the exploration policy p (see Section 3).
Using inequality (18) and the fact that , we obtain
Hence
Using the fact that we obtain
| (19) |
We are now ready to bound the expressions
. For any
, Qt+1 ∈
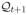 , and censoring survival function K: [0, τ] ↦ [Kmin, 1], where Kmin > 0, define
, and censoring survival function K: [0, τ] ↦ [Kmin, 1], where Kmin > 0, define
| (20) |
Note that similarly to (12) we have ErrQ̂t+1(Qt) = ε(Qt, Q̂t+1, SC), where SC is the censoring survival function.
Using this notation we have
where ŜC is the Kaplan-Meier estimator of SC, and (a)+ = max{a, 0}. Hence
| (21) |
| (22) |
| (23) |
Combining (19) and (21), and substituting in (16), we have
| (24) |
| (25) |
where we used the fact that for L ≥ 2 and the fact that .
In the following, we replace the bounds in (24) and (25)) with exponential bounds. We start with (24). Note that (Rt + maxat+1 Qt+1(St+1, At, at+1) − Qt)2 ≤ M1 = (2M + τ)2 for all Qt, Qt+1. Hence,
, and thus
| (26) |
where the first equality follows from the fact that
| (27) |
Using a Dvoretzky-Kiefer-Wolfowitz-type inequality for the Kaplan-Meier estimator (Bitouzé et al., 1999, Theorem 2), we have
| (28) |
where Co is some universal constant and Gmin is a lower bound on the survival function at τ (see Section 3).
Write , and thus . Note that . Applying the inequality (28) to the right hand-side of (26) and substituting for ε, we obtain
| (29) |
where and .
We now find an exponential bound for (25). We follow the same line of arguments, replacing the Dvoretzky-Kiefer-Wolfowitz type inequality used in the previous proof with the uniform entropy bound. Recall that by assumption, the uniform entropy bound (14) holds for the spaces
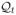 t and thus also for the spaces
. Hence, by Lemma A.6, and (27), for W′ = max{W, 1} and for all α > 0, we have
t and thus also for the spaces
. Hence, by Lemma A.6, and (27), for W′ = max{W, 1} and for all α > 0, we have
| (30) |
where C3 = Ca exp{(4L)−(T+1)}, C4 = Cb(4L)(T+1)/2, and U = W′(6 − W′)/(2 + W′).
Take n large enough such that the right hand side of (29) and (30) are less than η/2 and substitute in (24) and (25), respectively, and the result of the theorem follows.
7. Simulation Study
We simulate a randomized clinical trial with flexible number of stages to examine the performance of the proposed censored Q-learning algorithm. We compare the estimated individualized treatment policy to various possible fixed treatments. We also compare the given expected survival times of different censoring levels. Finally, we test the effect of ignoring the censoring.
This section is organized as follows. We first describe the setting of the simulated clinical trial (Section 7.1). We then describe the implementation of the simulation (Section 7.2). The simulation results appear in Section 7.3.
7.1. Simulated Clinical Trial
We consider the following hypothetical cancer trial. The duration of the trial is 3 years. The state of each patient at each time-point u ∈ [0, 3] includes the tumor size (0 ≤ T(u) ≤ 1), and the wellness (0.25 ≤ W(u) ≤ 1). The time-point uo such that W(uo) < 0.25 is considered the failure time. We define the critical tumor size to be 1. At time ui such that T(ui) = 1, we begin a treatment. We call the duration [ui, ui+1] the i-th stage. Note that different patients may have different numbers of stages.
At each time-point ui, we consider two optional treatments: a more aggressive treatment (A), and a less aggressive treatment (B). The immediate effects of treatment A are
| (31) |
i.e., the wellness at time ui after treatment A (denoted by ) decreases by 0.5 wellness units. The tumor size at time ui after treatment A (denoted by ) decreases by a factor of 1=(10W (ui)) which reflects a greater decrease of tumor size for a larger wellness value. Similarly, the immediate effects of the less aggressive treatment B are
| (32) |
which, in comparison to the treatment A, has lower effect on the tumor size but also lower decrease of wellness. The wellness and tumor size at time ui < u ≤ ui+1 follows the dynamics
| (33) |
The stage that begins at time-point ui ends when either T(ui+1) = 1 for some ui < ui+1 < 3 or when a failure event occurs or at the end of the trial when u = 3. During this stage, we model the survival function of the patient as an exponential distribution with mean .
The trajectories are constructed as follows. We assume that patients are recruited to the trial when their tumor size reaches the critical size, i.e., for all patients T(0) = 1, and hence u1 = 0 is the beginning of the first stage. The wellness at the beginning of the first stage, W(0), is uniformly distributed on the segment [0.5, 1]. With equal probability, a treatment a1 ∈ {A, B} is chosen. If no failure event occurs during the first stage, the first stage ends when either T(u2) = 1 for some 0 = u1 < u2 < 3 or at the end of the trial. If the first stage ends before the end of the trial, then with equal probability another treatment a2 ∈ {A, B} is chosen. The trial continues in the same way until either a failure time occurs or the trial ends. We note that the actual number of stages for each patient is a random function of the initial state and the treatments chosen during the trial. Due to the choices of model parameters, the number of stages in the above dynamics is at least one and not more than three.
For each trajectory, a censoring variable C is uniformly drawn from the segment [0, c] for some constant c > 3, where the choice of the constant c determines the expected percentage of censoring. When an event is censored, the trajectory (i.e., the states and treatments) up to the point of censoring and the censoring time are given.
7.2. Simulation Implementation
The Q-learning algorithm presented in Section 5 was implemented in the Matlab environment. For the implementation we used the Spider library for Matlab1. The Matlab code, as well as the data sets, are available online (see Supplement A).
The algorithm is implemented as follows. The input for the algorithm is a set of trajectories obtained according to the dynamics described in Section 7.1. First, the Kaplan-Meier estimator for the survival function of the censoring variable is computed from the given trajectories. Then, we set Q̂4 ≡ 0 and compute Q̂i, i = 3, 2, 1 backwardly, as the minimizer of (13) over all the functions Qi(si, ai) which are linear in the first variable. The policy π̂ is computed from the functions {Q̂1, Q̂2, Q̂3} using (4).
We tested the policy π̂ = (π̂1, π̂2, π̂3) by constructing 1000 new trajectories, in which the choice of treatment at each stage is according to π̂. 1000 initial wellness values were drawn uniformly from the segment [0.5, 1]. For each wellness value, a treatment was chosen from the set {A, B}, according to the policy π̂1. The immediate effect of the treatment was computed according to (31)–(32). A failure time was drawn from the exponential distribution with mean as described in the previous section; denote this time by f1. The time that the tumor reached the critical size was computed according to the dynamics (33), and we denote this time by u2. If both f1 and u2 are greater than 3 (the end of the trial) then the trajectory was ended after the first stage and the survival time for this patient was given as 3. Otherwise, if f1 ≤ u2, the trajectory is ended after the first stage and the survival time for this patient was given as f1. If u2 < f1, then at time u2, a second treatment is chosen according to the policy π̂2. The computation of the reminder of the trajectory is done similarly. The expected value of the policy π̂ is estimated by the mean of the survival time of all 1000 patients.
We compared the results of the algorithm to all fixed treatment sequences A1A2A3, where Ai ∈ {A, B}. The expected values of the fixed treatment sequences were computed explicitly. We also compared the results to that of the optimal policy, which was also computed explicitly.
7.3. Simulation and Results
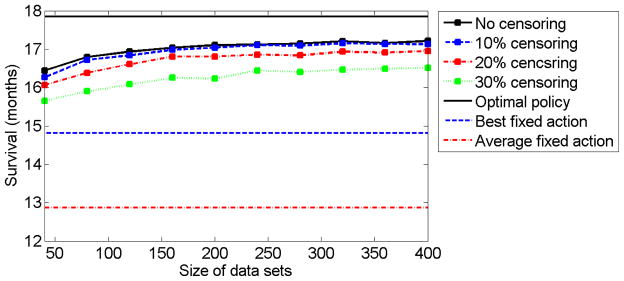
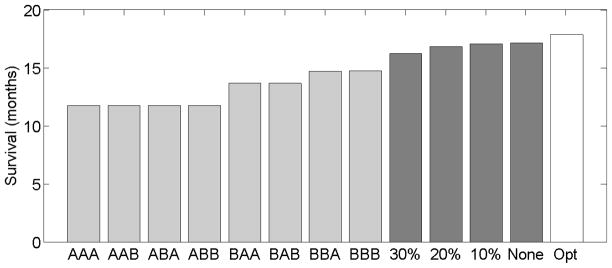
First, we would like to examine the influence of the sample size and censoring percentage on the algorithm’s performance. We simulated data sets of trajectories of sizes 40, 80, 120, …, 400. For each set of trajectories we considered four levels of censoring: no censoring, 10%-censoring, 20%-censoring, and 30%-censoring. Higher levels of (uniform) censoring were not considered since this requires drawing the censoring variable from a segment [0, c] for c < 3, which is in contrast to the assumption on the censoring variable (see the beginning of section 3). A policy π̂ was computed for each combination of data set size and censoring percentage. The policy π̂ was evaluated on a data set of size 1000, as described in Section 7.2. We repeated the simulation 400 times for each combination of data set size and censoring percentage. The mean values of the estimated mean survival time are presented in Figure 1. A comparison between the different fixed policies, polices obtained by the algorithm for different censoring levels, and the optimal policy appears in Figure 2. As can be seen from both figures, the individualized treatment polices obtained by the algorithm are better than any fixed policy. Moreover, as the number of observed trajectories increases, the expected survival time increases, for all censoring percentages.
Fig 1.
The solid black curve, dashed blue curve, dot-dashed red curve, and dotted green curve correspond to the expected survival time (in months) for different data set sizes with no censoring, 10% censoring, 20% censoring, and 30% censoring, respectively. The expected survival time was computed as the mean of 400 repetitions of the simulation. The black straight line, blue dashed straight line, and the dot-dashed red straight line correspond to the expected survival times of the optimal policy, the best fixed treatment policy, and the average of the fixed treatment policies, respectively.
Fig 2.
The eight light gray bars represent the expected survival times for different fixed treatments where A1A2A3 indicates the policy that chooses Ai at the i-th stage. The four dark gray bars represent the expected survival times for policy π̂ obtained by the algorithm with no censoring, 10% censoring, 20% censoring, and 30% censoring. The white bar is the expected value of the optimal policy. The values of the fixed treatments and the optimal policy were computed analytically while the values of π̂ are the means of 400 repetitions of the simulation on 200 trajectories.
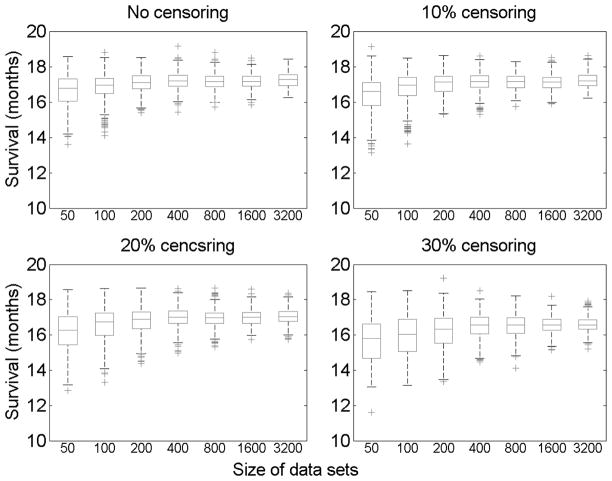
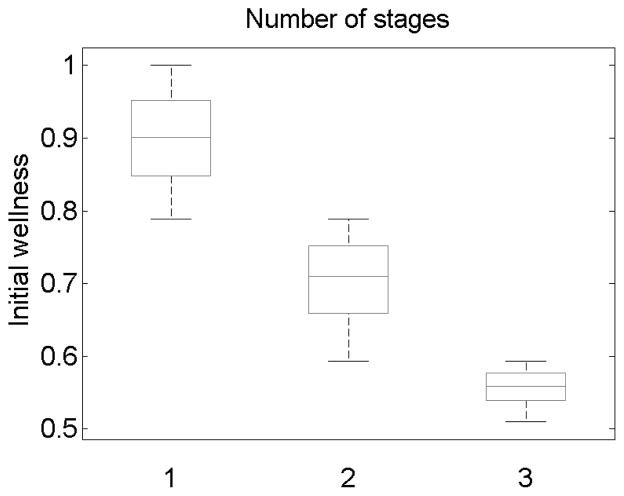
We also examined the influence of the sample size and censoring percentage on the distribution of estimated expected survival time. We simulated data sets of sizes 50, 100, 200, …, 3200 and we considered the four levels of censoring as before. As can be seen from Figure 3, the variance decreases when the sample size becomes larger. Also, the variance is smaller for smaller percentage of censoring, although the difference is modest.
Fig 3.
Distribution of expected survival time (in months) for different data set sizes, with no censoring, 10% censoring, 20% censoring, and 30% censoring. Each box plot is based on 400 repetitions of the simulation for each given data set size and censoring percentage.
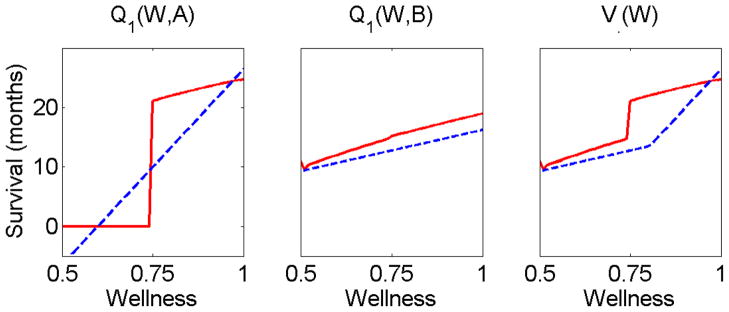
Note that the maximum expected survival times obtained by the algorithm are a little bit above 17 months (see both Figures 1 and 2), while the value of the optimal policy is 17.85. The difference follows from the fact that the Q-functions estimated by the algorithm are linear while the optimal Q-function is not (see Figure 4). It is worth mentioning that even in the class of linear functions on which the optimization is done there are Q-functions that yield higher values. This fact is often referred to as the “mismatch” that follows from the fact that optimization of the value function is not performed explicitly, but rather through optimization of the Q-functions (see Tsitsiklis and van Roy, 1996; Murphy, 2005b, for more details).
Fig 4.
The Q-functions computed by the proposed algorithm for a size 200 trajectory set. The left panel presents both the optimal Q-function (solid red curve) and the estimated Q-function (dashed blue curve) for different wellness levels and when treatment A is chosen. Similarly, the middle panel shows both Q-functions when treatment B is chosen. The right panel shows the optimal value function (solid red curve) and the estimated value function (dashed blue curve).
Figure 5 shows the number of treatments that were needed for patients that followed the policy π̂ and did not have a failure event during the trial. As can be seen from this figure, patients with high initial wellness need only one treatment. On the other hand, patients with very low initial wellness value need three treatments.
Fig 5.
The number of required treatments for patients that follow the policy π̂, when no failure event occurs during the trial. The policy π̂ was estimated from 100 trajectories. The results were computed using a size 100, 000 testing set.
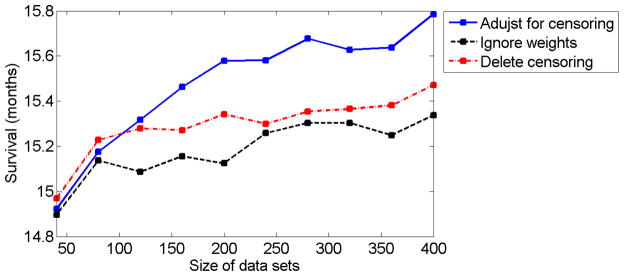
Finally, we checked the effect of ignoring the censoring on the expected survival time. We considered two ways of ignoring the censoring. First, we consider an algorithm that ignores the weights in the minimization problem (13). This is equivalent to deleting the last stage from each trajectory that was censored. We also consider an algorithm that deletes all censored trajectories. In the example presented in Figures 1–5, where uniform censoring takes place, there is a relatively moderate difference between the expected survival time for the proposed algorithm and the other two algorithms that ignore censoring. However, when the censoring variable follows the exponential distribution (leaving fewer observations with longer survival times) the bias from ignoring the censored trajectories is substantial, as can be seen in Figure 6.
Fig 6.
The solid blue curve, dashed black curve, and dot-dashed red curve correspond to the expected survival times (in months) for different data set sizes, for the proposed algorithm, the algorithm that ignores the weights, and the algorithm that deletes all censored trajectories, respectively. The censoring variable follows the exponential distribution with 50% censoring on average. The expected survival time was computed as the mean of 400 repetitions of the simulation.
8. Summary
We studied a framework for multistage-decision problems with flexible number of stages in which the rewards are survival times and are subject to censoring. We proposed a novel Q-learning algorithm adjusted for censoring. We derived the generalization error properties of the algorithm and demonstrated the algorithm performance using simulations.
The work as presented is applicable to real-world multi-stage decision problems with censoring. However, two main issues should be noted. First, we assumed that censoring is independent of observed trajectories. It would be useful to relax this assumption and allow censoring to depend on the covariates. Developing an algorithm that works under this relaxed assumption is a challenge. Second, we have used the inverse-probability-of-censoring weighting to correct the bias induced by censoring. When the percentage of censored trajectories is large, the algorithm may be inefficient. Finding a more efficient algorithm is also an open question.
Supplementary Material
APPENDIX A: SUPPLEMENTARY PROOFS
The main goal of this section is to provide an exponential bound on the difference between the empirical expectation
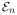 (Qt, Qt+1, K) and the true expectation
(Qt, Qt+1, K) and the true expectation
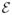 (Qt, Qt+1, K) as a function of the uniform entropy of the class of functions (see (20)). This result appears in Lemma A.6. Similar results for Glivenko–Cantelli classes, Donsker classes, and bounded uniform entropy integral (BUEI) classes can be found in van der Vaart and Wellner (1996) and Kosorok (2008).
(Qt, Qt+1, K) as a function of the uniform entropy of the class of functions (see (20)). This result appears in Lemma A.6. Similar results for Glivenko–Cantelli classes, Donsker classes, and bounded uniform entropy integral (BUEI) classes can be found in van der Vaart and Wellner (1996) and Kosorok (2008).
Lemma A.1
Let
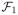 , …,
, …,
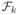 be k sets of functions. Assume that for every j ∈ {1, …, k}, supf∈
be k sets of functions. Assume that for every j ∈ {1, …, k}, supf∈
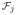 ||f||∞ ≤ Mj. Let φ : ℝk ↦ ℝ satisfy
||f||∞ ≤ Mj. Let φ : ℝk ↦ ℝ satisfy
| (34) |
for every f = (f1, …, fk), g = (g1, …, gk) ∈
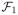 × … ×
× … ×
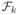 , where 0 < c < ∞. Let P be a finitely discrete probability measure. Define φ ∘ (
, where 0 < c < ∞. Let P be a finitely discrete probability measure. Define φ ∘ (
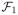 , …,
, …,
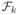 ) = {φ(f1, …, fk) : (f1, …, fk) ∈
) = {φ(f1, …, fk) : (f1, …, fk) ∈
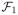 × … ×
× … ×
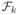 }. Then
}. Then
| (35) |
Proof
The proof is similar to the proof of Kosorok (2008, Lemma 9.13). Let f, g ∈
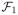 × … ×
× … ×
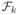 satisfy ||fj − gj||P,2 < εMj for 1 ≤ j ≤ k. Note that
satisfy ||fj − gj||P,2 < εMj for 1 ≤ j ≤ k. Note that
which implies (35).
The following two corollaries are direct result of Lemma A.1:
Corollary A.2
Let
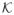 = {K : K is monotone decreasing K : [0, τ] ↦ [Kmin, 1]}. Define
= {K : K is monotone decreasing K : [0, τ] ↦ [Kmin, 1]}. Define
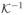 = {1/K : K ∈
= {1/K : K ∈
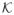 }. Let P be a finitely discrete probability measure. Then
}. Let P be a finitely discrete probability measure. Then
Proof
Note that inequality (34) holds for k = 1 and , and the results follow from Lemma A.1.
Corollary A.3
Let
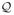 = {Q(x, a) : x ∈ ℝp, a ∈ {1, …, k}, ||Q||∞ ≤ M}. Define
= {Q(x, a) : x ∈ ℝp, a ∈ {1, …, k}, ||Q||∞ ≤ M}. Define
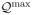 = {maxa Q(x, a) : Q ∈
= {maxa Q(x, a) : Q ∈
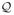 }. Let P be a finitely discrete probability measure. Then
}. Let P be a finitely discrete probability measure. Then
Proof
Since (maxa h(a) − maxa h′(a))2 ≤ maxa(h(a) − h′(a))2, inequality (34) holds for c = 1. The results now follow from Lemma A.1.
We also need the following lemma and its corollary:
Lemma A.4
Let
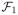 and F2 be two function classes uniformly bounded in absolute value by M1 and M2, respectively. Define
and F2 be two function classes uniformly bounded in absolute value by M1 and M2, respectively. Define
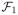 ·
·
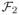 = {f1·f2 : fi ∈
= {f1·f2 : fi ∈
 }. Then
}. Then
Proof
Let ||fj −gj||P,2 ≤ εMj where fj, gj ∈
 , j = {1, 2}. Note that
, j = {1, 2}. Note that
The result follows.
Corollary A.5
Let
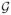 be a function class uniformly bounded in absolute value by M. Define
be a function class uniformly bounded in absolute value by M. Define
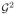 = {g2 : g ∈
= {g2 : g ∈
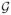 }. Then
}. Then
Proof
Apply Lemma A.4 with
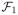 =
=
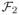 =
=
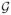 .
.
We use the previous results to prove the following lemma:
Lemma A.6
Let
where t ∈ 1, …, T and
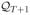 = {0}. Assume that the uniform entropy bound for each of the spaces
= {0}. Assume that the uniform entropy bound for each of the spaces
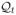 (14) holds. Then
(14) holds. Then
-
1
There are constants D′ and W′ such that , where W′ = max{W, 1}.
-
2For every α > 0 and t > 0,
where U = W′(6−W′)/(2+W′), the constants Ca and Cb depend only on D′, W′ and α, and where P* is outer probability.
Proof
Let W′ = max{W, 1}. Note that uniform entropy bound (14) for the spaces
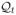 holds also for W′. Note that by Corollary A.3,
. Since (x+y+z)2 < 3(x2+y2+z2), we can apply Lemma A.1 to the class
holds also for W′. Note that by Corollary A.3,
. Since (x+y+z)2 < 3(x2+y2+z2), we can apply Lemma A.1 to the class
with and φ(x, y, z) = x+y+z to obtain , where we used the fact that the segment [0, τ] can be covered by no more than τ/ε+1 balls of radius ε and that log(1+τ/ε) ≤ τ/ε. By Corollary A.5, we have or, equivalently,
where M1 = (2M +τ)2 is a uniform bound for
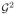 , and D1 = 2(τ+DkW′+1+ D)6−W′.
, and D1 = 2(τ+DkW′+1+ D)6−W′.
By Kosorok (2008, Lemma 9.11), log N(ε,
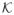 , L2(P)) ≤ D2ε−1 for some universal constant D2 which is independent of the choice of probability measure P. By Corollary A.2,
, L2(P)) ≤ D2ε−1 for some universal constant D2 which is independent of the choice of probability measure P. By Corollary A.2,
Applying Lemma A.4 to
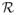 =
=
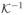 ·
·
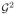 , we obtain
, we obtain
Since this inequality holds for every finitely discrete probability measures P, assertion 1 is proved. The second assertion follows from van der Vaart and Wellner (1996, Theorem 2.14.10).
Footnotes
The Spider library for Matlab can be downloaded form http://www.kyb.tuebingen.mpg.de/bs/people/spider/
Supplement A: Code and data sets
(). Please read the file README.pdf for details on the files in this folder.
Contributor Information
Yair Goldberg, Email: ygoldber@bios.unc.edu.
Michael R. Kosorok, Email: kosorok@unc.edu.
References
- Anthony M, Bartlett PL. Neural Network Learning: Theoretical Foundations. Cambridge University Press; 1999. [Google Scholar]
- Bellman R. Dynamic Programming. Princeton University Press; 1957. [Google Scholar]
- Biganzoli E, Boracchi P, Mariani L, Marubini E. Feed forward neural networks for the analysis of censored survival data: A partial logistic regression approach. Statist Med. 1998;17:1169–1186. doi: 10.1002/(sici)1097-0258(19980530)17:10<1169::aid-sim796>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- Bitouzé D, Laurent B, Massart P. A Dvoretzky-Kiefer-Wolfowitz type inequality for the Kaplan-Meier estimator. Ann Inst H Poincaré Probab Statist. 1999;35:735–763. [Google Scholar]
- Chen P, Tsiatis AA. Causal inference on the difference of the restricted mean lifetime between two groups. Biometrics. 2001;57:1030–1038. doi: 10.1111/j.0006-341x.2001.01030.x. [DOI] [PubMed] [Google Scholar]
- Goldberg Y, Kosorok MR, Lin DY. Unpublished manuscript. 2011. Support vector regression under right censoring. [Google Scholar]
- Karrison TG. Use of Irwin’s restricted mean as an index for comparing survival in different treatment groups–Interpretation and power considerations. Controlled Clinical Trials. 1997;18:151–167. doi: 10.1016/s0197-2456(96)00089-x. [DOI] [PubMed] [Google Scholar]
- Kosorok MR. Introduction to Empirical Processes and Semiparametric Inference. Springer; New York: 2008. [Google Scholar]
- Krzakowski M, Ramlau R, Jassem J, Szczesna A, Zatloukal P, Von Pawel J, Sun X, Bennouna J, Santoro A, Biesma B, Delgado FM, Salhi Y, Vaissiere N, Hansen O, Tan E, Quoix E, Garrido P, Douillard J. Phase III trial comparing Vinflunine with Docetaxel in second-line advanced nonsmall-cell lung cancer previously treated with platinum-containing chemotherapy. Journal of Clinical Oncology. 2010;28:2167–2173. doi: 10.1200/JCO.2009.23.4146. [DOI] [PubMed] [Google Scholar]
- Laan MJvd, Petersen ML. Causal effect models for realistic individualized treatment and intention to treat rules. The International Journal of Biostatistics. 2007;3:3. doi: 10.2202/1557-4679.1022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laber E, Qian M, Lizotte DJ, Murphy SA. Statistical inference in dynamic treatment regimes. 2010 Avaliable at http://arxiv.org/abs/1006.5831.
- Lavori PW, Dawson R. Dynamic treatment regimes: Practical design considerations. Clinical Trials. 2004;1:9–20. doi: 10.1191/1740774s04cn002oa. [DOI] [PubMed] [Google Scholar]
- Lunceford JK, Davidian M, Tsiatis AA. Estimation of survival distributions of treatment policies in two-stage randomization designs in clinical trials. Biometrics. 2002;58:48–57. doi: 10.1111/j.0006-341x.2002.00048.x. [DOI] [PubMed] [Google Scholar]
- Miyahara S, Wahed AS. Weighted Kaplan-Meier estimators for two-stage treatment regimes. Statistics in medicine. 2010 doi: 10.1002/sim.4020. [DOI] [PubMed] [Google Scholar]
- Moodie EEM, Richardson TS, Stephens DA. Demystifying optimal dynamic treatment regimes. Biometrics. 2007;63:447–455. doi: 10.1111/j.1541-0420.2006.00686.x. [DOI] [PubMed] [Google Scholar]
- Murphy SA. Optimal dynamic treatment regimes. Journal of the Royal Statistical Society Series B (Statistical Methodology) 2003;65:331–366. [Google Scholar]
- Murphy SA. An experimental design for the development of adaptive treatment strategies. Statistics in medicine. 2005a;24:1455–1481. doi: 10.1002/sim.2022. [DOI] [PubMed] [Google Scholar]
- Murphy SA. A generalization error for Q-learning. Journal of Machine Learning Research. 2005b;6:1073–1097. [PMC free article] [PubMed] [Google Scholar]
- Murphy SA, Oslin DW, Rush AJ, Zhu J. Methodological challenges in constructing effective treatment sequences for chronic psychiatric disorders. Neuropsychopharmacology. 2006;32:257–262. doi: 10.1038/sj.npp.1301241. [DOI] [PubMed] [Google Scholar]
- Orellana L, Rotnitzky A, Robins JM. Dynamic regime marginal structural mean models for estimation of optimal dynamic treatment regimes, Part I: Main content. The International Journal of Biostatistics. 2010:6. [PubMed] [Google Scholar]
- Robins J, Orellana L, Rotnitzky A. Estimation and extrapolation of optimal treatment and testing strategies. Statist Med. 2008;27:4678–4721. doi: 10.1002/sim.3301. [DOI] [PubMed] [Google Scholar]
- Robins JM. Association, causation, and marginal structural models. Synthese. 1999;121:151–179. [Google Scholar]
- Robins JM. Optimal structural nested models for optimal sequential decisions. In: Lin D, Heagerty PJ, editors. Proceedings of the Second Seattle Symposium in Biostatistics Proceedings of the Second Seattle Symposium in Biostatistics. 2004. pp. 189–326. [Google Scholar]
- Robins JM, Rotnitzky A, Zhao LP. Estimation of regression coefficients when some regressors are not always observed. Journal of the American Statistical Association. 1994:89. [Google Scholar]
- Satten GA, Datta S. The Kaplan-Meier estimator as an inverse-probability-of-censoring weighted average. The American Statistician. 2001;55:207–210. doi: 10.1198/000313001317098185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shim J, Hwang C. Support vector censored quantile regression under random censoring. Comput Stat Data Anal. 2009;53:912–919. [Google Scholar]
- Shivaswamy PCW, Jansche M. A support vector approach to censored targets. Data Mining, 2007 ICDM 2007; Seventh IEEE International Conference on; 2007. pp. 655–660. [Google Scholar]
- Steinwart I, Chirstmann A. Support Vector Machines. Springer; 2008. [Google Scholar]
- Stinchcombe TE, Socinski MA. Considerations for second-line therapy of non-small cell lung cancer. Oncologist. 2008;13:28–36. doi: 10.1634/theoncologist.13-S1-28. [DOI] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Reinforcement Learning: An Introduction. MIT Press; 1998. [Google Scholar]
- Thall PF, Wooten LH, Logothetis CJ, Millikan RE, Tannir NM. Bayesian and frequentist two-stage treatment strategies based on sequential failure times subject to interval censoring. Statist Med. 2007;26:4687–4702. doi: 10.1002/sim.2894. [DOI] [PubMed] [Google Scholar]
- TSITSIKLIS JN, van Roy B. Feature-based methods for large scale dynamic programming. Machine Learning. 1996;22:59–94. [Google Scholar]
- van der VAART AW, WELLNER JA. Weak Convergence and Empirical Processes: With Applications to Statistics. Springer; 1996. [Google Scholar]
- VAPNIK V. The Nature of Statistical Learning Theory. 2. Springer; 1999. [DOI] [PubMed] [Google Scholar]
- WAHED AS. Estimation of survival quantiles in two-stage randomization designs. Journal of Statistical Planning and Inference. 2009:139. [Google Scholar]
- WAHED AS, TSIATIS AA. Semiparametric efficient estimation of survival distributions in two-stage randomization designs in clinical trials with censored data. Biometrika. 2006;93:163–177. [Google Scholar]
- WATKINS CJCH. PhD thesis. Cambridge University; 1989. Learning from Delayed Rewards. [Google Scholar]
- WATKINS CJCH, DAYAN P. Q-learning. Machine Learning. 1992;8:279–292. [Google Scholar]
- WELLNER J. On an exponential bound for the KaplanMeier estimator. Lifetime Data Analysis. 2007;13:481–496. doi: 10.1007/s10985-007-9055-z. [DOI] [PubMed] [Google Scholar]
- ZHAO Y, KOSOROK MR, ZD, SMA Reinforcement learning strategies for clincal trials in non-small cell lung cancer. The University of North Carolina at Chapel Hill Department of Biostatistics Technical Report Series. 2010 Working Paper 13. Avaliable at http://biostats.bepress.com/uncbiostat/papers/art13.
- ZHAO Y, KOSOROK MR, ZENG D. Reinforcement learning design for cancer clinical trials. Statistics in Medicine. 2009;28:3294–3315. doi: 10.1002/sim.3720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ZUCKER DM. Restricted mean life with covariates: Modification and extension of a useful survival analysis method. Journal of the American Statistical Association. 1998;93:702–709. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.