A Novel Method for Determining the Inhibitory Potential of Anti-HIV Drugs

Abstract

In the absence of a cure, most HIV-1-infected individuals will require life-long treatment. It is therefore essential to optimize highly active antiretroviral therapy. Recent research has shown that the slope parameter or Hill coefficient, which describes the steepness of a dose-response curve, is a critical missing dimension in the evaluation of antiviral drug activity. Based on this finding, the instantaneous inhibitory potential (IIP) has been derived as a new measure of antiviral drug activity. IIP incorporates the slope parameter and thus is a more accurate pharmacodynamic measure of antiviral activity than current measures such as IC₅₀ and inhibitory quotient. However, it remains important to determine how to use IIP to predict the in vivo efficacy of anti-HIV-1 drugs. This article discusses recent advances in in vitro measures of antiviral activity and the therapeutic implications of the dose-response curve slope and IIP.

Introduction

There are approximately 33 million people currently infected with HIV-1, making this one of the major public health problems worldwide [1]. In the absence of antiviral drugs, HIV-1 replicates continuously at high rate in CD4⁺ T lymphocytes, setting in motion a complex chain of events that cause gradual depletion of CD4⁺ T lymphocytes, immunodeficiency, and eventually death from opportunistic infections. Since the introduction of highly active antiretroviral therapy (HAART) in 1997 [2–4], morbidity and mortality from HIV-1 infection have markedly decreased. Although it was originally hoped that HAART would cure the infection [4], it is now clear that eradication is an unrealistic goal. A stable reservoir of HIV-1 in resting memory CD4⁺ T cells presents one major barrier to eradication [5–7]. Therefore, treatment is a lifelong challenge, and the correct choice of antiretroviral drugs is crucial for achieving and maintaining suppression of viral replication. Other major problems include drug toxicity [8–10] and the evolution of drug resistance [11–13]. Some of the most important therapeutic challenges are how to evaluate drug efficacy in vitro and in vivo, and how to use this information to guide treatment and achieve lifetime control of viral replication with minimal side effects.

Data from randomized clinical trials have been the gold standard for evaluating the efficacy of HAART regimens [14, 15]. Although these trials have proven useful in guiding the choice of regimens for treatment-naive patients, the choice of salvage regimens for patients for whom therapy is failing is difficult and often involves educated guesswork based on genotypic and phenotypic analysis of viral variants present in individual patients. Because of the close correlation between genotype and phenotype, physicians can use genotypic information to predict the residual activity of a drug when there are only a few resistance mutations present [16–18]. For patients with complex patterns of resistance, commercial phenotypic assays provide a direct measure of the “fold change” in drug potency [19, 20].

In principle, the in vivo efficacy of a regimen could be evaluated by considering the relationship between the amount of viral replication occurring in a patient and the degree of inhibition of replication produced by the drugs. A regimen is likely to halt viral replication if it can block all of the new infection events occurring in one viral generation. Based on the classical model of viral dynamics [21, 22], it can be estimated that the number of new infection events per generation is on the order of 10⁶ (range 10⁵~5×10⁷) for a patient with a typical set point viral load of 30,000 copies/ml (Box 1, equation 1). This means that HAART must produce a 6 log reduction in infection events in a single round in order to immediately halt viral replication in the average patient.

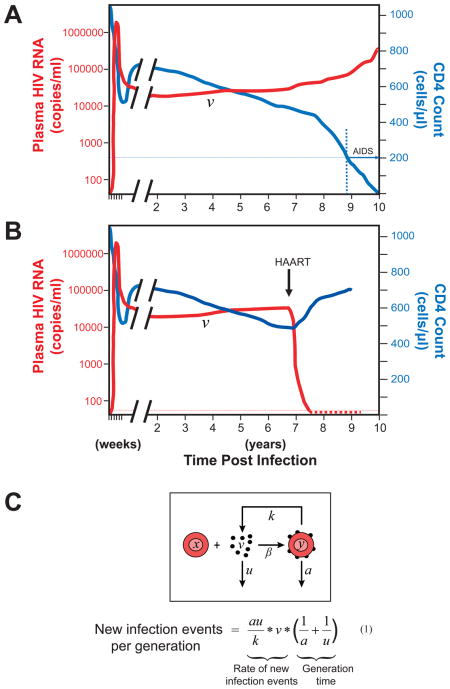
Box 1. HIV-1 pathogenesis and viral dynamics [21, 22].

During the first weeks after exposure, the virus replicates rapidly and produces a high level of viremia (Figure A). As the immune response develops, viremia falls to a steady state or “set point” level (v), typically 10,000–100,000 viral genomes/ml of plasma. The virus continues to replicate at this level throughout the asymptomatic phase of the illness. During this period, there is graduate depletion of CD4⁺ T cells driven by virus-induced immune activation. When the CD4 count falls below 200 cells/μl, opportunistic infections develop and the patient is considered to have AIDS. In patients who start on HAART and remain adherent (Figure B), viremia decays rapidly to below the limit of detection of clinical assays (50 copies of HIV-1 RNA/ml), and CD4 counts increase.

In order for HAART to produce an immediate and complete block in viral replication, it must achieve a degree of inhibition that is comparable to or greater than the number of new infection events per viral generation. The number of new infection events can be estimated using the classical model of viral dynamics (Figure C) [21, 22], in which uninfected cells (x) interact with free virus (v) and become infected at a rate determined by the concentration of each and the rate constant β. The productively infected cells produce virus at rate k, and free virus and productively infected cells both decay exponentially with the rate constants u and a, respectively. The rate at which newly infected cells arise is given by βxv. From the steady state relationships βxv=ay and ky=uv, it can be seen that βxv=auv/k. The values of a and u are known [21]. k can be estimated from the range of reported values for the burst size N and the relationship N = k/a, where burst size is the number of virus generated per infected cell [25–27]. The maximal time for one viral generation can be estimated as (1/a + 1/u) [21]. Thus, the total body number of newly infected cells per viral generation can be estimated from the viral load and the constants u, a, and k by multiplying the rate at which new infection events occur and the time for one viral generation as shown in equation 1. Values must be adjusted for extracellular fluid volume (~15 L). Based on reported estimates of a, u, and k [21, 23–27], the number of new infection events per generation is on the order of 10⁶ (range 10⁵~5×10⁷) for a patient with a typical set point viral load of 30,000 copies/ml.

Neither the standard pharmacodynamic measures such as IC₅₀ and inhibitory quotient (IQ=clinical concentration/IC₅₀) nor the commercial genotypic and phenotypic assays provide sufficient information to determine whether HAART regimens will achieve the 6-log target level of inhibition in vivo (Box 1). In order to evaluate the effectiveness of antiviral drugs in halting viral replication, we have recently derived instantaneous inhibitory potential (IIP) as a new measure of antiviral activity [28]. IIP may be superior to traditional measures because it directly and accurately measures the degree of inhibition that can be achieved by antiviral drugs at clinically relevant concentrations. Since in vitro models that accurately predict antiviral drug activity are useful in guiding HIV-1 treatment and stimulating hypotheses to be tested in clinical trials, we here review these recent advances in the in vitro measurement of antiviral drug activity and the potential clinical applications of IIP.

In vitro measures of antiviral activity

In vitro analysis of the antiviral activity is typically accomplished by measuring viral replication in the presence of various concentrations of the relevant drug. Dose-response curves can be analyzed using the median effect model (Box 2, equations 2–4) [29]. IC₅₀, the drug concentration that inhibits replication by 50%, is the most widely used measure of drug. Although IC₅₀ is a useful measure for drugs with a maximum efficacy (e.g. most agonists), it may not be ideal for evaluating inhibitors such as antivirals. For anti-HIV-1 drugs, 50% inhibition is small compared to the 6 logs of inhibition required to completely suppress replication in a typical patient (Box 1), and antiviral activity cannot be fully appreciated when a linear 0–100% scale is used. Instead, the inhibition of an exponential process such as viral replication should be evaluated on a logarithmic scale (Figure 1a). For these reasons, a more direct measure of antiviral activity is the log reduction in infectivity produced by an antiviral at a clinically relevant concentration (see below).

Box 2 . The median effect model [29].

The Median effect model describes the dose-effect relationship of a drug. It is based on the law of mass action and is closely related to the widely used sigmoidal E_max model. It classically takes the form of equation 2, where f_a is the fraction of binding (or infection) events affected or inhibited by a drug, f_u is the fraction that are not inhibited, D is the dose of drug, IC₅₀ is the dose that causes 50% inhibition, and m is the slope parameter which reflects the steepness of the dose-response curve. Since f_u = 1 − f_a, equation 2 can be restated in the form of equations 3 or 4. Equation 3 directly calculates the fraction of viruses that are inhibited or uninhibited by a drug. Equation 4 linearizes the dose-response curves by plotting log (f_a/f_u) vs. log (D). m is the slope of this line. Inhibitory quotient (IQ) is ratio of the clinical drug concentration to the IC₅₀. From equation 3, it is clear that the degree of inhibition of infection by a given concentration of an antiretroviral drug is dependent on three factors: the drug concentration D, the IC₅₀, and the slope parameter m.

$$\frac{f_a}{f_u}={\left(\frac{D}{{IC}_{50}}\right)}^m={IQ}^m$$ (2)

$$f_u=1-f_a=\frac{1}{1+{\left(\frac{D}{{IC}_{50}}\right)}^m}$$ (3)

$$log(f_a/f_u)=\mathit{m}log\mathit{D}-mlog({IC}_{50})$$ (4)

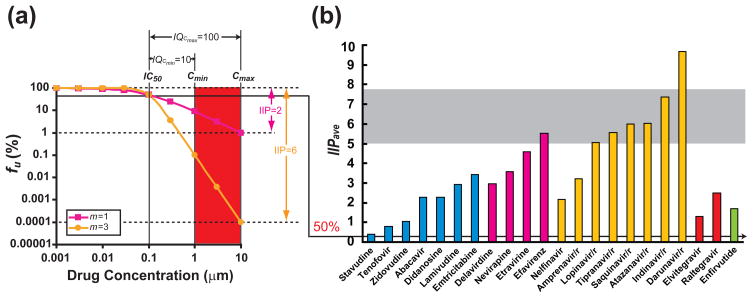
Figure 1. Instantaneous inhibitory potential of current antiretroviral drugs.

(a) Dose-response curves for hypothetical drugs with IC₅₀ = 0.1 μM, C_min = 1 μM, C_max = 10 μM, and m = 1 or 3. For the drug with m = 1, there is a 100-fold or 2-log decrease in infection events at C_max. The other drug has the same IC₅₀ and IQ but a higher m value. This drug causes a 1,000,000-fold or 6-log reduction in infectivity at C_max. Thus the slope difference results in a 10,000 fold difference in antiviral activity. The biological meaning of IC₅₀ (see the arrow connecting Figure 1a and 1b), IQ, and IIP are also illustrated in the Figure. (b) Estimated IIP_ave of current antiretroviral drugs. IIP_ave is the average IIP value during the dosing interval and is calculated using equation (6). Values are approximate and depend on reported pharmacokinetic parameters. The gray shaded area is the estimated range of IIP_ave values needed to completely halt amount of viral replication in a patient with a viral load of 30,000 copies/ml based on the HIV-1 dynamic model shown in Box 1. Note that the PI darunavir is the only drug that may achieve the required inhibition by itself. Calculations assume the use of ritonavir boosting and, for NRTIs, utilize the t_1/2 value of the intracellular triphosphate forms of the drugs.

In addition to the IC₅₀, a second critical factor in determining drug activity is the drug concentration (D) that can be achieved in vivo (Box 2). Effective antivirals have toxicity profiles that allow plasma concentrations substantially greater than the IC₅₀ to be achieved. This is reflected in the IQ, which is the ratio of drug level D (usually the minimum or trough plasma drug concentration C_min) achieved during standard dosing to the IC₅₀ (for example, IQ = C_min/IC₅₀, see Figure 1a) [30,31]. There are means for normalizing the IQ and taking into account drug resistance mutations [32, 33], but these approaches are somewhat arbitrary and lack clear biological meaning. IQ and normalized IQ are useful in predicting the virological response to some regimens based on protease inhibitors (PIs), but consensus on experimental approaches to measure cut-off IQ values is lacking (reviewed by Morse, G.D. et al and la Porte, C. [33, 34]). Although IQ captures two critical dimensions of antiviral activity, including both the pharmacokinetic and pharmacodynamic properties, it cannot quantify the number of logs of inhibition achieved by the drug at clinical concentrations because it ignores a critical third parameter involving the shape of the dose-response curve.

Slope and instantaneous inhibitory potential

The median effect model clearly states that, in addition to IC₅₀ and drug concentration, antiviral activity is affected by a third parameter, the slope parameter m (Box 2). This parameter measures the steepness of the dose-response curve and is analogous to the Hill coefficient [35], which reflects cooperativity in the binding of multiple ligands to a multivalent receptor. Because the HIV-1 enzymes are univalent with respect to their inhibitors, m has been assumed to be ~1 for antiretroviral drugs and has been largely ignored. However, in a recent study [28], we showed that for anti-HIV-1 drugs, m varies in a class-dependent manner. While nucleoside analogue reverse transcriptase inhibitors (NRTIs) and integrase inhibitors have slope values of ~1, non-nucleoside reverse transcriptase inhibitors (NNRTIs) and entry inhibitors have slope values of ~1.7. Strikingly, PIs have slopes ranging from 2 to 4.5. The mechanisms underlying the slope differences are not yet fully understood. We believe that the slope values close to 1 observed for NRTIs and integrase inhibitors reflect that fact that these drugs block reactions in which a single copy of the relevant viral enzyme mediates a critical step in the virus life cycle. The slope values may be affected by drug resistance mutations. Importantly, differences in slope have a marked effect on antiviral activity. A drug with m = 3 produces 10,000 fold greater inhibition at IQ = 100 than a drug that would be judged equally potent based on the IC₅₀ or IQ, but with m = 1 (Figure 1a). Thus, conventional pharmacodynamic indices (IC₅₀ and IQ) are insufficient to compare the antiviral activity of different drugs because neither considers possible differences in the slope parameter.

As discussed above, it is useful to consider the antiviral activity in terms of the log reduction in infectivity produced by a drug at a clinically relevant concentration. We therefore derived a new index called instantaneous inhibitory potential (IIP), which directly quantifies the log decrease in single round infection events caused by a drug at a clinically relevant concentration such as C_min or C_max (the maximum or peak plasma drug concentration) during the standard dosing [28]. IIP can be calculated as log₁₀ (1/f_u) where f_u is the fraction of infection events that remain unaffected by the drug. IIP can also be calculated using equation 5:

$$\mathit{IIP}=log\left(\frac{1}{f_u}\right)=log\left(1+{\left(\frac{D}{{IC}_{50}}\right)}^m\right)$$ (5)

if the level of inhibition is beyond the dynamic range of the assay. Importantly, IIP captures the marked effect of the slope parameter on antiviral activity. For NRTIs and integrase inhibitors, antiviral activity is intrinsically limited by the shallow dose-response curve slopes. These agents can achieve IIP values ranging from only 1 to ~3.5. Interestingly, viremia decays rapidly in patients starting regimens containing the integrase inhibitor raltegravir [36], but this may in part be a reflection of the fact that decay dynamics are influenced by where a drug acts in the virus life cycle [37]. By contrast, the NNRTI efavirenz and some PIs have high slope values and produce >5 logs of inhibition at C_max. This extra degree of inhibition resulting from high slope values is not apparent when dose-response curves are analyzed on a traditional linear scale, but are critical for complete suppression of viral replication. Thus, by incorporating the slope parameter, IIP provides a more accurate pharmacodynamic measure of antiviral activity than the traditional measures. Interestingly, most current first-line HAART regimens [38] include at least one drug with an IIP value >5.

Treatment implications of IIP

The effectiveness of an antiretroviral regimen in vivo is determined by at least five factors: (1) the intrinsic pharmacodynamic properties (the IC₅₀ and slope) of each drug in the regimen; (2) the pharmacokinetic properties of each drug, which determine the value of D over time for a given dosing schedule; (3) synergistic, additive, and antagonistic effects of drug combinations; (4) tolerability of the regimen, which affects adherence, the likelihood that patient will take the drug regimen as recommended; and (5) genetic barriers to resistance, which determine how readily resistance will arise when viral replication is not controlled.

Factors 1 and 2, through median effect equation, determine the degree of inhibition of viral replication (the IIP) that each drug produces. IIP depends on the local drug concentration and may vary depending on drug penetration into different tissue compartments. Factors 1 and 2, together with factor 3, determine whether suppression of wild-type HIV-1 can be achieved by a particular combination. Factors 4 and 5 come into play over long-term administration and determine whether control of viral replication can be maintained. Factor 4 may also directly limit the choice of regimen for patients with other health problems. The concepts of IIP and slope are critical for understanding intrinsic antiviral activity, but also affect the other factors as we discuss below.

IIP, residual viremia and intensification

The high IIP values of some NNRTIs and PIs suggest that current HAART regimens have an extraordinary potential to suppress HIV-1 replication. Interestingly, patients responding well to HAART have residual viremia, averaging 1–3 copies of HIV-1 RNA/ml [39–46]. Genetic studies of the residual viremia [42–46] suggest that it reflects release of virus from stable reservoirs consisting of long-lived cells infected prior to therapy rather than ongoing cycles of replication not adequately suppressed by the drugs (reviewed by Shen, L and Siliciano, R.F. [47]).

In a recent intensification study [48], patients who had suppression of viremia to <50 copies/ml on an optimal initial HAART regimen (tenofovir disoproxil fumarate + emtricitabine + efavirenz) for > 6 months had a fourth drug, ritonavir-boosted atazanavir (ATV/r), added to their regimen for 8 weeks. The effect of intensification on residual viremia was measured using an RT-PCR assay with single copy sensitivity [40]. Intensification had no measurable effect on residual viremia. The concentrations of atazanavir measured in the plasma of these subjects can produce 5–7 logs of inhibition of laboratory wild-type virus in in vitro single-round infectivity assays. The failure of atazanavir to reduce residual viremia confirms that residual viremia is not due to ongoing viral replication in any drug-accessible compartment.

These results suggest that HAART can effectively halt viral replication in vivo, a conclusion that is no longer surprising given the extraordinary potential of some antiretroviral drugs to inhibit HIV-1 infection as a result of their high slope and IIP values. These findings also suggest that the theoretical potential of HAART to control replication of wild-type HIV-1 has been reached. Life-time suppression of HIV-1 replication is possible with current HAART as long as patients remain adherent.

Slope, pharmacokinetics, and adherence

There is an important interplay between slope, pharmacokinetics, and adherence. For drugs with high slope values, small increases in drug concentration produce large increases in inhibition. However, small decreases in drug concentration also lead to large decreases in inhibition. Thus for drugs with a high slope and a short half life, IIP varies dramatically during the dosing interval. The rate at which IIP initially decreases after the last dose is directly proportional to m and inversely proportional to t_1/2 [28]. The PIs indinavir and saquinavir have very high slope values but short half lives even with ritonavir boosting [28]. Thus, although IIP for these drugs is very high at C_max, the rapid decline in IIP is a disadvantage. Depending the half-life and the dosing interval, different drugs show different degrees of variation in drug concentration. With a high slope value, the effects of fluctuations in drug concentration on IIP are amplified. Drugs with longer half lives can maintain high IIP values long after the last dose. The drugs which maintain the highest IIP values 24 hours after the last dose (IIP₂₄) are efavirenz, darunavir/r, and ATV/r. Each has excelled in clinical trials [38]. Another way to incorporate pharmacokinetic parameters is to calculate the average IIP (IIP_ave) over the dosing interval (τ) (equation 6):

$${\mathit{IIP}}_{\mathit{ave}}=\frac{1}{\tau }\ast \underset{0}{\overset{\tau }{\int }}log\left(1+{\left(\frac{C_{max}{e}^{(-0.693t/t_{1/2})}}{{IC}_{50}}\right)}^m\right)\ast dt$$ (6)

where t_1/2 is the half life of the drug. IIP_ave values for current HIV-1 drugs are shown in Figure 1b. Measures such as IIP₂₄ and IIP_ave may be more generally useful because they capture the IIP values over time in a way that reflects the pharmacokinetic properties of the drug.

Patient adherence to HAART regimens is obviously a critical determinant of clinical outcome. Adherence is affected by side-effects and ease of administration. Interestingly, the concepts of slope and IIP are useful in understanding the consequences of lapses in adherence. For drugs with a high sustained IIP, viral replication will be controlled even if some doses are missed. For a given drug, the rate at which IIP initially declines after the last dose is directly proportional to the slope and inversely proportional to the half-life [28]. We have found that IIP₂₄, a measure of sustained antiviral activity that incorporates both pharmacodynamic and pharmacokinetic characteristics of a drug, correlates well with the virological response in comparative clinical trials [28].

Antiviral activity for drug-resistant viruses

The concept of the dose-response curve slope also has clinical utility in the analysis of drug resistance. Although genotypic analysis can provide some indication of which drugs are likely to be effective against resistant viruses [16–18], physicians frequently use commercial phenotypic assays in selecting salvage regimens for patients whose viruses have multiple resistance mutations. These assays analyze shifts in dose-response curves for recombinant viruses carrying patient-derived pol sequences relative to the dose-response curve of a wild-type construct [19, 20]. The fold change in IC₅₀ is taken as a measure of resistance. Interestingly, this analysis assumes that the slopes are the same for wild-type and drug-resistant viruses. However, if a drug resistance mutation also changes the slope, then the actual effect of the resistance mutation at clinically relevant concentrations of the drug might be overestimated or underestimated. Therefore, analysis of slope is essential for accurate analysis of the IIP that a drug or drug combination retains against drug-resistant viruses (residual IIP) and proper interpretation of phenotypic resistance tests.

Other relevant factors include viral fitness and the genetic barrier to resistance. Most drug resistance mutations have some effect on viral fitness [49]. If resistant viruses are less fit, the IIP required to suppress viral replication may be lower than that required for wild-type virus. The genetic barrier to resistance determines how readily resistance will arise in the setting of suboptimal suppression. Intuitively, the higher the genetic barrier to resistance, the more likely the regimen is to be tolerant to non-adherence. However, the best ways to quantify viral fitness and the genetic barrier to resistance remain unclear.

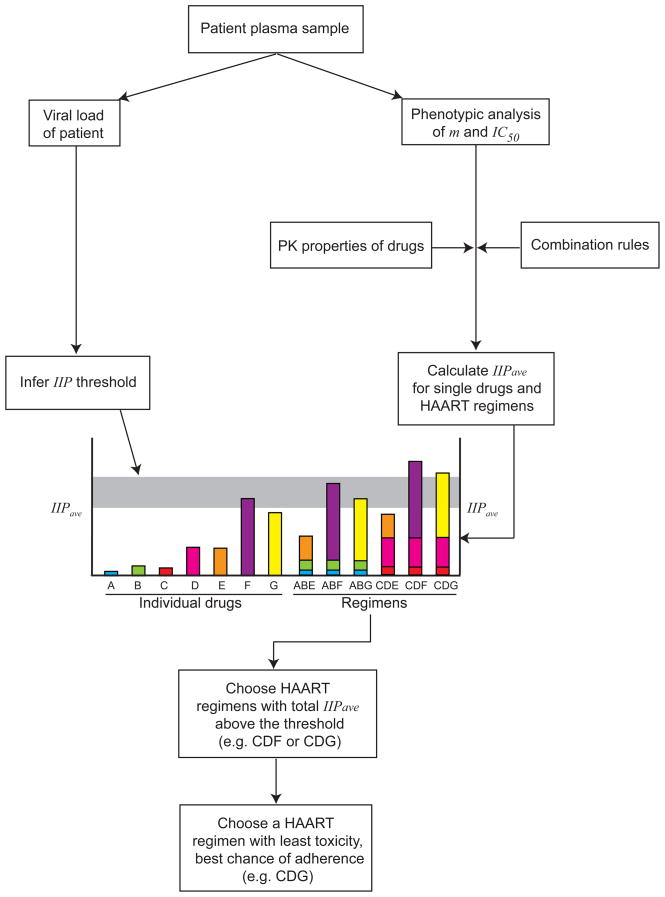
Although no single parameter or in vitro assay can predict clinical outcome, in vitro models incorporating the factors mentioned above may have some role in guiding therapy. As an example, we suggest here a rational approach to the choice of a salvage regimen (Figure 2). From an initial blood sample, the viral load would be determined, and phenotypic analysis similar to current commercial assays [19,20] would be done to assess the effects of the resistance mutations on the slope and IC₅₀ for each drug. It would then be possible to compute the IIP that each drug retains towards the most common resistant viruses present in the patient sample. Next, from the rules for combining IIPs, it should be possible to determine the total IIP for every possible salvage regimen. From viral load data and the classic model of viral dynamics, the threshold value of IIP needed to suppress viral replication completely may be determined. Among the regimens that have total IIP above this threshold, the optimal regimen may be the one that will be best tolerated by the patient. Although we still need to understand how to calculate the total IIP for combinations of antitretroiviral drugs, this approach may eventually offer a more rational and quantitative approach to choosing a salvage regimen.

Figure 2. Proposed scheme for choosing a salvage HAART regimen.

It may eventually be possible to calculate the IIP of a salvage regimen based on in vitro phenotypic analysis of the inhibition of a patient-derived virus by individual antiretroviral drugs. The amount of replication occurring in a patient may be calculated from the viral load as described in Box 1. The relationship between these values could identify regimens with the potential to control viral replication. This information, together with issues of drug toxicity and adherence, may help physicians to choose the optimal salvage regimen. In order to implement this approach, it will be necessary to understand understand the rules for computing the IIP of a combination from measurements on individual drugs. It should be noted that this approach does not take into account potential complexities resulting from the presence of minority resistant variants not detected in genotypic or phenotypic analysis. It also does not consider the potentially significant inter-patient variability the pharmacokinetics of antiretroviral drugs.

Conclusions

The inhibitory potential of antiretroviral drugs is strongly dependent on a previously ignored factor, the dose-response curve slope, which is analogous to the Hill coefficient. When the dose-response curve slope is considered, it becomes clear that antiretroviral drugs with high slope values, such as NNRTIs and PIs, can produce extraordinarily high levels of inhibition of viral replication in vitro. These levels can only be appreciated on a logarithmic scale. We propose that the log reduction in infection events produced by a drug at a clinically relevant concentration (the IIP) is a more appropriate measure of antiviral activity than are conventional pharmacodyamic measures. In future studies, it will be important to understand how to calculate the IIP of drug combinations from the IIPs if individual drugs, to determine how resistance mutations affect slope and IIP, and how to use various mearsures of IIP (IIP_Cmax, IIP₂₄, IIP_ave) to predict and optimize responses to therapy. These concepts have broad implications for understanding how HAART works and can also be applied to the treatment of other viral illness such as hepatitis C infection.

Glossary

HAART

Highly active antiretroviral therapy, current most effective combination therapy for control of HIV-1 infection

IC₅₀

The drug concentration leading to 50% inhibition of viral infection

IQ

Inhibitory quotient, the ratio of the clinical drug concentration (such as C_min or C_max) to the IC₅₀

C_min

The minimum or trough concentration of a drug during the dosing interval

C_max

The maximum or peak concentration of a drug during the dosing interval

C_ave

The average concentration of a drug during the dosing interval after reaching steady state. C_ave, is calculated as the area under the curve of drug concentration divided by the dosing interval

IIP

Instantaneous inhibitory potential, the log reduction of infectivity in a single round at a clinical relevant drug concentration

IIP_ave

The average IIP value during the dosing inteveral calculated using equation (6)

IIP₂₄

The IIP value of a drug at 24 h after taking the last dose of that drug

Salvage regimen

Drug therapy options for highly treatment-experienced individuals who generally carry viruses resistant to multiple classes of antiretroviral drugs