Heart wall myofibers are arranged in minimal surfaces to optimize organ function

Abstract

Heart wall myofibers wind as helices around the ventricles, strengthening them in a manner analogous to the reinforcement of concrete cylindrical columns by spiral steel cables [Richart FE, et al. (1929) Univ of Illinois, Eng Exp Stn Bull 190]. A multitude of such fibers, arranged smoothly and regularly, contract and relax as an integrated functional unit as the heart beats. To orchestrate this motion, fiber tangling must be avoided and pumping should be efficient. Current models of myofiber orientation across the heart wall suggest groupings into sheets or bands, but the precise geometry of bundles of myofibers is unknown. Here we show that this arrangement takes the form of a special minimal surface, the generalized helicoid [Blair DE, Vanstone JR (1978) Minimal Submanifolds and Geodesics 13–16], closing the gap between individual myofibers and their collective wall structure. The model holds across species, with a smooth variation in its three curvature parameters within the myocardial wall providing tight fits to diffusion magnetic resonance images from the rat, the dog, and the human. Mathematically it explains how myofibers are bundled in the heart wall while economizing fiber length and optimizing ventricular ejection volume as they contract. The generalized helicoid provides a unique foundation for analyzing the fibrous composite of the heart wall and should therefore find applications in heart tissue engineering and in the study of heart muscle diseases.

Histological studies of the mammalian heart (1–4) corroborate the finding that individual myofibers in the left ventricle (LV) are aligned to form helical curves (Fig. 1B). Several formal analyses (1, 2, 5–7) support the view that this alignment is mechanically optimal. Moving beyond considerations of individual fibers has proved difficult. An advantage of certain fibrous composites, such as those in plant cell walls, bone, insect cuticle, and fiberglass, is that their fiber geometries offer efficient reinforcement (8) by equalizing stiffness in all directions parallel to the plane in which fibers lie. Our approach has been to retain the mathematical precision available for the analysis of individual fibers while switching scales to that of the composite arrangement. Anatomical studies reveal that at such scales, fibers remain almost parallel locally (9), as illustrated in Fig. 1C with the colors depicting changes in orientation. We show that they are packed together to achieve this organization, while maintaining their helical form (4), via a unique structural arrangement in which they bundle into a special surface: a generalized helicoid (10–14). Because this object is a minimal surface (15, 16), it generalizes the geodesic properties of the individual helices (1, 2, 5–7) to the more global scale of the ventricular wall. We also show that this minimal surface structure can be maintained as the heart beats, with simulations revealing the power of using the proper mathematical coordinates. Previous models (1, 2, 5–7) apply to selected regions of the LV myocardium but exclude the apex. They describe the orientation of individual fibers but not volumetric bundles of them. The arrangement of myofibers in generalized helicoids characterizes their orientation throughout the heart wall.

Fig. 1.

Fiber geometry in the left ventricle of a rat. (A) An axial slice (gray) with both a single helical fiber passing through a voxel (B) and a bundle of fibers passing through neighboring locations (C–E). (B) The geometry of a single fiber is characterized locally by its rate of bending in the osculating tangent-normal (TN) plane (curvature) and out of it (torsion). The TN plane is shown in blue. (C) The geometry of a bundle of fibers is more complex. Here we show a narrow slice of fibers arranged across the thickness of the wall, emerging from the slice in A. The colors are used to visualize changes in orientation. (D) More abstractly, we now show fibers passing through a plane of voxels in green, and those in a neighboring plane in a cubic lattice in blue. The placement of a local coordinate frame allows fiber bundle geometry to be characterized by curvature measures in directions T, N, and B. (E) Comparing the model to data: The orientations corresponding to GHM fitting are overlaid in color on the principal eigenvector direction e₁ (shown with gray to black shading in the direction from below to above the slice plane), for an axial slice of the rat heart DT-MRI data (compare with C).

Model

Setting up the right local coordinate frame is critical to developing the generalized helicoid model (GHM). Fig. 1D depicts a myofiber passing through a particular location (voxel) in a rectangular grid in three-dimensional Euclidean space, with its tangent vector lying in the plane of the page, along with fibers passing through neighboring voxels. An orthogonal coordinate frame is placed using the fiber orientation for tangent vector T, the in-page direction for the binormal vector B, and their cross-product for the normal vector N. The differential geometry of the collection of myofibers can now be characterized by specifying the rates of change of fiber orientation for displacements in the directions of T, N, and B.

The GHM expresses fiber orientation in terms of these curvatures by prescribing an orientation function given by

at each point (x,y,z) within the LV wall with respect to a local coordinate frame (17, 18). Here θ(x,y,z) represents the orientation in the x–y plane with respect to the x axis, which is aligned with the local fiber direction, and with the z axis taken to be the component of the heart wall orthogonal to it (following heart myofiber geometry literature, refs. 19 and 20). This choice ensures that the reference frame rotates smoothly and consistently throughout the LV myocardium. Because it is small (21, 22) we do not directly model the component of fiber orientation out of the x–y plane in the local neighborhood of (x,y,z).

Fig. 2 illustrates the effects of the parameters of the GHM, with the orientation θ shown by a unit length vector field in the x–y plane and with fibers abstracted by streamline traces in θ (23). The K_T parameter causes bending in the direction tangential to a fiber (Fig. 2A). With positive K_N added, the fibers fan out. Finally, K_B defines angular change in the z direction. In this example, K_B has the effect of creating rotated copies of the same streamlines in planes parallel to the x–y plane (Fig. 2C). Mathematically the GHM’s scalar parameters K_T, K_N, and K_B correspond locally to the three curvatures of the myofiber bundle, describing the amount that the fiber orientation changes for displacements in the directions T, N, and B, respectively (17, 18). As such it provides coordinates for describing the geometry of a bundle of myofibers in three dimensions. In contrast, a helix (1, 2, 5–7) only describes the geometry of a single fiber viewed as a one-dimensional curve.

Fig. 2.

The effect of varying the parameters K_T,K_N, and K_B of the GHM. The x, y, and z axes of its reference frame are shown in red, green, and blue, and correspond to the directions T, N, and B. A slice of the unit length vector field specified by θ(x,y,z) in the x–y plane is shown in black. In each panel a single “fiber” is traced in red using a forward Euler approach (23) in the direction T, with neighboring fiber traces shown in black or gray. In A and B, fibers are only shown in the x–y plane because with K_B = 0, θ is only a function of (x,y). (A) With only tangential curvature K_T the fibers bend but remain locally parallel to one another in the x–y plane. (B) With positive normal curvature K_N added the fibers fan away from one another in the x–y plane. (C) The effect of adding K_B is to cause the fibers to rotate in planes parallel to the x–y plane. Here traced fibers are shown in six planes, one in the x–y plane (red), two above it (black), and three below it (gray). Notice the similarity between this and the rotation of fiber orientations from epicardium to endocardium in Fig. 1E.

A fundamental property of the GHM, as shown in ref. 17 and in the Appendix, is that (x,y,z,θ(x,y,z)) is a minimal surface when embedded in ; i.e., its mean curvature, given by the trace of the shape operator, vanishes everywhere. A more familiar example of a minimal surface is the bubble that results from dipping a wire frame into a soapy film; that is, the minimal surface required to enclose a given volume of air. Blair and Vanstone show in ref. 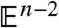10 that complete ruled minimal n-dimensional hypersurfaces in are products of and a helicoid in 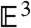. As such, in , a generalized helicoid is the product of a helicoid in and the real line. Barbosa et al. (11) and Thas (13, 14) independently derive the parametric equations of such minimal generalized helicoids. There is a relationship between these results and those on generalized helical curves. In ref. 24, Hayden proves that, in Riemannian spaces of n dimensions, with n even, at least one of the curvatures of a generalized helix must vanish. One can deduce from this result that, in , a generalized helix can have non-null curvature and torsion, but its higher-order curvatures must be null. Thus, in , a generalized helix must be the ordinary 3D helix with a linear coordinate function describing its fourth dimension.

Results

We have tested our model against data from diffusion tensor (DT) MRI from three different mammals: rat, dog, and human. DT-MRI provides estimates of myofiber orientation over the full myocardial volume at high spatial resolution by measuring the orientation dependence of the Brownian motion of water molecules (25). Diffusion in the myocardium is anisotropic due to its fibrous structure. Several studies (26–28) show that the principal eigenvector e₁ of a DT is locally aligned with myofiber orientation at the spatial scale of a typical image voxel. The use of DT-MRI has advantages over earlier dissection studies which were typically restricted to a small set of locations (3) and are therefore difficult to reproduce.

Returning to Fig. 1D, let T and B represent the x and z axis directions at each voxel. Applying GHM fitting to the fiber bundle shown in Fig. 1C, one expects a large binormal curvature K_B, capturing the variation of fiber angle in the direction perpendicular to the heart wall. In contrast, the curvatures K_T and K_N along and across fibers, respectively, appear to be small. Our results confirm this trend throughout the LV myocardium, consistent with the anatomical observation that fibers are almost parallel locally but turn as one penetrates the heart wall (1–3, 26, 29). Fig. 1E compares our model to the data by overlaying the orientations corresponding to the best fit GHMs in color on the DT-MRI based fiber directions (gray to black) in an axial slice of rat LV myocardium.

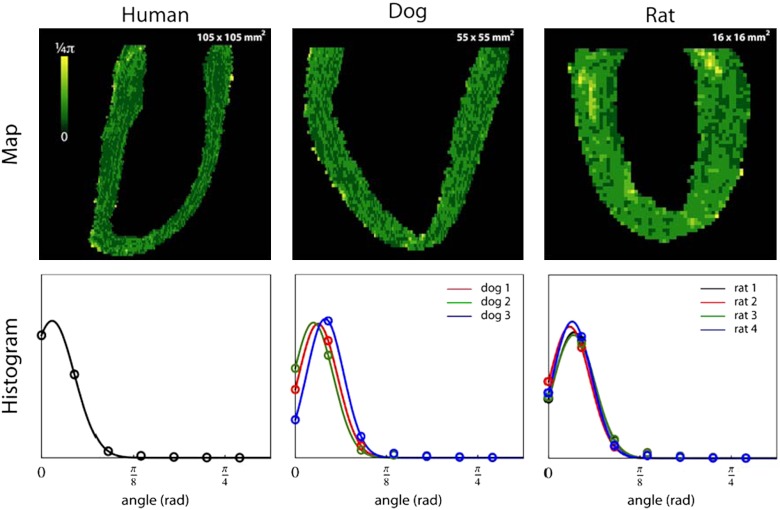
In Fig. 3, we plot histograms of the distributions of K_B, K_N, and K_T for one human, three dog, and four rat DT-MRI datasets. The human, dog, and rat datasets have spatial resolutions of 0.4297 × 0.4297 × 1.0, 0.3125 × 0.3125 × 0.8, and 0.25 × 0.25 × 0.25 mm³, respectively. To perform a cross-species comparison, all curvature parameters were normalized based on the maximum epicardial cross-sectional diameter (MD). The histograms were then normalized with respect to the number of voxels contained in the dataset. The histogram of normalized K_B values for each dataset peaks around -0.15 to -0.22 rad/mm, revealing a remarkable consistency of design across these three species. The mean K_B value for each dataset is also an order of magnitude larger than the mean K_N and K_T values, which are both centered at zero. The rightmost column of Fig. 3 depicts the spatial variation of the K_B parameter in a long-axis slice from a single dataset of each species, showing it to be homogeneous throughout the LV myocardial wall, including the apex, an area excluded by other models (1, 2, 5–7). GHM fits for transmural penetrations at locations near the base, the equator, and the apex of a rat heart dataset are shown in Fig. 4. Table 1 and Fig. 5 provide a quantitative and qualitative assessment of the GHM fitting angular errors over all the heart datasets. A von Mises distribution (30) fit shows these errors to be consistently low, with the μ parameter ranging from 2.63° (0.046 rad) to 7.63° (0.128 rad), and to have concentration κ higher than 100 (or equivalently, low variance). Locations of high error coincide with dataset boundaries, or are close to the base or insertions of the right ventricle.

Fig. 3.

Normalized K_B, K_N, and K_T histograms for GHM fits of the human, dog, and rat heart DT-MRI datasets. The right-most column shows the spatial variation of the normalized K_B parameter in a long-axis slice from one dataset of each species, with the color map ranging from -0.7 to 0.7 rad/mm. The plots show K_B to be consistent across species as well as homogenous in the heart wall, and K_N and K_T to be close to zero. Locations where K_B has a different sign and value (red arrows) reveal interesting anatomy near the insertions of the right ventricle and at the base close to the valves and the atria.

Fig. 4.

GHM fits at three locations in a rat heart dataset. (A) Transmural penetrations in red at the apex, equator, and base (counterclockwise from bottom). (B) The GHM fit at the base. (C) The GHM fit at the apex. (D) The GHM fit at the equator. In B–D, the measured DT-MRI fiber orientations are shown in pink with extrapolated fibers based on the GHM fits in blue. For each penetration the model smoothly interpolates the measured fiber orientations via its curvature parameter K_B.

Table 1.

Quantitative assessment of the GHM fits for all heart DT-MRI datasets

*	KB, rad/mm	KN, rad/mm	KT, rad/mm	μ, rad	κ(-)
Human	-0.17 ± 0.18	0.003 ± 0.085	-0.005 ± 0.081	0.046 ± 0.002	108 ± 8
Dog 1	-0.15 ± 0.16	0.001 ± 0.101	-0.001 ± 0.101	0.098 ± 0.002	141 ± 9
Dog 2	-0.17 ± 0.15	0.004 ± 0.096	-0.011 ± 0.090	0.078 ± 0.001	136 ± 9
Dog 3	-0.17 ± 0.16	0.006 ± 0.099	-0.011 ± 0.096	0.128 ± 0.003	157 ± 7
Rat 1	-0.19 ± 0.14	0.008 ± 0.053	0.003 ± 0.053	0.109 ± 0.003	128 ± 9
Rat 2	-0.21 ± 0.12	0.008 ± 0.045	0.005 ± 0.043	0.090 ± 0.002	132 ± 7
Rat 3	-0.22 ± 0.11	0.008 ± 0.043	0.006 ± 0.049	0.107 ± 0.003	121 ± 9
Rat 4	-0.20 ± 0.14	0.008 ± 0.053	0.000 ± 0.053	0.101 ± 0.001	144 ± 6

^*All values reported as mean ± standard deviation. A neighborhood of 5 × 5 × 5 about the central voxel v is used for each fit. Errors are measured only for the voxels closest to v. K_B, K_N, and K_T are species-normalized values.

Fig. 5.

Statistical analysis of the angular error of fit β. (Upper) The spatial variation of β in a long-axis slice from one dataset of each species. Locations of higher error in the rat dataset coincide with anatomically interesting regions, where K_B has a different sign (red arrows in Fig. 3). (Lower) A statistical analysis obtained by fitting a von Mises distribution (30) (solid lines), with the μ and κ parameters shown in Table 1, to the angular errors from discretized GHM fits (open circles).

In a second experiment, we assess the effect of increasing neighborhood size (N = 3, 5, 7, 9) on GHM fits for the human heart dataset. Here we measure error for all voxels within the associated spherical neighborhood, not just the closest voxel neighbors. The von Mises analysis, presented in Table 2, shows that, although the error increases slightly, the larger number of error samples now leads to much tighter von Mises fits, with the concentration parameter κ increasing by a factor of 4 or more. In interpreting these results, it is important to recall that because the mathematical framework we follow is motivated by Cartan’s moving frame construction, we adapt the local coordinate frame to the object under consideration. When this frame is made too large, the tangent plane approximation to the heart wall becomes less accurate.

Table 2.

Quantitative assessment of the effect of increasing neighborhood size on the GHM fit for the human heart dataset

Neighborhood*	μ, rad	κ(-)
3 × 3 × 3	0.125 ± 0.00077	610 ± 23
5 × 5 × 5	0.145 ± 0.00156	478 ± 33
7 × 7 × 7	0.162 ± 0.00198	444 ± 37
9 × 9 × 9	0.173 ± 0.00213	430 ± 38

^*All values reported as mean ± standard deviation. The errors are now measured for all voxels within the sphere of maximal radius inscribed in the neighborhood.

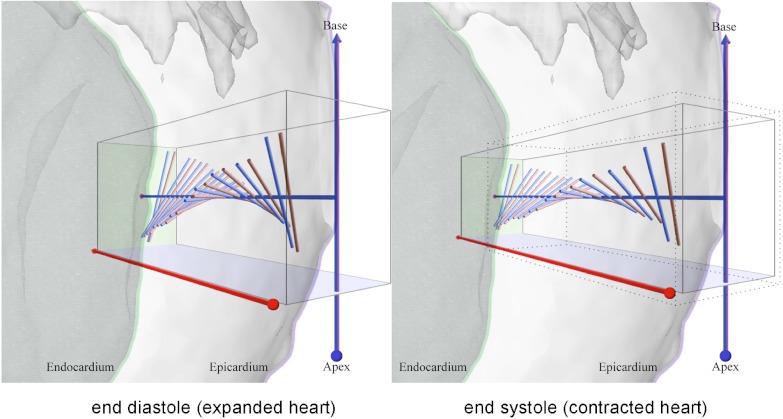
The changes implied by a beating heart, including fiber shortening and wall thickening (31), reveal another surprising aspect of the curvature parameter K_B. Chen et al. (26) have reported DT-MRI measurements of fiber orientation along transmural penetrations from epicardium to endocardium on rat hearts fixed at end systole and end diastole. Their results show the heart wall to thicken significantly as myofibers contract, but the total change in fiber orientation from outer wall to inner wall to be quantitatively preserved. Using parameters consistent with their findings and our GHM fits for a transmural sampling at a location near the equator of the dataset in Fig. 4, Fig. 6 and Movie S1 show how this rearrangement of fiber geometry is predicted simply by a decrease in K_B. Remarkably, throughout the contraction process, the minimal surface structure provided by the GHM is preserved.

Fig. 6.

A simulation of fiber contraction for an equatorial penetration of the rat heart in Fig. 4. To situate the anatomy the epicardium and endocardium are overlaid as transparent gray surfaces, with their contours shown in pink and green, respectively. The left subfigure shows the DT-MRI fiber orientations prior to contraction in pink with extrapolated fibers based on GHM fits and their corresponding K_B curvatures in blue. The simulation (left to right) shows the effect of decreasing the length of each fiber by 14.2%, increasing their radii by 8.0% to preserve fiber volume and increasing the wall thickness by 41.9%, as reported in the findings of Chen et al. (26). As a result, in the right subfigure, the endocardium patch (green rectangle) has been displaced in the direction of the ventricular chamber. The dotted box in the right panel is a copy of the box in the left panel to illustrate changes to scale. By reducing the description of myofiber geometry to the single curvature parameter K_B, the fiber rearrangement after contraction in the right subfigure is explained by simply decreasing it, while preserving the GHM structure. The full cycle from end diastole to end systole and back is visualized in Movie S1.

Discussion

Our bundling of heart wall myofibers into generalized helicoids adds significant dimensions to current knowledge of LV myofiber structure and function. First, this organization shows that myofiber orientation as a function of position is a minimal surface (15, 16) throughout the myocardium. Whereas previous models have considered only the geometry of individual (one-dimensional) fibers (1, 2, 6, 7) or their groupings in (two-dimensional) sheets (9, 19, 26, 28), our analysis of fiber orientation applies in three dimensions across the entire ventricular volume. The property that a minimal surface is locally area minimizing (15, 16) generalizes current understanding that individual helical fibers, being geodesic (1, 2, 6, 7), are length minimizing. Other properties of minimal surfaces are also inherited by the generalized helicoid organization. For example, for a harmonic minimal surface defined on a plane, it can be shown that the second variation of its area depends only on the component of a variation normal to it (15, 16). This property suggests that shortening fibers along their length in the direction given by θ could contribute to an efficient shrinkage of volume by yielding a displacement in the direction normal to the heart wall. It has in fact been established that a helical orientation of myofibers is essential to achieve a transmurally homogeneous workload for all myocytes within the healthy myocardium (32–34). More globally, the helicoidal myofiber architecture induces torsion of the left ventricle during contraction. Second, our GHM fits with small K_T and K_N but high K_B formalize Neville’s stacked helicoids model (8) and Bouligand’s generalized twisted model (35). These two models have been used as qualitative descriptions of helicoidal arrangements in a variety of biological and man-made fibrous composites (8, 35), but without a formal mathematical underpinning. Furthermore, they have never before been applied to the heart wall. Our formalization along with our experimental fits to DT-MRI data reveal an additional purpose of the generalized helicoid organization, which is that it allows for wall stiffness to be equalized in the plane approximately tangent to the heart wall (8, p. 95), giving it mechanical strength.

In tissue bioengineering, understanding the basic structural properties of heart wall myofibers is fundamental. Their higher-order structural arrangement in generalized helicoids is likely to find application in the design of scaffolds for artificial heart muscle growth (36), in the study of myocardial infarction or other heart pathologies that rearrange fiber geometry (37, 38), and in understanding the relationship between individual fibers and their laminar organization into sheets (9, 19, 26, 28).

Materials and Methods

Diffusion Tensor Magnetic Resonance Imaging.

DT-MRI data for the dog and human hearts were obtained from The Center for Cardiovascular Bioinformatics and Modeling (http://www.ccbm.jhu.edu/research/DTMRIDS.php) at Johns Hopkins University. The institutional animal care committee at the Eindhoven University of Technology approved the following procedures for the acquisition of the rat heart datasets. Male Wistar rats were sedated by 3% isoflurane in medical air. For each specimen, the skin and ribs were cut to expose the heart. The left ventricular wall was penetrated at the apex with an 18 gauge perfusion needle. The vena cava inferior was cut and the vascular bed was perfused with 10,000 units of heparin L-1 in 100 mL of PBS. Subsequently, the perfusate was switched to 100 mL 4% phosphate buffered paraformaldehyde to induce tissue fixation. After all muscular contractions ceased, the heart was excised, rinsed thoroughly with PBS, and stored overnight in PBS at 4 °C.

DT-MRI measurements were then obtained on a 6.3 T horizontal-bore MRI scanner (Oxford Instruments) equipped with a 12-cm inner diameter providing a maximum gradient strength of 400 mT/m and a quadrature driven birdcage coil with an inner diameter of 32 mm (RAPID Biomedical). Each heart was placed in a plastic tube filled with Fomblin (Fens) for susceptibility matching, with medical gauze used to immobilize the specimen against mechanical vibrations. The left ventricular long axis was visually aligned with the centerline of the magnet bore. Diffusion-weighted images were collected at room temperature using a three-dimensional spin-echo sequence with unipolar diffusion sensitizing pulsed field gradients. The field of view was 32 × 16 × 16 mm³, with matrix dimensions 128 × 64 × 64, yielding 250 × 250 × 250 μm³ isotropic voxels (echo time 25 ms, repetition time 1,000 ms, 1 signal average). Pulsed field gradients were applied in 10 directions (39), with a diffusion weighting b value of 900 s/mm². One additional measurement was performed without diffusion weighting. Paravision 4.0 was used to reconstruct the diffusion tensor which was diagonalized to obtain the three eigenvalues (λ₁, λ₂, and λ₃) and eigenvectors (e₁, e₂, and e₃) for each voxel. The principal eigenvector corresponds to the local orientation of myofibers (27, 28).

Generalized Helicoid Model Fitting.

In each dataset, the left ventricle was manually segmented by an expert. A GHM fit was obtained at each voxel v by searching over K_T, K_N, and K_B values in the range [-0.7,…,0.7] rad/mm, in increments of 0.1 rad/mm for the human and dog datasets (a total of 15 × 15 × 15 = 3,375 {K_T,K_N,K_B} triplets) and a range of [-2.75,…,2.75] rad/mm, in increments of 0.25 rad/mm, for the rat datasets (a total of 23 × 23 × 23 = 12,167 {K_T,K_N,K_B} triplets). For each triplet, the GHM equation was applied within a local neighborhood N of size 5 × 5 × 5 voxels with origin at v to provide a 3D orientation α at each voxel v∈N. This neighborhood size is about the largest that can be used for the rat heart datasets, where we have approximately 10 voxels from outer wall to inner wall. In our implementation, for storage reasons, we discretized a GHM’s orientation α to the closest direction among 100 uniformly distributed samples on the hemisphere. The angle between α and the fiber direction, indicated by the DT principal eigenvector e₁ at v was then computed, and this angular difference was averaged over all v∈N to provide a goodness-of-fit measure for the model. We note that, due to the discretization of the GHM’s orientation, even a perfect fit would result in an average error of about 5.4°. The goodness-of-fits measure was used to determine the best-fitting set of {K_T,K_N,K_B} parameter values. In order to control for overall heart size differences, the {K_T,K_N,K_B} parameters were normalized with respect to the MD of the human heart, such that, for example, K_Bnorm = K_B × MD/MDhuman. For each fit, the x axis of the GHM frame at v was aligned with e₁, with its z axis aligned with the projection of the local normal vector to the heart wall onto the plane orthogonal to e₁. The heart wall normal direction was estimated using the local gradient to a Euclidean distance function (40) within the heart wall. In this manner, the frame rotated smoothly throughout the heart wall and allowed the z axis to be associated with the penetration direction used to define a fiber angle in the literature (19, 20).

Quantitative Assessment of GHM Fitting Errors.

The angular error of fit β at v was computed as the average angular difference between data and model direction, within the six nearest neighbors of v. The calculated β values were placed in bins corresponding to the inherent discretization of the data directions and were statistically analyzed by obtaining a least squares fit of a von Mises probability density function (30):

Here μ is a measure of the amount of angular error β with κ a measure of its concentration at that amount—i.e., 1/κ is analogous to the variance of a normal distribution. We report the mean and standard deviation of K_T,K_N, and K_B and the μ and κ parameters for each dataset in Table 1, with an associated quantitative and qualitative assessment in Fig. 5. We carry out an additional experiment to assess the effect of increasing neighborhood size (N = 3, 5, 7, 9) on the human heart dataset, measuring the error for all voxels within the associated spherical neighborhood. The μ and κ parameters resulting from a von Mises fit are presented in Table 2.

Appendix: The GHM Model for θ Is a Minimal Surface

A minimal surface is one whose mean curvature vanishes everywhere (15, 16). The mean curvature is given by the trace of the shape operator, which is the differential dN expressed in terms of the local coordinates of the tangent space at a point p, of the surface normal vector N. We begin by expressing (x,y,z,θ) in the parametric form h(u,v,w) = (x(u,v,w),y(u,v,w),z(u,v,w),θ(u,v,w)), where θ is a three-dimensional surface in four-dimensional Euclidean space . We rearrange the GHM expression for θ as

[1]

and let z(u,v,w) = w and θ(u,v,w) = v to get 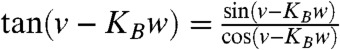. Multiplying the numerator and the denominator of the right-hand side of this equation by the parameter u and requiring equality with the right-hand side of [1] leads to the parametric equations

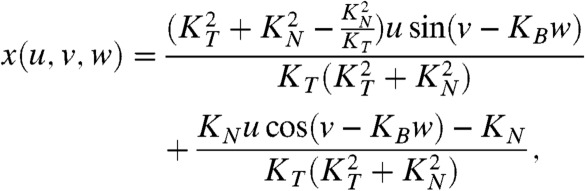[2]

[3]

[4]

An expression for the normal vector N at a given point of the surface is found by solving for the null space of J^T, where J is the Jacobian matrix of parametrization h. The solution space is a line in , and so N is taken as the direction vector of that line:

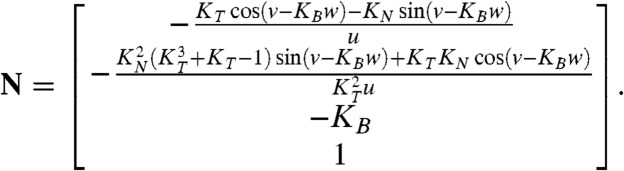[5]

Projected in the local coordinates of the tangent space at p, which are given by ∂h/∂u = (∂x/∂u,∂y/∂u,∂z/∂u,∂θ/∂u), ∂h/∂v, and ∂h/∂w, dN becomes

[6]

where denotes the Euclidean dot product in . With the expressions for h = (x,y,z,θ) provided in [2–4] and with the expression for the normal vector N provided in [5], one can verify that 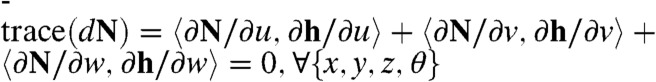, which completes the proof.